ABSTRAK
Dalam pengukuran ketinggian, masalah utamanya adalah menentukan titik-titik tinggi dengan ukuran galat sekecil mungkin. Salah satu metode yang dapat meminimalkan galat pada pengukuran ketinggian adalah metode kuadrat terkecil tebobot.
Tugas akhir ini bertujuan untuk menunjukan hubungan antara masalah jaringan ketinggian dengan sebuah graf dimana titik-titik tinggi dilambangkan dengan simpul dan beda ketinggian dilambangkan dengan ruas. Kemudian masalah jaringan ketinggian yang telah direpresentasikan dengan sebuah graf akan diselesaikan dengan meggunakan metode kuadrat terkecil tebobot. Pada bagian akhir tugas akhir ini, akan diberi contoh penerapan dari sebuah graf yang mempresentasikan suatu masalah jaringan ketinggian dan penyelesaiaannya dengan menggunakan metode kuadrat terkecil tebobot.
ABSTRACT
In the measurements of height, the main problem is to find the point of height which the size of error as small as possible. One method that can minimize the error in the measurements of height is weighted least squares.
This paper aims to show the relation of height network with a graph in which the points of height are assigned by nodes and the differences of height are assigned by edges.
Then the height network’s problems that have been represented by a graph will be solved by
weighted least squares method. At the end of this paper will be given an example of the application of a graph that presented a height network’s problem and it’s solution by weighted least squares method.
METODE KUADRAT TERKECIL TERBOBOT UNTUK MEMINIMALKAN GALAT PADA PENGUKURAN JARINGAN
KETINGGIAN MAKALAH
Diajukan untuk Memenuhi Salah Satu Syarat Memperoleh Gelar Sarjana Matematika
Program Studi Matematika
Disusun Oleh :
Sisilia Nov Ciptaning Pradini 103114018
PROGRAM STUDI MATEMATIKA JURUSAN MATEMATIKA FAKULTAS SAINS DAN TEKNOLOGI
UNIVERSITAS SANATA DHARMA YOGYAKARTA
ii
WEIGHTED LEAST SQUARES METHOD TO MINIMIZE THE ERROR IN THE MEASUREMENTS OF HEIGHT NETWORK
PAPER
Presented as Partial Fulfillment of the Requirements To Obtain the Degree of Sarjana Matematika
Mathematics Study Program
By :
Sisilia Nov Ciptaning Pradini 103114018
MATHEMATICS STUDY PROGRAM DEPARTMENT OF MATHEMATICS FACULTY OF SCIENCE AND TECHNOLOGY
SANATA DHARMA UNIVERSITY YOGYAKARTA
vii
MOTTO DAN PERSEMBAHAN
“There I
s No Elevator to Success,
You’ve to Take The Stairs”
Ku persembahkan Tugas akhir ini kepada :
My beloved Jesus
Mama dan Bapakku tercinta
Adik-adikku tersayang Fifin, Benny dan Ella
viii ABSTRAK
Dalam pengukuran ketinggian, masalah utamanya adalah menentukan titik-titik tinggi dengan ukuran galat sekecil mungkin. Salah satu metode yang dapat meminimalkan galat pada pengukuran ketinggian adalah metode kuadrat terkecil tebobot.
Tugas akhir ini bertujuan untuk menunjukan hubungan antara masalah jaringan ketinggian dengan sebuah graf dimana titik-titik tinggi dilambangkan dengan simpul dan beda ketinggian dilambangkan dengan ruas. Kemudian masalah jaringan ketinggian yang telah direpresentasikan dengan sebuah graf akan diselesaikan dengan meggunakan metode kuadrat terkecil tebobot. Pada bagian akhir tugas akhir ini, akan diberi contoh penerapan dari sebuah graf yang mempresentasikan suatu masalah jaringan ketinggian dan penyelesaiaannya dengan menggunakan metode kuadrat terkecil tebobot.
ix
ABSTRACT
In the measurements of height, the main problem is to find the point of height which the size of error as small as possible. One method that can minimize the error in the measurements of height is weighted least squares.
This paper aims to show the relation of height network with a graph in which the points of height are assigned by nodes and the differences of height are assigned by edges.
Then the height network’s problems that have been represented by a graph will be solved by
weighted least squares method. At the end of this paper will be given an example of the application of a graph that presented a height network’s problem and it’s solution by weighted least squares method.
x
KATA PENGANTAR
Puji dan syukur penulis haturkan kepada Tuhan Yesus Kristus dan Bunda Maria atas berkatNya yang selalu menyertai penulis dalam menyelesaikan tugas akhir ini.
Penulis menyadari, tugas akhir ini tidak akan selesai tanpa bantuan dari berbagai pihak, untuk itu dalam kesempatan ini, penulis ingin mengucapkan terima atas segala bimbingan, dorongan, semangat, sehingga tugas akhir ini terselesaikan dengan baik, kepada:
1. Ibu Paulina Heruningsih Prima Rosa, S.Si., M.Sc., selaku Dekan Fakultas Sains dan Teknologi Universitas Sanata Dharma.
2. Bapak Y.G.Hartono, Ph.D., selaku Ketua Program Studi Matematika Universitas Sanata Dharma.
3. Bapak Dr.rer.nat. Herry Pribawanto Suryawan selaku dosen pembimbing yang dengan penuh kesabaran, kesungguhan hati serta memberikan banyak ide serta masukan kepada penulis dalam menyelesaikan tugas akhir ini.
4. Ir. Ignatius Aris Dwiatmoko, M.Sc. yang telah memberikan ide dan masukan untuk menulis tugas akhir ini dan selaku dosen pembimbing akademik.
5. Seluruh Dosen Program Studi Matematika serta karyawan Fakultas Sains dan Teknologi. Terima kasih atas bimbingan, doa dan pelajaran yang diberikan selama berkuliah di Universitas Sanata Dharma.
xi
yang selalu bikin panik ini. Terima kasih atas kesabaran dan kasih sayang dalam mendidik anak-anaknya. Adik-adik penulis Fifin, Beni, Ella.
7. Sahabat-sahabat penulis di Program Studi Matematika , Anes, Bibi, Nyai, Juna, Yoyo, Selly, Aster, Ayu, Arga, Tika, Ratri, Pandu, Roy, Yohan, yang selalu setia mendengar keluh kesah, menemani dan memberi semangat untuk penulis yang sangat berarti.
8. Keluarga Besar Program Studi Matematika, terima kasih atas segala dukungan dan bantuannya kepada penulis.
9. Teman-teman sekaligus keluarga penulis, Mbak Rub yang selalu siap menyediakan keperluan penulis, Apin, Mbak Astrid, Mbak Arin yang terus memberi semangat, dukungan dan doa. Banyak suka dan duka telah kita lewati bersama selama ini.
10. Semua pihak yang telah mendukung dan membantu penulis dalam menyelesaikan tugas akhir ini yang tidak dapat disebutkan satu per satu. Terima kasih banyak atas semua bantuannya.
Akhirnya penulis menyadari bahwa tugas akhir ini memiliki berbagai kekurangan. Oleh karena itu penulis mengharapkan kritik dan saran dari pembaca. Semoga tugas akhir ini dapat menjadi referensi bagi rekan-rekan dalam mengembangkan ilmu pengetahuan.
Yogyakarta, 11 Februari 2015
xii DAFTAR ISI
JUDUL ... i
HALAMAN PERSETUJUAN PEMBIMBING ... iii
HALAMAN PENGESAHAN... iv
PERNYATAAN KEASLIAN KARYA ... v
LEMBAR PERNYATAAN PERSETUJUAN PUBLIKASI KARYA ILMIAH ... vi
MOTTO DAN PERSEMBAHAN ... vii
ABSTRAK ... viii
ABSTRACT ... ix
KATA PENGANTAR ... x
BAB I : PENDAHULUAN ... 1
I.1 Latar belakang ... 1
I.2 Rumusan Masalah ... 6
I.4 Tujuan Penulisan ... 7
I.5 Metode Penulisan ... 7
I.6 Manfaat Penulisan ... 7
I.7 Sistematika Penulisan ... 7
BAB II : LANDASAN TEORI ... 10
II.1 Matriks Singular dan Tak singular ... 10
II.2 Ruang Vektor... 11
II.3 Ruang Bagian ... 13
xiii
II.5 Basis dan Dimensi ... 18
II.6 Ruang Baris dan Ruang Kolom ... 22
II.7 Rank ... 24
II.8 Ruang Nol (Kernel/ Nullspace) ... 25
II.9 Ruang Hasil Kali Dalam ... 27
II.10 Norma ... 28
II.11 Ortogonalitas ... 33
II.12 Metode Kuadrat Terkecil ... 34
II.13 Matriks Definit Positif ... 37
II.14 Konsep-Konsep Penting Dalam Statistika ... 37
II.15 Dasar-Dasar Teori Graf ... 39
BAB III : JARINGAN KETINGGIAN ... 44
III.1 Pengukuran Ketinggian dengan Menggunakan Metode Kuadrat Terkecil ... 44
III.2 Kuadrat Terkecil Terbobot ... 66
III.3 Jaringan Ketinggian Dan Graf ... 70
BAB IV : PENUTUP ... 81
IV.1 Kesimpulan ... 81
IV.2 Saran ... 82
BAB I PENDAHULUAN
I.1 Latar Belakang
Pada kehidupan sekarang ini, tak dapat dipungkiri bahwa manusia sangat membutuhkan teknologi demi membantu kelangsungan hidup mereka. Contohnya adalah manusia sekarang tidak pernah terlepas dari alat komunikasi jarak jauh yang disebut handphone. Handphone selain dapat membantu manusia untuk dapat berkomunikasi dari jarak jauh, handphone juga dilengkapi dengan fitur-fitur yang semakin memanjakan penggunanya. Contohnya adalah fitur kamera, radio, games, dan lain-lain. Semakin mahal harga handphone maka biasanya semakin lengkap fitur yang dimilikinya. Salah satu fitur yang dimiliki sebuah handphone adalah GPS. GPS tidak hanya terdapat pada handphone, tetapi banyak dijumpai juga di mobil. Hal ini dikarenakan oleh fungsi GPS yang membantu pengguna sebagai penunjuk arah.
2
Gambar 1.1 (Global Positioning System)
Dalam menentukan posisi dan letak pada GPS, manusia membutuhkan ilmu pengetahuan tentang bumi yang disebut geodesi. Menurut IAG (International Association of Geodesy), geodesi adalah ilmu yang mempelajari pengukuran dan perepresentasian dari bumi dan benda-benda langit lainnya, termasuk medan gaya beratnya masing-masing dalam ruang tiga dimensi yang berubah dengan waktu. Dengan kata lain, geodesi adalah ilmu yang mempelajari tentang bentuk dan ukuran bumi termasuk berat dan kepadatannya. Dalam prakteknya, ilmuwan geodesi mengadakan pengamatan dan pengukuran secara teliti untuk menentukan posisi titik pada permukaan bumi untuk dipetakan.
3
pengukuran secara umum menurut Umar (1991) adalah kegiatan yang sistematis untuk mendapatkan informasi mengenai suatu objek secara kuantitatif dengan alat ukur yang dimiliki. Seringkali dalam melakukan pengukuran ketinggian, data yang didapat untuk suatu tempat tidak selalu akurat karena terdapat galat (kesalahan/error). Galat yang dimaksud di sini adalah kesalahan dalam proses pengambilan data. Menurut buku karangan Suntoyo Yitnosumarto (1993), galat adalah keanekaragaman (variabilitas) hasil pengukuran yang disebabkan oleh ketidakmampuan materi pengukuran atau objek pengukuran untuk berperilaku sama dalam pengukuran tersebut. Galat dapat berfungsi untuk menunjukkan efisiensi dari satu jenis pengukuran ke pengukuran yang lain. Secara normal, yang diharapkan dalam pengukuran adalah galat yang bernilai kecil. Untuk itu dibutuhkan metode matematis yang dapat meminimalkan galat pada pengukuran tersebut (dalam hal ini pengukuran ketinggian).
pengukuran 1 pengukuran 1 Pengukuran 1
galat
Objek pengukuran
4
Bagan (1.1) menjelaskan pengukuran suatu objek yang dilakukan beberapa kali. Pengukuran-pengukuran tersebut menghasilkan galat. Selanjutnya, galat tersebut akan diestimasi untuk memperkirakan ukuran atau bentuk objek yang sesungguhnya.
Salah satu metode yang dapat membantu meminimalkan galat adalah metode kuadrat terkecil. Matematikawan besar dari Jerman, Carl Friedrich Gauss adalah salah satu pencetus ide tentang metode kuadrat terkecil. Selain Gauss ada beberapa penemu lainnya yaitu Adrien Marie Legendre pada tahun 1805 dan Robert Adrian tahun 1808. Prinsip dari metode kuadrat terkecil adalah meminimalisasi jumlah kuadrat deviasi data dari pengukuran yang didapat.
Persamaan untuk meminimalisasi jumlah galat pada metode kuadrat terkecil adalah x = b, dengan adalah matriks koefisien yang berukuran m x n dan b adalah vektor yang berisi hasil-hasil pengukuran yang didapat dari data. Dalam hal ini harus dicari vektor sehingga ‖ ‖ seminimal mungkin, dengan ‖ ‖ adalah panjang vektor . Maksudnya adalah harus dicari sebuah vektor untuk yang terdekat ke .
Misalkan = ‖ ‖, menotasikan galat pada perhitungan. Biasanya jarang ditemukan = 0. Jika = 0 maka perhitungan x adalah perhitungan yang eksak untuk persamaan Ax = b. Jadi harus ditemukan ̂, sehingga ukuran =
5
Yang dimaksud terkecil adalah jumlah kuadrat dari elemen-elemen Ax - b diminimalisasikan.
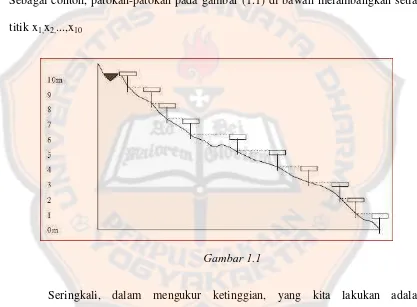
Dalam mengukur ketinggian, masalahnya adalah menemukan x1,x2,...,xn dimana n ditentukan dan x1,x2,...,xn adalah titik-titik ketinggian yang akan dicari. Sebagai contoh, patokan-patokan pada gambar (1.1) di bawah melambangkan setiap titik x1,x2,...,x10
Gambar 1.1
6 Gambar 1.2
Makalah ini akan membahas lebih lanjut tentang minimalisasi galat pada pengukuran ketinggian dengan menggunakan metode kuadrat terkecil terbobot..
I.2 Rumusan Masalah
a. Apa yang dimaksud dengan metode kuadrat terkecil terbobot?
b. Bagaimana menerapkan metode kuadrat terkecil terbobot tersebut ke dalam data jaringan ketinggian yang didapat?
I.3 Batasan Masalah
a. Perhitungan galat ini dilakukan hanya pada matriks yang mempunyai rank kolom penuh.
7
I.4 Tujuan Penulisan
a. Memahami metode kuadrat terkecil dalam meminimalkan galat dari suatu hasil pengukuran.
b. Memahami bagaimana metode kuadrat terkecil terbobot diaplikasikan dalam jaringan ketinggian.
c. Mengaplikasikan graf sebagai representasi dari jaringan untuk membantu memecahkan masalah menentukan titik-titik ketinggian.
I.5 Metode Penulisan
Metode yang digunakan adalah studi pustaka dengan menggunakan buku-buku referensi sebagai acuan penulisan serta pengambilan data.
I.6 Manfaat Penulisan
a. Dapat mengaplikasikan metode kuadrat terkecil untuk meminimalkan galat pada pengukuran jaringan ketinggian.
b. Membantu berbagai pihak dalam mengukur ketinggian agar galat dari hasil pengukuran yang diperoleh dapat diminimalkan.
I.7 Sistematika Penulisan
8 I.5 Metode Penulisan I.6 Manfaat Penulisan I.7 Sistematika Penulisan Bab II : Landasan Teori
II.1 Matriks Singular dan Taksingular II.2 Ruang Vektor
II.3 Kebebasan Linear II.4 Basis dan Dimensi
II.5 Ruang Baris dan Ruang Kolom II.6 Rank
II.7 Ruang Nol (Kernel) II.8 Ruang Hasil Kali Dalam II.9 Norma
II.10 Ortogonalitas
II.11 Metode Kuadrat Tekecil II.12 Matriks Definit Positif
II.13 Konsep-Konsep Penting Dalam Statistika A. Nilai Harapan Variabel Random B. Variansi Variabel Random
C. Kovariansi dari Dua Variabel Random II.14 Dasar-Dasar Teori Graf
9 B. Graf Berarah C. Graf Lengkap Bab III : Jaringan Ketinggian
III.1 Pengukuran Ketinggian dengan Menggunakan Metode Kuadrat Terkecil
III.2 Kuadrat Terkecil Terbobot III.3 Jaringan Ketinggian dan Graf
Bab IV : Penutup
BAB II
LANDASAN TEORI
II.1 Matriks Singular dan Tak singular
Definisi (2.1) : Suatu matriks A berorde n x n dikatakan tak singular (nonsingular) atau dapat dibalik (invertible) jika terdapat matriks B, sehingga AB = BA = I. Matriks B disebut sebagai invers perkalian (multiplicative inverse) dari A.
Jika B dan C keduanya adalah invers perkalian dari A, maka : B = BI = B(AC) = (BA)C = IC = C Jadi, satu matriks memiliki paling banyak satu invers perkalian.
Definisi (2.2) : Suatu matriks n x n dikatakan singular jika tidak memiliki invers perkalian.
Sebut invers perkalian dari suatu matriks taksingular A sebagai invers dari A dan ditulis sebagai .
Contoh :
Matriks-matriks
dan
adalah saling invers karena,
[
]
11
[
]
Teorema (2.1)
Suatu matriks A berorde n x n adalah singular jika dan hanya jika
Bukti (Leon, teorema 2.2.2, hal.90)
II.2 Ruang Vektor
Misalkan adalah himpunan tak kosong di mana didefinisikan operasi-operasi penjumlahan dan perkalian dengan skalar. Artinya bahwa untuk setiap pasangan elemen-elemen dan di dalam dapat diasosiasikan dengan elemen
yang tunggal yang juga berada di , dan dengan setiap elemen di dan setiap skalar , dapat diasosiasikan dengan elemen yang tunggal di dalam . Himpunan bersama-sama dengan operasi-operasi penjumlahan dan perkalian dengan skalar dikatakan membentuk ruang vektor jika aksioma-aksioma berikut dipenuhi :
A.1. untuk setiap dan di
A.2. untuk setiap di
A.3. Terdapat elemen 0 di sehingga = untuk setiap di
12
A.6. = untuk setiap skalar dan dan setiap A.7. untuk setiap skalar dan dan setiap A.8. 1. = setiap
Elemen-elemen dari V disebut vektor. Istilah skalar biasanya adalah suatu bilangan real, meskipun dalam beberapa kasus adalah bilangan kompleks. Seringkali istilah
ruang vektor real digunakan untuk menyatakan bahwa himpunan skalar-skalar adalah himpunan bilangan-bilangan real. Simbol 0 telah digunakan dalam Aksioma 3 untuk membedakan vektor nol dan skalar 0.
Beberapa contoh Ruang vektor :
1. Ruang vektor Euclides
Himpunan semua pasangan terurut dengan entri-entri bilangan real:
|
2. Ruang vektor
Misalkan himpunan semua matriks dengan entri-entri bilangan real. Jika dan , maka jumlahan didefinisikan sebagai matriks yang berorde . Jika diberikan skalar , maka dapat didefinisikan sebagai matriks dimana entri ke- adalah .
3. Ruang vektor
13
semestanya adalah himpunan fungsi-fungsi. Jadi vektornya adalah fungsi-fungsi di
. Jumlah dari dua fungsi di didefinisikan oleh
,
untuk semua di . Fungsi yang baru dari adalah elemen dari , karena jumlahan dari fungsi kontinu adalah kontinu. Jika adalah fungsi di dan suatu bilangan real, maka didefinisikan oleh
,
untuk semua di . Jelas bahwa berada di dalam karena jika konstan dikalikan dengan fungsi kontinu selalu kontinu.
4. Ruang vektor
Misalkan adalah himpunan semua polinom dengan derajat . Untuk
dan didefinisikan dan oleh
dan
II.3 Ruang Bagian
Definisi (2.3) : Jika S adalah subhimpunan tak kosong dari suatu ruang vektor . Dan memenuhi syarat-syarat berikut :
14 2.
maka disebut ruang bagian (subspace) dari .
Contoh :
Misalkan | . Maka adalah ruang bagian dari , karena
jika , maka :
1. .
jika dan maka :
2.
II.4 Kebebasan Linear
15
Untuk melihat bagaimana mencari himpunan perentang yang minimal perlu diperhatikan bagaimana vektor-vektor di dalam himpunan saling “bergantung” satu sama lain.
vektor-vektor dalam ruang vektor disebut bebas linear (linearly independent) jika
mengakibatkan semua skalar harus sama dengan 0.
Contoh :
Vektor-vektor dan
adalah bebas linear, karena jika
yaitu
maka satu-satunya penyelesaian dari sistem ini adalah dan .
16
Contoh :
Diberikan. Vektor-vektor ( ) ( ) ( ) ( ) adalah
bergantung linear karena apabila
( ) ( ) ( ) ( ) ( )
maka diperoleh :
Dalam kasus ini = 1, , , , jadi
.
Teorema (2.2)
Misalkan adalah vektor dalam dan misalkan
17
untuk . Jika , maka vektor-vektor adalah bergantung linear jika dan hanya jika adalah matriks singular.
Bukti (Leon, teorema 3.3.1, hal.122)
Teorema (2.2) dapat digunakan untuk menguji apakah vektor adalah bebas linear atau bergantung linear dalam . Langkah awalnya adalah bentuk suatu matriks yang elemen-elemennya adalah vektor-vektor yang akan diuji kebebasan linearnya, sebut matriks itu adalah matriks . Untuk menentukan apakah matriks singular atau tidak, hitunglah nilai dari det( . Jika det( = 0, maka vektor-vektornya bergantung linear. Jika det ( ≠ 0 maka vektor-vektornya bebas linear.
Contoh :
Tentukan apakah vektor-vektor dan bergantung linear atau bebas linear?
Penyelesaian :
Misalkan X = (
)
. Untuk menentukan apakah matriks singular atau tidak
singular adalah dengan mencari nilai determinannya
| | | | | |
18
.
Karena , maka menurut teorema (2.2), vektor-vektor tersebut adalah bergantung linear.
II.5 Basis dan Dimensi
Definisi (2.4) : Vektor-vektor membentuk basis untuk ruang vektor jika dan hanya jika :
i. bebas linear ii. merentang
Contoh :
“Basis baku” untuk adalah { ( ) ( ) ( )}, akan tetapi
terdapat banyak basis untuk yang dapat dipilih untuk (basis dari ruang vektor tidak tunggal). Sebagai contoh
{( ) ( ) ( )} dan {( ) ( ) ( )}
19 Buktinya adalah :
Diberikan {( ) ( ) ( )}, maka :
1. Harus dibuktikan bahwa himpunan vektor-vektor di atas merentang
( ) ( ) ( )
Menghasilkan :
maka,
20 sehingga ketiga vektor tersebut merentang .
2. Harus dibuktikan bahwa ketiga vektor tersebut bebas linear.
(
linear. Maka himpunan vektor tersebut adalah basis untuk .
Teorema (2.3)
Jika adalah basis dari suatu ruang vektor , maka himpunan sebarang vektor di , dengan adalah bergantung linear.
Bukti (Leon, teorema 3.4.1, hal.129)
21
Jika dan kedua-duanya adalah basis untuk suatu ruang vektor , maka .
Bukti (Leon, akibat 3.4.2, hal. 130)
Definisi (2.5) : Misalkan adalah ruang vektor. Jika memiliki basis yang terdiri dari vektor, maka dapat dikatakan bahwa memiliki dimensi . Ruang bagian dari dikatakan memilik dimensi 0. dikatakan memiliki dimensi hingga jika terdapat himpunan berhingga vektor yang merentang dan bebas linear; jika tidak demikian, maka dapat dikatakan bahwa memiliki dimensi tak hingga.
Contoh :
Ruang vektor memiliki basis . Karena terdapat vektor dalam basis tersebut, maka memiliki dimensi n.
Conotoh :
Teorema (2.4)
Jika adalah ruang vektor dengan dimensi
1. Sembarang himpunan n vektor bebas linear merentang
2. Sembarang himpunan vektor yang merentang adalah bebas linear.
22 Contoh :
Tunjukkan bahwa {( ) (
) ( )} adalah basis untuk .
Karena dim , maka hanya perlu ditunjukkan bahwa ketiga vektor ini bebas linear.
Misalkan (
), maka
| | | | | |
Karena ketiga vektor di atas bebas linear, maka menurut teorema (2.4) ketiga vektor di atas merentang . Jadi ketiga vektor di atas adalah basis untuk .
II.6 Ruang Baris dan Ruang Kolom
23
Definisi (2.6) : Jika adalah matriks berorde , maka ruang bagian dari yang direntang oleh vektor-vektor baris dari disebut ruang baris (row space) dari
dilambangkan dengan . Ruang bagian dari yang direntang oleh vektor-vektor kolom dari disebut ruang kolom (column space) dari dilambangkan dengan .
Contoh :
Misalkan
Ruang baris dari adalah himpunan tiga tupel yang berbentuk
Ruang kolom dari adalah himpunan semua vektor yang berbentuk
Jadi ruang baris dari adalah ruang bagian berdimensi dua dari dan ruang kolom dari adalah .
Teorema (2.5)
24 Bukti (Leon, teorema 3.6.1, hal. 144)
II.7 Rank
Rank dari suatu matriks adalah dimensi dari ruang baris dari . Untuk menentukan rank dari suatu matriks dapat dilakukan dengan cara mereduksi matriks yang bersangkutan menjadi bentuk eselon baris. Baris-baris taknol dari matriks eselon baris akan membentuk basis untuk ruang barisnya.
Contoh :
Misalkan
(
)
Dengan mereduksi menjadi bentuk eselon baris
(
) (
) (
)
( ) ( )
maka diperoleh matriks
25
Jelas bahwa dan membentuk basis untuk ruang baris dari . Karena dan ekivalen baris, maka matriks memiliki ruang baris yang sama dengan matriks sehinga rank dari adalah 2.
II.8 Ruang Nol (Kernel/ Nullspace)
Misalkan adalah matriks . Misalkan menyatakan himpunan semua penyelesaian dari sistem homogen , maka :
|
Akan ditunjukan bahwa adalah ruang bagian dari sebagai berikut :
Jika dan suatu skalar, maka
sehingga . , maka :
Oleh karena itu, . Ini berarti bahwa ruang bagian dari . Himpunan semua penyelesaian dari sistem homogen membentuk ruang bagian dari . Ruang bagian disebut ruang nol (kernel atau nullspace) dari .
Contoh :
26
Penyelesaian : Dengan menggunakan reduksi Gauss-Jordan untuk menyelesaikan
, maka diperoleh :
| |
| |
Bentuk eselon baris tereduksi melibatkan dua variable bebas dan
jadi, jika didefinisikan = dan , maka
(
)
27
di mana dan adalah skalar.
II.9 Ruang Hasil Kali Dalam
Hasil kali dalam pada ruang vektor adalah sebuah operasi pada yang memetakan setiap pasang vektor-vektor , dengan sebuah bilangan real yang memenuhi syarat berikut :
i , dengan kesamaan jika dan hanya jika ii untuk semua dan di dalam
iii untuk semua di dalam dan semua skalar dan
Ruang vektor yang dilengkapi dengan sebuah hasil kali dalam disebut ruang hasil kali dalam.
Sifat-sifat dasar ruang hasil kali dalam
Jika adalah sebuah vektor di dalam sebuah ruang hasil kali dalam , panjang atau norma dari diberikan oleh
‖ ‖ √
28 Teorema (2.6) (Hukum Pythagoras)
Jika dan adalah vektor-vektor ortogonal di dalam sebuah ruang hasil kali dalam , maka :
‖ ‖ ‖ ‖ ‖ ‖
Bukti (Leon, teorema 5.3.1, hal. 203)
Teorema (2.7) (Ketaksamaan Cauchy-Schwarz)
Jika dan adalah vektor-vektor di dalam sebuah ruang hasil kali dalam , maka
| | ‖ ‖‖ ‖
Kesamaan berlaku jika dan hanya jika dan bergantung linear.
Bukti (Leon, teorema 5.3.2, hal. 206)
II.10 Norma
Definisi (2.7) : Sebuah ruang vektor dikatakan ruang linear bernorma (normed linear space) jika untuk setiap vektor dikaitkan dengan sebuah bilangan real ‖ ‖ yang disebut norma dari yang memenuhi :
i ‖ ‖ dengan kesamaan berlaku jika dan hanya jika ii ‖ ‖ | |‖ ‖ untuk setiap skalar .
29 Teorema (2.8)
Jika sebuah ruang hasil kali dalam, maka
‖ ‖ √ untuk semua
mendefinisikan sebuah norma pada .
Bukti (Leon, teorema 5.3.3, hal. 207)
Ada banyak norma yang dapat didefinisikan pada sebuah ruang vektor yang diberikan. Sebagai contoh di :
i. ‖ ‖ ∑ | |, untuk setiap = ii. ‖ ‖ | |
iii. ‖ ‖ ∑ | | ⁄
Secara khusus, jika p = 2, maka :
‖ ‖ (∑| |
)
⁄
Bukti bahwa i, ii, iii adalah norma :
i. Misalkan ‖ ‖ | | | | | | 1. ‖ ‖ | | | | | |
30
| | | | | |
| | dan | | dan dan | |
dan dan dan
2. ‖ ‖ | | | | | |
| || | | || | | || | | | | | | | | | | | ‖ ‖
3. Misalkan ‖ ‖ | | | | | |
‖ ‖ | | | | | | | | | | | | | | | | | |
| | | | | | | | | | | | ‖ ‖ ‖ ‖
Jadi, terbutki bahwa (i) adalah norma.
ii. Misalkan ‖ ‖ | | | | | | 1. ‖ ‖ | | | | | |
Jelas bahwa nilai mutlak selalu bernilai positif maka ‖ ‖
‖ ‖
| | | | | |
31
dan dan dan
2. ‖ ‖ | | | | | |
| || | | || | | || | | | | | | | | | | | | | | | | | | | ‖ ‖
3. Misalkan ‖ ‖ | | | | | |
‖ ‖ | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | ‖ ‖ ‖ ‖
Jadi terbukti bahwa (ii) adalah norma.
iii. Misalkan ‖ ‖ ∑ | | ⁄ √ 1. ‖ ‖ √
√
‖ ‖
32
√
dan dan dan
dan dan dan
2. ‖ ‖ √
√
√
√ √
| |‖ ‖
3. Misalkan ‖ ‖ ∑ | | ⁄ √
‖ ‖
‖ ‖ ‖ ‖ ‖ ‖ ‖ ‖ Ketaksamaan Cauchy-Schwarz
‖ ‖ ‖ ‖
Diperoleh ‖ ‖ ‖ ‖ ‖ ‖ .
33 Contoh :
Misalkan adalah vektor di . Hitung ‖ ‖ ‖ ‖ ‖ ‖
Penyelesaian :
‖ ‖ | | | | | |
‖ ‖ √ √
‖ ‖ | | | | | |
II.11 Ortogonalitas
Definisi (2.8) : Dua ruang bagian dan dari dikatakan ortogonal jika untuk setiap dan . Notasi yang digunakan jika dan ortogonal adalah
Definisi (2.9) : Misalkan adalah ruang bagian dari . Himpunan semua vektor-vektor di dalam yang ortogonal pada setiap vektor di akan dinotasikan dengan
. Jadi,
|
Himpunan disebut komplemen ortogonal dari .
Teorema (2.9)
34 Bukti (Leon, teorema 5.2.1, hal.196).
II.12 Metode Kuadrat Terkecil
Masalah kuadrat terkecil pada umumnya dapat dirumuskan sebagai sebuah sistem kelebihan persamaan linear. Sistem kelebihan persamaan linear melibatkan lebih banyak persamaan daripada peubah yang tidak diketahui. Sistem yang demikian biasanya tidak konsisten (sistem persamaan tidak dapat diselesaikan). Jadi, jika diberikan sebuah sistem yaitu dengan .
Misalkan adalah sebuah matriks dengan . Untuk setiap , definisikan
‖ ‖ √ √
Tinjau sistem persamaan . Untuk setiap dapat dibentuk sebuah vektor sisa (residual)
Jarak antara dan diberikan oleh
‖ ‖ ‖ ‖
Akan dicari sebuah vektor sehingga ‖ ‖ minimum. Meminimumkan
35
vektor yang memenuhi ini disebut sebagai penyelesaian kuadrat terkecil untuk sistem .
Jika ̂ adalah penyelesaian kuadrat terkecil untuk sistem dan ̂, maka adalah sebuah vektor di dalam ruang kolom dari yang terdekat ke .
Teorema (2.10)
Misalkan adalah ruang bagian dari . Untuk setiap terdapat sebuah elemen tunggal dari yang terdekat ke , artinya:
‖ ‖ ‖ ‖
untuk semua di dalam . Lebih lanjut, vektor yang diberikan dalam akan paling dekat dengan vektor jika dan hanya jika .
Bukti (Leon, Teorema 5.4.1, hal. 212)
Sebuah vektor ̂ akan menjadi penyelesaian masalah kuadrat terkecil jika dan hanya jika ̂ adalah vektor di dalam yang terdekat ke . Vektor dikatakan sebagai proyeksi dari pada . Berdasarkan Teorema (2.10)
̂ ̂
36
̂
Kunci penyelesaian dari masalah kuadrat terkecil diberikan oleh Teorema (2.9) yang menyatakan bahwa :
Sebuah vektor ̂ akan menjadi penyelesaian kuadrat terkecil dari sistem jika dan hanya jika:
̂
atau, ekivalen dengan :
̂ ̂
Jadi, untuk menyelesaikan masalah kuadrat terkecil , harus diselesaikan :
̂
Persamaan di atas menggambarkan sebuah persamaan linear . Persamaan di atas disebut sebagai persamaan normal (normal equation).
Teorema (2.11).
Jika adalah matriks yang memiliki rank , maka persamaan normal
37
Definisi (2.10) : Nilai harapan suatu variabel random didefinisikan oleh
38
Definisi (2.11) : Variansi dari suatu variabel random dengan adalah nilai harapan dari . Yaitu
Contoh :
Dalam suatu keluarga, yang memiliki dua anak, distribusi probabilitas dari banyaknya anak yang terlahir, akan mengikuti ketentuan di bawah ini :
Banyaknya anak perempuan X
0 1 2
Probabilitas ¼ ½ ¼
Nilai harapan dan variansi dari banyaknya anak yang terlahir perempuan akan dihitung sebagai berikut :
∑ ( ) ( ) ( )
( ) ( ) ( )
39
Definisi (2.12) : Diberikan dan adalah variabel random dengan distribusi probabilitas bersama . Kovariansi dari dan adalah
[ ]
dengan dan
II.15 Dasar-Dasar Teori Graf
A. Teori Graf
Definisi (2.13) : Graf didefinisikan sebagai pasangan himpunan , yang dalam hal ini adalah himpunan tidak kosong dari simpul-simpul, yaitu
dan adalah himpunan sisi yang menghubungkan sepasang simpul, yaitu , atau dapat ditulis dengan notasi . Bila sisi menghubungkan simpul dan maka dapat ditulis .
Contoh :
Gambar 2.1 menyatakan graf dengan:
40
Definisi (2.14) : Dua buah simpul pada graf dikatakan berhubungan bila keduanya terhubung langsung oleh suatu sisi.
Untuk sebarang sisi , sisi dikatakan bersisian dengan titik dan titik . Contoh :
Pada gambar 2.1, simpul berhubungan dengan simpul , tetapi simpul tidak berhubungan dengan simpul .
Definisi (2.15) : Misal adalah graf, dan adalah titik-titik dalam graf , jalan
dari didefinisikan sebagai barisan titik-titik dan rusuk-rusuk yang dimulai dari dan diakhiri dengan sedemikian sehingga titik-titik dan rusuk-rusuk yang berurutan saling bersisian.
Sebuah jalan tanpa titik yang berulang disebut lintasan dan lintasan yang menghubungkan titik dan disebut lintasan .
Definisi (2.16) : Misalkan adalah graf. Graf merupakan graf terhubung bila hanya bila untuk setiap simpul dan di , ada jalan dari titik ke titik .
Contoh :
41
Graf merupakan graf terhubung, sedangkan graf merupakan graf tidak terhubung.
B. Terminologi Graf
Berikut ini diberikan diberikan beberapa definisi dari jenis-jenis graf
Definisi (2.17) : Garis parallel adalah dua buah garis yang menghubungkan titik yang sama. Loop adalah garis yang titik awal dan titik ujungnya sama.
Contoh:
Gambar 2.3
Gambar 2.3 adalah contoh graf yang memuat garis parallel dan loop.
42
Definisi (2.18) : Graf lengkap adalah graf yang memiliki titik dan setiap titik dihubungkan satu sama lain oleh sebuah rusuk. Graf lengkap disebut juga graf trivial.
Contoh :
Gambar 2.4
Gambar 2.4 merupakan beberapa contoh graf lengkap. D. Graf Berarah
Definisi (2.19): Suatu graf berarah (Directed Graph) D terdiri atas dua himpunan : (1) Himpunan V, anggotanya disebut simpul
(2) Himpunan A, merupakan himpunan pasangan terurut, yang disebut sisi berarah.
Graf berarah dinotasikan dengan D(V,A).
Simpul anggota V, digambarkan sebagai titik. Sedangkan sisi a = (u,v), digambarkan sebagai garis dilengkapi dengan tanda panah mengarah dari simpul u ke simpul v. simpul u disebut titik pangkal, dan simpul v disebut titik terminal.
Contoh :
43
Gambar di atas adalah sebuah contoh dari graf berarah dengan : (1) V mengandung 4 simpul, yakni 1,2,3 dan 4
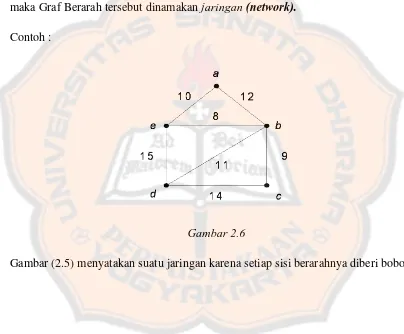
(2) A mengandung 4 sisi berarah yakni (1,4), (2,1),(4,2),(2,3),(4,3) dan (2,2) Definisi (2.18) : Apabila sisi berarah suatu graf berarah menyatakan suatu bobot, maka Graf Berarah tersebut dinamakan jaringan (network).
Contoh :
Gambar 2.6
BAB III
JARINGAN KETINGGIAN
III.1 Pengukuran Ketinggian dengan Menggunakan Metode Kuadrat
Terkecil
Pertama diberikan sebuah contoh permasalahan di dalam geodesi yaitu masalah leveling, dalam hal ini adalah penentuan tinggi. Masalahnya adalah menentukan ketinggian dari n titik yang ditentukan x1, x2, ... , xn. Di dalam prakteknya yang seringkali diukur adalah beda ketinggian. Ketinggian dari titik i diukur dari titik j, dengan menggunakan prinsip beda ketinggian bij (mungkin tidak eksak) adalah:
Beda-beda ketinggian ini diukur untuk pasangan tertentu (i,j). Dari pengukuran bij dapat diperkirakan ketinggian yang sebenarnya.
Pertama, diasumsikan tidak ada galat dalam pengukuran. Maka diharapkan penyelesaian dapat diselesaikan secara eksak. Tapi, jika dilihat pada persamaan dengan n = 3 variabel dan m = 3 persamaan, akan ditemukan masalah yaitu :
}
45 A = [
]
Matriks A tidak dapat dibalik (tidak invertibel). Determinan dari A sama dengan nol :
det (A) = 0 |
| | | | |
= 0 (-1 – 0)+1(0-1)+1(1-0)
= 0.
Jika ketiga persamaan pada (3.2) tersebut dijumlahkan akan menghasilkan :
0 = (3.3)
Sebuah sistem persamaan linear singular mempunyai dua kemungkinan, tidak ada penyelesaian atau ada banyak penyelesaian :
1. Tidak konsisten, artinya adalah tidak ada penyelesaian. Jumlahan dari
tidak sama dengan nol. (kasus 1)
46
Tidak dapat menentukan ketinggian yang sebenarnya semata-mata hanya dari
perhitungan beda tinggi. Satu atau lebih dari tinggi xj harus ditetapkan. Titik tinggi
yang telah ditetapkan akan dihilangkan dari variabel.
Misalkan titik ketinggian yang diketahui adalah x3 = H. Persamaan menjadi :
}
Sekarang terdapat tiga persamaan dan hanya dengan dua variabel. Catat bahwa persamaan tersebut memiliki kekonsistenan yang sama dengan ( ) yakni 0 =
. Masih terdapat dua kemungkinan, tetapi persamaan ( ) berbeda
47
1. Tidak ada penyelesaian (perhitungan tidak konsisten) 2. Hanya ada satu penyelesaian (jika kekonsistenan dipenuhi)
Bukti bahwa hanya ada satu penyelesaian :
48 kemungkinan yaitu tidak ada penyelesaian atau hanya ada satu penyelesesaian. Ruang nol dari matriks Areduced hanya terdiri dari vektor 0.
Bukti bahwa rank dari matriks Areduced adalah 2 :
Areduced = [
]
49
Bukti ruang nol dari matriks Areduced hanya terdiri dari vektor nol :
misalkan N(A) menyatakan himpunan semua penyelesaian dari sistem homogen Ax = 0. Jadi,
Masalah ini mirip dengan permasalahan menghitung tegangan pada sebuah jaringan listrik. Kekonsistenan pada permasalahan jaringan listrik, yakni persamaan 0 = dijamin oleh hukum tegangan Kirchhoff (perbedaan tegangan pada suatu jaringan listrik tertutup adalah nol). Tinggi yang telah ditetapkan pada ketinggian x3 = H sama seperti tegangan yang telah ditetapkan, yang memungkinkan tegangan lain ditemukan secara tunggal. Menetapkan x3 = 0 adalah kasus untuk tegangan yang bagian ujung dari jaringan diletakan di tanah. Selanjutnya dapat dikembangkan lebih lanjut analogi antara ketinggian pada jaringan ketinggian dan tegangan pada jaringan listrik (tidak akan dibahas dalam makalah ini)
50
otomatis terselesaikan. Walaupun hal ini adalah kasus yang mudah, tapi dalam prakteknya hampir tidak pernah terjadi.
Untuk perhitungan dengan galat, diharapkan ketiga persamaan pada (3.4) menjadi tidak konsisten. Persamaan-persamaan tersebut tidak dapat diselesaikan, akan dicari sebuah penyelesaian terbaik, yang mana dapat membuat pengukuran dari galat seluruh sistem menjadi sekecil mungkin. Penyelesaian tersebut diharapkan menjadi penyelesaian terbaik untuk pengukuran galat. Salah satu metode yang memiliki penyelesaian terbaik untuk meminimalkan galat adalah kuadrat terkecil, dimana kuadrat terkecil meminimalkan jumlah kuadrat dari m persamaan :
Persamaan di atas adalah kuadrat terkecil biasa. Ada beberapa pengukuran galat lain yang dapat memberikan penyelesaian-penyelesaian terbaik, yaitu :
…...(norma l2 terbobot)
2. | | | | | |...(norma l1)
3. | | | | | | ...(norma l∞)
Bukti bahwa ketiga pengukuran di atas adalah norma :
51 Misalkan r=( ), ‖ ‖= (∑ | | )
√
i. ‖ ‖ √
√
‖ ‖
√
√
dan dan
dan dan
ii. ‖ ‖ √
√
52 √ √
| |‖ ‖
iii. Misalkan t= (t1t2,t3), ‖ ‖ √ √
‖ ‖
=
‖ ‖ ‖ ‖‖ ‖ ‖ ‖ Cauchy-Schwarz ‖ ‖ ‖ ‖
Jadi, terbukti bahwa adalah norma (norma l2 terbobot).
2. Bukti | | | | | | adalah norma Misalkan r=( ), ‖ ‖ | | | | | | i. ‖ ‖ | | | | | |
‖ ‖
| | | | | |
| | dan | | dan | |
dan dan r = 0
53 | || | | || | | || |
| | | | | | | |
| | ‖ ‖
iii. Misalkan t= (t1t2,t3), ‖ ‖= | | | | | |
‖ ‖ | | | | | |
| | | | | | | | | | | | | | | | | | | | | | | | ‖ ‖ ‖ ‖
Jadi, terbukti bahwa | | | | | | adalah norma (norma l1).
3. Bukti bahwa | | | | | | adalah norma Misalkan r=( ), ‖ ‖ | | | | | |
i. ‖ ‖ | | | | | |
Jelas bahwa nilai mutlak selalu bernilai positif maka ‖ ‖ .
‖ ‖ = 0
| | | | | |
| | dan | | dan | |
dan dan
54 | || | | || | | || | | | | | | | | |
| | | | | | | |
| |‖ ‖
iii. Misalkan t= (t1t2,t3), ‖ ‖ | | | | | |
‖ ‖ | | | | | |
| | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | ‖ ‖ + ‖ ‖
Jadi, terbukti bahwa | | | | | | adalah norma.
Selanjutnya, makalah ini akan lebih banyak terfokus pada kuadrat terkecil terbobot. Pertama, harus dijelaskan kenapa bobot tertentu dipilih dalam dan bagaimana bobot-bobot tersebut mempengaruhi penyelesaian dari estimasi ̂ ̂ .
55 Ulasan 3.2
Pada bagian selanjutnya akan dibahas lebih detail mengenai variansi dan kovariansi. Output dari masalah ini harus menjadi perkiraan ketinggian ̂
dan juga merupakan indikasi dari kekonsistenan perkiraan-perkiraan tersebut. Akan dicari variansi dari output galat-galat ̂ , diberikan variansi-variansi dari input perhitungan galat-galat . Hal ini akan membuktikan bahwa output variansi-variansi adalah yang terkecil ketika bobot bersifat berkebalikan dengan input variansi. Hal ini yang menjadi alasan untuk bobot 1/ .
Lebih umum, suatu matriks bobot yang optimum adalah invers dari matriks kovariansi.
Ulasan 3.3
Pengukuran galat = ∑ | | dan = | | tidak kuadratik dan tidak terdiferensialkan karena adanya fungsi nilai mutlak.
56 Gambar 3.1
tidak terdiferensialkan di titik 0.
Turunan kiri fungsi f di titik 0 adalah :
Turunan kanan fungsi f di titik 0 adalah :
57
Karena turunan kanan fungsi f di titik 0 tidak sama dengan turunan kiri fungsi f di titik 0, maka tidak ada, yaitu fungsi f tidak terdiferensialkan di titik 0.
Pada prakteknya hampir selalu ada galat-galat besar pada perhitungan-perhitungan . Hal ini terjadi karena seringkali pengamatan diidentifikasi secara salah yang menyebabkan nilai-nilai pengamatan diproduksi kembali secara salah. Beberapa ilmuwan geodesi memperkirakan bahwa terdapat galat 5% dari data mereka.
Sebuah kuadrat-terkecil yang sesuai akan memperkecil galat-galat tersebut. Dengan meminimalkan bukan E, galat-galat besar dapat diidentifikasi pada sisa
̂ .
Penyelesaian dari sistem (3.3)
Kembali pada ketiga persamaan dengan dua variabel :
58
Sistemnya adalah yang akan diselesaikan dengan kuadrat terkecil dan juga dengan kuadrat terkecil terbobot. Pada kuadrat terkecil terbobot akan dipilih bobot-bobot yang tepat agar dapat menghasilkan perkiraan yang baik.
Jika melihat persamaan (3.5), matriks koefisien A dan b adalah :
A = [
Untuk kuadrat terkecil biasa dengan bobot satuan, persamaan normalnya adalah ̂ . Penyelesaian dari persamaan normal tersebut adalah perkiraan
̂ ̂ ̂ ) dari tinggi-tinggi yang tidak diketahui pada dua lokasi pengamatan pertama dan lokasi yang ketiga sudah ditetapkan sebagai .
59
tidak mudah dihitung dalam masalah yang memiliki ukuran matriks besar, tapi dalam masalah ini penyelesaiannya dapat dengan mudah dicari.
̂ mempunyai sebuah penyelesaian tunggal :
̂
[ ̂ ̂ ]
[ ]
[ ̂ ̂ ] [
]
[ ̂ ̂ ] [
]
Hal ini memberikan perkiraan kuadrat terkecil tidak terbobot :
[ ̂ ̂ ] [
]
[ ̂ ̂ ] [
]
̂
̂
}
60
Catat juga kemungkinan bahwa persamaan-persamaan asli (3.3) adalah konsisten : 0 = . Pada kasus ini, perkiraan ̂ juga merupakan penyelesaian x. Perkiraan ̂ adalah penyelesaian tunggal untuk .
Mengganti dengan nol memberikan penyelesaian yang tepat ketika hal tersebut muncul :
}
Sekali lagi, semua ketinggian memuat H. Tapi kuadrat terkecil mengatakan bahwa (3.8) adalah perkiraan yang lebih baik dari pada (3.9) ketika persamaan menjadi tak konsisten.
Selanjutnya, ubah perhitungan galat tidak terbobot mejadi perhitungan galat terbobot, yaitu :
menjadi
Variansi mewakili penyebaran dari rata-rata pengukuran galatnya. Untuk masalah jaringan ketinggian, ada sebuah aturan empiris yaitu : variansi adalah sebanding dengan jarak antar titik-titik pengamatan. Jadi, dipilih
61
Faktor merupakan suatu satuan bobot dari variansi (variance of unit weight).
Untuk menyelesaikan kasus pada bagian sebelumnya tapi dengan menambahkan bobot, masih tetap dibutuhkan penempatan dari satu ketinggian yaitu
. Ketiga persamaan masih tetap memiliki galat :
Penyelesaian terbaik ̂ ̂ meminimalkan . Variansi-variansi
menjadi penyebut. Ketika diambil turunan dari terhadap dan , maka akan didapat :
Dengan :
Dengan :
63
65
66
III.2 Kuadrat Terkecil Terbobot
Pada bagian sebelumnya telah dibahas contoh dari kuadrat terkecil terbobot. Matriks terbobot C adalah matriks diagonal, karena pengamatan dari galat-galat tidak berkorelasi. Matriks C menjadi C = (atau sungguh menjadi ketika seluruh galat mempunyai variansi yang sama. Hal ini termasuk pada kasus galat bebas linear dan teridentifikasi secara identik ( independent and identically distributed errors). Ketika galat-galat tidak bebas linear, maka setiap matriks simetris definit positif C =
∑ dengan C = ∑ adalah invers dari matriks kovariansi ∑
Pada bagian ini akan dikembangkan suatu persamaan normal ̂ dan dasar teori untuk membentuk matriks C. Ukuran kuadrat yang sebelumnya menjadi , termasuk juga bobot-bobot :
‖ ‖ berubah menjadi ‖ ‖ .
Ketika ukuran berubah, maka hasil kali dalam menjadi juga berubah. Sudutnya juga berubah, dua vektor a dan b sekarang menjadi tegak lurus ketika
67
atau ̂ atau ̂ (3.14)
Persamaan (3.14) adalah persamaan normal terbobot.
Vektor ̂ dipilih untuk membuat ‖ ‖ sekecil mungkin :
Meminimalkan ‖ ‖ (3.15)
Jabarkan (3.15) menjadi
. Sekarang yang ada adalah murni masalah kalkulus. Untuk dapat mencari nilai minimal dari (3.15) dapat dilakukan dengan menurunkan persamaan (3.15). Penyelesaian dari masalah tersebut memberikan persamaan-persamaan untuk setiap komponen dari ̂. Persamaan-persamaan menjadi linear karena ‖ ‖ adalah kuadratik.
Dalam aljabar, dapat ditemukan persamaan untuk mencari nilai ̂ (ada komponen) dengan menggunakan notasi matriks. Persamaan-persamaan tersebut adalah ̂ dengan dan :
Teorema (3.1):
Ketika adalah matriks simetri positif definit, bentuk kuadratik
68 Bukti :
Bandingkan ̂ dengan semua , untuk membuktikan bahwa ̂ adalah yang terkecil :
̂ ̂ ̂ ̂
̂ ̂ ̂
̂ ̂ ̂ ̂ ̂
̂ ̂ ̂
̂ ̂
Karena adalah matriks definit positif, maka selisih dari ̂ tidak pernah negatif. ̂ adalah nilai terkecil yang mungkin. Pada titik ̂ , minimum dari adalah :
(3.16)
Akibat (3.1.1):
Minimum dari galat terbobot ‖ ‖ tercapai ketika ̂ . Nilai minimumnya adalah :
‖ ‖
69
Jika adalah sebuah matriks persegi yang invertibel (dapat dibalik), maka keseluruhan galat akan dihilangkan menjadi nol! Penyelesaian ̂ akan menjadi penyelesaian yang eksak. Invers dari dapat ditulis menjadi
. Tapi penulisan seperti ini tidak dapat dilakukan pada sebuah
matriks persegi panjang A (matriks berukuran ). Hanya dapat diasumsikan bahwa memiliki kolom-kolom yang bebas linear, yang membuat definit positif (dan invertibel).
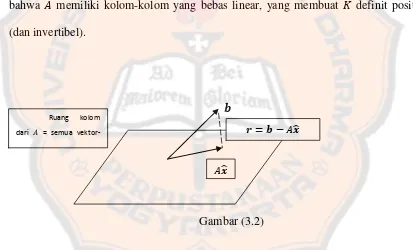
Gambar (3.2)
Gambar (3.2) proyeksi dari tegak lurus dalam perkalian dalam- :
untuk setiap kolom dari . Maka adalah persamaan normal terbobot. Segitiga siku-siku- memiliki ‖ ‖ ‖ ̂‖ ‖ ‖ , yang adalah .
Gambar (3.2) menunjukkan proyeksi secara geometri. Pengamatan yang dilakukan di atas adalah dengan menggunakan pengamatan hasil kali dalam. Jadi,
̂
̂
Ruang kolom
dari = semua vektor-
70
secara visual, tidak kelihatan tegak lurus terhadap proyeksinya. Tapi sudut siku-siku dalam perkalian dalam- , yang memberikan kunci persamaan adalah
̂ .
Ulasan 3.4
Sejak jaman Gauss, metode kuadrat terkecil sudah disebut teori penafsiran (adjustment theory) dalam geodesi dan digunakan dalam ilmu sains lainnya. Notasi sederhana mendefinisikan sisa oleh:
(3.17)
Dalam statistik dan aljabar linear numerik terdapat kesepakatan untuk mendefinisikan sisa dengan tanda yang berlawanan : . Gauss menggunakan notasi untuk bobot-bobot (latin : pondus). Untuk berbagai alasan akan diubah notasi menjadi .
III.3 Jaringan Ketinggian Dan Graf
Hubungan antar titik atau yang disebut dengan graf sudah banyak ditemukan dalam kehidupan sehari-hari. Contohnya adalah dibangunnya jalan besar yang menghubungkan beberapa kota. Dalam masalah mencari titik tinggi dari suatu ketinggian juga dapat disajikan dengan menggunakan graf.
71
menggunakan beda tinggi. Dalam graf, titik-titik tinggi tersebut dilambangkan dengan simpul-simpul dan beda tinggi dilambangkan dengan sisi.
Suatu graf berubah menjadi sebuah jaringan ketika ditetapkan bilangan
untuk setiap sisi. Setiap bilangan adalah suatu bobot dari pengamatan.
Secara statistik, adalah , suatu kebalikan dari variansi ketika diukur sebuah beda
ketinggian. Untuk masalah jaringan ketinggian ⁄ adalah sebanding dengan
suatu kebalikan dari suatu sisi. Bilangan-bilangan tersebut akan menjadi matriks yang mana berukuran .
Masalah utamanya adalah menentukan titik-titik yang tidak diketahui. Permasalahan dapat dipecahkan dengan menggunakan graf dan dengan menggunakan metode kuadrat terkecil terbobot.
Sebuah graf terdiri dari dari “simpul” dan “sisi”. Ada sebanyak simpul (titik-titik di mana ketinggian ditentukan). Dan ada juga sisi di antara simpul dan simpul yang melambangkan beda tinggi . Pengukuran beda tinggi tersebut membentuk sisi, umumnya dengan .
Semua simpul dinotasikan oleh setiap titik tinggi ̂ ̂ ̂ . Suatu beda ketinggian sepanjang sebuah loop adalah jmlahan dari ̂ ̂ ̂ ̂
72
Hukum loop : penjumlahan komponen-komponen dari ̂ adalah nol pada setiap putaran.
Untuk sisi , suatu galat terbobot sama dengan kali sisa ̂ . Persamaan vektornya adalah . Persamaan normal terbobot adalah
atau ̂ . Persamaan terbobot tersebut sama halnya dengan Hukum Arus Kirchhoff pada setiap simpul :
̂
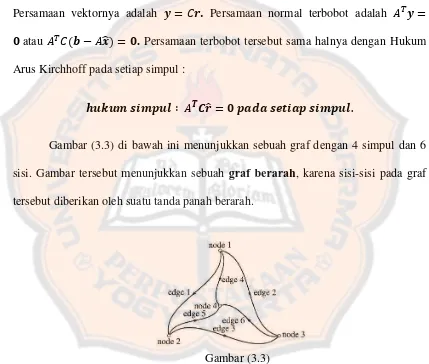
Gambar (3.3) di bawah ini menunjukkan sebuah graf dengan 4 simpul dan 6 sisi. Gambar tersebut menunjukkan sebuah graf berarah, karena sisi-sisi pada graf tersebut diberikan oleh suatu tanda panah berarah.
Gambar (3.3)
73
Selanjutnya akan dibahas lebih lanjut mengenai matriks insidensi atau matriks diferensi atau matriks koneksi dari graf.
Matriks insidensi mempunyai baris yang menginformasikan setiap sisi dan kolom yang menginformasikan setiap simpul. Pada contoh di atas, graf dengan 6 sisi dan 4 simpul memiliki matriks insidensi yang berukuran 6 x 4. Setiap baris memiliki dua entri tak nol yaitu +1 dan -1 untuk menunjukkan simpul mana yang ada tanda panah masuk dan simpul mana yang ditinggalkan. Maka membentuk matriks insidensi adalah dengan cara melihat simpul dan sisi yang berhubungan. Contoh pada gambar graf (3.3), ada 3 sisi yang menghubungkan simpul 1 yaitu sisi 1, sisi 2 dan sisi 4. Maka dalam matriks insidensi, entri tak nolnya adalah dan . Karena sisi 1 menunjukan panah yang meninggalkan simpul 1, maka entri adalah -1. Maka dengan cara yang sama dapat dibentuk sebuah matriks insidensi A dari sebuah graf.
74
memiliki sisi. Hubungan dari sebuah graf dengan matriks insidensinya adalah jika sebuah sisi dihilangkan dari graf maka sebuah baris dihilangkan dari matriks, dan lebih khususnya dalam masalah jaringan ketinggian, jika ada satu titik tinggi yang ditetapkan, maka suatu kolom yang berkorespondensi dengan simpul yang ditetapkan tersebut akan dihilangkan dari matriks insidensinya. Dalam masalah pengukuran jaringan ketinggian, tidak dapat dibuat dua buah sisi di antara simpul-simpul dan sebuah sisi dari sebuah simpul ke dirinya sendiri. Dua buah sisi hanya akan mengartikan bahwa beda ketinggian dihitung dua kali.
Dalam jaringan ketinggian, suatu matriks insidensi bukan hanya matriks yang melambangkan hubungan antara sisi dan simpul dalam suatu graf. Matriks insidensi berperan dalam menghitung beda tinggi dalam jaringan ketinggian. Ketika matriks dikalikan dengan sebuah vektor dari ketinggian, maka output dari adalah sebuah himpunan dari 6 beda ketinggian ;
75
atau dalam bentuk matriks
Sistem dengan 6 persamaan dan 4 variabel mungkin tidak konsisten (karena terdapat galat dalam pengukurannya).
Untuk menyelesaikan sistem dengan 6 persamaan dan 4 variabel dapat dilakukan dengan menggunakan metode kuadrat terkecil terbobot. Dibentuk persaman normal (terbobot) untuk mendapatkan perkiraan ̂. Tapi ada masalah yang harus ditangani terlebih dahulu :
Karena memiliki kolom yang bergantung linear, maka matriks dan
tidak dapat dibalik. Langkah selanjutnya yang harus diambil adalah satu atau lebih dari titik tinggi harus ditetapkan.
Dalam pengukuran yang sesungguhnya, menetapkan dapat dilakukan dengan berbagai cara. Misalnya adalah dengan melihat data pengukuran yang telah dilakukan sebelumnya atau dapat dilakukan dengan percobaan lapangan secara langsung. Contohnya adalah dalam mengukur suatu gunung akan ditentukan satu titik yang akan ditetapkan. Dengan menggunakan alat yang bernama LIDAR (Light Detection And Ranging) akan ditemukan nilai titik tinggi yang dicari.
Pada aljabar linear, persoalan seperti ini menyangkut tentang “ruang kolom” dari suatu matriks. Ruang nol dari matriks tersebut adalah berdimensi 1, berisi vektor
76
matriks baru memiliki rank penuh dan matriks baru dapat dibalik. Jika ditetapkan satu titik ketinggian (seperti pada bagian sebelumnya), maka semua ketinggian lain dapat diperkirakan.
Dengan bebas dapat ditentukan ketinggian (tidak hanya satu). Maka kolom dari matriks dapat dihilangkan. Matriks baru A (yang berorde ) memiliki rank penuh . Lalu dengan menyelesaikan persamaan normal terbobot
, maka dapat ditentukan estimasi dari nilai ̂.
Dalam praktek jaringan ketinggian, harus ada satu atau lebih titik tinggi yang ditetapkan. Misalkan adalah simpul yang telah ditetapkan tersebut, dan prosedur dalam menyelesaikan masalah jaringan ketinggian adalah :
1. Rincikan semua simpul dari 1 sampai . Rincikan juga simpul yang memiliki titik tinggi yang ditetapkan.
2. Bentuk matriks bersisian yang berukuran , dan suatu matriks bobot berukuran .
3. Hapus kolom pada matriks bersisian
4. Kalikan kolom k dengan sebuah kolom yang berisi titik tinggi tetap yang telah diketahui, kemudian jumlahkan dengan vektor . Suatu pengukuran memiliki persamaan dengan variabel tinggi yang tidak diketahui memiliki
77 Contoh 3.1
Untuk suatu jaringan ketinggian, ditunjukkan pada gambar 3.4 sebagai sebuah graf berarah. Titik-titik tersebut memiliki titik tetap
Gambar 3.4 graf berarah untuk sebuah jaringan ketinggian
Pengamatan dari beda-beda tinggi dan ukuran dari garis jaringan adalah
78
Matriks bersisiannya berukuran 5 x 5
79
Dan pada bagian sebelah kanan dari tanda sama dengan adalah
BAB IV PENUTUP
IV.1 Kesimpulan
Jaringan ketinggian dideskripsikan oleh graf dan matriks insidensi . Titik tinggi yang akan dicari dilambangkan dengan sebuah simpul, sedangkan beda tinggi dari titik ke titik dinotasikan dengan sebuah sisi. Suatu graf berubah menjadi sebuah jaringan ketika ditetapkan bilangan untuk suatu sisi.
Setiap bilangan adalah suatu bobot dari sebuah pengamatan. Secara statistik adalah ⁄ , suatu kebalikan dari variansi ketika diukur sebuah beda ketinggian.
Untuk masalah jaringan ketinggian ⁄ adalah sebanding dengan suatu
kebalikan panjang dari suatu sisi. Bilangan-bilangan tersebut akan menjadi matriks yang mana berukuran .
Dalam jaringan ketinggian, masalahnya adalah menentukan titik-titik tinggi ̂ (n komponen) dengan ukuran galat yang sekecil mungkin.
Salah satu metode yang dapat meminimalkan galat adalah metode kuadrat terkecil terbobot.
Persamaan normal metode kuadrat terkecil terbobot adalah :