DAFTAR ISI
Halaman
PERNYATAAN i
ABSTRAK ii
ABSTRACT iii
KATA PENGANTAR iv
RIWAYAT HIDUP vi
DAFTAR ISI vii
DAFTAR GAMBAR ix
BAB 1 PENDAHULUAN 1
1.1 Latar Belakang 1
1.2 Perumusan Masalah 5
1.3 Tujuan Penelitian 5
1.4 Manfaat Penelitian 6
1.5 Metode Penelitian 6
BAB 2 TINJAUAN PUSTAKA 7
BAB 3 GRAPH INTERVAL 12
3.1 Graph Interval 12
3.1.1 Sifat graph triangulated 13
3.1.2 Sifat orientasi transitif 13
BAB 4 POHON INTERVAL DAN APLIKASINYA 20
4.1 Pohon Interval 20
4.1.1 Sifat dari pohon interval 22
4.1.2 Representasi pohon interval 24
4.2 Aplikasi Pohon Interval 25
4.2.1 Pohon 3-spanner 25
4.3 Representasi Pohon 3 Spanner 26
BAB 5 KESIMPULAN DAN SARAN 28
5.1 Kesimpulan 28
5.2 Saran 28
DAFTAR GAMBAR
Nomor Judul Halaman
1.1 Digraph dengan 5 verteks dan 7 edge 2
1.2 Pohon 5
2.1 Graph lengkap G dan empat buah pohon perentangnya, T1, T2, T3,
dan T4 10
3.1 Graph interval 12
3.2 Sifat graph interval 15
3.3 Matriks clique 16
3.4 Graph induced 18
3.5 Graph interval 19
3.6 Representasi graph interval 19
3.7 Array dari Gambar 4.2 19
4.1 Pohon interval 25
PENDAHULUAN
1.1 Latar Belakang
Dalam perkembangan Ilmu Pengetahuan dan Teknologi sekarang ini salah satu cabang matematika yaitu graph banyak dipergunakan orang untuk menye-lesaikan berbagai permasalahan dalam kehidupan (Munir, 2005). Graph dapat digunakan untuk memecahkan suatu masalah, seperti masalah lalulintas, sistem saluran air, jaringan listrik, transpormasi udara, sistem telekomunikasi, dan lain-lain.
Secara sederhana graph didefinisikan sebagai kumpulan simpul-simpul yang dihubungkan dengan garis. Simpul biasa dinyatakan dengan istilah verteks dan garis biasa dinyatakan dengan istilah edges. Untuk selanjutnya dalam penelitian ini digunakan istilah verteks dan edge. Secara matematis suatu graph G adalah suatu objek yang terdiri atas dua himpunan, yakni :
1. Himpunan berhingga tak kosong V. Unsur dari V disebutverteks dari G. 2. Himpunan E yang merupakan himpunan bagian dari pasangan tak berurut
dari unsur-unsur diV. Unsur dari E disebut edgedari G.
Graph G dengan himpunan verteks V dan himpunan edge E dinotasikan dengan G(V, E). Definisi tersebut menyatakan bahwa V tidak boleh kosong, se-dangkan E boleh kosong. Dengan demikian sebuah graph dimungkinkan untuk tidak memiliki sebuah edge pun, tetapi minimal satu buah verteks harus dimili-ki. Graph yang hanya memiliki sebuah verteks tanpa memiliki edge disebutgraph trivial.
Verteks pada suatu graph dapat diberi label dengan huruf, seperti a, b, v, w, dengan bilangan asli, seperti 1,2,3,. . . , atau gabungan keduanya, sedangkan edge yang menghubungkan verteks vi dan vj dinyatakan dengan pasangan vivj atau dengan lambange1, e2, . . . , en. Dengan kata lain, jikae adalah edge yang
2
Contoh 1 : Himpunan verteks V ={v1, v2, v3, v4, v5}bersama dengan himpunan
edge A=v1−v5, v5−v4, v5−v2, v4−v2, v2−v1, v2−v3, v4−v3, v3−v3
adalah satu graph dengan 5 verteks dan 7 edge.
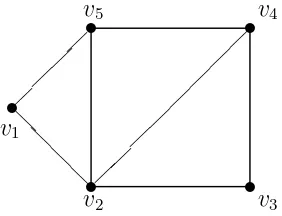
Sesuai dengan namanya, suatu graph biasanya direpresentasikan secara grafis dengan cara setiap verteks pada graph tersebut direpresentasikan sebagai suatu titik atau lingkaran kecil dan setiap edgevi−vj yang terdapat dalam digraph itu direpresentasikan sebagai garis tak berarah darivi kevj. Representasi graph pada contoh 1 diperlihatkan pada gambar 1.1.
t
Gambar 1.1 Digraph dengan 5 verteks dan 7 edge
Andaikanvi,vj ∈V. Suatu walk darivikevj dinotasikan denganwvivj. Suatu
walk dari vi kevj yang panjangnya m adalah suatu barisan edgedalam bentuk (vi =v0, v1),(v1, v2), . . . ,(vm−2, vm −1),(vm−1, vm =vj)
Walk diatas dapat juga direpresentasikan oleh
vi=v0−v1−v2−. . .−vm−1−vm =vj
Dari definisi walk diatas, panjang dari suatu walk adalah banyaknya edge yang terdapat pada walk tersebut.
Suatu walk dikatakan terbuka jika verteksvi 6=vj dan dikatakan tertutup jika vi =vj. Panjang dari suatu walkwvivj adalah banyaknya edge yang menyusun walk
tersebut dan dinotasikan dengan ℓ(wvivj). Suatu walk dengan edge yang
berbeda-beda disebut trail. Suatu path pvivj adalah suatu wvivj tanpa ada perulangan
verteks kecuali mungkin verteks awal dan verteks akhir dan panjangnya dinotasikan denganℓ(pvivj). Suatucycleadalah path dengan verteks awal sama dengan verteks
Perhatikan graph pada gambar 1.1. Berikut ini diperlihatkan contoh dari walk, trail, path, dan cycle.
1. Barisan v2−v1−v5−v2−v3 adalah walkwv2v3 dengan panjang 4. Walk ini
juga merupakan suatu trail karena tidak ada edge yang sama.
2. Barisan v2−v1−v5−v4−v3 adalah suatu pathpv2v3 dengan panjang 4.
3. Barisan v1−v5−v2−v1 adalah suatu cycle dengan panjang 3.
Misalkan G(V, E) adalah suatu graph dengan himpunan verteks V(G) dan himpunan edge E(G). Sedangkan G− = (V,E−), adalah suatu graph dengan him-punan verteksV(G) =V(G) dan himpunan edgeE(G)− 6=E(G). Dengan demikian graphG− adalah komplemen dari graph G .
Graph G(V, E) terdiri atas himpunan verteks yang dinyatakan dengan V = v1, v2, v3, . . . , vn dan himpunan edge yang dinyatakan dengan E =e1, e2, e3, . . . , en
dengan ei = (vi, vj) merupakan edge yang menghubungkan verteks vi dan verteks vj. Dua verteks vi dan vj dikatakan adjacent bila terdapat suatu edge yang menghubungkan kedua verteks tersebut.
Suatu graphG= (V, E) dikatakan graph tak berarah jika hubungan ketetang-gannya adalah simetris atau ekuivalen dengan E =E−. Misalkan graphG= (V, E) merupakan graph tak berarah. Maka didefenisikan komplemen dari G menjadi graphG− = (V,E−),dengan :
−
E = (x, y)∈V xV|x6=y dan (x, y)∈/E
Graph tak berarah G disebut graf terhubung (connected graph) jika untuk setiap pasang verteksvi dan vj di dalam himpunan V terdapat path dari vi kevj. Jika tidak, makaGdisebutgraph tak terhubung (disconnected graph). Setiap graph yang tidak terhubung dapat dipecah menjadi beberapa subgraph yang dinamakan komponen terhubung.
4
V(H) dan himpunan edge E(H). H adalah subgraph dari G jika V(H) ⊆ V(G) danE(H)⊆E(G). Dengan kata lain, H subgraph dariGjika verteks-verteks dari H juga verteks-verteks dari G dan edge-edge dari H juga edge-edge dari G.
Suatu subset S ⊆ E dari edge yang merentang pada subgraph H = (Vs, S) dengan Vs = {v ∈ V|v adalah titik akhir dari sebarang edge di S}, H disebut subgraph perentang oleh S.
Andaikan S adalah himpunan tak kosong dari G, dengan S ⊆ G. Subgraph inducedoleh S adalah graph Gs = (A, ES) dengan
Es ={xy∈E|x ∈S dan y ∈S}.
Suatu clique dari graph G adalah himpunan dari pasangan verteks yang adjacent. Suatu clique maksimal dari graph G adalah suatu clique yang tidak termuat di dalam clique manapun dari graph G.
Pohon merupakan terapan khusus dari teori graph. Pohon merupakan suatu struktur data yang sangat penting. Sebuah pohon adalah sebuah graph terhubung yang tidak memuat cycle . Karena merupakan graph terhubung maka pada pohon selalu terdapat path yang menghubungkan kedua verteks di dalam pohon.
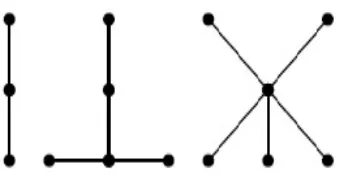
Karena defenisi pohon mengacu dari teori graph, maka sebuah pohon dapat mempunyai hanya sebuah verteks tanpa sebuah edge. Dengan kata lain, jika G= (V, E) adalah pohon, maka V tidak boleh berupa himpunan kosong, namun E boleh kosong. Pada sebagian literatur, pohon yang dimaksudkan oleh defenisi pohon diatas sering juga disebut pohon bebas (free tree) untuk membedakannya dengan pohon berakar (rooted tree). Pohon juga seringkali didefinisikan sebagai graph tak-berarah dengan sifat bahwa hanya terdapat sebuah walk tunggal antara setiap pasangan verteks. Sebuah daun pada sebuah pohon adalah sebuah verteks yang mempunyai derajat 1. Gambar 1.2 berikut merupakan gambar dari pohon.
Gambar 1.2 Pohon
Suatu graphG= (V, E) dikatakan suatu graph interval jika himpunan verteks V berkorespondensi satu-satu dengan suatu himpunan I dari interval pada garis real sedemikian hingga dua verteks adjacent di G jika dan hanya jika korespon-densi interval tersebut mempunyai irisan tak kosong. Contoh : Diberikan suatu pemetaan bijektiff : V →I (Anita et al., 2009).
Suatu himpunan I disebut suatu representasi interval dari G dan G dinya-takan sebagai graph interval dari I. Graph interval dibentuk melalui proses me-modelkan banyak situasi di kehidupan nyata, khususnya masalah yang melibatkan ketergantungan waktu atau permasalahan yang lain yang linier di alam. Graph ini dan variasi subclas nya digunakan pada arkeologi, biologi molekular, sosiologi, genetika, lalulintas, desain VLSI, psikologi, penjadwalan, transportasi, dan lainnya (Anita et al., 2009).
1.2 Perumusan Masalah
Andaikan pohon interval dari sebuah graph terhubung pada graph interval ada dan tunggal. Rumusan masalah dari penelitian ini adalah bagaimana caranya menemukan pohon interval tersebut.
1.3 Tujuan Penelitian
6
1.4 Manfaat Penelitian
Penelitian ini memberikan gambaran terkait dengan pohon interval agar dap-at memudahkan persoalan graph interval dan dapdap-at memperkaya literdap-atur tentang persoalan graph interval.
1.5 Metode Penelitian
TINJAUAN PUSTAKA
Istilah- istilah baku graph dalam tulisan ini, diambil dari Gilmore dan Hoff-man (1964), Anitaet al., (2009), Lekkerkerker dan Boland (1962).
Suatu pohon merupakan suatu graph terhubung yang tidak memuat suatu cycle. Oleh karena itu, apabila setiap edge dari suatu pohon dihapus maka akan menghasilkan graph tak terhubung. Berikut diberikan definisi dan sifat-sifat dari pohon.
Teorema 2.1 JikaGadalah graph terhubung (connected graph), maka pernyataan-pernyataan berikut ini adalah ekivalen :
1. G adalah pohon.
2. G memiliki tepat n1 edge dan tidak memilik cycle.
3. G adalah graph terhubung yang memiliki tepat n−1 edge. 4. G adalah graph terhubung yang setiap edgenya adalah jembatan.
5. Setiap dua verteks dari G dihubungkan oleh tepat satu walk.
6. Gtidak memiliki cycle, tetapi jika banyaknya edge ditambah satu yang menghubungkan sebarang dua verteks, maka hasilnya ialah graph yang memiliki tepat satu
cy-cle.
Bukti :
Kasus I :n = 1
1. Jelas bahwa pohon adalah pohon yang menyusut.
8
3. Gterhubung dan memiliki tepat n−1 edge.
4. G terhubung dan tidak ada edge dari G yang bukan jembatan, jadi setiap edge dari Gadalah jembatan.
5. Tidak ada pasangan verteks dari G (dua verteks yang berbeda ) yang tidak dihubungkan dengan path.
6. Gtidak memuat cycle dan jika banyaknya edge dariG ditambah satu berarti graph yang terjadi terdiri atas tepat satu cycle.
Pernyataaan diatas dapat disimpulkan bahwa :
1. AndaikanG adalah pohon. Maka menurut definisi Gtidak memiliki cycle. Berarti bahwa pengurangan satu edge dari G akan menghasilkan dua graph baru yang terpisah, yang masing-masing merupakan pohon. KarenaGhanya memilikinverteks berarti bahwa jika dilakukan pengurangann−1 edge pada G, yang tersisa hanyalah verteks. Jadi Gmemiliki tepat n−1 edge.
2. Seandainya G tidak memiliki cycle dan memilikin−1 edge, maka G terdiri atask pohon, misalkanp1, p2, ..., pndengan banyaknya verteks berturut-turut
adalah n1, n2, ..., nk dan n1+n2+...+nk =n.
Ternyata Ghanya terdiri atas satu komponen. Jadi G terhubung.
3. Andaikan G adalah graph terhubung yang memiliki tepat n−1 edge. Jika salah satu edge dari G dibunag maka yang terjadi adalah graph K yang memiliki tepat n verteks dan tepat n − 2 edge. Jadi setiap edge dari G adalah jembatan.
bertentangan dengan keadaan bahwa setiap edge dari G adalah jembatan. Jadi setiap dua verteks dari G dihubungkan oleh tepat satu path.
5. Andaikan G memuat cycle, maka setiap dua verteks pada cycle itu dihu-bungkan oleh paling sedikitnya dua path. Jadi kalau (5) benar, maka G tidak memuat cycle. JikaGditambah dengan edge yang menghubungkan ke-dua verteks itu maka terjadilah tepat satu cycle yang melalui keke-dua verteks tersebut.
6. MisalkanGtidak memiliki cycle, dan setiap penambahan edge padaG meng-hasilkan tepat satu cycle. SeandainyaGtidak terhubung, maka penambahan satu edge yang menghubungkan satu verteks dari salah satu komponen dan verteks, salah satu komponen yang lain tidak akan menghasilkan cycle. Ber-arti G pasti terhubung. Jadi jika (6) benar maka G terhubung dan tidak memiliki cycle. Artinya, jika (6) benar maka (1) benar.
Pohon perentang suatu graph G adalah subgraph G yang merupakan pohon dan semua memuat verteks dalam G. Disebut pohon perentang karena semua verteks pada pohon T sama dengan semua verteks pada graph G, dan edge-edge pada pohonT merupakan himpunan bagian dari edge-edge pada graphG. Dengan kata lain,V1 =V dan E1 ⊂E.
Pohon perentang didefenisikan hanya untuk graph terhubung, karena pohon selalu terhubung. Pada graph tak terhubung dengan n buah verteks tidak dapat ditemukan subgraph terhubung dengannbuah verteks. Tiap komponen dari graph tak-terhubung mempunyai satu buah pohon perentang.
Teorema 2.2 Setiap graph terhubung mempunyai sekurang-kurangnya satu pohon perentang.
10
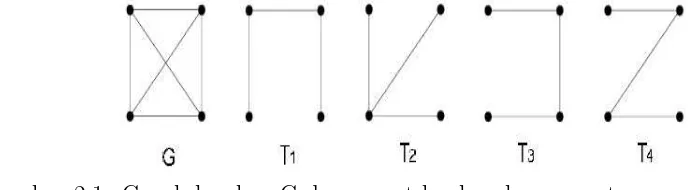
Pada Gambar 2.3 berikut akan diberikan bagaimana cara menentukan pohon perentang dari sebuah graph.
Gambar 2.1 Graph lengkap G dan empat buah pohon perentangnya, T1, T2, T3, dan T4
Suatu graph adalah graph interval jika dan hanya jika memenuhi beberapa kondisi, dengan demikian dalam sebuah graph G terdapat sebuah graph interval.
Gilmore Hoffman (1964) memberikan ide bahwa suatu graph adalah graph interval jika memiliki model irisan yang terdiri dari interval pada garis real. Se-buah graph interval adalah graph yang menunjukkan interval berpotongan pada sebuah garis. Andaikan himpunan interval E = (E1, ..., En), pada baris dengan
graph Interval G = (V, E), dengan V = (1, ..., n) dan dua verteks, x dan y, yang dihubungkan dengan sebuah edge jika dan hanya jika Gadalah graph interval.
Lekkerkerker Boland (1962) memberikan ide tentang karakteristik dari graph interval. Suatu graph disebut graph interval jika dan hanya jika memenuhi kondisi berikut:
1. Gadalah graph segitiga.
2. Setiap tiga verteks dari G dapat dibuat sedemikian rupa sehingga walk dari verteks pertama, verteks ketiga melewati tetangga dari verteks kedua.
Anita et al., (2009) memberikan ide bahwa pada dasarnya pohon interval itu adalah pohon perentang. Dengan mengambil akar pohon sebagai n dan tingkat akar sebagai 0. Setiap anak tingkat dari akar tersebut adalah 1. Jika tingkat verteks adalah l maka tingkat masing masing anak adalah l+ 1.
dalam graph nyata. Secara khusus, pohon perentang T dikatakan pohon t −