PELABELAN SUPER VERTEX MAGIC RAHMALIA YULIARNI

(1)

PELABELAN

SUPER VERTEX MAGIC

RAHMALIA YULIARNI

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM

INSTITUT PERTANIAN BOGOR

BOGOR

2013

(2)

ABSTRAK

RAHMALIA YULIARNI. Pelabelan Super Vertex Magic. Dibimbing oleh TEDUH WULANDARI MAS’OED dan FARIDA HANUM.

Pelabelan super vertex magic pada suatu graf dengan adalah himpunan simpul dan

adalah himpunan sisi, merupakan pelabelan yang memiliki pelabelan total vertex magic dengan

himpunan sisinya dipetakan ke dan himpunan simpulnya dipetakan ke , dengan adalah banyaknya simpul dan adalah banyaknya sisi pada suatu graf. Karya ilmiah ini membuktikan bahwa graf path, graf cycle, dan disjoint union pada graf cycle memiliki pelabelan super vertex magic serta fungsi bijektif dari himpunan sisi ke pada suatu graf dapat diperluas menjadi pelabelan super vertex magic. Terdapat empat teorema yang dibahas dalam karya ilmiah ini. Teorema pertama membuktikan bahwa suatu graf path adalah graf super vertex magic jika dan hanya jika ganjil dan . Teorema kedua membuktikan bahwa sebuah graf cycle adalah super vertex magic jika dan hanya jika ganjil. Teorema ketiga membuktikan bahwa fungsi bijektif dari himpunan sisi ke pada suatu graf dapat diperluas menjadi pelabelan super vertex magic jika dan hanya jika himpunan jumlah label sisi yang incident dengan suatu simpul pada graf tersebut terdiri dari bilangan bulat berurutan sebanyak simpul pada graf tersebut. Teorema keempat membuktikan bahwa gabungan tak terhubung (disjoint union) graf cycle yang terdiri dari m graf cycle dengan setiap graf memiliki n simpul adalah super vertex magic jika dan hanya jika dan keduanya ganjil.

Kata kunci: disjoint union, graf cycle, graf path, pelabelan super vertex magic, pelabelan total vertex magic.

(3)

ABSTRACT

RAHMALIA YULIARNI. Super Vertex Magic Labeling. Supervised by TEDUH WULANDARI MAS’OED and FARIDA HANUM.

Super vertex magic labeling is labeling on graph with is a set of edges mapped into and is a set of vertices mapped into . It has a vertex magic labeling in which and represents the size and order of the graph respectively. This manuscript proves that paths, cyclics, and disjoint union of cyclics have a super vertex magic labeling. There are four theorems to be discussed. The first theorem proves that path is super vertex magic if and only if is odd and . The second theorem proves that cyclic is super vertex magic if and only if is odd. The third theorem proves that bijection function from an edge set onto of graph can be extended to a super vertex magic labeling if and only if the set amount of edge label that incidents with a vertex in the graph, consists of sequential integers as many as vertices in the graph. The fourth theorem proves that disjoint union of the cyclics consists of cyclics with each cyclic has vertices is super vertex magic if and only if and are odd.

Keywords: cyclics, disjoint union, paths, super vertex magic labeling, total vertex magic labeling.

(4)

PELABELAN

SUPER VERTEX MAGIC

RAHMALIA YULIARNI

Skripsi

Sebagai salah satu syarat untuk memperoleh gelar

Sarjana Sains pada

Departemen Matematika

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM

INSTITUT PERTANIAN BOGOR

BOGOR

2013

(5)

Judul Skripsi : Pelabelan Super Vertex Magic

Nama : Rahmalia Yuliarni

NIM : G54080060

Menyetujui

Pembimbing I

Teduh Wulandari Mas’oed, M.Si. NIP. 19740915 199903 2 001

Pembimbing II

Dra. Farida Hanum, M.Si. NIP. 19651019 199103 2 002

Tanggal Lulus : ... Mengetahui

Ketua Departemen Matematika

Dr. Berlian Setiawaty, MS. NIP. 19650505 198903 2 004

(6)

PRAKATA

Puji syukur penulis panjatkan kepada Allah Subhanahu wa ta’ala atas nikmat dan karunia-Nya sehingga penulisan skripsi dengan judul “Pelabelan Super Vertex Magic” berhasil diselesaikan. Penyusunan skripsi ini tidak lepas dari bantuan berbagai pihak. Untuk itu penulis mengucapkan terima kasih kepada:

1 Keluarga tercinta : Bapak dan Ibuyang tiada hentimemberikan doa, motivasi, kasih sayang dan inspirasi dalam hidup, untuk kakakku, terima kasih atas doa dan dukungannya.

2 Ibu Teduh Wulandari Mas’oed, M.Si. selaku dosen pembimbing I dan Ibu Dra. Farida Hanum, M.Si. selaku dosen pembimbing II, terima kasih atas bimbingan, saran, dan ilmu yang diberikan,

3 Ibu Dra. Nur Aliatiningtyas, M.Si selaku dosen penguji, terima kasih atas ilmu dan sarannya,

4 semua dosen Departemen Matematika IPB, terima kasih atas semua ilmu yang telah diberikan,

5 staf Departemen Matematika: Bu Susi, Bu Ade, Pak Yono, Mas Deni, dan Mas Heri, terima kasih atas bantuannya selama ini,

6 sahabat-sahabat terbaikku : Janah, Yanti, Widya, Roby, Erlan, Antho, Dian, Dinis, Ita, Fika, Chichi, Arifah, Chanif, Chanchan, Ana, dan Rahmah yang selalu memberikan keceriaan dan motivasi, terima kasih atas persaudaraannya selama ini,

7 teman-teman matematika angkatan 45: Nova, Maya, Prama, Dimas, Pipin, dan teman-teman 45 lainnya, terima kasih atas kebersamaannya selama ini,

8 teman-teman angkatan 46 dan 47: Mput, Onya, Ami, Heni, Ivonne, Uwie, Meda, Puri, dan Putri, terima kasih atas bantuan dan motivasinya untuk segera menyelesaikan skripsi ini, 9 seluruh pihak yang tidak dapat disebutkan satu per satu.

Penulis menyadari bahwa tulisan ini masih jauh dari sempurna. Penulis sangat menghargai segala kritik dan saran yang membangun. Semoga skripsi ini bermanfaat bagi dunia ilmu pendidikan khususnya bidang matematika dan menjadi inspirasi bagi penelitian-penelitian selanjutnya.

Bogor, Juli 2013

(7)

RIWAYAT HIDUP

Rahmalia Yuliarni dilahirkan di Bekasi pada tanggal 10 Juli 1990. Penulis merupakan anak kedua dari pasangan Purwanto Gendroyono dan Endang Sedyarni.

Pada tahun 2002, penulis menyelesaikan pendidikan di SDN Jatimulya 09 Bekasi. Kemudian melanjutkan pendidikan di SLTPN 2 Bekasi. Pada tahun 2008, penulis menyelesaikan pendidikannya di SMAN 42 Jakarta dan berhasil menjadi mahasiswa Departemen Matematika, Fakultas Matematika dan Ilmu Pengetahuan Alam, Institut Pertanian Bogor melalui jalur USMI (Undangan Seleksi Masuk IPB).

Selama mengikuti kegiatan perkuliahan penulis pernah aktif dalam Badan Eksekutif Mahasiswa TPB periode 2008/2009 menjabat sebagai Sekretaris Umum dan Badan Eksekutif Mahasiswa FMIPA periode 2009/2010 sebagai Sekretaris Departemen Internal. Selain itu penulis juga aktif menjadi panitia di beberapa kegiatan mahasiswa antara lain Masa Perkenalan Kampus Mahasiswa Baru tahun 2009, Masa Perkenalan Fakultas tahun 2010, 2011, dan 2012, Masa Perkenalan Departemen 2010, Bina Desa FMIPA tahun 2011/2012, dan SPIRIT tahun 2011.

(8)

DAFTAR ISI

Halaman

DAFTAR GAMBAR ... viii

I. PENDAHULUAN ... 1

1.1 Latar Belakang ... 1

1.2 Tujuan ... 1

II. LANDASAN TEORI ... 2

2.1 Teori Graf ... 2

2.2 Pelabelan Graf ... 3

III. PEMBAHASAN ... 4

IV. SIMPULAN DAN SARAN 5.1 Simpulan ... 15

5.2 Saran ... 15

DAFTAR PUSTAKA ... 15

(9)

DAFTAR GAMBAR

Halaman

1 Graf ... 1

2 Graf taktrivial dengan 5 simpul ... 2

3 Graf cycle dengan 5 simpul ... 2

4 Graf tak terhubungkan (disconncted) ... 2

5 Graf ... 3

6 Graf cycle ber-order 3 ... 3

7 Pelabelan total vertex magic pada graf ... 4

8 Pelabelan super vertex magic pada graf ... 4

9 Graf path ber-order 5 ... 5

11 Graf cycle ber-order 7 ... 7

(10)

I PENDAHULUAN

1.1 Latar Belakang

Teori graf merupakan cabang ilmu dalam bidang matematika yang mempelajari himpunan simpul (vertex)yang dihubungkan dengan himpunan sisi (edge). Teori ini pertama kali diperkenalkan pada tahun 1736 oleh seorang matematikawan Swiss bernama Leonhard Euler. Ia menggunakan teori graf untuk menyelesaikan masalah jembatan Königsberg.

Teori graf terus berkembang hingga saat ini,pengaplikasiannya dapat dikaitkan dengan berbagai bidang dalam kehidupan sehari-hari seperti masalah penjadwalan, transportasi, ilmu komputer, riset operasi, dan lain sebagainya. Salah satu yang menjadi permasalahan dalam teori graf ialah bagaimana menandai suatu simpul dan sisi, sedemikian sehingga setiap simpuldan sisi memiliki tanda yang berbeda. Ada beberapa metode yang dapat digunakan, salah satunya adalah metode pelabelan.

Pelabelan pada suatu graf merupakan pemetaan injektif yang memetakan unsur himpunan simpul (vertex)dan unsur himpunan sisi (edge)ke bilangan asli yang disebut label (Gallian 2009). Terdapat beberapa jenis pelabelan graf yang dikenal hingga saat ini, antara lain pelabelan graceful, pelabelan harmoni, pelabelan total tak

beraturan (irregular total), pelabelan ajaib (magic), danpelabelan antiajaib (antimagic). Dari bentukpelabelan ajaib (magic), ada yang disebut pelabelan vertex magic, pelabelan super vertex magic, pelabelan total edge magic ataupun pelabelan super edge magic.

Pada karya ilmiah sebelumnya, Sari (2012) telah membahas tentang pelabelansuper edge magic pada graf cycle dan graf wheel. Oleh karena itu, penulis tertarik untuk melengkapi kajian mengenai pelabelan ajaib (magic), dengan pembahasan mengenai pelabelan super vertex magic. Dalam karya ilmiah ini akan dibuktikan bahwa beberapa graf sederhana yaitu graf path, graf cycle, dan disjoint union darigraf cycle memiliki pelabelan yang super vertex magic. Sumber utama karya ilmiah ini ialah artikel yang ditulis Swaminathan & Jeyanthi pada tahun 2003.

1.2 Tujuan

Tujuan dari karya ilmiah ini ialah: 1. membuktikan bahwa graf path, grafcycle,

dan disjoint union dari graf cycle memiliki pelabelan super vertex magic. 2. membuktikan bahwa fungsi bijektif dari

himpunan sisike pada suatu graf dapat diperluas menjadi pelabelan super vertex magic.

II LANDASAN TEORI

Pada bab ini akan dijelaskan beberapa definisi dalam teori graf dan pelabelan graf yang akan digunakan dalam pembahasan pada bab-bab selanjutnya.

2.1 Teori Graf Definisi 1 (Graf)

Suatu graf adalah pasangan terurut

dengan adalah himpunan takkosong

dan berhingga dan adalah himpunan pasangan tak terurut yang menghubungkan elemen-elemen Graf dinotasikan

Elemen disebut simpul (vertex,

node) sedangkan elemen disebut sisi (edge). Himpunan dari simpul-simpul pada graf dinotasikan dengan sedangkan himpunan dari sisi-sisi pada graf dinotasikan dengan .

(Foulds 1992)

Misalkan dan merupakan simpul-simpul suatu graf maka sisi (edge) dari graf tersebut ialah . Sebagai contoh, graf pada Gambar 1 mempunyai } : Gambar 1 Graf .

(11)

Definisi 2 (Graf Taktrivial)

Suatu graf disebut graf taktrivialjika suatu graf memiliki simpulpaling sedikit dua.

(Chartrand & Oellermann 1993) Berikut ini contoh graf taktrivialdengan 5 simpul.

Gambar 2 Graf taktrivial dengan 5 simpul.

Definisi 3 (Order dan Size)

Misalkan diberikan graf Banyaknya simpul (vertex) pada graf disebut order dan banyaknya sisi (edge)disebut size.Order pada graf dinotasikan dengan | | dan size pada graf dinotasikan dengan | |.

(Chartrand & Oellermann 1993) Graf pada Gambar 1 memiliki order| |

dan size| | .

Definisi 4 (Incident dan Adjacent)

Misalkan diberikan graf . Jika

dengan maka

dan dikatakan adjacent di dan

dikatakan incident dengan (dan ).

(Chartrand & Oellermann 1993) Pada Gambar 1, sisi maka dan dikatakan adjacent di dan dikatakan incident dengan dan .

Definisi 5 (Walk)

Suatu walk pada graf adalah suatu barisan simpul dan sisi dari graf dengan bentuk: { } dan dapat dituliskan sebagai

{ atau . Suatu walk

yang menghubungkan dengan dikatakan tertutup (closed walk) jika . Jika maka walk tersebut dikatakan terbuka.

(Foulds 1992) Berdasarkan Gambar 1, terdapat walk terbuka yaitu walk .

Definisi 6 (Path)

Path pada suatu graf adalah walk dengan setiap simpulnya berbeda. Graf ber-

order yang berbentuk path disebut graf path ber-order , dituliskan sebagai .

(Chartrand & Oellermann 1993)

Pada Gambar 1,

merupakan salah satu contoh path.

Definisi 7 (Cycle)

Cycle pada suatu graf adalah walk tertutup yang mengandung setidaknya tiga simpul dan semua simpulnya berbeda.

(Foulds 1992) Graf ber-order yang berbentuk disebut , dan dituliskan sebagai .

(Chartrand & Oellermann 1993) Contoh graf cycle dengan 5 simpul diberikan pada Gambar 3.

Gambar 3 Graf cycle dengan 5 simpul.

Definisi 8 (Graf Terhubungkan)

Misalkan dan merupakan simpul padagraf . Simpul dikatakan dihubungkan dengan jika mempunyai path .Suatu graf dikatakan terhubungkan(connected) jika untuk setiap pasangan simpul u dan vdi , maka dihubungkan dengan dan dikatakan tak terhubungkan (disconnected) jika terdapat pasangan simpul dan di , sehingga tidak ada path .

(Chartrand & Oellermann 1993) Berikut ini diberikan contoh graf tak terhubung(disconnected).

Gambar 4 Graf tak terhubung (disconnected).

(12)

Definisi 9 (Union dari Dua Graf)

Misalkan dan adalah graf dengan himpunan simpul yang disjoint, maka union dari dan dituliskan , adalah graf yang memiliki dan .

(Chartrand & Oellermann 1993)

Definisi 10 (Disjoint Uniondari Graf Cycle)

Disjoint uniondari graf cycleadalah gabungan tak terhubung graf cycle sebanyak m dengan setiap graf memiliki n simpul, dituliskan Graf memiliki himpunan

simpul dan himpunan sisi dengan himpunan simpul setiap graf dapat dituliskan

dengan merupakan

simpul ke-j pada graf cycleke-i dan himpunan sisi setiap graf dapat dituliskan

dengan merupakan sisi

ke-j pada graf cycle ke-i dan untuk .

(Swaminathan & Jeyanthi 2003) Berikut ini diberikan contoh disjoint uniondari graf cycle. Diberikan 3 graf cycle tak terhubung dengan setiap graf memiliki 3 simpul, dituliskan maka

dan dengan himpunan setiap simpul dan sisi pada graf cycle ke-i dapat ditulis } dan } dengan seperti pada Gambar 5.

Gambar 5 Graf . 2.2 Pelabelan Graf

Untuk memahami masalah pelabelan graf super vertex magic diperlukan pengertian dan konsep dasar mengenai pelabelan sebagai berikut.

Misalkan himpunan dari simpul-simpul yang adjacent dengan simpul pada graf dilambangkan dengan dan adalah himpunan bilangan asli.

Definisi 11 (Pelabelan Total Vertex Magic)

Misalkan graf dengan simpul dan sisi. Suatu pemetaan satu-satu dari ke himpunan bilangan bulat disebut pelabelan totalvertex magic jika terdapat sebuah konstanta untuk setiap simpul u sehingga ∑

dengan merupakan simpul-simpul yang adjacent dengan simpul .

(Swaminathan & Jeyanthi 2003) Berikut ini diberikan contoh pelabelan totalvertex magic. Misalkan diberikan graf cycle dengan 3 simpul dan 3 sisi seperti Gambar 6 dan .

Gambar 6 Graf cycle ber-order 3. Misalkan sisi-sisi pada graf dipadankan

dengan suatu nilai, yaitu

Label suatu simpul dapat diperoleh dari pengurangan nilai magic dengan jumlah semua label sisi yang incident dengan simpul tersebut.

Pada kasus ini dipilih nilai magic maka diperoleh label simpul sebagai berikut. ( ) ( ) ( )

(13)

maka dengan sehingga

dan dapat digambarkan seperti Gambar 7 (a). Sedangkan untuk nilai magic dan misalkan sisi-sisinya dipadankan dengan suatu nilai, yaitu sehingga diperoleh

dan digambarkan seperti Gambar 7 (b). (a)

(b)

Gambar 7Pelabelan totalvertex magic pada graf

Definisi 12 (Pelabelan dari Graf Super Vertex Magic)

Sebuah pelabelan total vertex magicf disebut pelabelan super vertex magic jika

dan

. Sebuah graf disebut super

vertex magic jika terdapat pelabelan super vertex magic pada .

(Swaminathan & Jeyanthi 2003) Berikut ini diberikan contoh pelabelan supervertex magic. Diberikan graf seperti

pada Gambar 6dan

Misalkan sisi-sisi pada graf

dipadankan dengan suatu nilai, yaitu

.

Dipilih nilai magick = 9, maka diperoleh label simpul, sehingga

dan dapat digambarkan sebagai berikut.

Gambar 8Pelabelan super vertex magic pada graf .

III PEMBAHASAN Karya ilmiah ini membahas lema dan

teorema-teorema yang akan membuktikan bahwa graf path, graf cycle, dan disjoint union graf cycle memiliki pelabelan super vertex magic.

Misalkan diberikan graf seperti pada Gambar 6. Banyaknya simpul dan sisi ialah 3,sehingga nilai magic dapat diperoleh dengan cara berikut.

.

Berikut ini diberikan lema yang akan digunakan untuk mencari nilai magic k yang juga akan digunakan untuk membuktikan teorema-teorema selanjutnya.

Lema 1

Jika adalah graf taktrivialyang super vertex magic, maka nilai magic diberikan oleh

(Swaminathan & Jeyanthi 2003)

Bukti :

Misalkan graf taktrival yang super vertex magicdengan simpul dan sisi. Akan dibuktikan bahwa memiliki nilai magic .

Karena graf super vertex magic maka terdapat konstanta sehingga untuk setiap simpul u di graf berlaku

(14)

∑ dengan merupakan simpul-simpul yang adjacent dengan simpul dan , .

Misalkan ( ) merupakan pelabelan

dari sisi yang menghubungkan simpul dengan simpul , dengan dan

( ) ( ) . Karena

graf taktrivialmaka memiliki |V| sehingga dapat dirumuskan sebagai berikut.

. . . . . . . . .

Dengan menjumlahkan semua kolom secara vertikal maka akan diperoleh rumusan sebagai berikut

[ ] [ ] [ ] [ ] [ ] [ ] ∑ [ ] ∑ [ ] ∑ ∑ (2.1a) Akibatnya ∑ dan ∑ [ ] ( ) (2.1c)

Dengan menyubstitusikan Persamaan (2.1b) dan (2.1c) ke dalam Persamaan (2.1a) maka akan diperoleh bilanganmagic sebagai berikut.

∑ ∑ (2.1b)

(15)

Terbukti Berikut ini diberikan contoh cara

pelabelan super vertex magic pada graf path sebelum dibuktikan Teorema 1.

Misalkan diberikan graf path yang memiliki 4 sisi dan 5 simpul seperti pada Gambar 9.

Gambar 9 Graf path ber-order 5. Berdasarkan Lema 1 maka akan diperoleh nilai magic untuk graf sebagai berikut.

Graf tersebut dilabeli ( )

( ) Didefinisikan: { , dengan

sehingga untuk graf diperoleh label sisi dan simpul sebagai berikut.

Akibatnya

dan pelabelannya dapat digambarkan sebagai berikut.

Gambar 10Pelabelan super vertex magic pada graf .

Cara pelabelan tersebut merupakan salah satu contoh cara pelabelan super vertex magic pada suatu graf path. Cara ini juga digunakan untuk membuktikan Teorema 1.

Berikut akan dibuktikan Teorema 1 yang menyatakan bahwa graf path memiliki pelabelan super vertex magic.

Teorema 1

Sebuah path adalah grafsuper vertex magic jika dan hanya jika ganjil dan .

Bukti:

Misalkan path adalah super vertex magic. Akan dibuktikan merupakan bilangan ganjil dan .

Karena path adalah grafsuper vertex magic maka dari Lema 1 terdapat bilangan magic sebagai berikut.

dengan dan . Graf adalah grafpathdengan n simpul maka memiliki | | | |

dengan | | sehingga pelabelannya dapat ditulis ,

Akibatnya diperoleh nilai magic k sebagai berikut. [ ]

Diketahui k dan n bilangan bulat maka 2k bilangan genap, sehingga genap. Akibatnya ganjil, sehingga n ganjil.

Misalkan adalah bilangan ganjil, untuk setiap bilangan bulat. Akan dibuktikan bahwa .

Karena adalah graf yang taktrivial, artinya , sehingga diperoleh

Karena bilangan bulat maka pilihan terkecil adalah , sehingga

(16)

Akibatnya .

Terbukti Misalkan adalah bilangan ganjil

dengan . Akan dibuktikan path adalahsuper vertex magic.

Misalkan Diberikan graf . Didefinisikan : ( ) ( ) { , dengan Untuk

Ambil sembarang dengan dan i ganjil, maka

∑ ( ) ( )

Dengan perhitungan yang sama, maka akan diperoleh hasil yang sama juga untuk i genap. Untuk ∑ ( )

Karenan ganjil maka juga ganjil, sehingga genap. Akibatnya bilangan genap, maka bilangan bulat. Jadi, fadalah pelabelan super vertex magic

dengan bilangan magic

Terbukti

Berikut ini diberikan contoh cara pelabelan super vertex magic pada graf cycle sebelum dibuktikanTeorema 2.

Misalkan diberikan graf cycle ber-order 7 seperti Gambar 11.

Gambar 11Graf cycle ber-order 7. Berdasarkan Lema 1 maka akan diperoleh nilai magic untuk graf sebagai berikut.

Graf tersebut dilabeli ( )

( ) Didefinisikan: , dengan { C C C C C C C

(17)

sehingga untuk graf diperoleh lebel sisi dan simpulnya sebagai berikut.

Akibatnya

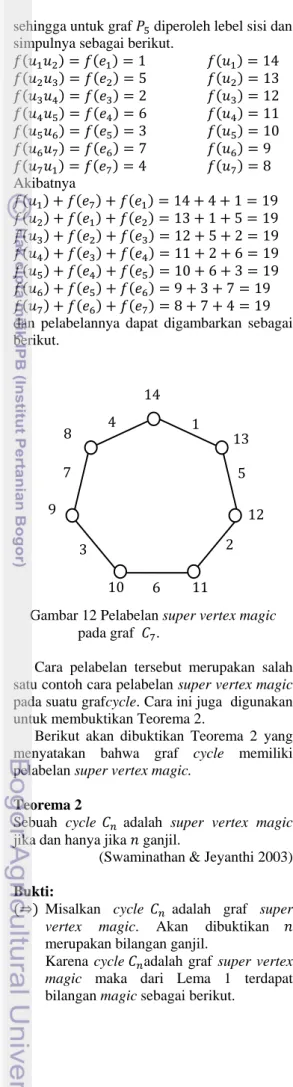
Gambar 12 Pelabelan super vertex magic pada graf .

Cara pelabelan tersebut merupakan salah satu contoh cara pelabelan super vertex magic pada suatu grafcycle. Cara ini juga digunakan untuk membuktikan Teorema 2.

Berikut akan dibuktikan Teorema 2 yang menyatakan bahwa graf cycle memiliki pelabelan super vertex magic.

Teorema 2

Sebuah cycle adalah super vertex magic jika dan hanya jika ganjil.

Bukti:

Misalkan cycle adalah graf super vertex magic. Akan dibuktikan merupakan bilangan ganjil.

Karena cycle adalah graf super vertex magic maka dari Lema 1 terdapat bilangan magic sebagai berikut.

dengan dan .

Graf adalah grafcycledengan n simpul maka memiliki | | | |

, sehingga pelabelannyadapat ditulis

Akibatnya diperoleh

nilai bilangan magic k sebagai berikut.

Diketahui k dan n bilangan bulat maka 2k bilangan genap, sehingga

harus genap. Akibatnya ganjil, sehingga n ganjil.

Terbukti Misalkan adalah bilangan ganjil. Akan dibuktikan cycle adalah graf super vertex magic.

Misalkan adalah bilangan ganjil. Diberikan graf cycle . Didefinisikan ( ) ( ) , dengan { Untuk

Ambil sembarang dengan

dan i ganjil maka

∑ ( ) C C C C C C C

(18)

Dengan perhitungan aljabar yang sama, akan diperoleh hasil yang sama juga untuk i genap. Untuk ∑ ( )

Karenan ganjil maka juga ganjil, sehingga genap. Akibatnya bilangan genap, maka bilangan bulat. Jadi, fadalah pelabelan super vertex magic dengan bilangan magic .

Terbukti Sebelum membuktikan Teorema 3, berikut ini akan diberikan suatu ilustrasi. Misalkan diberikan sebuah graf seperti Gambar 9 dengan dan Dimisalkan juga merupakan fungsi bijektif dari ke

pada graf Didefinisikan:

maka fungsi dapat diperluas menjadi { sehingga

Akibatnya merupakan pelabelan super vertex magic dengan nilai magic

Berikut ini diberikan Teorema 3 yang akan membuktikan bahwa fungsi bijektif dari himpunan sisike pada suatu graf dapat diperluas menjadi pelabelan super vertex magic.

Teorema 3

Misalkan sebuah graf dan fungsibijektif dari ke Kemudian dapat diperluas menjadi pelabelan super vertex magic untuk G jika dan hanya jika{ ∑ | } terdiri dari | |bilangan bulat berurutan.

Bukti:

Misalkan adalah grafyang super vertexmagic. Akan dibuktikan{ ∑ | } terdiri dari | |bilangan bulat berurutan.

Misalkan memiliki simpul dan sisi. Karena graf super vertex magic maka terdapat konstanta untuk setiap simpul sehingga ∑ ,dengan v merupakan simpul-simpul yangadjacent dengan simpul u. Dimisalkan juga merupakan pelabelan sisi dari simpulvyang adjacent dengan simpul u.Didefinisikan w(u)sebagai jumlah dari label sisiyang incidentdengan simpul u. Akibatnya

∑ |

Karena juga merupakan pelabelan sisi dari simpulvyang adjacent dengan simpulumaka

∑ ∑

sehingga dapat dituliskan

∑ | .

(19)

∑ Didefinisikan dengan . . . . . . . . .

maka akan diperoleh sebagai berikut . . . . . . . . .

Karena merupakan pengurang bagi maka semakin besar nilai akan semakin kecil nilai akibatnya Dimisalkan | sehingga dengan merupakan himpunan bulat dengan nilai terkecil dan perbedaan antara dua nilai yang berurutanialah 1 dan maksimum . Jadi, himpunan adalah bilangan bulat teratur sejumlah | |.

Terbukti Misalkan { ∑ |

} terdiri dari | | bilangan bulat berurutan. Akan dibuktikan merupakan graf super vertexmagic. Misalkan merupakan himpunan bilangan bulat berurutan dengan

| . Didefinisikan dengan dan

Akan dibuktikan pelabelan super vertex magicdengan .

Ambil sebarang

dengansimpulvyang

adjacentdengansimpulu. Pilih ,akan diperoleh nilai sebagai berikut. . . . . . . . . . dengan | |, sehingga ∑

Karena dan merupakan pelabelan dari simpulvyang adjacent dengan simpulu, maka ∑ . Akibatnya merupakan graf super vertexmagic dengan

∑ .

Terbukti Sebelum membuktikan Teorema 4 akan diperlihatkan ilustrasi pelabelan super vertex magic pada gabungan tak terhubung (disjoint union) graf cycle.

Misalkan diberikan sebuah graf seperti pada Gambar 5. Banyaknya graf cycle ialah 3, dengan banyaknya sisi dan simpul setiap graf adalah 3, maka berdasarkan Lema 1 akan diperoleh nilai magic untuk graf

sebagai berikut.

Graf tersebut dilabeli ( ( ))

( ( ))

Didefinisikan:

(20)

 Untuk ( ) { {  Untuk ( ) { {

sehingga diperoleh label sisi dan simpulnya sebagai berikut. 1 Akibatnya

 Untuk graf ke-1

 Untuk graf ke-2

 Untuk graf ke-3

Gambar 13 Pelabelan super vertex magic pada graf .

Cara pelabelan tersebut merupakan salah satu contoh cara pelabelan super vertex magic pada suatu graf . Cara ini juga digunakan

untuk membuktikan Teorema 4.

Berikut ini diberikan Teorema 4 yang akan membuktikan bahwa graf memiliki

pelabelan super vertex magic.

Teorema 4

adalah super vertex magic jika dan hanya

jika dan keduanya ganjil.

Bukti:

Misalkan adalah graf super vertex

magic. Akan dibuktikan

memiliki ganjil.

Karena adalah graf super vertex

magic maka dari Lema 1 terdapat nilaimagic sebagai berikut.

dengan dan . Karena adalah cycle sebanyak

(21)

dengan dan Akibatnya diperoleh nilai bilangan magic k .

Karena k adalah bilangan bulat maka 2k bilangan genap, sehingga harus genap. Akibatnya ganjil, maka m dan n ganjil.

Terbukti Misalkan adalah bilangan bulat ganjil. Akan dibuktikan graf adalah

graf super vertex magic.

Misalkan dan adalah bilangan bulat ganjil. Diberikan

graf cycle . Diasumsikan bahwa graf mempunyai simpul yang

merupakan gabungan dari himpunan simpulpada graf cycle pertama hingga graf cycle ke-m dan dapat dituliskan sebagai dengan setiap himpunan simpulpada setiap graf dapat dituliskan sebagai

dengan merupakan

simpulke-j pada graf cycle ke-i dan mempunyai sisi yang merupakan gabungan dari himpunan sisipada graf cycle pertama hingga graf cycle ke-m dan dapat dituliskan sebagai

dengan setiap himpunan

sisipada setiap graf dapat dituliskan sebagai dengan merupakan sisi ke-j pada graf cycle ke-i dan dengan

Didefinisikan untuk dan Untuk ( ) { { Untuk ( ) { {

Ambil sembarang pada graf cycle ke-i dengan danj bilangan ganjil, maka Untuk

(22)

( ) ( ) ( ) ( ₎ [ ] [ ] [ ] [ ] [ ] [ ]  Untuk ( ) ( ) ( ) [ ] [ ] [ ]  untuk ( ) ( ) ( ) ( _{) (} _{) (} ₎ [ ] [ ] [ ] [ ] [ ] * +

(23)

Ambil sembarang pada graf cycle ke-i dengan danj bilangan ganjil, maka Untuk ( ) ( ) ( ) ( ) [ ] [ ] [ ] Untuk ( ) ( ) ( ) [ ] [ ] [ ] [ ] [ ] [ ] Untuk ( ) ( ) ( ) ( _{) (} _{) (} ₎

(24)

[ ] [ ] [ ] [ ] [ ] [ ]

Karena dan m ganjil maka juga ganjil, sehingga genap. Akibatnya bilangan bulat, maka bilangan bulat. Jadi, f adalah pelabelan

super vertex magic dengan bilangan magic .

Terbukti

IV SIMPULAN DAN SARAN

4.1 Simpulan

Dalam karya ilmiah ini dibuktikan bahwa graf path, graf cycle, dan disjoint union graf cycle memiliki pelabelan graf yang super vertex magic. Graf path dan graf cycle yang memiliki n simpul merupakan graf super vertex magic jika dan hanya jika n merupakan bilangan ganjil. Selain itu, gabungan tak terhubung (disjoint union) graf cycleyang terdiri dari graf cyclesebanyak m dengan setiap graf memilikin simpulatau graf

juga merupakan graf super vertex magic jika dan hanya jika m dan n merupakanbilangan ganjil.

Dalam karya ilmiah ini juga ditunjukkan bahwa fungsi bijektif dari himpunan sisi ke

pada suatu graf dapat diperluas menjadi pelabelan super vertex magic jika dan hanya jika himpunan jumlah label sisi yang incident dengan suatu simpul pada graf tersebut terdiri dari bilangan bulat terurut sebanyak simpul pada graf tersebut.

4.2 Saran

Dalam karya ilmiah ini telah dibahas pelabelan super vertex magic yang difokuskan pada graf cycle, graf path,dan disjoint uniondarigraf cycle.Bagi yang berminat membuat karya ilmiah yang berhubungan dengan pelabelan super vertex magic dapat mencari pada graf reguler, graf star, graf circulantatau pada graf lainnya.

DAFTAR PUSTAKA

Chartrand G, Oellermann OR. 1993. Applied and Algorithmic Graph Theory. New York: McGraw-Hill.

Foulds LR. 1992. Graph Theory Applications. New York: Spinger-Verlag.

Gallian JA. 2009. A dynamic survey of graph labeling. The Electronic Journal of Combinatorics 16:7-65.

Swaminathan V, Jeyanthi P. 2003. Super vertex magic labeling. Indian J. Pure Appl. Math. 34(6):935-939.

Sari NNI. 2012. Pelabelan super edge magic pada graf cycle dan graf wheel [skripsi]. Bogor: Fakultas Matematika dan Ilmu Pengetahuan Alam, Institut Pertanian Bogor.

(25)