OPTIMASI TANAMAN PANGAN DI KOTA MAGELANG DENGAN PEMROGRAMAN KUADRATIK DAN
METODE FUNGSI PENALTI EKSTERIOR
SKRIPSI
Diajukan kepada Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Negeri Yogyakarta
untuk Memenuhi Sebagian Persyaratan guna Memperoleh Gelar Sarjana Sains
Oleh : Sativa Nurin Insani NIM. 13305141006
PROGRAM STUDI MATEMATIKA JURUSAN PENDIDIKAN MATEMATIKA
MOTTO
Kepuasan terbesar dalam hidup adalah berhasil melakukan sesuatu yang orang lain kira Anda tak mampu melakukannya
-Walter Bagehot-
Syukuri apa yang ada, hidup adalah anugerah. Tetap menjalani hidup dan lakukan yang terbaik
-Rian Ekky Pradipta- MAN SHABARA ZHAFIRA. Siapa yang bersabar pasti beruntung
PERSEMBAHAN
Karya ini saya persembahkan untuk
ayah dan ibu saya, Bambang Isiantono dan Endang Pudji Hastuti
Kalau bukan karena mereka, saya tidak akan bisa mencapai titik
ini.
Novera Rahmi Annisa,
Dialah motivasi saya untuk terus berusaha menjadi contoh yang
baik.
Ani Budiati, Sigit Edhi Nugroho, Dwi Agus Nurswantoro, Akbar Farid,
Bahagia bisa mengenal dan menyebut kalian “SAHABAT”.
Hanif Sri Yulianto
Terima kasih sudah menjadi alasanku untuk tersenyum dan
membuat hidupku jadi nano-nano.
Orang-orang yang pernah datang dan pergi di kehidupanku
Terima kasih sudah membuatku mengerti rasanya disakiti dan
OPTIMASI TANAMAN PANGAN DI KOTA MAGELANG DENGAN PEMROGRAMAN KUADRATIK DAN
METODE FUNGSI PENALTI EKSTERIOR
Oleh :
Sativa Nurin Insani NIM. 13305141006
ABSTRAK
Optimasi merupakan suatu cara untuk menemukan hasil yang terbaik, yaitu dengan meminimumkan atau memaksimalkan suatu fungsi tujuan dengan tetap memperhatikan batasan yang ada. Selain bidang industri, transportasi, dan perencanaan keuangan, optimasi juga dapat diterapkan dalam bidang pertanian. Salah satu contohnya yaitu optimasi rata-rata produksi tanaman pangan. Tujuan dari penelitian ini adalah membentuk model matematika untuk mengoptimalkan rata-rata produksi tanaman pangan di kota Magelang serta menyelesaikan model dengan pemrograman kuadratik dan metode fungsi penalti eksterior (metode
penalty).
Model matematika dalam penelitian ini merupakan model nonlinear yang dibentuk menggunakan metode kuadrat terkecil. Fungsi tujuan dari model tersebut adalah memaksimalkan rata-rata produksi tanaman pangan di kota Magelang yang dalam penelitian ini dipilih tiga jenis, yaitu padi, ketela pohon, dan jagung. Pemrograman kuadratik menyelesaikan masalah nonlinear dengan mengubahnya menjadi masalah linear menggunakan syarat Kuhn Tucker, selanjutnya masalah linear tersebut diselesaikan menggunakan simpleks metode wolfe. Sedangkan metode fungsi penalti eksterior (metode penalty) menyelesaikan masalah nonlinear berkendala menjadi masalah nonlinear tak berkendala. Solusi diperoleh berdasarkan syarat perlu dan cukup keoptimalan masalah tak berkendala.
Berdasarkan perhitungan, diperoleh hasil optimal yang sama baik dari pemrograman kuadratik maupun metode fungsi penalti eksterior untuk rata-rata produksi tanaman pangan padi, ketela pohon, dan jagung di kota Magelang, yaitu 387,0586 kwintal dengan luas panen padi 520,75 hektar, luas panen ketela pohon 33,6426 hektar, dan luas panen jagung 8,4817 hektar.
KATA PENGANTAR
Puji syukur penulis panjatkan kehadirat Allah SWT, yang telah melimpahkan segala rahmat, karunia dan hidayah-Nya sehingga penulis dapat menyelesaikan skripsi yang berjudul “Optimasi Tanaman Pangan di Kota Magelang Dengan Pemrograman Kuadratik dan Metode Fungsi Penalti Eksterior”. Skripsi ini disusun untuk memenuhi sebagian persyaratan memperoleh gelar Sarjana Sains Program Studi Matematika di Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Negeri Yogyakarta.
Penyusunan skripsi ini dapat berhasil dengan baik dan lancar berkat bantuan dari berbagai pihak. Oleh karena itu dalam kesempatan ini penulis mengucapkan terima kasih kepada :
1. Bapak Dr. Hartono selaku Dekan Fakultas Matematika dan Ilmu Pengetahuan Alam atas izin yang diberikan untuk melakukan penelitian.
2. Bapak Dr. Ali Mahmudi selaku Ketua Jurusan Pendidikan Matematika atas izin kepada penulis untuk menyusun skripsi dan memberikan kelancaran pelayanan dalam urusan akademik.
3. Bapak Dr.Agus Maman Abadi selaku Ketua Prodi Matematika dan Penasehat Akademik yang telah memberikan motivasi dan kelancaran pelayanan dalam urusan akademik.
4. Ibu Eminugroho Ratna Sari, M.Sc. selaku dosen pembimbing yang telah meluangkan waktunya untuk memberikan bimbingan, motivasi, bantuan dan arahan dengan sabar dalam penyusunan skripsi ini.
5. Bapak Ibu dosen Jurusan Pendidikan Matematika FMIPA UNY yang telah mengajarkan ilmunya selama perkuliahan.
6. Teman teman Matematika B 2013 yang selalu menemani dan memberi semangat serta bantuan demi kelancaran penyusunan skripsi ini.
DAFTAR ISI
HALAMAN JUDUL ... i
PERSETUJUAN ... ii
PENGESAHAN ... iii
PERNYATAAN ... iv
MOTTO ... v
PERSEMBAHAN ... vi
ABSTRAK ... vii
KATA PENGANTAR ... viii
DAFTAR ISI ... x
DAFTAR TABEL ... xii
DAFTAR GAMBAR ... xiii
DAFTAR LAMPIRAN ... xiv
DAFTAR SIMBOL ... xv
BAB I PENDAHULUAN ... 1
A. LATAR BELAKANG ... 1
B. RUMUSAN MASALAH ... 5
C. TUJUAN PENELITIAN ... 6
D. MANFAAT PENELITIAN ... 6
BAB II KAJIAN PUSTAKA ... 8
A. Optimasi ... 8
B. Fungsi ... 8
1. Fungsi Konveks dan Konkaf ... 10
2. Fungsi Kontinu ... 11
C. Turunan ... 11
D. Matriks Hessian ... 13
E. Matriks Definit Positif dan Definit Negatif ... 14
F. Titik Kritis ... 15
H. Metode Simpleks ... 21
I. Teorema Dualitas ... 24
J. Pemrograman Nonlinear ... 31
K. Persyaratan Karush Kuhn Tucker ... 34
L. Pemrograman Kuadratik ... 36
M. Metode Fungsi Penalti ... 39
BAB III PEMBAHASAN ... 44
A. Pembentukan Fungsi Tujuan dengan Metode Kuadrat Terkecil ... 44
B. Penyelesaian Masalah Nonlinear ... 47
1. Pemrograman Kuadratik dengan Metode Wolfe ... 47
2. Metode Fungsi Penalti Eksterior (Metode Penalty) ... 53
C. Penerapan Model Nonlinear pada Rata-Rata Produksi Tanaman Pangan di Kota Magelang ... 55
1. Pembentukan Model ... 56
2. Penyelesaian dengan Pemrograman Kuadratik Metode Wolfe ... 66
3. Penyelesaian dengan Metode Fungsi Penalti Eksterior (Metode Penalty) 71 4. Analisa Hasil Penyelesaian dengan Pemrograman Kuadratik dan Metode Penalty ... 75
BAB IV PENUTUP ... 77
A. Kesimpulan ... 77
B. Saran ... 79
DAFTAR PUSTAKA ... 81
DAFTAR TABEL
Tabel 2. 1 Bentuk tabel simpleks ... 23
Tabel 2. 2 Contoh tabel dualitas ... 29
Tabel 3. 1 Tabel simpleks dengan metode wolfe ... 51
Tabel 3. 2 Iterasi pertama metode wolfe ... 52
Tabel 3. 3 Tabel optimum metode wolfe ... 52
Tabel 3. 4 Data Luas Tanam, Luas Panen, dan Rata-rata Produksi Padi, Ketela Pohon dan Jagung tahun 1994-2014 ... 57
Tabel 3. 5 Hasil Perhitungan Selisih Nilai dan Errornya ... 64
Tabel 3. 6 Tabel Nilai Conditional Number Padi, Ketela Pohon, dan Jagung ... 65
DAFTAR GAMBAR
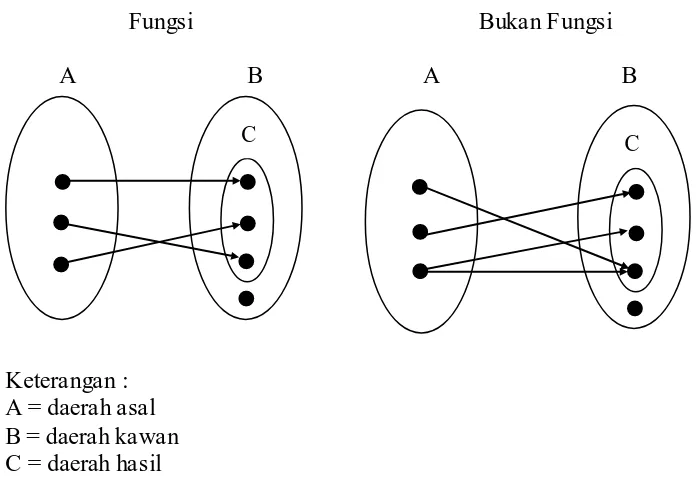
Gambar 2. 1 Ilustrasi Fungsi dan Bukan Fungsi ... 9
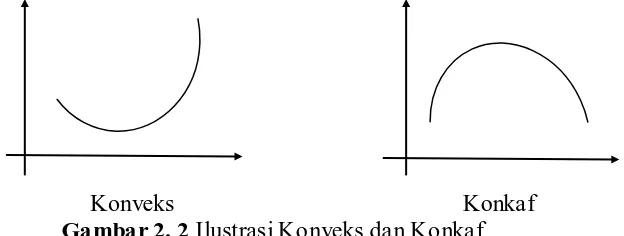
Gambar 2. 2 Ilustrasi konveks dan konkaf ... 10
Gambar 3. 1 Bagan Langkah Penyelesian Pemrograman Kuadratik Metode Wolfe ... 53
Gambar 3. 2 Bagan Langkah Penyelesaian Metode Penalty ... 54
Gambar 3. 3 Alur Pembentukan Model dan Penyelesaian Model Non Linear ... 55
Gambar 3. 4 Tampilan Output MKTX pada Command Window ... 60
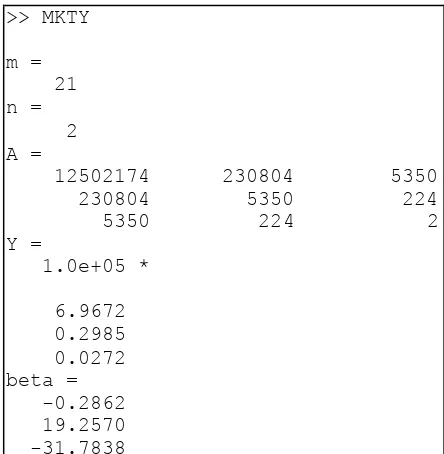
Gambar 3. 5 Tampilan Output MKTY pada Command Window ... 61
Gambar 3. 6 Tampilan Output MKTZ pada Command Window... 62
DAFTAR LAMPIRAN
Lampiran 1 Input Data dan Script untuk Membentuk Fungsi Tujuan ... 84
Lampiran 2 Iterasi Simpleks Metode Wolfe pada Pemrograman Kuadratik ... 87
Lampiran 3 Script dan Output untuk Mencari Conditional Number... 88
DAFTAR SIMBOL
: parameter fungsi tujuan
� : sisa (galat)
� : jumlah kuadrat sisa
: pengali pada kondisi Kuhn Tucker untuk kendala ke-i
� : variabel slack untuk kondisi Kuhn Tucker ke-i
� ′ : variabel slack untuk kondisi Kuhn Tucker kendala ke-i
� : variabel buatan untuk kondisi Kuhn Tucker ke-i : fungsi tujuan linear pada pemrograman kuadratik � : fungsi kendala pertidaksamaan ke-m
: fungsi penalti
� : fungsi tambahan/ fungsi masalah tak berkendala pada metode penalty
: parameter penalti
BAB I PENDAHULUAN
A. LATAR BELAKANG
Operations Research (Riset Operasi) merupakan suatu bagian dari ilmu
pengetahuan yang mulai berkembang pada tahun 1945, yaitu pada saat Perang Dunia II (Siswanto, 2007 : 3). Selama Perang Dunia II para ilmuwan serta militer Inggris dan Amerika bahu- membahu mengupayakan optimum-alokasi bahan-bahan logistik yang jumlahnya terbatas untuk perang sehingga dapat memenuhi kebutuhan pasukan sekutu daratan Eropa. Mereka yang terdiri dari ahli berbagai disiplin ilmu (teknik, matematika, sosiologi, psikologi, dan ahli perilaku atau
behavioral scientist) merupakan pionir yang memprakarsai penggunaan Riset
Operasi sebagai alat bantu dalam proses pengambilan keputusan yang berkaitan dengan Perang Dunia II (Suyadi, 2005 : 3).
Menurut BPS Provinsi Jawa Tengah (2013) peran sektor pertanian dalam pertumbuhan ekonomi masih sangat besar, yaitu menjadi salah satu sektor penopang utama. Tantangan yang sangat berat dalam pertumbuhan sektor pertanian diantaranya meningkatnya permintaan terhadap produksi pertanian khususnya kebutuhan bahan pangan. Hal ini merupakan dampak dari pertumbuhan penduduk yang relatif tinggi setiap tahunnya. Kebutuhan bahan pangan masyarakat Indonesia sebagian besar bertumpu pada komoditas beras, dan sebagian kecil mengkonsumsi palawija seperti jagung dan ubi. Dengan demikian produk utama padi dan palawija menjadi pemasok utama dalam pemenuhan kebutuhan pangan nasional.
Melihat produksi tanaman pangan di kota Magelang yang mengalami penurunan, maka perlu dianalisis optimasi tanaman pangan di kota Magelang agar dapat dijadikan acuan untuk meningkatkan produksi tanaman pangan di kota Magelang. Hasil optimal yang diperoleh dapat digunakan untuk mengetahui apakah produksi dari masing – masing tanaman telah mencapai nilai optimal atau belum. Jika belum itu artinya pemerintah perlu meningkatkan produksi tanaman tersebut. Berdasarkan data dari buku Kota Magelang Dalam Angka, padi, ketela pohon, dan jagung adalah tanaman yang paling banyak diproduksi dari tahun 1994 hingga tahun 2014. Oleh karena itu dipilihlah ketiga tanaman tersebut.
Teknik optimasi masalah nonlinear berkendala dibagi menjadi dua kategori, yaitu metode langsung (direct method) dan metode tidak langsung (indirect
method). Metode langsung meliputi metode Pencarian Acak, metode Pencarian
Heuristik, metode Pendekatan Kendala, dan metode Arah Layak. Metode Pendekatan Kendala terbagi lagi menjadi dua yakni metode Pemrograman Linear dan metode Pemrograman Kuadratik. Sedangkan metode tidak langsung antara lain Transformasi Variabel dan metode Fungsi Penalti. Metode Fungsi Penalti dibagi lagi menjadi dua yakni metode Fungsi Penalti Interior (metode Barrier) dan metode Fungsi Penalti Eksterior (metode Penalty) (Rao, 2009 : 381).
Pemrograman kuadratik merupakan pendekatan penyelesaian permasalahan optimasi nonlinear dengan kendalanya berupa fungsi linear dan fungsi tujuannya merupakan fungsi non linear. (Hillier & Lieberman, 2001 : 665). Pemrograman Kuadratik disini akan diubah ke bentuk pemrograman linear menurut kondisi
wolfe, dalam pemrograman kuadratik terdapat kondisi complementary slackness
khusus, hal inilah yang membedakan simpleks metode wolfe dengan simpleks biasa.
Beberapa penelitian mengenai pemrograman kuadratik pernah dilakukan oleh Vina (2013) untuk mencari periode tanam padi yang optimal dengan pemodelan kuadratik yang fungsi tujuannya dibentuk dengan metode kuadrat terkecil dan diselesaikan dengan bantuan software Matlab. Pada penelitian Vina, diperoleh hasil yaitu periode tanam padi yang optimal adalah periode III (September-Desember). Selain itu, ada pula Efria (2015) yang mengaplikasikan pemrograman kuadratik pada portofolio saham. Pada penelitian Efria diperoleh model nonlinear pada portofolio saham perbankan beserta persentase proporsi dana yang diinvestasikan.di masing- masing bank.
Metode fungsi penalti eksterior (metode penalty) adalah metode yang digunakan untuk menyelesaikan masalah optimasi nonlinear berkendala menjadi masalah tidak berkendala dengan menambahkan fungsi penalti da n parameter penalti pada fungsi tujuannya (Rao, 2009 : 443). Metode ini dapat menyelesaikan masalah dengan kendala berupa pertidaksamaan maupun persamaan, sedangkan metode fungsi penalti interior hanya menyelesaikan masalah dengan kendala pertidaksamaan. Solusi optimal pada beberapa kasus dapat diperoleh dengan memadukan metode penalty dengan metode penyelesaian masalah tanpa kendala.
yaitu kasus umum yang memerlukan titik awal dan kasus khusus yang tidak memerlukan titik awal. Selain itu, ada pula Tri Wahyu (2006) yang menggunakan metode barrier (fungsi penalti interior) dan metode penalty (fungsi penalti eksterior) untuk optimasi masalah nonlinear dengan kendala. Pada penelitiannya, Tri memperoleh hasil bahwa barisan minimisasi pada metode penalty adalah barisan naik yang konvergen ke solusi optimal masalah berkendala dan barisan minimisasi pada metode barrier adalah barisan turun yang konvergen ke solusi optimal masalah berkendala.
Pemrograman kuadratik dipilih karena setelah diubah ke bentuk linear, dapat diselesaikan dengan metode simpleks. Sedangkan metode fungsi penalti eksterior dipilih karena metode ini dapat menyelesaikan masalah dengan kendala secara lebih umum. Berdasarkan latar belakang tersebut, tugas akhir ini akan melakukan penelitian tentang optimasi tanaman pangan di kota Magelang dengan pendekatan Pemrograman Kuadratik dan Metode Fungsi Penalti Eksterior.
B. RUMUSAN MASALAH
Berdasarkan latar belakang diatas, dapat ditentukan rumusan masalah sebagai berikut :
1. Bagaimana membentuk model matematika untuk pengoptimalan rata-rata produksi tanaman pangan di kota Magelang?
2. Bagaimana penyelesaian model dengan pemrograman kuadratik?
C. TUJUAN PENELITIAN
Sesuai dengan rumusan masalah diatas, maka tujuan dari penelitian ini adalah : 1. Membentuk model matematika untuk pengoptimalan rata-rata produksi
tanaman pangan di kota Magelang.
2. Menyelesaikan model menggunakan pemrograman kuadratik. 3. Menyelesaikan model menggunakan metode fungsi penalti eksterior.
D. MANFAAT PENELITIAN
Adapun manfaat dari penulisan skripsi ini adalah : 1. Bagi Penulis
a. Untuk mengetahui produksi tanaman bahan pangan di kota Magelang.
b. Sebagai sarana untuk menambah pengetahuan dan wawasan dalam penerapan teori-teori yang sudah diperoleh di perkuliahan.
c. Dapat mengaplikasikan dan mensosialisasikan teori tentang pemrograman kuadratik dan metode fungsi penalti eksterior.
2. Bagi Institusi
a. Memberikan luas panen yang optimal untuk tanaman pangan di kota Magelang agar didapat rata-rata produksi yang optimal.
b. Dapat dijadikan acuan untuk meningkatkan produksi tanaman pangan di Kota Magelang.
3. Bagi Pembaca
b. Menambah pemahaman tentang optimasi model non linear dengan menggunakan pemrograman kuadratik dan metode fungsi penalti eksterior.
BAB II
KAJIAN PUSTAKA
Pada bab ini akan diberikan landasan teori tentang optimasi, fungsi, turunan, pemrograman linear, metode simpleks, teorema dualitas, pemrograman nonlinear, persyaratan karush kuhn tucker, pemrograman kuadratik, dan metode fungsi penalty (metode penalty).
A. Optimasi
Menurut Kamus Besar Bahasa Indonesia optimasi merupakan upaya atau cara untuk memperoleh hasil yang terbaik. Menurut Yuni (2015 : 10) optimasi adalah suatu cabang ilmu dalam matematika untuk memaksimumkan atau meminimumkan fungsi tujuan dengan mempertimbangkan beberapa kendala yang diberikan. Menurut Rao (2009 : 1) optimasi dapat didefinisikan sebagai proses untuk menemukan kondisi yang memberikan nilai maksimum dan minimum dari suatu fungsi. Berdasarkan beberapa definisi tersebut maka dapat disimpulkan bahwa optimasi adalah suatu proses atau cara untuk memperoleh nilai maksimum atau minimum dari sebuah fungsi dengan mempertimbangkan beberapa kendala yang diberikan.
B. Fungsi
Definisi 2.1 Fungsi (Varberg & Purcell, 2010 : 29 )
Sebuah fungsi adalah suatu aturan korespondensi yang
menghubungkan tiap obyek dalam suatu himpunan, yang disebut daerah
yang disebut daerah kawan (kodomain). Himpunan nilai yang diperoleh
secara demikian disebut daerah hasil (range) fungsi.
Untuk menambah pemahaman, berikut ini akan diberikan ilustrasi dari suatu fungsi dan bukan fungsi.
Fungsi Bukan Fungsi
A B A B
Keterangan : A = daerah asal B = daerah kawan C = daerah hasil
Gambar 2. 1 Ilustrasi Fungsi dan Bukan Fungsi
Sebuah fungsi yang berbentuk , dengan konstanta (bilangan real) disebut fungsi konstanta. Fungsi , dengan variabel disebut fungsi identitas. Sebarang fungsi yang dapat diperoleh dari fungsi konstanta dan fungsi identitas dengan menggunakan operasi penambahan, pengurangan, dan perkalian disebut fungsi polinomial. (Varberg & Purcell, 2010 : 39)
Suatu fungsi polinomial dapat ditulis dalam bentuk
dengan anggota bilangan real. Jika , maka adalah derajat fungsi polinomial tersebut. Secara khusus, bentuk adalah fungsi polinomial berderajat satu atau disebut
. .
fungsi linear, dan adalah fungsi polinomial berderajat dua atau fungsi kuadrat. (Varberg & Purcell, 2010 : 39). Berikut ini akan dijelaskan tentang fungsi konveks dan konkaf serta fungsi kontinu.
1. Fungsi Konveks dan Konkaf
Definisi 2.2 (Varberg dan Purcell, 2010 : 156)
Misalkan terdiferensial untuk semua , dikatakan cekung
keatas atau konveks jika naik untuk semua dan dikatakan
cekung kebawah atau konkaf jika turun untuk semua .
Turunan kedua fungsi adalah turunan pertama dari , sehingga dapat disimpulkan bahwa naik jika positif dan turun jika negatif atau dapat ditulis dalam teorema berikut ini
Teorema 2.1 (Varberg dan Purcell, 2010 : 157)
Misalkan terdiferensial dua kali untuk semua
i. Jika , maka cekung keatas atau konveks untuk semua
,
ii. Jika , maka cekung kebawah atau konkaf untuk semua
.
Gambar 2.1 merupakan ilustrasi dari himpunan konveks dan konkaf
Konveks Konkaf
2. Fungsi Kontinu
Sebelum memahami tentang fungsi kontinu, akan dibahas terlebih dahulu mengenai limit fungsi.
Definisi 2.3 (Varberg dan Purcell, 2010 : 62)
Suatu limit untuk mendekati adalah , dan dapat ditulis
yang berarti untuk setiap yang diberikan
terdapat sedemikian sehingga jika maka
.
Dengan kata lain nilai mendekati limit untuk mendekati , jika nilai mutlak dari selisih nilai dan dibuat sekecil mungkin dengan cara mengambil cukup dekat tetapi tidak sama dengan . Perlu diperhatikan bahwa definisi tersebut tidak mengharuskan ada , agar fungsi mempunyai nilai limit.
Definisi 2.4 (Varberg dan Purcell, 2010 : 83)
Misalkan terdefinisi pada suatu interval terbuka yang mengandung .
Fungsi dikatakan kontinu di jika .
Dengan kata lain dikatakan kontinu di jika memenuhi : i. ada
ii. ada iii.
C. Turunan
Definisi 2.5 (Varberg dan Purcell, 2010 : 100)
Turunan fungsi adalah fungsi lain yang nilainya pada sebarang
bilangan adalah
Asalkan limit ini ada.
Teorema 2.2 (Varberg dan Purcell, 2010 : 102)
Jika ada maka kontinu di .
Bukti :
Bukti teorema ini menggunakan syarat fungsi kontinu, sebagai berikut i. ada
ii. ada iii.
Dari yang diketahui ada, maka
sehingga ada. Jadi syarat i terpenuhi. Selanjutnya
sehingga
Syarat ii dan iii terpenuhi. Sehingga Teorema 2.2 terbukti bahwa jika ada maka kontinu di .
Jika suatu fungsi memiliki variabel, maka turunan fungsi merupaka n turunan parsial.
Definisi 2.6 (Varberg dan Purcell, 2011 : 245)
Jika suatu fungsi dengan variabel, maka turunan parsial fungsi
terhadap di dinyatakan oleh atau
didefinisikan oleh :
Turunan parsial terhadap didefinisikan dengan cara yang sama.
D. Matriks Hessian
Matriks Hessian adalah matriks yang tiap elemennya dibentuk dari turunan parsial kedua dari suatu fungsi. Misalkan suatu fungsi dengan variabel, matriks Hessian dari yaitu :
E. Matriks Definit Positif dan Definit Negatif
Salah satu cara untuk menentukan apakah suatu matriks persegi merupakan definit positif, definit negatif atau tidak definit yaitu seperti yang dijelaskan berikut ini
Definisi 2.7 (Anton, 1995 : 320)
Diberikan A matriks persegi , maka berlaku :
a. Matriks A disebut Definit Positif
b. Matriks A disebut Definit Negatif
c. Matriks A disebut Semi Definit Positif
d. Matriks A disebut Semi Definit Negatif
Bentuk disebut bentuk kuadratik, dimana merupakan matriks dari variabel dan merupakan transpose dari matriks . Untuk menambah pemahaman, diberikan sebuah contoh berikut
Contoh 2.1
Diketahui matriks
. Akan diselidiki apakah H definit positif, definit negatif atau tidak definit. Jika H dinyatakan dalam bentuk kuadratik, maka
F. Titik Kritis
Tempat terjadinya nilai ekstrim baik itu nilai maksimum atau nilai minimum adalah di titik kritis (Varberg dan Purcell, 2010 : 152). Teorema 2.3 berikut akan menjelaskan keberadaan titik kritis.
Teorema 2.3 (Varberg dan Purcell, 2010 : 152)
Misalkan didefinisikan pada interval yang memuat titik . Jika
adalah nilai ekstrim, maka haruslah berupa suatu titik kritis; dengan kata
lain, adalah salah satu dari
i. Titik ujung dari ,
ii. Titik stasioner dari ; yaitu titik dimana ,
iii. Titik singular dari ; yaitu titik dimana tidak ada.
Bukti :
Misal berupa nilai maksimum pada dan bukan titik ujung ataupun titik singular. Akan dibuktikan bahwa adalah titik stasioner. Karena adalah nilai maksimum maka untuk semua dalam , yaitu .
Jadi, jika sehingga , maka
(2.1)
Sedangkan jika , maka
(2.2)
diperoleh dan . Sehingga dapat disimpulkan bahwa
Definisi 2.8 (Varberg dan Purcell, 2010 : 162)
Misalkan daerah asal , memuat titik . Dapat dikatakan bahwa
i. nilai maksimum lokal jika terdapat interval yang memuat
sedemikian sehingga adalah nilai maksimum pada ,
ii. nilai minimum lokal jika terdapat interval yang memuat
sedemikian sehingga adalah nilai minimum pada ,
iii. nilai ekstrim lokal jika ia berupa nilai maksimum lokal atau minimum lokal.
Titik-titik kritis (titik ujung, titik stasioner, dan titik singular) adalah titik tempat kemungkinan terjadinya ekstrim lokal (Varberg dan Purcell, 2010 : 163).
Definisi 2.9 (Varberg dan Purcell, 2010 : 155)
Misalkan terdefinisi pada interval (terbuka, tertutup, atau tidak satupun).
Dapat dikatakan bahwa :
i. naik pada jika, untuk setiap pasang bilangan dan dalam ,
,
ii. turun pada jika, untuk setiap pasang bilangan dan dalam ,
,
Teorema 2.4 (Varberg dan Purcell, 2010 : 155)
Misalkan f kontinu pada interval dan terdiferensial pada setiap titik-dalam
dari
i. Jika untuk semua titik-dalam , maka f naik pada ,
ii. Jika untuk semua titik-dalam , maka f turun pada .
Bukti :
Misalkan terdefinisi pada selang untuk semua titik-dalam dari . Jika , maka dapat ditulis
i. berarti
Menurut Definisi 2.9 i, fungsi naik. ii. berarti
Menurut Definisi 2.9 ii, fungsi turun. Teorema 2.5 (Varberg dan Purcell, 2010 : 163)
Misalkan kontinu pada interval terbuka yang memuat sebuah titik
kritis .
i. Jika untuk semua dalam dan untuk semua
dalam , maka adalah nilai maksimum lokal ,
ii. Jika untuk semua dalam dan untuk semua
iii. Jika bertanda sama pada kedua pihak , maka bukan nilai
ekstrim lokal .
Bukti :
i. Karena untuk semua dalam , maka menurut Teorema 2.4 naik pada . Demikian pula karena untuk semua dalam , maka turun pada . Jadi untuk semua dalam , kecuali di . Dapat disimpulkan bahwa adalah maksimum lokal.
Demikian pula untuk pembuktian ii dan iii. Teorema 2.6 (Varberg dan Purcell, 2010 : 164)
Misalkan dan ada pada setiap titik interval terbuka yang memuat
, dan misalkan .
i. Jika , maka adalah nilai minimum lokal ,
ii. Jika , maka adalah nilai maksimum lokal .
Bukti :
i. Jika dan , maka ada selang buka yang memuat sedemikian sehingga
G. Pemrograman Linear
Pemrograman Linear adalah metode matematis ya ng berkarakteristik linear untuk menemukan suatu penyelesaian optimal dengan cara memaksimumkan atau meminimumkan fungsi tujuan terhadap satu susunan kendala. (Siswanto, 2007 : 26). Model pemrograman linear mempunyai tiga unsur utama yaitu (Siswanto, 2007 : 25-26) :
1. Variabel Keputusan
Variabel keputusan adalah variabel yang akan mempengaruhi nilai tujuan yang hendak dicapai. Pada proses pembentukan suatu model, menentukan variabel keputusan harus dilakukan terlebih dahulu sebelum menentukan fungsi tujuan dan kendala-kendalanya.
2. Fungsi Tujuan
Pada pemrograman linear, tujuan yang hendak dicapai harus berbentuk fungsi linear. Selanjutnya, fungsi tujuan tersebut dimaksimalkan atau diminimumkan terhadap fungsi- fungsi kendala yang ada.
3. Fungsi Kendala
Kendala merupakan suatu pembatas terhadap variabel- variabel keputusan yang dibuat. Fungsi kendala suatu pemrograman linear juga harus berbentuk linear.
Secara umum, masalah pemrograman linear dapat dirumuskan sebagai berikut (B. Susanta, 1994 : 6)
Mencari nilai yang memaksimumkan (atau meminimumkan)
dengan kendala
(2.4)
Dalam hal ini,
(2.5)
(2.6)
(2.7)
(2.8)
Matriks merupakan matriks satu kolom dari variabel yang akan dicari, merupakan matriks satu baris dari koefisien ongkos ( ), matriks adalah matriks koefisien dari persamaan kendala dan adalah matriks kolom dari ruas kanan persamaan kendala.
Jika Persamaan (2.3) dan (2.4) diuraikan menjadi penjumlahan aljabar maka akan menjadi
Mencari nilai yang memaksimumkan (atau meminimumkan)
(2.9)
dengan kendala
(2.10a) (2.10b)
(2.10c)
H. Metode Simpleks
Menghadapi persoalan pemrograman linear yang memiliki variabel keputusan lebih dari dua digunakan metode yang lebih efisien yaitu metode simpleks. Metode simpleks merupakan pengembangan metode aljabar yang hanya menguji sebagian dari jumlah solusi yang layak dalam bentuk tabel. Tanpa mengurangi keumuman, metode simpleks yang akan dibahas dalam hal ini untuk fungsi tujuan memaksimalkan.
Adapun pokok-pokok metode simpleks yaitu (Zulian, 1991 : 41) :
a. Mengubah persoalan pemrograman linear ke dalam bentuk kanonik, yaitu kondisi dimana nilai ruas sama dengan ruas pada Persamaan (2.4) dengan cara memasukkan variabel slack/surplus atau variabel buatan. b. Mengubah bentuk fungsi kendala ke dalam bentuk kanonik untuk
mendapatkan solusi basis awal yang layak.
c. Memperbaiki solusi basis awal untuk mendapatkan solusi basis layak lainnya yang akan memperbaiki harga fungsi tujuan.
d. Mencari solusi basis layak lainnya, sehingga tidak ditemukan lagi solusi basis layak lainnya yang dapat memperbesar nilai fungsi tujuan.
Contoh 2.2 :
Tentukan bentuk kanonik dari masalah pemrograman linear berikut Memaksimumkan
(2.11)
Dengan kendala
(2.12a)
(2.12b)
Setelah dirubah ke bentuk kanonik Persamaan (2.11) dan (2.12) menjadi : Memaksimumkan
(2.13)
Dengan kendala
(2.14a)
(2.14b)
Variabel merupakan variabel surplus dengan koefisien -1 sehingga tidak bisa menjadi basis. Oleh karena itu perlu ditambahkan suatu variabel yang bernilai +1 untuk menjadi basis, variabel tersebut dinyatakan sebagai variabel buatan ( ). (B. Susanta, 1994 : 88)
dan merupakan bilangan positif yang cukup besar. Dengan demikian diharapkan variabel buatan segera keluar dari basis karena koefisien ongkosnya negatif besar. (B. Susanta, 1994 : 89)
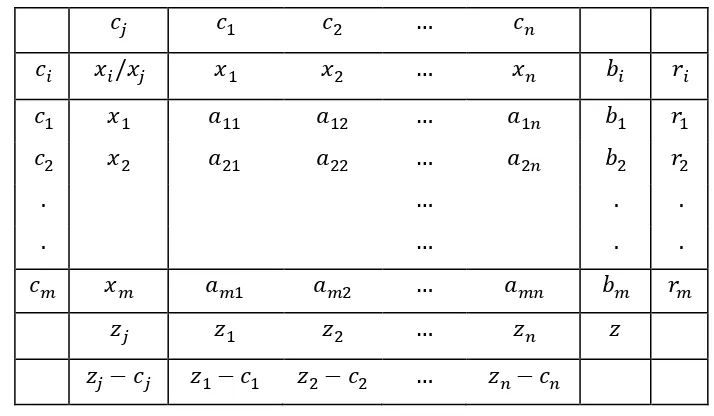
[image:38.596.141.498.276.484.2]Setelah fungsi kendala diubah ke bentuk kanonik dan didapatkan solusi basis awal yang layak, maka langkah selanjutnya adalah membuat tabel simpleks yang ditunjukkan pada Tabel 2.1.
Tabel 2. 1 Bentuk tabel simpleks
Keterangan
: variabel-variabel keputusan
: variabel yang menjadi basis dalam tabel yang ditinjau : koefisien ongkos
: koefisien ongkos variabel basis
: koefisien teknis (koefisien dalam kendala utama) : suku tetap (nilainya tidak negatif)
: (jumlah hasil kali dengan kolom ) : (jumlah hasil kali dengan kolom )
Apabila tabel yang bersangkutan belum optimum dan terpilih sebagai basis baru maka disusun kolom yang diperoleh dengan
, hanya untuk (B. Susanta, 1994 : 75)
Kasus dimana semua fungsi kendalanya berupa pertidaksamaan satu jenis disebut sebagai kasus maksimum atau minimum baku (B. Susanta, 1994 : 77). Pada soal memaksimumkan, yang terpilih untuk masuk menjadi basis adalah yang memiliki yang paling kecil. Variabel yang terpilih untuk keluar dari basis adalah variabel yang memiliki nilai terkecil (B. Susanta, 1994 : 78). Tabel pada masalah pemrograman linear dengan bentuk fungsi tujuan maksimum, dikatakan sudah optimum jika nilai pada baris
(Zulian, 1991 : 48). I. Teorema Dualitas
Konsep dualitas menjelaskan secara matematis bahwa sebuah kasus pemrograman linear berhubungan dengan sebuah kasus pemrograman linear yang lain. Bila kasus pemrograman linear pertama disebut primal maka kasus pemrograman linear kedua disebut dual, sehingga penye lesaian kasus primal secara otomatis akan menyelesaikan kasus dual, demikian pula sebaliknya (Siswanto, 2007 : 149). Tanpa mengurangi keumuman, dualitas yang akan dibahas dalam hal ini untuk bentuk primal memaksimalkan.
Primal
dengan kendala : , dan (2.16) Dual
Meminimumkan : (2.17)
dengan kendala : , dan (2.18)
Dalam hal ini, , (2.19)
(2.20)
(2.21)
dan (2.22)
Matriks dan merupakan transpose dari matriks dan matriks , sedangkan adalah matriks satu kolom untuk setiap koefisien ongkos ( ), dan merupakan matriks satu kolom dari variabel-variabel dual yang dicari. Jika Persamaan (2.17) dan (2.18) langsung ditulis dalam bentuk matriks secara keseluruhan, maka akan didapat bentuk :
Meminimumkan :
dengan kendala :
Bentuk perkalian matriks tersebut jika diuraikan menjadi penjumlahan aljabar akan menjadi :
Meminimumkan
(2.23)
dengan kendala
(2.24a) (2.24b)
(2.24c)
Lemma 2.1 (Winston, 2003 : 306)
merupakan solusi layak masalah primal, dan
merupakan solusi layak masalah dual, maka nilai primal dual. Bukti :
Masalah primal yang dinyatakan dalam bentuk :
Memaksimumkan dengan kendala :
Sehingga bentuk masalah dualnya menjadi :
Meminimumkan dengan kendala :
Diketahui bahwa , jika dikalikan dengan kendala masalah primal maka akan diperoleh
Jika ada kendala maka
(2.25)
Diketahui bahwa , jika dikalikan dengan kendala masalah dual maka akan diperoleh
Jika ada kendala maka
(2.26)
Dari Persamaan (2.25) dan (2.26) diperoleh
Jadi Lemma 2.1 terbukti.
Teorema 2.7 Teore ma Dualitas (Winston, 2003 : 309)
Jika terdapat solusi optimal bagi suatu pemrograman primal, maka juga
terdapat solusi optimal bagi pemrograman dual, dan kedua fungsi tujuannya
Bukti :
Jika masalah primal ditulis dalam bentuk : Meminimalkan / Memaksimalkan Dan bentuk dualnya adalah :
Memaksimalkan / Meminimumkan
i. Berdasarkan Lemma 2.1 didapatkan . Suatu titik layak pada masalah primal harus menghasilkan sebuah nilai primal yang tidak melebihi . Mengingat merupakan solusi layak primal dan mempunyai suatu nilai fungsi tujuan primal yang memenuhi
, maka haruslah solusi optimal primal.
ii. Berdasarkan Lemma 2.1 didapatkan , karena solusi layak primal. Suatu titik layak masalah dual, yaitu harus menghasilkan sebuah nilai dual yang melebihi . Mengingat merupakan solusi layak dual dan mempunyai suatu nilai fungsi tujuan dual yang memenuhi , maka haruslah solusi optimal dual.Berdasarkan penjelasan pada i dan ii, maka Teorema 2.9 terbukti. Berikut ini adalah contoh permasalahan primal dan dual
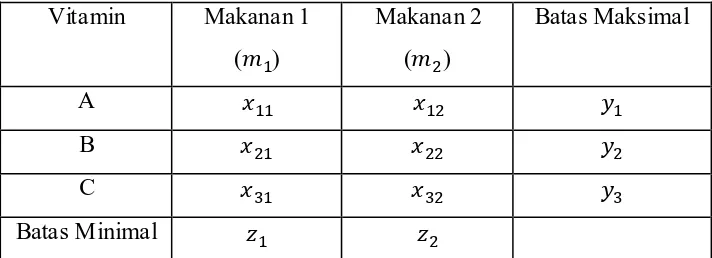
Contoh 2.3
makanan yang dinyatakan sebagai , sedangkan harga beli kedua jenis makanan dinyatakan sebagai .
[image:44.596.134.490.196.325.2]Dari ilustrasi Contoh 2.3 dapat dipresentasikan dalam Tabel 2.2. Tabel 2.2 Contoh Tabel Dualitas
Vitamin Makanan 1 ( )
Makanan 2 ( )
Batas Maksimal
A
B
C
Batas Minimal
Bila Tabel 2.2 dibaca ke kanan diperoleh soal primal dan bila dibaca ke bawah diperoleh soal dual. Sehingga diperoleh :
Soal dual :
Memaksimumkan dengan kendala :
Soal primal :
Meminimumkan dengan kendala :
Menurut Siswanto (2007) hubungan penyelesaian optimal antara primal dan dual sebuah kasus pemrograman linear adalah sebagai berikut
1. Nilai maksimum fungsi tujuan primal sama dengan nilai minimum fungsi tujuan dual.
2. Nilai optimal variabel keputusan primal sama dengan nilai (ruas kanan kendala) dual.
3. Nilai (ruas kanan kendala) primal sama dengan nilai optimal variabel keputusan dual.
Keoptimalan masalah dual dan masalah primal mengakibatkan suatu kondisi yang disebut dengan kondisi complementary slackness (B. Susanta, 1994 : 186) :
1. Jika dalam penyelesaian optimal masalah primal, kendala ke- berupa pertidaksamaan maka dalam penyelesaian optimal masalah dual variabel ke- bernilai nol.
2. Jika dalam penyelesaian optimal masalah primal, variabel ke- bernilai positif (kendala tak negatif untuk berupa pertidaksamaan ) maka dalam penyelesaian optimal masalah dual kendala ke- akan berupa persamaan.
Pada kondisi complementary slackness tersebut dapat ditulis secara matematis yaitu :
1.
Dimana
kendala variabel variabel kendala
ke-J. Pemrograman Nonlinear
Tidak semua permasalahan dalam kehidupan sehari- hari bisa diselesaikan dengan pemrograman linear. Oleh karena itu munculah pemrograman non linear. Bentuk umum masalah pemrograman nonlinear adalah menemukan nilai dari variabel keputusan agar
Memaksimumkan (atau meminimumkan) Dengan kendala
(2.27)
Dengan fungsi non linear dan fungsi linear atau non linear. (Winston, 2003 : 619)
Menurut Hillier (2001 : 664) terdapat 3 bentuk permasalahan pemrograman nonlinear, yaitu :
1. Pemrograman Nonlinear Tanpa Kendala
pemrograman nonlinear tanpa kendala untuk menentukan nilai ( ) dengan
Fungsi tujuan : maksimum / minimum
Untuk menyelesaikan permasalahan pemrograman nonlinear tanpa kendala terdapat dua syarat keoptimalan, yaitu :
a. Syarat Perlu Keoptimalan
Syarat perlu keoptimalan digunakan untuk mencari titik-titik optimal pada pendekatan analitis. Syarat perlu keoptimalan mengatakan bahwa :
Jika solusi adalah titik optimal dari maka :
di untuk (2.28) b. Syarat Cukup Keoptimalan
Syarat cukup keoptimalan digunakan untuk menentukan apakah titik optimal yang didapatkan dari syarat perlu keoptimalan merupakan titik minimum atau titik maksimum.
Syarat cukup keoptimalan yaitu : Jika
dan definit positif maka titik minimum Jika
dan definit negatif maka titik maksimum 2. Pemrograman Nonlinear Dengan Kendala Linear
nonlinear. Untuk menentukan nilai dengan bentuk umum adalah :
Maksimum/minimum : dengan kendala :
Untuk
3. Pemrograman Nonlinear Dengan Kendala Nonlinear
Menurut Taha (2007 : 699) pemrograman nonlinear dengan kendala non linear merupakan masalah optimasi dengan fungsi tujuan nonlinear dan fungsi kendala nonlinear. Pemrograman nonlinear berkendala nonlinear dibedakan menjadi dua yaitu :
a. Untuk bentuk umum pemrograman nonlinear dengan kendala kesamaan (equality) adalah
Fungsi tujuan : Maksimum/minimum : Fungsi kendala :
Dimana menunjukkan jumlah kendala dan menunjukkan jumlah variabel dengan .
b. Bentuk umum pemrograman nonlinear dengan kendala pertidaksamaan adalah
Maksimum/minimum :
K. Persyaratan Karush Kuhn Tucker
Pada tahun 1951 Kuhn Tucker menemukan suatu teknik optimasi yang dapat digunakan untuk mencari titik optimum dari permasalahan berkendala baik permasalahan dalam bentuk linear maupun nonlinear. Metode ini membahas suatu kondisi untuk menjadi solusi optimal untuk pemrograman non linear berikut
Memaksimumkan (atau meminimumkan) Dengan kendala
(2.29)
Semua kendala yang akan diselesaikan dengan metode Karush Kuhn Tucker harus menggunakan tanda ( ) . Kendala yang berbentuk harus ditulis sebagai . Kendala dengan bentuk harus diganti dengan h dan (Winston, 2003 : 673).
Teorema 2.8 (Winston, 2003 :676)
Andaikan Persamaan (2.29) adalah masalah maksimisasi. Jika
merupakan solusi optimal untuk Persamaan (2.29) , maka
harus memenuhi kendala pada Persamaan (2.29) dan
harus ada pengali serta variabel slack yang
memenuhi : (2.30) (2.31) (2.32) (2.33) (2.34)
Teorema 2.9 (Winston, 2003 : 676)
Andaikan Persamaan (2.29) adalah masalah minimisasi. Jika
merupakan solusi optimal untuk Persamaan (2.29) , maka
harus memenuhi kendala pada Persamaan (2.29) dan
harus ada pengali serta variabel surplus yang
Pada Persamaan (2.31) dan Persamaan (2.36) jika dan menurut bentuk umum fungsi kendala, yaitu maka berakibat
Menurut Hillier (2001 : 679) untuk masalah berkendala, kondisi Karush
Kuhn Tucker merupakan syarat perlu keoptimalan, dan akan menjad i syarat
cukup jika fungsi tujuannya merupakan fungsi konkaf dan fungsi kendalanya berupa fungsi konveks.
Corollary 2.1 (Hillier, 2001 : 680)
Diasumsikan bahwa f(x) adalah fungsi konkaf dan
adalah fungsi konveks, dimana semua fungsi memenuhi bentuk Persamaan
(2.29), adalah solusi optimal jika dan hanya jika semua
kondisi Karush Kuhn Tucker terpenuhi.
L. Pemrograman Kuadratik
Pemrograman kuadratik merupakan pendekatan penyelesaian permasalahan optimasi nonlinear dengan kendalanya berupa fungsi linear dan fungsi tujuannya berupa fungsi nonlinear. Bentuk umum dari masalah pemrograman kuadratik menurut Peressini, dkk (1988) adalah
Meminimalkan (2.40)
dengan kendala
(2.41a)
(2.41b)
tersusun dari nilai , dimana diperoleh dari turunan parsial kedua terhadap dan dari fungsi tujuan. Matriks merupakan matriks simetris sehingga nilai
.
Persamaan (2.40) bila ditulis dalam bentuk penjumlahan aljabar maka akan menjadi
(2.40)
Pada dasarnya, masalah pemrograman kuadratik dapat diselesaikan dengan persyaratan Karush Kuhn Tucker seperti pada Teorema 2.8 dan 2.9. Persyaratan Karush Kuhn Tucker digunakan untuk mengubah masalah nonlinear menjadi masalah linear melalui syarat Persamaan (2.30) dan (2.35) . Selanjutnya, masalah linear tersebut dapat diselesaikan dengan berbagai cara, salah satunya menggunakan metode simpleks. Pada pemrograman kuadratik terdapat kondisi
complementary slackness khusus, hal inilah yang membedakan dari metode
simpleks biasa yang kemudian disebut simpleks metode wolfe.
Sifat 2.1 Complementary Slackness pada Pemrograman kuadratik (Winston, 2003 : 687)
1) dan pada kondisi Kuhn Tucker dan tidak dapat kedua-duanya
bernilai positif.
2) Variabel surplus (excess) ataupun slack untuk kendala ke-i dan tidak
Bukti :
1) Diketahui syarat Persamaan (2.30) dan (2.32) pada Teorema 2.8 , yaitu : Syarat Persamaan (2.30)
, sehingga
Kemudian disubstitusikan ke Persamaan (2.32)
Diperoleh .
Jika maka , yaitu .
Jika maka , yaitu atau . Berdasarkan syarat Persamaan (2.33) maka .
Hal ini juga berlaku pada Teorema 2.9 , sehingga terbukti bahwa dan pada kondisi Kuhn Tucker dan tidak dapat kedua-duanya bernilai positif.
2) Diketahui syarat Persamaan (2.31) dan (2.36) yaitu Pada fungsi kendala maka bentuk kanonik kendala tersebut yaitu
, sehingga syarat Persamaan (2.31) dan (2.36) menjadi :
Jika maka , yaitu .
Pada fungsi kendala dapat diubah menjadi . Dengan cara yang sama maka didapat pula , sehingga terbukti bahwa variabel surplus ataupun slack untuk kendala ke- i dan tidak dapat kedua-duanya bernilai positif.
M. Metode Fungsi Penalti
Metode fungsi penalti adalah metode yang digunakan untuk menyelesaikan masalah optimasi nonlinear berkendala menjadi masalah tidak berkendala dengan menambahkan fungsi penalti dan parameter penalti pada fungsi tujuannya. Fungsi Penalti terjadi karena adanya pelanggaran terhadap fungsi tujuan, yaitu menghilangkan kendala pada permasalahan (Bazaraa, 2006 : 470). Metode Fungsi Penalti dibagi menjadi dua, yaitu Metode Fungsi Penalti Interior (Metode Barrier) dan Metode Fungsi Penalti Eksterior (Metode Penalty).
Fungsi Penalti Eksterior merupakan bentuk fungsi tambahan yakni, fungsi tujuan ditambahkan fungsi penalti. Jika merupakan fungsi penalti, yaitu
Fungsi merupakan fungsi tujuan, maka diperoleh yang merupakan fungsi tambahan, yaitu
Jadi bentuk umum masalah Fungsi Penalti Eksterior adalah : Meminimalkan
(2.42)
(Bazaraa, 2006 : 471)
Berikut ini teorema-teorema yang menjamin hasil dari penyelesaian dengan metode fungsi penalti eksterior adalah solusi dari masalah nonlinear.
Lemma 2.2 (Chong, 2001 : 448)
Jika
Maka relasi-relasi berikut akan benar untuk setiap :
i.
ii.
iii.
iv.
Bukti :
i. Diketahui dan solusi dicari dari luar daerah layak (eksterior) sehingga , maka diperoleh
Kedua ruas ditambah dengan , maka
Selanjutnya, karena meminimalkan , maka
Jadi terbukti bahwa
ii. Karena dan masing- masing meminimalkan dan , maka
(2.44) (2.45)
Jika Persamaan (2.44) dan (2.45) dijumlahkan, maka diperoleh
(2.46) Tetapi karena , maka Persamaan (2.46) akan berlaku jika
Jadi terbukti bahwa iii. Dari Persamaan (2.43) diperoleh
(2.47) Karena dan maka Persamaan (2.47) akan berlaku jika
iv. Karena meminimalkan , maka diperoleh
Karena nilai minimum untuk masalah optimasi berkendala, maka , sehingga diperoleh
Karena dan maka
Teorema 2.10 (Chong, 2001 : 449)
Jika fungsi tujuan kontinu, dan ketika , maka limit dari
barisan konvergen adalah solusi masalah optimasi berkendala.
Bukti :
Diketahui merupakan barisan naik yang dibatasi oleh solusi optimal masalah berkendala yaitu . Dimisalkan
(2.48)
Karena fungsi kontinu dan berdasarkan relasi ke (iv) Lemma 2.2, maka diperoleh
(2.49) Jika Persamaan (2.48) dikurangi Persamaan (2.49) maka diperoleh
Berdasarkan relasi (ii) Lemma 2.2, merupakan barisan turun dengan batas bawahnya yaitu nol. Sehingga
Karena kontinu maka dapat dipilih titik layak , sehingga diperoleh
,
sehingga merupakan titik layak. Berdasarkan relasi (iv) Lemma 2.2, sehingga
BAB III PEMBAHASAN
Pada bab ini akan dijelaskan tentang konsep dasar metode kuadrat terkecil yang digunakan untuk membentuk fungsi tujuan dari masalah pemrograman nonlinear dan langkah- langkah penyelesaiannya menggunakan pemrograman kuadratik metode wolfe dan metode fungsi penalti eksterior (metode penalty). Selanjutnya akan dipaparkan penerapan model nonlinear pada rata-rata produksi tanaman pangan di kota Magelang beserta penyelesaiannya dengan kedua metode tersebut.
A. Pembentukan Fungsi Tujuan denga n Metode Kuadrat Terkecil
Masalah yang dibahas dalam tugas akhir ini adalah masalah pemrograman nonlinear, sehingga fungsi tujuan yang akan dibentuk berupa fungsi nonlinear yang dalam hal ini berupa fungsi kuadrat, yaitu fungsi dengan pangkat tertinggi dari variabelnya adalah dua. Fungsi kuadrat memiliki satu nilai titik ekstrim yaitu maksimum atau minimum, sedangkan fungsi kubik memiliki sebuah titik belok, yaitu titik peralihan bentuk kurva dari cekung menjadi cembung atau sebaliknya dan mungkin pula memiliki satu atau dua titik ekstrim. Karena fungsi kubik belum tentu memiliki titik ekstrim, maka dipilihlah fungsi kuadrat yang sudah pasti memiliki satu titik ekstrim.
Model yang diselesaikan dengan metode k uadrat terkecil adalah sebagai berikut
(3.1a)
Dimana adalah parameter dan adalah sisa (galat). Menurut Setijo Bismo (2008), fungsi kuadrat atau fungsi parabola mempunyai bentuk umum yang dapat dituliskan sebagai berikut :
(3.1b)
Dari Persamaan (3.1a) dan (3.1b) diperoleh model fungsi kuadrat yang akan diselesaikan dengan metode kuadrat terkecil, yaitu
(3.1c)
Metode kuadrat terkecil disini digunakan untuk mencari nilai- nilai tetapan
, dan berdasarkan set data yang diberikan, (dimisalkan banyaknya data = ) , yaitu dengan meminimumkan jumlah kuadrat sisa ( dari Persamaan (3.1) berikut
Selanjutnya diturunkan terhadap , dan dengan syarat optimumnya adalah
Jika diturunkan terhadap , maka diperoleh
(3.2a)
Jika diturunkan terhadap , maka diperoleh
(3.2b)
Jika diturunkan terhadap , maka diperoleh
(3.2c)
Persamaan (3.2) disebut persamaan normal. Apabila ditulis kedalam bentuk matriks Persamaan (3.2) akan menjadi
Selanjutnya nilai , dan dapat ditaksir dengan menggunakan rumus
B. Penyelesaian Masalah Nonlinear
1. Pemrograman Kuadratik dengan Metode Wolfe
Kuhn Tucker dicari solusi optimalnya dengan simpleks metode wolfe. Adapun
langkah-langkah penyelesaiannya adalah sebagai berikut (Yuni, 2015)
a. Membentuk kondisi Kuhn Tucker dari syarat Kuhn Tucker yang diperoleh.
b. Mengidentifikasi complementary slackness sesuai Sifat 2.1.
c. Menambahkan variabel buatan untuk setiap kondisi Kuhn Tucker yang tidak memiliki variabel basis.
d. Membuat fungsi tujuan baru yang linear yaitu fungsi tujuan untuk meminimalkan jumlah nilai variabel buatan .
e. Melakukan proses iterasi simpleks dengan menggunakan metode
wolfe.
Untuk menjamin bahwa solusi akhir (variabel buatan bernilai nol) memenuhi kondisi complementary slackness, metode wolfe memiliki modifikasi untuk pilihan variabel simpleks yang masuk menjadi basis, yaitu
1) dari kondisi Kuhn Tucker dan variabel keputusan tidak bisa menjadi variabel basis secara bersamaan.
2) Variabel surplus atau variabel slack dari kendala ke- i dan dari kondisi Kuhn Tucker tidak boleh kedua-duanya menjadi variabel basis.
tabel optimal akan ada complementary slackness yang tidak terpenuhi.
f. Mensubstitusikan hasil dari tabel optimum ke dalam fungsi tujuan awal (nonlinear) untuk didapatkan solusi optimum.
Jika dalam tabel optimum terdapat variabel buatan maka dapat disubstitusikan ke fungsi tujuan linear. Begitu pula untuk variabel
slack, surplus, buatan ataupun maka dapat disubstitusikan ke bentuk kanonik yang telah dibentuk di awal.
Untuk menambah pemahaman, maka diberikan ilustrasi penyelesaian pemrograman kuadratik dengan metode wolfe melalui contoh berikut : Contoh 3.1 :
Memaksimumkan (3.3) dengan kendala
(3.4a)
(3,4b)
(3.4c)
Langkah - langkah penyelesaian Persamaan (3.3) dan (3.4) dengan pemrograman kuadratik metode wolfe adalah sebagai berikut :
a. Membentuk kondisi Kuhn Tucker dari fungsi tujuan dan fungsi kendala yang telah dimiliki.
Berdasarkan Persamaan (3.3) dan (3.4) maka ditentukan bentuk kanoniknya yaitu :
(3.5b)
(3.5c)
(3.5d)
b. Mengidentifikasi complementary slackness yang ada.
Diperhatikan bahwa Persamaan (3.5) merupakan kondisi
complementary slackness, sehingga mengakibatkan :
c. Menambahkan variabel buatan untuk setiap kondisi Kuhn Tucker yang tidak memiliki variabel basis.
Berdasarkan Persamaan (3.5), hanya Persamaan (3.5c) dan (3.5d) yang memiliki variabel basis. Pada Persamaan (3.5a) dan (3.5b) perlu ditambah variabel buatan sehingga bentuk kanoniknya menjadi :
(3.6a)
(3.6b)
(3.6c)
(3.6d)
d. Membuat fungsi tujuan baru yang linear yaitu fungsi tujuan untuk meminimalkan jumlah nilai variabel buatan .
Bentuk fungsi tujuan baru yang linear untuk Contoh 3.1 adalah
Meminimumkan
dengan kendala
(3.6a)
(3.6b)
(3.6c)
(3.6d)
Semua variabel non negatif.
e. Melakukan proses iterasi simpleks dengan menggunakan metode
wolfe.
[image:66.596.180.503.384.518.2]Pada proses iterasi, semua koefisien ongkos variabel non basis diganti dengan 0. (Winston, 2003 : 687)
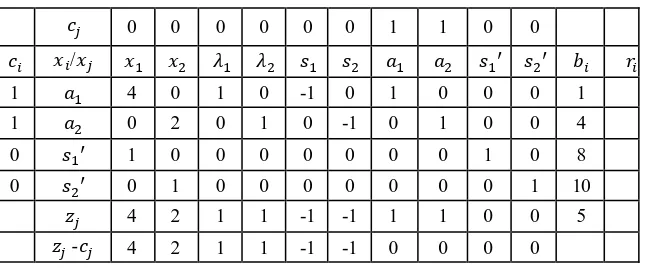
Tabel 3. 1 Tabel simpleks dengan metode wolfe 0 0 0 0 0 0 1 1 0 0
/
1 4 0 1 0 -1 0 1 0 0 0 1
1 0 2 0 1 0 -1 0 1 0 0 4
0 1 0 0 0 0 0 0 0 1 0 8
0 0 1 0 0 0 0 0 0 0 1 10
4 2 1 1 -1 -1 1 1 0 0 5
- 4 2 1 1 -1 -1 0 0 0 0
Nilai pada adalah yang paling besar, maka semua nilai pada kolom dibagi dengan nilai pada kolom variabel sehingga didapatkan nilai seperti dijelaskan pada Tabel 3.2.
Tabel 3. 2 Iterasi pertama metode wolfe
0 0 0 0 0 0 1 1 0 0
/
1 4 0 1 0 -1 0 1 0 0 0 1 0,25
1 0 2 0 1 0 -1 0 1 0 0 4 -
0 1 0 0 0 0 0 0 0 1 0 8 8
0 0 1 0 0 0 0 0 0 0 1 10 -
4 2 1 1 -1 -1 1 1 0 0 5
- 4 2 1 1 -1 -1 0 0 0 0
Karena nilai terkecil adalah maka keluar dan masuk menjadi variabel basis dengan koefisien ongkos 0. Selanjutnya proses iterasi dilanjutkan hingga diperoleh tabel optimum seperti Tabel 3.3.
Tabel 3. 3 Tabel optimum metode wolfe
0 0 0 0 0 0 1 1 0 0
/
0 1 0 0,25 0 -0,25 0 0,25 0 0 0 0,25
0 0 1 0 1 0 -1 0 1 0 0 2
0 0 0 -0,25 0 0,25 0 -0,25 0 1 0 7,75
0 0 0 0 -1 0 1 0 -1 0 1 8
0 0 0 0 0 0 0 0 0 0 0
- 0 0 0 0 0 0 -1 -1 0 0
Karena nilai maka iterasi berhenti, dan tabel dinyatakan optimum. Dari tabel optimum tersebut diperoleh nilai variabel
dan . Selain itu juga didapatkan nilai variabel
mengetahui nilai maksimum yang dicari maka nilai variabel- variabel tersebut disubstitusikan kedalam fungsi tujuan awal yaitu
. Sehingga penyelesaian optimal dari Contoh 3.1 adalah 10,125.
Secara umum, penyelesaian pemrograman kuadratik metode Wolfe dapat digambarkan dalam Gambar 3.1
2. Metode Fungsi Penalti Eksterior (Metode Penalty)
Metode fungsi penalti eksterior pada prinsipnya adalah mentransformasikan masalah nonlinear berkendala menjadi masalah tidak berkendala sedemikian sehingga penyelesaiannya dicari secara numerik. Masalah berkendala diubah ke masalah tanpa kendala dengan cara menambahkan fungsi penalti dan parameter penalti pada fungsi tujuan. Proses pencarian solusi pada metode penalty dimulai dari luar daerah layak, oleh karena itu disebut dengan metode fungsi penalti eksterior.
Kondisi
Kuhn
Tucker
Fungsi
Linear
Simpleks
Metode
Wolfe
Tabel
Optimum Fungsi
Tujuan Non
Linear
Gambar 3. 1 Bagan Langkah Penyelesian Pemrograman Kuadratik Metode
Berikut adalah langkah penyelesaian metode fungsi penalti eksterior
a. Mengecek kekontinuan fungsi tujuan dan fungsi kendala
b. Membentuk fungsi tujuan untuk masalah optimasi tidak berkendala
, dengan
1) adalah fungsi tujuan masalah berkendala 2) adalah parameter penalti
3) Fungsi penalti 4) adalah fungsi kendala pertidaksamaan
5) adalah fungsi kendala persamaan 6) adalah bilangan bulat positif
c. Menentukan penyelesaian dari masalah minimalkan , yakni . Menurut syarat perlu keoptimalan masalah nonlinear tanpa kendala, titik optimal akan dicapai ketika turunannya sama dengan nol. d. Menyelidiki apakah nilai optimal yang dicapai merupakan titik
minimum atau maksimum berdasarkan syarat cukup keoptimalan masalah nonlinear tanpa kendala.
Secara umum, penyelesaian metode fungsi penalti eksterior dapat digambarkan dalam Gambar 3.2
Solusi
Optimal Fungsi Tujuan
Nonlinear Tak
Berkendala Fungsi Tujuan
Non Linear
Berkendala
Metode
[image:69.596.149.510.598.696.2]Penalty
C. Penerapan Model Nonlinear pada Rata-Rata Produksi Tanaman Pangan di Kota Magelang
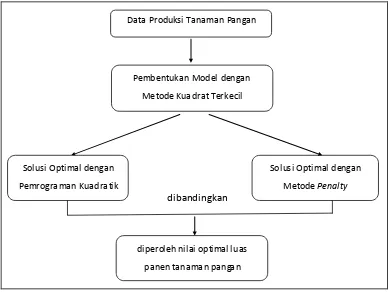
[image:70.596.124.512.305.597.2]Pada subab ini akan dijelaskan langkah pembentukan model non linear untuk rata-rata produksi tanaman pangan menggunakan metode kuadrat terkecil yang perhitungannya diselesaikan dengan bantuan software matlab. Kemudian model yang diperoleh akan diselesaikan dengan pemrograman kuadratik metode wolfe dan metode fungsi penalti eksterior. Gambar 3.3 adalah alur penelitian dalam tugas akhir ini
Gambar 3. 3 Alur Pembentukan Model dan Penyelesaian Model Non Linear
dibandingkan
Solusi Optimal dengan
Metode Penalty Solusi Optimal dengan
Pemrograman Kuadratik
Pemb entukan Mod el dengan
Metode Kuadrat Terkecil Data Produksi Tanaman Pangan
diperoleh nilai optimal luas
1. Pembentukan Model
Salah satu sektor penopang utama pertumbuhan ekonomi yang masih sangat besar adalah sektor pertanian. Setiap tahun, permintaan terhadap produksi pertanian selalu meningkat, khususnya kebutuhan bahan pangan. Kebutuhan bahan pangan masyarakat bertumpu pada padi dan palawija. Oleh karena itu produksi padi dan palawija menjadi pemasok utama dalam pemenuhan kebutuhan pangan.
Di kota Magelang, jenis tanaman pangan yang diproduksi setiap tahunnya selalu berubah ubah. Jenis-jenis tanaman yang diproduksi yaitu padi, jagung, ketela pohon, ketela rambat, kacang tanah, dan kedelai. Namun menurut data dari buku Magelang Dalam Angka, dari tahun 1994 hingga tahun 2014 jenis tanaman pangan yang paling banyak diproduksi yaitu padi, ketela pohon, dan jagung maka dipilihlah ketiga jenis tanaman tersebut.
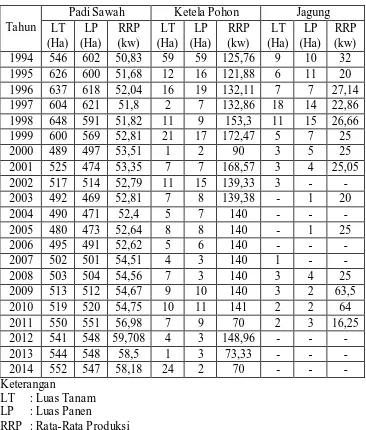
Tabel 3. 4 Data Luas Tanam, Luas Panen, dan Rata-rata Produksi Padi, Ketela Pohon dan Jagung tahun 1994-2014
Tahun
Padi Sawah Ketela Pohon Jagung
LT (Ha) LP (Ha) RRP (kw) LT (Ha) LP (Ha) RRP (kw) LT (Ha) LP (Ha) RRP (kw) 1994 546 602 50,83 59 59 125,76 9 10 32 1995 626 600 51,68 12 16 121,88 6 11 20 1996 637 618 52,04 16 19 132,11 7 7 27,14 1997 604 621 51,8 2 7 132,86 18 14 22,86 1998 648 591 51,82 11 9 153,3 11 15 26,66 1999 600 569 52,81 21 17 172,47 5 7 25
2000 489 497 53,51 1 2 90 3 5 25
2001 525 474 53,35 7 7 168,57 3 4 25,05 2002 517 514 52,79 11 15 139,33 3 - -
2003 492 469 52,81 7 8 139,38 - 1 20
2004 490 471 52,4 5 7 140 - - -
2005 480 473 52,64 8 8 140 - 1 25
2006 495 491 52,62 5 6 140 - - -
2007 502 501 54,51 4 3 140 1 - -
2008 503 504 54,56 7 3 140 3 4 25
2009 513 512 54,67 9 10 140 3 2 63,5
2010 519 520 54,75 10 11 141 2 2 64
2011 550 551 56,98 7 9 70 2 3 16,25
2012 541 548 59,708 4 3 148,96 - - -
2013 544 548 58,5 1 3 73,33 - - -
2014 552 547 58,18 24 2 70 - - -
Keterangan
LT : Luas Tanam LP : Luas Panen
RRP : Rata-Rata Produksi
a. Membentuk Fungsi Tujuan
Fungsi tujuan dari permasalaan ini dibentuk dari rata – rata produksi yang diartikan sebagai hasil panen per hektar yang dihitung beratnya dalam satuan kwintal. Sedangkan luas panen diasumsikan sebagai banyaknya tanaman yang dipungut hasilnya setelah cukup umur termasuk yang gagal panen. Karena tidak memungkinkan untuk menghitung tanaman satu persatu, maka jumlah tanaman dianggap setara dengan luas tanaman yang dihitung dalam satuan hektar.
Rata-rata produksi tanaman pangan total merupakan jumlahan dari rata-rata produksi tanaman padi, ketela pohon, dan jagung. Sehingga fungsi tujuan yang akan dibentuk dapat dinyatakan sebagai jumlahan dari rata-rata produksi padi, ketela pohon, dan jagung.
(3.8)
Adapun variabel yang digunakan adalah sebagai berikut = data Luas Panen Padi ke - dalam satuan ha
= data Luas Panen Ketela Pohon ke - dalam satuan ha = data Luas Panen Jagung ke - dalam satuan ha
= data Rata – Rata Produksi ke - dalam satuan kw = 1