OPTIMASI TRANSPORTASI TAK SEIMBANG MENGGUNAKAN MODIFIKASI METODE ASM SKRIPSI MIFTAHUN NADHIRAH

(1)

OPTIMASI TRANSPORTASI TAK SEIMBANG MENGGUNAKAN MODIFIKASI

METODE ASM

SKRIPSI

MIFTAHUN NADHIRAH 130803045

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SUMATERA UTARA

MEDAN 2019

Universitas Sumatera Utara

(2)

SKRIPSI

Diajukan untuk melengkapi tugas dan memenuhi syarat mencapai gelar Sarjana Sains

MIFTAHUN NADHIRAH 130803045

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SUMATERA UTARA

MEDAN 2019

(3)

i

PERSETUJUAN

Judul : Optimasi Transportasi Tak Seimbang Menggunakan Modifikasi Metode ASM

Kategori : Skripsi

Nama : Miftahun Nadhirah

Nomor Induk Mahasiswa : 130803045

Program Studi : Sarjana (S1) Matematika

Departemen : Matematika

Fakultas : Matematika dan Ilmu Pengetahuan Alam Universitas Sumatera Utara

Disetujui di Medan, Januari 2019

Disetujui oleh

Departemen Matematika FMIPA USU Pembimbing, Ketua,

Dr. Suyanto, M.Kom Dr. Suyanto, M.Kom

NIP. 19590813 198601 1 002 NIP. 19590813 198601 1 002

(4)

PERNYATAAN

OPTIMASI TRANSPORTASI TAK SEIMBANG MENGGUNAKAN MODIFIKASI

METODE ASM

SKRIPSI

Saya mengakui bahwa skripsi ini adalah hasil karya sendiri. Kecuali beberapa kutipan dan ringkasan yang masing-masing disebutkan sumbernya.

Medan, Januari 2019

Miftahun Nadhirah 130803045

(5)

iii

PENGHARGAAN

Puji dan syukur penulis ucapkan kehadirat Allah Ta‟ala yang telah melimpahkan rahmat dan karunia-Nya sehingga penulis dapat menyelesaikan skripsi yang berjudul “Optimasi Transportasi Tak Seimbang Menggunakan Modifikasi Metode ASM”. Sholawat dan salam semoga selalu tercurahkan kepada Nabi Muhammad SAW yang telah memberikan contoh teladan kepada umat manusia.

Terima kasih penulis sampaikan kepada Bapak Dr. Suyanto, M.Kom selaku dosen pembimbing, penasehat akademik dan Ketua Departemen Matematika FMIPA USU yang senantiasa membantu dan mengarahkan penulis dalam menyelesaikan skripsi ini. Terima kasih kepada bapak Dr. Open Darnius, M.Sc dan Ibu Dra. Normalina Napitupulu, M.Sc selaku dosen pembanding yang telah memberikan kritik dan saran yang membangun dalam menyelesaikan skripsi ini. Terima kasih kepada Bapak Dr. Kerista Sebayang, MS selaku Dekan FMIPA USU serta seluruh staf pegawai di FMIPA USU. Terima kasih kepada seluruh Bapak dan Ibu dosen yang telah mendidik saya selama menjalani pendidikan di FMIPA USU. Teristimewa kepada kedua orangtua tercinta Buya Syahrul dan Ummi Mailin Fauziah Nst, adik-adik tercinta Zati Hulwani dan Fakhira Salsabila yang selalu memberikan kasih sayang dan dukungan do‟a dan motivasi sehingga penulis memiliki semangat untuk menyelesaikan skripsi ini. Terima kasih kepada sahabat-sahabat tersayang penulis yang tak bisa disebutkan namanya satu persatu, rekan-rekan kuliah di Matematika 2013 serta teman-teman di berbagai organisasi yang telah memberikan semangat dan dukungan kepada penulis. Semoga Allah Ta‟ala memberikan balasan atas kebaikan semua.

Medan, Januari 2019

Miftahun Nadhirah 130803045

(6)

OPTIMASI TRANSPORTASI TAK SEIMBANG MENGGUNAKAN MODIFIKASI

METODE ASM

ABSTRAK

Masalah transportasi merupakan masalah pendistribusian barang dari beberapa sumber (persediaan atau supply) ke beberapa tujuan (permintaan atau demand) dengan tujuan untuk meminimumkan biaya transportasi atau memaksimumkan keuntungan. Terdapat beberapa metode untuk menyelesaikan masalah transportasi. Salah satu metode langsung untuk meyelesaikan masalah transportasi adalah metode ASM yang diperkenalkan oleh Abdul Quddoos, Dr. Shakeel Javaid, dan Prof. Mohd Masood Khalid pada tahun 2012. Metode ASM ini memberikan solusi optimal tanpa memerlukan solusi awal dengan karakteristik menitikberatkan pada hasil reduksi yang bernilai nol dengan indeks terkecil.

Quddoos et al. (2016) melakukan revisi metode ASM untuk masalah transportasi tak seimbang yaitu adanya penambahan baris/kolom dummy dengan nilai awal 0 dimana sangat berpengaruh pada hasil reduksi. Maka dilakukan modifikasi algoritma pada revisi metode ASM yaitu mengganti nilai dummy dengan nilai tereduksi terbesar yang berfungsi sebagai pengoptimalan angka 0 yang muncul pada tabel. Algoritma ini diambil dari metode Improved Zero Point. Diperoleh hasil dari modifikasi metode ASM sebesar 75 sedangkan dari revisi metode ASM diperoleh hasil 79. Dengan demikian, terjadi penurunan nilai optimasi sebesar 5%, sehingga modifikasi metode ASM memberikan solusi yang tetap optimal.

Kata kunci: Improved Zero Point, Modifikasi Metode ASM, Reduksi, Solusi Optimal, Transportasi Tak Seimbang.

(7)

v

UNBALANCED TRANSPORTATION OPTIMIZATION USING ASM METHOD MODIFICATION

ABSTRACT

Transportation problem is the problem of distributing goods from several sources (fulfilling or supplying) to several destinations (demand or demand) with the aim of minimizing transportation costs or maximizing profits. Several methods appear to deal with transportation problems. One of the direct methods to solve transportation problems is the ASM method introduced by Abdul Quddoos, Dr.

Shakeel Javaid, and Prof. Mohd Masood Khalid in 2012. This ASM method provides optimal solutions without the need for an initial solution with the characteristics of focusing on the reduction results which are zero with the smallest index. Quddoos et al (2016) revised the ASM method for unbalanced transportation problems, namely the addition of a dummy row /column with an initialvalue of 0 which is very influential on the reduction results. Then the algorithm is modified to revise the ASM method, which is to replace the dummy value with the largest reduced value that serves as an optimization of the number 0 that appears in the table. This algorithm is taken from the Improved Zero Point method. The result of modification of ASM method is 75 while from the revision of the ASM method 79 results are obtained. Therefore, an optimization value decreases of 5%, so the modification of the ASM method provides a solution that remains optimal.

Keywords: Modification of ASM Method, Reduction, Optimal Solution, Unbalanced Transportation

(8)

DAFTAR ISI

Halaman

PERSETUJUAN i

PERNYATAAN ii

PENGHARGAAN iii

ABSTRAK iv

ABSTRACT v

DAFTAR ISI vi

DAFTAR TABEL viii

DAFTAR GAMBAR ix

BAB 1 PENDAHULUAN

1.1 Latar Belakang 1

1.2 Rumusan Masalah 3

1.3 Batasan Masalah 3

1.4 Tujuan Penelitian 4

1.5 Manfaat Penelitian 4

1.6 Metodologi Penelitian 4

BAB 2 TINJAUAN PUSTAKA

2.1 Program Linier 5

2.2 Masalah Transportasi 6

2.2.1 Solusi Optimal 8

2.2.2 Masalah Transportasi Seimbang 9

2.2.3 Masalah Transportasi Tidak Seimbang 9

2.3 Metode Transportasi 10

2.3.1 Metode Zero Neighbouring 10

2.3.2 Metode Zero Suffix 11

2.3.3 Metode Zero Point 12

2.3.4 Metode Exponential Approach 15

2.3.5 Metode ASM 16

BAB 3 MODIFIKASI METODE ASM

3.1 Analisis Metode ASM 20

3.2 Rancangan Optimasi 21

3.3 Metodologi Penelitian 22

BAB 4 IMPLEMENTASI DAN PEMBAHASAN 25

BAB 5 KESIMPULAN

5.1 Kesimpulan 36

DAFTAR PUSTAKA 37

(9)

vii

DAFTAR TABEL

Nomor Tabel

Judul Halaman

2.1 Masalah Transportasi 7

4.1 Masalah Transportasi Tak Seimbang 26

4.2 Masalah Transportasi Seimbang dengan Penambahan Kolom

Dummy 26

4.3 Hasil Reduksi Kolom 27

4.4 Penggantian Nilai Dummy 28

4.5 Hasil Reduksi Baris 29

4.6 Hasil Reduksi Kolom 30

4.7 Penetapan Indeks 31

4.8 4.9

Pengalokasian ke Indeks Terkecil Pengalokasian (1)

31 32

4.10 Pengalokasian (2) 32

4.11 Pengaolkasian (3) 32

4.16 Pengalokasian dengan Seluruh Permintaan dan Persediaan 34 Terpenuhi

4.17 Perbaikan Tabel Transportasi 34

(10)

DAFTAR GAMBAR

Nomor Gambar

Judul Halaman

2.1 Masalah Umum Transportasi 7

3.1 Rancangan Optimasi 22

(11)

BAB 1

PENDAHULUAN

1.1 Latar Belakang

Salah satu studi dalam riset operasi adalah masalah transportasi. Terdapat beberapa metode untuk menyelesaikan masalah transportasi, misalnya dalam mendapatkan solusi fisibel awal yaitu dengan Metode Pojok Barat Laut (North West Corner Method), Metode Biaya Terendah (Least Cost Method), dan Metode Aproksimasi Vogel (VAM). Setelah solusi awal di dapat, maka langkah selanjutnya adalah uji optimalitas dengan Metode Batu Loncat (Stepping Stone), atau Metode MODI (Modified Distribution) (Winston, 2004). Kelemahan dari serangkaian metode tersebut adalah memiliki dua proses penyelesaian. Metode ini dipandang kurang efisien.

Seiring dengan perkembangan waktu, muncul metode-metode baru yang lebih efisien dan sederhana untuk memecahkan masalah transportasi. Beberapa metode baru tersebut mudah dipahami dan memiliki perhitungan dengan sedikit iterasi. Dalam perhitungannya metode-metode tersebut langsung didapatkan solusi optimum tanpa harus mencari solusi fisibel awalnya terlebih dahulu atau disebut metode langsung.

Sebagian besar beberapa metode langsung telah berhasil memberikan solusi optimal pada masalah transportasi seimbang, sedangkan untuk masalah transportasi tak seimbang belum tentu menghasilkan solusi optimal. Salah satu metode langsung tersebut adalah metode ASM (Abdul, Shakel, dan M. Khalid).

Quddoos et al. (2012) menunjukkan karakteristik dari metode ASM ini menitikberatkan pada nilai hasil reduksi yang bernilai nol, lanjut ke penetapan indeks pada angka 0, hingga pengalokasian dari indeks terkecil. Metode ASM ini telah berhasil memberikan solusi optimal pada masalah transportasi seimbang.

Quddoos et al. (2016) kembali melakukan studi revisi metode ASM pada masalah transportasi tak seimbang tetapi terdapat Initial Basic Feasible Solution (IBFS)

(12)

yang sangat dekat ke solusi optimum. Sehingga perlu adanya perbaikan agar metode ASM dapat memberikan solusi optimal pada masalah transportasi tak seimbang. Pada revisi metode ASM terdapat algoritma berupa penambahan baris/kolom dummy dimana biaya pada baris/kolom dummy tersebut bernilai 0 sehingga sangat berpengaruh terhadap hasil reduksi. Maka harus diberikan penambahan algoritma untuk mengoptimalkan angka 0 yang muncul pada baris/kolom dummy.

Masalah transportasi adalah jenis khusus dari masalah program linier yang muncul di banyak aplikasi praktis. Dan ini adalah salah satu aplikasi teknik program linier yang paling awal dan paling bermanfaat. Telah dipelajari secara luas dalam Manajemen Logistik dan Operasi dimana distribusi barang dan komoditas dari sumber ke tujuan merupakan masalah penting. Masalah itu diformulasikan oleh matematikawan asal Prancis, Gaspard Monge pada tahun 1781. (He D et al. 2014)

Masalah transportasi adalah salah satu yang sering didengar dan paling penting dari masalah program linier. Masalah transportasi dapat dideskripsikan sebagai sejumlah komoditas homogen tertentu tersedia di sejumlah sumber dan jumlah yang tetap diperlukan untuk memenuhi permintaan di sejumlah tujuan.

Kondisi yang seimbang yaitu total permintaan sama dengan total persediaan.

Kemudian menemukan jadwal pengiriman barang yang optimal dengan kepuasan permintaan di setiap tujuan adalah tujuan utama dari masalah transportasi. Pada tahun 1941, Hitchcock mengembangkan masalah transportasi dasar bersama dengan metode konstruktif solusi dan kemudian pada tahun 1949 Koopmans mendiskusikan masalah secara rinci. Selanjutnya pada tahun 1951 Dantzig merumuskan masalah transportasi sebagai masalah pemograman linier dan juga menyediakan metode solusi. Sekarang masalah transportasi sehari-hari telah menjadi aplikasi standar untuk perkumpulan industri yang memiliki beberapa unit manufaktur, gudang, dan pusat distribusi (Quddoos et al. 2012).

Metode transportasi dirancang untuk melakukan optimalisasi variabel yang digunakan dalam memecahkan masalah transportasi, termasuk didalamnya masalah pengiriman dari beberapa sumber ke beberapa tujuan dengan tetap

(13)

3

berorientasi pada biaya minimum, dimana setiap sumber mempunyai kapasitas tertentu dan setiap tujuan mempunyai permintaan tertentu pula. Perusahaan yang menjadikan model transportasi sebagai alat strategi akan mempunyai keunggulan dalam merebut persaingan diantara perusahaan dengan produk sejenis. Hal itu dikarenakan tidak semua perusahaan mampu melakukan penghematan biaya operasional terutama biaya transportasi. Pada masalah transportasi yang merupakan bagian dari program linier ini, yang harus diperhatikan adalah bahwa total kuantitas pada seluruh sumber harus sama dengan total kuantitas pada seluruh tujuan, dengan kata lain harus seimbang, jika tak seimbang, maka perlu ditambahkan kuantitas dummy. Dan cara penyelesaian dapat dilakukan dengan menggunakan metode simpleks atau dengan menggunakan teknik-teknik khusus yang penyelesaiannya lebih efisien dan beraneka ragam.

Berdasarkan uraian diatas, maka penulis memberi tulisan ini dengan judul

“Optimasi Transportasi Tak Seimbang Menggunakan Modifikasi Metode ASM”

1.2 Rumusan Masalah

Berdasarkan pengamatan penulis, maka rumusan masalah pada penelitian ini adalah adanya pada revisi metode ASM masih terdapat hasil Initial Basic Feasible Solution (IBFS) yang sangat dekat ke solusi optimum. Hal ini terjadi untuk beberapa masalah transportasi tak seimbang dikarenakan adanya penambahan dummy dengan nilai awal 0 sehingga mempengaruhi hasil reduksi.

1.3 Batasan Masalah

Batasan masalah pada penelitian ini adalah penambahan algoritma nantinya memudahkan untuk melakukan perhitungan matematik dan hasil yang diberikan tetap termasuk optimal dari hasil pada metode sebelumnya.

(14)

1.4 Tujuan Penelitian

Tujuan penelitian ini adalah menunjukkan bahwa modifikasi metode ASM merupakan solusi optimal pada masalah transportasi tak seimbang.

1.5 Manfaat Penelitian

1. Menambah wawasan dan informasi dalam bidang operasi riset yang berhubungan dengan masalah transportasi tak seimbang menggunakan metode ASM.

2. Sebagai bahan referensi bacaan untuk penelitian sejenisnya.

1.6 Metodologi Penelitian

Metodologi yang digunakan dalam penelitian ini didasarkan pada studi literatur dan studi kasus yang bersumber dari buku atau jurnal. Adapun langkah-langkah yang digunakan dalam menyelesaikan permasalahan pada penelitian ini adalah sebagai berikut:

1. Mengamati keseimbangan masalah transportasi

2. Membuat tabel transportasi seimbang dengan menambahkan dummy dengan nilai awal 0

3. Reduksi tabel transportasi dengan dummy

4. Menetapkan indeks untuk setiap sel yang bernilai 0 5. Mengalokasikan sel ke indeks terkecil

6. Membuat kesimpulan dari hasil yang diperoleh

(15)

BAB 2

TINJAUAN PUSTAKA

2.1 Program Linier

Program linier adalah suatu cara yang digunakan untuk menyelesaikan masalah optimasi suatu model linier dengan berbagai tujuan dan kendala yang dihadapinya. Masalah program linier ini berkembang pesat setelah ditemukan suatu metode penyelesaian program linier dengan metode simpleks yang dikemukakan oleh George Dantzig pada tahun 1947. Selanjutnya, berbagai cara dan metode dikembangkan untuk menyelesaikan masalah program linier bahkan sampai pada masalah riset operasi hingga tahun 1950-an seperti pemrograman dinamik, teori antrian, dan teori persediaan.

Tujuan utama dari program linier ini adalah menentukan nilai optimum (maksimal/minimal) dari fungsi tujuan yang telah ditetapkan. Secara umum, fungsi pada model ini ada dua macam, yaitu fungsi tujuan dan fungsi pembatas/kendala.

1. Fungsi tujuan adalah fungsi yang menggambarkan tujuan/sasaran di dalam program linier yang dimaksudkan untuk menentukan nilai optimum dari fungsi tersebut yaitu nilai maksimal untuk masalah keuntungan dan nilai minimal untuk masalah biaya.

2. Fungsi pembatas merupakan bentuk penyajian secara matematika yang diperlukan berkenaan dengan adanya keterbatasan sumber daya yang tersedia, misalnya jumlah bahan baku yang terbatas, luas wilayah, waktu kerja, jumlah tenaga kerja, luas gudang persediaan.

Seperti yang telah dijelaskan diatas, optimasi program linier memiliki formula sebagai berikut:

Fungsi tujuan max/min (2.1)

Dengan kendala i = 1, 2, ..., m

(16)

Untuk memperoleh solusi yang optimum, formula tersebut dapat diselesaikan dengan metode grafik atau metode simpleks. Metode grafik digunakan apabila permasalahan yang diselesaikan cukup sederhana dan hanya dapat menyelesaikan maksimal 2 variabel. Metode simpleks merupakan prosedur aljabar yang bersifat iteratif, yang bergerak selangkah demi selangkah, dimulai dari suatu titik ekstrim pada daerah fisibel menuju titik ekstrim yang optimum (Zenis dkk, 2015).

2.2 Masalah Transportasi

Masalah transportasi merupakan masalah pendistribusian barang dari beberapa sumber (persediaan atau supply) ke beberapa tujuan (permintaan atau demand) dengan tujuan untuk meminimumkan biaya transportasi atau memaksimumkan keuntungan (Siswanto, 2016).

Pada masalah transportasi terdapat beberapa sumber dan tujuan tertentu, komoditas atau barang yang didistribusikan dari setiap sumber dan yang diminta oleh setiap tujuan dengan jumlah tertentu. Komoditas yang akan dikirim dari sumber ke tujuan, besarnya disesuaikan dengan permintaan atau kapasitas sumber dan biaya pengangkutan komoditas. Oleh karena itu, permasalahan yang dibahas pada masalah transportasi adalah bagaimana mengatur distribusi barang untuk meminimumkan biaya total distribusi barang (Dimyati dan Akhmad, 1992).

Dalam masalah transportasi, pola pengiriman optimal antara sumber atau pusat persediaan dan tujuan atau pusat permintaan harus ditentukan. Misalkan sumber m adalah menyediakan n tujuan dengan produk tertentu. Terdapat sebagai jumlah produk yang tersedia di sumber i, dan sebagai jumlah produk yang diperlukan di tujuan j. Selanjutnya, biaya pengiriman satu unit produk dari sumber i ke tujuan j diasumsikan sebagai , dan terdapat adalah jumlah yang dikirim dari sumber i ke tujuan j. Jika biaya pengiriman diasumsikan proporsional dengan jumlah yang dikirim dari setiap sumber ke setiap tujuan sehingga untuk meminimalkan total biaya pengiriman ternyata menjadi masalah program linier (He D et al. 2014).

(17)

7

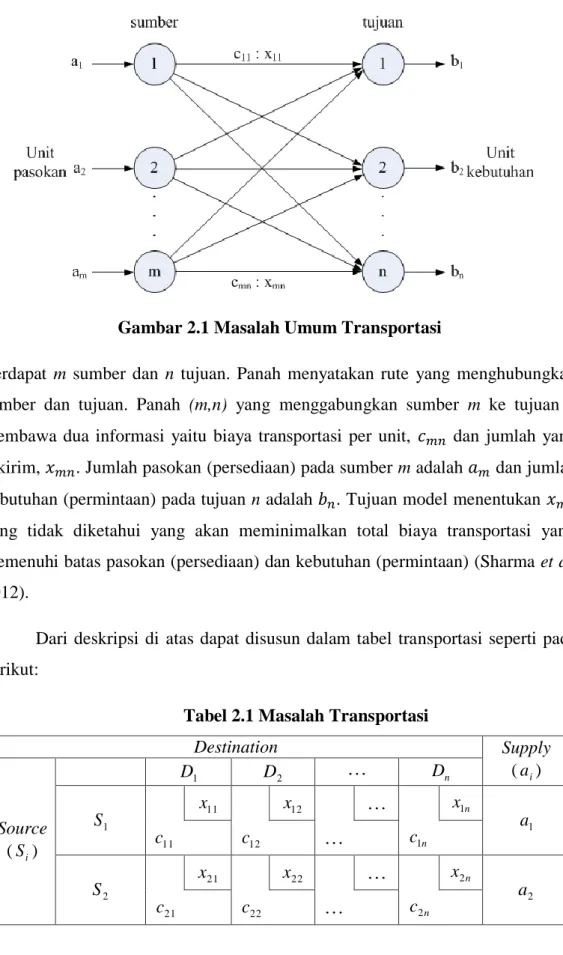
Masalah umum transportasi direpresentasikan oleh gambar berikut

Gambar 2.1 Masalah Umum Transportasi

Terdapat m sumber dan n tujuan. Panah menyatakan rute yang menghubungkan sumber dan tujuan. Panah (m,n) yang menggabungkan sumber m ke tujuan n membawa dua informasi yaitu biaya transportasi per unit, dan jumlah yang dikirim, . Jumlah pasokan (persediaan) pada sumber m adalah dan jumlah kebutuhan (permintaan) pada tujuan n adalah . Tujuan model menentukan yang tidak diketahui yang akan meminimalkan total biaya transportasi yang memenuhi batas pasokan (persediaan) dan kebutuhan (permintaan) (Sharma et al.

2012).

Dari deskripsi di atas dapat disusun dalam tabel transportasi seperti pada berikut:

Tabel 2.1 Masalah Transportasi

Destination Supply

(a ) _i

Source (S ) _i

D 1 D ₂  D n

S 1 ¹¹

x x ₁₂  x₁ⁿ

a 1

c 11 c ₁₂  c₁ⁿ

S 2 x ²¹ x ₂₂  x₂ⁿ

a 2

c 21 c ₂₂  c₂ⁿ

(18)

Destination Supply (a ) _i

Source (S ) _i

D 1 D ₂  D n

    

    

S m ^m¹

x x_m₂ 12 xmn

a m 1

c m c_m₂  ^c^mn

Demand

(b_j) b¹ b ₂  b ⁿ

Sumber: Patel et al. (2017) dalam Global Journal of Pure and Applied Mathematics

keterangan:

: sumber ke i, i = 1, 2, ..., m : tujuan ke j, j = 1, 2, ..., n : persediaan ke i, i = 1, 2, ..., m : permintaan ke j, j = 1, 2, ..., n

: biaya transportasi barang dari sumber i ke tujuan j, i = 1, 2, ..., m j = 1, 2, ..., n

: banyak barang yang diangkut dari sumber i ke tujuan j, i = 1, 2, ..., m j = 1, 2, ..., n Secara matematis, masalah ini dapat dinyatakan sebagai

Minimum ∑∑ (2.2) bergantung pada

∑ i = 1, 2, ..., m (2.3)

∑ j = 1, 2, ..., n (2.4)

2.2.1 Solusi Optimal

Solusi optimal adalah solusi yang layak (belum tentu dasar) dikatakan optimal jika meminimalkan total biaya transportasi. (Mamidi et al. 2014)

(19)

9

2.2.2 Masalah Transportasi Seimbang

Masalah transportasi seimbang adalah jumlah persediaan dari beberapa sumber sama dengan jumlah permintaan beberapa tempat tujuan, yaitu



^ ⁿ

j j m

i

i a

b _(2.5)

2.2.3 Masalah Transportasi Tidak Seimbang

Masalah transportasi tidak seimbang adalah jumlah persediaan dari beberapa sumber tidak sama dengan jumlah permintaan beberapa tempat tujuan. Dalam kasus masalah transportasi tak seimbang, dimana persediaan lebih besar dari permintaan atau sebaliknya yaitu sebagai berikut.



^ ⁿ

j j m

i

i a

b (2.6)



^ ⁿ

j j m

i

i a

b (2.7)

Batasan di atas dikemukakan hanya karena ia menjadi dasar dalam pengembangan teknik transportasi. Namun, setiap persoalan transportasi dapat dibuat seimbang dengan cara memasukkan variable artifisial (semu). Jika jumlah demand melebihi jumlah supply, maka dibuat suatu sumber dummy yang akan men-supply kekurangan tersebut, yaitu sebanyak ∑ ∑ .

Sebaliknya, jika jumlah supply melebihi jumlah demand, maka dibuat suatu tujuan dummy untuk menyerap kelebihan tersebut, yaitu sebanyak ∑

∑ .

Biaya pengiriman barang dari sumber dummy ke seluruh tujuan adalah nol. Hal ini dapat dipahami karena pada kenyataannya dari sumber dummy tidak terjadi pengiriman. Begitu pula dengan biaya pengiriman barang dari semua sumber ke tujuan dummy adalah nol.

(20)

2.3 Metode Transportasi

Masalah transportasi dapat diselesaikan dengan beberapa metode, misalnya dalam mendapatkan solusi fisibel awal yaitu dengan Metode Pojok Barat Laut (North West Corner Method), Metode Biaya Terendah (Least Cost Method), dan Metode Aproksimasi Vogel (VAM). Setelah solusi awal di dapat, maka langkah selanjutnya adalah uji optimalitas dengan Metode Batu Loncat (Stepping Stone), atau Metode MODI (Modified Distribution) (Winston, 2004).

Beberapa metode langsung yang berhasil dikembangkan diantaranya Metode Zero Neigbouring, Metode Zero Suffix, Metode Zero Point, Metode Exponential Approach, Metode ASM, dan sebagainya. Karakteristik dari beberapa metode ini menitikberatkan pada biaya hasil reduksi yang bernilai nol.

2.3.1 Metode Zero Neighbouring

Metode Zero Neighbouring diterapkan untuk menemukan solusi yang layak untuk masalah transportasi secara langsung. Metode yang diusulkan memberikan solusi yang selalu layak (mungkin optimal untuk sebagian) tanpa gangguan kondisi degenerasi. Metode ini membutuhkan iterasi minimal untuk mencapai optimalitas.

Pada metode langsung ini di hitung nilai rata-rata sekitar angka 0 yang bukan bernilai 0, kemudian pengalokasian bergantung pada nilai rata-rata terbesar (Thiagarajan et al. 2013).

Algoritma metode Zero Neighbouring (Thiagarajan et al. 2013):

1. Membuat tabel transportasi.

2. Pilih nilai minimum dari setiap baris dan kurangi dengan setiap elemen di baris yang sesuai.

3. Pilih nilai minimum dari setiap kolom dan kurangi dengan setiap elemen di kolom yang sesuai.

4. Dalam matriks biaya tereduksi akan ada setidaknya satu nol di setiap baris dan kolom, kemudian cari rata-rata sekitar 0 yang bukan bernilai 0 di posisi nol.

5. Temukan nilai maksimum di antara sekitar 0. Jika memiliki satu nilai maksimum, maka pertama-tama berikan permintaan yang sesuai dengan sel.

(21)

11

Jika memiliki nilai yang sama maka pilih { } dan berikan permintaan semaksimal mungkin.

6. Setelah langkah diatas, permintaan (kolom) atau persediaan (baris) yang habis untuk diratakan. Matriks yang dihasilkan harus memiliki setidaknya satu nol pada setiap baris dan kolom, kalau tidak, ulangi langkah ke 5.

7. Ulangi langkah 2 hingga langkah 6 sampai solusi yang layak diperoleh.

2.3.2 Metode Zero Suffix

Sama seperti Metode Zero Neighbouring, Metode Zero Suffix juga mempunyai karakteristik menghitung nilai rata-rata sekitar angka 0 yang bukan bernilai 0, kemudian pengalokasian bergantung pada nilai rata-rata terbesar.

Algoritma Metode Zero Suffix (Fegade et al. 2012):

1. Membuat tabel transportasi

2. Kurangi setiap entri baris dari tabel transportasi dari baris minimum yang sesuai setelah itu kurangi setiap entri kolom dari tabel transportasidari kolom minimum yang sesuai.

3. Dalam matriks biaya yang dikurangi akan ada setidaknya satu nol di setiap baris dan kolom, kemudian cari nilai akhiran dari semua nol dalam matriks biaya yang dikurangi yang dilambangkan dengan S, oleh karena itu S = {tambahkan biaya dari sisi terdekat dari nol / biaya tambahan}

4. Pilih maksimum S, jika memiliki satu nilai maksimum maka persediaan pertama ke permintaan tersebut sesuai dengan sel. Jika memiliki nilai yang lebih sama maka pilih { } dan berikan pemintaan semaksimal mungkin 5. Setelah langkah diatas, permintaan (kolom) atau persediaan (baris) yang habis

harus diratakan. Matriks yang dihasilkan harus memiliki setidaknya satu nol pada setiap baris dan kolom, jika tidak, ulangi langkah ke 2

6. Ulangi langkah 3 hingga langkah 5 sampai solusi optimal diperoleh.

Sharma et al. (2013) melakukan modifikasi metode Zero Suffix yang bebas dari masalah degenerasi, dan membutuhkan sedikitnya jumlah iterasi untuk mencapai optimalitas sehingga lebih sederhana, mudah dimengerti dan diterapkan.

(22)

Algoritma metode Zero Suffix (Sharma et al. 2013):

1. Membuat tabel transportasi untuk masalah transportasi yang diberikan

2. Kurangi elemen terkecil dari setiap baris dari semua elemen baris yang sesuai 3. Kurangi elemen terkecil dari setiap kolom dari semua elemen kolom yang

sesuai dari tabel transportasi yang diperoleh pada langkah 2

4. Temukan nilai akhiran, S dari setiap nol dalam tabel transportasi biaya rendah sebagai berikut: S = rata-rata perbedaan dari elemen terkecil dan elemen terkecil selanjutnya dari barisnya dan elemen terkecil selanjutnya dari kolomnya.

5. Cari nilai akhiran terbesar dari noldan alokasikan ke sel yang sesuai dan hapus baris/kolom yang habis untuk mendapatkan tabel transportasi yang dikurangi. Lanjutkan ke langkah 2.

6. Ulangi langkah 2 hingga 5 sampai semua permintaan dan persediaan habis.

2.3.3 Metode Zero Point

Metode Zero Point adalah sebuah prosedur sistematis untuk masalah transportasi dan mudah diterapkan dan dapat digunakan untuk semua jenis masalah transportasi apakah memaksimalkan atau meminimalkan fungsi objektif. Metode Zero Point memberikan solusi optimal tanpa bantuan metode modifikasi lainnya.

Pada metode Zero Point diperhatikan permintaan dan persediaan pada sel dengan biaya tereduksi 0 yang bersangkutan (Sharma et al. 2012).

Algoritma Metode Zero Point (Sharma et al. 2012):

1. Membuat tabel transportasi untuk masalah transportasi yang diberikan, kemudian jika tidak seimbang, mengubahnya menjadi seimbang

2. Kurangi setiap entri baris dari tabel transportasi dari baris minimum

3. Kurangi setiap entri kolom dari tabel transportasisetelah menggunakan langkah 2 dari minimum kolom

4. Periksa apakah setiap kolom permintaan kurang dari jumlah persedian yang biaya berkurang dalam kolom itu adalah nol. Juga periksa apakah setiap baris persediaan kurang dari jumlah permintaan yang biaya berkurang dalam baris

(23)

13

itu adalah nol. Jika demikian, lanjutkan ke langkah 7 (tabel yang dikurangi itu disebut tabel peruntukan). Jika tidak, lanjut ke langkah 5

5. Gambarkan jumlah minimum garis horizontal dan garis vertikal untuk menutup semua nol dari tabel transportasi yang dikurangi sehingga beberapa entri dari baris atau kolom yang tidak memenuhi kondisi langkah 4, tidak tertutupi

6. Kembangkan tabel transportasi tereduksi yang baru dan direvisi sebagai berikut:

(i) Menemukan entri terkecil dari matriks biaya rendah yang tidak tercakup oleh jalur apapun.

(ii) Kurangi entri ini dari semua entri yang tidak ditemukan dan yang sama untuk semua entri yang terletak di persimpangan dua baris, dan kemudian lanjutkan ke langkah 4.

7. Pilih sel di tabel transportasi berkurang yang mengurangi biaya adalah biaya maksimum. Katakan (a,b). Jika ada lebih dari satu, maka pilih siapa saja.

8. Pilih sel dalam baris a atau kolom b dari tabel transportasi berkurang yang merupakan satu-satunya sel yang mengurangi biaya adalah nol dan kemudian membagikan setinggi mungkin ke sel itu. Jika sel seperti itu tidak terjadi untuk nilai apa pun, kita pilih sel apa pun dalam tabel transportasi yang dikurangi yang mengurangi biaya nol.

9. Mereformasi tabel transportasi yang dikurangi setelah menghapus titik persediaan yang digunakan sepenuhnya dan titik permintaan yang diterima dan juga memodifikasinya untuk memasukkan titik persediaan yang tidak sepenuhnya digunakan dan tidak menerima titik permintaan

10. Ulangi langkah 7 hingga langkah 9 sampai semua titik persediaan dan semua titik permintaan diterima sepenuhnya

11. Pembagian ini menghasilkan solusi untuk masalah transportasi.

Selanjutnya metode ini ditingkatkan dengan metode yang lebih sederhana dan efisien, mudah dimengerti dan memberikan solusi optimal untuk masalah transportasi teratur atau fuzzy. Metode ini ditingkatkan oleh Samuel (2012) dengan nama Improved Zero Point Method.

(24)

Algoritma IZPM (Samuel, 2012):

1. Inisialisasi

Sudah diketahui bahwa suatu ketidakseimbangan pada masalah transportasi adalah setara dengan masalah transportasi seimbang yang biasa dengan satu kolom dummy atau satu baris dummy dengan penambahan biaya 0.

2. Mengembangkan Tabel Biaya

(a) Jika kolom dummy (baris) ditambahkan, kurangi nilai terkecil dari setiap kolom (baris) dari tabel biaya yangdiberikan dan mengurangi dari setiap elemen dari kolom (baris).

(b) Dalam matriks yang diturunkan diperoleh dari 2(a), ganti biaya dummy terbesar dari biaya transportasi.

3. Penentuan Nilai Nol

(a) Temukan elemen terkecil dari setiap baris pada nilai tabel dan kemudian kurangi itu dari setiap elemen dari baris.

(b) Dalam matriks yang diturunkan diperoleh dari 3(a), temukan elemen terkecil di setiap kolom dan kemudian kurangi itu dari setiap elemen dari kolom. Setiap baris dan kolom sekarang mempunyai paling sedikit satu 0.

4. Kriteria Optimalitas

(a) Verifikasi setiap elemen persediaan kurang dari atau sama dengan permintaan, yang mengurangi biaya nol.

(b) Sekarang verifikasi setiap elemen permintaan kurang dari atau sama dengan persediaan, yang mengurangi biaya nol.

(c) Jika 4(a) dan 4(b) terpenuhi, maka lanjut ke langkah 7, jika tidak, lanjut ke langkah 5.

5. Merevisi Tabel Biaya Peluang

(a) Gambarkan jumlah minimum garis horizontal dan vertikal untuk menutup semua nol dalam tabel biaya revisi yang diperoleh dari langkah 3. (Menghilangkan baris dan kolom yang tidak terpenuhi).

6. Kembangkan Tabel Biaya Peluang Revisi yang Baru

(25)

15

(a) Dari sel-sel yang tidak tercakup oleh garis apa pun, pilih elemen terkecil.

Sebut nilai ini k.

(b) Kurangi k dari setiap elemen di dalam sel yang tidak ditutupi oleh garis.

(c) Tambahkan k ke setiap elemen di dalam sel yang di cakup oleh dua garis, yaitu perpotongan dua garis.

(d) Elemen dalam sel tertutup oleh satu baris tetap tidak berubah.

(e) Kemudian lanjutkan ke langkah 4.

7. Penentuan Sel untuk Alokasi

(a) Identifikasi biaya transportasi unit terbesar dalam matriks berkurang yang diperoleh dari langkah 4. Jika ikatan terjadi, gunakan sembarang pilihan pemutusan ikatan. Sebut sel ini (i,j).

(b) Pilih satu sel nol untuk alokasi, sesuai baris ke-i dan atau kolom ke-j, jika ada.

(c) Mengalokasikan semaksimal mungkin ke sel itu, dan menyeberang dengan cara biasa.

(d) Jika sel tunggal nol tidak ada di kedua baris ke-i dan kolom ke-j kemudian pilih biaya transportasi unit terbesar berikutnya dan ulangi proses dari langkah 7(b) ke langkah 7(c) sampai semua persyaratan rim puas. (Jika tidak, akhirnya pilih sewenang-wenang).

2.3.4 Metode Exponential Approach

Metode Exponential Approach menetapkan penalti eksponensial pada setiap sel biaya yang bernilai 0. Penalti eksponensial adalah banyaknya angka 0 pada baris ke-i dan kolom ke-j selain angka 0 yang terpilih. Pengalokasian pada sel dengan penalti eksponensial terkecil. Jika terdapat penalti eksponensial terkecil yang sama, maka pengalokasian bergantung pada rata-rata permintaan dan persediaan terkecil untuk sel yang bersesuaian (Vannan dan Rekha, 2013).

Algoritma Exponential Approach (Mamidi et al. 2014):

1. Membuat model transportasi dalam tabel dari masalah transportasi yang diberikan

(26)

2. Kurangi setiap entri baris dari tabel transportasi dari baris minimum masing- masing dan kemudian kurangi setiap entri kolom dari tabel transportasi dari minimum kolom terkait, sehingga setiap baris dan kolom akan memiliki setidaknya satu nol

3. Sekarang akan ada setidaknya satu nol di setiap baris dan kolom dalam matriks biaya yang dikurangi. Pilih nol pertama (baris bijaksana) yang terjadi dalam matriks biaya. Hitung jumlah total nol tidak termasuk yang dipilih di baris dan kolom yang sesuai. Dan kemudian tetapkan hukuman eksponensial (jumlah nol di baris dan kolom masing-masing). Ulangi prosedur untuk semua nol dalam matriks

4. Sekarang pilih nol dengan mana hukuman eksonensial minimum ditetapkan dari langkah 3 dan alokasikan masing-masing nilai sel dengan jumlah maksimumyang mungkin. Jika dasi terjadi untuk sel mana pun dalam nilai penalti, maka pertama-tama periksa nilai yang sesuai dalam permintaan dan penawaran, temukan nilai rata-ratanya dan tetapkan alokasi untuk nilai rata- rata terkecil. Dan jika lagi ikat terjadi maka periksa nilai yang sesuai di baris dan kolom dan pilih minimum

5. Setelah melakukan langah 4, hapus baris atau kolom (dimana persediaan atau permintaan menjadi nol) untuk perhitungan lebih lanjut

6. Perikasa apakah matriks yang dihasilkan memiliki setidaknya satu nol di setiap kolom dan di setiap baris. Jika tidak ulangi langkah 2, jika tidak lanjutkan ke langkah 7

7. Ulang langkah 3 hingga langkah 6 sampai dan kecuali semua permintaan dipenuhi dan semua persediaan habis

8. Untuk nilai yang dialokasikan, hitunglah biaya optimal.

2.3.5 Metode ASM

Metode ASM merupakan salah satu metode optimasi masalah transportasi yang langsung menguji keoptimalan dari tabel transportasi. Metode ASM memberikan solusi optimal secara langsung dengan iterasi yang lebih sedikit untuk masalah transportasi. Karena metode ini menghabiskan lebih sedikit waktu dan sangat

(27)

17

mudah untuk dimengerti dan diterapkan, maka akan menjadi sangat membantu untuk pengambilan keputusan yang menangani masalah permintaan dan persediaan (Quddoos et al. 2012).

Algoritma metode ASM (Quddoos et al. 2012):

1. Menyusun tabel transportasi dari masalah transportasi yang diberikan

2. Mengurangi biaya setiap baris pada tabel transportasi dengan biaya minimum masing-masing baris dan kemudian mengurangi biaya setiap kolom dengan nilai minimum masing-masing kolom.

3. Sekarang akan ada setidaknya satu nol di setiap baris dan setiap kolom dalam matriks biaya yang telah dikurangi. Pilih nol pertama, perhatikan (i, ) nol j yang dipilih, hitung jumlah total nol (tidak termasuk nol yang dipilih) di baris i dan kolom j . Kemudian pilih nol selanjutnya dan hitung jumlah total nol pada baris dan kolom dengan cara yang sama. Ulangi untuk semua nol pada matriks biaya.

4. Sekarang pilih nol dari sejumlah nol yang telah terhitung pada langkah 3 yang minimum dan berikan jumlah maksimum yang mungkin pada sel. Jika terjadi seri untuk beberapa nol yang terhitung dari langkah 3, pilih salah satu nol.

Alokasikan jumlah yang mungkin untuk sel tersebut.

5. Setelah melakukan langkah 4, hapus baris dan kolom untuk perhitungan lebih lanjut dimana persediaan dari sumber tertentu habis atau permintaan untuk tujuan tertentu terpenuhi.

6. Periksa apakah hasil perhitungan matriks terdapat minimal satu nilai nol di setiap baris dan di setiap kolom. Jika tidak, ulangi langkah 2, jika sebaliknya ke langkah 7.

7. Mengulangi langkah 3 sampai langkah 6 sampai seluruh permintaan terpenuhi dan seluruh persediaan habis.

Metode ini mampu memberikan solusi optimal untuk masalah transportasi seimbang tetapi untuk masalah transportasi tak seimbang belum tentu memberikan solusi optimal. Maka dilakukan revisi metode ASM pada penelitian selanjutnya untuk menyelesaikan masalah transportasi tak seimbang.

(28)

Algoritma Revisi Metode ASM (Quddoos et al. 2016):

1. Menyusun tabel transportasi dari masalah transportasi yang diberi. Periksa apakah masalahnya seimbang atau tidak. Jika masalah seimbang, langsung ke tahap 4, jika tidak, lanjut ke tahap 2.

2. Jika masalah tidak seimbang, kemudian salah satu dari dua kasus berikut mungkin terjadi:

a. Jika total persediaan melebihi total permintaan, masukkan kolom dummy tambahan pada tabel transportasi untuk menyerap kelebihan persediaan.

Biaya transportasi untuk sel di kolom dummy ini diatur ke „M‟ dimana M

> 0 adalah sangat besar tetapi batas nilai positif. atau

b. Jika total permintaan melebihi total persediaan, masukkan baris dummy tambahan pada tabel transportasi untuk memenuhi kelebihan permintaan.

Biaya transportasi untuk sel di baris dummy ini diatur ke „M‟ dimana M

> 0 adalah sangat besar tetapi batas nilai positif.

3. a. Di kasus (a) pada langkah 2, identifikasi elemen terendah dari setiap baris dan kurangi dari setiap elemen dari masing-masing baris dan kemudian yang dihasilkan tabel, identifikasi elemen terendah dari setiap kolom dan kurangi dari setiap elemen dari masing-masing kolom dan lanjut ke langkah 5. atau

b. Di kasus (b) pada langkah 2, identifikasi elemen terendah dari setiap kolom dan kurangi dari setiap elemen dari masing-masing kolom dan kemudian yang dihasilkan tabel, identifikasi elemen terendah dari setiap baris dan kurangi dari setiap elemen dari masing-masing baris dan lanjut ke langkah 5.

4. Identifikasi elemen terendah dari setiap baris dan kurangi dari setiap elemen dari masing-masing baris dan setelah dihasilkan tabel, identifikasi elemen terendah dari setiap kolom dan kurangi dari setiap elemen dari masing- masing kolom.

5. Dalam tabel yang telah dikurangi, setiap baris dan setiap kolom memiliki setidaknya satu nol. Sekarang, pilih nol pertama (katakan 0) dan hitung jumlah nol (tidak termasuk nol yang dipilih) di baris dan kolom dan catat

(29)

19

sebagai tanda dari nol yang telah dipilih. Ulangi proses ini untuk semua nol pada tabel transportasi.

6. Sekarang, pilih sel yang mengandung nol yang mana nilai yang bertanda adalah minimum dan berikan jumlah maksimum yang memungkinkan pada sel tersebut. Jika terjadi seri untuk beberap nol di langkah 5, pilih salah satu nol dari beberapa nol tersebut di baris dan kolom maksimum. Sediakan jumlah maksimum yang mungkin untuk sel tersebut.

7. Hapus baris atau kolom untuk dipertimbangkan lebih lanjut dimana persediaan dari sumber tertentu habis (atau permintaan untuk tujuan tertentu terpenuhi). Jika pada tahap apapun, kolom permintaan telah terpenuhi dan baris persediaan telah habis, kemudian hapus hanya satu kolom (atau baris) dan baris (atau kolom) yang tersisa diberikan persediaan (atau permintaan) nol dalam perhitungan lebih lanjut.

8. Sekarang periksa apakah tabel yang telah dikurangi mengandung setidaknya satu nol di setiap baris dan setiap kolom. Jika ini tidak terjadi, ulangi langkah 4, jika sebaliknya ke langkah 9.

9. Ulangi langkah 5 sampai langkah 8 sampai semua permintaan terpenuhi dan persediaan habis.

(30)

BAB 3

MODIFIKASI METODE ASM

3.1 Analisis Metode ASM

Metode ASM merupakan metode langsung untuk menyelesaikan masalah transportasi. Metode ini diperkenalkan oleh Abdul Quddoos, Dr. Shakeel Javaid, dan Prof. Mohd Masood Khalid yang selanjutnya disingkat menjadi ASM. Pada tahun 2012, Quddoos et al. telah menunjukkan bahwa metode ASM memberikan solusi optimal untuk menyelesaikan masalah transportasi seimbang. Algoritma pada metode ASM ini menitikberatkan pada hasil reduksi yang bernilai nol dari reduksi baris dan reduksi kolom. Selanjutnya menetapkan indeks dari angka 0 pada setiap baris dan kolom, dilanjutkan dengan pengalokasian sebesar mungkin dari jumlah persediaan dan permintaan pada indeks terkecil. Tetapi selama dalam penelitian, Quddoos et al temui sedikit masalah dimana metode ASM tidak langsung memberikan solusi optimal tetapi memberikan Initial Basic Feasible Solution (IBFS) terbaik yang mana sangat dekat ke solusi optimal. Satu dasar masalah yang ditemui adalah masalah transportasi tak seimbang. Untuk mengatasi masalah ini, Quddoos et al menghadirkan revisi metode ASM pada tahun 2016.

Solusi dari revisi metode ASM ini adalah adanya penambahan algoritma yaitu penambahan sel dummy. Sel dummy ini berfungsi untuk membuat tabel transportasi tak seimbang menjadi seimbang. Selanjutnya, untuk melakukan reduksi, tergantung dari penambahan baris atau kolom dummy. Jika baris dummy yang ditambahkan, maka dilakukan reduksi kolom terlebih dahulu setelah itu reduksi baris, begitu pula sebaliknya. Dan untuk algoritma selanjutnya sama seperti algoritma metode ASM sebelumnya yaitu menetapkan indeks dari angka 0 pada setiap baris dan kolom (termasuk baris/kolom dummy) dan dilanjutkan dengan pengalokasian sebesar mungkin dari jumlah persediaan dan permintaan (termasuk sel dummy yang ditambahkan) pada indeks terkecil.

(31)

21

Sehingga pada revisi metode ASM ini memberikan solusi optimal untuk masalah transportasi tak seimbang. Dan revisi metode ASM ini tetap mempunyai algoritma yang sederhana dan mudah dipahami.

3.2 Rancangan Optimasi

Pada penelitian ini, akan dilakukan modifikasi dari revisi metode ASM untuk menunjukkan bahwa modifikasi ini tetap memberikan solusi optimal pada masalah transportasi tak seimbang. Pada revisi metode ASM, terdapat algoritma berupa penambahan baris/kolom dummy dimana biaya pada baris/kolom dummy tersebut bernilai 0 sehingga sangat berpengaruh terhadap hasil reduksi. Maka diberikan penambahan algoritma untuk mengoptimalkan angka 0 yang muncul pada baris/kolom dummy. Untuk melakukan reduksi, sesuai dengan penambahan baris/kolom dummy. Jika baris dummy yang ditambahkan, maka lakukan reduksi baris terlebih dahulu selanjutnya lakukan penggantian nilai dummy dengan nilai tereduksi terbesar dan selanjutnya dilakukan reduksi kembali sehingga syarat pengoptimalan angka 0 terpenuhi. Dan sebaliknya dilakukan seperti itu jika kolom dummy yang ditambahkan. Penambahan algoritma ini diambil dari metode Improved Zero Point dimana metode ini juga merupakan metode langsung untuk menyelesaikan masalah transportasi. Dalam hal ini algoritma yang ditambahkan yaitu pada bagian reduksi dari penambahan dummy dan penggantian nilai dummy dengan nilai tereduksi terbesar.

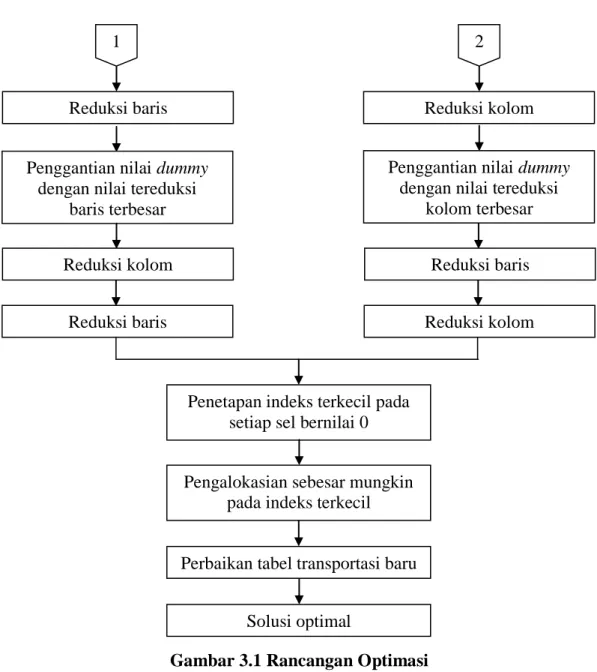
Rancangan optimasi ini digambarkan sebagai berikut:

Transportasi tak seimbang Transportasi seimbang dengan

penambahan dummy

Penambahan baris dummy Penambahan kolom dummy

1 2

(32)

Gambar 3.1 Rancangan Optimasi

3.3 Metodologi Penelitian

Adapun langkah penyelesaiannya sebagai berikut:

1. Mengamati keseimbangan masalah transportasi

Dengan melihat teori keseimbangan, maka kita bisa menentukan apakah masalah transportasi tersebut seimbang atau tak seimbang

2. Membentuk tabel transportasi seimbang

Dengan menambahkan dummy pada baris atau kolom dengan biaya awal 0 3. Reduksi tabel transportasi dengan dummy

Reduksi kolom

1 2

Penggantian nilai dummy dengan nilai tereduksi

baris terbesar

Penggantian nilai dummy dengan nilai tereduksi

kolom terbesar

Reduksi kolom Reduksi baris

Reduksi baris Reduksi kolom

Penetapan indeks terkecil pada setiap sel bernilai 0

Pengalokasian sebesar mungkin pada indeks terkecil

Perbaikan tabel transportasi baru

Solusi optimal Reduksi baris

(33)

23

3.1. Jika baris dummy yang ditambahkan, maka ke langkah ke-4. Kemudian mengganti biaya dummy dengan biaya terbesar dari hasil reduksi baris.

Selanjutnya ke langkah ke-5 kemudian langkah ke-4.

3.2. Jika kolom dummy yang ditambahkan, maka ke langkah ke-5.

Kemudian mengganti biaya dummy dengan biaya terbesar dari hasil reduksi kolom. Selanjutnya ke langkah ke-4 kemudian langkah ke-5.

4. Reduksi Baris

Mengurangi setiap entri baris dengan masing-masing biaya terkecilnya, yaitu

. 5. Reduksi kolom

Mengurangi setiap entri kolom dengan masing-masing biaya terkecilnya, yaitu .

6. Penetapan indeks

Menetapkan indeks e untuk setiap sel ij yang bernilai 0, yang mana indeks e adalah banyaknya angka 0 pada baris ke-i dan kolom ke-j dan tidak termasuk angka 0 yang terpilih pada sel-ij.

7. Pengalokasian

Memilih angka 0 dengan indeks e terkecil dan mengalokasikan sel dengan jumlah terbesar yang mungkin dengan melihat persediaan dan permintaan sel yang bersangkutan. Jika terdapat indeks e terkecil yang sama (lebih dari satu), maka menghitung masing-masing jumlah pada baris ke-i dan kolom ke-j dari sel-ij yang bersangkutan (sel yang memiliki indeks e terkecil yang sama) dan mengalokasikan sebesar mungkin pada sel dengan hasil penjumlahan terbesar. Jika masih terjadi kesamaan, maka memilih sel-ij (sel yang memiliki indeks e terkecil yang sama) yang memiliki rata-rata persediaan dan permintaan terkecil.

8. Perbaikan tabel transportasi

Membuat tabel transportasi baru untuk perhitungan selanjutnya dengan mengabaikan baris atau kolom yang permintaan atau persediaannya telah terpenuhi. Mengecek apakah tabel transportasi baru memiliki paling sedikit satu angka 0 pada setiap baris dan kolom.

Jika tidak terdapat, kembali ke langkah ke-4.

(34)

9. Mengulangi langkah ke-6 sampai langkah ke-8 sedemikian sehingga semua permintaan terpenuhi dan semua persediaan habis.

(35)

BAB 4

IMPLEMENTASI DAN PEMBAHASAN

Pada penelitian ini, data diperoleh dari jurnal “A Revised Version of ASM- Method for Solving Transportation Problem” (sumber: Int. J. Agricult. Sat. Sci tahun 2016).

Diketahui bahwa terdapat 4 sumber ( ) dan 3 tujuan ( ), dimana sumber dan tujuan ini saling terhubung membawa dua informasi yaitu biaya transportasi ( ) dan jumlah yang dikirim ( ). Dalam hal ini telah diketahui biaya dari setiap sumber ke setiap tujuan serta jumlah persediaan (supply) pada sumber dan jumlah permintaan (demand) pada tujuan.

Biaya yang diketahui dari setiap sumber ke setiap tujuan sebagai berikut Dari sumber ke tujuan = 2

Dari sumber ke tujuan = 7 Dari sumber ke tujuan = 14 Dari sumber ke tujuan = 3 Dari sumber ke tujuan = 3 Dari sumber ke tujuan = 1 Dari sumber ke tujuan = 5 Dari sumber ke tujuan = 4 Dari sumber ke tujuan = 7 Dari sumber ke tujuan = 1 Dari sumber ke tujuan = 6 Dari sumber ke tujuan = 2

Jumlah persediaan (supply) pada setiap sumber adalah sebagai berikut Pada sumber jumlah persediaan ( ) sebanyak 5

Pada sumber jumlah persediaan ( ) sebanyak 8 Pada sumber jumlah persediaan ( ) sebanyak 7

(36)

Pada sumber jumlah persediaan ( ) sebanyak 15 Maka



^aⁱ 35

Jumlah permintaan (demand) pada setiap tujuan adalah sebagai berikut Pada tujuan jumlah permintaan ( ) sebanyak 7

Pada tujuan jumlah permintaan ( ) sebanyak 9 Pada tujuan jumlah permintaan ( ) sebanyak 18 Maka



^b^j 34

Dari deskripsi diatas, dapat digambarkan pada tabel 4.1 berikut Tabel 4.1 Masalah Transportasi Tak Seimbang

D 1 D ₂ D ₃ Supply (a ) _i

S 1 2 7 14 5

S 2 3 3 1 8

S 3 5 4 7 7

S 4 1 6 2 15

Demand (b_j) 7 9 18

Terdapat jumlah persediaan (



^aⁱ)35 dan jumlah permintaan (



^b^j)34, maka diperoleh



^aⁱ^>



b , sehingga dibuat suatu tujuan dummy (kolom) untuk ^j menyerap kelebihan tersebut yaitu sebesar



^aⁱ 



^b^j 35341^{. Maka} diperoleh tabel 4.2 berikut.

Tabel 4.2 Masalah Transportasi Seimbang dengan Penambahan Kolom Dummy

D 1 D ₂ D ₃ Dummy Supply (a ) _i

S 1 2 7 14 0 5

S 2 3 3 1 0 8

S 3 5 4 7 0 7

S 4 1 6 2 0 15

Demand (b_j) 7 9 18 1 35

(37)

27

Diketahui bahwa terjadi penambahan kolom dummy, sehingga dilakukan reduksi kolom dengan mengurangi setiap entri kolom dengan masing-masing biaya terkecilnya.

Pada biaya terkecilnya terletak pada , sehingga

Pada kolom dummy yang ditambahkan, setiap entri kolom tetap bernilai 0, sehingga . Maka diperoleh tabel 4.3 berikut

Tabel 4.3 Hasil Reduksi Kolom

D 1 D ₂ D 3 Dummy Supply (a ) _i

S 1 1 4 13 0 5

S 2 2 0 0 0 8

(38)

S 3 4 1 6 0 7

S 4 0 3 1 0 15

Demand (b_j) 7 9 18 1 35

Selanjutnya dilakukan penggantian nilai dummy dengan nilai tereduksi kolom terbesar. Dari tabel hasil reduksi kolom diatas, diperoleh nilai tereduksi terbesar pada setiap entri kolom yaitu 13, sehingga diperoleh tabel 4.4 berikut

Tabel 4.4 Penggantian Nilai Dummy

S 1 1 4 13 13 5

S 2 2 0 0 13 8

S 3 4 1 6 13 7

S 4 0 3 1 13 15

Demand (b_j) 7 9 18 1 35

Selanjutnya dilakukan reduksi baris dengan mengurangi setiap entri baris dengan masing-masing biaya terkecilnya.

Pada , biaya terkecilnya terletak pada , sehingga

Pada , biaya terkecilnya terletak pada atau , sehingga

(39)

29

Maka diperoleh tabel 4.5 berikut

Tabel 4.5 Hasil Reduksi Baris

S 1 0 3 12 12 5

S 2 2 0 0 13 8

S 3 3 0 5 12 7

S 4 0 3 1 13 15

Demand (b_j) 7 9 18 1 35

Kembali dilakukan reduksi kolom agar setidaknya ada satu nol pada kolom dummy dengan mengurangi setiap entri kolom dengan masing-masing biaya terkecilnya.

(40)

Pada kolom dari penggantian nilai dummy, biaya terkecil terletak pada atau

, sehingga

Maka diperoleh tabel 4.6 berikut

Tabel 4.6 Hasil Reduksi Kolom

D 1 D ₂ D 3 Dummy Supply (a ) _i

S 1 0 3 12 0 5

S 2 2 0 0 1 8

(41)

31

S 3 3 0 5 0 7

S 4 0 3 1 1 15

Demand (b_j) 7 9 18 1 35

Selanjutnya dilakukan penetapan indeks e untuk setiap sel ij yang bernilai nol dimana indeks e adalah banyaknya angka 0 pada baris ke-i dan kolom ke-j. Maka diperoleh tabel 4.7 berikut

Tabel 4.7 Penetapan Indeks

S 1 02 3 12 01 5

S 2 2 0₂ 0₁ 1 8

S 3 3 0₁ 5 0₂ 7

S 4 01 3 11 1 15

Demand (b_j) 7 9 18 1 35

Selanjutnya dilakukan pengalokasian dengan cara memilih angka 0 dengan indeks e terkecil dan mengalokasikan sel dengan jumlah terbesar yang mungkin dengan melihat persediaan dan permintaaan sel yang bersangkutan sampai permintaan dan persediaan terpenuhi. Diperoleh indeks terkecil pertama pada sel ( , Dummy) dan dapat diperlihatkan pada tabel 4.8 berikut

Tabel 4.8 Pengalokasian ke Indeks Terkecil

S 1 02 3 12 01 5

S 2 2 0₂ 0₁ 1 8

S 3 3 01 5 02 7

S 4 01 3 11 1 15

Demand (b_j) 7 9 18 1 35

Diketahui indeks terkecil pertama terdapat pada sel ( , Dummy) dan dilakukan pengalokasian permintaan yang berjumlah 1, sehingga permintaan pada kolom dummy terpenuhi dan persediaan pada baris , bersisa 4. Selanjutnya dilakukan penetapan indeks kembali pada sel ( , ) dan diperoleh tabel 4.9 berikut

(42)

Tabel 4.9 Pengalokasian (1)

S 1 0₁ 3 12 1 4

S 2 2 02 01 8

S 3 3 0₁ 5 7

S 4 0₁ 3 1₁ 15

Demand (b_j) 7 9 18 0 35

Diketahui indeks terkecil selanjutnya terdapat pada sel ( , ) dan dilakukan pengalokasian persediaan yang berjumlah 4, sehingga persediaan pada baris terpenuhi dan permintaan pada kolom bersisa 3. Selanjutnya dilakukan penetapan indeks kembali pada sel ( , ) dan diperoleh tabel 4.10 berikut

S 1 4 1 0

S 2 2 02 01 8

S 3 3 0₁ 5 7

S 4 01 3 11 15

Demand (b_j) 3 9 18 0 35

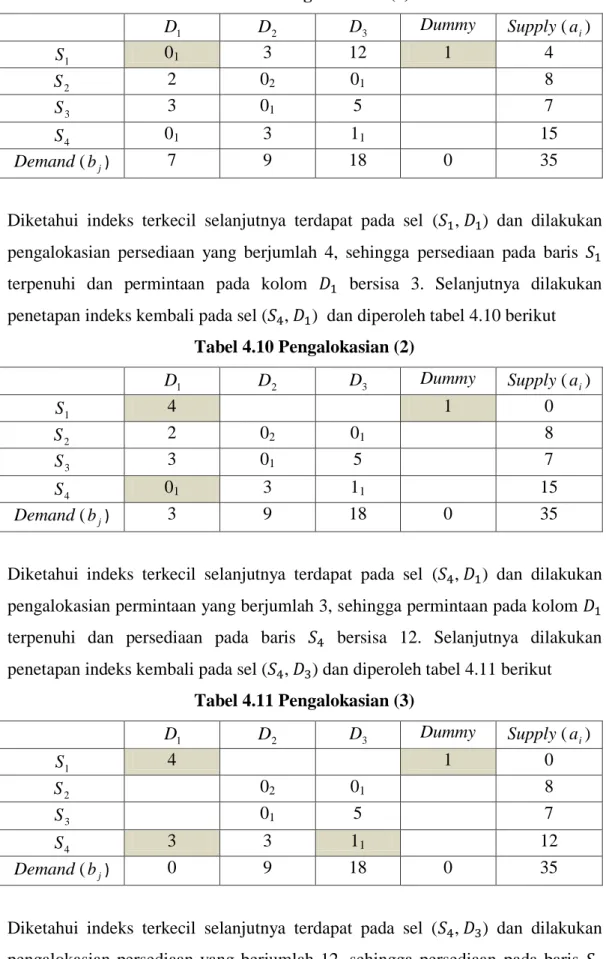
Diketahui indeks terkecil selanjutnya terdapat pada sel ( , ) dan dilakukan pengalokasian permintaan yang berjumlah 3, sehingga permintaan pada kolom terpenuhi dan persediaan pada baris bersisa 12. Selanjutnya dilakukan penetapan indeks kembali pada sel ( , ) dan diperoleh tabel 4.11 berikut

S 1 4 1 0

S 2 0₂ 0₁ 8

S 3 0₁ 5 7

S 4 3 3 11 12

Demand (b_j) 0 9 18 0 35

Diketahui indeks terkecil selanjutnya terdapat pada sel ( , ) dan dilakukan pengalokasian persediaan yang berjumlah 12, sehingga persediaan pada baris