Informasi Dokumen
- Penulis:
- A. Wagiyo
- Sri Mulyono
- Susanto
- Pengajar:
- Dian Pramani
- Suharyati
- Sekolah: Pusat Perbukuan, Departemen Pendidikan Nasional
- Mata Pelajaran: Matematika
- Topik: Pegangan Belajar Matematika 3 Untuk SMP/MTs Kelas IX
- Tipe: buku
- Tahun: 2008
- Kota: Jakarta
Ringkasan Dokumen
I. Kesebangunan
Bab ini membahas konsep kesebangunan dalam geometri, yang merupakan dasar untuk memahami hubungan antara bangun datar. Siswa diajarkan untuk mengenali bangun datar yang sebangun dan kongruen, serta sifat-sifat yang dimiliki oleh dua segitiga yang sebangun. Materi ini penting karena memberikan landasan bagi siswa untuk memahami transformasi geometri dan aplikasinya dalam kehidupan sehari-hari. Melalui latihan yang diberikan, siswa diajarkan untuk menganalisis dan memecahkan masalah yang berkaitan dengan kesebangunan, yang memperkuat kemampuan berpikir kritis dan analitis mereka.
1.1 Bangun Datar yang Sebangun dan Kongruen
Materi ini membahas definisi bangun datar yang sebangun dan kongruen, serta memberikan contoh-contoh konkret dari kehidupan sehari-hari. Siswa diajarkan untuk membedakan antara dua konsep ini dan memahami pentingnya dalam konteks geometri. Dengan menggunakan gambar dan diagram, siswa dapat lebih mudah memahami perbedaan antara kesebangunan dan kongruensi, yang merupakan konsep dasar dalam geometri.
1.2 Sifat-sifat Dua Segitiga Sebangun dan Kongruen
Di bagian ini, siswa mempelajari sifat-sifat segitiga yang sebangun dan kongruen. Sifat-sifat ini sangat penting untuk memahami bagaimana segitiga dapat digunakan dalam berbagai aplikasi, termasuk dalam perhitungan luas dan volume. Dengan latihan soal yang bervariasi, siswa dapat menerapkan teori yang telah dipelajari untuk menyelesaikan masalah praktis.
1.3 Penerapan Kesebangunan
Bab ini menekankan penerapan konsep kesebangunan dalam situasi nyata. Melalui studi kasus dan contoh, siswa diajarkan bagaimana konsep ini dapat digunakan untuk memecahkan masalah yang kompleks. Penerapan ini tidak hanya meningkatkan pemahaman siswa tentang teori, tetapi juga membantu mereka mengembangkan keterampilan praktis yang berguna dalam kehidupan sehari-hari.
II. Bangun Ruang Sisi Lengkung
Bab ini membahas berbagai jenis bangun ruang yang memiliki sisi lengkung, seperti tabung, kerucut, dan bola. Siswa akan belajar tentang unsur-unsur bangun ruang ini serta cara menghitung luas permukaan dan volume. Pemahaman tentang bangun ruang sisi lengkung sangat penting dalam berbagai bidang, termasuk arsitektur dan teknik. Melalui latihan dan contoh yang relevan, siswa diharapkan dapat menerapkan konsep ini dalam situasi nyata.
2.1 Unsur-unsur Bangun Ruang Sisi Lengkung
Materi ini mengidentifikasi unsur-unsur yang membentuk bangun ruang sisi lengkung. Siswa diajarkan untuk mengenali bagian-bagian penting dari bangun ini, seperti jari-jari, tinggi, dan garis pelukis. Dengan pemahaman yang baik tentang unsur-unsur ini, siswa dapat lebih mudah menghitung luas dan volume bangun ruang.
2.2 Luas Sisi dan Volume Bangun Ruang Sisi Lengkung
Di bagian ini, siswa belajar cara menghitung luas permukaan dan volume dari berbagai bangun ruang sisi lengkung. Rumus-rumus yang digunakan dijelaskan secara rinci, dan siswa diberikan latihan untuk memperkuat pemahaman mereka. Penerapan rumus dalam konteks nyata membantu siswa memahami pentingnya konsep ini dalam kehidupan sehari-hari.
2.3 Penyelesaian Masalah Bangun Ruang Sisi Lengkung
Bab ini fokus pada penerapan konsep yang telah dipelajari untuk menyelesaikan masalah yang berkaitan dengan bangun ruang sisi lengkung. Siswa diajarkan untuk menganalisis situasi dan memilih rumus yang tepat untuk menyelesaikan masalah. Latihan soal yang bervariasi memberikan siswa kesempatan untuk menerapkan pengetahuan mereka dalam konteks yang lebih luas.
2.4 Perbandingan Volume Tabung, Kerucut, dan Bola (Pengayaan)
Materi ini membahas perbandingan antara volume tabung, kerucut, dan bola. Siswa diajarkan untuk memahami hubungan antara ketiga bangun ini dan bagaimana perbandingan volume dapat digunakan dalam berbagai aplikasi. Dengan latihan tambahan, siswa dapat memperdalam pemahaman mereka tentang konsep ini.
III. Statistika
Statistika merupakan bagian penting dari matematika yang berfokus pada pengumpulan, analisis, dan interpretasi data. Dalam bab ini, siswa diperkenalkan pada konsep dasar statistika, termasuk penyajian data dalam bentuk tabel dan grafik. Pemahaman tentang statistika sangat penting untuk menganalisis informasi dan membuat keputusan berdasarkan data. Melalui latihan yang diberikan, siswa diharapkan dapat menerapkan konsep statistika dalam situasi nyata.
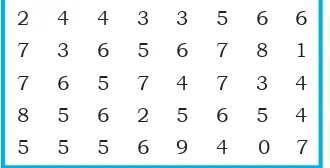
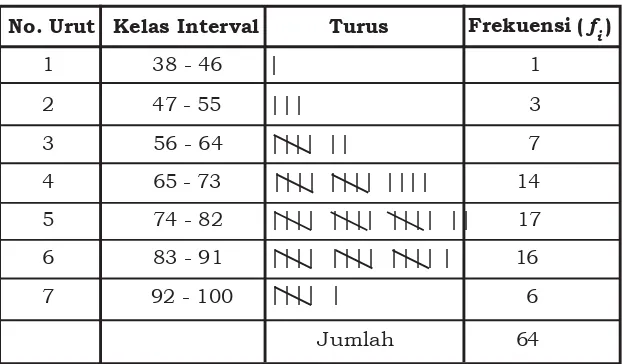
3.1 Penyajian Data Statistika
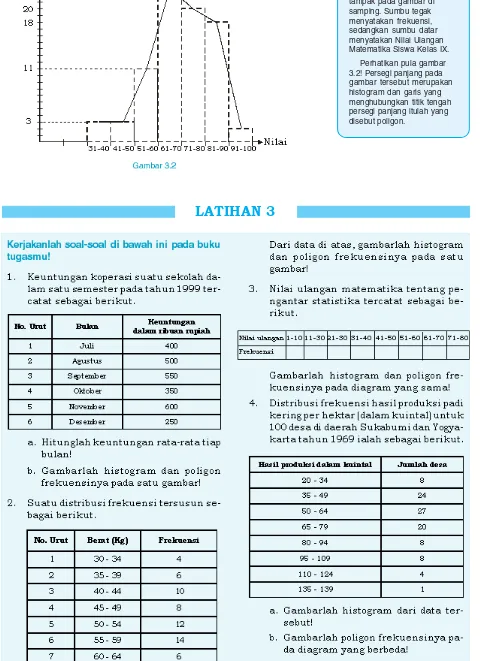
Materi ini membahas cara menyajikan data dalam bentuk tabel dan grafik. Siswa diajarkan untuk membuat tabel frekuensi dan diagram batang, yang merupakan alat penting untuk menganalisis data. Dengan latihan yang diberikan, siswa dapat memahami bagaimana data dapat disajikan dengan cara yang jelas dan menarik.
3.2 Ukuran Pemusatan
Di bagian ini, siswa belajar tentang ukuran pemusatan, termasuk rata-rata, median, dan modus. Pemahaman tentang ukuran pemusatan penting untuk menganalisis data dan menarik kesimpulan. Dengan contoh dan latihan, siswa dapat menerapkan konsep ini dalam situasi nyata.
3.3 Ukuran Pencaran (Pengayaan)
Materi ini membahas ukuran pencaran dalam data, seperti rentang dan deviasi standar. Siswa diajarkan untuk memahami pentingnya ukuran pencaran dalam analisis data. Dengan latihan tambahan, siswa dapat memperdalam pemahaman mereka tentang konsep ini.
IV. Peluang
Bab ini memperkenalkan konsep peluang, yang merupakan bagian penting dari statistika. Siswa diajarkan untuk memahami ruang sampel, kejadian sederhana, dan cara menghitung peluang. Pemahaman tentang peluang sangat penting dalam pengambilan keputusan dan analisis risiko. Dengan latihan yang diberikan, siswa diharapkan dapat menerapkan konsep peluang dalam situasi nyata.
4.1 Ruang Sampel Percobaan
Materi ini membahas ruang sampel dalam percobaan acak. Siswa diajarkan untuk mengenali berbagai jenis ruang sampel dan bagaimana cara menghitung peluang dari kejadian tertentu. Dengan latihan yang diberikan, siswa dapat memahami konsep ini dengan lebih baik.
4.2 Peluang Suatu Kejadian
Di bagian ini, siswa belajar cara menghitung peluang suatu kejadian. Siswa diajarkan untuk menggunakan rumus peluang dan menerapkannya dalam situasi nyata. Latihan yang bervariasi membantu siswa memperkuat pemahaman mereka tentang konsep ini.
V. Bilangan Berpangkat
Bab ini membahas konsep bilangan berpangkat dan aplikasinya dalam matematika. Siswa diajarkan untuk memahami sifat-sifat bilangan berpangkat dan cara melakukan operasi aljabar pada bilangan berpangkat. Pemahaman tentang bilangan berpangkat penting untuk memecahkan masalah yang lebih kompleks. Dengan latihan yang diberikan, siswa diharapkan dapat menerapkan konsep ini dalam situasi nyata.
5.1 Sifat Bilangan Berpangkat dan Bentuk Akar
Materi ini membahas sifat-sifat bilangan berpangkat dan bagaimana cara mengubah bentuk akar menjadi bilangan berpangkat. Siswa diajarkan untuk memahami hubungan antara kedua konsep ini dan bagaimana cara menerapkannya dalam masalah.
5.2 Operasi Aljabar pada Bilangan Berpangkat dan Bentuk Akar
Di bagian ini, siswa belajar cara melakukan operasi aljabar pada bilangan berpangkat. Siswa diajarkan untuk menerapkan rumus dan sifat yang telah dipelajari untuk menyelesaikan masalah. Latihan yang diberikan membantu siswa memperkuat pemahaman mereka.
5.3 Penerapan Bilangan Berpangkat dan Bentuk Akar
Bab ini menekankan penerapan bilangan berpangkat dalam situasi nyata. Siswa diajarkan untuk menganalisis dan memecahkan masalah yang berkaitan dengan bilangan berpangkat. Dengan latihan tambahan, siswa dapat memperdalam pemahaman mereka tentang konsep ini.
VI. Barisan dan Deret Bilangan
Bab ini membahas konsep barisan dan deret bilangan, termasuk pola barisan aritmetika dan geometri. Siswa diajarkan untuk mengenali pola dan menghitung suku ke-n dalam barisan. Pemahaman tentang barisan dan deret penting dalam banyak aplikasi matematika. Dengan latihan yang diberikan, siswa diharapkan dapat menerapkan konsep ini dalam situasi nyata.
6.1 Pola Barisan Bilangan
Materi ini membahas pola dalam barisan bilangan, termasuk cara mengidentifikasi dan menggambarkan pola tersebut. Siswa diajarkan untuk mengenali pola yang berbeda dan bagaimana cara menghitung suku ke-n dalam barisan.
6.2 Suku ke-n Barisan Aritmetika dan Barisan Geometri
Di bagian ini, siswa belajar cara menghitung suku ke-n dalam barisan aritmetika dan geometri. Siswa diajarkan untuk menggunakan rumus yang tepat untuk menghitung suku dan memahami aplikasinya dalam situasi nyata.
6.3 Jumlah n Suku Pertama Deret Aritmetika dan Deret Geometri
Bab ini membahas cara menghitung jumlah n suku pertama dalam deret aritmetika dan geometri. Siswa diajarkan untuk memahami hubungan antara suku dan jumlah, serta bagaimana cara menerapkannya dalam masalah.
VII. Persamaan dan Fungsi Kuadrat (Pengayaan)
Bab ini membahas persamaan kuadrat dan fungsi kuadrat, yang merupakan konsep penting dalam aljabar. Siswa diajarkan untuk menyelesaikan persamaan kuadrat dengan berbagai metode dan memahami grafik fungsi kuadrat. Pemahaman tentang fungsi kuadrat sangat penting untuk analisis data dan pemecahan masalah. Dengan latihan yang diberikan, siswa diharapkan dapat menerapkan konsep ini dalam situasi nyata.
7.1 Persamaan Kuadrat
Materi ini membahas cara menyelesaikan persamaan kuadrat dengan berbagai metode, termasuk pemfaktoran dan menggunakan rumus kuadrat. Siswa diajarkan untuk memahami konsep dasar dan bagaimana menerapkannya dalam masalah.
7.2 Penyelesaian Persamaan Kuadrat dengan Pemfaktoran
Di bagian ini, siswa belajar cara menyelesaikan persamaan kuadrat dengan pemfaktoran. Siswa diajarkan untuk mengenali bentuk persamaan dan bagaimana cara memfaktorkannya dengan benar.
7.3 Penyelesaian Persamaan Kuadrat dengan Melengkapkan Kuadrat Sempurna
Bab ini membahas metode melengkapkan kuadrat sempurna untuk menyelesaikan persamaan kuadrat. Siswa diajarkan untuk memahami langkah-langkah dalam metode ini dan bagaimana menerapkannya dalam masalah.