Try Out MATEMATIKA IPS

(1)

NASKAH SOAL

MATA UJIAN : MATEMATIKA

PROGRAM : IPS

WAKTU UJIAN : 90 MENIT JUMLAH SOAL : 40 SOAL

1. Isikan identitas Anda ke dalam lembar kerja komputer (LJK) yang tersedia dengan menggunakan pensil 2B, sesuai petunjuk di Lembar Jawaban Komputer (LJK).

2. Tersedia waktu 90 menit untuk mengerjakan paket tes tersebut.

3. Jumlah soal sebanyak 40 butir, pada setiap butir terdapat 5 (lima) pilihan jawaban. 4. Periksa dan bacalah soal-soal sebelum anda menjawabnya.

5. Laporkan kepada pengawas ujian apabila terdapat lembar soal yang kurang jelas, rusak, atau tidak lengkap. 6. Mintalah kertas buram pada pengawas ujian, bila diperlukan.

7. Tidak diizinkan menggunakan kalkulator, HP, tabel matematika atau alat bantu hitung lainnya. 8. Periksalah pekerjaan Anda sebelum diserahkan kepada pengawas ujian.

1. Perhatikan tabel di bawah ini.

p q (p~q)  ~p

B B S S

B S B S

... ... ... ...

Nilai kebenaran dari pernyataan majemuk yang dinyatakan dengan lambang (p~q)  ~p pada tabel di atas adalah ...

A. BBSS D. BSBS

B. BSBB E. BSSB

C. SBSB

2. Ingkaran dari pernyataan “ Jika samy mendapatkan nilai 10 maka ia diberi hadiah“. Adalah ...

A. Jika samy tidak mendapatkan nilai 10 maka ia diberi hadiah

B. Jika samy diberi hadiah, maka ia mendapat nilai 10 C. Samy mendapat nilai 10, dan ia diberi hadiah D. Samy mendapat nilai 10, tetapi ia tidak diberi

hadiah

E. Jika samy tidak diberi hadiah, maka ia tidak mendapat nilai 10.

3. Diberikan beberapa pernyataan:

Premis 1 : Jika santi sakit maka ia pergi ke doktor Premis 2 : Jika santi pergi ke doktor maka santi

membeli obat.

Kesimpulan yang sah dari dua pernyataan di atas adalah ...

A. santi tidak sakit dan pergi ke doktor B. santi tidak sakit atau membeli obat C. santi sakit dan membeli obat

D. jika santi sakit maka ia membeli obat E. jika santi membeli obat maka ia sakit.

4. Bentuk sederhana dari ₂

 

2 3 3 5

3 15

q q p

q p

 

adalah

A. ₅p3q _D.₅_p7_q2 B. ₅_p3_q2 _E.₅_p7_q5 C. ₅p7q

5. Bentuk sederhana dari



125 63



... 3

28

45   

A. 12 57 7 D. 12 57 7

B.  12 5  7 7 E. 12 5  7 7

C.  12 5  11 7

6. Diketahui 2log3p_dan2_log₅__q_{, maka} ...

45 log

2 _

A. p2q D. p2 q2 B. 2pq _E.p2q

C.2



pq



7. Titik balik fungsi f

 

x 2



x2



23 adalah ... A.



 2, 3



D.



2, 3



B.



 2,3



E.



2,3



C.



3, 2



8. Persamaan grafik fungsi kuadrat yang memotong sumbu X di titik



3,0



_dan



 5,0



, serta melalui titik



 3,24



adalah ... A. _y__x2 _ 2_x_15 B. yx2 2x15 C. _y_2_x2 _ 4_x_ 30 D. _y_2_x2 _4_x_ 30 E. y3x2 6x 45

9. Fungsi f :R Rdan g:R R_{yang di rumuskan} oleh f

 

x 3 2xdan _g

 

_x __x2 _4_x_ 6 Rumus fungsi



g f

 

x ...

A. 4x2  20x15 D. 4x2  4x15 B. 4_x2 _14_x_15 _E.₄_x2 _₂₀_x_₁₅ C. 4x2  8x15

10. Diketahui

 

, 3

3 5 4

  



 x

x x x

f dan _f 1_adalah

invers dari f , maka f 1

 

x ...

A. , 4

4 5 3

  

 

x x

x

D.

4 , 4

5 3

 



x x

x

B. , 4

4 5 3

 

 

x x

x

E. , 4

4 5 3

  



x x

x

C. , 4

4 5 3

 



x x

x

11. Diketahui akar-akar perasamaan kuadrat 0

4 3

2x2  x  adalah p dan q. Nilai ...

3 2

2 __q _ _pq_ p

A. 4 1

4 D.

4 1 12

B. 4 1

6 E.

4 1 13

C. 4 1 8

Try Out UN 2014 Irfan Juliansyah, S. Pd

PETUNJUK UMUM

(2)

12. Akar –akar persamaan 3_x2 __px_1_0_adalah



_dan

 _{, jika} 1  1 2



 , maka nilai p = ...

A. 2 D. – 1

B. 1 E. – 2 C. 0

13. Penyelesaian dari



x 4



2 2xadalah ... A. x4atau x 4

B. x2atau x8 C. x2atau x2 D. 2x8

E. 4x4

14. Diketahui sistem persamaan sebagai berikut.















7

5

6

4

3

4

y

x

y

x

Nilai

x



y

yang memenuhi sistem persamaan tersebut adalah ...

A. 3 D.

2 3 

B. 2 1

E. – 3

C. – 1

15. Uang Ana ditambah dua kali uang Ani sama dengan Rp425.000,00. selisih uang Ana dengan seperlima uang Ani adalah Rp150.000,00. Uang Ana Sebanyak ... A. Rp250.000,00 D. Rp175.000,00 B. Rp225.000,00 E. Rp125.000,00 C. Rp200.000,00

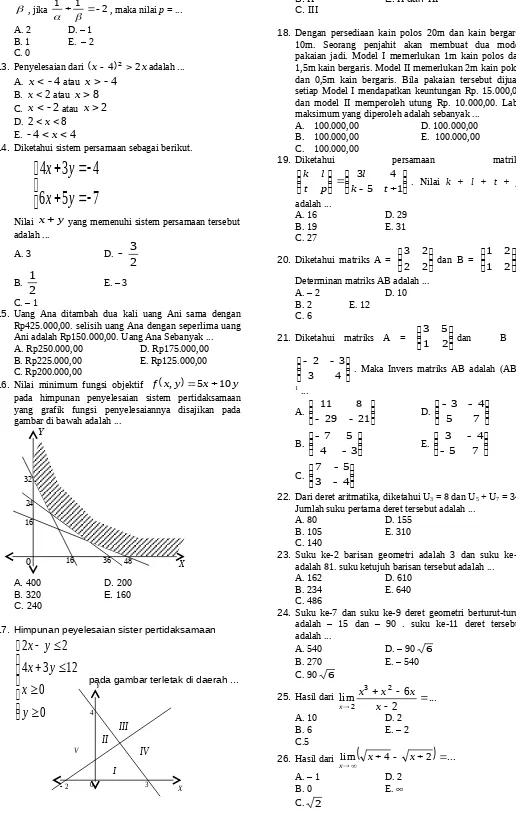
16. Nilai minimum fungsi objektif f



x,y



5x10y pada himpunan penyelesaian sistem pertidaksamaan yang grafik fungsi penyelesaiannya disajikan pada gambar di bawah adalah ...

A. 400 D. 200

B. 320 E. 160

C. 240

17. Himpunan peyelesaian sister pertidaksamaan













0

12

3

4

2

y

x

y

x

y

x

pada gambar terletak di daerah ...

A. I D. I dan IV

B. II E. II dan III

C. III

18. Dengan persediaan kain polos 20m dan kain bergaris 10m. Seorang penjahit akan membuat dua model pakaian jadi. Model I memerlukan 1m kain polos dan 1,5m kain bergaris. Model II memerlukan 2m kain polos dan 0,5m kain bergaris. Bila pakaian tersebut dijual, setiap Model I mendapatkan keuntungan Rp. 15.000,00 dan model II memperoleh utung Rp. 10.000,00. Laba maksimum yang diperoleh adalah sebanyak ...

A. 100.000,00 D. 100.000,00 B. 100.000,00 E. 100.000,00 C. 100.000,00

19. Diketahui persamaan matriks

   

 

        

1 5

4 3

t k

l p

t l k

. Nilai k + l + t + p

adalah ...

A. 16 D. 29

B. 19 E. 31

C. 27

20. Diketahui matriks A = _

    

2 2

2 3

dan B = _

    

2 1

.

Determinan matriks AB adalah ...

A. – 2 D. 10

B. 2 E. 12

C. 6

21. Diketahui matriks A = _

    

2 1

5 3

dan B =

   



 

4 3

3 2

. Maka Invers matriks AB adalah (AB)

-1_...

A. _

  

 



 29 21

8 11

D. _

  



 

7 5

4 3

B. _

  

 

 

3 4

5 7

E. _

  

  



7 5

4 3

C. _

  

 

 

4 3

5 7

22. Dari deret aritmatika, diketahui U3 = 8 dan U5 + U7 = 34. Jumlah suku pertama deret tersebut adalah ...

A. 80 D. 155

B. 105 E. 310

C. 140

23. Suku ke-2 barisan geometri adalah 3 dan suku ke-5 adalah 81. suku ketujuh barisan tersebut adalah ...

A. 162 D. 610

B. 234 E. 640

C. 486

24. Suku ke-7 dan suku ke-9 deret geometri berturut-turut adalah – 15 dan – 90 . suku ke-11 deret tersebut adalah ...

A. 540 D. – 90 6

B. 270 E. – 540

C. 90 6

25. Hasil dari ...

2 6 lim

2 3

2 _ 

 

 x

x x x

x

A. 10 D. 2

B. 6 E. – 2

C.5

26. Hasil dari lim



4 2



...



 x x

x

A. – 1 D. 2

B. 0 E. 

C. 2

X Y

48

0 36

32

24

16

X Y

2

 0 3

4

I II

III

IV

(3)

27. Turunan pertama dari f

 

x _2x2_ 6x_adalah

 

x

f' _{. Nilai dari} f'

 

0 ...

A. 0 D. – 7

B. – 4 E. – 8

C. – 6

28. Interval agar fungsi f yang ditentukan oleh

 

x x x x

f _2 3 _ 9 2_12 _{naik adalah ...} A. x1atau x2

B. x2atau x1 C. x1atau x2 D. 1x2

E. 2x1

29. Persamaan garis singgung kurva _y__x2 _3_x_1 melalui titik



1,3



adalah ...

A. y 5x8 _D.y 5x 3 B. y5x3 _E.y5x 2 C. y5x2

30. Nilai maksimum dari fungsi f

 

x x33x28 adalah ...

A. 8 D. 24

B. 12 E. 32

C. 16

31. Suatu proyek kan dikerjakan dalam x hari, biaya proyek

per hari adalah 

  

 



1000 50

40

x

x juta rupiah.

Biaya proyek minimum per hari adalah ... A. Rp450.000.000,00

B. Rp400.000.000,00 C. Rp375.000.000,00 D. Rp350.000.000,00 E. Rp300.000.000,00

32. Banyaknya bilangan 3 angka berbeda dapat disusun dari angka-angka 4, 5, 6, 7, dan 8 adalah ...

A. 10 D. 120

B. 20 E. 125

C. 60

33. Dalam sebuah kotak berisi 5 bola merah, 3 bola putih, dan 2 bola biru, diambil 3 bola sekaligus. Banyak cara pengambilan bola dari kotak adalah ...

A. 2520 D. 120

B. 1440 E. 30

C. 720

34. Dua buah dadu dilempar bersama-sama satu kali. Peluang muncul mata dadu keduanya bilangan prima adalah ...

A. 6 1

D. 8 3

B. 4 1

E. 2 1

C. 3 1

35. Sebuah dadu dilemparkan sebanyak 24 kali. Besarnya frekuensi harapan munculnya sisi dadu kurang dari atau sama dengan 4 adalah ...

A. 16 D. 6

B. 12 E. 4

C. 8

36. Perhatikan diagram di bawah ini.

Diagram di atas menunjukkan cara yang ditempuh oleh 180 siswa SMA N 2 BENDAHARA untuk berangkat ke sekolah. Jumlah siswa yang tidak naik mobil ke sekolah adalah ... A. 18 Siswa D. 72 Siswa

B. 36 Siswa E. 171 Siswa C. 45 Siswa

37. Perhatikan gambar diagram berikut.

Nilai rata-rata berat badan adalah ....

A. 49,33 D. 48,83

B. 49,16 E. 48,50 C. 49,00

38. Perhatikan tabel distribusi nilai ulangan matematika berikut ini!

No Nilai Frekuensi 1

2 3 4 5

11 – 20 21 – 30 31 – 40 41 – 50 51 – 60

2 5 8 3 1

Modus dari data pada tabel adalah ....

A. 33,75 D. 3450

B. 34,00 E. 34,75 C. 34,25

39. Simpangan baku dari data 6, 8, 7, 7, 7 adalah ...

A. 35 5 1

D. 10 5 1

B. 5 2

E. 5 1

C. 5

5 2

40. Dari data : 8, 9, 3, 6, 3, 10, 7, 6, 5, 6, 2, 9. Nilai kuartil ketiga data di atas adalah ...

A. 5,5 D. 8,

B. 6 E. 9

C. 8

Naik sepeda motor

40% Jalan kaki

20%

Naik sepeda 25%

Naik Mobil

5%

Naik becak 10%

1 3 6 9 11