4 Analitik Data Tingkat Lanjut Clustering Big Data L1617 v2

26 September 2016

Analitik Data Tingkat Lanjut

(Clustering)

Pokok Bahasan

1. Konsep Clustering

2. K-means vs Kernel K-Means

3. Studi Kasus

Konsep Clustering



Cluster data diartikan kelompok. Dengan demikian,

pada dasarnya analisis cluster akan menghasilkan

sejumlah cluster (kelompok).



Analisis ini diawali dengan pemahaman bahwa sejumlah

data tertentu sebenarnya mempunyai kemiripan di antara anggotanya.

Konsep Clustering



Karena itu, dimungkinkan untuk mengelompokkan

anggota-anggota yang mirip atau mempunyai

karakteristik yang serupa tersebut dalam satu atau lebih dari satu cluster.



Hierarchical clustering adalah suatu metode

pengelompokan data yang dimulai dengan

Konsep Clustering



Metode non-hierarchical clustering justru dimulai dengan

menentukan terlebih dahulu jumlah cluster yang

diinginkan (dua cluster, tiga cluster, atau lain

sebagainya). Contoh metodenya adalah k-means

K-means Clustering



K-means clustering merupakan salah satu metode data

clustering non-hirarki yang mengelompokan data dalam bentuk satu atau lebih cluster (kelompok).



Data-data yang memiliki karakteristik yang sama

dikelompokan dalam satu cluster (kelompok) dan data

yang memiliki karakteristik yang berbeda dikelompokan

dengan cluster (kelompok) yang lain sehingga data

K-means Clustering



Langkah-langkah melakukan clustering dengan metode

k-means:

1. Tentukan jumlah cluster k.

2. Inisialisasi k pusat cluster ini bisa dilakukan dengan berbagai

cara. Namun yang paling sering dilakukan adalah dengan cara random (acak).

3. Alokasikan semua data atau obyek ke cluster terdekat

berdasarkan jarak kedua obyek tersebut (jarak Euclidean):

4. Hitung kembali pusat cluster dengan keanggotaan cluster yang

sekarang



 

 



2





2

2 2

2 1

1 ..

, _{j i j i j id jd}

i x x x x x x x

x

D       





 



 i mi

j

jd i

id m

j

j i

i x

m C

x m

C

1 1

1 1

1

K-means Clustering



Langkah-langkah clustering metode k-means:

1. Tentukan jumlah cluster k.

2. Inisialisasi k pusat cluster ini bisa dengan berbagai cara. Namun

yang sering dilakukan adalah dengan cara random (acak).

3. Alokasikan semua data atau obyek ke cluster terdekat

berdasarkan jarak kedua obyek tersebut (jarak Euclidean):

4. Hitung pusat cluster dengan keanggotaan yang sekarang

5. Jika pusat cluster tidak berubah lagi maka proses clustering

selesai. Atau, kembali ke langkah nomor 3 sampai pusat cluster tidak berubah.



 

 



2





2

2 2

2 1

1 ..

, _{j i j i j id jd}

i x x x x x x x

x

D       





 



 i mi

j

jd i

id m

j

j i

i x

m C

x m

C

1 1

1 1

1

K-means Clustering



Hasil clustering data 2 dimensi dengan menggunakan

K-means vs Kernel K-Means



K-means adalah algoritma unsupervised learning yang

membagi kumpulan data ke dalam sejumlah cluster

(kelompok).



Akan tetapi k-means clustering memiliki kelemahan di

dalam memproses data yang berdimensi banyak

khususnya untuk data yang bersifat non-linierly

separable.



Sedangkan dalam dunia nyata saat ini, data yang

tersedia atau yang diperoleh memiliki dimensi yang banyak dan bervariasi.



Dalam hal ini, penambahan fungsi kernel pada input

K-means vs Kernel K-Means

K-means vs Kernel K-Means

K-means vs Kernel K-Means



Kita dapat menggunakan beberapa jenis transformasi

pada data, dengan memetakan data pada ruang baru

dimana machine learning dapat digunakan.



Fungsi kernel memberikan kepada kita sebuah alat

untuk mendefinisikan transformasi.

o

_{Kernel Polynomial}

o

_{Kernel RBF}



 



d

j i

j

i

x

x

x

c

x

k

,

































₂

2

2

exp

,



j i

j i

x

x

Kernel K-means



Pada umumnya, perluasan dari means ke kernel

k-means direalisasi melalui pernyataan jarak dalam

bentuk fungsi kernel.



Dengan menggunakan Jarak Euclidean pada tradisional

k-means dan fungsi pemetaan Φ, maka algoritma

k-means clustering pada slide ke-8 dapat diubah menjadi :

1. Tentukan jumlah cluster k.

2. Inisialisasi k pusat cluster ini bisa dengan berbagai cara. Namun

yang sering dilakukan adalah dengan cara random (acak).

3. Alokasikan semua data atau obyek ke cluster terdekat

berdasarkan jarak yang dihitung menggunakan rumus fungsi

pemetaan Φ dan fungsi kernel.





 

n

i m

j

ij _{i j}

u

x

c

1 1

2

~

)

(

Kernel K-means

3. Alokasikan semua data atau obyek ke cluster terdekat

berdasarkan jarak yang dihitung menggunakan rumus fungsi

pemetaan Φ dan fungsi kernel.

merupakan cluster centers dan dihitung dengan

menggunakan rumus :





 

n

i

m

j

ij _{i j}

u

x

c

1 1

2

~

)

(

min



j

c

~







n

i

i ij

j

j

u

x

n

c

1

)

(

1

~









  _

n

i

m

j

ij

n

l lj l

j i

u

u

x

n

x

1 1

2

1

Kernel K-means







  _ n i m j ij n

l lj l

j i

u

u

x

n

x

1 1

2

1

min



(

)

1



(

)

                        



n

l lj l j i n i m j n

l lj l j

i

ij u x

n x x u n x u 1

1 1 1

) ( 1 ) ( ) ( 1 ) (

min















                                 n i m j n

l lj l j

n

l lj l j

i i

i

ij u x

n x u n x x x u 1 1 2 1 1 ) ( 1 ) ( ) ( 2 ) ( ). (

min     

 

 

 



                                   n i m j n l n

p lj l p j

n

l lj l i j

i i

ij u K x x

n x x K u n x x K u

1 1 1 1

Kernel K-means

 Keterangan:  

 

 



                                   n i m j n l n

p lj l p j

n

l lj l i j

i i

ij u K x x

n x x K u n x x K u

1 1 1 1

2 2 1 ) , ( 1 ) , ( 1 2 ) , ( min

n = Jumlah data. m = Jumlah cluster. K = Fungsi kernel.

i = Index untuk keseluruhan data. j = Index untuk cluster.

l = Index untuk data yang terdapat pada cluster ke-j. p = Index untuk data yang terdapat pada cluster ke-j.

u_ij = Nilai keanggotaan data ke-i terhadap cluster ke-j. Bernilai 1 apabila merupakan anggota, bernilai 0 jika bukan merupakan anggota dari cluster yang diproses. u_lj = Nilai keanggotaan data ke-l terhadap cluster ke-j

= Fungsi yang memetakan titik x ke ruang baru yang berdimensi lebih tinggi. x_i = Titik data ke-i. x_l = Titik data ke-l. x_p = Titik data ke-p.



Kernel K-means

4. Setelah mendapat jarak titik data terhadap masing-masing

cluster pada langkah 3, jarak terdekat titik data dengan suatu cluster berarti titik data tersebut termasuk dalam cluster tersebut.

5. Perhatikan kondisi berhenti (Next Slide), misal jika pusat

Kondisi Berhenti

(Termination Condition)



Langkah selanjutnya adalah menentukan apakah

diperlukan iterasi selanjutnya atau tidak (stop condition).

a.

Jumlah Iterasi Maksimum

b.

Fungsi Obyektif dan Threshold

Fungsi obyektif dihitung dan nilai threshold pada sistem

ini diperoleh dari masukan user.

Note: jika delta ≥ threshold, maka iterasi berlanjut. Jika

delta < threshold, maka iterasi berhenti.



 

 ndata

j k i

i j jiD x C

a F

1 1

) ,

( F = Fungsi Objektif k = Jum. cluster. ndata = Jum. data. a_ji = Nilai keanggotaan data ke-j terhadap cluster ke-i. D(x_j,C_i) = Jarak antara titik data ke-j terhadap cluster ke-i.

lama

baru F

F

delta  

Kernel K-means Clustering



Hasil clustering data 2 dimensi dengan menggunakan

k-means Vs Kernel k-k-means clustering (Chitta, Radha, Rong Jin, Timothy C. Havens, dan Anil K. Jain., 2011):



Terbukti bahwa Kernel K-mean clustering dapat

digunakan untuk menyelesaikan cluster yang komplek.

Analisis Cluster



Analisis cluster berkepentingan dengan penggolongan

hasil kelompok yang sudah didapatkan. Atau

menyiapkan draft nama atau label yang tepat untuk kelompok tersebut.



Sedangkan analisis faktor berkepentingan dengan

Studi Kasus: Clustering data 2 dimensi



Diketahui data 2 dimensi:

No. X Y Cluster 1 0.50 0.00 1

2 0.48 0.13 2

3 0.43 0.25 2 4 0.35 0.35 2

5 0.25 0.43 1

6 0.13 0.48 1

7 0.00 0.50 2

8 -0.13 0.48 2

9 -0.25 0.43 1

10 -0.35 0.35 1

11 -0.43 0.25 1

12 -0.48 0.13 2

13 -0.50 0.00 2

14 -0.48 -0.13 2

15 -0.43 -0.25 2

16 -0.35 -0.35 1

17 -0.25 -0.43 2

18 -0.13 -0.48 2

19 0.00 -0.50 1

20 0.13 -0.48 1

21 0.25 -0.43 1

22 0.35 -0.35 1

23 0.43 -0.25 2

24 0.48 -0.13 2 25 0.50 0.00 2

26 15.00 0.00 2

27 14.94 1.31 1

28 14.77 2.61 2

29 14.49 3.88 1

30 14.09 5.13 1

31 13.59 6.34 1

32 12.99 7.50 1

33 12.29 8.61 2

No. X Y Cluster 34 11.49 9.65 1

35 10.60 10.61 2

36 9.64 11.49 2

37 8.60 12.29 2

38 7.49 12.99 1

39 6.33 13.60 2

40 5.12 14.10 2

41 3.87 14.49 2

42 2.60 14.77 1

43 1.30 14.94 2

44 -0.01 15.00 1

45 -1.32 14.94 1

46 -2.62 14.77 2

47 -3.89 14.49 1

48 -5.14 14.09 1

49 -6.35 13.59 1

50 -7.51 12.98 2

51 -8.61 12.28 1

52 -9.65 11.48 1 53 -10.62 10.60 2

54 -11.50 9.63 1

55 -12.30 8.59 2

56 -13.00 7.49 2

57 -13.60 6.32 2

58 -14.10 5.11 1

59 -14.49 3.87 2

60 -14.78 2.59 1

61 -14.94 1.29 2

62 -15.00 -0.02 1

63 -14.94 -1.33 2

64 -14.77 -2.62 1

65 -14.48 -3.90 2

66 -14.09 -5.15 2

No. X Y Cluster 67 -13.59 -6.36 1

68 -12.98 -7.52 1

69 -12.27 -8.62 1

70 -11.48 -9.66 2

71 -10.59 -10.62 2

72 -9.62 -11.51 1

73 -8.58 -12.30 2

74 -7.48 -13.00 2

75 -6.32 -13.61 1

76 -5.11 -14.10 1

77 -3.86 -14.50 1

78 -2.58 -14.78 2

79 -1.28 -14.95 1

80 0.03 -15.00 1

81 1.34 -14.94 1

82 2.63 -14.77 1

83 3.91 -14.48 2

84 5.16 -14.08 2

85 6.37 -13.58 2

86 7.53 -12.97 2

87 8.63 -12.27 2

88 9.67 -11.47 1

89 10.63 -10.58 2

90 11.51 -9.62 1

91 12.31 -8.58 1

92 13.01 -7.47 1

93 13.61 -6.31 2

94 14.11 -5.10 2

95 14.50 -3.85 1

96 14.78 -2.57 1

97 14.95 -1.27 2

Studi Kasus: Clustering data 2 dimensi



Visualisasi data 2 dimensi:

Langkah-langkah penyelesaian dengan Kernel K-Means: Misal dengan kernel Polynomial

1.

Tentukan jumlah cluster k = 2. Iterasi maksimum (t_max) =

5, dan nilai threshold = 0.05.

2.

Inisialisasi k pusat cluster. Misal dilakukan inisialisasi

secara random nilai indek clusternya (1 atau 2, pada

kolom cluster) dari semua data pada slide ke-21.

No. X Y Cluster 1 0.50 0.00 1

2 0.48 0.13 2

3 0.43 0.25 2 4 0.35 0.35 2

5 0.25 0.43 1

. . . .

97 14.95 -1.27 2

98 15.00 0.04 1

-20 -15 -10 -5 0 5 10 15 20

-20 -10 0 10 20

X

Y

Keterangan:

Cluster 1

Cluster 2



 



d

j i

j

i x x x c

x

Studi Kasus: Clustering data 2 dimensi

3.

Alokasikan semua data atau obyek ke cluster terdekat

berdasarkan jarak yang dihitung menggunakan rumus

fungsi pemetaan Φ dari fungsi kernel.

Mulai masuk pada iterasi ke-1 (t = 1). Sebelum

dilakukan pengalokasian data ke cluster terdekat,

lakukan perhitungan centroid masing-masing cluster

dari hasil pemetaan Φ.

o

_{Menghitung Centroid Cluster}







n

i

i ij

j

j

u

x

n

c

1

)

(

1

~



No. X Y Cluster 1 0.50 0.00 1

. . . .

97 14.95 -1.27 2

98 15.00 0.04 1

No. X Y Cluster X2 √2.X.Y Y2

1 0.50 0.00 1 0.25 0.00 0.00

. . . .

9714.95 -1.27 2

9815.00 0.04 1

)

(

x

_i



i

x

fungsi pemetaan Φ = (X2_, √2_{XY, Y}2₎



 



d

j i

j

i x x x c

x

Studi Kasus: Clustering data 2 dimensi

o

_{Menghitung Centroid Setiap Cluster}







n i i ij j

j

u

x

n

c

1

)

(

1

~



No. X2 √2_{.X.Y Y}2

Cluster 10.25 0.00 0.00 1

. .

97 2

98 1

Total .. .. ..

)

(

x

_i



Data X Y Cluster X2 _{√2XY Y}2

1 0.50 0.00 1 0.25 0.00 0.00 2 0.25 0.43 1 0.06 0.15 0.19 3 0.13 0.48 1 0.02 0.09 0.23 4 -0.25 0.43 1 0.06 -0.15 0.19

. . . .

48 14.78 -2.57 1 218.40 -53.68 6.60 49 15.00 0.04 1 225.00 0.80 0.00 Total 49 4312.54 1.63 4240.21

centroid cluster 1 pada iterasi 1:

                      86.53 0.03 88.01 49 / 4240.21 49 / 1.63 49 / 4312.54 ~ 1 c

Data X Y Cluster X2 _{√2XY Y}2

1 0.48 0.13 2 0.23 0.09 0.02 2 0.43 0.25 2 0.19 0.15 0.06 3 0.35 0.35 2 0.12 0.18 0.13 4 0.00 0.50 2 0.00 0.00 0.25

. . . .

48 14.11 -5.10 2 199.02 -101.68 25.98 49 14.95 -1.27 2 223.39 -26.85 1.61

Total 49 4018.97 -1.22 3859.54

centroid cluster 2 pada iterasi 1:

Studi Kasus: Clustering data 2 dimensi

3.

Alokasikan semua data atau obyek ke cluster terdekat

berdasarkan jarak yang dihitung menggunakan rumus

fungsi pemetaan Φ dan fungsi kernel.





 

n

i

m

j

ij _{i j}

u

x

c

1 1

2

~

)

(

min









n

i

i ij

j

j

u

x

n

c

1

)

(

1

~



Data X Y Jarak ke C1 Jarak ke C2 K baru K lama 1 0.50 0.00 15190.29 12890.39 2 1 2 0.25 0.43 15190.84 12891.62 2 1 3 0.13 0.48 15190.98 12891.91 2 1 4 -0.25 0.43 15190.86 12891.60 2 1

. . . .

48 14.78 -2.57 26277.54 26687.92 1 1 49 15.00 0.04 26254.64 26647.91 1 1 50 0.48 0.13 15190.35 12890.51 2 2

. . . .

97 14.11 -5.10 26337.65 26811.35 1 2 98 14.95 -1.27 26260.58 26656.34 1 2

Total 1177274.15 1138242.98

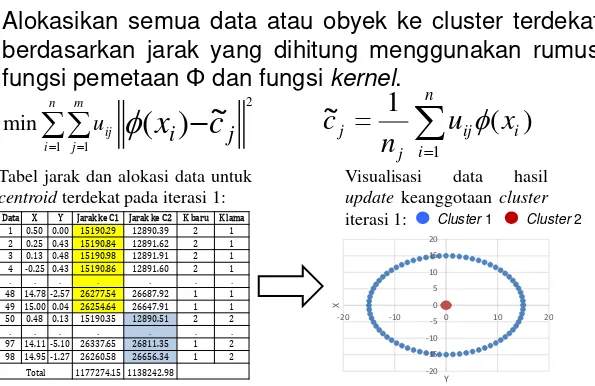
Tabel jarak dan alokasi data untuk centroid terdekat pada iterasi 1:

-20 -15 -10 -5 0 5 10 15 20

-20 -10 0 10 20

X

Y

Visualisasi data hasil update keanggotaan cluster iterasi 1: Cluster 1 Cluster 2

Studi Kasus: Clustering data 2 dimensi

4.

Setelah mendapat jarak titik data terhadap

masing-masing cluster pada langkah 3, jarak terdekat titik data dengan suatu cluster berarti titik data tersebut termasuk dalam cluster tersebut.

Data X Y Jarak ke C1 Jarak ke C2 K baru K lama 1 0.50 0.00 15190.29 12890.39 2 1 2 0.25 0.43 15190.84 12891.62 2 1 3 0.13 0.48 15190.98 12891.91 2 1 4 -0.25 0.43 15190.86 12891.60 2 1

. . . .

48 14.78 -2.57 26277.54 26687.92 1 1 49 15.00 0.04 26254.64 26647.91 1 1 50 0.48 0.13 15190.35 12890.51 2 2

. . . .

97 14.11 -5.10 26337.65 26811.35 1 2 98 14.95 -1.27 26260.58 26656.34 1 2

Total 1177274.15 1138242.98

Tabel jarak dan alokasi data untuk centroid terdekat pada iterasi 1:

-20 -15 -10 -5 0 5 10 15 20

-20 -10 0 10 20

X

Y

Visualisasi data hasil update keanggotaan cluster iterasi 1: Cluster 1 Cluster 2

Fbaru = 1177274.15 + 1138242.98 = 2315517.13

Studi Kasus: Clustering data 2 dimensi



Visualisasi data 2 dimensi:

Cara ke-2 penyelesaian dengan Kernel K-Means: Misal dengan kernel Polynomial

1.

Tentukan jumlah cluster k = 2. Iterasi maksimum (t_max) =

5, dan nilai threshold = 0.05.

2.

Inisialisasi k pusat cluster. Misal dilakukan inisialisasi

secara random nilai indek clusternya (1 atau 2, pada

kolom cluster) dari semua data pada slide ke-21.

No. X Y Cluster 1 0.50 0.00 1

2 0.48 0.13 2

3 0.43 0.25 2 4 0.35 0.35 2

5 0.25 0.43 1

. . . .

97 14.95 -1.27 2

98 15.00 0.04 1

-20 -15 -10 -5 0 5 10 15 20

-20 -10 0 10 20

X

Y

Keterangan:

Cluster 1

Cluster 2



 



d

j i

j

i x x x c

x

Studi Kasus: Clustering data 2 dimensi

3.

Alokasikan semua data atau obyek ke cluster terdekat

berdasarkan jarak yang dihitung menggunakan rumus

fungsi pemetaan Φ dan fungsi kernel.

o

_{Penghitungan jarak data terhadap masing-masing}

cluster menggunakan persamaan berikut

 

 

 



                                  n i m j n l n

p lj l p j

n

l lj l i j

i i

ij u K x x

n x x K u n x x K u

1 1 1 1

2 2 1 ) , ( 1 ) , ( 1 2 ) , ( min





  n i m j

ij _{i j}

u

x

c

1 1

2

~

)

(

min









n i i ij j

j

u

x

n

c

1

)

(

1

~



Studi Kasus: Clustering data 2 dimensi

o

_{Untuk memudahkan dalam perhitungan, persamaan}

di atas dibagi menjadi 3 bagian yaitu a, b, dan c. Sebagai contoh, berikut ini ditampilkan perhitungan

jarak antara data 1 terhadap cluster 1.

 

 

 



                                  n i m j n l n

p lj l p j

n

l lj l i j

i i

ij u K x x

n x x K u n x x K u

1 1 1 1

2 2 1 ) , ( 1 ) , ( 1 2 ) , ( min

a b c

i = 1

j = 1

x_i = (0.50, 0.00)

Untuk menghitung bagian a:

K(x_i, x_i) = (x_i.x_i+ c)d

= ( 0.50

0.00 . 0.500.00 + 0)2

= (((0.50 x 0.50)+(0.00 x 0.00)) + 0)2

Studi Kasus: Clustering data 2 dimensi

o

_{Untuk memperoleh b terlebih dahulu dilakukan}

penjumlahan nilai fungsi kernel antara data i

terhadap seluruh data pada cluster j. Sebagai contoh diambil satu data pada cluster j yaitu :

x_l = (0.25, 0.43) K(x_i, x_l) = (x_i.x_l+ c)d

= ( 0.50

0.00 . 0.250.43 + 0)2

= (((0.50 x 0.25)+(0.00 x 0.43)) + 0)2

= 0.016

No. x_l K(x_i, x_l) 1 0.5, 0 0.0625 2 0.25, 0.43 0.015625 3 0.13, 0.48 0.004225 4 -0.25, 0.43 0.015625

. . .

48 14.78, -2.57 54.6121 49 15, 0.04 56.25

Total 1078.15

Nilai fungsi kernel antara data i terhadap seluruh data pada cluster j untuk iterasi 1

b = -2(baris (Total)) / jumlah data padaclusterj = -2(1078.15) / 49

Studi Kasus: Clustering data 2 dimensi

o

_{Selanjutnya yaitu menghitung c. Untuk memperoleh c}

terlebih dahulu dilakukan penjumlahan nilai fungsi kernel antar data pada cluster j. Sebagai contoh diambil satu data pada cluster j yaitu

o

_{Asumsikan total nilai tersebut dengan T. Untuk}

memperoleh nilai c dengan cara

x_l = (0.25, 0.43) K(x_l, x_l) = (x_l.x_l+ c)d

= ( 0.25

0.43 . 0.250.43 + 0)2

= (((0.25 x 0.25)+(0.43 x 0.43)) + 0)2

= 0.66

xl 1 2 3 . . . 49

1 0.06 0.02 0 . . . 56.25 2 0.02 0.06 0.06 . . . 14.19 3 0 0.06 0.06 . . . 3.88

. . . .

. . . .

. . . .

49 56.25 14.19 3.88 . . . 50625.72

Tabel nilai fungsi kernel antar data pada cluster j untuk iterasi 1

c = (T) / (jumlah data padaclusterj)2

= 36577410.24 / (49)2

Studi Kasus: Clustering data 2 dimensi

o

_{Jumlahkan nilai a, b, dan c. Hasil jumlah a, b, dan c}

adalah :  

 

 



                                  n i m j n l n

p lj l p j

n

l lj l i j

i i

ij u K x x

n x x K u n x x K u

1 1 1 1

2 2 1 ) , ( 1 ) , ( 1 2 ) , ( min

a b c

a + b + c =0.625 + (-44.006) + 15234.24

Tugas Kelompok

1. Jelaskan perbedaan antara K-Means dengan Kernel K-Means!

2. Jelaskan bagaimana cara untuk memilih kernel yang terbaik untuk K-means!

3. Diketahui data berikut, Tentukan hasil K(x₁,x₂) dengan menggunakan kernel Polynomial dan RBF:

a.

b.

4. Tentukan hasil perhitungan jarak kuadrat dari data ke-1 dari slide ke-21 terhadap cluster 2, berdasarkan perhitungan pada slide ke-29!

26 September 2016

Terimakasih