SIFAT-SIFAT FUNGSI KONVEKS DAN APLIKASINYA DALAM OPTIMISASI

Skripsi

Diajukan untuk Memenuhi Salah Satu Syarat Memperoleh Gelar Sarjana

Program Studi Matematika

Disusun oleh :

CICILIA RIRIN WAHYUNDARI NIM : 043114011

PROGRAM STUDI MATEMATIKA JURUSAN MATEMATIKA FAKULTAS SAINS DAN TEKNOLOGI

UNIVERSITAS SANATA DHARMA YOGYAKARTA

Thesis

Presented as Partial Fulfillment of the Requirements To Obtain the SARJANA SAINS Degree

In Mathematics

by:

CICILIA RIRIN WAHYUNDARI

Student number : 043114011

STUDY PROGRAM OF MATHEMATICS SCIENCE

DEPARTMENT OF MATHEMATICS

FACULTY OF SCIENCE AND TECHNOLOGY

SANATA DHARMA UNIVERSITY

YOGYAKARTA

2008

APLIKASII\YA I}ALAM OPTIMISASI

Pembimbing

^0

Lusia Krismiyati Budiasih, J.Si, M.Si tanggal: Juli 2008

Dipersiapkan dan ditulis oleh:

Cicilia Ririn Wahyundari

NIM : 043114{fl1

Tangan

r - r (

Fakultas Sains dan Teknologi

lv

I

Yogyakarta, Juli 2008

i

Serahkanlah hidupmu kepada TUHAN dan

percayalah kepada-Nya, dan Ia akan bertindak

Mazmur 37:5

Kupersembahkan skripsiku ini kepada :

Jesus Christ

sumber Kekuatan dan harapanku

Bapak dan ibux

atas cinta dan doa setiap waktu

Norbertus Deutz

atas doa, dukungan, perhatian dan cinta.

serta

Almamaterku

tercinta

vii

~nn~

Janganlah hendaknya kamu kuatir tentang apapun juga,

tetapi nyatakanlah dalam segala hal keinginanmu kepada Allah

dalam doa dan permohonan dengan ucapan syukur.

Filipi 4:6

Segala yang kamu ingini akan terjadi jika kamu yakin

pada Allah dan kamu melakukannya dengan

sungguh-sungguh

konveks dapat menggunakan definisi atau sifat dari matriks Hessian. Suatu fungsi dikatakan konveks jika matriks Hessian fungsi tersebut semidefinit positif dan dikatakan konveks tegas jika matriks Hessian fungsi tersebut definit positif. Fungsi konveks mempunyai sifat kontinu dan diferensiabel.

Fungsi konveks berguna dalam masalah optimisasi. Jika suatu fungsi konveks yang didefinisikan pada himpunan konveks mencapai minimum lokal pada suatu titik maka fungsi tersebut mencapai minimum pada titik tersebut. Suatu fungsi akan mempunyai nilai minimum jika fungsi tersebut konveks dan diferensiabel, dan nilai gradien fungsi tersebut sama dengan nol.

ix

the characteristic of Hessian matrix can be used. A function is a said to be convex if the Hessian matrix of the function is positive semidefinite and called a strictly convex if the Hessian matrix of the function is positive definite. Convex function is continuous and differentiable.

dan kasih karunia yang telah diberikan sehingga penulis dapat menyelesaikan skripsi yang berjudul ”Sifat–sifat Fungsi Konveks dan Aplikasinya Dalam Optimisasi”.

Dalam proses penulisan skripsi ini banyak hambatan yang dialami oleh penulis. Namun, berkat bantuan dan dukungan dari banyak pihak, akhirnya skripsi ini dapat terselesaikan. Oleh karena itu penulis ingin mengucapkan terima kasih kepada:

1. Ibu Lusia Krismiyati Budiasih, S.Si, M.Si selaku pembimbing dan ketua program studi Matematika yang telah memberikan banyak saran dan telah banyak meluangkan waktu, pikiran, tenaga, dan yang telah sabar membimbing penulis sampai pada tahap penyusunan skripsi ini.

2. Ibu MV. Any Herawati dan Bapak Herry Pribawanto Suryawan selaku dosen penguji dan telah memberi masukan.

3. Ir. Gregorius Heliarko, S.J., S.S., BST., M.A., M.Sc. selaku Dekan Fakultas Sains dan Teknologi Universitas Sanata Dharma.

4. Bapak dan Ibu Dosen FMIPA yang telah memberikan ilmu pengetahuan yang sangat berguna bagi penulis.

5. Pak Tukijo dan Ibu Linda yang telah memberikan pelayanan administrasi dan urusan–urusan akademik kepada penulis selama masih kuliah.

xii

7. Norbertus Deutz Yunianta Tinitih yang telah memberikan banyak cinta, perhatian, pengertian, kesabaran, waktu dan semangat. Terima kasih buat doa dan kenangan indah yang telah diberikan kepada penulis.

8. Sahabat–sahabatku terkasih, Ipus, Mbak Liul, Dek Embix, Yayas, Toro. Terima kasih atas persahabatan, kenangan, dukungan, doa dan perjalanan hidup yang berarti banget untuk penulis.

9. Teman–teman Kost Sekar Ayu, Mbak Die, Mbak Lia, Mbak Wie, Watiex, Mbak Ria, Sisca, terima kasih atas keceriaan yang kalian berikan kepada penulis.

10.Teman–teman angkatan 2003 dan 2004, Septi, Dewi, Valent, Merry, Mekar, Ridwan, Anin, Anggie, Koko, Eko, Nancy, Eni, Theo, Lili, Retno, Ratna, Siska, dan Yo. Terima kasih telah mau berbagi pengetahuan dan memberikan keceriaan dalam melewati kebersamaan selama di Matematika USD.

Penulis juga mengucapkan terima kasih kepada teman dan sahabatku yang tidak bisa disebutkan satu persatu serta semua pihak yang telah membantu penulis dalam menyelesaikan skripsi ini. Penulis berharap semoga skripsi ini dapat bermanfaat bagi semua pihak.

Yogyakarta, Juli 2008

HALAMAN JUDUL……… i

HALAMAN JUDUL DALAM BAHASA INGGRIS ………….. ii

HALAMAN PERSETUJUAN PEMBIMBING……… iii

HALAMAN PENGESAHAN………. iv

HALAMAN KEASLIAN KARYA ……… v

PERNYATAAN PERSEMBAHAN ……….. vi

ABSTRAK……… viii

ABSTRACT………. ix

LEMBAR PERNYATAAN PERSETUJUAN PUBLIKASI KARYA ILMIAH UNTUK KEPENTINGAN AKADEMIS ……… x

KATA PENGANTAR ……… xi

DAFTAR ISI……….. xiii

DAFTAR GAMBAR ………. xv

BAB I PENDAHULUAN………. 1

A. Latar Belakang Masalah……….. 1

B. Perumusan Masalah……….. 2

C. Pembatasan Masalah………. 2

D. Tujuan Penulisan……… 2

E. Metode Penulisan……… 2

F. Manfaat Penulisan………. 3

A. Ruang Vektor……….. 5

B. Topologi Metrik pada n ……… 7

C. Kekompakkan……… 10

D. Peminimal fungsi……… 13

E. Garis dan Hyperplane dalam n ……… 14

F. Sifat Himpunan Konveks dalam n……….. 22

G. Supporting Hyperplane atau Bidang Hiper Penyangga dan Titik Ekstrim……… 28

BAB III SIFAT-SIFAT FUNGSI KONVEKS DALAM n … 31 A. Definisi dan Sifat Dasar……… 31

B. Fungsi Konveks yang Diferensiabel……… 53

BAB IV OPTIMISASI FUNGSI KONVEKS………. 71

BAB V PENUTUP……… 81

A. Kesimpulan……… 81

B. Saran……….. 82

DAFTAR PUSTAKA……… 83

xv

Gambar 2.4.1 ……… 15

Gambar 2.4.2 ……… 19

Gambar 3.1.1 ……… 32

Gambar 3.1.2 ……… 35

Gambar 3.1.3 ……… 41

Gambar 3.1.4 ……… 50

Gambar 3.2.1 ……… 54

BAB I PENDAHULUAN

A. Latar Belakang Masalah

Fungsi–fungsi konveks membentuk kelas fungsi yang mempunyai peranan penting dalam analisis real. Fungsi konveks berguna dalam masalah optimisasi. Dalam masalah optimisasi kadang ada suatu fungsi yang sulit untuk dincari penyelesaiannya. Sumber kesulitan dari masalah optimisasi tersebut bergantung pada fungsi sasaran atau fungsi kendala, juga banyaknya variabel dan kendala dari fungsi tersebut.

Jika suatu fungsi adalah fungsi konveks maka fungsi tersebut unimodal, yaitu hanya mempunyai satu titik minimum saja. Fungsi konveks bersifat kontinu dan mempunyai turunan atau diferensiabel.

Pada umumnya, masalah–masalah optimisasi berkaitan dengan memaksimumkan atau meminimumkan suatu fungsi sasaran dengan kendala atau tanpa kendala. Salah satu cabang dari permasalahan optimisasi yang ada adalah masalah optimisasi konveks, yaitu jika fungsi sasaran dan fungsi kendalanya bersifat konveks. Jika suatu fungsi adalah konveks dan diferensiabel maka fungsi tersebut mencapai minimum jika gradien fungsi tersebut sama dengan nol.

B. Perumusan Masalah

Masalah-masalah yang akan dibahas dalam skripsi ini adalah: 1. Bagaimana sifat-sifat dasar fungsi konveks dalam n

? 2. Bagaimana terapan fungsi konveks dalam optimisasi?

C. Pembatasan Masalah

Pembahasan dari skripsi ini hanya dibatasi pada sifat-sifat fungsi konveks dalam n

dan masalah optimisasi dengan meminimumkan fungsi sasaran tanpa kendala. Masalah meminimumkan dengan kendala tidak dibahas di dalamnya.

D. Tujuan Penulisan

Tujuan dari penulisan skripsi ini adalah membahas: 1. Sifat-sifat dasar fungsi konveks dalam n

.

2. Masalah optimisasi fungsi konveks dalam meminimumkan suatu fungsi tanpa kendala.

E. Metode Penulisan

F. Manfaat Penulisan

Manfaat yang diharapkan dari penulisan skripsi ini adalah dapat memberikan kejelasan mengenai sifat-sifat fungsi konveks dan masalah optimisasi dari fungsi konveks.

G. Sistematika Penulisan

BAB I PENDAHULUAN

Dalam bab I akan dibahas tentang latar belakang masalah, perumusan masalah, pembatasan masalah, tujuan penulisan, metode penulisan, manfaat penulisan, dan sistematika penulisan.

BAB II TOPOLOGI METRIK DAN HIMPUNAN KONVEKS

DALAM n

Dalam bab II akan dibahas tentang topologi metrik pada n, kekompakkan, peminimal fungsi, garis dan hyperplane dalam n

, sifat himpunan konveks, dan supporting hyperplane atau bidang hiper penyangga dan titik ekstrim.

BAB III SIFAT-SIFAT FUNGSI KONVEKS DALAM n

BAB IV OPTIMISASI FUNGSI KONVEKS

Dalam bab IV akan dibahas tentang optimisasi fungsi konveks dengan meminimumkan fungsi sasaran tanpa kendala.

BAB V PENUTUP

BAB II

TOPOLOGI METRIK

DAN HIMPUNAN KONVEKS DALAM n

A. Ruang Vektor

Elemen–elemen dalam 

disebut sebagai vektor. Vektor x∈ n-merupakan matriks berordo n×1. Selanjutnya vektor x ditulis dengan

(

)

T

n

x x x1, 2,...,

=

x atau

⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎝ ⎛ =

n

x x

M 1

x . Bilangan real x_i, i=1,2,K,n disebut

komponen dari vektor x.

Definisi 2.1.1

Perkalian skalar dua vektor x dan y dalam n

yang dinotasikan dengan x,y

didefinisikan sebagai :

∑

=

= n i

i iy

x

1 ,y x

Definisi 2.1.2

Panjang vektor dalam n

, dinotasikan dengan x didefinisikan sebagai :

2 1

1 2 2

1

, _⎥

⎦ ⎤ ⎢ ⎣ ⎡ =

=

∑

= n

i i

x

Definisi 2.1.3

Dua vektor x dan y dalam n

, dikatakan saling tegak lurus atau ortogonal jika 0

,y = x .

Definisi 2.1.4

Misalkan adalah vektor-vektor dalam suatu ruang vektor V.

Kombinasi linear dari vektor-vektor adalah

n

v v v1, 2,...,

n

v v v1, 2,...,

n nv

v

v α α

α1 1+ 2 2+...+

dimana α1,α2,...,α_n∈.

Himpunan semua kombinasi linear dari disebut rentang dari , dan dilambangkan dengan

n

v v v1, 2,...,

n

v v

v₁, ₂,..., Rentang

(

v1,v2,...,vn

)

.

Definisi 2.1.5

Vektor-vektor v1,v2,...,vn dalam ruang vektor V disebut bebas linear jika

0 v v

v +α + +α_{n n} =

α_{1 1 2 2} ...

mengakibatkan semua skalar-skalar α1,α2,...,αn harus sama dengan 0.

Definisi 2.1.6

Vektor-vektor dalam ruang vektor V disebut bergantung linear

jika terdapat skalar-skalar n

v v v1, 2,...,

n

α α

α₁, ₂,..., yang tidak semuanya nol sehingga

0 v v

v +α + +α_{n n} =

Definisi 2.1.7

Vektor-vektor membentuk basis untuk ruang vektor V jika dan hanya jika:

n

v v v1, 2,...,

(i) v1,v2,...,vn bebas linear, (ii) v1,v2,...,vn merentang V.

Definisi 2.1.8

Misalkan V adalah ruang vektor. Jika V mempunyai basis yang terdiri dari n vektor, maka dikatakan bahwa V memiliki dimensi n. Ruang bagian

{

dari V dikatakan memiliki dimensi 0. V dikatakan memiliki dimensi hingga jika terdapat himpunan berhingga vektor yang merentang V, jika tidak demikian halnya, maka V memiliki dimensi tak hingga.

}

0

B. Topologi Metrik pada n

Definisi 2.2.1 (Kitar Terbuka dan Kitar Tertutup)

Kitar Terbuka dengan pusat x dan radius , yang diberi notasi

adalah himpunan titik-titik y yang jaraknya dari x kurang dari r, yang dapat juga ditulis :

0

>

r B

( )

x,r

( )

r

B x, =

{

y| y−x <r

}

.

Sedangkan Kitar Tertutup, B

( )

x,r dengan pusat x dan radius didefinisikan dengan

0

>

r

Definisi 2.2.2 (Titik Interior)

Misalkan n

. Suatu titik x disebut titik interior dari S, jika ada sedemikian sehingga .

⊆

S r>0

( )

r S B x, ⊂

Jika himpunan titik interior S adalah tidak kosong, maka himpunan titik-titik interior ini dapat disebut sebagai interior dari S yang dinotasikan dengan

.

( )

S

int

Contoh 2.2.1

i). Perhatikan himpunan titik-titik pada 1, maka semua titik tersebut adalah titik interior.

ii). Perhatikan himpunan titik-titik dalam bidang (2) dengan bentuk

(

x1,0

)

dengan 0 < x1<1. Interval 0 < x1<1 terletak pada sumbu−x1. Ambil

1

=

r , maka ada r>0 sedemikian sehingga

( )

{

1

}

bukan subset S. Maka titik-titik pada 2 ini tidak mempunyai titik interior.

|

, = y y−x < x r

B

Definisi 2.2.3 (Himpunan Terbuka)

Suatu himpunan S dikatakan terbuka jika semua titik S adalah titik interior yaitu untuk setiap titik x∈S, ada bilangan positif , yang bergantung pada

x, sedemikian sehingga kitar

0

>

r

( )

r

Definisi 2.2.4 (Titik Limit)

Titik x disebut titik limit dari himpunan S jika untuk setiapε>0 ada titik sedemikian sehingga

x

x_ε ≠ x_ε ∈S∩B

( )

x,ε . Titik biasanya bergantung pada

ε x

ε.

Himpunan titik-titik limit dari himpunan S dinotasikan denganS'.

Suatu himpunan tidak harus mempunyai titik limit dan suatu titik limit tidak harus berada dalam himpunan tersebut.

Contoh 2.2.2

Himpunan bilangan asli positif pada himpunan 1 merupakan salah satu contoh himpunan yang tidak mempunyai titik limit.

Contoh titik limit yang anggotanya tidak berada dalam himpunan

⎭ ⎬ ⎫ ⎩

⎨

⎧ _{= =}

K

, 3 , 2 , 1 , 1

| n

n x

x di 1. Nol adalah titik limit dari himpunan S, tetapi nol

tidak berada dalam S.

Definisi 2.2.5 (Closure atau Pemampat)

Closure atau pemampat dari himpunan S, yang dinotasikan dengan S

didefinisikan sebagai S= , dengan adalah himpunan titik limit dari S.

' S

Definisi 2.2.6 (Himpunan Tertutup)

Suatu himpunan S dikatakan tertutup jika S = S, yaitu bahwa S memuat semua titik limitnya.

Teorema 2.2.1

Komplemen himpunan tertutup adalah terbuka. Komplemen himpunan terbuka adalah tertutup.

Pembuktian dapat dilihat pada Berkovitz, L. D, 2002: 7. ∎

C. Kekompakkan

Definisi 2.3.1

Misalkan S adalah himpunan di n

dan A sebarang himpunan. Kumpulan himpunan terbuka

{ }

O_{α α∈A} dikatakan selimut terbuka S jika setiap x∈S

berada di O_α untuk suatu α∈A.

Definisi 2.3.2

Himpunan S⊂n

dikatakan kompak jika untuk setiap selimut terbuka dari S ada koleksi himpunan berhingga dari kumpulan

sedemikian sehingga kumpulan berhingga juga

merupakan selimut terbuka S.

{ }

O_{α α∈A}

{ }

Oα α∈A

m O O

O1, 2,K,

O

Teorema 2.3.1

Himpunan S n

adalah kompak jika dan hanya jika S adalah tertutup dan terbatas.

⊂

Pembuktian dapat dilihat pada Rudin, W, 1976: 40. ∎

Contoh 2.3.1

Himpunan S di 1 yang didefinisikan dengan S=

( ) {

0,1 = x|0<x<1

}

adalah tidak kompak, karena S tidak tertutup. Misalkan S1 =

[ ]

0,1 =

{

x|0≤x≤1

}

adalah himpunan kompak karena S tertutup dan terbatas.

Teorema 2.3.2 (Teorema Bolzano-Weierstrass)

Himpunan S n adalah kompak jika dan hanya jika setiap barisan dari titik-titik di S mempunyai subbarisan

⊂

{ }

xk

{ }

xkj yang konvergen untuk titik di S.

Pembuktian dapat dilihat pada Rudin, W, 1976: 38. ∎

Definisi 2.3.3

Misalkan n

, n

, dan

⊆

A f:A→ c∈A. Fungsi f dikatakan kontinu pada jika diberikan sebarang

(

c1,c2,K,cn

)

=

c ε>0 ada δ>0 sedemikian

sehingga jika x adalah sebarang titik di A yang memenuhi x−c <δ , maka

( ) ( )

x −f c <ε

Definisi 2.3.4

Misalkan n

, n

. Fungsi f dikatakan kontinu seragam pada A jika untuk setiap

⊆

A f:A→

0

>

ε ada δ

( )

ε >0 sedemikian sehingga jika

memenuhi

A

∈

u x,

( )

ε

δ

< −u

x , maka f

( ) ( )

x − f u <ε.

Definisi 2.3.5

Suatu himpunan S∈n

dikatakan terbatas jika ada bilangan positif M sedemikian sehingga x ≤M untuk semua x∈S.

Contoh 2.3.2

Himpunan S di 1 dikatakan terbatas jika untuk setiap x∈S, x ≤M atau .

M x

M ≤ ≤

−

Himpunan S di 1 dikatakan terbatas ke atas jika ada bilangan asli A sedemikian sehingga x ≤ A,∀x∈S.

Himpunan S disebut terbatas ke bawah jika ada bilangan asli B sedemikian sehingga x ≥ B, ∀x∈S.

Bilangan A disebut batas atas dari S, dan bilangan B adalah batas bawah dari S.

Definisi 2.3.6

(i). U adalah batas atas dari S, dan (ii). U' batas atas dari S maka U'≥U

Suatu bilangan L dikatakan batas bawah terbesar atau infimum dari himpunan S yang dinotasikan dengan L=inf

( )

S jika

(i). L adalah batas bawah dari S, dan (ii). L' batas bawah dari S, maka L'≤L.

D. Peminimal Fungsi

Masalah dasar dalam teori optimisasi adalah sebagai berikut: diberikan himpunan S dan fungsi bernilai real f yang didefinisikan pada himpunan S, apakah dapat ditemukan s_*∈S sedemikian sehingga f

( )

s* ≤ f

( )

s , ∀s∈S.

Tiik dikatakan peminimal untuk f . Dapat juga dikatakan bahwa f mencapai minimum pada S di . Masalah memaksimalkan f atas S atau menemukan

sedemikian sehingga

*

s

S

*

s

s*∈

( )

s* ≥ f

( )

s

f

Contoh 2.4.1

Sebagai contoh dalam 1 ini, apakah ada peminimal untuk f ?

(i). Misalkan S=

{

x| x≥1

}

dan

( )

x x

f =1. Disini jelas bahwa

}

0

1 , karena tidak ada nilai x yang membuat

( )

{

|

inf f x x≥ = f

( )

x

minimum, maka tidak ada x_*∈S sedemikian sehingga

( )

x* = 0. Jadi tidak ada peminimal untuk fungsi tersebut atau f tidak mencapai minimum pada S.

f

(ii). Misalkan S=

[ ]

1,2 dan

( )

x x

f =1. Maka inf

{

f

( )

x |1≤x≤2

}

=2. Jadi

2

*=

x adalah peminimal untuk fungsi tersebut atau f mencapai minimal di x*=2.

E. Garis dan Hyperplane dalam n

Persamaan garis (vektor) dan persamaan bidang telah dibahas dalam perkuliahan Geometri Analitik Ruang, oleh karena itu disini tidak akan dibahas tentang bagaimana cara mendapatkan suatu persamaan garis dan persamaan bidang.

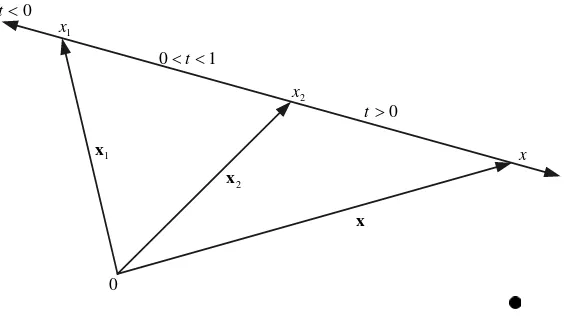
Persamaan vektor yang melalui dua titik dan dalam 2 dan 3 dinyatakan dengan (lihat gambar 2.4.1):

1

x x₂

(

2 1

)

1 x x

x

1

x

2

x

x 0

<

t

1 0<t<

0

>

t

0

1 x

2 x

x

Gambar 2.5.1 Garis

Pada gambar 2.4.1, penggal garis yang berawal dari dan berakhir di , berkorespondensi dengan nilai t dalam interval [0, 1] disebut dengan

segmen garis tertutup. Penggal garis yang berawal dari dan berakhir di

, tetapi tidak memuat dan , berkorespondensi dengan nilai t dalam interval

(

disebut segmen garis terbuka.

1

x

1

x

2

x

2

x x₁ x₂

)

1 , 0

Sinar garis positif berawal dari atau dari berkorespondensi dengan nilai t 0, dan sinar garis negatif berawal dari atau dari berkorespondensi dengan nilai t

1

x x₂

≥ x₁ x₂

≤ 0, sinar garis demikian disebut segmen garis setengah terbuka.

Definisi 2.5.1

Garis pada n

yang melewati dua titik dan didefinisikan menjadi himpunan titik–titik x sedemikian sehingga

1

x x₂

(

2 1

)

1 x −x

x

(

)

{

x|x= x1+t x2−x1 ,−∞<t<∞

}

(2.5.2)

dapat juga ditulis sebagai

( )

{

x|x= 1−t x1 +tx2,−∞<t<∞

}

. (2.5.3)

Dengan mengambil α=

( )

1−t danβ=t diperoleh

{

x|x=α x1+βx2,α≥0,β≥0,α +β=1

}

. (2.5.4)

Definisi 2.5.2

Segmen garis tertutup yang menghubungkan titik–titik dan dalam n

dinotasikan dengan

[

dan didefinisikan sebagai :

1

x x₂

]

2 1,x

x

[

x1,x2

]

=

{

x|x=

( )

1−t x1+tx2,0≤t≤1

}

Untuk α=

( )

1−t dan β=t, diperoleh :

[

x₁,x₂

]

=

{

x|x=αx₁+βx₂,α≥0,β≥0,α+β=1

}

.

Definisi 2.5.3

Segmen garis terbuka yang menghubungkan titik–titik dan dalam n

dinotasikan dengan

(

dan didefinisikan sebagai :

1

x x₂

)

2 1,x

x

(

x1,x2

)

=

{

x|x=

( )

1−t x1+tx2,0<t<1

}

Untuk α=

( )

1−t dan β=t, diperoleh :

Definisi 2.5.4

Segmen garis setengah terbuka yang memuat titik tetapi tidak memuat titik yang dinotasikan dengan

1

x

2

x

[

x₁,x₂

)

dan dibatasi dengan 0≤t<1 didefinisikan sebagai :

[

x₁,x₂

)

=

{

x|x=

( )

1−t x₁ +tx₂,0≤t<1

}

Untuk α=

( )

1−t dan β=t, diperoleh :

[

x₁,x₂

) {

= x|x=αx₁ +βx₂,α>0,β≥0,α+β=1

}

.

Segmen garis setengah terbuka yang memuat titik tetapi tidak memuat titik yang dinotasikan dengan

2

x

1

x

(

x₁,x₂

]

dan dibatasi dengan 0<t≤1 didefinisikan sebagai :

(

x₁,x₂

]

=

{

x|x=

( )

1−t x₁ +tx₂,0<t≤1

}

Untuk α=

( )

1−t dan β=t, diperoleh

(

x₁,x₂

]

=

{

x|x=αx₁ +βx₂,α≥0,β>0,α+β=1

}

.

Lema 2.5.1

Misalkan y sebarang titik dalam segmen garis terbuka

(

yang didefinisikan dengan

)

2 1,x

x

1 ,

0 , 0 ,

2

1+ > > + =

=αx βx α β α β

y , berlaku :

α β

= − −

2 1

x y

x y

Bukti :

Ambil sebarang titik y∈

(

x1,x2

)

, maka y=αx1+βx2,α>0,β>0,α+β=1.

1

x

y− = αx1 +βx2 −x1

⇔ y−x₁ =

(

α−1

)

x₁ +βx₂

⇔ y−x₁ = βx₂ −

(

1−α

)

x₁

⇔ y−x₁ = βx₂ −βx₁

⇔ y−x₁ = β

(

x₂ −x₁

)

⇔ y−x₁ = β

(

x₂−x₁

)

⇔ y−x₁ = β x₂−x₁ (2.5.6)

Dengan cara yang sama akan didapatkan :

2 2 1

2 x x x

x

y− =α +β −

⇔ y−x2=αx1+

(

β−1

)

x2

⇔ y−x2=αx1−

(

1−β

)

x2

⇔ y−x₂=αx₁−αx₂ (karena α+β=1)

⇔ y−x2=α

(

x1−x2

)

⇔ y−x2 = α

(

x1−x2

)

⇔ y−x2 =α x1−x2 (2.5.7)

Dari persamaan (2.5.6) dan (2.5.7) diperoleh :

2 1

1 2

2 1

x x

x x

x y

x y

− − =

− −

⇔

2 1

2 1

2 1

x x

x x

x y

x y

− − =

− −

α β

⇔

α β

= − −

2 1

x y

x y

∎

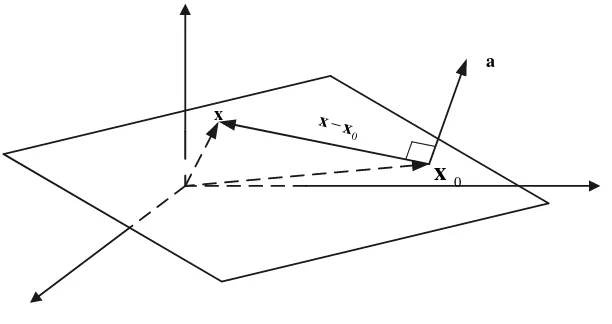
Dalam 3 bidang yang melewati titik x0=

(

x01,x02,x03

)

dengan normal

yang terdiri atas semua titik x =

(

a1,a2,a3

=

a

)

(

x₁,x₂,x₃

)

sedemikian

sehingga x−x0 tegak lurus terhadap a , sehingga memenuhi persamaan :

(

1 01

)

2

(

2 02

)

3

(

3 03

)

0

1 x −x +a x −x +a x −x =

a (2.5.8)

Atau

γ

= +

+ _{2 2 3 3}

1

1x a x a x

a (2.5.9)

dimana γ=a1 x01+a2 x02+a3x03.

Bentuk ini merupakan bentuk umum persamaan bidang di 3.

x

0

x

0

x x₋

a

Dalam persamaan vektor, persamaan (2.5.8) dan (2.5.9) dapat ditulis sebagai

γ

= =

−x a x

x

a, ₀ 0 atau , (2.5.10)

dimana γ = a,x0 . Persamaan (2.5.10) adalah persamaan bidang dengan normal a dalam 3.

Persamaan (2.5.10) dapat digunakan untuk mendefinisikan hyperplane atau bidang hiper dalam n_.

Definisi 2.5.5 (Hyperplane atau Bidang Hiper)

Hyperplane atau bidang hiper di n

didefinisikan sebagai himpunan dari titik–titik yang memenuhi persamaan

α a

H

α

=

x

a, yang dapat ditulis sebagai

{

α

}

α _{= =}

x a x

a | ,

H .

Vektor a dikatakan sebagai normal of hyperplane atau normal bidang hiper.

Persamaan bidang hiper H_aα =

{

x| a,x =α

}

dapat ditulis sebagai :

{

x| a,x−x₀ =0

}

.

Untuk sebarang x0 memenuhi a,x0 =α atau ekuivalen untuk sebarang

dengan a adalah normalnya, selanjutnya persamaan bidang hiper cukup ditulis dengan :

0

x ∈H_aα

0 ,x−x₀ =

Contoh 2.5.1

Dalam 4 diketahui titik–titik A

(

1,1,0,1

)

, B

(

2,-1,1,0

)

, dan . Bagaimana persamaan bidang hiper yang melalui titik A, B, C, dan D?

(

2,0,1,0

)

C

(

1,-1,1,0

D

)

Penyelesaian :

Misalkan Dx₁=A,x₂ =B,x₃ =C,dan x₄ = .

Misalkan p=x2 −x1, q=x3 −x2, r=x4 −x3, maka

(

)

T AB = 1,−2,1,−1

=

p ,

(

)

T 0 , 0 , 1 , 0 BC=

=

q dan r=CD=

(

−1,−1,0,0

)

T, dengan normal bidang hiper , sehingga dapat dicari dengan syarat sebagai berikut :

(

T

a a₃, ₄

,

)

a a₁, ₂

=

a

i). a⊥p ⇔ a,p =0 ⇔

(

a1,a2,a3,a4

) (

⋅1,−2,1,−1

)

= 0

⇔ a₁−2a₂+a₃−a₄=0 (2.5.11)

ii). a⊥q ⇔ a,q =0 ⇔

(

a1,a2,a3,a4

) (

⋅ 0,1,0,0

)

=0

⇔ a2=0 (2.5.12) iii). a⊥r ⇔ a,r =0 ⇔

(

a1,a2,a3,a4

) (

⋅ −1,−1,0,0

)

=0

⇔ −a1−a2=0 (2.5.13)

Untuk mendapatkan nilai–nilai skalar vektor a dari persamaan di atas dapat diperoleh dengan cara substitusi dan eliminasi.

Substitusikan nilai a2=0 ke persamaan (2.5.13) diperoleh: 0

0 1

2

1− = ⇒ =

Substitusikan nilai a2=0 dan a1=0 ke persamaan (2.5.11) diperoleh :

4 3 4

3 2

1 2a a a 0 a a

a − + − = ⇒ =

Untuk sebarang skalar α di mana a3=a4=α, normal . Jadi

persamaan bidang hiper yang melalui titik

(

_{α α} T

, , 0 , 0

=

a

)

(

1,1,0,1

)

A dengan normal

adalah :

(

_{α α} T

, , 0 , 0

=

a

)

(

x3−0

) (

+α x4−1

)

α = 0

⇔ α x3+αx4−α = 0

⇔ α

(

x₃+x₄

)

= α

F. Sifat Himpunan Konveks dalam n

Suatu himpunan dikatakan konveks jika diberikan sebarang dua vektor dan yang merupakan anggota himpunan tersebut, segmen garis yang menghubungkan kedua vektor juga terdapat dalam himpunan tersebut.

1

x x₂

Definisi 2.6.1

Himpunan C n

disebut konveks jika untuk setiap pasangan titik–titik dan di C, maka segmen garis

⊆ x₁

2

x

[

x1,x2

]

=

{

x|x=α x1+βx2,α≥0,β≥0,α +β=1

}

Contoh 2.6.1

Dari himpunan–himpunan dalam 2_{, gambar berikut mengilustrasikan}

himpuna e s atau himpunan tidak konveks. (a).

beberapa n konv k

( )

{

, | 2 ₊ 2 _≤1

}

y x y x

Konveks

).

{

( )

, |0_< 2 ₊ 2 _≤1

}

y x y x (b

Tidak Konveks

).

{

( )

x,y |y≥x2

}

(c

(d).

{

( )

x,y |x + y≤1

}

Konveks

(e).

{

( )

(

2

)

}

1 / 1 |

,y y x

x ≥ +

Tidak Konveks

Untuk setiap bilangan bulat positif n, didefinisikan

(

)

⎭ ⎬ ⎫ ⎩

⎨ ⎧

= ≥

=

=

∑

= n

i i i

T n

n p p p p

P

1 1,..., | 0, 1

p

Jika n=1, P₁ adalah titik 1. Jika n=2, adalah segmen garis tertutup yang menghubungkan dan

2

P

(

0,1

)

( )

1,0 . Jika n=3, adalah segitiga tertutup

dengan titik-titik sudut

3

P

(

1,0,0

)

,

(

0,1,0

)

, dan

(

0,0,1

)

. Mudah dipahami bahwa,

untuk setiap n, Pn adalah himpunan konveks tertutup.

Definisi 2.6.2

Titik n

disebut kombinasi konveks dari titik–titik jika ada dimana adalah himpunan konveks tertutup sedemikian sehingga

∈

x

(

1,K,

k

x x1,K,

)

k

k P

p

p ∈

=

p

p x x

k P

k k p

p x + + x

+ ₂ L

1

Lema 2.6.1

Sebuah himpunan C∈n

adalah konveks jika dan hanya jika setiap kombinasi konveks dari titik–titik di C juga ada di dalam C.

Bukti :

(

⇒

)

Jika C konveks maka akan ditunjukkan bahwa setiap kombinasi konveks

dari titik-titik C juga ada di dalam C. Pembuktian ini akan menggunakan induksi matematika.

Untuk k = 1, jelas benar karena kombinasi konveksnya adalah titik itu sendiri. Andaikan benar untuk k titik, yakni bahwa

C ...

2 2 1

1 + + + ∈

=l x l x l_kx_k

x dengan l=

(

l1,...,lk

)

∈Pk Akan ditunjukkan benar untuk k + 1 titik, yakni bahwa

C p

p

p + + _{k k} + _{k k} ∈

= ₁x₁ ... x ₊₁x ₊₁

x dengan p=

(

p1,...,pk,pk+1

)

∈Pk+1

Jika 1pk+1 =

...= pk =

, maka dari syarat , berakibat bahwa

, sehingga kombinasi konveksnya adalah titik itu sendiri.

∑

+

=

=

≥ 1

1

1 dan

0 k

i i

i p

p

0

1=

p

Jika 1pk+₁ <

0

>

i p

, maka dari syarat , berakibat bahwa

sehingga kombinasi konveksnya ditulis sebagai berikut:

∑

+

=

=

≥ 1

1

1 dan

0 k

i i

i p

p

1

∑

= k

i

x = p₁x₁ + p₂x₂ +...+ pkxk + pk₊₁xk₊₁

⇔ x =

(

_{1 1 2 2}

)

_{1 1} 1 1 _... + + = = _{+ + +}

∑

∑

k k k k k i i k i i p p p p p p x x x x

⇔ x = _{1 1}

1 2 1 2 1 1 1 1 ... + + = = = = + ⎟ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎜ ⎝ ⎛ + +

∑

∑

∑

∑

k k k k

i i k k i i k i i k i i p p p p p p p

p x x x x (2.5.1)

Perhatikan bentuk dalam tanda kurung pada persamaan (2.5.1).

Misalkan ⎟ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎜ ⎝ ⎛ =

∑

∑

∑

= = = k i i k k i i k i i p p p p p p 1 1 2 1

1 _{, ,...,}

q dengan 0. Maka

1 >

∑

= k i i p

∑

∑

∑

∑

= = = = + + + = _k i i k k i i k i i k i i p p p p p p q 1 1 2 1 1 1 ... ⇔

∑

∑

= = + + + = _k i i k k i i p p p p q 1 2 1 1 ... ⇔

∑

∑

∑

= = = = _k i i k i i k i i p p q 1 1 1 ⇔ 1 1 =

∑

= k i i q

(

⇐

)

Jika setiap kombinasi konveks dari titik–titik di C juga ada di dalam C,

maka akan ditunjukkan bahwa konveks.

Ambil x₁danx₂∈C. Akan ditunjukkan

[

x₁,x₂

]

⊆C.

Misalkan x∈

[

x₁,x₂

]

, maka x=αx₁+β x₂ dengan α ≥0,β ≥0,α +β =1. Nampak bahwa α dan β memenuhi definisi sehingga x merupakan suatu

kombinasi konveks dari x . Jadi

k P

2

x

1dan

[

x1,x2

]

⊆C. ∎

Untuk sebarang himpunan A, misalkan K

( )

A dinotasikan sebagai himpunan semua kombinasi konveks dari titik-titik dalam A. Maka menurut Lema 2.6.1, adalah konveks dengan memandang sebagai C. Untuk lebih jelasnya

( )

A

K K

( )

A

( )

A A ⊆ K .

Definisi 2.6.3

Konveks hull dari himpunan A yang dinotasikan dengan adalah irisan

dari semua himpunan konveks yang memuat A.

( )

A

co

Lema 2.6.2

Jika sebarangA⊂ n adalah kompak, maka A =co

( )

A .

G. Supporting Hyperplane atau Bidang Hiper Penyangga dan Titik Ekstrim

Definisi 2.7.1 (Titik Batas)

Titik z dikatakan titik batas dari himpunan S jika untuk setiap ε>0, kitar

( )

z,ε

B memuat titik x∈S dan titik y∉S.

Contoh 2.7.1

Dalam 2, misalkan S=

{

x=

(

x₁,x₂

)

|0< x <1

}

, maka 0 adalah titik batas S dan untuk setiap 0<ε<1, titik tersebut hanya di dalam B

( )

0,ε . Jadi 0 tidak berada di dalam S.

Definisi 2.7.2 (Bidang Hiper Penyangga)

Bidang hiper dikatakan supporting hyperplane atau bidang hiper

penyangga untuk himpunan S jika untuk setiap

α a

H

S

∈

x , a,x ≤α dan ada

sekurang-kurangnya satu titik x₀∈S sedemikian sehingga a,x₀ ≤α .

Teorema 2.7.1

Misalkan C adalah himpunan konveks dan misalkan y∉C, maka ada bidang hiper Haα sedemikian sehingga untuk semua x∈C berlaku

α

≤

x

a, dan a,y =α Jika int

( )

C ≠φ, maka untuk semua x∈int

( )

C

α

<

Pembuktian dapat dilihat pada Berkovitz, L. D, 2002: 51. ∎

Teorema 2.7.2

Misalkan C adalah himpunan konveks dan z adalah titik batas dari C. Maka ada bidang hiper penyangga Haα untuk C sedemikian sehingga . Jika

α a

z∈H

( )

C ≠φ

int , bidang hiper penyangga adalah tak trivial.

Bukti :

Jika , maka menurut Teorema 2.7.1 dengan y = z, ada bidang hiper sedemikian sehingga untuk semua

C

∉

z H_aα

C

∈

x

α

α =

≤ a z

x

a, dan , .

Karena z∉C dan z adalah titik batas dari C, maka z∈C. Jadi adalah bidang hiper penyangga untuk C dengan .

α a

H

α

•

∈ _a

z H

Jika , menurut definisi dari titik batas maka ada barisan titik–titik

{ }

dengan sedemikian sehingga . Menurut Teorema 2.7.1 untuk setiap bilangan bulat positif k ada vektor

C

∈

z

k

y

k y C

∉ y_k→z

0

a_k ≠ sedemikian sehingga

C

k k

k x ≤ a y ∀x∈

a , , , . (2.7.1)

Jika pertidaksamaan (2.7.1) dibagi dengan ak ≠0, maka dapat diasumsikan

bahwa ak =1. Karena S

( )

0,1 adalah kompak, maka ada subbarisan dari

{ }

dan vektor a dengan

k

a

1

=

a sedemikian sehingga . Pada pertidaksamaan (2.7.1) misalkan

a

a_k →

∞ →

C

∈ ∀

≤ a z x

x

a, , , .

Jika diambil α= a,z , dapat dilihat bahwa bidang hiper memuat z dan

merupakan bidang hiper penyangga untuk C. ∎

α a

H

Definisi 2.7.3 (Titik Ekstrim)

Suatu titik x dalam himpunan konveks C dikatakan titik ekstrim dari C jika ada dua titik berbeda u,v∈Csedemikian sehingga x=αu+βv untuk

1 ,

0 ,

0 > + =

> β α β

α .

Teorema 2.7.3

Misalkan C adalah himpunan konveks kompak. Misalkan dinotasikan

sebagai himpunan titik ekstrim C, maka

e C

( )

Ce

C=co .

BAB III

SIFAT-SIFAT FUNGSI KONVEKS DALAM n

A. Definisi dan Sifat Dasar Definisi 3.1.1

Suatu fungsi bernilai real f yang didefinisikan pada himpunan konveks C di n dikatakan konveks jika untuk setiap x₁ dan x₂di C dan α≥0,β≥0,α+β=1 maka

(

x1 x2

)

f

( )

x1 f

( )

x2

f α +β ≤α +β (3.1.1)

Fungsi f disebut konveks tegas jika

(

x1 x2

)

f

( )

x1 f

( )

x2

f α +β <α +β (3.1.2)

untuk setiap x₁ dan x₂ di C dengan x₁≠x₂.

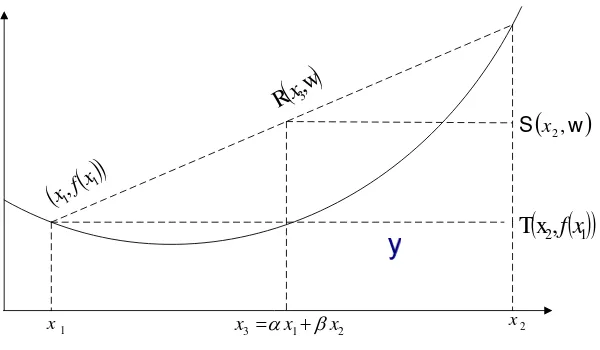
Apabila diinterpretasikan secara geometris, fungsi konveks f adalah fungsi sedemikian sehingga jika z1dan z2 sebarang dua titik di 

n+1

pada grafik f, maka titik–titik segmen garis

[

z1,z2

]

yang menghubungkan z1danz2 terletak pada atau di atas grafik f.

( )

(

x2, 1

)

T fx

2 1 3 x x

x =α +β

( )

(

1

)

1,

x f x

( )

,w Rx3

(

w

)

S x2,

1

x x2

Gambar 3.1.1 Fungsi konveks di 2

Misalkan R=

(

x3,w

)

dengan x3 =α x1 +βx2,α>0,β>0,α+β=1

( )

(

1, 1

)

P= x f x

, adalah titik pada segmen garis yang menghubungkan titik dan

( )

(

2, 2

Q= x f x

)

pada grafik f, dan misalkan S=

(

x2,w

)

dan ,

maka

( )

(

2, 1

)

T= x f x

( )

( ) ( )

1 2

1 2

1 2 2

x x

x f x f PT QT RS

QS x

x w x f

− − =

= =

− −

α

Dari syarat–syarat di atas maka kita peroleh persamaan

( ) (

x1 1

) ( )

f x2

f

w=α + −α

( )

x1 f

( )

x2

f β

α +

= .

Dengan demikian

(

terletak di atas atau pada grafik jika dan hanya jika persamaan (3.1.1) terpenuhi.

Contoh3.1.1

Misalkan f

( )

z =z1z2 dengan z=

(

z1,z2

)

{

z2 ≥0

}

. Apakah f konveks atau konveks sempurna pada C= z |z1≥0, ?

Penyelesaian :

Misalkan, x=

[

x₁,x₂

]

T ∈C dan y=

[

y₁,y₂

]

T ∈ C. Maka

(

)

(

)

(

)

(

)

⎥_⎦⎤ ⎢ ⎣ ⎡ + − + − = ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ − + − + = ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ − − + ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ = ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ − + ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ = − + 2 2 2 1 1 1 2 2 2 1 1 1 2 2 1 1 2 1 2 1 2 1 1 1 y y x y y x y y x y y x y y y y x x y y x x α α α α α α α α α α α α α

αx y

Karena itu

(

)

(

αx+ 1−α y

)

f =

(

α

(

x1−y1

)

+y1

) (

(

α x2−y2

)

+y2

)

=

(

α x1−α y1+y1

)(

αx2−α y2+y2

)

= + − + − +

− 2 _{1 2 1 2}

1 2 2 2 1 2 1 2 2 1 2 y y y y y x y x y x x

x α α α α α

α 2 1 2 1 1

2y y y y y

x −α +

α

= − − + 1 2+

2 1 2 2 2 1 2 2 1 2 y y y x y x x

x α α α

α

α x1y2+α x2y1−2α y1y2+y1y2

=

(

1 2− 1 2− 2 1+ 1 2

)

+ 1

(

2− 2+ 2

)

+ 2

2 y y

x y y y y x y x x

x α α

α

dan

( ) (

x

) ( )

f y

f α

α + 1− = α

(

x1∗x2

) (

+ 1−α

)(

y1∗y2

)

= α x1x2+y1y2−α y1y2

= α

(

x₁x₂−y₁y₂

)

+y₁y₂

Karena α=

[

0,1

]

maka α2<α sehingga diperoleh :

(

)

(

αx+ 1−α y

)

f

=

(

1 2− 1 2− 2 1+ 1 2

)

+ 1

(

2− 2+ 2

)

+ 2

2 y y

x y y y y x y x x

x α α

α α x₁y₂

(

x1x2 x1y2 x2y1 y1y2

)

y1

(

α x2 2α y2 y2

)

α x1y2

α − − + + − + +

<

2 1 2 1 2 1 1

2 2 1 1 2 2 1 2

1x x y x y y y x y 2 y y y y x y

x α α α α α α

α − − + + − + +

<

2 1 2 1 2

1x y y y y

x − +

=α α

(

x1x2−y1y2

)

+y1y2

=α = α f

( ) (

x + 1−α

) ( )

f y

Jadi, untuk sebarang α maka f

(

αx+

(

1−α

)

y

)

≤α f

( ) (

x + 1−α

) ( )

f y .

Karena f

(

αx+

(

1−α

)

y

)

≤α f

( ) (

x + 1−α

) ( )

f y untuk sebarang α, jadi f adalah konveks.

Definisi 3.1.2

Suatu fungsi f yang didefinisikan pada himpunan konveks C disebut konkaf

jika – f adalah konveks.

Contoh 3.1.2

Misalkan f

( )

z =−z1.z2 dengan z =

(

z1,z2

)

. Apakah f konkaf pada

?

{

| 1≥0,z2≥0

}

= z

Penyelesaian :

Ya. Karena − f

( ) (

z =− −z1z2

)

=z1z2 konveks pada C menurut Contoh 3.1.1.

Definisi 3.1.3

Misalkan f adalah fungsi bernilai real yang didefinisikan pada suatu himpunan

A. Epigraph dari fungsi f, yang dinotasikan dengan epi

( )

f adalah himpunan

( ) ( )

f =

{

,y | ∈A,y∈

epi x x ,y≥ f

( )}

x

Epigraph dari suatu fungsi adalah himpunan titik–titik

( )

x,y di n+1

yang terletak pada atau di atas grafik f.

Gambar 3.1.2 Epigraph

Lema 3.1.1

Bukti :

(

⇐

)

Diketahui epi

( )

f konveks.

Misalkan dan akan ditunjukkan f konveks. Fungsi f didefinisikan pada himpunan konveks C, maka

C

∈

2 1,x x

( )

(

x1, f x1

)

dan

(

x2, f

( )

x2

)

dalam .

Karena konveks untuk sebarang

( )

f

epi

( )

f

epi

(

α,β

)

∈P2, dimana adalah segmen

garis tertutup yang menghubungkan

2

P

( )

0,1 dan

( )

1,0 maka

( )

(

x1, f x1

)

β

(

x2, f

( )

x2

)

(

αx1,α f

( )

x1

)

(

βx2,β f

( )

x2

)

α + = +

=

(

αx1+βx2,α f

( )

x1 +β f

( )

x2

)

berada dalamepi

( )

f . Menurut definisiepi

( )

f ,

( )

x1 β

( ) (

x2 αx1 βx2

)

α f + f ≥ f + .

Jadi f adalah konveks.

(

⇒

)

Diketahui f adalah konveks.

Misalkan

(

x1,y1

)

)

y2

dan adalah sebarang dua titik dalam . Maka dan . Untuk sebarang

(

x2,y2

( )

x2

)

epi

( )

f

(

1

1 f x

y ≥ ≥ f

(

α,β

)

∈P₂, misalkan

(

x3,y

)

= α

(

x1,y1

) (

+β x2,y2

)

=

(

αx1,α y1

) (

+ βx2,β y2

)

=

(

αx1+βx2,α y1+β y2

)

Karena

(

x₁,y₁

)

dan

(

x₂,y₂

)

dalam epi

( )

f dan karena f adalah konveks, maka

( )

1

( ) (

2 1 2

) (

3

2

1 y f x f x f x x f x

y

y=α +β ≥α +β ≥ α +β =

)

Teorema 3.1.2 Pertidaksamaan Jensen

Misalkan adalah fungsi konveks yang didefinisikan pada himpunan konveks subset C n

. Jika

( )

x

f

⊆ λ1,λ2,K,λ_k

k

x

adalah bilangan tak negatif dengan

dan jika adalah titik di C, maka 1 1 =

∑

= k i i

λ x1,x2,K,

( )

i k i i k i i i f

f

∑

x

∑

x

= = ≤ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ 1 1 λ

λ (3.1.3)

Bukti :

Teorema di atas akan dibuktikan dengan menggunakan induksi matematik pada bilangan k.

i). Untuk k = 2, karena f konveks berlaku

(

1 1 2 2

)

1

( )

1 2 2 2 1 x f x f x x f f i i

i λ λ λ λ

λ _⎟⎟ = + ≤ + ⎠ ⎞ ⎜⎜ ⎝ ⎛

∑

=

x

( )

=

( )

i i

i f x

∑

=

2

1

λ

Jadi pertidaksamaan (3.1.3) benar untuk k = 2. ii). Misalkan pertidaksamaan berlaku untuk k = n, maka

( )

∑

∑

= = ≤ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ n i i i n i i i f f 1 1 x x λ λ

iii). Akan dibuktikan pertidaksamaan benar untuk k = n + 1

Misalkanλ₁,λ₂,K,λn+₁ adalah bilangan tak negatif sehingga memenuhi ,

0

≥

i

Misalkan

∑

maka = = Ω n i i 1

λ Ω>0,Ω+λn+1=1, 1

1 = Ω

∑

= n i i λ sehingga ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛

∑

+ = 1 1 n i i i

f λ x = _⎟⎟

⎠ ⎞ ⎜ ⎜ ⎝ ⎛ + ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ Ω Ω _{+ +} =

∑

1 1

1 n n n i i i

f λ x λ x

= _⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ Ω Ω

∑

= + + n i n n i i f 1 1 1x x λ λ

1

( )

1

1 + + = + ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ Ω Ω

≤

∑

n n

n

i

i i

f

f λ x λ x

= f

(

λ1x1+λ2x2 +L+λnxn

)

+λn+1f

( )

xn+1

≤ λ₁f

( )

x₁ +λ₂f

( )

x₂ +L+λn₊₁f

( )

xn₊₁

=

( )

i n

i

i f x

∑

+

=

1

1

λ

Jadi pertidaksamaan (3.1.3) benar untuk k = n + 1, ∀n∈.

Jadi

( )

i benar untuk semua k k i i k i i i f

f

∑

x

∑

x

= = ≤ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ 1 1 λ λ ∈. ∎

Misalkan C adalah himpunan konveks. Untuk n , didefinisikan

∈ ∈ v

x Cdan

{

∈ =

Ω λ|λ , x+λv∈C

}

.

Misalkan l₁=inf

{

λ|λ∈Ω

}

dan l₂ =sup

{

λ|λ∈Ω

}

. Maka . Karena C adalah konveks, jika

2

1 0 l

l ≤ ≤

2

1 l

terbuka

(

l₁,l₂

)

. Bergantung pada struktur himpunan C, x+λv dapat berada di C untuk semua λ di

[

l₁,l₂

)

atau

[ ]

l₁,l₂ atau

(

l₁,l₂

]

.

Misalkan f adalah fungsi konveks yang didefinisikan pada himpunan konveks C. Maka dari pembahasan sebelumnya, untuk setiap x∈C dan v∈n terdapat suatu interval  yang bergantung pada x dan v sedemikian sehingga fungsi

⊆

I

(

⋅;x,v

)

didefinisikan dengan

ϕ

(

λ x v

) (

=f x λv

)

(3.1.4)

ϕ ; , +

memiliki domain I. Interval I selalu memuat titik asal.

Lema 3.1.3

Suatu fungsi f yang didefinisikan pada himpunan konveks C adalah konveks jika dan hanya jika untuk setiap x∈C dan v∈n

sedemikian sehingga

(

⋅;x,v

)

ϕ terdefinisi pada interval nondegenerate I, maka fungsi ϕ

(

⋅;x,v

)

adalah konveks pada I.

Bukti :

(

⇒

)

Misalkan f adalah konveks. Akan ditunjukkan ϕ

(

⋅; x,v

)

adalah konveks.

Untuk sebarang λ₁,λ₂ pada I dan

(

α,β

)

∈P₂ maka

(

αλ₁ βλ₂;x,v

)

=

(

x

(

₁ βλ₂

)

v

)

ϕ + f + αλ +

(

) (

)

(

x ₂ v

)

= f α+β + αλ₁+βλ (karena α+β=1)

(

) (

)

(

x ₁v β x λ₂v

)

f

= α +λ + +

= αϕ

(

λ₁;x,v

)

+βϕ

(

λ₂;x,v

)

Jadi terbukti ϕ

(

⋅; x,v

)

adalah konveks.

( )

⇐ Diketahui untuk setiap x ∈ C dan v ∈ n

sedemikian sehingga

{ } (

0, ⋅;x,v

)

≠ ϕ

I

1dan

x

adalah konveks. Akan dibuktikan f adalah konveks. Misalkan

2

x ∈C dan

(

α,β

)

∈P₂, maka

(

αx₁+βx₂

)

= f

(

(

1−β

)

x₁+βx₂

)

f

(

x₁−βx₁+βx₂

)

= f

(

)

(

x1+ x2−x1

)

= f β

(

;x1,x2−x1

)

=ϕ β

=ϕ

(

α⋅0+β⋅1;x₁,x₂−x₁

)

. (3.1.5) Karena

(

λ;x1,x2−x1

)

=

(

x1+λ

(

x2−x1

)

)

ϕ f

dan C adalah konveks, maka ϕ

(

λ;x₁,x₂−x₁

)

terdefinisi untuk 0≤λ≤1 dan

(

0;x₁,x₂ −x₁

)

= f

(

x₁+0

(

x₂−x₁

))

= f

( )

x₁

ϕ serta

(

1;x₁,x₂ −x₁

)

=f

(

x₁+1

(

x₂ −x₁

)

) (

= f x₁+x₂−x₁

) ( )

= f x₂

ϕ (3.1.6)

Karena ϕ

(

⋅;x,v

)

adalah konveks dan dari persamaan (3.1.6) maka diperoleh

(

αx1 +βx2

) (

=ϕ α⋅0+β⋅1;x1,x2 −x1

)

f

≤αϕ

(

0;x₁,x₂ −x₁

) (

+β1;x₁,x₂ −x₁

)

=α f

( )

x₁ +β f

(

x₂

)

Jadi terbukti bahwa f adalah konveks.

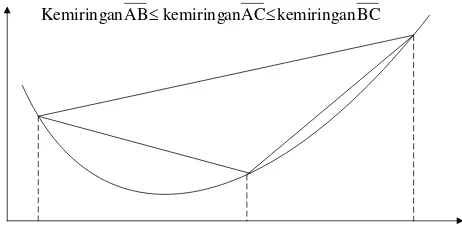
Teorema 3.1.4 Sifat Tiga Busur

Misalkan g adalah fungsi konveks yang didefinisikan pada interval . Maka untuk

⊂

I

z y

x< < dengan x,y,z∈I berlaku

( ) ( ) ( ) ( ) ( ) ( )

y z y g z g x z x g z g x y x g y g − − ≤ − − ≤ − − (3.1.7)

Jika g adalah konveks sempurna maka

( ) ( ) ( ) ( ) ( ) ( )

y z y g z g x z x g z g x y x g y g − − < − − < − − Bukti :

Ilustrasi Teorema 3.1.4 dapat dilihat pada gambar 3.1.3 berikut

BC kemiringan AC

kemiringan AB

Kemiringan ≤ ≤

Gambar 3.1.3 Sifat Three-chord

i). Akan dibuktikan

( ) ( ) ( ) ( )

x z x g z g x y x g y g − − ≤ − − .

Karena x<y<z ada 0<t<1 sedemikian sehingga y=x+t

(

z−x

)

. Karena g adalah konveks,

( ) ( )

y g x g

(

( )

t x tz

) ( )

g x g − = 1− + −

= g

( )

x −tg

( )

x +tg

( ) ( )

z −g x

= −tg

( )

x +tg

( )

z

= t

(

g

( ) ( )

z −g x

)

(3.1.8) Jika persamaan (3.1.8) dibagi dengan t

(

z−x

)

>0 dan maka diperoleh

(

z x t x

y− = −

)

( ) ( )

(

( ) ( )

)

x y x g z g t x y x g y g − − ≤ − −

( ) ( )

(

( ) ( )

)

(

z x

)

t x g z g t x y x g y g − − = − −

( ) ( ) ( ) ( )

x z x g z g x y x g y g − − ≤ − −

ii). Akan dibuktikan

( ) ( )

( ) ( )

y z y g z g x z x g z g − − ≤ − − .

Karena g konveks berlaku

( )

(

t x tz

) ( ) ( )

t g x tg

( )

z g 1− + ≤ 1− + maka

( )

(

t x tz

) ( ) ( )

t g x tg

( )

z g − + ≥− − −

− 1 1

dengan demikian

( ) ( )

z g y g

( )

z g

(

x t

(

z x

)

)

g − = − + −

= g

( ) (

z −g x+tz−tx

)

= g

( )

z −g

(

( )

1−t x+tz

)

≥ g

( ) ( ) ( )

z − 1−t g x −tg

( )

z

=

( ) ( ) ( )

1−t

[

g z −g x

]

atau dapat ditulis

( ) ( ) ( )

1−t

[

g z −g x

]

≤g

( ) ( )