Metode Elemen Batas (MEB) Untuk Solusi Numerik Masalah Statik Dari Material Elastis Isotropik Tak-Homogen

Masalah Statik Dari Material Elastis Isotropik

Tak-Homogen

Mohammad Ivan Azis

†

Abstract

A boundary element method is derived for the solution of static boundary value problems for inhomogeneous isotropic elastic materials. Some particular problems are considered to illustrate the application of the method.

Keywords: Boundary element method, static, boundary value problem, inhomogeneous, isotropic, elastic.

1. Pendahuluan

Pendekatan persamaan integral untuk masalah nilai batas elastostatik lama telah diperkenalkan oleh Rizzo (1967). Sejak saat itu sudah banyak penulis yang ikut menggunakan metode elemen batas untuk menentukan solusi numerik dari berbagai masalah statik untuk material elastis, isotropik dan homogen (Brebbia & Dominguez, 1989).

Dalam pertentangan, aplikasi dari metode elemen batas ke masalah untuk material elastis isotropik tak-homogen sangat terbatas jumlahnya dan hal ini disebabkan oleh karena kesulitan dalam memperoleh fungsi Green sebagai kernel dari persamaan integral batas yang bersesuaian. Baru-baru ini Manolis & Shaw (1996) menurunkan suatu fungsi Green dari persamaan gelombang vektor untuk media isotropik heterogen lemah (mildly heterogeneous). Fungsi Green ini diturunkan untuk material dengan parameter yang bervariasi secara tertentu dan secara khusus terbatas untuk kasus dimana parameter Lamé



dan



sama. Hal ini berarti nilai rasio Poison adalah 0, 25 yang membatasi aplikasi. Akan tetapi, menurut Manolis & Shaw (1996) nilai rasio Poison ini adalah sesuatu biasa untuk material batuan (Turcotte & Schubert, 1982).

Tulisan ini mengembangkan kerja Manolis & Shaw (1996) untuk membangun suatu prosedur perturbasi untuk menentukan solusi masalah statik dua dimensi untuk media isotropik tak-homogen dengan parameter Lamé

) ( ) ( ) ( ) ( ) ( ) ( ) 1 ( 0 ) 1 ( 0 x x g x x x g x













   

dimana x(x1,x2,x3)adalah suatu vektor di

3

R ,

g

(

x

)

suatu fungsi yang memenuhi batasan tertentu,



(0) 



(0) adalah konstanta dan



suatu parameter kecil. Dalam batasan ini, bentuk parameter Lamé di atas menawarkan pilihan keberagaman parameter



(

x

)

dan

)

(

x



yang cukup luas.

2.

Persamaan Dasar

Dengan merujuk pada kerangka Cartesian Ox₁x₂x₃ persamaan kesetimbangan (the equilibrium equations) dalam suatu material elastis tanpa gaya badan (body force) dapat ditulis dalam bentuk



_ij,j



0

(1)

dimana



_ij untuk

i

,

j



1

,

2

,

3

melambangkan tensor stress, tanda koma terindeks mengindikasikan turunan parsial terhadap kordinat spasial

x

_j dan konvensi penjumlahan indeks berulang (jumlahan dari 1 sampai 3) diterapkan. Hubungan displacement-stress dapat dituliskan sebagai

)

)(

(

)

(

_{ij k,k i,j j,i} ij





x



u





x

u



u



(2)

dimana u_kuntuk

k



1

,

2

,

3

menyatakan displacement dan



_ij adalah operator delta Kronecker.



(

x

)

dan



(

x

)

dengan x(x1,x2,x3) dalam persamaan (2) adalah parameter

Lamé yang diasumsikan fungsi yang punya turunan kedua (twice differentiable). Subtitusi persamaan (2) ke (1) menghasilkan





(x)



ijuk,k 



(x)





i,j 



j,i





_j 0 (3)

3.

Masalah Nilai Batas

Suatu material isotropik tak-homogen berada pada daerah



dalam ruang tiga dimensi R3dengan batas  yang terdiri atas sejumlah berhingga permukaan tertutup dan mulus (smooth), pada bagian demi bagian. Pada 1displacement uiditentukan, dan pada

2



 vektor stress

P

_i





_ij

n

_j diketahui, dimana ₁₂ dan n(n1,n2,n3)

melambangkan vektor normal satuan mengarah keluar pada permukaan. Dikehendaki untuk menentukan displacement dan stress dalam material. Dengan demikian solusi untuk persamaan (3) yang berlaku dalam domain



dan memenuhi syarat batas pada  akan dicari.

4.

Penurunan Persamaan dengan Koefisien Konstan

Dalam pasal ini prosedur yang dikembangkan dalam Manolis & Shaw (1996) dipakai untuk menurunkan suatu metode persamaan integral batas untuk kelas kofisien



(

x

)

dan



(

x

)

tertentu. Penurunan ini diperoleh dengan memperkenalkan suatu transformasi dari peubah tak-bebas ui(x) untuk mentransformasikan persamaan (3) ke suatu persamaan

dengan koefisien konstan. Kofisien



(

x

)

dan



(

x

)

disyaratkan mengikuti bentuk



(x)



(0)g(x) ,



(x)



(0)g(x), (4) dimana



(0) dan



(0) konstan. Misalkan



_i

(

x

)



g

1/2

(

x

)

u

_i

(

x

)

(5)

Subtitusi persamaan (4) dan (5) ke dalam persamaan (3), menghasilkan

(6)

















0

2

1

)

(

, , , , 2 / 1 ) 0 ( ) 0 ( 2 / 1 , ) 0 ( 2 / 1 , ) 0 ( 2 / 1 , ) 0 ( , , ) 0 ( , ) 0 ( 2 / 1









































k k i i k k ij j ji i ki k j i j j i k k ij

g

g

g

g

g

g

g

















Jika

g

(

x

)

diasumsikan memiliki bentuk





2 3 2 1 ) (x 



x 



x 



x 



g (7)

dimana



,



,



dan  adalah konstanta, dan



(0) 



(0) (8)

sehingga



(x)



(0)





x₁



x₂ 



x₃ 





2 



(x), maka persamaan (6) dapat ditulis sebagai







(0)



_,



(0)



_,





_,





0

j i j j i k k ij







(9)

dengan



(0) 



(0). Dengan kata lain, jika _i adalah solusi displacement dari persamaan kesetimbangan untuk material isotropik homogen dengan konstanta Lamé



(0)dan



(0), maka solusi bersesuaian dari persamaan kesetimbangan untuk material elastis isotropik tak-homogen dengan parameter Lamé



(

x

)

dan



(

x

)

yang diberikan dalam bentuk multiparameter pada persamaan (4) dapat ditulis dari (5), dalam bentuk





(

)

)

(

)

(

)

(

1 3 2 1 2 / 1

x

x

x

x

x

x

g

x

u

i i i















 









Tensor stress yang diperoleh dari persamaan (2), dituliskan dalam bentuk

 _      ik g ijk k ij



g





1/2 dimana   ) ( _{, ,} ) 0 ( , ) 0 ( i j k k k k ij ik      

_

_

_



dan vektor stress

 

_

 







g _i ik k i

P

g

P

P

1/2 (10) dimana         n P n P j i ij g ijk g ik   _ 



,



(11)

Persamaan integral batas untuk solusi persamaan (9) dengan i diberikan pada 1 dan ]

[

i

P

diberikan pada ₂ (dalam Brebbia & Dominguez , 1989), dalam bentuk

j

x





ij

P

i  ij i



ds

  

_

_

_









(

0

)

(12)

dimana x0 adalah titik sumber,





0

jika x01,



1 jika x0 , dan

2 1 



jika    0

x , dan  memiliki tangen membelok secara kontinyu pada x0. Juga untuk kasus

tiga dimensi  

₍

₎



₍

₎

₍

₎



_,

, 2 / 1 , 2 / 1 ) 0 ( , 2 / 1 ) 0 ( i kj j ki k ij g ijk





g





g



g















3

4

,

,



,

)

1

(

16

1

) 0 ( ij i j ij

v

d

d

d

v















(13)





_







_

_

_

_

_













i j j i j i ij ij

d

n

d

n

v

d

d

v

n

d

d

v

,

,

)(

2

1

(

,

,

3

)

2

1

(

)

1

(

8

1

2





(14)

Sedangkan untuk kasus dua dimensi,





_   _{ }   ij ij d id j d v d v , , 1 log 4 3 ) 1 ( 8 1 ) 0 (





(15)





_







_

_

_

_

_













i j j i j i ij ij

d

n

d

n

v

d

d

v

n

d

d

v

,

,

)(

2

1

(

,

,

2

)

2

1

(

)

1

(

4

1

2





(16)

dimana

d



x



x

₀

,

v





(0)

/



2

(



(0)





(0)



dan d/nd,k



k. Subtitusi persamaan

(5) dan (10) ke persamaan (12), menghasilkan

 



g

P

g

P

u



ds

x

u

x

g

_j



_{ij i kj ki}g _{ij k}    

_

_

_



(

)

(

)

)

(

)

(

_{0 0} 1/2 1/2 2 / 1







(17)

Persamaan integral batas ini dapat dipakai untuk penentuan solusi ui dan



ij pada semua titik

dalam domain



.

5.

Metode Perturbasi

Prosedur elemen batas yang disebutkan dalam pasal sebelumnya menawarkan metode numerik efektif untuk penentuan solusi u_i(x) pada saat

g

(

x

)

memiliki bentuk (7) dan parameter



(0) dan



(0) yang memenuhi persamaan (8). Pada pasal ini suatu prosedur baru ditemukan untuk kasus pada saat koefisien



(

x

)

dan



(

x

)

diganggu sedikit (perturbed) di sekitar



(0)(x) dan



(0)(x), sementara persamaan (7) dan (8) tetap dipertahankan.

Koefisien



(

x

)

dan



(

x

)

disyaratkan mengambil bentuk

) ( ) ( ) (x



(0)g x



(1) x



  (18) ) ( ) ( ) (x



(0)g x



(1) x



  (19) dengan ) 0 ( ) 0 (





 dan gi1/j2 0

dimana



(1)dan



(1) fungsi yang memiliki turunan kedua. Sehingga dari persamaan (3)



g



ij

u

kk





u

i,j



u

j,i







_j



) 0 ( , ) 0 (















(1)



_ij

u

_k,k





(1)



u

_i,j



u

_j,i





_j

.

(20)

Penggunaan transformasi (5) dan mengikuti analisis yang digunakan untuk memenuhi persamaan (6) dari (3) menghasilkan







ijkk  i,i j,i



 ) 0 ( , ) 0 (















j i j i i k k ij

cg

1/2



(1)





_,





(1)



_,





_,



 (21) Solusi dari persamaan (21) dicari dalam bentuk

( ) ( )( ) 0 x x _i r r r i







_

   (22)

Dari persamaan (5) dan (22) displacement uk dapat dituliskan dalam bentuk deret

) ( ) ( ( ) 0 x u x u _k r r r k



  



(23)

dimana

u

_k(r)berkorespondensi dengan



_k(r)menurut relasi

),

(

)

(

1/2 ( ) ) (

x

u

g

x

_kr r k





untuk

r



0

,

1

,...

(24)

Subtitusi persamaan (22) ke dalam (21), dan menyamakan koefisien dari suku-suku dalam



berpangkat menghasilkan



(0) (_,) (0)



(_,) (_,)





(r) j r i j r j i r k k ij















h





(25) dimana 0 ) ( ) 0 (  x h (26)







r



_j i j r j i r k k ij r

u

u

u

g

x

h

( )

(

)





1/2



(0)



(_,1)





(1) (_,1)



(_,1) (27) untuk

r



1

,

2

,

...

.

Persamaan integral untuk persamaan (25) adalah



(

,

)

(

)

(

,

)

(

)



(

)

)

(

)

(

x

₀ (_jr)

x

₀



_ij

x

x

_{0 i}(r)

x

_ij

x

x

₀

P

_i (r)

x

ds

x

  

























h

_i(r)

(

x

)

_ij

(

x

,

x

₀

)

ds

(

x

)

(28) untuk

r



0

,

1

,

...

, dimana

 

_

_

_

_

j r i j r j i r k k ij i

n

P

(r)





(0)





(_,)





(0)



(_, )





(_,) Juga

 

 g ik r i r P r k P g i

u

P

( )



1/2 ( )



( ) , untuk

r



0

,

1

,

...

(29) dimana

 

_

_

_

_

j r i j r j i r k k ij i

x

u

u

u

n

P

(r)

(

)





(0)



(_,)





(0) (_,)



(_,) (30) dan

P

_ik g diberikan dalam persamaan (11). Sehingga persamaan integral (28) dapat ditulis dalam bentuk



 







{

(

)[

(

)

(

,

)

)

(

)

(

)

(

x

₀

g

1/2

x

₀

u

(_jr)

x

₀

u

_i(r)

x

g

1/2

x

_ij

x

x

₀



P_{k i}

 

g (x)_{k j}(x,x₀)]

  P_i(r)(x)[g1/2(x) _ij(x,x₀)]}ds(x)







(

,

)

(

)

)

(

{

h

_i(r)

x

_ij

x

x

₀

ds

x

(31) Nilai P_i dapat ditulis sebagai







 









1 ) ( ) ( ) 0 ( r r i r i r i i

gP

r

gP

G

P



(31) dimana









j r ji r ij r k k ij r i x u u u n G (, 1) (1) ( 1) ( 1) ) 1 ( ) ( ) ( 





 



   .

Untuk memenuhi syarat batas seperti yang disebutkan dalam pasal sebelumnya disyaratkan bahwa i i

u

u

(0)



pada ₁, i i

g

P

P

(0)



1 pada ₂,

dimana ui mengambil nilai tetapannya pada 1 dan Pi mengambil nilai tetapannya pada

2



 . Akibatnya, bahwa untuk

r



1

,

2

,

...

dari persamaan (23) dan (31) diperoleh

0

) (r



i

u

pada ₁, ) ( 1 ) ( r i r i

g

G

P





 pada 2

Sekarang, persamaan integral (31) dapat digunakan untuk menentukan nilai numerik dari anu (unknowns) pada batas , dan nilai numerik dari

u

_i(r) dan turunannya dalam domain



untuk r = 0, 1, .... Persamaan (23) dan (31) kemudian memberikan nilai u_i dan

i

P di seluruh domain .

6.

Hasil Numerik

Dalam pasal ini beberapa masalah renggangan bidang (plane strain) akan diselesaikan secara numerik dengan menggunakan persamaan integral yang diperoleh pada pasal sebelumnya. Dalam pemakaian metode ini, untuk mendapatkan hasil numerik prosedur elemen batas baku, digunakan misalnya metode yang terdapat dalam Clements (1981). Untuk variasi parameter elastisitas terpilih ruas kanan dari persamaan (27) dianggap sangat kecil sehingga hanya perlu untuk mempertahankan dua suku pertama dari ekspresi deret persamaan (23).

Untuk semua masalah yang diperhatikan domain



berupa suatu bujur sangkar bersisi l dan masing-masing sisi dari bujur sangkar itu dibagi menjadi sejumlah M (kelipatan dari 5) segmen dengan panjang sama. Integral numerik Gaussian dipakai untuk penghitungan integral garis pada setiap segmen. Sedangkan untuk integral domain dalam persamaan (31), domain dibagi atas sejumlah M2 sel bujur sangkar yang sama dan fungsi yang diintegralkan (integrand) diasumsikan konstan dan mengambil nilainya pada titik pusat dari setiap sel. Tetapi, nilai dari solusi iterasi sebelumnya

u

_i(r1) beserta turunannya dalam persamaan (27) dihitung hanya pada sejumlah 5 × 5 titik pusat dari bujur sangkar bagian bersisi l/5, dan diasumsikan konstan di dalam setiap bujur sangkar bagian itu. Dengan kata lain nilai

u

_i(r1) beserta turunannya dalam suatu bujur sangkar bagian tertentu adalah sama untuk sejumlah

2

5

/

Problem 1. Perhatikan masalah nilai batas yang memenuhi solusi analitik







'



1 ' 2 ' 2 ' 1 ' 1 ' 1 x /4.4(1 0.1x , u x /4.4(1 0.1x u     dan ' 1 ' 22 ' 1 ' 11 10.12x ,



10.32x



untuk suatu material dengan kofisien elastisitas

2 ' 1 ' ) 1 . 0 1 ( 2 . 1 ) (x   x



, (32) 2 ' 1 ' ) 1 . 0 1 ( ) (x   x



(33) dimana  







x

l

u

u

u

P

x

_i' _i

/

,

_i' _i

/

,



_ij'



_ij

/

(untuk

i

,

j



1

.

2

),     















' / , ' / ,l, dan 

u

masing-masing adalah panjang, modulus elastis dan displacement rujukan, serta

P

u

/

l

 





. Koefisien elastisitas persamaan (32) dan (33)

memiliki bentuk persamaan (18) dan (19) dengan

0 , ) 1 . 0 ( , , ) 1 . 0 1 ( ) (   ₁' 2 (0)  (0)  (1)   ₁' 2 (1)   













x x x g dan



0.2.

Syarat batasnya (lihat Gambar 1) adalah

' 1

P dan u'₂diketahui pada AB,

' 1

P dan u'₂diketahui pada BC,

' 1

P dan u'₂diketahui pada CD,

' 1

P dan u'₂diketahui pada AD

dimana



 P P P_i' _i / .

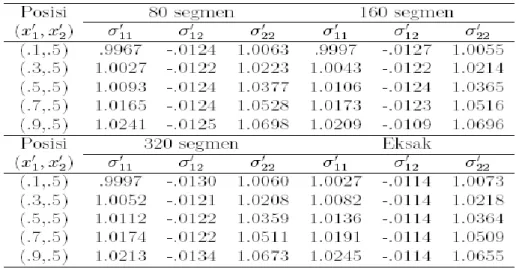
Tabel 1 dan 2 memperlihatkan solusi eksak dan MEB untuk beberapa titik dalam domain dan untuk kasus dimana batas domain dibagi atas 80, 160 dan 320 segmen. Hasil dalam tabel konvergen ke solusi eksak sejalan dengan bertambahnya jumlah segmen. Hal ini sesuai dengan apa yang diharapkan, karena semakin kecil ukuran segmen semakin akurat nilai integral numerik. Khusus untuk kasus 320 segmen solusi displacement memperlihatkan keakuratan sampai pada desimal keempat, dan solusi stress pada desimal ketiga.

Problem 2. Perhatikan masalah nilai batas untuk suatu material bujur sangkar tak homogen yang diberi beban dari atas dan terklem pada bagian bawah serta dibiarkan bebas pada sisi kiri dan kanan, seperti yang diberikan pada gambar berikut.

Tabel 1. Solusi MEB dan eksak untuk



_ij' dari Problem 1.

Tabel 2. Solusi MEB dan eksak untuk

u

_i' dari Problem 1.

Pada Gambar 2 di bawah ini, terlihat material ini memiliki koefisien elastisitas

2 ' 2 ' 1 ' ) 1 ( 5 . 1 ) (x



x



x



   (34) 2 ' 2 ' 1 ' ) 1 ( ) (x



x



x



   (35)

Koefisien elastisitas pada persamaan (34) dan (35) memiliki bentuk persamaan (18) dan (19) dengan g(x)(1



x₁' 



x₂')2, (0)  (0)  , (1)  (1 ₁'  ₁')2, (1) 0  

















x x dan



0.5. Bila



2

.

49



10

3 



ksi, maka material yang diperhatikan adalah magnesium alloy. Kordinat titik sudut material ini adalah A(-0.5,-0.5), B(0.5,-0.5), C(0.5,0.5) dan D(0.5,0.5), dan syarat pada batas adalah

0 , 0 ₂' ' 1  u  u pada AB, 0 , 0 ₂' ' 1  u  u pada BC, 0 , 0 ₂' ' 1  u  u pada CD, 0 , 0 ₂' ' 1  u  u pada AD

Empat kasus yang diperhatikan menyangkut kofisien keelastikan material



dan



yaitu kasus material homogen (









0

) dan tiga kasus material tak-homogen

)

1

.

0

,

1

.

0

,

0

,

1

.

0

,

1

.

0

,

0

(

























.

Gambar 2. Geometri untuk Problem 2.

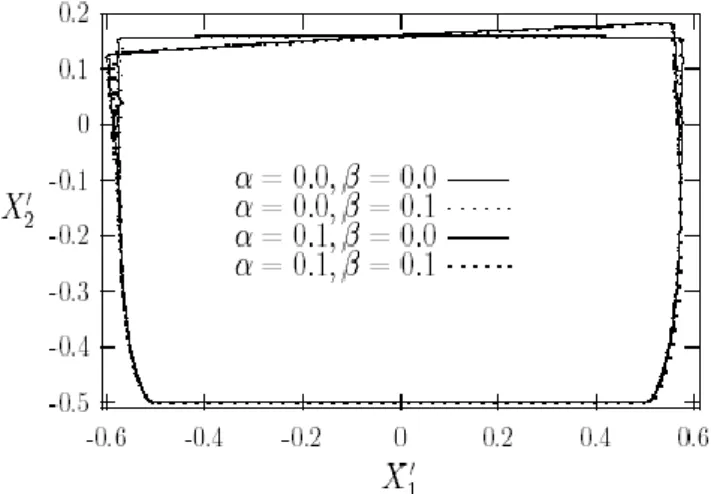
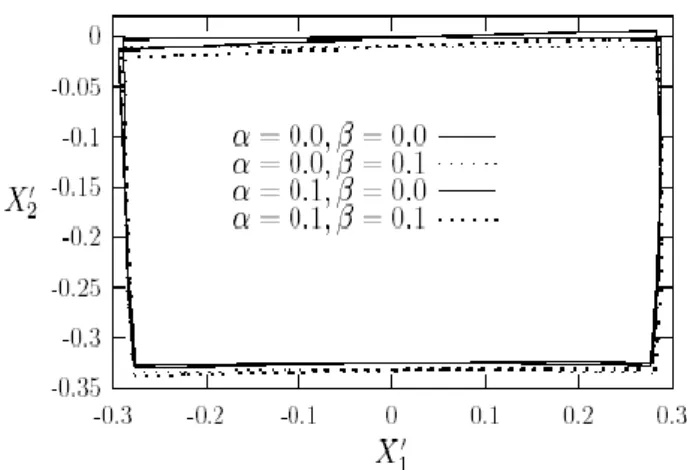
Gambar 3 dan 4 memperlihatkan hasil deformasi sisi material dan sisi daerah

25 . 0 25 . 0 , 25 . 0 25 . 0  ₁'    ₂' 

 x x dalam material. Dari kedua gambar ini dapat

disimpulkan bahwa fungsi ketakhomogenan g sangat mempengaruhi hasil deformasi. Dalam hal ini peningkatan nilai fungsi ketakhomogenan g akan meningkatkan nilai koefisien keelastikan khususnya rigiditas



. Sistem kordinat baru

X

_i' dalam Gambar 3 dan 4 adalah sistem untuk material hasil deformasi. Dalam hal ini variabel kordinatnya didefinisikan sebagai

X

_i'



x

_i'



u

_i' untuk

i



1

,

2

.

7.

Penutup

Metode elemen batas untuk solusi suatu kelas masalah nilai batas untuk material isotropik tak-homogen telah berhasil ditemukan.

Gambar 4. Hasil Deformasi Sisi Daerah 0.25 x₁' 0.25, 25 . 0 25 . 0  ₂'   x Dalam Material.

Metode ini cukup mudah digunakan untuk memperoleh solusi numerik dari suatu masalah tertentu. Hasil numerik yang telah diperoleh mengindikasikan bahwa metode ini mampu memberikan solusi yang akurat.

Daftar Pustaka

[1] Brebbia, C.A. dan Dominguez, J., (1989), “Boundary Elements An Introductory Course”, Computational Mechanics Publications, Boston.

[2] Clements, D.L., (1981),”Boundary Value Problems Governed By Second Order Elliptic Systems”, Pitman.

[3]. Manolis, R.P. dan Shaw, R.P., (1996), “Green’s function for the vector wave equation in a mildly heterogeneous continuum”, Wave Motion, Volume 24, pp : 59–83.

[4]. Rizzo, F.J., (1967), “An integral equation approach to boundary value problems of classical elastostatics”, Quarterly of Applied Mathematics”, Volume 25, pp : 83–95. [5]. Turcotte, D.L. & Schubert, P., (1982), Geodynamic Applications of Continuum Physics