BAB 2
LANDASAN TEORI
2.1 Matrix Rotasi 3D dengan Representasi Euler
Matriks Rotasi untuk grafik 3D dengan representasi euler ( euler angle ) terdiri atas rotasi terhadap sumbu x , y , dan z
Gambar 2.1 Vektor di Ruang 3 Dimensi
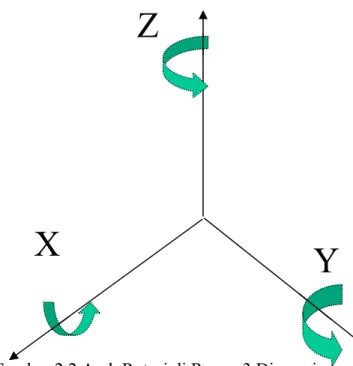
Gambar 2.2 Arah Rotasi di Ruang 3 Dimensi
X
Y
Z
v
v
1
v
2
v
3
X
Y
Z
Matriks Rotasi terhadap sumbu x :
Matriks Rotasi terhadap sumbu y :
Matriks Rotasi terhadap sumbu z :
Karena perkalian matriks tidak bersifat komutatif , maka dengan representasi euler , terdapat 12 urutan rotasi yang dapat dihasilkan , yaitu : xyz , xzy, xyx , xzx , yxz , yzx , yxy , yzy , zxy , zyx , zxz , zyz.
= × × ( ) ( ) ) (α y β z γ x R R R = ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎣ ⎡ ⋅ − ⋅ α α α α cos sin 0 sin cos 0 0 0 1 ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎣ ⎡ ⋅ − ⋅ β β β β cos 0 sin 0 1 0 sin 0 cos ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎣ ⎡ ⋅ − ⋅ 1 0 0 0 cos sin 0 sin cos γ γ γ γ sehingga didapatkan = ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎣ ⎡ − + + − − β α γ α γ β α γ α γ β α β α γ α γ β α γ α γ β α β γ β γ β cos cos cos sin sin sin cos sin sin cos sin cos cos sin cos cos sin sin sin sin cos cos sin sin sin sin cos cos cos
Berikut adalah hasil dari setiap urutan rotasi yang mungkin : = × × ( ) ( ) ) (α z γ y β x R R R ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎣ ⎡ + − + − + + − − β α γ β α γ α β α γ β α β α γ β α γ α β α γ β α β γ γ β γ cos cos sin sin sin cos sin sin cos sin cos sin cos sin sin sin cos cos cos sin sin sin cos cos sin cos sin cos cos = × × ( ) ( ) ) (α y β x α x R R R ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎣ ⎡ + − − − + − − β α α β α α α α β α β α α α α β α α β α β α β α β cos cos sin cos cos sin cos sin sin cos cos cos sin cos sin cos sin cos sin sin sin cos sin sin cos 2 2 2 2 = × × ( ) ( ) ) (α z γ x α x R R R ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎣ ⎡ + − − − − + − − α γ α α α γ α α γ α α α γ α α α γ α γ α γ α γ α γ 2 2 2 2 cos cos sin cos sin cos cos sin cos sin cos sin cos cos sin sin cos cos sin cos sin sin sin cos cos = × × ( ) ( ) ) (β x α z γ y R R R ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎣ ⎡ − + − − + − β α γ β α γ β γ β α γ α α γ α γ α β α γ β α γ β γ β α γ β cos cos cos cos sin sin sin sin cos sin cos sin sin cos cos sin cos sin cos cos sin sin sin cos sin sin sin cos cos
= × × ( ) ( ) ) (β z γ x α y R R R ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎣ ⎡ + − − − + β α γ β α β α γ β α γ β γ α γ α γ β α γ β α β α γ β α γ β cos cos sin sin sin cos sin sin sin cos cos sin cos sin cos cos sin sin cos sin cos sin sin sin sin cos cos cos cos = × × ( ) ( ) ) (β x α y β y R R R ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎣ ⎡ + − + − − − β α β β α α β β β β β α α β α β β α β β β α α β β 2 2 2 2 cos cos sin cos sin cos cos sin cos sin cos sin cos sin sin sin cos cos cos sin sin sin cos sin cos = × × ( ) ( ) ) (β z γ y β y R R R ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎣ ⎡ + − + − − − − β γ β γ β β β γ β β γ β γ β γ β β γ β β γ β β γ β 2 2 2 2 cos cos sin sin sin cos sin cos cos sin sin sin cos cos sin cos sin cos cos sin sin cos sin cos cos = × × ( ) ( ) ) (γ x α y β z R R R ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎣ ⎡ − + + − + − + β α α β α γ β α γ β γ α γ β α γ β γ β α γ β γ α γ β α γ β cos cos sin sin cos cos cos sin sin sin cos cos cos sin sin sin cos sin cos sin cos sin sin cos sin sin sin cos cos = × × ( ) ( ) ) (γ y β x α z R R R ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎣ ⎡ − + − − − + β α β α β γ β α γ α γ β α γ α β γ γ β α γ α γ β α α γ γ β cos cos cos sin sin sin sin cos cos sin sin sin sin cos cos cos sin cos sin cos sin sin cos sin sin cos sin cos cos = × × ( ) ( ) ) (γ x α z γ z R R R ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎣ ⎡ − + − − − + − α γ α γ α γ α α γ γ γ α γ γ γ γ α γ γ γ γ γ γ γ cos cos sin sin sin cos sin cos cos sin cos cos sin cos sin sin sin cos sin cos sin cos sin cos 2 2 2 2 2
= × × ( ) ( ) ) (γ y β z γ z R R R ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎣ ⎡ − − − − − + − β γ β γ β γ β γ β γ γ γ γ γ β γ β γ γ γ γ β γ β γ cos sin sin cos sin sin sin cos cos sin cos sin cos sin cos cos sin cos sin cos sin cos sin cos cos 2 2 2 2
Karena menggunakan aturan tangan kanan ( Right – Hand rule ) maka α,β,γ, adalah sudut antara 0-360° , berlawanan arah dengan arah jarum jam.
Representasi Euler memiliki masalah yang signifikan , yaitu terjadinya gimbal lock. Gimbal lock ini disebabkan karena representasi euler terhadap orientasi tertentu tidak bersifat unik ( aliasing ) . Aliasing terjadi karena orientasi menggunakan representasi euler dapat di wujudkan dengan beberapa kombinasi matriks. Apabila menggunakan urutan rotasi xyz , gimbal lock dapat dilihat jika merotasikan sumbu y sebesar 90° . Menggunakan rumus rotasi di atas , maka apabila β=90° diperoleh :
= × × y z x R R R ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎣ ⎡ − + + − − 90 cos cos cos sin sin 90 sin cos sin sin cos 90 sin cos 90 cos sin cos cos sin 90 sin sin sin cos cos 90 sin sin 90 sin sin 90 cos cos 90 cos α γ α γ α γ α γ α α γ α γ α γ α γ α γ γ = ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎣ ⎡ − + + − − 0 cos sin sin cos sin sin cos cos 0 cos cos sin sin sin cos cos sin 1 0 0 γ α γ α γ α γ α γ α γ α γ α γ α = ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎣ ⎡ − − − − − − 0 ) sin( ) cos( 0 ) cos( ) sin( 1 0 0 γ α γ α γ α γ
Sehingga rotasi terhadap sudut α maupun γ hanya akan menghasilkan rotasi terhadap 1 sumbu rotasi ( kehilangan 1 sumbu rotasi). Hal ini juga terjadi pada setiap kombinasi rotasi pada representasi euler.
2.2 Struktur Aljabar
2.2.1 Semigrup
Semigrup (G,*) adalah himpunan tak kosong dengan operasi “*” yang bersifat : - Tertutup terhadap operasi “*”
- Assosiatif (x*y)*z = x*(y*z) untuk setiap x,y,z ε G
2.2.2 Grup
Grup adalah himpunan tak kosong dengan satu operasi * yang mempunyai sifat sebagai berikut :
- Tertutup terhadap * - Asosiatif untuk operasi * - Mempunyai Unsur Kesatuan - Setiap elemen memiliki invers Grup yang komutatif disebut juga grup abelian.
2.2.3 Ring
Suatu struktur aljabar dengan dua operasi biner “+” dan “*” , R(+,*) disebut Ring , jika :
- (R , + ) grup komutatif ( grup abelian ) - (R , * ) semi grup
- Berlaku distributif kiri dan kanan o a*(b+c) = a*b + a*c o (a+b)*c = a*c + b*c R c b a ∈ ∀ , , 2.2.4 Quaternion
Bentuk umum Quaternion adalah a + bi + cj + dk , di mana a , b , c , d adalah bilangan Real. Quaternion dapat dibagi menjadi 2 bagian , bagian skalar dan bagian vector . Bagian skalar dari Quaternion a+bi+cj+dk adalah a , dan bagian vektor nya adalah bi+cj+dk .
Quaternion adalah Struktur aljabar yang ditemukan oleh William Rowan
Hamilton. Quaternion adalah division Ring yang nonkomutatif
(http://mathworld.wolfram.com/Quaternion.html ) , sehingga quaternion memiliki sifat – sifat sebagai berikut :
1. (Q , + ) merupakan grup komutatif 2. (Q-{0}, * ) merupakan grup
3. Operasi * distributif terhadap + Q = {a+bi+cj+dk:a,b,c,d∈R
}
Bukti :1. (Q , + ) merupakan grup komutatif a. Tertutup
Quaternion + Quaternion = Quaternion
a + bi + cj + dk + e + fi + gj + hk = (a+e) + (b+f)i + (c+g)j + (d+h)k al h g f e d c b a, , , , , , , ∈Re b. Assosiatif
( Quaternion + Quaternion ) +Quaternion = Quaternion + (Quaternion+Quaternion)
c. Memiliki Unit Kesatuan
a +bi+cj+dk + 0 +0i+0j+0k = a+bi+cj+dk
al d c b
a, , , ∈Re
d. Setiap Elemen Quaternion memiliki invers ) ( ) ( 1 dk cj bi a dk cj bi a+ + + − = − − − − al d c b a, , , ∈Re e. Komutatif ) ( ) ( ) ( ) (a+bi+cj+dk+ w+xi+yj+zk = w+xi+yj+zk+ a+bi+cj+dk al z y x w d c b a, , , , , , , ∈Re 2.(Q-{0} , *) merupakan grup a. Tertutup
Quaternion * Quaternion = Quaternion k dw cx by az j dx cw bz ay i dy cz bw ax dz cy bx aw zk yj xi w dk cj bi a )*( ) ( ) ( ) ( ) ( ) ( + + + + + + = − − − + + + − + − + + + + − + al z y x w d c b a, , , , , , , ∈Re b. Assosiatif ) ( * )) ( * ) (( )) ( * ) (( * ) (a+bi+cj+dk w+xi+yj+zk e+fi+gj+hk = a+bi+cj+dk w+xi+yj+zk e+fi+gj+hk Bukti : ) ( * )
(w+xi+yj+zk e+ fi+gj+hk = (we –xf-yg –zh) + (wf +xe + yh – zg)i +(wg –xh
+ye +zf)j + (wh + xg – yf + ze)k )) ( * ) (( * ) (a+bi+cj+dk w+xi+yj+zk e+ fi+gj+hk =
=( a (we-xf-yg-zh) – b(wf+xe+yh-zg)-c(wg-xh+ye+zf) –d(wh+xg-yf+ze)) + (a (wf+xe+yh-zg) + b(we-xf-yg-zh) + c(wh+xg-yf+ze) –d(wg-xh+ye+zf))i + (a(wg –xh+ye+zf) –b (wh+xg-yf+ze) +c (we-xf-yg-zh) +d(wf+xe+yh-zg))j + (a(wh+xg-yf+ze) + b ( wg-xh+ye+zf)- c(wf+xe+yh-zg) + d(we-xf-yg-zh))k
=(awe –axf-ayg-azh –bwf-bxe-byh+bzg –cwg+cxh-cye-czf-dwh-dxg+dyf-dze) + (awf+axe+ayh-azg +bwe –bxf-byg-bzh+ cwh +cxg –cyf +cze –dwg +dxh –dye –dzf)i (awg-axh+aye+azf-bwh-bxg+byf-bze +cwe-cxf-cyg-czh + dwf+dxe +dyh-dzg)j (awh+axg-ayf+aze + bwg-bxh+bye+bzf –cwf-cxe-cyh+czg +dwe-dxf-dyg-dzh)k
) (
* )
(a+bi+cj+dk w+xi+yj+zk = (aw –bx-cy –dz) + (ax +bw + cz – dy)i +(ay –bz
) ( * )) ( * ) ((a+bi+cj+dk w+xi+yj+zk e+ fi+gj+hk =
=( ( aw –bx-cy-dz)e - (ax+bw+cz-dy)f – (ay-bz+cw+dx)g –(az+by-cx+dw)h ) + ( (aw-bx-cy-dz)f + (ax+bw+cz-dy)e + (ay-bz+cw+dx)h –(az+by-cx+dw)g)i + ( (aw-bx-cy-dz)g - (ax+bw+cz-dy)h + (ay-bz+cw+dx)e +(az+by-cx+dw)f )j + ( (aw-bx-cy-dz)h + (ax+bw+cz-dy)g - (ay-bz+cw+dx)f + (az+by-cx+dw)e)k
= ( awe-bxe-cye-dze –axf-bwf-czf+dyf –ayg +bzg-cwg-dxg-azh-byh+cxh-dwh ) + ( awf – bxf-cyf-dzf + axe+bwe+cze-dye + ayh-bzh+cwh+dxh –azg-byg+cxg-dwg)I + ( awg-bxg-cyg-dzg –axh-bwh-czh+dyh +aye-bze+cwe+dxe+ azf +byf-cxf-dwf) j + ( awh-bxh-cyh-dzh +axg+bwg+czg-dyg-ayf+bzf-cwf-dxf +aze +bye-cxe+dwe)k
R z y x w h g f e d c b a, , , , , , , , , , , ∈ ) ( * )
(w+xi+yj+zk e+ fi+gj+hk = (we –xf-yg –zh) + (wf +xe + yh – zg)i +(wg –xh
Terbukti
c. Mempunyai Unsur Kesatuan
(a+bi+cj+dk)*(1+0i+0j+0k) = (a+bi+cj+dk) R d c b a, , , ∈
d. Setiap elemen memiliki invers
Setiap elemen Quaternion selain 0 mempunyai invers sebagai berikut :
2 _ 1
q q
jika q=(a+bi+cj+dk) maka q = (a−bi−cj−dk) q = q.q = a2 +b2 +c2 +d2 al d c b a, , , ∈Re , q≠0 , q−1∈ Quaternion
3.Operasi * distributif terhadap + q*(w+z) = qw + qz q = (a+bi+cj+dk) w =(w+xi+yj+zk) z = (e+ fi+gj+hk) al z y x w h g f e d c b a, , , , , , , , , , , ∈Re
2.2.4.1 Operasi Quaternion
Berbeda dengan Bilangan kompleks , quaternion tidak bersifat komutatif .
Sifat – sifat dasar quaternion i2 = j2 = k2 = ijk = − 1 dk cj bi t v t p= + = + + + zk yj xi a u a q= + = + + + p q q p× ≠ × ( non komutatif ) r q p r q p×( × )=( × )× ( assosiatif )
Sekawan ( conjugate ) dari quaternion p=t+v adalah p* =t−v
Nilai Mutlak dari quaternion didapat dengan * 2 2 2 2
d c b t pp p = = + + +
Jika p =1 , maka p disebut unit quaternion.
Karena 2 * 1 z z p− =
dan untuk unit quaternion , berlaku p =1 , maka p−1 = p*
- Penambahan dk cj bi t v t p= + = + + + , q=a+u =a+xi+yj+zk k z d j y c i x b t a v u a t q p+ = + + + =( + )+( + ) +( + ) +( + ) - Perkalian dk cj bi t v t p= + = + + + , q=a+u =a+xi+yj+zk u v u t v a v u at pq= − + + + × pq = (at − bx − cy − dz) + (bt + ax + cz − dy)i + (ct + ay + dx − bz)j + (dt + az + by − cx)k - Perkalian dot
- Perkalian cross - Invers 2 * 1 p p p− =
( )
−1 = −1 −1 q p pq2.2.4.2 Penggunaan Quaternion Dalam Rotasi
Bentuk umum Quaternion : q=(a+bi+cj+dk)Titik di ruang 3D dengan bentuk quaternion adalah p(0,x,yz ) = 0+xi+yj+zk , sehingga jika ingin merotasikan titik dengan menggunakan quaternion maka
1 − = qpq
protated , karena q adalah unit quaternion , sehingga q = q untuk operasi *. −1
q qp protated =
rotated
p = (-bx-cy-dz+i ( ax + cz- dy) + j (ay - bz + dx) + k (az + by - cx ) )*(a- bi - cj -
dk)
rotated
p = (- bx -cy- dz)*a - ( ax + cz- dy)*(-b) -(ay - bz + dx)(-c) - (az + by - cx )*(-d)
+ i (( ax + cz- dy)(a) + (- bx -c y- dz)(-b) + (ay - bz + dx)(-d) - (az + by - cx )(-c) ) + j ((- bx -c y- dz)(-c) - ( ax + cz- dy)(-d) + (ay - bz + dx)(a) + (az + by - cx )(-b)) + k ((- bx -cy- dz)(-d) + ( ax + cz- dy)(-c) - (ay - bz + dx)(-b) + (az + by - cx )(a))
rotated
p = - bax – cay – daz + abx + cbz – dby + acy - bcz + dcx + adz + bdy - cdx
+ j ( bcx +cc y+ dcz + adx +cdz- ddy + aay - baz + dax - abz - bby + cbx ) + k (bdx +cd y+ ddz - acx - ccz+ dcy + aby - bbz + dbx + aaz + bay - cax )
rotated
p = 0+ i ( aax + caz- day + bbx +cby+ dbz - ady + bdz - ddx + acz + bcy – ccx)
+ j ( bcx +cc y+ dcz + adx +cdz- ddy + aay - baz + dax - abz - bby + cbx )
+ k (bdx +cd y+ ddz - acx - ccz+ dcy + aby - bbz + dbx + aaz + bay - cax )
Apabila dikelompokkan x , y , z maka akan menjadi matriks sebagai berikut
aa + bb- dd- cc -da+cb- ad+ bc ca + db + bd + ac
bc+ ad+ da+ cb cc- dd+ aa - bb dc+cd- ba- ab
bd- ac+ db- ca cd + dc+ ab+ ba dd- cc- bb+ aa
Dalam merepresentasikan rotasi dengan quaternion , hanya diperlukan unit quaternion , sehingga karena unit Quaternion memiliki sifat 2+ 2+ 2+ 2 =1
d c b
a maka matrix diatas
menjadi :
1-2dd - 2cc - 2da+2cb 2ca +2db
2bc+ 2ad 1 - 2dd - 2bb 2dc- 2ba
Karena quaternion terdiri atas bagian skalar dan bagian vector maka dari a+bi+cj+dz , a adalah besar dari rotasi yang diinginkan , dan bi+cj+dz adalah vektor.
a =cos ( 2 θ ) b = axis x * sin ( 2 θ ) c = axis y * sin ( 2 θ ) d = axis z * sin ( 2 θ )