MODEL MATEMATIS DINAMIKA PERTUMBUHAN
POPULASI DUNIA
SKRIPSI
Diajukan untuk Memenuhi Salah Satu Syarat Memperoleh Gelar Sarjana Matematika
Program Studi Matematika
Oleh:
Stanislaus Warih Priyo Tomo 163114033
PROGRAM STUDI MATEMATIKA JURUSAN MATEMATIKA FAKULTAS SAINS DAN TEKNOLOGI
UNIVERSITAS SANATA DHARMA YOGYAKARTA
i
MODEL MATEMATIS DINAMIKA PERTUMBUHAN
POPULASI DUNIA
SKRIPSI
Diajukan untuk Memenuhi Salah Satu Syarat Memperoleh Gelar Sarjana Matematika
Program Studi Matematika
Oleh:
Stanislaus Warih Priyo Tomo 163114033
PROGRAM STUDI MATEMATIKA JURUSAN MATEMATIKA FAKULTAS SAINS DAN TEKNOLOGI
UNIVERSITAS SANATA DHARMA YOGYAKARTA
ii
MATHEMATICAL MODEL OF WORLD POPULATION
GROWTH DYNAMICS
THESIS
Presented as Partial Fulfillment of the
Requirements to Obtain the Degree of Sarjana Matematika Mathematics Study Program
Written by
Stanislaus Warih Priyo Tomo 163114033
MATHEMATICS STUDY PROGRAM FACULTY OF SCIENCE AND TECHNOLOGY
SANATA DHARMA UNIVERSITY YOGYAKARTA
v
HALAMAN PERSEMBAHAN
Janganlah hendaknya kamu kuatir tentang apapun juga, tetapi nyatakanlah dalam segala hal keinginanmu kepada Allah dalam doa dan permohonan dengan ucapan
syukur. Filipi 4:6
Skirpsi ini saya persembahkan untuk kedua orang tua tercinta, Petrus Purwanta dan Sri Suprihati serta kakak saya, Theresia Dhian Puspita
viii
ABSTRAK
Model kependudukan adalah model matematis yang merepresentasikan pertumbuhan populasi dalam bentuk matematika. Pada skripsi ini akan dibahas tentang model pertumbuhan hiperbolik, model Kapitsa dan model Dolgonosov. Model tersebut akan diselesaikan secara analitik untuk model yang mempunyai penyelesaian analitik dan menggunakan metode numerik untuk semua model. Metode numerik yang akan digunakan adalah metode Euler, aturan trapesium untuk persamaan diferensial biasa, dan modifikasi aturan trapesium untuk persamaan diferensial biasa. Penyelesaian dari metode ini digunakan untuk memperkirakan jumlah penduduk dunia di tahun mendatang. Skripsi ini menghasilkan perkiraan jumlah populasi penduduk dunia untuk model Kapitsa dan model Dolgonosov, sedangkan untuk model pertumbuhan hiperbolik adalah model yang tidak realistik. Kata kunci : Model pertumbuhan hiperbolik, model Kapitsa, model Dolgonosov.
ix
ABSTRACT
The population model is a mathematical modelling that represents population growth in mathematical form. In thesis we discuss about hyperbolic growth model, Kapitsa model, and Dolgonosov model. The model will be solved analytically for a model that has a solution and using numerical method for all model. The numerical method used is Euler method, trapezoidal rule for ordinary differential equation, and modified trapezoidal rule for ordinary differential equation. Solution of this method is used to predict the number of world population in the coming year. This thesis produces an estimate of the world’s population for the Kapitsa model and Dolgonosov model, while the hyperbolic growth model is an unrealistic model.
x
KATA PENGANTAR
Puji syukur kepada Tuhan Yesus Kristus karena limpahan rahmat-Nya penulis bisa menyelesaikan skripsi ini dengan baik. Skripsi ini disusun sebagai salah satu syarat memperoleh gelar Sarjana Matematika dari Program Studi Matematika, Fakultas Sains dan Teknologi, Universitas Sanata Dharma.
Penulis sadar bahwa selama penulisan skripsi ini banyak pihak yang telah terlibat hingga dapat diselesaikannya skripsi ini. Oleh karena itu penulis mengucapkan terima kasih kepada:
1. Bapak Sudi Mungkasi, S.Si., M.Math.Sc., Ph.D., selaku dekan Fakultas Sains dan Teknologi, sekaligus sebagai dosen pembimbing skripsi.
2. Bapak Hartono, S.Si., M.Sc., Ph.D., selaku Kaprodi Matematika.
3. Bapak Ir. Ig. Aris Dwiatmoko, M.Sc., selaku Dosen Pembimbing Akademik. 4. Romo Prof. Dr. Frans Susilo, SJ., Ibu M. V. Any Herawati, S.Si., M.Si., Bapak
Dr. rer. nat. Herry P. Suryawan, S.Si., M.Si., dan Bapak Ricky Aditya, M.Sc., selaku dosen Prodi Matematika yang telah memberi pengetahuan kepada penulis selama masa perkuliahan.
5. Bapak/Ibu karyawan Fakultas Sains dan Teknologi yang telah berdinamika dengan penulis selama masa perkuliahan.
6. Kedua orang tua, dan kakak yang telah mendukung dan mendoakan penulis sehingga dapat menyusun skripsi ini.
7. Teman-teman dan orang-orang yang dekat dengan penulis: Aji, Gabby, Egi, Reinald, Dani, Ikhsan, Pandu, Tasya, Leo, Shinta, om dan tante Ros yang telah mendukung dan memberi semangat dalam proses pengerjaan skripsi.
8. Teman-teman Matematika 16 yang telah berdinamika dengan penulis selama proses perkuliahan.
9. Semua pihak yang penulis tidak dapat disebut satu per satu atas dukungan dalam penyusunan skripsi ini.
xii DAFTAR ISI
HALAMAN JUDUL ... i
TITLE PAGE ... ii
HALAMAN PERSETUJUAN PEMBIMBING ... iii
HALAMAN PENGESAHAN ... iv
HALAMAN PERSEMBAHAN ... v
PERNYATAAN KEASLIAN KARYA ... vi
LEMBAR PERNYATAAN PERSETUJUAN PUBLIKASI... vii
ABSTRAK ... viii
ABSTRACT ... ix
KATA PENGANTAR ... x
DAFTAR ISI ... xii
BAB I PENDAHULUAN ... 1 A. Latar Belakang ... 1 B. Rumusan Masalah ... 3 C. Batasan Masalah ... 3 D. Tujuan Penulisan ... 4 E. Manfaat Penulisan ... 4 F. Metode Penulisan ... 4 G. Sistematika Penulisan ... 4
BAB II PEMODELAN MATEMATIS ... 6
A. Persamaan Diferensial Biasa ... 6
1. Turunan Fungsi ... 6 2. Integral Fungsi ... 18 3. Persamaan Diferensial ... 21 B. Pemodelan Matematis ... 25 C. Metode Numerik ... 27 1. Metode Euler ... 27
xiii
2. Metode Heun (Aturan Trepesium untuk
Persamaan Diferensial Biasa) ... 28
3. Modifikasi Aturan Trapesium untuk Persamaan Diferensial Biasa ... 30
D. Verifikasi Model ... 31
BAB III MODEL KEPENDUDUKAN ... 32
A. Model Pertumbuhan Hiperbolik ... 32
B. Model Kapitsa ... 35
C. Model Dolgonosov ... 39
D. Penyelesaian Model dengan Aturan Trapesium ... 45
1. Aturan Trapesium untuk Persamaan Diferensial Biasa... 46
2. Modifikasi Aturan Trapesium untuk Persamaan Diferensial Biasa ... 60
BAB IV ANALISIS GALAT... 76
A. Analisis Galat Metode Euler... 76
B. Analisis Galat Aturan Trapesium ... 78
C. Analisis Galat Modifikasi Aturan Trapesium ... 80
BAB V PENUTUP ... 84
A. Kesimpulan ... 84
B. Saran ... 85 DAFTAR PUSTAKA
1
BAB I
PENDAHULUAN
A. Latar Belakang
Pertumbuhan ekonomi yang luar biasa dan perubahan geopolitik yang ter-jadi pada abad ke-20 disebabkan oleh ledakan populasi yang belum pernah terter-jadi. Ledakan jumlah penduduk itu terjadi dari 1,656 miliar penduduk pada tahun 1900 menjadi 6,055 miliar di tahun 2000 (Akaev and Sadovnichii, 2010). Sedangkan penggunaan sumber daya alam secara intensif yang disebabkan oleh pertumbuhan tajam populasi dunia menyebabkan kerusakan biosfer bumi, pencemaran ling-kungan, dan akhirnya kerusakan kondisi lingkungan yang akan menimbulkan ancaman serius bagi manusia. Hal ini mendorong pengembangan model matematis yang mampu menunjukkan batas ekspansi manusia dalam biosfer dan kendala global maupun lokal berdasarkan keadaan lingkungan pada populasi dunia.
Pada pertengahan abad ke-20, data yang ada menujukkan populasi dunia dapat dirumuskan dengan model pertumbuhan hiperbolik (Hathout, 2013)
𝑁(𝑡) = 𝑁0
1 − 𝑘𝑡 (1.1) dengan 𝑁(𝑡) adalah populasi penduduk saat 𝑡, 𝑁0 adalah populasi awal, 𝑘 adalah konstanta, dengan 0 < 𝑘 < 1 dan 𝑡 adalah waktu dalam tahun masehi.
Analisis hukum pertumbuhan hiperbolik populasi dunia yang menghu-bungkan ukuran populasi dunia dan perkembangan manusia, menyarankan suatu mekanisme kerja sama ukuran perkembangan yang direpresentasikan oleh kuadrat ukuran populasi. Karena alasan tersebut, Kapitsa (1992) mengusulkan ketergan-tungan kuadratik untuk laju pertumbuhan penduduk
𝑑𝑁 𝑑𝑡 =
𝑁2
𝐶 = 𝑎𝑁
2 (1.2)
Untuk menggambarkan transisi demografis global, Kapitsa menyusun kem-bali persamaaannya dan memperkenalkan 𝜏 yang merupakan karakteristik umur hidup manusia, untuk membatasi tingkatan pertumbuhan penduduk. Model yang ditemukan oleh Kapitsa menjadi
𝑑𝑁 𝑑𝑡 = 𝐶 (𝑇1 − 𝑡)2+ 𝜏2 (1.3) 𝑁 = 𝐾2arccot (𝑇1− 𝑡 𝜏 ) (1.4) dengan 𝐾2 = 𝐶/𝜏, 𝑇
1 adalah konstanta, dan 𝑡 adalah waktu dalam tahun masehi. Setelah itu, Dolgonosov (2009) melengkapi persamaan yang didapat oleh Kapitsa. Menurut Dolgonosov, ukuran populasi ditentukan oleh 𝑞 tingkat produksi informasi:
𝑑𝑞
𝑑𝑡 = 𝜔𝑁 (1.5) dengan ω adalah tingkat rata-rata pemrosesan informasi oleh manusia.
Model Dolgonosov untuk ukuran populasi dunia adalah:
𝑑𝑁 𝑑𝑡 = 𝑟𝑁 2[1 − 𝑁 𝐾(𝑞)] (1.6) 𝐾(𝑞) = 𝑁𝑐 1 − exp (−𝛼𝑞𝑞 𝑐) (1.7) dengan 𝑟 =𝜔
𝑞 adalah koefisien pertumbuhan populasi dunia, 𝐾(𝑞) adalah kapasitas lingkungan seketika, 𝑁𝑐 = 𝑞𝑐
𝜔𝑡𝑐 daya muat dari biosfer bumi, 𝑞𝑐 dan 𝑡𝑐 adalah karaktersitik skala jumlah, 𝛼 adalah konstanta dan 𝑁 adalah populasi penduduk dunia.
Gorshkov (1995) memperkirakan, populasi dunia mengkonsumsi sekitar 22-23% biomassa planet. Pengaruh teknologi pendukung kehidupan dimulai pada
abad ke-19 ketika populasi dunia mencapai 1 miliar. Untuk memperhitungkan keadaan ini 𝐾(𝑞) pada persamaan (1.6) menjadi
𝐾 = 𝑁𝑐+ 𝛾(𝑁 − 𝑁0) exp[−𝜅(𝑁 − 𝑁0)] (1.8) dengan 𝑁𝑐 adalah daya muat biosfer, 𝛾 dan 𝜅 adalah konstanta, dan 𝑁0 adalah po-pulasi awal.
Skripsi ini membahas penerapan pemodelan matematis dalam mem-perkirakan jumlah penduduk dunia pada tahun-tahun mendatang. Model-model pertumbuhan hiperbolik, Kapitsa dan Dolgonosov, digunakan untuk mem-perkirakan jumlah penduduk dunia pada tahun-tahun mendatang.
B. Rumusan Masalah
Perumusan masalah yang akan dibicarakan dalam skripsi ini adalah:
1. Bagaimana menyusun model matematis untuk memprediksi jumlah penduduk dunia?
2. Berapa perkiraan jumlah penduduk dunia pada tahun-tahun mendatang?
C. Batasan Masalah
Skripsi ini dibatasi oleh model pertumbuhan penduduk dan metode numerik sebagai berikut:
1. Model pertumbuhan hiperbolik 2. Model Kapitsa
3. Model Dolgonosov 4. Metode Euler
5. Aturan trapesium untuk persamaan diferensial biasa
D. Tujuan Penulisan
Tujuan dari penulisan skripsi ini, untuk mengetahui teori dasar dan penerapan pemodelan matematis dalam bidang kependudukan. Skripsi ini akan difokuskan untuk memprediksi jumlah penduduk dunia pada tahun-tahun mendatang menggunakan penyelesaian analitik dan metode numerik dengan menggunakan model pertumbuhan hiperbolik, model Kapitsa, model Dolgonosov.
E. Manfaat Penulisan
Manfaat dari penulisan skripsi ini adalah:
1. Dapat mengetahui penerapan pemodelan matematis pada bidang kependu-dukan.
2. Mengetahui pembentukan model kependudukan. 3. Dapat memperkirakan pertumbuhan penduduk dunia.
F. Metode Penulisan
Metode penulisan yang digunakan dalam tugas akhir ini adalah metode studi pustaka, yaitu dengan membaca dan mempelajari buku dan jurnal yang berkaitan dengan model pertumbuhan penduduk.
G. Sistematika Penulisan BAB I PENDAHULUAN A. Latar Belakang B. Rumusan Masalah C. Batasan Masalah D. Tujuan Penulisan E. Manfaat Penulisan F. Metode Penulisan G. Sistematika Penulisan
BAB II PEMODELAN MATEMATIS A. Persamaan Diferensial Biasa B. Pemodelan Matematis C. Metode Numerik D. Verifikasi Model
BAB III MODEL KEPENDUDUKAN A. Model Pertumbuhan Hiperbolik B. Model Kapitsa
C. Model Dolgonosov
D. Penyelesaian Model dengan Aturan Trapesium BAB IV ANALISIS GALAT
A. Analisis Galat Metode Euler B. Analisis Galat Aturan Trapesium
C. Analisis Galat Modifikasi Aturan Trapesium BAB V PENUTUP
A. Kesimpulan B. Saran
DAFTAR PUSTAKA LAMPIRAN
6
BAB II
PEMODELAN MATEMATIS
A. Persamaan Diferensial Biasa
Pada Subbab ini sebelum membahas tentang persamaan diferensial, terlebih dahulu akan membahas tentang turunan dan integral fungsi.
1. Turunan Fungsi
Definisi turunan fungsi dengan menggunakan limit (Larson and Edwards, 2009)
Definisi 2.1
Turunan dari fungsi 𝑓 dinyatakan dengan 𝑓′ yang didefinisikan 𝑓′(𝑥) = lim
∆𝑥→0
𝑓(𝑥 + ∆𝑥) − 𝑓(𝑥) ∆𝑥
di setiap titik 𝑥 sehingga limit ada dan hingga.
Proses menemukan turunan dari suatu fungsi disebut diferensiasi (differentiation). Suatu fungsi dikatakan terdiferensial (differentiable) pada 𝑥 jika fungsi tersebut mempunyai turunan pada 𝑥 dan suatu fungsi dikatakan terdiferensial pada interval (𝑎, 𝑏) jika fungsi mempunyai turunan untuk setiap titik pada interval. Notasi untuk menunjukan turunan dari fungsi 𝑦 = 𝑓(𝑥) yaitu 𝑓’(𝑥). Selain notasi tersebut, notasi lain yang digunakan untuk menunjukan turunan fungsi 𝑦 = 𝑓(𝑥), yang umumnya digunakan yaitu (Larson and Edwards, 2009)
𝑓′(𝑥), 𝑑𝑦
𝑑𝑥, 𝑦
′, 𝑑
𝑑𝑥[𝑓(𝑥)], 𝐷𝑥[𝑦] (2.1)
Contoh 2.1
a) 𝑓(𝑥) = 𝑥2 b) 𝑔(𝑥) =1 𝑥 Penyelesaian a) Untuk fungsi 𝑓(𝑥) = 𝑥2 𝑓′(𝑥) = lim ∆𝑥→0 𝑓(𝑥 + ∆𝑥) − 𝑓(𝑥) ∆𝑥 = lim ∆𝑥→0 (𝑥 + ∆𝑥)2− 𝑥2 ∆𝑥 = lim ∆𝑥→0 2𝑥 ∙ ∆𝑥 + ∆𝑥2 ∆𝑥 = lim ∆𝑥→0(2𝑥 + ∆𝑥) = 2𝑥 b) Untuk fungsi 𝑔(𝑥) =1 𝑥 𝑔′(𝑥) = lim ∆𝑥→0 𝑔(𝑥 + ∆𝑥) − 𝑔(𝑥) ℎ = lim ∆𝑥→0 1 𝑥 + ∆𝑥 − 1 𝑥 ∆𝑥 = lim ∆𝑥→0 𝑥 − (𝑥 + ∆𝑥) ∆𝑥(𝑥 + ∆𝑥)𝑥 = lim ∆𝑥→0− 1 (𝑥 + ∆𝑥)𝑥 = − 1 𝑥2 ∎
Setelah mengetahui definisi dari turunan menggunakan limit, akan dibahas sifat-sifat dari turunan fungsi (Larson and Edwards, 2009).
Teorema 2.1
Turunan dari fungsi konstan adalah nol. Jika 𝑐 merupakan bilangan real maka 𝑑
Bukti
Misalkan 𝑓(𝑥) = 𝑐, dengan menggunakan definisi limit pada turunan didapat 𝑑 𝑑𝑥[𝑐] = 𝑓 ′(𝑥) = lim ∆𝑥→0 𝑓(𝑥 + ∆𝑥) − 𝑓(𝑥) ∆𝑥 = lim ∆𝑥→0 𝑐 − 𝑐 ∆𝑥 = lim ∆𝑥→00 = 0 ∎ Contoh 2.2
Tentukan turunan dari fungsi i. 𝑦 = 7
ii. 𝑓(𝑥) = −3
iii. 𝑦 = 𝑘𝜋, dengan 𝑘 adalah konstanta
Penyelesaian
Dengan menggunakan teorema didapat i. 𝑦′= 0
ii. 𝑓′(𝑥) = 0 iii. 𝑑𝑦
𝑑𝑥 = 0
Teorema 2.2
Jika 𝑓 fungsi terdiferensial dan 𝑐 adalah bilangan real, maka 𝑐𝑓 juga terdiferensial dan 𝑑
Bukti 𝑑 𝑑𝑥[𝑐𝑓(𝑥)] = lim∆→0 𝑐𝑓(𝑥 + ∆𝑥) − 𝑐𝑓(𝑥) ∆𝑥 = lim ∆→0𝑐 [ 𝑓(𝑥 + ∆𝑥) − 𝑓(𝑥) ∆𝑥 ] = 𝑐lim ∆→0[ 𝑓(𝑥 + ∆𝑥) − 𝑓(𝑥) ∆𝑥 ] = 𝑐𝑓′(𝑥) ∎ Teorema 2.3
Jumlahan dan pengurangan dua fungsi yang terdiferensial, juga merupakan fungsi yang terdiferensial 𝑑 𝑑𝑥[𝑓(𝑥) + 𝑔(𝑥)] = 𝑓 ′(𝑥) + 𝑔′(𝑥) 𝑑 𝑑𝑥[𝑓(𝑥) − 𝑔(𝑥)] = 𝑓 ′(𝑥) − 𝑔′(𝑥) Bukti 𝑑 𝑑𝑥[𝑓(𝑥) ± 𝑔(𝑥)] = lim∆𝑥→0 [𝑓(𝑥 + ∆𝑥) ± 𝑔(𝑥 + ∆𝑥)] − [𝑓(𝑥) ± 𝑔(𝑥)] ∆𝑥 = lim ∆𝑥→0[ 𝑓(𝑥 + ∆𝑥) − 𝑓(𝑥) ∆𝑥 ± 𝑔(𝑥 + ∆𝑥) − 𝑔(𝑥) ∆𝑥 ] = lim ∆𝑥→0 𝑓(𝑥 + ∆𝑥) − 𝑓(𝑥) ∆𝑥 ± lim∆𝑥→0 𝑔(𝑥 + ∆𝑥) − 𝑔(𝑥) ∆𝑥 = 𝑓′(𝑥) ± 𝑔′(𝑥) ∎
Teorema 2.4
Turunan dari perkalian dua fungsi yang terdiferensial, juga merupakan fungsi yang terdiferensial. 𝑑 𝑑𝑥[𝑓(𝑥)𝑔(𝑥)] = 𝑓(𝑥)𝑔′(𝑥) + 𝑔(𝑥)𝑓′(𝑥) Bukti 𝑑 𝑑𝑥[𝑓(𝑥)𝑔(𝑥)] = lim∆𝑥→0 𝑓(𝑥 + ∆𝑥)𝑔(𝑥 + ∆𝑥) − 𝑓(𝑥)𝑔(𝑥) ∆𝑥 = lim ∆𝑥→0 𝑓(𝑥 + ∆𝑥)𝑔(𝑥 + ∆𝑥) − 𝑓(𝑥 + ∆𝑥)𝑔(𝑥) + 𝑓(𝑥 + ∆𝑥)𝑔(𝑥) − 𝑓(𝑥)𝑔(𝑥) ∆𝑥 = lim ∆𝑥→0[𝑓(𝑥 + ∆𝑥) 𝑔(𝑥 + ∆𝑥) − 𝑔(𝑥) ∆𝑥 + 𝑔(𝑥) 𝑓(𝑥 + ∆𝑥) − 𝑓(𝑥) ∆𝑥 ] = 𝑓(𝑥)𝑔′(𝑥) + 𝑔(𝑥)𝑓′(𝑥) ∎ Teorema 2.5
Pembagian dari dua fungsi 𝑓 dan 𝑔 yang terdiferensial, juga merupakan fungsi terdiferensial, dengan semua nilai 𝑥 pada 𝑔(𝑥) ≠ 0
𝑑 𝑑𝑥[ 𝑓(𝑥) 𝑔(𝑥)] = 𝑔(𝑥)𝑓′(𝑥) − 𝑓(𝑥)𝑔′(𝑥) [𝑔(𝑥)]2 , 𝑔(𝑥) ≠ 0 Bukti 𝑑 𝑑𝑥[ 𝑓(𝑥) 𝑔(𝑥)] = lim∆𝑥→0 𝑓(𝑥 + ∆𝑥) 𝑔(𝑥 + ∆𝑥)− 𝑓(𝑥) 𝑔(𝑥) ∆𝑥 = lim ∆𝑥→0 𝑔(𝑥)𝑓(𝑋 + ∆𝑥) − 𝑓(𝑥)𝑔(𝑥 + ∆𝑥) ∆𝑥𝑔(𝑥)𝑔(𝑥 + ∆𝑥)
= lim ∆𝑥→0 𝑔(𝑥)𝑓(𝑥 + ∆𝑥) − 𝑓(𝑥)𝑔(𝑥) + 𝑓(𝑥)𝑔(𝑥) − 𝑓(𝑥)𝑔(𝑥 + ∆𝑥) ∆𝑥𝑔(𝑥)𝑔(𝑥 + ∆𝑥) = lim ∆𝑥→0 𝑔(𝑥)[𝑓(𝑥 + ∆𝑥) − 𝑓(𝑥)]∆𝑥 − 𝑓(𝑥)[𝑔(𝑥 + ∆𝑥) − 𝑔(𝑥)]∆𝑥 𝑔(𝑥)𝑔(𝑥 + ∆𝑥) =𝑔(𝑥)𝑓 ′(𝑥) − 𝑓(𝑥)𝑔′(𝑥) [𝑔(𝑥)]2 ∎ Teorema 2.6
jika 𝑛 adalah bilangan rasional, maka fungsi 𝑓(𝑥) = 𝑥𝑛 terdiferensial dan 𝑑
𝑑𝑥[𝑥
𝑛] = 𝑛𝑥𝑛−1
Bukti
Kasus I: untuk 𝑛 ≥ 0, 𝑛 ∈ ℤ
Jika 𝑛 = 0 maka 𝑓(𝑥) = 𝑥0 = 1, karena 𝑥0 adalah konstan, menurut teorema 2.1 𝑓′(𝑥) = 0 jika 𝑛 > 0, maka 𝑑 𝑑𝑥[𝑥 𝑛] = lim ∆𝑥→0 (𝑥 + ∆𝑥)𝑛− 𝑥𝑛 ∆𝑥 = lim ∆𝑥→0 𝑥𝑛 + 𝑛𝑥𝑛−1(∆𝑥) +𝑛(𝑛 − 1)𝑥2 𝑛−2(∆𝑥)2+ ⋯ + (∆𝑥)𝑛− 𝑥𝑛 ∆𝑥 = lim ∆𝑥→0𝑛𝑥 𝑛−1+𝑛(𝑛 − 1)𝑥𝑛−2 2 (∆𝑥) + ⋯ + (∆𝑥) 𝑛−1 = 𝑛𝑥𝑛−1
Kasus II: Untuk 𝑛 bilangan bulat negatif Misalkan 𝑛 = −𝑘 𝑑 𝑑𝑥[𝑥 𝑛] = 𝑑 𝑑𝑥[ 1 𝑥𝑘]
=𝑥 𝑘(0) − (1)(𝑘𝑥𝑘−1) (𝑥𝑘)2 =0 − 𝑘𝑥 𝑘−1 𝑥2𝑘 = −𝑘𝑥−𝑘−1 = 𝑛𝑥𝑛−1
Kasus III: untuk 𝑛 bilangan rasional, bukti akan dibahas setelah teorema mengenai
aturan rantai. ∎
Contoh 2.3
Tentukan turunan dari fungsi berikut i. 𝑓(𝑥) = 𝑥3
ii. 𝑔(𝑥) = (3𝑥 − 2𝑥2)(5 + 4𝑥), dengan menggunakan aturan perkalian iii. ℎ(𝑥) =5𝑥−2 𝑥2+1 Penyelesaian i. 𝑓′(𝑥) = 𝑑 𝑑𝑥[𝑥 3] = 3𝑥2 ii. 𝑔′(𝑥) = (3𝑥 − 2𝑥2) 𝑑 𝑑𝑥(5 + 4𝑥) + (5 + 4𝑥) 𝑑 𝑑𝑥(3𝑥 − 2𝑥 2) = (3𝑥 − 2𝑥2)(4) + (5 + 4𝑥)(3 − 4𝑥) = 12𝑥 − 8𝑥2+ 15 − 8𝑥 − 16𝑥2 = −24𝑥2+ 4𝑥 + 15 iii. ℎ′(𝑥) =(𝑥 2+1)𝑑 𝑑𝑥[5𝑥−2]−(5𝑥−2) 𝑑 𝑑𝑥[𝑥 2+1] (𝑥2+1)2 =(𝑥 2+ 1)(5) − (5𝑥 − 2)(2𝑥) (𝑥2+ 1)2 =5𝑥 2 + 5 − 10𝑥2+ 4𝑥 (𝑥2+ 1)2 =−5𝑥 2+ 4𝑥 + 5 (𝑥2+ 1)2 ∎
Teorema 2.7 Aturan Rantai
Jika 𝑦 = 𝑓(𝑢) adalah fungsi terdiferensial di 𝑢 dan 𝑢 = 𝑔(𝑥) adalah fungsi terdiferensial di 𝑥, maka 𝑦 = 𝑓(𝑔(𝑥)) adalah fungsi terdiferensial di 𝑥 dan
𝑑𝑦 𝑑𝑥 = 𝑑𝑦 𝑑𝑢∙ 𝑑𝑢 𝑑𝑥 atau ekivalen 𝑑 𝑑𝑥[𝑓(𝑔(𝑥))] = 𝑓 ′(𝑔(𝑥))𝑔′(𝑥) Bukti 𝑑 𝑑𝑥[𝑓(𝑔(𝑥))] = lim∆𝑥→0 𝑓(𝑔(𝑥 + ∆𝑥)) − 𝑓(𝑔(𝑥)) ∆𝑥 = lim ∆𝑥→0[ 𝑓(𝑔(𝑥 + ∆𝑥)) − 𝑓(𝑔(𝑥)) ∆𝑥 ] [ 𝑔(𝑥 + ∆𝑥) − 𝑔(𝑥) 𝑔(𝑥 + ∆𝑥) − 𝑔(𝑥)] = lim ∆𝑥→0[ 𝑓(𝑔(𝑥 + ∆𝑥)) − 𝑓(𝑔(𝑥)) 𝑔(𝑥 + ∆𝑥) − 𝑔(𝑥) ] [ 𝑔(𝑥 + ∆𝑥) − 𝑔(𝑥) ∆𝑥 ] = lim ∆𝑥→0[ 𝑓(𝑔(𝑥 + ∆𝑥)) − 𝑓(𝑔(𝑥)) 𝑔(𝑥 + ∆𝑥) − 𝑔(𝑥) ] ∙ lim∆𝑥→0[ 𝑔(𝑥 + ∆𝑥) − 𝑔(𝑥) ∆𝑥 ] = lim ∆𝑥→0[ 𝑓(𝑔(𝑥 + ∆𝑥)) − 𝑓(𝑔(𝑥)) 𝑔(𝑥 + ∆𝑥) − 𝑔(𝑥) ] ∙ 𝑔′(𝑥)
misal 𝑘 = 𝑔(𝑥 + ∆𝑥) − 𝑔(𝑥), didapat 𝑔(𝑥 + ∆𝑥) = 𝑔(𝑥) + 𝑘, dan ∆𝑥 → 0 akibatnya 𝑘 → 0, sehingga = lim 𝑘→0[ 𝑓(𝑔(𝑥) + 𝑘) − 𝑓(𝑔(𝑥)) 𝑘 ] ∙ 𝑔′(𝑥) = 𝑓′(𝑔(𝑥))𝑔′(𝑥) ∎
Setelah membuktikan aturan rantai, akan dibuktikan Teorema 2.6 untuk 𝑛 bilangan rasional. Misalkan 𝑦 = 𝑥𝑛, dimana 𝑛 = 𝑝/𝑞, 𝑝, 𝑞 ∈ ℤ, dan 𝑞 ≠ 0 didapat
𝑦 = 𝑥 𝑝
𝑞 (2.2) sehingga,
𝑦𝑞= 𝑥𝑝 (2.3) dengan menggunakan aturan rantai dan Teorema 2.6 untuk 𝑛 ∈ ℤ didapat
𝑞𝑦𝑞−1𝑑𝑦
𝑑𝑥= 𝑝𝑥
𝑝−1 (2.4)
Karena 𝑦 = 𝑥 𝑝
𝑞, persamaan diatas menjadi
𝑑𝑦 𝑑𝑥 = 𝑝𝑥𝑝−1 𝑞𝑥𝑝− 𝑝 𝑞 (2.5) didapat 𝑑𝑦 𝑑𝑥 = 𝑝 𝑞𝑥 𝑝 𝑞−1 (2.6)
jadi untuk 𝑛 bilangan rasional berlaku 𝑦 = 𝑥𝑛, 𝑦′= 𝑛𝑥𝑛−1
Contoh 2.4
Tentukan turunan dari fungsi 𝑦 = √1 − 𝑥
Penyelesaian
𝑦 = √1 − 𝑥 = (1 − 𝑥)12
Dengan menggukanan persamaan (2.6) dan aturan rantai didapat
𝑦′=1
2(1 − 𝑥) −12
dengan bentuk yang lebih sederhana
𝑦′= 1
2√1 − 𝑥 ∎
Teorema 2.8
Fungsi turunan trigonometri yaitu
i. 𝑑 𝑑𝑥[sin 𝑥] = cos 𝑥 ii. 𝑑 𝑑𝑥[cos 𝑥] = sin 𝑥 iii. 𝑑 𝑑𝑥[tan 𝑥] = sec 2𝑥 iv. 𝑑
𝑑𝑥[sec 𝑥] = sec 𝑥 tan 𝑥
v. 𝑑 𝑑𝑥[cot 𝑥] = − csc 2𝑥 vi. 𝑑 𝑑𝑥[csc 𝑥] = − csc 𝑥 cot 𝑥 Bukti i. 𝑑 𝑑𝑥[sin 𝑥] = lim∆𝑥→0 sin(𝑥+∆𝑥)−sin(𝑥) ∆𝑥 = lim ∆𝑥→0
sin 𝑥 cos ∆𝑥 + cos 𝑥 sin ∆𝑥 − sin 𝑥 ∆𝑥
= lim ∆𝑥→0
cos 𝑥 sin ∆𝑥 − sin 𝑥 (1 − cos ∆𝑥) ∆𝑥 = cos 𝑥 lim ∆𝑥→0 sin ∆𝑥 ∆𝑥 − sin 𝑥 lim∆𝑥→0 1 − cos ∆𝑥 ∆𝑥 = cos 𝑥 (1) − sin 𝑥 (0) = cos 𝑥 ii. 𝑑 𝑑𝑥[cos 𝑥] = 𝑑 𝑑𝑥[sin ( 𝜋 2 − 𝑥)] = (−1) cos ( 𝜋 2− 𝑥) = − sin 𝑥 iii. 𝑑 𝑑𝑥[tan 𝑥] = 𝑑 𝑑𝑥[ sin 𝑥 cos 𝑥]
=cos 𝑥 𝑑 𝑑𝑥[sin 𝑥] − sin 𝑥 𝑑 𝑑𝑥[cos 𝑥] cos2𝑥
=cos 𝑥 cos 𝑥 − sin 𝑥 (− sin 𝑥) cos2𝑥 =cos 2𝑥 + sin2𝑥 cos2𝑥 = 1 cos2𝑥= sec2𝑥 iv. 𝑑 𝑑𝑥[sec 𝑥] = 𝑑 𝑑𝑥[ 1 cos 𝑥] = (−1)(cos 𝑥)−2 𝑑 𝑑𝑥[cos 𝑥] = − sec2𝑥 (− sin 𝑥) = sec 𝑥 tan 𝑥
v. 𝑑 𝑑𝑥[cot 𝑥] = 𝑑 𝑑𝑥[ 1 tan 𝑥] = (−1) tan−2𝑥 𝑑 𝑑𝑥[tan 𝑥] = − cot2𝑥 sec2𝑥 = − csc2𝑥 vi. 𝑑 𝑑𝑥[csc 𝑥] = 𝑑 𝑑𝑥[ 1 sin 𝑥] = (−1) sin−2𝑥 𝑑 𝑑𝑥[sin 𝑥] = −csc2𝑥 (cos 𝑥) = − csc 𝑥 cot 𝑥 ∎ Contoh 2.5
Tentukan turunan dari fungsi berikut: i. 𝑓(𝑥) = 𝑥 + cos 𝑥
ii. 𝑔(𝑥) = 𝑥 sec 𝑥
Penyelesaian
i. 𝑓′(𝑥) = 1 − sin 𝑥
Teorema 2.9
Fungsi turunan arccot 𝑥 yaitu 𝑑
𝑑𝑥[arccot 𝑥] = − 1 1 + 𝑥2
Bukti
misal 𝑦 = arccot 𝑥 maka cot 𝑦 = 𝑥 𝑑 𝑑𝑥cot 𝑦 = 𝑑 𝑑𝑥𝑥 − csc2𝑦𝑑𝑦 𝑑𝑥= 1 𝑑𝑦 𝑑𝑥 = − 1 csc2𝑦 = − 1 1 + cot2𝑦 = − 1 1 + 𝑥2 Jadi, didapat 𝑑 𝑑𝑥[arccot 𝑥] = − 1 1 + 𝑥2 ∎ Contoh 2.6
Tentukan turunan dari fungsi
Penyelesaian
Dengan menggunakan aturan rantai didapat
𝑦′= − 1
1 + 𝑥4∙ 2𝑥 = − 2𝑥
1 + 𝑥4 ∎
2. Integral Fungsi
Andaikan terdapat fungsi 𝐹(𝑥) = 𝑥3, dan menggunakan rumus turunan dapat diketahui turunan dari 𝐹(𝑥), yaitu 𝑓(𝑥) = 𝑑
𝑑𝑥[𝑥
3] = 3𝑥2. Pada hal ini dikatakan fungsi 𝐹 adalah anti turunan (𝑎𝑛𝑡𝑖𝑑𝑒𝑟𝑖𝑣𝑎𝑡𝑖𝑣𝑒𝑠) dari 𝑓 (Larson and Edwards, 2009). Pada sub bab ini hanya akan dibahas mengenai integral tak tentu atau anti turunan.
Definisi 2.2
Suatu fungsi 𝐹 adalah anti turunan dari fungsi 𝑓 pada interval 𝐼 jika 𝐹’(𝑥) = 𝑓(𝑥) untuk setiap 𝑥 di 𝐼.
Teorema 2.10
Jika 𝐹 adalah anti turunan dari 𝑓 pada interval 𝐼, maka 𝐺 merupakan anti turunan dari 𝑓 pada imterval 𝐼 jika dan hanya jika G memiliki bentuk persamaan 𝐺(𝑥) = 𝐹(𝑥) + 𝐶, untuk setiap 𝑥 pada interval 𝐼, dimana 𝐶 adalah konstanta.
Bukti
Pembuktikan teorema dari kanan ke kiri, Jika 𝐺(𝑥) = 𝐹(𝑥) + 𝐶, 𝐹′(𝑥) = 𝑓(𝑥) dan 𝐶 konstanta, maka
𝐺′(𝑥) = 𝑑
𝑑𝑥[𝐹(𝑥) + 𝐶] = 𝐹
′(𝑥) + 0 = 𝑓(𝑥) jadi didapat 𝐺 merupakan anti turunan dari 𝑓.
Untuk membuktikan teorema tersebut dari arah yang lain, andaikan 𝐺 anti turunan dari 𝑓, didefinisikan fungsi 𝐻 seperti berikut
𝐻(𝑥) = 𝐺(𝑥) − 𝐹(𝑥)
ambil sebarang 2 titik 𝑎 dan 𝑏 (𝑎 < 𝑏) pada interval, 𝐻 kontinu pada [𝑎, 𝑏] dan terdiferensial pada [𝑎, 𝑏], sehingga
𝐻′(𝑐) =𝐻(𝑏) − 𝐻(𝑎) 𝑏 − 𝑎
untuk 𝑐 pada (𝑎, 𝑏). Namun, 𝐻′(𝑐) = 0, sehingga 𝐻(𝑎) = 𝐻(𝑏). Karena 𝑎 dan 𝑏 adalah sebarang titik pada interval, dapat di ketahui 𝐻 adalah fungsi konstan 𝐶. Sehingga, 𝐺(𝑥) − 𝐹(𝑥) = 𝐶 dan 𝐺(𝑥) = 𝐹(𝑥) + 𝐶 ∎
Contoh 2.7
Tentukan penyelesaian dari persamaan 𝑦′= 2
Penyelesaian
Dengan menggukanan teorema didapat 𝑦 = 2𝑥 + 𝑐 ∎
Operasi untuk mencari solusi dari persamaan 𝑦′= 𝑓(𝑥) disebut anti turunan atau integral tak tentu yang dinotasikan dengan ∫. Solusi dari persamaan dinotasikan dengan (Larson and Edwards, 2009)
𝑦 = ∫ 𝑓(𝑥) 𝑑𝑥 = 𝐹(𝑥) + 𝐶 (2.7) notasi ∫ 𝑓(𝑥) 𝑑𝑥 disebut anti turunan dari 𝑓 terhadap 𝑥.
Sifat invers dari integral dan turunan dapat diverifikasi dengan mengganti 𝑓(𝑥) dengan 𝐹′(𝑥) dalam definisi integral untuk memperoleh (Larson and Edwards, 2009)
𝑦 = ∫ 𝐹′(𝑥) 𝑑𝑥 = 𝐹(𝑥) + 𝐶 (2.8) lebih lanjut, jika ∫ 𝑓(𝑥) 𝑑𝑥 = 𝐹(𝑥) + 𝐶, maka
𝑑
persamaan tersebut memberikan langsung formula integral dari rumus turunan, se-perti berikut: i. ∫ 0𝑑𝑥 = 𝐶 ii. ∫ 𝑐𝑓(𝑥)𝑑𝑥 = 𝑐 ∫ 𝑓(𝑥)𝑑𝑥 iii. ∫[𝑓(𝑥) ± 𝑔(𝑥)]𝑑𝑥 = ∫ 𝑓(𝑥) 𝑑𝑥 ± ∫ 𝑔(𝑥)𝑑𝑥 iv. ∫ 𝑥𝑛𝑑𝑥 = 𝑥𝑛+1 𝑛+1 + 𝐶, 𝑛 ≠ 1 v. ∫ cos 𝑥 𝑑𝑥 = sin 𝑥 + 𝐶 vi. ∫ sin 𝑥 𝑑𝑥 = − cos 𝑥 + 𝐶 vii. ∫ sec2𝑥 𝑑𝑥 = tan 𝑥 + 𝐶 viii. ∫ sec 𝑥 tan 𝑥 𝑑𝑥 = sec 𝑥 + 𝐶
ix. ∫ csc2𝑥 𝑑𝑥 = − cot 𝑥 + 𝐶 x. ∫ csc 𝑥 cot 𝑥 𝑑𝑥 = − csc 𝑥 + 𝐶
Contoh 2.8
Tentukan integral dari fungsi berikut i. ∫ 1
𝑥3𝑑𝑥 ii. ∫(𝑥 + 2)𝑑𝑥 iii. ∫cossin 𝑥2𝑥𝑑𝑥
Penyelesaian i. ∫𝑥13𝑑𝑥 = ∫ 𝑥 −3𝑑𝑥 =𝑥−2 −2 + 𝐶 = − 1 2𝑥2+ 𝐶 ii. ∫(𝑥 + 2)𝑑𝑥 = ∫ 𝑥𝑑𝑥 + ∫ 2 𝑑𝑥 =𝑥 2 2 + 𝐶1+ 2𝑥 + 𝐶2 =𝑥 2 2 + 2𝑥 + 𝐶, 𝐶 = 𝐶1+ 𝐶2 iii. ∫cossin 𝑥2𝑥𝑑𝑥 = ∫ (
1 cos 𝑥) (
sin 𝑥 cos 𝑥) 𝑑𝑥
3. Persamaan Diferensial
Persamaan diferensial adalah persamaan yang memuat derivatif atau turunan dari suatu fungsi. Penyelesaian dari persamaan diferensial merupakan suatu fungsi. Persamaan diferensial diperlukan untuk mengetahui dan menyelidiki fenomena laju perubahan gerak fluida, gerak sistem mekanik, pelepasan panas benda padat, dinamika populasi, dan sebagainya (Boyce and DiPrima, 2012).
Contoh 2.9
Persamaan berikut merupakan contoh persamaan diferensial i. 𝑦′= 𝑦
ii. 𝑦′′ = −𝑦 iii. 𝑦′′ = 2𝑦′+ 𝑦
Pada subab ini hanya akan dibahas tentang persamaan diferensial orde satu. Persamaan diferensial orde satu merupakan persamaan diferensial yang orde tertinggi turunannya adalah satu. Bentuk umum persamaan diferensial orde satu (Boyce and DiPrima, 2012)
𝑑𝑦
𝑑𝑡 = 𝑓(𝑡, 𝑦) (2.10) dimana 𝑓 merupakan fungsi dari variabel bebas 𝑡 dan variabel terikat 𝑦.
Contoh 2.10
Persamaan berikut merupakan contoh persamaan diferensial orde satu i. 𝑑𝑦 𝑑𝑡 = 2 − 𝑦, dimana 𝑓(𝑡, 𝑦) = 2 − 𝑦 ii. 𝑑𝑦 𝑑𝑡 = 𝑦 + 𝑡, dimana 𝑓(𝑡, 𝑦) = 𝑦 + 𝑡 iii. 𝑑𝑦 𝑑𝑡 = 𝑡𝑦, dimana 𝑓(𝑡, 𝑦) = 𝑡𝑦
Contoh 2.11
Persamaan 𝑦′′= sin(𝑡) − 𝑦′− 2𝑦 bukan merupakan persamaan diferensial orde satu karena turunan orde tertingginya bukan satu.
Pada persamaan diferensial orde satu, salah satu cara menyelesaikan persamaan dengan menggunakan persamaan diferensial orde satu variabel terpisah. Persamaan diferensial orde satu variabel terpisah adalah persamaan dimana 𝑓(𝑡, 𝑦) dapat ditulis sebagai perkalian dari fungsi 𝑡 dan fungsi 𝑦. Dengan demikian persamaan diferensial orde satu dapat ditulis (Adkins and Davidson, 2012) 𝑑𝑦
𝑑𝑡 = 𝑔(𝑡)ℎ(𝑦) (2.11) Penyelesaian dari persamaan diferensial orde satu variabel terpisah dapat dicari dengan memisahkan fungsi 𝑡 dan fungsi 𝑦, sehingga persamaan (2.11) menjadi
𝑑𝑦
ℎ(𝑦)= 𝑔(𝑡)𝑑𝑡 (2.12) dengan mengintegralkan kedua ruas didapat
∫ 𝑑𝑦
ℎ(𝑦)= ∫ 𝑔(𝑡) 𝑑𝑡 (2.13) Persamaan (2.13) adalah penyelesaian dari persamaan diferensial orde satu variabel terpisah.
Contoh 2.12
Tentukan penyelesaian dari persamaan diferensial 𝑑𝑦 𝑑𝑡 = 𝑡𝑦
Penyelesaian
Persamaan tersebut dapat dipisahkan antara fungsi 𝑡 dan fungsi 𝑦 sehingga persamaan tersebut menjadi
𝑑𝑦
𝑦 = 𝑡 𝑑𝑡 dengan mengintegralkan kedua ruas didapat
∫𝑑𝑦
ln|𝑦| =1 2𝑡
2+ 𝐶
|𝑦| = 𝑒12𝑡2𝑒𝑐 𝑦 = ±𝑒𝐶𝑒12𝑡2
sehingga didapat penyelesaian dari persamaan diferensial
𝑦 = 𝑘𝑒12𝑡2, 𝑘 = ±𝑒𝐶 ∎
Masalah nilai awal dan masalah nilai batas dapat digunakan untuk menemukan penyelesaian khusus dari persamaan diferensial. Bentuk dari masalah nilai awal dari persamaan diferensial
𝑦′ = 𝑓(𝑡, 𝑦) 𝑡 ∈ [𝑡0, 𝑡1], 𝑦(𝑡0) = 𝑦0 (2.14) dimana 𝑡0 adalah nilai awal dari varibel bebas 𝑡, 𝑦(𝑡0) adalah nilai awal dari variabel terikat 𝑦 saat 𝑡 = 𝑡0. Sedangkan, bentuk dari masalah nilai batas persamaan diferensial
𝑦′= 𝑓(𝑡, 𝑦) 𝑡 ∈ [𝑡0, 𝑡1], 𝑦(𝑡1) = 𝑦1 (2.15) dimana 𝑡1 adalah nilai batas dari variabel bebas 𝑡, 𝑦(𝑡1) adalah nilai batas dari variabel terikat 𝑦 saat 𝑡 = 𝑡1.
Contoh 2.13
Tentukan penyelesaian khusus dari persamaan diferensial 𝑑𝑦
𝑑𝑡 = 𝑡 dengan 𝑦(0) = 1, dimana 𝑡 ∈ [0, ∞]
Penyelesaian
Persamaan tersebut dapat diselesaikan menggunakan persamaan diferensial orde satu variabel terpisah.
𝑑𝑦 𝑑𝑡 = 𝑡 𝑦 = ∫ 𝑡 𝑑𝑡 didapat penyelesaian umum persamaan diferensial,
𝑦 =1 2𝑡 2 + 𝐶 𝑦(0) = 0 maka 𝑦(0) =1 2∙ 0 + 𝐶 = 1 didapat 𝐶 = 1
sehingga penyelesaian khusus persamaan diferensial 𝑦 =1
2𝑡
2 + 1 ∎
Contoh 2.14
Tentukan penyelesaian khusus dari persamaan diferensial 𝑑𝑦
𝑑𝑡 = 𝑡 dengan 𝑦(1) = 1
2, dimana 𝑡 ∈ [0,1]
Penyelesaian
Persamaan tersebut dapat diselesaikan menggunakan persamaan diferensial orde satu variabel terpisah.
𝑑𝑦 𝑑𝑡 = 𝑡 𝑦 = ∫ 𝑡 𝑑𝑡 didapat penyelesaian umum persamaan diferensial,
𝑦 =1 2𝑡 2 + 𝐶 𝑦(1) =1 2 maka 𝑦(1) = 1 2∙ 1 + 𝐶 = 1 2 didapat 𝐶 = 0
sehingga penyelesaian khusus persamaan diferensial 𝑦 =1
2𝑡
B. Pemodelan Matematis
Pemodelan matematis merupakan suatu bentuk matematis yang digunakan untuk mempelajari kejadian atau fenomena dunia nyata. Pada suatu kejadian nyata model matematis tidak hanya terdapat satu model, akan tetapi terdapat beberapa model yang berbeda untuk suatu kejadian. Perbedaan tersebut terjadi karena dalam pembentukan model terdapat perbedaan eksperimen dan simulasi. Dalam model matematis model yang dibuat harus dapat merepresentasikan kenyataan dan dapat mengontrol kondisi yang mempengaruhi model seperti data yang dikumpulkan (Giordano et al., 2003).
Dalam penyusunan model matematis terdapat langkah-langkah dan prosedur dalam pembuatan model matematis. Langkah-langkah dalam pembuatan model matematis yaitu (Giordano et al., 2003)
1. Mengidentifikasi masalah
Langkah awal dalam pembuatan model matematis adalah mengidentifaksi masalah. Dalam langkah identifikasi masalah merupakan langkah yang sulit dilakukan, biasanya dalam langkah ini harus memilah data dan mengindentifikasi beberapa aspek dari situasi yang dipelajari. Pada saat mengidentifikasi masalah harus sesuai dengan masalah yang dihadapi sehingga memudahkan dalam langkah-langkah selanjutnya.
2. Membuat asumsi
Umumnya dalam pembuatan model matematis tidak bisa menggunakan semua faktor yang mempengaruhi masalah yang diindentifikasi, oleh karena itu dalam pembuatan model matematis disederhanakan dengan mengurangi jumlah faktor yang dipertimbangkan. Hubungan dari faktor-faktor yang tersisa harus ditentukan, dengan mengasumsikan hubungan antar faktor kompleksitas masalah dapat berkurang. Asumsi terbagi menjadi 2 bagian yaitu:
a. Mengklasifikasikan variabel
Daftar hal-hal yang mempengaruhi masalah yang diidentifikasi dalam langkah pertama disebut sebagai variabel. Dalam mengklasifikasikan variabel, setiap variabel diklasifikasikan sebagai variabel terikat, bebas, atau tidak keduanya. Beberapa variabel bebas dapat diabaikan karena salah satu dari dua alasan berikut:
Pertama, pengaruh variabel relatif kecil. Kedua, faktor yang mempengaruhi berbagai alternatif dengan cara yang hampir sama, meskipun memiliki pengaruh penting. Sebagai contoh, pertimbangan bentuk optimal ruang kuliah, dimana keterbacaan papan tulis merupakan kriteria yang penting. Pencahayaan merupakan hal yang penting, akan tetapi itu akan mempengaruhi semua bentuk ruangan.
b. Menentukan keterkaitan antar variabel yang dipilih
Dalam menentukan keterkaitan antar variabel tidak mudah, sehingga membuat pada awalnya tidak bisa melihat hubungan di antara semua variabel. Dalam kasus ini dimungkinkan untuk mempelajari sub model, yaitu mempelajari satu atau lebih variabel bebas secara terpisah. Pada akhirnya dapat dihubungkan submodel bersama.
3. Menyelesaikan model
Setelah membuat asumsi model langkah yang selanjutnya yaitu menyelesaikan model. Model matematis dapat terdiri dari persamaan atau ketidaksamaan matematika yang harus diselesaikan untuk menemukan solusi dari masalah. Dalam penyelesaian masalah terkadang terdapat model yang sangat sulit untuk dipecahkan. Karena hal tersebut kembali ke langkah kedua dan membuat asumsi penyederhanaan tambahan untuk menyelesaikan masalah.
4. Verifikasi model
Model yang telah diselesaikan pada langkah sebelumnya akan dilakukan tes dengan menggunakan data asli. Dalam verifikasi model ada beberapa hal yang menjadi kriteria yaitu model menjawab masalah yang diidentifikasi pada langkah pertama, data yang diperlukan memungkinkan untuk didapatkan, model tersebut realistik atau tidak realistik.
5. Implementasi model
Pengimplementasian model ini diharapkan model tersebut dapat menjadi pertimbangan dalam pembuatan suatu keputusan dan model ini dapat dimengerti dengan mudah. Selain mudah digunakan juga dimasukkan suatu langkah tambahan untuk memfasilitasi pengumpulan dan input data yang diperlukan untuk menentukan keberhasilan atau kegagalan model.
6. Mempertahankan model
Model tersebut dibuat berdasarkan identifikasi masalah pada langkah 1 dan asumsi pada langkah 2. Pada langkah ini model yang dibuat harus dipertahankan berdasarkan identifikasi masalah dan asumsi-asumsi yang dibuat.
C. Metode Numerik
Metode numerik dapat menyelesaiakan persamaan diferensial yang sulit untuk diselesaikan dengan metode analitik. Pada subbab ini akan dibahas metode numerik untuk menyelesaikan persamaan diferensial orde satu dengan metode Euler dan metode Heun.
1. Metode Euler
Metode Euler merupakan salah satu metode numerik yang dapat menyelesaiakan persamaan diferensial. Persamaan umum diferensial orde satu yaitu (Boyce and DiPrima, 2012)
𝑑𝑦
𝑑𝑡 = 𝑓(𝑡, 𝑦) (2.16) dimana 𝑓 merupakan fungsi dari variabel bebas 𝑡 dan variabel terikat 𝑦. Pada persamaan (2.16) 𝑑𝑦/𝑑𝑡 didekati dengan
lim ℎ→0
𝑦(𝑡 + ℎ) − 𝑦(𝑡)
ℎ (2.17) Sehingga persamaan (2.16) menjadi
lim ℎ→0 𝑦(𝑡 + ℎ) − 𝑦(𝑡) ℎ = 𝑓(𝑡, 𝑦) (2.18) 𝑦(𝑡 + ℎ) − 𝑦(𝑡) ℎ ≈ 𝑓(𝑡, 𝑦) (2.19) 𝑦(𝑡 + ℎ) ≈ 𝑦(𝑡) + ℎ𝑓(𝑡, 𝑦) (2.20) Persamaan (2.20) merupakan metode Euler.
Contoh 2.15
𝑦′= 1 − 𝑡 + 4𝑦 pada [0,1] dengan ℎ = 0.05 dan 𝑦(0) = 1
Penyelesaian
Diketahui ℎ = 0.05 dan 𝑦(0) = 1, dengan menggunakan metode Euler untuk menyelesaikan persamaan 𝑦′= 1 − 𝑡 + 4𝑦 pada [0,1] diperoleh
untuk 𝑡 = 0.05,
𝑦(0.05) ≈ 1 + 0.05 ∙ (1 − 0 + 4) = 1.25 untuk 𝑡 = 0.1,
𝑦(0.1) ≈ 1.25 + 0.05 ∙ (1 − 0.05 + 4 ∙ 1.25) = 1.5475 dengan menggunakan cara yang sama didapat
𝑦(0.15) ≈ 1.902, 𝑦(0.2) ≈ 2.3249, 𝑦(0.25) ≈ 2.8299, 𝑦(0.3) ≈ 3.4334, 𝑦(0.35) ≈ 4.155, 𝑦(0.4) ≈ 5.0185, 𝑦(0.45) ≈ 6.0522, 𝑦(0.5) ≈ 7.2902, 𝑦(0.55) ≈ 8.7732, 𝑦(0.6) ≈ 10.5504, 𝑦(0.65) ≈ 12.6804, 𝑦(0.7) ≈ 15.234, 𝑦(0.75) ≈ 18.2958, 𝑦(0.8) ≈ 21.9675, 𝑦(0.85) ≈ 26.371 𝑦(0.9) ≈ 31.6527, 𝑦(0.95) ≈ 37.9882, 𝑦(1) ≈ 45.5884. ∎
2. Metode Heun (Aturan Trapesium untuk Persamaan Diferensial Biasa) Metode Heun merupakan salah satu metode numerik untuk menyelesaikan persamaan diferensial. Metode Heun dapat juga dikenali dengan aturan trapesium untuk persamaan diferensial biasa atau metode Runge-Kutta orde dua. Metode Heun memperkenalkan ide baru untuk membentuk algoritma dalam menyelesaikan masalah nilai awal pada persamaan diferensial (Mathews and Fink, 1999)
𝑦′(𝑡) = 𝑓(𝑡, 𝑦(𝑡)) 𝑡 ∈ [𝑡0, 𝑡1], 𝑦(𝑡0) = 𝑦0 (2.21) untuk mendapatkan solusi pada (𝑡1, 𝑦1) dapat menggunakan teorema fundamental kalkulus dan integral 𝑦′(𝑡) pada [𝑡0, 𝑡1] untuk medapatkan
∫ 𝑓(𝑡, 𝑦(𝑡))𝑑𝑡 𝑡1 𝑡0 = ∫ 𝑦′(𝑡)𝑑𝑡 = 𝑡1 𝑡0 𝑦(𝑡1) − 𝑦(𝑡0) (2.22) dimana anti turunan dari 𝑦′(𝑡) adalah fungsi 𝑦(𝑡). Ketika persamaan (2.22) adalah penyelesaian dari 𝑦(𝑡1), didapat
𝑦(𝑡1) = 𝑦(𝑡0) + ∫ 𝑓(𝑡, 𝑦(𝑡))𝑑𝑡 𝑡1
𝑡0
(2.23) Metode integral numerik dapat digunakan untuk mendekati integral tentu dari persamaan (2.23). Jika aturan trapesium digunakan dengan jarak ℎ = 𝑡1 − 𝑡0, maka didapat
𝑦(𝑡1) ≈ 𝑦(𝑡0) + ℎ
2(𝑓(𝑡0, 𝑦(𝑡0)) + 𝑓(𝑡1, 𝑦(𝑡1))). (2.24) Formula pada ruas kanan persamaan (2.24) mengadung nilai 𝑦(𝑡1) yang belum diketahui. Untuk dapat memproses formula tersebut, digunakan pendekatan dari 𝑦(𝑡1) dengan menggunakan metode Euler. Hasil dari subtitusi metode Euler pada pesamaan (2.24) disebut metode Heun
𝑦1 = 𝑦(𝑡0) + ℎ
2(𝑓(𝑡0, 𝑦(𝑡0)) + 𝑓(𝑡1, 𝑦0+ ℎ𝑓(𝑡0, 𝑦0)) (2.25) Proses ini diulangi dan menghasilkan urutan titik yang mendekati solusi kurva 𝑦 = 𝑦(𝑡). Pada setiap langkah, metode Euler digunakan sebagai prediksi dan kemudian aturan trapesium digunakan untuk melakukan koreksi dalam mendapatkan nilai akhir. Langkah umum untuk metode Heun adalah
𝑝𝑘+1= 𝑦𝑘+ ℎ𝑓(𝑡𝑘, 𝑦𝑘), 𝑡𝑘+1= 𝑡𝑘+ ℎ (2.26) 𝑦𝑘+1 = 𝑦𝑘+ℎ
2(𝑓(𝑡𝑘, 𝑦𝑘) + 𝑓(𝑡𝑘+1, 𝑝𝑘+1)). (2.27)
Contoh 2.16
Dengan menggunakan metode Heun tentukan nilai perkiraan dari persamaan 𝑦′= 𝑡−𝑦
2 pada [0,1] dengan ℎ = 0.125 dan 𝑦(0) = 1
Penyelesaian
Diketahui ℎ = 0.125 dan 𝑦(0) = 1, dengan menggunakan metode Heun untuk menyelesaikan persamaan 𝑦′= 𝑡−𝑦
2 pada [0,1] diperoleh Untuk 𝑡 = 0.125,
𝑝0.125= 1 + 0.125 ∙0 − 1
𝑦0.125= 1 + 0.125 2 ( 0 − 1 2 + 0.125 − 0.9375 2 ) = 0.9434 Untuk 𝑡 = 0.25, 𝑝0.25= 0.934 + 0.125 ∙0.125 − 0.934 2 = 0.8867 𝑦0.25= 0.934 +0.125 2 ( 0.125 − 0.934 2 + 0.25 − 0.8867 2 ) = 0.8979
dengan menggunakan cara yang sama didapat
𝑦0.375= 0.8624, 𝑦0.5 = 0.8368, 𝑦0.625 = 0.8203,
𝑦0.75= 0.8124, 𝑦0.875= 0.8125, 𝑦1 = 0.8202. ∎
3. Modifikasi Aturan Trapesium untuk Persamaan Diferensial Biasa Modifikasi dari aturan trapesium digunakan untuk menyelesaikan masalah nilai awal dalam persamaan diferensial biasa (Sukale and Daftardar-Gejji, 2016) 𝑦′= 𝑓(𝑡, 𝑦(𝑡)), 𝑦(0) = 𝑦
0 (2.28) dengan rumus prediktor-korektor sebagai berikut
𝑢0 = 𝑦𝑛+ℎ 2𝑓(𝑡𝑛, 𝑦𝑛) = 𝑦𝑛+1 𝑝 (2.29) 𝑢1 = 𝑁(𝑢0) =ℎ 2𝑓(𝑡𝑛+1, 𝑦𝑛+1 𝑝 ) = 𝑧𝑛+1𝑝 (2.30) 𝑢2 = 𝑁(𝑢0+ 𝑢1) − 𝑁(𝑢0) (2.31) Tiga pendekatan solusi 𝑢0 + 𝑢1+ 𝑢2 memberikan modifikasi aturan berikut untuk menyelesaikan persamaan diferensial biasa
𝑦𝑛+1𝑐 = 𝑦𝑛+1𝑝 +ℎ
2𝑓(𝑡𝑛+1, 𝑦𝑛+1 𝑝
+ 𝑧𝑛+1𝑝 ) (2.32) dimana, 𝑦𝑛+1𝑝 dan 𝑧𝑛+1𝑝 diberikan pada persamaan (2.29) dan pada persamaan (2.30).
Contoh
Dengan menggunakan modifikasi aturan trapesium untuk persamaan diferensial biasa, tentukan nilai perkiraan dari persamaan 𝑦′= 𝑡 + 𝑦 pada [0,1] dengan ℎ = 0.125 dan 𝑦(0) = 1
Penyelesaian
Diketahui 𝑦(0) = 1 dan ℎ = 0.125, Dengan menggunakan modifikasi aturan trapesium untuk persamaan diferensial biasa untuk menyelesaikan persamaan 𝑦′= 𝑡 + 𝑦 pada [0,1] didapat untuk 𝑡 = 0.125, 𝑦0.125𝑝 = 1 +0.125 2 (0 + 1) = 1.0625 𝑧0.125𝑝 = 0.125 2 (0.125 + 1.0625) = 0.07422 𝑦0.125= 1.0625 +0.125 2 (0.125 + (1.0625 + 0.07422)) = 1.1414 untuk 𝑡 = 0.25, 𝑦0.25𝑝 = 1.1414 +0.125 2 (0.125 + 1.1414) = 1.22055 𝑧0.25𝑝 =0.125 2 (0.25 + 1.22055) = 0.0919 𝑦0.25= 1.22055 +0.125 2 (0.25 + (1.22055 + 0.0919)) = 1.3182 dengan menggunakan cara yang sama didapat
𝑦0.375= 1.5351, 𝑦0.5 = 1.7976, 𝑦0.625 = 2.1116,
𝑦0.75= 2.4840, 𝑦0.875= 2.9226, 𝑦1 = 3.4362. ∎
D. Verifikasi Model
Untuk memverikasi model akan digunakan metode grafis, galat relatif, dan galat kuadrat rata-rata (mean square error). Metode grafis yaitu dengan membandingkan grafik dari data asli dan grafik dari model. Galat relatif dan galat kuadrat rata-rata merupakan metode yang dapat digunakan untuk mengukur tingkat keakuratan model yang digunakan. Galat relatif (𝑒𝑟) dan galat kuadrat rata-rata (𝑀𝑆𝐸) memiliki bentuk sebagai berikut
𝑒𝑟= |𝑦 − 𝑦̂ 𝑦 | , 𝑀𝑆𝐸 = 1 𝑛∑(𝑦𝑡− 𝑦̂𝑡) 2 𝑛 𝑡=1 (2.33)
32
BAB III
MODEL KEPENDUDUKAN
A. Model Pertumbuhan Hiperbolik
Model pertumbuhan hiperbolik menggunakan model pertumbuhan ekspo-nensial sebagai dasar dalam pembentukan model. Bentuk dari model pertumbuhan eksponensial yaitu (Hathout, 2013)
𝑑𝑁
𝑑𝑡 = 𝑘𝑁 (3.1) dengan 𝑘 adalah konstanta, dan 𝑁 adalah populasi penduduk. Dalam pembentukan model pertumbuhan hiperbolik diasumsikan 𝑘 merupakan sebuah fungsi dari 𝑁, sehingga persamaan (3.1) menjadi
𝑑𝑁
𝑑𝑡 = 𝑘(𝑁)𝑁 (3.2) Persamaan (3.2) merupakan bentuk sederhana dari model pertumbuhan hiperbolik. Untuk mempertahankan ukuran dalam persamaan, 𝑘(𝑁) dapat ditulis
𝑘(𝑁) =𝑐𝑁
𝑁0 (3.3) dimana 𝑐 adalah konstanta, dan 𝑁0 adalah populasi awal. Dengan mensubstitusikan persamaan (3.3) ke dalam persamaan (3.2) didapat
𝑑𝑁 𝑑𝑡 = 𝑐𝑁 𝑁0𝑁 (3.4) 𝑑𝑁 𝑑𝑡 = 𝑐𝑁2 𝑁0 (3.5) Persamaan (3.5) dapat diselesaikan dengan menggunakan persamaan diferensial orde satu variable terpisah. Persamaan (3.5) dapat ditulis
𝑑𝑁 𝑁2 =
𝑐 𝑁0
𝑑𝑡 (3.6) dengan mengintegralkan kedua ruas, persamaan (3.6) menjadi
∫𝑑𝑁 𝑁2 = ∫ 𝑐 𝑁0 𝑑𝑡 (3.7) −1 𝑁 = 𝑐 𝑁0 𝑡 + 𝐶 (3.8) dengan mengamsumsikan bahwa populasi 𝑁0 saat 𝑡 = 0, didapat
𝐶 = − 1
𝑁0 (3.9) sehingga persamaan (3.8) menjadi
− 1 𝑁= 𝑐 𝑁0 𝑡 − 1 𝑁0 (3.10) didapat 𝑁(𝑡) = 𝑁0 1 − 𝑐𝑡 (3.11) persamaan (3.11) merupakan penyelesaian dari model pertumbuhan hiperbolik.
Untuk mendapatkan konstanta 𝑐 akan digunakan data 1960 dan data 2009. Diambil 𝑁0 = 𝑁(1960) = 3.0402, dengan memanipulasi persamaan (3.11) diperoleh bentuk persamaan (Hathout, 2013)
𝑁(2009) = 𝑁0 1 − 𝑐(2009 − 1960)= 𝑁0 1 − 49𝑐 (3.12) atau 𝑐 = 1 −𝑁(2009)𝑁0 49 (3.13) Didapat 𝑐 =1 − 3.0402 6.8158 49 = 0.0113 (3.14) sehingga persamaan (3.11) dapat ditulis
𝑁(𝑡) = 𝑁0
Model pertumbuhan hiperbolik merupakan model dimana populasi bertambah dengan laju pertumbuhan yang cenderung naik, sehingga pada model ini untuk 𝑡 menuju tak hingga jumlah populasi penduduk juga menuju tak hingga. Karena hal tersebut, model ini bukan merupakan model yang realistik. Gambar 3.1 merupakan ilustrasi dari model pertumbuhan hiperbolik.
Gambar 3.1 Model Pertumbuhan Hiperbolik
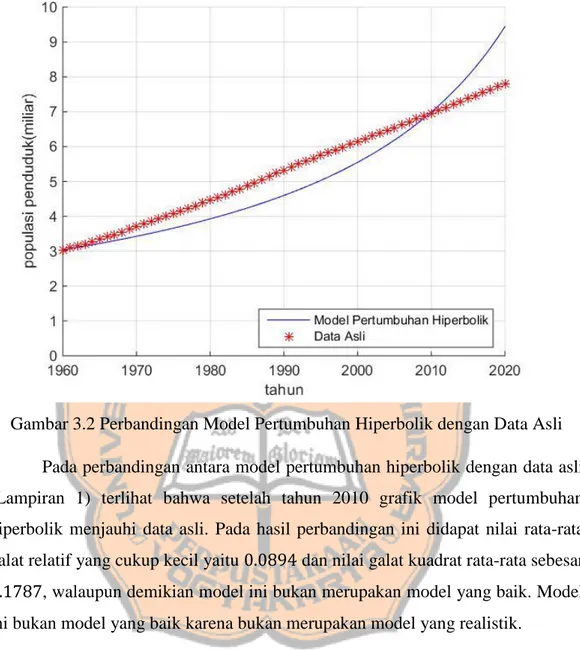
Model pertumbuhan hiperbolik ini akan dibandingkan dengan data asli pada tahun 1950 sampai dengan tahun 2020. Karena pada model ini perhitungan dimulai dari tahun 1960, perbandingan antara model dan data asli dilakukan untuk tahun 1960 sampai tahun 2020. Pada perbandingan ini juga akan dicari rata-rata galat relatif dan galat kuadrat rata-rata dari model. Perbandingan antara model dan data asli ini dilakukan dengan bantuan program MATLAB. Gambar 3.2 adalah hasil perbandingan antara model pertumbuhan hiperbolik dan data asli.
Gambar 3.2 Perbandingan Model Pertumbuhan Hiperbolik dengan Data Asli Pada perbandingan antara model pertumbuhan hiperbolik dengan data asli (Lampiran 1) terlihat bahwa setelah tahun 2010 grafik model pertumbuhan hiperbolik menjauhi data asli. Pada hasil perbandingan ini didapat nilai rata-rata galat relatif yang cukup kecil yaitu 0.0894 dan nilai galat kuadrat rata-rata sebesar 8.1787, walaupun demikian model ini bukan merupakan model yang baik. Model ini bukan model yang baik karena bukan merupakan model yang realistik.
B. Model Kapitsa
Kapitsa merumuskan prinsip fenomenologis imperatif demografis, dimana pertumbuhan populasi ditentukam oleh populasi sistem dunia itu sendiri dan proses pengembangan sosial (Kapitsa, 2008).
Analisis hukum pertumbuhan hiperbolik populasi dunia yang menghu-bungkan ukuran populasi dunia dan perkembangan manusia, menyarankan suatu mekanisme kerja sama ukuran perkembangan yang direpresentasikan oleh kuadrat
ukuran populasi. Karena alasan tersebut, Kapitsa (1992) mengusulkan ketergan-tungan kuadratik untuk laju pertumbuhan penduduk
𝑑𝑁 𝑑𝑡 =
𝑁2
𝐶 = 𝑎𝑁
2 (3.16)
dimana 𝐶 adalah konstanta, 𝑎 = 1/𝐶 dan 𝑁 adalah populasi penduduk. Pada persamaan (3.16) karena bentuk matematis dari dinamika populasi tidak memerlukan faktor apapun selain ukuran populasi, Kapitsa menyebut fenomena tersebut sebagai the demographic imperative (imperatif demografis).
Pada bentuk matematis persamaan (3.16) untuk waktu mendekati tak hingga, jumlah populasi penduduk dunia akan mendekati tak hingga pula. Sedangkan pada kenyataannya pertumbuhan populasi yang tinggi seiring berjalannya waktu makin lama berkurang jumlahnya. Fenomena ini pertama kali ditemukan oleh ahli demografi Perancis yaitu Adolphe Landry, yang kemudian Adolphe Landry menyebut fenomena tersebut sebagai demographic revolution (revolusi demografis) (Kapitsa, 2008). Sekarang fenomena tersebut disebut sebagai
global demographic transiton (transisi demografis global).
Untuk menggambarkan transisi demografis global, Kapitsa menyusun kem-bali persamaaannya dan memperkenalkan 𝜏 yang merupakan karakteristik umur hidup manusia, untuk membatasi tingkatan pertumbuhan penduduk. Model yang ditemukan oleh Kapitsa yaitu (Kapitsa, 2008)
𝑑𝑁 𝑑𝑡 =
𝐶 (𝑇1− 𝑡)2+ 𝜏2
(3.17) dimana 𝑇1 dan 𝐶 adalah konstanta, dan 𝑡 adalah waktu dalam tahun masehi. Persamaan (3.17) merupakan model Kapitsa.
Persamaan (3.17) dapat diselesaikan dengan menggunakan persamaan diferensial orde satu variabel terpisah. Persamaan (3.17) dapat ditulis
𝑑𝑁 = 𝐶
(𝑇1− 𝑡)2 + 𝜏2𝑑𝑡 (3.18) dengan mengintegralkan kedua ruas persamaan (3.18) menjadi
∫ 𝑑𝑁 = ∫ 𝐶 (𝑇1− 𝑡)2 + 𝜏2 𝑑𝑡 (3.19) ∫ 𝑑𝑁 = ∫ 𝐶 𝜏 ((𝑇1− 𝑡)𝜏 2+ 𝜏) 𝑑𝑡 (3.20)
misalkan 𝐾 = √𝐶/𝜏, persamaan (3.20) menjadi ∫ 𝑑𝑁 = ∫ 𝐾 2 ((𝑇1− 𝑡)𝜏 2+ 𝜏) 𝑑𝑡 (3.21) ∫ 𝑑𝑁 = 𝐾2∫ (− 1 (𝑇1− 𝑡)2 𝜏2 + 1 ∙ −1 𝜏) 𝑑𝑡 (3.22)
dengan menggunakan invers dari persamaan 𝑑 𝑑𝑥[arccot 𝑥] = − 1 1 + 𝑥2 (3.23) persamaan (3.22) menjadi 𝑁 = 𝐾2arccot (𝑇1− 𝑡 𝜏 ) (3.24) persamaan (3.24) merupakan penyelesaian model Kapitsa. Model Kapitsa menggambarkan pertumbuhan populasi dunia dengan stabilisasi dan hanya berlaku dalam kasus perkembangan manusia yang berkelanjutan. Gambar 3.3 merupakan ilustrasi dari model Kapitsa dengan 𝐶 = 163 × 109, 𝜏 = 45, dan 𝑇1 = 1995.
Gambar 3.3 Model Kapitsa
Model Kapitsa dapat digunakan dengan baik untuk perhitungan dinamika demografis pada suatu negara dengan perkembangan penduduk yang kuat, ketika populasi tumbuh sesuai dengan skenario stabilisasi tanpa penurunan (Yakunin, 2011).
Pada model Kapitsa ini akan dilakukan perbandingan dengan data asli. Data asli yang digunakan yaitu data pada tahun 1950 sampai tahun 2000. Pada perbandingan ini juga akan dicari rata-rata galat relatif dan galat kuadrat rata-rata model. Perbandingan ini dilakukan dengan bantuan program MATLAB. Gambar 3.4 merupakan perbandingan model Kapitsa dengan data asli.
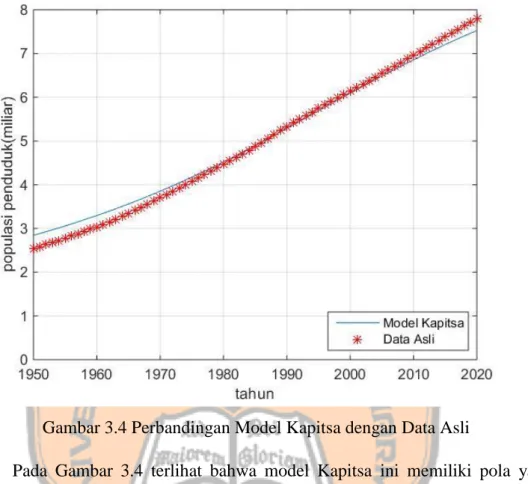
Gambar 3.4 Perbandingan Model Kapitsa dengan Data Asli
Pada Gambar 3.4 terlihat bahwa model Kapitsa ini memiliki pola yang hampir sama dengan data asli. Pada hasil perbandingan didapat nilai rata-rata galat relatif dan galat kuadrat rata-rata yang kecil yaitu 0.0353 dan 0.0268, yang berarti model ini mendekati nilai dari data asli dan cukup baik untuk menghitung jumlah populasi penduduk dunia. Model Kapitsa ini merupakan model yang baik karena memiliki nilai galat yang kecil dan model ini merupakan model yang realistik.
C. Model Dolgonosov
Dolgonosov (2009) melengkapi persamaan yang didapat oleh Kapitsa. Menurut Dolgonosov, ukuran populasi ditentukan oleh 𝑞 tingkat produksi informasi:
𝑑𝑞
𝑑𝑡 = 𝜔𝑁 (3.25) dimana ω adalah tingkat rata-rata pemrosesan informasi oleh manusia.
Model Dolgonosov untuk populasi dunia adalah: 𝑑𝑁 𝑑𝑡 = 𝑟𝑁 2[1 − 𝑁 𝐾(𝑞)] (3.26) 𝐾(𝑞) = 𝑁𝑐 1 − exp (−𝛼𝑞𝑞 𝑐) (3.27) dimana 𝑟 = 𝜔
𝑞 adalah koefisien dari pertumbuhan populasi dunia, 𝐾(𝑞) adalah kapasitas lingkungan sesaat, 𝑁𝑐 =
𝑞𝑐
𝜔𝑡𝑐 daya muat dari biosfer bumi, 𝑞𝑐 dan 𝑡𝑐 adalah karaktersitik skala jumlah, 𝛼 adalah konstanta dan 𝑁 adalah populasi penduduk dunia.
Model Dolgonosov dapat dipandang sebagai model universal yang dapat digunakan untuk menganalisis melalui simulasi numerik berbagai skenario perkembangan manusia, yaitu pertumbuhan populasi dunia dengan stabilisasi, penurunan jumlah populasi, dan osilasi teredam. Dolgonosov berpendapat bahwa osilasi teredam merupakan pendekatan yang paling cocok untuk mendiskripsikan dinamika populasi. Namun, model yang sesuai dari produksi informasi mengandung frekuensi osilasi 𝛽, yang tidak dapat ditentukan karena kurangnya data empiris. Untuk alasan ini, dinamika populasi dideskripsikan menggunakan model sederhana dengan pengembalian aperiodik. Selain itu, skema komputasi yang didasarkan pada model Dolgonosov diperumit oleh fakta bahwa pertumbuhan produksi informasi harus dihitung terlebih dahulu diikuti dengan menghitung dinamika populasi. Untuk mengatasi kesulitan-kesulitan ini, desain fungsi yang menggambarkan kapasitas lingkungan sesaat yaitu 𝐾 = 𝐾(𝑁) harus dibatasi pada imperatif demografis.
Kremer (1993) menunjukkan bahwa, untuk setiap periode waktu, ada ukuran populasi terbatas 𝐾(𝐴) yang tidak dapat melebihi tingkat perkembangan teknologi 𝐴. 𝐾 merupakan kapasitas lingkungan saat ini. Dengan demikian, kapasitas lingkungan sesaat ditentukan oleh tingkat perkembangan teknologi dan berkembang dengan peningkatan tingkat perkembangan teknologi. Kremer
mengasumsikan bahwa tingkat pertumbuhan teknologi sebanding dengan ukuran populasi saat ini
𝑑𝐴
𝐴𝑑𝑡= 𝑐𝑁 (3.28) Persamaan 3.28 menyiratkan bahwa 𝐾 dapat meningkat secara proporsional dengan laju pertumbuhan tingkat perkembangan teknologi, oleh karena itu
𝐾(𝐴)~𝑁 (3.29) Di sisi lain, ketika populasi dunia tumbuh saat kondisi kegiatan ekonomi yang tidak tekendali, beban antropogenik pada biosfer bumi yang juga meningkat, yang mengarah pada degradasi ekosistem biosfer pada banyak wilayah, mengakibatkan berkurangnya kapasitas lingkungan sesaat. Oleh karena itu, laju penurunan kapasitas sesaat berbanding lurus dengan laju pertumbuhan penduduk
𝑑𝐾
𝐾𝑑𝑡= −𝜅
𝑑𝑁
𝑑𝑡 (3.30) dimana 𝜅 adalah konstanta. Dengan mengikuti hal tersebut
𝐾~ exp(−𝜅𝑁). (3.31) Dengan mengkombinasikan (3.29) dan (3.31) di dapat
𝐾~ Nexp(−𝜅𝑁) (3.32) menambahkan tingkat stasioner populasi dunia menjadi (3.32), diperoleh formula akhir untuk kapasitas sesaat, yang hanya ditentukan oleh ukuran populasi, yaitu oleh imperatif demografis
𝐾 = 𝑁𝑐 + 𝛾 Nexp(−𝜅𝑁) (3.33) dimana 𝛾 adalah konstanta.
Ada berbagai metode untuk memperkirakan ukuran stasioner populasi dunia 𝑁𝑐. Ukuran stasioner populasi sutau negara dapat diperkirakan dengan membagi ukuran stasioner populasi dunia dengan indeks antropogenik negara. Antropogenik
adalah sumber pencemaran yang tidak alami, timbul karena ada pengaruh atau campur tangan manusia.
Gorshkov (1995) memperkirakan, populasi dunia mengkonsumsi sekitar 22-23% biomassa planet. Pengaruh teknologi pendukung kehidupan dimulai pada abad ke-19 ketika populasi dunia mencapai 1 miliar. Untuk memperhitungkan keadaan ini 𝐾(𝑞) dapat ditulis
𝐾 = 𝑁𝑐+ 𝛾(𝑁 − 𝑁0) exp[−𝜅(𝑁 − 𝑁0)] (3.34) dimana 𝑁𝑐 adalah daya muat biosfer, 𝛾 dan 𝜅 adalah konstanta, dan 𝑁0 adalah po-pulasi awal.
Persamaan populasi dinamik pada persamaan (3.26) dapat ditulis ulang dengan mensubstitusikan persamaan (3.34), sehingga persamaan (3.26) dapat ditulis
𝑑𝑁
𝑑𝑡 = 𝑟𝑁
2[1 − 𝑁
𝑁𝑐 + 𝛾(𝑁 − 𝑁0)exp [−𝜅(𝑁 − 𝑁0)]] (3.35) dengan karakteristik waktu tunda, persamaan (3.35) dapat ditulis
𝑑𝑁 𝑑𝑡 = 𝑟𝑁(𝑡 − 𝜏1) 2[1 − 𝑁 𝐾(𝑁, 𝜏2, 𝜏3) ] (3.36) dimana, 𝐾(𝑁, 𝜏2, 𝜏3) = 𝑁𝑐+ 𝛾(𝑁(𝑡 − 𝜏2) − 𝑁0)exp [−𝜅(𝑁(𝑡 − 𝜏3) − 𝑁0)]
dengan 𝜏1 adalah rata-rata umur reproduksi, 𝜏2 adalah waktu difusi dari teknologi basis, 𝜏3 adalah keterlambatan dalam respon biosfer terhadap beban antropogenik. Karena karakteristik waktu tunda yang diberikan dalam model, untuk menggunakan model tersebut butuh data dinamika populasi sebelumnya selama sekitar 100 tahun. Berikut merupakan ilustrasi model Dolgonosov, seperti ditunjukkan dalam Gambar 3.5 dan Gambar 3.6. Metode numerik Heun akan dijelaskan dalam subbab beri-kutnya. Gambar hasil metode Heun dan metode Euler ditampilkan terlebih dahulu agar pembaca memahami perilaku solusi model Dolgonosov.
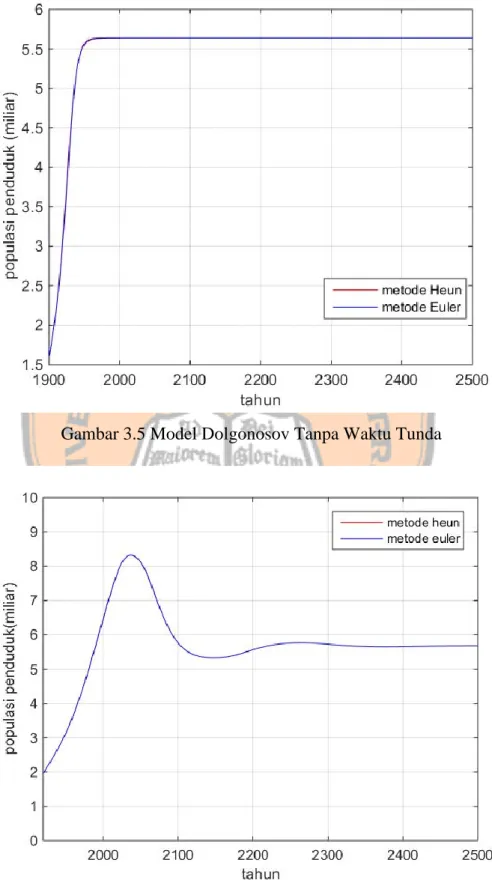
Gambar 3.5 Model Dolgonosov Tanpa Waktu Tunda
Dari Gambar 3.5 dan Gambar 3.6 dapat diketahui bahwa pengaruh peng-gunaan metode Euler dan metode Heun dalam model Dolgonosov tidak ada perbedaaan yang signifikan. Untuk model ini nilai yang didapat dengan menggunakan metode Euler hampir sama dengan menggunakan metode Heun. Setelah ini akan dilihat perbedaan pengunaan waktu tunda dalam model Dolgonosov. Perbedaan penggunaan waktu tunda seperti pada Gambar 3.7 dan Gambar 3.8.
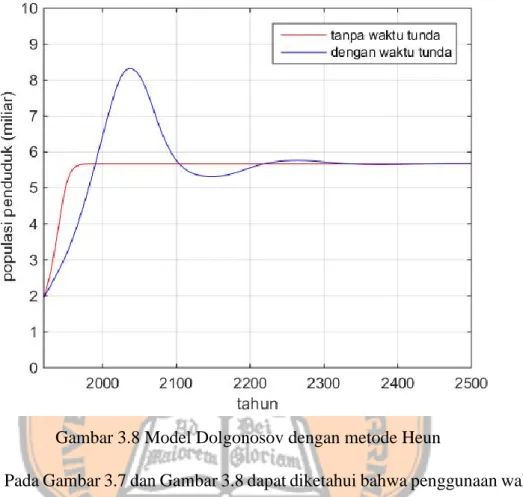
Gambar 3.8 Model Dolgonosov dengan metode Heun
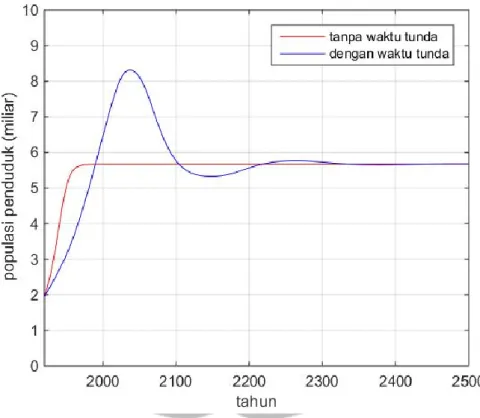
Pada Gambar 3.7 dan Gambar 3.8 dapat diketahui bahwa penggunaan waktu tunda sangat berpengaruh untuk model Dolgonosov, baik menggunakan metode Euler maupun metode Heun. Penggunaan waktu tunda dapat membuat model naik mencapai puncak dan setelah itu turun mendekati stasioner. Apabila pada model ini tidak menggunakan waktu tunda, model langsung menuju stasioner tanpa kenaikan yang sangat tajam terlebih dahulu.
D. Penyelesaian Model dengan Aturan Trapesium
Pada subbab ini akan dibahas mengenai penggunaan aturan trapesium (metode Heun) untuk menyelesaikan ketiga model kependudukan yang telah dibahas pada sub bab sebelumnya. Untuk menyelesaikan ketiga model tersebut akan digunakan aturan trapesium untuk persamaan diferensial biasa dan modifikasi aturan trapesium untuk persamaan diferensial biasa.
1. Aturan Trapesium untuk Persamaan Diferensial Biasa
Aturan trapesium untuk persamaan diferensial biasa merupakan salah satu metode numerik untuk menyelesaikan persamaan diferensial. Pada sub bab ini akan dibahas menggunakan aturan trapesium untuk menyelesaikan ketiga model kepen-dudukan yaitu model pertumbuhan hiperbolik, model Kapitsa dan model Dolgonosov. Aturan trapesium untuk Persamaan Diferensial Biasa sebagi berikut 𝑝𝑛+1= 𝑦𝑛+ ℎ𝑓(𝑡𝑛, 𝑦𝑛), 𝑡𝑛+1 = 𝑡𝑛+ ℎ (3.37) 𝑦𝑛+1= 𝑦𝑛 +
ℎ
2(𝑓(𝑡𝑛, 𝑦𝑛) + 𝑓(𝑡𝑛+1, 𝑝𝑛+1)). (3.38) Model Pertama yang akan diselesaikan menggunakan aturan trapesium adalah model pertumbuhan hiperbolik
𝑑𝑁
𝑑𝑡 = 𝑘(𝑁)𝑁 (3.39) dimana 𝑁 adalah populasi penduduk dan
𝑘(𝑁) =𝑐𝑁 𝑁0
(3.40) dengan 𝑐 adalah konstanta, dan 𝑁0 adalah populasi awal. Dari persamaan (3.39) dan (3.40) didapat persamaan diferensial
𝑑𝑁
𝑑𝑡 =
𝑐𝑁2 𝑁0
(3.41) persamaan (3.41) merupakan persamaan yang akan diselesaikan dengan aturan trapesium untuk persamaan diferensial biasa.
Untuk menyelesaikan persamaan (3.41) dipilih nilai awal 𝑡0 = 1960, dan 𝑁(0) = 3.0402 miliar, 𝑁(0) adalah jumlah populasi penduduk saat 𝑡0 (Hathout, 2013). Selain itu, untuk menyelesaikan persamaan tersebut dipilih juga nilai 𝑐 = 0.0113 dan ℎ = 1. Sehingga dengan menggunakan (3.37) dan (3.38) didapat Untuk 𝑡1 = 1961 𝑝1 = 3.0402 + 1 ∙ 0.0113(3.0402)2 3.0402 = 3.0746 𝑦1 = 3.0402 +1 2( 0.0113(3.0402)2 3.0402 + 0.0113(3.0746)2 3.0402 =) = 3.0749
Untuk 𝑡2 = 1962 𝑝2 = 3.0749 + 1 ∙ 0.0113(3.0749)2 3.0402 = 3.1101 𝑦2 = 3.0749 +1 2( 0.0113(3.0749)2 3.0402 + 0.0113(3.1101)2 3.0402 ) = 3.1105 Untuk 𝑡3 = 1963 𝑝3 = 3.1105 + 1 ∙0.0113(3.1105) 2 3.0402 = 3.1465 𝑦3 = 3.1105 + 1 2( 0.0113(3.1105)2 3.0402 + 0.0113(3.1465)2 3.0402 ) = 3.1469 Untuk 𝑡4 = 1964 𝑝4 = 3.1469 + 1 ∙ 0.0113(3.1469)2 3.0402 = 3.1837 𝑦4 = 3.1469 +1 2( 0.0113(3.1469)2 3.0402 + 0.0113(3.1837)2 3.0402 ) = 3.1841 Untuk 𝑡5 = 1965 𝑝5 = 3.1841 + 1 ∙0.0113(3.1841) 2 3.0402 = 3.2218 𝑦5 = 3.1841 +1 2( 0.0113(3.1841)2 3.0402 + 0.0113(3.1837)2 3.0402 ) = 3.2222
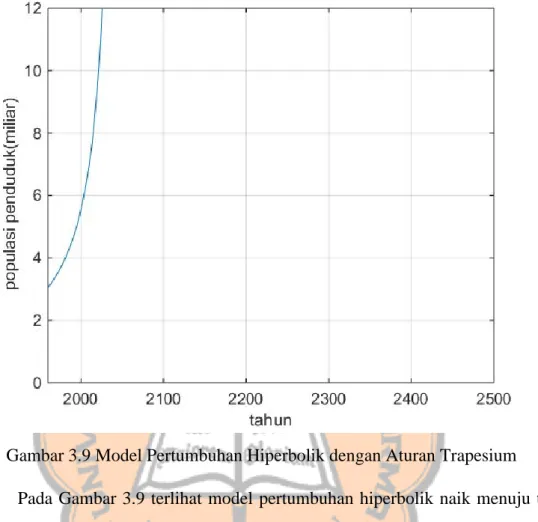
Dengan menggunakan cara yang sama dapat dihitung untuk iterasi-iterasi selanjutnya. Pada hal ini akan dihitung dari tahun 1900 hingga tahun 2500, dengan menggunakan bantuan program MATLAB didapatkan grafik seperti pada Gambar 3.9.
Gambar 3.9 Model Pertumbuhan Hiperbolik dengan Aturan Trapesium Pada Gambar 3.9 terlihat model pertumbuhan hiperbolik naik menuju tak hingga seperti penyelesaian analitiknya. Setelah diketahui penyelesaian model dengan menggunakan aturan trapesium akan dilakukan perbandingan dengan penyelesaian analitik dari model. Perbandingan antara penyelesaian analitik dan penyelesaian menggunakan aturan trapesium ini juga akan dicari nilai galat kuadrat rata-rata dan rata-rata galat realatif dari metode yang digunakan. Perbandingan antara penyelesaian analitik dan penyelesaian dengan aturan trapesium ini dilakukan dengan bantuan program MATLAB. Gambar 3.10 merupakan perbandingan penyelesaian analitik dan aturan trapesium untuk model.
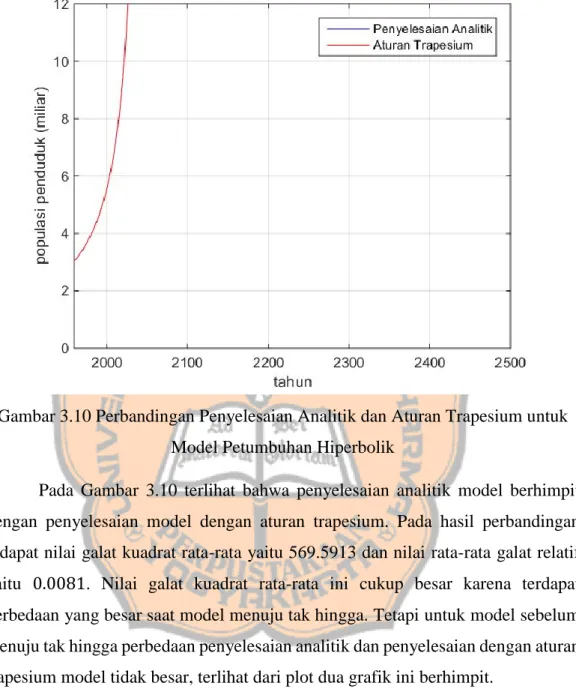
Gambar 3.10 Perbandingan Penyelesaian Analitik dan Aturan Trapesium untuk Model Petumbuhan Hiperbolik
Pada Gambar 3.10 terlihat bahwa penyelesaian analitik model berhimpit dengan penyelesaian model dengan aturan trapesium. Pada hasil perbandingan didapat nilai galat kuadrat rata-rata yaitu 569.5913 dan nilai rata-rata galat relatif yaitu 0.0081. Nilai galat kuadrat rata-rata ini cukup besar karena terdapat perbedaan yang besar saat model menuju tak hingga. Tetapi untuk model sebelum menuju tak hingga perbedaan penyelesaian analitik dan penyelesaian dengan aturan trapesium model tidak besar, terlihat dari plot dua grafik ini berhimpit.
Model yang selanjutnya yang akan diselesaikan dengan menggunakan aturan trapesium adalah model Kapitsa yaitu
𝑑𝑁 𝑑𝑡 =
𝐶 (𝑇1− 𝑡)2+ 𝜏2
(3.42)
dimana 𝑇1 dan 𝐶 adalah konstanta, 𝑡 adalah waktu dalam tahun masehi dan 𝜏 adalah karakteristik umur hidup manusia. Model Kapitsa ini adalah model kependudukan dimana untuk 𝑡 mendekati tak hingga, jumlah populasi penduduk akan menuju ke
suatu nilai tertentu. Model ini berbeda dengan model pertumbuhan hiperbolik karena untuk model pertumbuhan hiperbolik, jika 𝑡 mendekati tak hingga maka jumlah populasi penduduk akan menuju tak hingga.
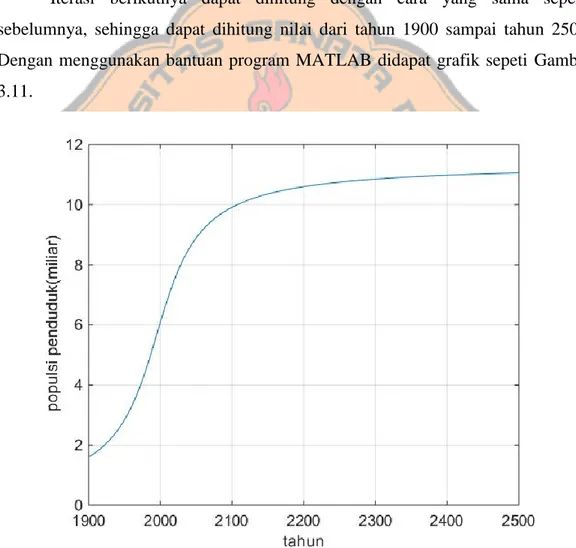
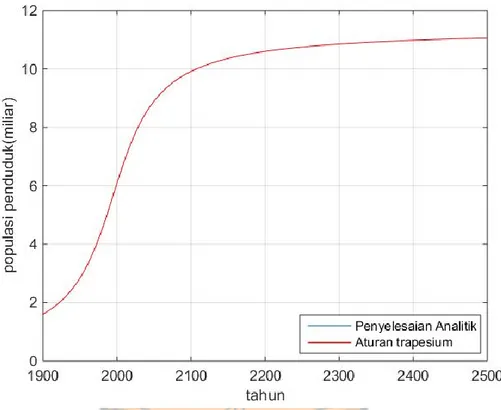
Untuk menyelesaikan persamaan (3.42) dengan aturan trapesium dipilih nilai awal 𝑡0 = 1900 dan 𝑁(0) = 1.6024 miliar. 𝑁(0) diambil dari nilai eksak model Kapitsa saat 𝑡 = 1900. Untuk menyelesaikan persamaan tersebut dipilih pula nilai 𝑇1 = 1995, 𝐶 = 163 × 109 dan 𝜏 = 45. Karena nilai dari variabel persamaan (3.42) sudah diketahui, persamaan tersebut dapat diselesaikan dengan aturan trapesium untuk persamaan diferensial biasa. Sehingga dari aturan trapesium untuk persamaan diferensial biasa dengan ℎ = 1 didapat
Untuk 𝑡1 = 1901 𝑝1 = 1.6024 + 1 ∙ 163 (1995 − 1900)2+ 452 = 1.6172 𝑦1 = 1.6024 +1 2( 163 (1995 − 1900)2+ 452 + 163 (1995 − 1901)2+ 452) = 1.6173 Untuk 𝑡2 = 1902 𝑝2 = 1.6173 + 1 ∙ 163 (1995 − 1901)2+ 452 = 1.6323 𝑦2 = 1.6173 + 1 2( 163 (1995 − 1901)2+ 452+ 163 (1995 − 1902)2 + 452) = 1.6324 Untuk 𝑡3 = 1903 𝑝3 = 1.6324 + 1 ∙ 163 (1995 − 1903)2+ 452 = 1.6477 𝑦2 = 1.6324 +1 2( 163 (1995 − 1903)2+ 452+ 163 (1995 − 1904)2 + 452) = 1.6478 Untuk 𝑡4 = 1904 𝑝4 = 1.6478 + 1 ∙ 163 (1995 − 1904)2+ 452 = 1.6634