1
AN APPLICATION OF LEFT / RIGHT INVERSE
IN PUBLIC KEY CRYPTOSYSTEM
Budi Murtiyasa
Department of Mathematics Education, Muhammadiyah University of Surakarta e-mail : bdmurtiyasa@yahoo.com
Fax : +62 271 715448
Subanar, RetantyoWardoyo, SriHartati
Faculty of Mathematics and Natural Science, Gadjah Mada University
Abstract
The theory of matrices becomes a potential tool in cryptographic research. The paper addreses to develop a public key cryptosystem based on right inverse of matrices. The idea is similar to the previous public key cryptosystem, that is McElice’s public key and Wu-Dawson’s public key, in term of the usage of a coding theory. Properties of the public key cryptosystem are analyzed and compared with the previous public key cryptosystem.
Key word : left inverse, right inverse, public key cryptosystem
Introduction
For a public key cryptosystem with information expansion, i.e. the length of ciphertext blocks is larger than that of plaintext blocks, it is possible that one plaintext block may correspond to several valid ciphertext blocks. For example, McEliece’s public key cryptosystem and Wu-Dawson’s public key cryptosystem have information expansion (Wu and Dawson, 1998:321). Both of them have an advantage that is fast encryption and decryption. Disadvantages need large key space and have message expansion.
This paper proposes a public key cryptoystem based on the left / right inverses of matrices in the field Z2 = {0, 1}. The algorithms of encryption and decryption, which are
2 Encryption by McEliece’s public key can be explained as follows. For a message
m, cipherptext c = mG’ ⊕ e, G’ = SGP, where G is a kxn generator matrix of linear code C[n,k], S is a kxk a nonsingular matrix, P is a nxn permutation matrix, and e is a binary vector of length n with Hamming weight t. G’ is public, and G, S, and P are secret. Conversely, the decryption processes of ciphertext c to obtain the plaintext m are : (1) compute c1 = cP-1, (2) m1 = c1 ⊕ e1, (3) retrieve m0 from m0G = m1, (4) compute m
= m0S-1 (Stinson, 1995:196). Meanwhile, Wu-Dawson’s public key can be summarized
as in Table 1 below.
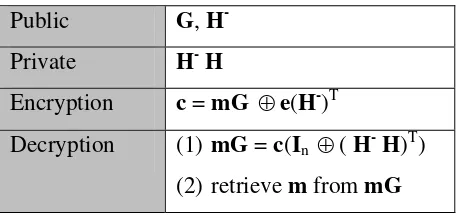
Table 1. Wu-Dawson’s public key cryptosystem Public G, H
-Private H-H
Encryption c = mG ⊕e(H-)T
Decryption (1) mG = c(In ⊕( H-H)T)
(2) retrieve m from mG
where c is a ciphertext of a message m, G is a kxn generator matrix of linear code C[n,k],
H is (n-k)xn parity check of matrix, H- is nx(n-k) generalized reinverses of matrix H. (Wu and Dawson, 1998:323).
Permutation Matrix and Left / Right Inverse of Matrices
For a nonsingular and square matrix A, the inverse of A is A-1, so that
AA-1 = A-1A = I (1)
The matrix A-1 can be found by (i) adjoint matrix, (ii) elementary row operation, and/or (iii) elementary column operation.
Definition 1. Permutation matrix is a matrix which is by permute i-th row and j-th row of the identity matrix I.
3 (interchange of row), in this case interchange of i-th row and j-th row from identity matrix I. So, permutation matrix is also elementary matrix. If Pij is permutation matrix by
permute i-th and j-th row of I, PijPij = I or:
Pij2 = I (2)
From relation (2), it can be concluded that inverse of permutation matrix is also permutation matrix.
Lemma 1. For nxn identitity matrix I, the number of permutation matrix is n!. Proof :
Because matrix I has dimension n, the number of permutation is n !.. So, the number of permutation matrices is n!.
Moreover, if A is non-square, it is possible to find a left inverse or a right inverse of A.
Definition 2. For a matrix A, if LA = I but AL ≠ I, with more than one L, the matrices L are called left inverse of A. Conversely, for a matrix A, if AR = I but
RA≠I, with more than one R, the matrices R are called right inverse of A.
Furthermore, AL denotes the left inverse of A, and AR denoted the right inverse of A. So, if left inverse exist, ALA = I, meanwhile if right inverse exist, A AR = I.
Theorem 1. An mxn matrix A has left inverses only if m≥n and rank of A is n.
Theorem 2. An mxn matrix A has right inverses only if m≤n and rank of A is m. Proof: we prove that a contradictory result can be obtained as m > n and A having right
inverse. For m > n, let A = ⎟⎟
⎠ ⎞ ⎜⎜
⎝ ⎛
−nxn m nxn Y X ) (
, and suppose nxm matrix AR is right inverse of A,
AR=
(
P
nxnQ
nx(m−n))
, then :AAR =
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
−nxn m nxn
Y
X
) ((
P
nxnQ
nx(m−n))
= ⎟⎟⎠ ⎞ ⎜⎜ ⎝ ⎛ YQ YP XQ XP
= Im =
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
−) (0
0
n m nI
I
4
YP = YX-1 = 0
YX-1X = 0 (multiple by X)
Y = 0
and YQ = 0Q = 0≠I. It is contradictory. Therefore, if m > n, an mxn matrix A has no right inverse. Meanwhile, because A has rank m, there exists an mxm non-singular
submatrix X of A. Let A = (Xmxm Ymx(n-m)), and suppose AR =
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
− −
xm m n
mxm
X
) (
1
0
is right inverseof A, then AAR = Im.
Theorem 3. A matrix A has right inverse if and only if AT has left inverse. Proof :
• Suppose an mxn matrix A has right inverse, by Theorem 2, matrix A has rank m and
m ≤n. Hence, AT has dimension nxm, rank m, and n≥m. By Theorem 1, AT has left inverse.
• Suppose an nxmAT has left inverse, by Theorem 1, AT has rank m and n≥m. Hence,
(AT)T = A has dimension mxn, rank m, and m ≤ n. By Theorem 2, A has right inverse.
Theorem 4. A matrix A has left inverse if and only if AT has right inverse.
Theorem 5. If a matrix A has right inverse, (AR)T is left inverse of AT. Proof :
Suppose A has right inverse AR,
A AR = I
(A AR)T = IT
(AR)TAT = I
Its mean (AR)T is left inverse of AT.
5 From Theorem 5 and Theorem 6, if left inverse or right inverse exist,
(AR)T = (AT)L (3) (AL)T = (AT)R (4)
Constructing of left inverse. If an nxm matrix A has rank m and n ≥ m, there is nxn
nonsingular matrix P so that PA =
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
−mxm n mxm
O
I
) (, or :
A = P-1
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
−mxm n mxm
O
I
) ( (5)where P is product of elementary row matrix.
Theorem 7. A left inverse of A in form (5) is:
AL = (Im Smx(n-m)) P (6)
which is an arbitrary S. Proof :
ALA = (Im Smx(n-m)) P P-1
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
−mxm n mxm
O
I
) (= Im.
The Theorem 7 above gives way to construct a left inverse of A. Because an mx(n-m) matrix S is an arbitrary, in the field of real number R, the number of left inverses of A is infinite. In the field of computer science, discussion in the field R is meaningless. Therefore, a discussion will be meaningfull if in the field Z2 = {0, 1}. It can be show that
in the field Z2, the number of left inverses is finite.
Lemma 2. In the field Z2, a number of left inverses of A in the form (6) are 2mx(n-m).
Proof:
The number of different left inverses of A is the number of different choices of S which is totally 2mx(n-m).
Constructing of right inverse. An mxn matrix A which has rank m, there exists an nxn
nonsingular matrix Q, so that AQ = (Im Omx(n-m)) or :
A = (Im Omx(n-m)) Q-1 (7)
6
Theorem 8. In form (7), right inverses of A is
AR = Q
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
−mxm n
m
W
I
) (
(8)
where W is an arbitrary. Proof :
A AR = (Im Omx(n-m)) Q-1Q
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
−mxm n
m
W
I
) (
= Im.
The Theorem 8 above gives way to construct right inverse of A. Every different choice of
W, gives different rigt inverse.
Lemma 3. In the field Z2, a number of right inverses of A in the form (8) are 2(n-m)xm.
Proof :
The number of different right inverses of A is the number of different choices of W
which is totally 2(n-m)xm.
Design of Public Key Cryptosystem
An arbitrary linear code C[n,k] can be treated as a vector subspace of Vn(Z2). A
Generator matrix for C is a kxn matrix G that has rank k. For message m, c = mG is codeword, see for detail on error correcting code (Vanstone and Oorschot, 1989; MacWilliams and Sloane, 1993). By reconstruction of generator matrix G, that is G = (PR S-1)T, the ciphertext of plaintext m with length k is c = mG. S is a kxk permutation matrix, and P is a kxn matrix with rank k. Matrix G is public to encrypt message m. The decryption to obtain message m can be performed as follows :
compute c(SP)T = mG(SP)T = m (PRS-1)T (SP)T = m (S-1)T (PR)TPTST = m.
The above description can be summarized as in Table 2 below. Table 2. Our public key cryptosystem
Public G = (PRS-1)T Private R = SP
Encryption c = mG
7 A key generation of the public key cryptosystem can be performed according to the following steps : (1) select G1 = [Ik A] with an arbitrary kx(n-k) matrix A, (2) select an arbitrary kxk permutation matrix S, (3) P = SG1 , (4) find a right inverse of P, i.e. PR, (5) find inverse of S, i.e. S-1, (6) G = (PRS-1)T, (7) R = SP. Thus, R is a private key and
G is a public key.
Properties of the Cryptosystem
1. Key space.
The public key space is size of G, which are kn bits. Meanwhile, the private key space is size of R, which are also kn bits. So, the total of key space needs 2kn bits. 2. Encryption and decryption complexity.
We assume that both binary addition and multiplication are bit operation. For encryption, computation c = mG needs (k + k – 1)n = (2k –1) n = 2kn – n. Encryption complexity is the order of O(kn). For decryption, ciphertext c has length n, so that computation m = cRT needs (n + n – 1)k = (2n –1)k = 2kn – k. Decryption complexity is the order of O(kn). Therefore, both encryption and decryption process needs 2kn –
n + 2kn – k = 4kn – k – n . So, encryption and decryption complexity are also the order of O(kn).
3. message expansion.
A cryptosystem is said to have message expansion if the length of ciphertext blocks is longer than the length of the plaintext blocks. If r denotes the proportion of the length of the ciphertext blocks from the length of plaintext blocks, in our cryptosystem r = n/k.
Table 3. Comparison of cryptosystem Cryptosystem Private key
space
Public key space
Complexity of encryption and decryption
Ratio of message
expansion Our cryptosystem kn kn 4kn – n – k Æ O(kn) n/k
McEliece k2 + kn + n2 kn 2kn+(2n-1)n+(2k-1)k Æ O(n2) n/k
8 From Table 3 above, it can be concluded that the cryptosystem are:
(1) efficient in key space, i.e its total 2kn bits. (2) low complexity, i.e the order of O(kn)
(3) have a message expansion. This is a characteristic of cryptosystem based on coding theory.
Therefore the cryptosystem is efficient enough and faster in encryption and decryption than McEliece’s and Wu-Dawson’s cryptosystem.
Risk Analysis
The risk analysis is based on security of ciphertext c, which is by possibly attacks by the intruder. If the intruder has known a private key R, the ciphertext c can be broken. By computation m = cRT, the intruder will obtain message m. The intruder will perhaps find out of the private key R by : (1) find a matrix that generates R, i.e. S and P, (2) find a right inverse of G, and (3) try an arbitrary matrix R.
(1) Attack 1: find a matrix that generates the private key R. By procedure of key generation, P = SG1, where G1 = [IkA]. This means that matrix P depends on matrix S and A. As a consequence, finding a matrix that generates matrix R means looking for a permutation matrix Skxk and an arbitrary matrix Akx(n-k). According Lemma 1, in
the field of Z2 = {0,1}, the number of permutation matrix S is n!. Meanwhile, the
number of possibilities of matrix A is 2k(n-k). So, the number of ways to findout the private key R is : n! 2k(n-k). It is very large to get one of the private keys R.
(2) Attack 2 : find a right inverse of G. Because of c = mG, the message m will be found
if the intruder got a right inverse of G. Therefore, if GR is right inverse of G, by computation cGR = mGGR = mIk = m. Matrix G has a size kxn and rank k, by lemma
3, the number of right inverses of G is 2(n-k)xk. Matrix GRthatsatisfies the condition is
only one. So, that the probability of the intruder will succeed is only (n k)xk
2
1
− . It is
9 (3) Attack 3: try an arbitrary matrixR. Matrix R has size kxn, the number of element of
matrix R is kn. In the field Z2 = {0, 1}, the number of possibilities of different matrix R is 2kn. It is large enough to get one of the private keys R.
From above discussion, it can be concluded that if k and n are large, the ciphertext c is still secure. We would like to point out that by removing error pattern e in our cryptosystem, we hope our cryptosystem is still secure and efficient, because error patterns e, both in McElice’s and Wu-Dawson’s cryptosystem, became a weak key of the cryptosystem (Wu and Dawson, 1998).
Conclusion
By the right inverses of matrices, a public key cryptosysem which has a good performance is proposed. It is shown that the theory of matrices became a potential tool in cryptographic research. The complexity of the matrix operation is low. Hence, it can work very quickly. It is anticipated that the theory of matrices over finite field may have more cryptographic applications.
We would like to remind that although we have found a method to find out left inverses in form (6) and right inverses in form (8), an efficient algorithm to find right inverses needs further investigation. Further research about authentication scheme of the cryptosystem is still needed.
References
MacWilliams, F.J., and Sloane, N.J.A., 1993, The Theory of Error Correcting Codes, Eight Impression, Amsterdam : North-Holland Mathematical Library.
Stinson, D. R., 1995, Cryptography Theory and Practice, Florida : CRC Press LLC.
Vanstone, S.A., and Oorscot, V.P.C., 1989, An Introduction to Error Correcting Code with Applications, Kluwer Academic Publisher.
Wu, C.K., and Dawson, E., 1998, “Generalised Inverses in Public Key Cryptosystem Design” in IEE Proceedings Computer Digit. Tech. Vol. 145 No. 5, September 1998, Pp:321-326.