1 BAB I PENDAHULUAN A. Latar Belakang
Perkembangan investasi di Indonesia saat ini semakin pesat. Semakin banyak masyarakat yang tertarik untuk melakukan investasi. Instrumen dalam melakukan kegiatan berinvestasi yang menguntungkan banyak ditawarkan, instrumen investasi yang ada di Indonesia antara lain adalah properti, deposito, saham, emas, dan obligasi. Saham merupakan salah satu instrumen investasi yang paling banyak diminati masyarakat, hal ini dibuktikan dengan naiknya nilai Indeks Harga Saham Gabungan (IHSG) dari tahun ke tahun.
Investasi adalah penanaman modal untuk satu atau lebih sekuritas yang dimiliki dan biasanya berjangka waktu lama dengan harapan mendapatkan keuntungan di masa-masa yang akan datang (Sunariyah, 2003). Menurut Abdul Halim (2005) Investasi pada hakikatnya merupakan penempatan sejumlah dana pada saat ini dengan harapan memperoleh keuntungan di masa mendatang.
2
pemilihan portofolio dari sekian banyak sekuritas untuk memaksimalkan return yang diharapkan pada tingkat risiko tertentu yang bersedia ditanggung investor. Dengan kata lain, teori portofolio membahas bagaimana cara untuk membentuk portofolio yang optimal (Eduardus Tandelilin, 2001).
Model Black Litterman merupakan salah satu model untuk membentuk portofolio optimal. Model Black Litterman muncul pada tahun 90an oleh Robert Litterman dan Fisher Black dengan mengkombinasikan dua sumber informasi yaitu return ekuilibrium Capital Assets Pricing Model (CAPM) dan prediksi return yang diberikan oleh investor pada masing-masing saham atau hanya pada beberapa saham. Menurut Retno Subekti (2008) model Black Litterman merupakan salah satu model optimasi portofolio yang menghasilkan kinerja lebih baik dan menguntungkan bagi seorang investor karena keterlibatan opini investor dalam portofolio yang dibentuknya tidak terabaikan.
3
(Jogiyanto Hartono, 2014), sehingga strategi ini cocok untuk investor yang cenderung tidak menyukai risiko, atau biasa disebut dengan investor tipe konservatif.
Beberapa penelitian telah dilakukan mengenai model Black Litterman dan pengembangannya. Beberapa di antaranya adalah penelitian yang dilakukan oleh Vita Susilo Dewi (2014) yang membahas mengenai aplikasi neural network algoritma backpropagation pada pembentukan views untuk model Black Litterman dengan implementasi pada saham-saham yang tergabung dalam indeks saham LQ-45. Penelitian tentang pengaruh ukuran data return saham terhadap kinerja model Black Litterman pada saham syariah JII (Jakarta Islamic Index) dianalisis oleh Agnes Dwi Wulandari (2015). Penelitian tersebut menggunakan beberapa ukuran data return saham yaitu 60, 120 dan 240 data return saham. Diperoleh kinerja yang paling baik yaitu pada ukuran data return saham yang tidak terlalu banyak yaitu 60 saham.
4
adalah data bulanan pada pasar modal United State (U.S) selama periode Januari 1993-Desember 2011. Hasil dari optimasi portofolio tersebut kemudian diukur kinerjanya dengan beberapa ukuran yaitu Sharpe ratio, Omega Ratio, Maximum Drawdown (MDD), dan Portofolio Turnover (PT). Black Litterman dengan minimum variance menghasilkan kinerja lebih baik dengan nilai Sharpe ratio dan nilai omega ratio lebih tinggi serta memiliki nilai portofolio turnover lebih rendah.
Berdasarkan penelitian yang dilakukan oleh Bessler, dkk penulis tertarik untuk membahas dua pengembangan portofolio model Black Litterman, yaitu Black Litterman dengan diversifikasi naive 1/N dan Black Litterman dengan minimum variance sekaligus mengukur kedua model portofolio tersebut menggunakan Sharpe ratio dengan implementasi pada pasar saham Indonesia, khususnya pada saham-saham
yang tergabung dalam indeks saham syariah JII (Jakarta Islamic Index). B. Batasan Masalah
5 C. Rumusan Masalah
Berdasarkan uraian latar belakang, maka dapat dirumuskan permasalahan sebagai berikut:
1. Bagaimana kinerja model Black Litterman dengan strategi diversifikasi naive 1/N (BL-1/N) pada portofolio saham syariah JII ?
2. Bagaimana kinerja model Black Litterman dengan minimum variance (BL-MinVar) pada portofolio saham syariah JII ?
3. Bagaimana perbandingan kinerja kedua model portofolio yang digunakan ? D. Tujuan Penulisan
Sesuai dengan rumusan masalah, maka tujuan dari penulisan skripsi ini adalah 1. Menjelaskan kinerja model Black Litterman dengan strategi diversifikasi naive
1/N (BL-1/N) pada portofolio saham syariah JII.
2. Menjelaskan kinerja model Black Litterman dengan minimum variance (BL-MinVar) pada portofolio saham syariah JII.
6 E. Manfaat Penulisan
Manfaat dari penulisan skripsi ini adalah sebagai berikut: 1. Bagi penulis
Menambah pengetahuan mengenai portofolio menggunakan model Black Litterman dengan strategi diversifikasi naive 1/N (BL-1/N) serta model Black Litterman dengan minimum variance (BL-MinVar).
2. Bagi Jurusan Pendidikan Matematika
Menambah referensi tentang penerapan ilmu matematika khususnya portofolio dan keuangan yang dapat dijadikan dasar untuk penelitian selanjutnya.
3. Bagi Investor
7 BAB II
LANDASAN TEORI
Pada bab ini dibahas tentang materi dasar yang digunakan untuk mendukung pembahasan pada bab-bab berikutnya, yaitu varians dan kovarians, distribusi normal, matriks, investasi, portofolio, saham, Jakarta Islamic Index (JII), metode Lagrange, model Mean Variance markowitz, Capital Assets Pricing Model (CAPM), metode Diversifikasi Naive 1/N, model Minimum Variance, dan model Black Litterman. A. Varians dan Kovarians
Definisi 2. 4 (Murray R. Spiegel, 2004)
Varians dari variabel random didefinisikan dengan: ]
) [(
)
(X E X 2
Var . (2. 1)
Notasi varians yang lain adalah 2,x2, atau � . Standar deviasi dari
didefinisikan sebagai akar positif dari varians yaitu
x
Var
(
X
)
. Rumus varians pada (2.1) dapat dinyatakan dalam persamaan berikut:� =∑��− �− ̅
− (untuk suatu populasi) (2. 2)
=∑��− �− ̅
�− (untuk suatu sampel) (2. 3)
Definisi 2. 4 (Murray R. Spiegel, dkk, 2004)
Kovarians adalah suatu ukuran yang menyatakan varians bersama dari dua variabel random. Kovarians dari pasangan variabel random X dan Y didefinisikan sebagai:
8
Jika X dan Y adalah variabel random dan dan konstan, maka berlaku: 1. Cov(aX,bY)abCov(X,Y).
1. Cov(X a,Y b)Cov(X,Y). 2. Cov(X,aX b)aVar(X).
3. Cov(X,Y)0, jika X dan Y independen. B. Distribusi Normal
Definisi Distribusi Normal
Definisi 2. 6 (Bain & Engelhardt, 1992)
Variabel random X dikatakan berdistribusi normal yang dinotasikan X~N(µ, σ2)
dengan mean µ dan varians σ2 mempunyai fungsi densitas probabilitas yaitu: 2
/ } / ) {( 2
2 1 ) , ;
(
xe x
f
(2. 5)
untuk –∞ < x < ∞, dengan –∞ < µ< ∞ dan 0 < σ< ∞. Uji Normalitas
9
investor. Uji normalitas return saham dapat dilakukan dengan uji Kolomogorov-Smirnov sebagai berikut:
a. Hipotesis:
H0: data return saham diasumsikan berdistribusi normal.
H1: data return saham tidak dapat diasumsikan berdistribusi normal.
b. Tingkat signifikansi α. c. Statistik uji:
Kolmogornov-Smirnov (KS)SupX F*(X)S(X) . F*(X) adalah distribusi kumulatif data sampel.
S(X) adalah distribusi kumulatif yang berdistribusi normal.
d. Kriteria uji:
H0ditolak jika KS>KSTabel atau p-value KS < α. e. Perhitungan.
f. Kesimpulan. C. Matriks
Definisi 2. 8 (Anton, 2010)
10 A m n m m n in a a a a a a a a a 2 1 2 22 21 12 11 n m
. (2. 6)
Perkalian matriks
Definisi 2. 9 (Anton, 2010)
Jika A adalah suatu matriks dan c adalah skalar, maka hasil kali (product) cA adalah matriks yang diperoleh dengan mengalikan masing-masing entri dari A oleh c. Jika A
] [aij
, maka perkalian matriks ini dinotasikan sebagai c(A)ij (cA)ij[caij].
Jika A[aij]sebuah matriks berukuran m × r dan B[bij] sebuah matriks berukuran r × n, maka hasil kali A dengan B yaitu C = AB adalah matriks yang entrinya didefinisikan dengan
rl il lj
m n a b
C 1 (2. 7)
dengan matriks � berukuran m × n. Contoh: A , 2 1 4 1 2 1
B
1 1 2
Maka, AB
11 Transpose Matriks
Definisi 2. 10 (Anton, 2010)
Jika A adalah sebarang matriks m × r, maka transpose A dinyatakan oleh A' yang merupakan matriks berukuran r ×m dengan mengubah baris dari A menjadi kolom pada A'. Transpose matriks A dapat dinyatakan dengan:
(A)ij(A') ji.
(2. 8)
Contoh:
A
2 1 4
1 2 1
maka, A'
2 1
1 2
4 1
.
Minor dan Kofaktor Matriks Definisi 2. 11 (Anton, 2010)
Jika A merupakan matriks berukuran n × n, maka minor dari entri aijdinotasikan dengan Mijyaitu determinan dari submatriks A yang didapat dengan menghapus baris
ke- dan kolom ke- . Nilai ij j i
M
1
)
(
dinotasikan dengan cij disebut kofaktor dari entri aij. Sehingga matriks kofaktor dari A dapat dinyatakan dengan:
nn n
n
n n
c c
c
c c
c
c c
c
2 1
2 22
21
1 12
11
12 Contoh:
A
2 4 5
3 4 2
0 1 3
maka, minor dari entri a11 yaitu:
4 12 8 4 . 3 ) 2 ).( 4 ( 2 4
3 4
11
M ,
kofaktor dari entri a11 yaitu:
4 ) 4 .( 1 )
1
( 11
1 1
11
M
c .
Determinan Matriks
Definisi 2. 12 (Anton, 2010)
Determinan matriks A berukuran n × n dapat dihitung dengan mengalikan entri pada suatu baris ke-i atau kolom ke-j dengan masing-masing kofaktor dan menjumlahkan hasil perkalian tersebut. Determinan matriks A dinyatakan sebagai berikut:
|A|
a
1j.
c
1j
a
2j.
c
2j
a
nj.
c
nj atau|A|
a
i1.
c
i1
a
i2.
c
i2
a
in.
c
in. Contoh:�
2 4 5
3 4 2
13 maka, |�| 2 4 5 3 4 2 0 1 3 3 4 0 1 5 2 4 0 1 ) 2 ( 2 4 3 4 3 )] 4 .( 0 3 . 1 .[ 5 ] 4 . 0 ) 2 .( 1 .[ 2 ] 4 . 3 ) 2 ).( 4 .[(
3
3 . 5 ) 2 .( 2 ) 4 .(
3
15 4 12 1 . Invers Matriks
Definisi 2. 13 (Anton, 2010)
Jika A matriks persegi dan jika terdapat suatu matriks B dengan ukuran yang sama sedemikian sehingga AB=BA=I dengan I merupakan matriks identitas, maka A invertible (dapat dibalik) dan B adalah invers dari A. Invers dari A dinotasikan dengan A1, sehingga AA1I dan A1AI
Jika matriks A berukuran n × n maka invers adalah: �− =
|�| [adj(A)]
(2. 10) dengan,
14 Contoh: A 2 2 6 1 1 2 0 1 3 , ��� � 1 0 2 3 6 2 1 2 0
det � 3.1.2 1.1.6 0.2.2 6.1.0 2.1.3 2.2.1 2 2 6 1 2 1 3 2 2 6 1 1 2 0 1 3 maka, A A 1 1
[adj(A)]
15 D. Analisis Multivariat
Definisi 2. 14 (Johnson & Wichern, 2007)
Analisis statistik multivariat merupakan metode statistik untuk menganalisis hubungan antara lebih dari dua variabel secara bersamaan. Data sampel analisis multivariat secara umum dapat digambarkan dalam bentuk matriks dengan n objek dalam p variabel sebagai berikut:
Variabel 1 Variabel 2 Variabel k Variabel p Objek 1
11
x
x
12 x
1k x
1pObjek 2
21
x
x
22 x
2k x
2p
Objek j
1
j
x
x
j2 x
jk x
jp
Objek n
1
n
x
x
n2 x
nk x
npatau dapat ditulis dalam bentuk matriks X dengan n baris dan p kolom berikut:
16 Multivariat Berdistribusi Normal
Definisi 2. 15 (Johnson & Wichern, 2007)
Fungsi distribusi multivariat normal merupakan perluasan dari fungsi distribusi univariat normal untuk ≥ . Jika �~ � , � adalah p-variat multivariat normal dengan rata-rata µ dan varians-kovarians matriks �, dimana:
pp p p p p p p X X X 1 1 2 22 21 1 12 11 2 1 2 1 Σ , μ , X
Maka fungsi densitas multivariat normal adalah:
2 2 1 2 p 1 e 2 1
f (X μ)' (X μ)/
/ / | Σ | ) ( ) X ( (2. 11) dengan Xi,i1,2,...,p.
Vektor random dan matriks random Definisi 2. 16 (Johnson & Wichern, 2007)
17 Mean dan Kovarians Vektor Random Definisi 2. 17 (Johnson & Wichern, 2007)
Dimisalkan X adalah variabel random dengan mean μE(X)dan matriks kovarians �. Mean vektor random X dengan ordo × dapat dinyatakan dengan:
μ ) ( ) ( ) ( ) X ( E p 2 1 p 2 1 X E X E X E . (2. 12) Sedangkan kovarians vektor random X dengan ordo × adalah
μ)' μ)(X
E(X
2 2 ( 1 1 2 2 )
1 1 p p p p X X X X X X
E
2 2 2 1 1 2 2 2 2 2 1 1 2 2 1 1 2 2 1 1 2 1 1 ) ( ) )( ( ) )( ( ) )( ( ) ( ) )( ( ) )( ( ) )( ( ) ( p p p p p p p p p p X X X X X X X X X X X X X X X E 2 2 2 1 1 2 2 2 2 2 1 1 2 2 1 1 2 2 1 1 2 1 1 ) ( ) )( ( ) )( ( ) )( ( ) ( ) )( ( ) )( ( ) )( ( ) ( p p p p p p p p p p X E X X E X X E X X E X E X X E X X E X X E X E .
Atau dapat dinyatakan
18
Dengan
ij: kovarians dari Xi dan Xj,i1,2,p dan j1,2,p.Kovarians untuk sampel dinyatakan
pp p
p
p p
s s
s
s s
s
s s
s
2 1
2 22
21
1 12
11
S .
(2. 14) Dengan
s
ij: kovarians dariX
i
dan Xj,i 1,2,p dan j1,2,p E. Investasi
Menurut Abdul Halim (2005) Investasi pada hakikatnya merupakan penempatan sejumlah dana pada saat ini dengan harapan memperoleh keuntungan di masa mendatang. Proses investasi menunjukkan bagaimana seharusnya seorang investor membuat keputusan investasi, yaitu sekuritas apa yang akan dipilih, seberapa banyak investasi tersebut, dan kapan investasi tesebut akan dilakukan (Suad Husnan, 1998). Untuk itu diperlukan tahapan sebagai berikut:
1. Penentuan tujuan investasi
Tahap pertama dalam proses keputusan investasi adalah menentukan tujuan investasi yang akan dilakukan. Tujuan investasi untuk masing-masing investor bisa berbeda tergantung pada investor yang membuat keputusan tersebut.
2. Penentuan kebijakan investasi
19 3. Pemilihan strategi portofolio
Strategi portofolio yang bisa dipilih yaitu strategi portofolio aktif dan strategi portofolio pasif. Strategi portofolio aktif meliputi kegiatan penggunaan informasi yang tersedia untuk mencari kombinasi portofolio yang lebih baik. Strategi portofolio pasif meliputi aktivitas investasi pada portofolio yang seiring dengan kinerja indeks pasar. 4. Pemilihan sekuritas
Pemilihan sekuritas yang dilakukan untuk membentuk suatu portofolio. Tahap ini memerlukan pengevaluasian setiap sekuritas yang ingin dimasukkan dalam portofolio untuk mencari kombinasi portofolio yang efisien oleh perusahaan. Apabila kinerja keuangan perusahaan cukup bagus dan sudah mampu membayar kewajiban keuangan lainnya.
F. Portofolio
Pengertian Portofolio
Menurut Jogiyanto Hartono (2014) portofolio adalah suatu kumpulan sekuritas keuangan dalam suatu unit yang dipegang atau dibuat oleh seorang investor, perusahaan investasi, atau instansi keuangan. Tujuan dari pembentukan portofolio adalah untuk mendiversifikasi dana yang dimiliki investor pada beberapa sekuritas dengan harapan dapat memaksimalkan return dengan tingkat risiko yang minimal.
Return Portofolio
Return adalah hasil yang diperoleh dari suatu investasi. Hubungan positif antara
20
yang artinya semakin besar risiko yang diambil, maka semakin besar pula return yang diperoleh. Hal ini dimaksudkan bahwa harus ada pertambahan return sebagai kompensasi dari pertambahan risiko yang ditanggung oleh investor.
Return dapat berupa realized return yang sudah terjadi atau expected return yang belum terjadi dan diharapkan akan diperoleh pada masa mendatang (Jogiyanto Hartono, 2003).
Realized return portofolio dapat dirumuskan:
� = ∑�= . (2. 15)
keterangan:
Rp: realized return portofolio,
i
w : bobot dana investor pada sekuritas ke-i,
i
R : realized return dari sekuritas ke-i,
: banyaknya sekuritas.
Return suatu sekuritas untuk dapat dihitung menggunakan rumus:
1 1 1
1
t t t
t t t
P P P P
P
R . (2. 16)
keterangan:
21
Expected return portofolio merupakan rata-rata tertimbang dari expected return
masing-masing sekuritas dalam portofolio. Expected return portofolio dapat dirumuskan sebagai berikut:
� = ∑�= . . (2. 17)
keterangan: ) (Rp
E : expected return dari portofolio,
i
w : bobot dana investor pada sekuritas ke-i,
) (Ri
E : expected return dari sekuritas ke-i,
: banyaknya sekuritas.
Nilai expected return pada persamaan (2.17) secara matematis dapat dibentuk dalam matriks adalah sebagai berikut:
E R
w
E
R
wn
E
Rn
wRp
E( ) 1 1 2 2
R E w'
n n
R E
R E
R E
w w
w
2
1 2
1 .
(2. 18) keterangan:
w: matriks bobot tiap sekuritas dalam portofolio,
� � : matriks expected return tiap sekuritas dalam portofolio. Risiko Portofolio
22
dengan besarnya varians dari nilai return saham-saham yang ada di dalam portofolio (Jogiyanto Hartono, 2003). Jika semakin besar nilai varians maka risiko yang ditanggung semakin tinggi. Banyaknya sekuritas dalam suatu portofolio dapat mempengaruhi nilai varians dari risiko. Untuk membentuk suatu portofolio diperlukan minimal dua sekuritas. Varians dengan dua sekuritas adalah sebagai berikut (Jogiyanto Hartono, 2003):
2P
Rp
Var
= [ �− ( �)]
22 2 1 1 2 2 1
1
R
w
R
E
w
R
w
R
w
E
22 2 1 1 2 2 1
1
R
w
R
E
w
R
E
w
R
w
E
22 2 1 1 2 2 1
1
R
w
R
w
E
R
w
E
R
w
E
22 2 2 1 1
1
R
E
R
w
R
E
R
w
E
2
2 2 2 2 2 2 1 1 2 1 2 1 1 2
1
R
E
R
2
w
w
R
E
R
R
E
R
w
R
E
R
w
E
2
2 2 2 2 2 2 1 1 2 1 2 1 1 2
1
E
R
E
R
2
w
w
E
R
E
R
R
E
R
w
E
R
E
R
w
2 2 2 2 12 2 1 2 1 21
2
w
w
w
w
. (2. 19)Selanjutnya varians dengan n sekuritas dapat dinyatakan sebagai berikut:
n n
n n n n
P w w w w1w2 12 w1w3 13 w 1w 1
2 2 2 2 2 2 2 1 2 1 2 2 2
2
ni
n
j i j ij n
i 1wi i 1 1ww 2
2
2
.
23
Persamaan (2. 20) dapat dinyatakan dalam bentuk matriks yaitu:
w' Σ ww w w
w w
w
n nn n
n
n n
n
p
2
1
2 1
2 22
21
1 12
11 2
1 2
(2. 21)
keterangan:
Σ: matriks varians kovarians n x n, w: matriks bobot tiap sekuritas n x 1.
Risiko portofolio dihitung menggunakan rumus standar deviasi yang merupakan akar positif dari varians sebagai berikut:
2
p
p
(2. 22) Risiko portofolio dapat dihitung dengan mensubstitusikan persamaan (2.21) pada rumus standar deviasi (2.22) sebagai berikut:
w
Σ
w'
p
(2. 23)
keterangan:
��: standar deviasi portofolio. G. Saham
24
kertas tersebut) untuk memperoleh bagian dari prospek atau kekayaan organisasi yang menerbitkan sekuritas tersebut dan berbagai kondisi yang memungkinkan pemodal tersebut menjalankan haknya. Saham merupakan salah satu alternatif dari beberapa instrumen lainnya yang dapat dipilih untuk berinvestasi.
Pada dasarnya saham dapat digunakan untuk mencapai tiga tujuan investasi utama sebagaimana yang dikemukakan oleh Kertonegoro Senatnoe (2000) yaitu:
1. Sebagai gudang nilai, berarti investor mengutamakan keamanan prinsipal, sehingga akan dicari saham blue chips dan saham non-spekulatif lainnya.
2. Untuk pemupukan modal, berarti investor mengutamakan investasi jangka panjang, sehingga para investor akan mencari saham pertumbuhan untuk memperoleh capital gain atau saham sumber penghasilan untuk mendapat dividen.
3. Sebagai sumber penghasilan, berarti investor mengandalkan pada penerimaan dividen sehingga para investor akan mencari saham yang bermutu baik yaitu saham
yang mempunyai tingkat pengembalian yang tinggi dan konsisten dalam membayar dividen.
H. Jakarta Islamic Index (JII)
25
mengembangkan pasar modal syariah. JII diperbarui setiap 6 bulan sekali, yaitu pada awal bulan Januari dan Juli.
Jakarta Islamic Index (JII) merupakan indeks yang berisi 30 saham perusahaan terdapat di lampiran 5 Halaman 96 dengan kriteria investasi yang telah dipenuhi berdasarkan syariah Islam (metode keuangan dalam Islam), dengan prosedur berikut ini:
1. Memilih kumpulan saham dengan jenis usaha utama yang tidak bertentangan dengan prinsip syariah dan sudah tercatat paling tidak 3 bulan terakhir, kecuali saham yang termasuk dalam 10 kapitalisasi terbesar.
2. Mempunyai rasio utang terhadap sekuritas tidak lebih dari 90% di laporan keuangan tahunan atau tengah tahun.
3. Dari yang masuk kriteria nomer 1 dan 2, dipilih 60 saham dengan rata-rata kapitalisasi pasar terbesar selama satu tahun terakhir. Kemudian dipilih 30 saham dengan urutan tingkat likuiditas rata-rata nilai perdagangan reguler selama satu tahun terakhir.
4. Kemudian dipilih 30 saham dengan urutan tingkat likuiditas rata-rata nilai perdagangan regular selama satu tahun terakhir.
I. Pengali Lagrange (Lagrange Multiplier)
26
tertentu. Misalkan akan dicari harga optimasi suatu fungsi tujuan , dengan kendala-kendala tertentu yang harus dipenuhi yaitu , = .
Cara yang dilakukan adalah dengan menyusun fungsi bantu yang disebut fungsi Lagrange sebagai berikut :
, = , + , (2. 24)
Dengan syarat : ��
� = dan ��
� = (2. 25)
Dalam hal ini parameter λ yang bebas dari dan dinamakan Lagrange Multiplier atau pengali Lagrange.
Jika pengali Lagrange melibatkan lebih dari satu kendala, maka penggunaan parameter yang dipilih dapat ditambahkan menjadi λ, µ atau parameter yang lain.
Misalnya fungsi yang akan dicari maksimum atau minimum , , dengan kendala , , = dan kendala ℎ , , = , maka fungsi Lagrangenya adalah:
, , = , , + , , + ℎ , , (2. 26)
Syarat adanya harga maksimum atau minimum adalah: ��
� = , ��
� = , dan ��
� = (2. 27)
Permasalahan di atas dapat diperluas untuk fungsi yang memiliki n variabel , , … , � dengan k kendala.
Misal fungsi yang akan dicari maksimum atau minimum adalah: , , … , �
27
� , , … , � = , � , , … , � = , …, � , , … , � = Maka fungsi Lagrangenya adalah:
, , … , � = + � + � + + � (2. 28)
Dengan syarat: ��
� = , ��
� = , … , �� � � =
Dalam hal ini parameter , , … , adalah pengali Lagrange. J. Model Mean Variance Markowitz
Harry Markowitz memperkenalkan model tentang pemilihan portofolio optimal pada tahun 1952 yang dikenal dengan model mean variance Markowitz (Markowitz, 1952). Menurut Eduardus Tandelilin (2001) Model mean variance Markowitz didasari oleh tiga asumsi yaitu:
1. Waktu yang digunakan hanya satu periode 2. Tidak ada biaya transaksi
3. Preferensi investor hanya berdasarkan pada return yang diharapkan dan risiko dari portofolio.
Berdasarkan asumsi ketiga, maka portofolio optimal menggunakan model mean variance Markowitz dapat dilakukan dengan mengoptimalkan portofolio efisien
dengan preferensi investor yang dirumuskan dalam bentuk sebagai berikut: a. Meminimumkan risiko untuk tingkat return tertentu:
28
( �) = �′ dengan � ( �) = �′ �� (2. 30) Bobot untuk masing-masing sekuritas dapat dinyatakan dengan �′= [ … �] dan merupakan matriks expected return masing-masing sekuritas × .
Optimasi untuk memaksimumkan return dengan tingkat risiko tertentu dapat diselesaikan dengan menggunakan fungsi Lagrange L dan faktor pengali Lagrange λ sebagai berikut:
L
w
'μ
λ
(
w
'Σw
)
(2. 31) Turunan parsial terhadap � adalah sebagai berikut:w
Σw
w'
μ
w'
( λ( )
w L
Σw μ2λ
(2. 32)
Optimasi harus memenuhi syarat 0 w L
sehingga:
0
2
Σw
μ
0
2
Σw
μ , karena
2
= �Ʃ� (2. 33)
Dengan � merupakan koefisien risk aversion (He & Litterman, 1999).
Rumus bobot portofolio model mean variance Markowitz untuk masing-masing sekuritas dalam pasar berdasarkan rumus (2.33) adalah sebagai berikut :
29 K. Capital Assets Pricing Model (CAPM)
Capital Assets Pricing Model (CAPM) diperkenalkan pertama kali oleh William Sharpe, John Lintner, dan Jan Mossin antara tahun (1964-1966). CAPM merupakan suatu model yang bertujuan untuk memprediksi hubungan antar risiko dengan return yang diharapkan dari suatu sekuritas. Untuk memahami model CAPM, maka harus memahami asumsi-asumsi yang melandasi model ini walaupun dianggap tidak realistis. Oleh karena itu ada beberapa penyederhanaan asumsi supaya model CAPM lebih realistis. Berikut adalah hasil penyederhanaan asumsi-asumsi CAPM menurut Eduardus Tandelilin (2001) :
1. Semua investor mempunyai distribusi probabilitas tingkat return di masa depan yang sama, karena mereka mempunyai harapan yang hampir sama. Ini berarti para investor sepakat tentang expected return, standar deviasi, dan koefisien korelasi antar tingkat keuntungan.
2. Semua investor mempunyai satu periode waktu yang sama, misalnya satu tahun. 3. Semua investor dapat meminjamkan sejumlah dananya atau meminjam sejumlah
dana dengan jumlah yang tidak terbatas pada tingkat return bebas risiko. 4. Tidak ada biaya transaksi.
5. Tidak terjadi inflasi.
30
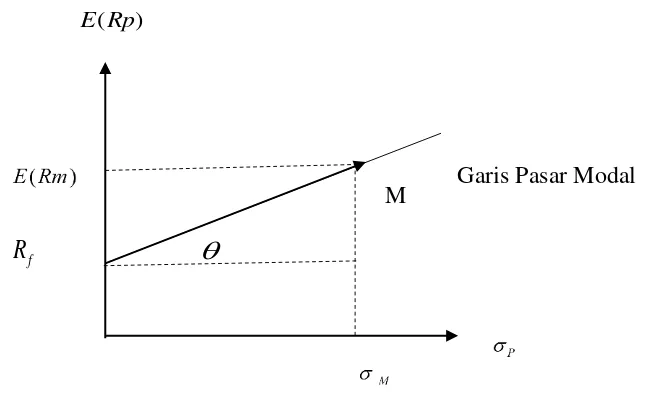
Jika semua asumsi tersebut dipenuhi, maka akan terbentuk kondisi pasar yang ekuilibrium. Hubungan expected return dan risiko dalam keadaan ekuilibrium pasar dapat digambarkan pada Gambar 2.1.
E(Rp)
f
R
[image:30.612.145.471.192.390.2]
Gambar 2. 1 Capital Market Line
Slope dalam Capital Market Line (CML) disimbolkan � merupakan harga pasar dari risiko untuk portofolio. Besarnya slope CML mengindikasikan tambahan return yang disyaratkan pasar untuk setiap 1% kenaikan risiko portofolio. Slope CML dapat dihitung dengan menggunakan rumus:
M f
M r
R E
.
(2. 35) Perubahan � yang semakin kecil mengakibatkan risiko portofolio semakin besar dan sebaliknya. Capital Market Line (CML) menunjukan semua kemungkinan kombinasi portofolio efisien yang terdiri sekuritas-sekuritas berisiko dan sekuritas
31
bebas risiko (Jogiyanto Hartono, 2003). Capital Market Line (CML) terbentuk sepanjang titik expected return sekuritas bebas risiko � sampai titik M. Expected return sekuritas bebas risiko didekati dengan tingkat return suku bunga Bank sentral,
di Indonesia umumnya diambil dari tingkat return suku bunga Bank Indonesia. Portofolio CAPM diharapkan memberikan keuntungan lebih besar dibandingkan sekuritas yang di investasikan pada Bank (Jogiyanto Hartono, 2003). Expected return dalam portofolio CAPM berdasarkan Gambar 2. 1 dapat dirumuskan dengan:
pM f M f
p
r R E r R
E
.
(2. 36)
keterangan:
� : expected return portofolio f
r : return sekuritas bebas risiko
RM
E : expected return portofolio pasar
M
: standar deviasi dari return portofolio pasar
�� : standar deviasi dari return portofolio efisien yang ditentukan.
32
besarnya kovarians return sekuritas tersebut terhadap portofolio pasar. Besarnya kontribusi risiko sekuritas terhadap risiko portofolio pasar yaitu:
M M i
,
dimana �, adalah kovarians dari sekuritas ke- dengan portofolio pasar. Dengan mensubstitusikan kontribusi sekuritas ke- terhadap risiko portofolio pasar pada persamaan (2.36), maka dapat dihitung expected return CAPM untuk sekuritas ke-i adalah sebagai berikut:
M M i
M f M f
i
r R E r r E
, .
M f
i f
M i M
f M f
r R E r
r R E r
2 . ,
(2. 37)
dengan
M M iM M , i i
R Var
R , R Cov
2
sebagai pengukur tingkat risiko dari suatu sekuritas
terhadap risiko portofolio pasar dan sebagai expected return CAPM masing-masing sekuritas. Expected return CAPM untuk suatu sekuritas dapat dinyatakan dengan persamaan sebagai berikut:
M f
i f
i ) r E(R ) r
r (
E . (2. 38)
33
merupakan salah satu indeks pasar saham yang digunakan oleh Bursa Efek Indonesia (BEI).
L. Diversifikasi Naive 1/N
Investor perlu melakukan diversifikasi ke beberapa sekuritas untuk menurunkan risiko portofolio, dengan demikian konsep diversifikasi berhubungan dengan jumlah sekuritas yang ada di dalam portofolio. Semakin banyak sekuritasnya, semakin tersebar risikonya. Dengan bertambahnya sekuritas di dalam portofolio, maka risiko akan didistribusikan ke sekuritas-sekuritas tersebut. Secara naluri manusia juga melakukan diversifikasi, misalnya tidak menyimpan semua uangnya di satu Bank, tetapi disebarkan ke beberapa Bank, tidak menyimpan file di komputernya dalam satu USB, tetapi dua atau lebih USB, dan lainnya. (Jogiyanto Hartono, 2014). Menurut Jogiyanto Hartono (2014) diversifikasi Naive 1/N adalah strategi diversifikasi dengan bobot yang sama untuk masing-masing sekuritasnya.
Diversifikasi untuk sekuritas di dalam portfolio, berarti bobot masing-masing sekuritas di dalam portofolio adalah =
�. Untuk menghitung risiko portofolio yang terdiri dari sekuritas digunakan rumus (2.20) sebagai berikut:
1 1 1 1
2 2 2
2 ni n
j i j ij n
i i i p
i j
w w
w
Untuk sekuritas, setiap sekuritas memiliki bobot yang sama yaitu = �, sehingga persamaan (2.20) menjadi:
34 Jika sekuritas ≠ , maka rumus (2.39) menjadi:
�� = ∑�= ∑�= � � (2. 40)
Persamaan (2.39) dan (2.40) digunakan untuk menghitung varians maupun kovarians portofolio, jika = maka rumus (2.39) dapat digunakan untuk menghitung varians, jika ≠ maka rumus (2.40) dapat digunakan untuk menghitung kovarians portofolio.
M. Minimum Variance Portofolio (MVP)
Metode optimasi Minimum Variance Portofolio (MVP) disebut juga dengan portofolio optimal risiko terkecil yang dibentuk dengan meminimumkan fungsi tujuan. Fungsi tujuan yang digunakan adalah fungsi risiko berdasarkan metode Markowitz yaitu meminimumkan risiko untuk tingkat return tertentu. Fungsi tujuan ini kemudian diminimalkan dengan beberapa kendala. Kendala yang pertama adalah total bobot yang diinvestasikan di masing-masing sekuritas untuk seluruh sekuritas adalah sama dengan 1 atau dana yang diinvestasikan seluruhnya berjumlah 100%. Misalnya adalah bobot sekuritas ke- yang diinvestasikan di dalam portofolio yang terdiri dari
sekuritas, maka kendala pertama ini dapat dituliskan sebagai:
1 1
n
i i w
35
≥ untuk = sampai dengan .
Kendala yang ketiga adalah jumlah expected return masing-masing sekuritas dengan masing-masing bobot saham dibatasi oleh return minimal yang diinginkan oleh investor ( ) atau dapat ditulis sebagai berikut:
R w ) R (
E i
n
i i
1
Dengan demikian, model penyelesaian optimasi ini dapat ditulis sebagai berikut ini: Fungsi Tujuan:
Meminimumkan
ij j n
i n
j i
n
i i i
w w
w
1 1 1
2 2
(2. 41)
dengan kendala:
1. 1
1
n
i i w
2. ≥ untuk i=1 sampai dengan n. 3. n E(R )wi R
i i
1
N. Model Black Litterman
Pengertian Model Black Litterman
36
(2000) menjelaskan mengenai pendekatan Bayes untuk menyelesaikan kombinasi distribusi probabilitas model Black Litterman. Model Black Litterman dengan pendekatan Bayes menggunakan views investor (views) sebagai informasi prior dan informasi pasar sebagai data sampel yang kemudian dikombinasikan untuk membentuk data baru (data posterior).
Views model Black Litterman digunakan untuk menyesuaikan expected return ekuilibrium dalam memprediksi return di masa yang akan datang. Manajer investasi dapat menyatakan opininya yang berbeda dengan kondisi ekuilibrium, informasi yang berbeda ini mungkin karena berkaitan dengan expected return suatu sekuritas apakah akan meningkat atau turun berdasarkan views investor terhadap keadaan pasar, perekonomian ataupun isu-isu politik dan kenegaraan yang mungkin mempengaruhi pergerakan sekuritas di pasar.
Views Investor
37
pandangannya dengan views relatif (relative views) maupun views pasti (absolute views).
a. Views pasti (absolute views)
Views pasti terbentuk apabila seorang investor memberikan prediksinya terhadap
dua buah saham, maka investor tersebut akan mengungkapkan views dengan yakin terhadap besarnya return yang akan diberikan oleh masing-masing saham.
Contoh:
Views 1 : “Saya prediksikan return saham A akan meningkat sebesar 2%”.
Views 2 : “Saya prediksikan return saham B akan meningkat sebesar 3%”.
a. Views relatif (relative views)
Ketika seorang investor diminta untuk memberikan views tentang dua buah saham, kemudian investor tersebut melakukan perbandingan antara return yang akan diberikan kedua saham tersebut, maka terbentuklah views relatif atau relative views.
Contoh: “Saya prediksikan bahwa return saham A akan melebihi return saham B
sebesar 2%”. Contoh :
Suatu portofolio terbentuk dari 4 saham, yaitu saham A, B, C dan D. Investor dapat menyatakan views terhadap keempat saham tersebut maupun hanya pada beberapa saham yang menjadi perhatian investor. Pada contoh ini, investor hanya menyatakan keempat saham tersebut dalam 3 views sebagai berikut:
38
Views 2: “Saya yakin saham C akan memberikan return 4%”. Views 3: “Saya yakin saham D akan memberikan return 0,5%”.
Jika E(r) adalah estimasi return investor dengan 4 saham, yaitu A , B , C dan D, maka ketiga views investor tersebut dapat dinyatakan dengan:
02 0, ) r ( E ) r (
E B A ;
;
,
)
r
(
E
C
0
04
;. , ) r (
E D 0005
Estimasi return investor tersebut jika dibentuk dalam matriks, maka:
P ,
1 0 0 0
0 1 0 0
0 0 1 1
� =
[ ]
, = [ , , , ]
Baris dalam matriks P menjelaskan tentang views dan kolom matriks P menjelaskan tentang saham. Saham yang akan memberikan return lebih dari saham yang lain (outperforming) akan dinyatakan dalam nilai positif, sedangkan saham yang underperforming akan diberikan nilai negatif. Sehingga, jumlah dari bobot views
absolut yang diberikan dalam matriks P adalah 1 dan views relatif berjumlah 0. Matriks adalah matriks berukuran × yang elemen-elemennya berisi nilai expected return yang diperoleh dari views investor.
Tingkat Keyakinan Investor
39
ini dinyatakan dalam matriks diagonal � (kovarians dari views) sebagai berikut (Idzorek, 2005) :
� = P(τΣ)P' (2. 42)
dengan,
� = matriks views dari return
� = skala tingkat keyakinan dalam views (range 0-1) Σ = matriks varians-kovarians dari return saham
Jika elemen � adalah nol maka investor dianggap sangat yakin terhadap pandangannya, sedangkan ketika informasi prior yang dimiliki investor memiliki tingkat views yang tidak pasti, maka hal ini diindikasikan dengan nilai matriks kovarians views � adalah tidak nol.
Asumsi Model
Aturan Bayes menyatakan bahwa distribusi probabilitas dari suatu kejadian B terjadi apabila kejadian A diketahui, maka:
) Pr(
) Pr( ) | Pr( ) | Pr(
A B B A A
B . (2. 43)
Aturan Bayes di atas lebih sering diungkapkan dalam bentuk berikut: )
Pr( ) | Pr( ) |
Pr(B A A B B . (2. 44)
dengan notasi ∞ menyatakan “proposional terhadap” )
|
40 )
|
Pr(A B : probabilitas dari kejadian A, dengan syarat kejadian B diketahui. Disebut juga dengan distribusi bersyarat.
)
Pr(B : probabilitas B, disebut juga informasi prior. )
Pr(A : probabilitas A, disebut juga normalisasi konstan.
Untuk membentuk model Black Litterman dibutuhkan dua jenis informasi yaitu expected return ekuilibrium CAPM dan views investor. Kedua informasi tersebut kemudian dikombinasikan dengan menggunakan aturan Bayes, dengan mengganti kejadian A adalah return ekuilibrium CAPM dan kejadian B adalah expected return investor, menggunakan persamaan Bayes dapat diperoleh:
) Pr(
)) Pr( ) | Pr( ) | Pr(
π
E(r E(r)
π π
E(r) (2. 45)
dengan, :
E(r): vektor expected return investor ukuran × �: return ekuilibrium CAPM
dengan asumsi-asumsi sebagai berikut (Retno Subekti, 2008) : a. Asumsi Pertama
Diasumikan bahwa keyakinan prior E(r) dinyatakan sebagai PE(r), yang mempunyai bentuk kendala linear dari vektor expected return E(r) dan ditulis dengan matriks � berukuran × sehingga:
41
Notasi q adalah vektor k x 1 dari views return yang diberikan investor, sedangkan adalah vektor error k x 1 yang menandakan adanya views yang masih belum pasti. Persamaan (2.46) dapat ditulis dalam bentuk matriks sebagai berikut:
[
� �
� � … �… ���
� � … �⋱ �
] [ �
]=[ ] + [ ]
Diasumsikan v berdistribusi normal dengan mean nol dan variansi �, dinotasikan v~N(0, �), � adalah matriks kovarians × , sehingga :
) , ( N
~ q Ω
E(r)
P (2. 47)
b. Asumsi Kedua
Data return ekuilibrium � dengan syarat informasi prior diasumsikan berdistribusi normal multivariat dengan mean � dan varians �Σ, sehingga dapat dinyatakan:
) , ( N ~
|E(r) E(r) Σ
π (2. 48)
42
Kombinasi Return Ekuilibrium dan Views Investor Teorema Model Black Litterman (Salomons, 2007):
) |
(E(r) π berdistribusi multivariat normal dengan mean E(r)=
]
'
)
[(
]
'
)
[(
Σ
1
P
Ω
1P
1
Σ
1π
P
Ω
1P
dan variansnya adalah[(
Σ
)
1
P'
Ω
1P
]
1 Bukti:Asumsi 1:
PE(r) berdistribusi normal multivariat dengan mean dan varians � dinotasikan
) , ( N
~ q Ω
PE(r) , sehingga fungsi probabilitasnya adalah:
) (
)' (
exp ) det( ) ( )
k Ω PE(r) q Ω PE(r) q
π
E(r)
f(P 1
2 1 2
1
(2. 49)
Asumsi 2: E(r)
π| berdistribusi normal multivariat dengan mean π dan varians-kovarians matriks
dinotasikanπ|E(r)~ N(E(r),Σ), sehingga fungsi probabilitasnya:
exp ( )'( ) ( )
) det( ) ( )
n Σ π-E(r) Σ π-E(r)
π
E(r) |
f(π 1
2 1 2
1
(2. 50)
Teorema Bayes dalam konteks ini dapat dinyatakan sebagai:
) Pr(
)) Pr( ) | Pr( ) | Pr(
π
E(r E(r)
π π
E(r)
atau dapat dinyatakan sesuai dengan persamaan (2.44)sebagai berikut:
43
Fungsi probabilitas (2.49) dan (2.50) disubstitusikan pada rumus (2.44) sehingga
diperoleh: ) ( ) ( )' ( exp ) det( ) ( . ) ( ( )' ( exp ) det( ) ( ) | Pr( k n q PE(r) Ω q PE(r) Ω π E(r) π Σ) E(r) π Σ π π E(r) 1 1 2 1 2 1 2 1 2 1
Dengan menghilangkan semua konstanta, maka yang tersisa adalah:
exp ( )'( ) ( )) ( )' ( )
) | ) (
Pr(E r π π E(r) Σ 1 π E(r PE(r) q Ω 1 PE(r) q
2 1 2 1 2 1 exp ) |
Pr(E(r) π
44
untuk,
C =
(
Σ
)
1π
P'
Ω
1q
,H =
(
Σ
)
1
P'
Ω
1P
, dimana H simetris dengan H = H', A =π
'
(
Σ
)
1π
q'
Ω
1q
.
Menggunakan notasi di atas, maka dapat ditulis kembali mejadi:
C) HE(r) H C H(E(r) C H C A A E(r H H C' E(r) H H H E(r)' = A E(r) C' HE(r) E(r)' 1 - ( )' ( ' ) ' 1 1 1 2 2
Dengan demikian AC' H1C akan menjadi konstanta dan selanjutnya
C)
HE(r)
H
C
HE(r)
)'
(
(
1 = �� − � ′�− �� − � = �− �� − �− � ′��− � �− �� − �− � = � − �− � ′� � − �− � Sehingga diperoleh: )] ( )' exp[ ) |Pr(E(r) π (E(r) H 1C H E(r) H 1C
2
1
Maka mean posteriornya �− � adalah
]
'
)
[(
]
'
)
[(
Σ
P
Ω
P
Σ
π
P
Ω
q
C
45
Jadi distribusi return kombinasi yang baru � |� sebagai distribusi posterior berdistribusi normal
)
]
'
)
[(
],
'
)
[(
]
'
)
([(
N
~
)
(
E(r)
|
π
Σ
1
P
Ω
1P
1
Σ
1π
P
Ω
1q
Σ
1
P
Ω
1P
1Selanjutnya, ). ( ) ' ( ' ) ( ) ' ( ' )] ' ( ) ' [( ) ( ) P ' )( ' ' ' ( ) ' ( ) }( ) P ' )( ' {( ' ( ) ' ( )) ( ' ( ) ' ( )] ( ' ) ' [( ] ' [ ] ' [ ] ' [ ] ' ) )[( ( ) ( ] ' ) [( ] ' ) [( ] ' ) [( Pπ q ΣP Ω ΣP π Pπ q ΣP P Ω ΣP P Ω ΣP I P Ω ΣP I π Pπ q Σ P Ω ΣP P Ω P ΣP P Ω ΣP I π Pπ q Σ P Ω ΣP P q Ω ΣP P Ω ΣP I π Pπ q Ω ΣP P Ω ΣP I π Pπ q Ω ΣP π P Ω ΣP I P Ω ΣP I q Ω ΣP π P Ω ΣP I q Ω P π Σ Σ Σ P Ω P Σ q Ω P π Σ P Ω P Σ μBL 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
Sehingga, expected return Black Litterman dapat dirumuskan sebagai berikut:
)
(
)
'
(
'
Ω
P
ΣP
1q
P
π
ΣP
π
)
E(r
μ
BL
BL
(2. 51)dengan,
)
E(rBL : expected return model Black Litterman
π : vektor k x 1 untuk return ekuilibrium CAPM � : skala tingkat keyakinan dalam views (range 0-1)
Ʃ : matriks varians kovarians return Ω : matriks diagonal kovarians dari views
P : matriks k x n untuk views yang berkaitan dengan return
46
Pembobotan portofolio model Black Litterman dihitung menggunakan rumus (2.34) pada model mean variance Markowitz sehingga diperoleh sebagai berikut:
BL
BL
Σ
μ
w
(
)
1 (2. 52)dengan, BL
w : bobot sekuritas pada model Black Litterman
δ : koefisien risk aversion
Ʃ : matriks varians kovarians return
BL
μ : expected return Black Litterman. O. Sharpe Ratio
Sharpe ratio dikembangkan oleh William Sharpe dan sering disebut juga dengan
reward-to-variability ratio (RVAR). Sharpe Ratio membandingkan selisih antara return sekuritas dan risk free rate dengan standar deviasi dari sekuritas tersebut, artinya
Sharpe mengukur besarnya perbedaan ( �− �) atau risk premium yang dihasilkan untuk tiap unit risiko yang diambil. Semakin tinggi nilai Sharpe ratio, maka semakin baik kinerja yang dihasilkan. Perhitungan Sharpe ratio dengan menggunakan risk free rate adalah sebagai berikut:
p f p p
r R S
(2. 53)
47 p
p * p
R S
(2. 54)
Keterangan:
� = Sharpe ratio
� = Return portofolio dalam suatu periode
77
DAFTAR PUSTAKA
Abdul Halim. (2005). Analisis Investasi Edisi 2. Jakarta: Salemba Empat.
Agnes Dwi Wulandari. (2015). Pengaruh Ukuran Data Return Terhadap Kinerja Portofolio Black Litterman pada Saham Syariah Jakarta Islamic Indeks. Skripsi. Yogyakarta: UNY.
Anton, Howard. (2010). Elementary Linear Algebra. New York: Anton Textbook. Bain, L. J., & Engelhardt, M. (1992). Introduction to Probability and Mathematical
Statistic. California: Duxbury Press.
Benartzi and Thaler. (2001). Naive Diversification Strategies in Defined Contribution Saving Plans. The American Economic Review, Vol 91, Maret ; 79-98.
Bessler Wolfgang., Heiko Offer., & Dominik Wolf. (2014). Multi-Asset Portofolio Optimization and Out-of-Sample Performance: An Evaluation of Black-Litterman, Mean Variance, and Naive Diversification Approaches. Europan Journal of Finance, Forthcoming, 1-38.
Black., Fischer and Litterman, Robert. (1992). Global Portfolio Optimization. Financial Analysts Journal, Sep/Oct; 48.
Clarke Roger., Harindra de Silva., and Steven Thorley. (2011). Minimum Variance Portfolio Composition. The Journal of Portfolio Management, Juli, 1-27. Eduardus Tandelilin. (2001). Analisis Investasi dan Manajemen Portofolio.
Yogyakarta: BPPE-Yogyakarta.
He, G., and Litterman, R. (1999). The Intuition Behind Black Litterman Model Portofolio. Investment Management Research. Goldman, Sachs & Company Idzorek, Thomas. (2005). A Step by Step to The Black Litterman Model. 1-34.
Jogiyanto Hartono. (2014). Teori dan Praktik Portofolio dengsn Excel. Jakarta: Salemba Empat.
78
Johnson, R. A., & Wichern, D. W. (2007). Applied Multivariate Statistical Analysis. New Jersey: Pearson Education, Inc.
Kempf Alexander. (2006). Estimating The Global Minimum Variance Portfolio. Schmalenbach Business Review, Vol. 58, Oktober, 332-348 .
Kertonegoro Senatnoe. (2000). Analisa dan Manajemen Investasi, Edisi Pertama. Jakarta: PT Widya Press.
Markowitz, Harry. (1952). Portofolio Selection. Jurnal of Finance, Vol. 7, No. 1, 77-91.
Murray R. Spiegel, J. S. (2004). Probabilitas dan Statistik Edisi Kedua. Jakarta: Erlangga.
Nurhidayah & Adrianto, O. (2014). Penerapan Capital Asset Pricing Model Untuk Menilai Kinerja Saham. Jurnal JIBEKA, Vol 8, No 2, Agustus, 45-54.
Pudjiastuti. (2006). Matriks Teori dan Aplikasi. Yogyakarta: Graha Ilmu.
Retno Subekti. (2008). Model Black Litterman Untuk Optimasi Portofolio. Tesis. Yogyakarta: UGM.
Salomons, Annisa. (2007). The Black Litterman Model Hype or Improvement. Gro-ningen.
Satchell, S., and Scowcroft, A. (2000). A Demystification of The Black Litterman: Managing Quantitive and Traditional Construction. Journal of Asset Management , 138-150.
Sharpe, W. F. (2001). Mutual Fund Performance. The Journal of Business, Vol 39, Jan ; 119-138.
Suad Husnan. (2005). Dasar-Dasar Teori Portofolio dan Analisis Sekuritas. Yogyakarta: Unit Penerbit dan Percetakan AMP YKPN.
Sunariyah. (2011). Pengantar Pengetahuan Pasar Modal. Yogyakarta: UPP-AMP YKPN.
Varberg & Purcell. (1987). Calculus With Analytic Geometry, 5th Edition. Prentice Hall, Inc.
79
www.bi.go.id, diakses pada Rabu, 3 Februari 2016 pukul 13.14 WIB.
www.evestment.com, diakses pada Selasa, 26 Januari 2016 pukul 11.35 WIB. www.finance.yahoo.com, diakses pada Sabtu, 6 Februari 2016 pukul 19.35 WIB. www.investopedia.com. diakses pada Selasa, 26 Januari 2016 pukul 11.40 WIB. www.parahita.wordpress.com, 24 Januari 2016 pada pukul 12.10 WIB.