DIKTAT
PROGRAM LINEAR
Disusun Oleh
Abdul Jabar, M.Pd
PROGRAM STUDI PENDIDIKAN MATEMATIKA
STKIP PGRI BANJARMASIN
SEPTEMBER
2011
Diktat Program Linear Oleh Abdul Jabar Halaman ke - i
KATA PENGANTAR
Alhamdulillah, Segala kesempurnaan hanya milik ALLAH SWT, berkat RAHMAT dari ALLAH SWT, penulis dapat menyelesaikan diktat PROGRAM LINEAR ini. Penulis juga mengucapkan terima kasih kepada semua pihak yang telah membantu sehingga penulisan diktat ini dapat selesai.
Materi pada diktat ini disusun untuk membantu mahasiswa Program Studi Pendidikan Matematika STKIP PGRI Banjarmasin. mendalami persoalan-persoalan yang berkaitan dengan pemograman linear.Prasyarat mata kuliah ini adalah Aljabar Linear.
Semoga dengan adanya diktat ini dapat membantu belajar mahasiswa dalam meraih yang terbaik di mata kuliah ini khususnya, serta mata kuliah lain yang terkait. Penulis menyadari bahwa isi diktat ini masih jauh dari kesempurnaan oleh sebab itu kritik dan saran sangat diperlukan.
Banjarmasin, September 2011
Diktat Program Linear Oleh Abdul Jabar Halaman ke - ii DAFTAR ISI Halaman KATA PENGANTAR ……… i DAFTAR ISI ………. ii PENDAHULUAN ……….. 1
BAB I PEMOGRAMAN LINEAR ……….. 2
1.1 Formulasi Model Program Linear ……….. 2
1.2 Masalah Maksimisasi ………. 2
1 .3 Masalah Minimisasi ………. 4
BAB II METODE SIMPLEKS ……….. 6
2.1 Pengantar ……… 6
2.2 BENTUK BAKU ... 7
2.3 PEMBENTUKAN TABEL SIMPLEKS ……… 8
2.4 LANGKAH-LANGKAH PENYELESAIAN ... 8
2.5 MEMBACA TABEL OPTIMAL ... 11
2.6 DUA FASE ... 11
BAB III PERSOALAN TRANSPORTASI ………. 14
3.1 MASALAH TRANSPORTASI SEIMBANG ……….. 14
3.2 TABEL TRANSPORTASI ………. 15
3.3 METODE NORTH WEST CORNER ………. 16
3.4 STEPPING STONE ……….. 16
3.5 Metode VAM ……….. 17
3.6 METODE MODI ……….. 19
BAB IV PENUGASAN ………. 23
4.1 Algoritma dengan Tujuan Meminimumkan ……… 23
4.2 Algoritma dengan Tujuan Memaksimalkan………. 25
Diktat Program Linear Oleh Abdul Jabar Halaman ke - 1
PENDAHULUAN
Dalam kehidupan sehari-hari sering kali kita menjumpai masalah yang dalam penyelesaiannya kita menghendaki hasil yang optimum padahal sumber daya yang kita punyai untuk mencapai hasil tersebut terbatas. Kumpulan cara atau metode untuk memecahkan masalah tersebut di atas dikenal dengan Riset Operasional. Sebutan ini dikenal sejak selesainya perang dunia II (akhir tahun 1950-an). Sebenarnya masalah serupa serta metode penyelesaiannya sudah diketengahkan sejak lama. Namun, perkembangannya kurang begitu pesat, belum banyak ahli yang berkecimpung dalam penyelesaian masalah tersebut maupun belum banyak hasil temuan metode yang dipublikasikan. Akan tetapi,sejak adanya perang dunia kedua, dengan dipicu oleh keinginan pihak sekutu untuk mengakhiri perang secepatnya, para ahli strategi militer maupun ilmuwan banyak mencurahkan diri untuk mencari perencanaan strategi operasi militer yang diharapkan dapat menyelesaikan perang secepatnya. Masalah yang dihadapi sebenarnya serupa dengan masalah di atas, yaitu berangkat dari keterbatasan sumber daya (personil, biaya, peralatan), diharapkan diperoleh hasil yang optimum. Hasil yang optimum tersebut berhubungan dengan biaya, waktu maupun risiko yang minimum ataupun berhubungan dengan keuntungan, manfaat yang maksimum.
Setelah selesainya perang dunia kedua, kumpulan metode yang telah ditemukan beralih diterapkan pada masalah yang berhubungan dunia industri sejalan dengan beralihnya kebutuhan yang dihadapi. Mulai saat itulah terjadi perkembangan pesat baik ragam masalah maupun metode penyelesaiannya. Untuk selanjutnya kumpulan metode penyelesaiannya tersebut disebut orang dengan Riset Operasional, sesuai dengan awal banyak digunakannya metode tersebut untuk keperluan operasi militer. Sejak saat itu bidang kajian masalah maupun metode penyelesaian masalahnya berkembang menjadi suatu disiplin keilmuan (bidang kajian) tersendiri.Dari uraian tersebut di atas, kita dapat menyatakan secara lebih umum bahwa disiplin keilmuan Riset Operasional berawal dari upaya untuk memecahkan masalah sebagai berikut.
Dengan mempertimbangkan keterbatasan sumber daya yang ada, bagaimana kita dapat melakukan tugas yang diberikan agar diperoleh hasil yang optimum?Sebelum tugas yang diberikan dilaksanakan, dilakukan dahulu riset (atau penelitian) untuk memperoleh rancangan. Diharapkan rancangan yang diperoleh dapat dioperasionalkan (dapat dilaksanakan) dan dapat memberikan hasil yang optimum dengan mempertimbangkan keterbatasan yang ada. Kumpulan metode atau teknik yang digunakan untuk menghasilkan rancangan tersebut disebut selanjutnya dengan Riset Operasional.
Diktat Program Linear Oleh Abdul Jabar Halaman ke - 2
BAB I
PEMOGRAMAN LINEAR
Program Linier merupakan metode matematik dalam mengalokasikan sumberdaya yang langka untuk mencapai tujuan tunggal seperti memaksimumkan keuntungan atau meminimumkan biaya. Program Linier banyak diterapkan dalam membantu menyelesaikan masalah ekonomi, indutri, militer, social dan lain-lain.
1.1 Formulasi Model Program Linier
Masalah keputusan yang sering dihadapi analis adalah alokasi optimum sumberdaya langka. Sumberdaya dapat berupa uang, tenaga kerja, bahan mentah, kapasitas mesin, waktu, ruang atau teknologi. Tugas analis adalah mencapai hasil terbaik yang mungkin dengan keterbatasan sumber daya itu. Hasil yang dinginkan mungkin ditunjukkan sebagai maksimasi dari beberapa ukuran profit, penjualan dan kesejahteraan, atau minimisasi pada biaya, waktu dan jarak.
Setelah masalah di identifikasikan, tujuan ditetapkan, langkah selanjutnya adalah formulasi model matematika yang meliputi tiga tahap seperti berikut :
1. Tentukan variable yang tidak diketahui (Variabel keputusan) dan nyatakan dalam symbol matematika.
2. Membentuk fungsi tujuan yang ditunjukkan sebagai suatu hubungan linier (bukan perkalian) dari variable keputusan.
3. Menentukan semua kendala masalah tersebut dan mengekspresikan dalam persamaan atau pertidaksamaan yang juga merupakan hubungan linier dari variable keputusan yang mencerminkan keterbatasan sumberdaya masalah itu.
1.2 Masalah Maksimalisasi
Maksimalisasi dapat berupa memaksimalkan keuntungan atau hasil. Contoh:
PT LAQUNATEKSTIL memiliki sebuah pabrik yang akan memproduksi 2 jenis produk, yaitu kain sutera dan kain wol. Untuk memproduksi kedua produk diperlukan bahan baku benang sutera, bahan baku benang wol dan tenaga kerja. Maksimum penyediaan benang sutera adalah 60 kg per hari, benang wol 30 kg per hari dan tenaga kerja 40 jam per hari. Kebutuhan setiap unit produk akan bahan baku dan jam tenaga kerja dapat dilihat dalam tabel berikut:
Jenis bahan baku dan tenaga kerja
Kg bahan baku & Jam tenaga kerja Maksimum
penyediaan
Kain sutera Kain wol
Benang sutera 2 3 60 kg
Benang wol - 2 30 kg
Tenaga kerja 2 1 40 jam
Kedua jenis produk memberikan keuntungan sebesar Rp 40 juta untuk kain sutera dan Rp 30 juta untuk kain wol. Masalahnya adalah bagaimana menentukan jumlah unit setiap jenis produk yang akan diproduksi setiap hari agar keuntungan yang diperoleh bisa maksimal.
Langkah-langkah: 1) Tentukan variabel X1=kain sutera X2=kain wol 2) Fungsi tujuan Zmax= 40X1 + 30X2
3) Fungsi kendala / batasan
1. 2X1 + 3X2 ≤ 60 (benang sutera)
2. 2X2 ≤ 30 (benang wol)
Diktat Program Linear Oleh Abdul Jabar Halaman ke - 3 4) Membuat grafik 1. 2X1 + 3 X2 = 60 X1=0, X2 =60/3 = 20 X2=0, X1= 60/2 = 30 2. 2X2 ≤ 30 X2=15 3. 2X1 + X2 ≤ 40 X1=0, X2 = 40 X2=0, X1= 40/2 = 20
Cara mendapatkan solusi optimal adalah dengan mencari nilai Z setiap titik ekstrim. Titik A
X1=0, X2=0
masukkan nilai X1 dan X2 ke Z
Z = 40 . 0 + 30 . 0 = 0 Titik B
X1=20, X2=0
masukkan nilai X1 dan X2 ke Z
Z = 40 . 20 + 30 . 0 = 800 Titik C
Mencari titik potong (1) dan (3) 2X1 + 3X2 = 60 2X1 + X2 = 40 - 2X2 =20 X2=10 Masukkan X2 ke kendala (1) 2X1 + 3X2 = 60 2X1 + 3 . 10 = 60 2X1 + 30 = 60 2X1 = 30 X1 = 15
masukkan nilai X1 dan X2 ke Z
40X1 + 30X2 = 40 . 15 + 30 . 10 = 600 + 300 = 900 (optimal) Titik D 2X2 = 30 X2 = 15 masukkan X2 ke kendala (1) 2X1 + 3 . 15 = 60 2X1 + 45 = 60 2X1 = 15 X1 = 7,5
masukkan nilai X1 dan X2 ke Z
Diktat Program Linear Oleh Abdul Jabar Halaman ke - 4
Titik E X2 = 15
X1 = 0
masukkan nilai X1 dan X2 ke Z
Z = 40 . 0 + 30 .15 = 450 Kesimpulan :
untuk memperoleh keuntungan optimal, maka X1 = 15 dan X2 = 10 dengan
keuntungan sebesar Rp 900 juta. 1 .3 Masalah Minimalisasi
Minimalisasi dapat berupa meminimumkan biaya produksi. Solusi optimal tercapai pada saat garis fungsi tujuan menyinggung daerah fasible yang terdekat dengan titik origin.
Contoh :
Perusahaan makanan ROYAL merencanakan untuk membuat dua jenis makananyaitu Royal Bee dan Royal Jelly. Kedua jenis makanan tersebut mengandung vitamin dan protein. Royal Bee paling sedikit diproduksi 2 unit dan Royal Jelly paling sedikit diproduksi 1 unit. Tabel berikut menunjukkan jumlah vitamin dan protein dalam setiap jenis makanan:
Jenis makanan Vitamin
(unit)
Protein (unit)
Biaya per unit (ribu rupiah) Royal Bee 2 2 100 Royal Jelly 1 3 80 minimum kebutuhan 8 12
Bagaimana menentukan kombinasi kedua jenis makanan agar meminimumkan biaya produksi. Langkah – langkah: 1. Tentukan variabel X1 = Royal Bee X2 = Royal Jelly 2. Fungsi tujuan Zmin = 100X1 + 80X2 3. Fungsi kendala 1) 2X1 + X2 ≥ 8 (vitamin) 2) 2X1 + 3X2 ≥ 12 (protein) 3) X1 ≥ 2 4) X2 ≥1 4. Membuat grafik 1) 2X1 + X2 = 8 X1 = 0, X2 = 8 X2 = 0, X1 = 4 2) 2X1 + 3X2 = 12 X1 = 0, X2 = 4 X2 = 0, X1 = 6 3) X1 = 2 4) X2 = 1
Diktat Program Linear Oleh Abdul Jabar Halaman ke - 5
Solusi optimal tercapai pada titik B (terdekat dengan titik origin), yaitupersilangan garis kendala (1) dan (2). 2X1 + X2 = 8 2X1 + 3X2 = 12 - -2X2 = -4 ó X2 = 2 masukkan X2 ke kendala (1) 2X1 + X2 = 8 2X1 + 2 = 8 2 X1 = 6 X1 = 3
masukkan nilai X1 dan X2 ke Z
Z min = 100X1 + 80X2 = 100 . 3 + 80 . 2 = 300 + 160 = 460
Kesimpulan :
Untuk meminimumkan biaya produksi, maka X1 = 3 dan X2 = 2 dengan biaya produksi 460 ribu
rupiah. SOAL LATIHAN 1. Maksimumkan Z = 3X1 + 5X2 Kendala : 1) 2X1 ≤ 8 2) 3X2 ≤ 15 3) 6X1 + 5X2 ≤ 30 X1≥ 0 , X2 ≥ 0 2. Minimumkan Z = 5 X1 + 2X2 Kendala: 1) 6X1 + X2 ≥ 6 2) 4X1 + 3X2 ≥ 2 3) X1 + 2X2 ≥ 4 , X1 ≥ 0
Diktat Program Linear Oleh Abdul Jabar Halaman ke - 6
BAB II
METODE SIMPLEKS 2.1 Pengantar
Salah satu teknik penentuan solusi optimal yang digunakan dalam pemrograman linier adalah metode simpleks. Penentuan solusi optimal menggunakan metode simpleks didasarkan pada teknik eleminasi Gauss Jordan. Penentuan solusi optimal dilakukan dengan memeriksa titik ekstrim satu per satu dengan cara perhitungan iteratif. Sehingga penentuan solusi optimal dengan simpleks dilakukan tahap demi tahap yang disebut dengan iterasi. Iterasi ke-i hanya tergantung dari iterasi sebelumnya (i-1).
Ada beberapa istilah yang sangat sering digunakan dalam metode simpleks, diantaranya : 1. Iterasi adalah tahapan perhitungan dimana nilai dalam perhitungan itu tergantung dari nilai
tabel sebelumnya.
2. Variabel non basis adalah variabel yang nilainya diatur menjadi nol pada sembarang iterasi. Dalam terminologi umum, jumlah variabel non basis selalu sama dengan derajat bebas dalam sistem persamaan.
3. Variabel basis merupakan variabel yang nilainya bukan nol pada sembarang iterasi. Pada solusi awal, variabel basis merupakan variabel slack (jika fungsi kendala merupakan pertidaksamaan ≤ ) atau variabel buatan (jika fungsi kendala menggunakan pertidaksamaan ≥ atau =). Secara umum, jumlah variabel basis selalu sama dengan jumlah fungsi pembatas (tanpa fungsi non negatif).
4. Solusi atau nilai kanan merupakan nilai sumber daya pembatas yang masih tersedia. Pada solusi awal, nilai kanan atau solusi sama dengan jumlah sumber daya pembatas awal yang ada, karena aktivitas belum dilaksanakan.
5. Variabel slack adalah variabel yang ditambahkan ke model matematik kendala untuk mengkonversikan pertidaksamaan ≤ menjadi persamaan (=). Penambahan variabel ini terjadi pada tahap inisialisasi. Pada solusi awal, variabel slack akan berfungsi sebagai variabel basis.
6. Variabel surplus adalah variabel yang dikurangkan dari model matematik kendala untuk mengkonversikan pertidaksamaan ≥ menjadi persamaan (=). Penambahan ini terjadi pada tahap inisialisasi. Pada solusi awal, variabel surplus tidak dapat berfungsi sebagai variabel basis.
7. Variabel buatan adalah variabel yang ditambahkan ke model matematik kendala dengan bentuk ≥ atau = untuk difungsikan sebagai variabel basis awal. Penambahan variabel ini terjadi pada tahap inisialisasi. Variabel ini harus bernilai 0 pada solusi optimal, karena kenyataannya variabel ini tidak ada. Variabel hanya ada di atas kertas.
8. Kolom pivot (kolom kerja) adalah kolom yang memuat variabel masuk. Koefisien pada kolom ini akn menjadi pembagi nilai kanan untuk menentukan baris pivot (baris kerja). 9. Baris pivot (baris kerja) adalah salah satu baris dari antara variabel basis yang memuat
variabel keluar.
10. Elemen pivot (elemen kerja) adalah elemen yang terletak pada perpotongan kolom dan baris pivot. Elemen pivot akan menjadi dasar perhitungan untuk tabel simpleks berikutnya. 11. Variabel masuk adalah variabel yang terpilih untuk menjadi variabel basis pada iterasi
berikutnya. Variabel masuk dipilih satu dari antara variabel non basis pada setiap iterasi. Variabel ini pada iterasi berikutnya akan bernilai positif.
12. Variabel keluar adalah variabel yang keluar dari variabel basis pada iterasi berikutnya dan digantikan oleh variabel masuk. Variabel keluar dipilih satu dari antara variabel basis pada setiap iterasi. Variabel ini pada iterasi berikutnya akan bernilai nol.
Diktat Program Linear Oleh Abdul Jabar Halaman ke - 7
2.2 BENTUK BAKU
Sebelum melakukan perhitungan iteratif untuk menentukan solusi optimal, pertama sekali bentuk umum pemrograman linier dirubah ke dalam bentuk baku terlebih dahulu. Bentuk baku dalam metode simpleks tidak hanya mengubah persamaan kendala ke dalam bentuk sama dengan, tetapi setiap fungsi kendala harus diwakili oleh satu variabel basis awal. Variabel basis awal menunjukkan status sumber daya pada kondisi sebelum ada aktivitas yang dilakukan. Dengan kata lain, variabel keputusan semuanya masih bernilai nol. Dengan demikian, meskipun fungsi kendala pada bentuk umum pemrograman linier sudah dalam bentuk persamaan, fungsi kendala tersebut masih harus tetap berubah.
Ada beberapa hal yang harus diperhatikan dalam membuat bentuk baku, yaitu :
1. Fungsi kendala dengan pertidaksamaan ≤ dalam bentuk umum, dirubah menjadi persamaan (=) dengan menambahkan satu variabel slack.
2. Fungsi kendala dengan pertidaksamaan ≥ dalam bentuk umum, dirubah menjadi persamaan (=) dengan mengurangkan satu variabel surplus.
3. Fungsi kendala dengan persamaan dalam bentuk umum,ditambahkan satu artificial variabel (variabel buatan).
Perhatikan kasus A berikut :
Fungsi tujuan : minimumkan z = 2 x1 + 5.5 x2
Kendala : x1 + x2 = 90 0.001 x1 + 0.002 x2 ≤ 0.9 0.09 x1 + 0.6 x2 ≥ 27 0.02 x1 + 0.06 x2 ≤ 4.5 x1, x2 ≥ 0
Bentuk di atas adalah bentuk umum pemrograman liniernya. Kedalam bentuk baku, model matematik tersebut akan berubah menjadi :
Fungsi tujuan : z - 2 x1- 5.5 x2 = 0 Kendala : x1 + x2 + s1 = 90 0.001 x1 + 0.002 x2 + s2 = 0.9 0.09 x1 + 0.6 x2 – s3 + s4 = 27 0.02 x1 + 0.06 x2 + s5 = 4.5 x1, x2 , s1, s2, s3, s4, s5 ≥ 0
Fungsi kendala pertama mendapatkan variable buatan (s1), karena bentuk umumnya sudah
menggunakan bentuk persamaan. Fungsi kendala kedua dan keempat mendapatkan variabel slack (s2 dan s5) karena bentuk umumnya menggunakan pertidaksamaan ≤, sedangkan fungsi kendala
ketiga mendapatkan variabel surplus (s3) dan variabel buatan (s4) karena bentuk umumnya
menggunakan pertidaksamaan ≥. Perhatikan pula kasus B berikut ini :
Maksimumkan z = 2x1 + 3x2 Kendala : 10 x1 + 5 x2 ≤ 600 6 x1 + 20 x2 ≤ 600 8 x1 + 15 x2 ≤ 600 x1, x2 ≥ 0
Bentuk di atas juga merupakan bentuk umum. Perubahan ke dalam bentuk baku hanya membutuhkan variabel slack, karena semua fungsi kendala menggunakan bentuk pertidaksamaan ≤ dalam bentuk umumnya. Maka bentuk bakunya adalah sebagai berikut :
z - 2x1- 3x2 + 0s1 + 0s2 + 0s3= 0 (Maksimum)
Kendala :
10 x1 + 5 x2 + s1 = 600
6 x1 + 20 x2 + s2 = 600
Diktat Program Linear Oleh Abdul Jabar Halaman ke - 8
x1, x2 , s1 , s2 , s3 ≥ 0
s1 , s2 , s3 merupakanvariable slack.
2.3 PEMBENTUKAN TABEL SIMPLEKS
Dalam perhitungan iterative, kita akan bekerja menggunakan tabel. Bentuk baku yang sudah diperoleh, harus dibuat ke dalam bentuk tabel.
Semua variabel yang bukan variabel basis mempunyai solusi (nilai kanan) sama dengan nol dan koefisien variabel basis pada baris tujuan harus sama dengan 0. Oleh karena itu kita harus membedakan pembentukan tabel awal berdasarkan variabel basis awal. Gunakan kasus B di atas, maka tabel awal simpleksnya adalah :
VB X1 X2 S1 S2 S3 Solusi Z -2 -3 0 0 0 0 S1 10 5 1 0 0 600 S2 6 20 0 1 0 600 S3 8 15 0 0 1 600 2.4 LANGKAH-LANGKAH PENYELESAIAN
Langkah-langkah penyelesaian adalah sebagai berikut :
1. Periksa apakah tabel layak atau tidak. Kelayakan tabel simpleks dilihat dari solusi (nilai kanan). Jika solusi ada yang bernilai negatif, maka tabel tidak layak. Tabel yang tidak layak tidak dapat diteruskan untuk dioptimalkan.
2. Tentukan kolom pivot. Penentuan kolom pivot dilihat dari koefisien fungsi tujuan (nilai di sebelah kanan baris z) dan tergantung dari bentuk tujuan. Jika tujuan maksimisasi, maka kolom pivot adalah kolom dengan koefisien paling negatif. Jika tujuan minimisasi , maka kolom pivot adalah kolom dengan koefisien positif terbesar. Jika kolom pivot ditandai dan ditarik ke atas, maka kita akan mendapatkan variabel keluar. Jika nilai paling negatif (untuk tujuan maksimisasi) atau positif terbesar (untuk tujuan minimisasi) lebih dari satu, pilih salah satu secara sembarang.
3. Tentukan baris pivot. Baris pivot ditentukan setelah membagi nilai kanan dengan nilai kolom pivot yang bersesuaian (nilai yang terletak dalam satu baris). Dalam hal ini, nilai negatif dan 0 pada kolom pivot tidak diperhatikan, artinya tidak ikut menjadi pembagi. Baris pivot adalah baris dengan rasio pembagian terkecil. Jika baris pivot ditandai dan ditarik ke kiri, maka kita akan mendapatkan variabl keluar. Jika rasio pembagian terkecil lebih dari satu, pilih salah sau secara sembarang.
4. Tentukan elemen pivot. Elemen pivot merupakan nilai yang terletak pada perpotongan kolom dan baris pivot.
5. Bentuk tabel simpleks baru. Tabel simpleks baru dibentuk dengan pertama sekali menghitung nilai baris pivot baru. Baris pivot baru adalah baris pivot lama dibagi dengan elemen pivot. Baris baru lainnya merupakan pengurangan nilai kolom pivot baris yang bersangkutan dikali baris pivot baru dalam satu kolom terhadap baris lamanya yang terletak pada kolom tersebut.
6. Periksa apakah tabel sudah optimal. Keoptimalan tabel dilihat dari koefisien fungsi tujuan (nilai pada baris z) dan tergantung dari bentuk tujuan. Untuk tujuan maksimisasi, tabel sudah optimal jika semua nilai pada baris z sudah positif atau 0. Pada tujuan minimisasi, tabel sudah optimal jika semua nilai pada baris z sudah negatif atau 0. Jika belum, kembali ke langkah no. 2 , jika sudah optimal baca solusi optimalnya.
Rumus yang digunakan: yr’ =
rk r
x y
(untuk baris ke – r yang terdapat elemen pivot)
yi’ = yi – bi ar (untuk baris ke – i yang tidak terdapat elemen pivot)
Keterangan:
Diktat Program Linear Oleh Abdul Jabar Halaman ke - 9
yi’ = elemen baris ke – i pada tabel yang baru
yr = elemen baris ke – r pada tabel yang lama
yi = elemen baris ke – i pada tabel yang lama
bi = elemen baris ke – i pada tabel lama yang se-kolom dengan elemen pivot
ar = elemen baris ke – r pada tabel yang baru
Selesaikan kasus berikut ini menggunakan metode simpleks : Maksimum z = 8 x1 + 9 x2 + 4x3 Kendala : x1 + x2 + 2x3 ≤ 2 2x1 + 3x2 + 4x3 ≤ 3 7x1 + 6x2 + 2x3 ≤ 8 x1,x2,x3 ≥ 0 Penyelesaian :
Bentuk bakunya adalah :
Maksimum z = 8 x1 + 9 x2 + 4x3 + 0s1 + 0s2 + 0s3 atau z - 8 x1 - 9 x2 - 4x3 + 0s1 + 0s2 + 0s3 = 0 Kendala : x1 + x2 + 2x3 + s1 = 2 2x1 + 3x2 + 4x3 + s2 = 3 7x1 + 6x2 + 2x3 + s3 = 8 x1,x2,x3 ,s1 , s2 , s3 ≥ 0
Solusi / table awal simpleks :
VB X1 X2 X3 S1 S2 S3 NK Rasio
Z -8 -9 -4 0 0 0 0
S1 1 1 2 1 0 0 2
S2 2 3 4 0 1 0 3
S3 7 6 2 0 0 1 8
Karena nilai negative terbesar ada pada kolom X2, maka kolom X2 adalah kolom pivot dan X2 adalah
variabel masuk. Rasio pembagian nilai kanan dengan kolom pivot terkecil adalah 1 bersesuaian dengan baris s2, maka baris s2 adalah baris pivot dan s2 adalah varisbel keluar. Elemen pivot adalah
3. VB X1 X2 X3 S1 S2 S3 NK Rasio Z -8 -9 -4 0 0 0 0 S1 1 1 2 1 0 0 2 2 S2 2 3 4 0 1 0 3 1 S3 7 6 2 0 0 1 8 8/6 Iterasi 1
Nilai pertama yang kita miliki adalah nilai baris pivot baru (baris x2). Semua nilai pada baris s2
pada tabel solusi awal dibagi dengan 3 (elemen pivot).
VB X1 X2 X3 S1 S2 S3 NK Rasio
Z S1
x2 2/3 1 4/3 0 1/3 0 1
S3
Perhitungan nilai barisnya : Baris z :
Diktat Program Linear Oleh Abdul Jabar Halaman ke - 10 -8 -9 -4 0 0 0 0 -9 ( 2/3 1 4/3 0 1/3 0 1 ) - -2 0 8 0 3 0 9 Baris s1 : 1 1 2 1 0 0 2 1 (2/3 1 4/3 0 1/3 0 1 ) - 1/3 0 2/3 1 -1/3 0 1 Baris s3 : 7 6 2 0 0 1 8 6 ( 2/3 1 4/3 0 1/3 0 1 ) - 3 0 -6 0 -2 1 2
Maka tabel iterasi 1 ditunjukkan tabel di bawah. Selanjutnya kita periksa apakah tabel sudah optimal atau belum. Karena nilai baris z di bawah variabel x1 masih negatif, maka tabel belum
optimal. Kolom dan baris pivotnya ditandai pada tabel di bawah ini :
VB X1 X2 X3 S1 S2 S3 NK Rasio
Z -2 0 8 0 3 0 9 -
S1 1/3 0 2/3 1 -1/3 0 1 3
X2 2/3 1 4/3 0 1/3 0 1 3/2
S3 3 0 -6 0 -2 1 2 2/3
Variabel masuk dengan demikian adalah X1 dan variabel keluar adalah S3 . Hasil perhitungan iterasi ke 2 adalah sebagai berikut :
Iterasi 2 : VB X1 X2 X3 S1 S2 S3 NK Rasio Z 0 0 4 0 5/3 2/3 31/3 S1 0 0 4/3 1 -1/9 -1/9 7/9 X2 0 1 8/3 0 7/9 -2/9 5/9 X1 1 0 -2 0 -2/3 1/3 2/3
Tabel sudah optimal, sehingga perhitungan iterasi dihentikan !
Perhitungan dalam simpleks menuntut ketelitian tinggi, khususnya jika angka yang digunakan adalah pecahan. Pembulatan harus diperhatikan dengan baik. Disarankan jangan menggunakan bentuk bilangan desimal, akan lebih teliti jika menggunakan bilangan pecahan. Pembulatan dapat menyebabkan iterasi lebih panjang atau bahkan tidak selesai karena ketidaktelitian dalam melakukan pembulatan.
Perhitungan iteratif dalam simpleks pada dasarnya merupakan pemeriksaan satu per satu titik-titik ekstrim layak pada daerah penyelesaian. Pemeriksaan dimulai dari kondisi nol (dimana semua aktivitas/variabel keputusan bernilai nol). Jika titik ekstrim berjumlah n, kemungkinan terburuknya kita akan melakukan perhitungan iteratif sebanyak n kali.
Diktat Program Linear Oleh Abdul Jabar Halaman ke - 11
2.5 MEMBACA TABEL OPTIMAL
Membaca tabel optimal adalah bagian penting bagi pengambil keputusan. Ada beberapa hal yang bisa dibaca dari table optimal :
1. Solusi optimal variable keputusan 2. Status sumber daya
3. harga bayangan (dual/shadow prices). Menggunakan table optimal :
VB X1 X2 X3 S1 S2 S3 NK
Z 0 0 4 0 5/3 2/3 31/3
S1 0 0 4/3 1 -1/9 -1/9 7/9
X2 0 1 8/3 0 7/9 -2/9 5/9
X1 1 0 -2 0 -2/3 1/3 2/3
Solusi optimal X1 = 2/3, X2 = 5/9 , X3 = 0 dan Z = 31/3, artinya untuk mendapatkan keuntungan
maksimum sebesar $ 31/3 , maka perusahaan sebaiknya menghasilkan produk 1 sebesar 2/3 unit dan produk 2 sebesar 5/9 unit.
Status sumber daya :
Sumber daya pertama dilihat dari keberadaan variable basis awal dari setiap fungsi kendala pada table optimal. Dalam kasus di atas, untuk fungsi kendala pertama periksa keberadaan S1 pada
variable basis table optimal. Periksa keberadaan S2 pada variable basis table optimal untuk fungsi
kendala kedua. Periksa keberadaan S3 pada variable basis table optimal untuk fungsi kendala
ketiga.
S1 = 7/9. Sumber daya ini disebut berlebih (abundant)
S2 = S3 = 0. Kedua sumber daya ini disebut habis terpakai (scarce).
Harga bayangan :
Harga bayangan dilihat dari koefisien variable slack atau surplus pada baris fungsi tujuan.
Koefisien S1 pada baris fungsi tujuan table optimal = 0, dengan demikian harga bayangan sumber
daya pertama adalah 0
Koefisien S2 pada baris fungsi tujuan table optimal = 5/3, dengan demikian harga bayangan sumber
daya kedua adalah 5/3
Koefisien S3 pada baris fungsi tujuan table optimal = 2/3, dengan demikian harga bayangan sumber
daya kedua adalah 2/3. 2.6 DUA FASE
Metode ini digunakan untuk menyelesaikan persoalan PL yang memuat variabel buatan Contoh: Min Z = 4 X1 + X2 Kendala 3 X1 + X2 = 3 4 X1 + 3 X2 ≥ 6 X1 + 2 X2 ≤ 4 X1 , X2 ≥ 0 Tahap 1 :
Diktat Program Linear Oleh Abdul Jabar Halaman ke - 12 Min r = R1 + R2 Kendala 3 X1 + X2 + R1 = 3 4 X1 + 3 X2 - X3 +R2 = 6 X1 + 2 X2 + X4 = 4 X1 , X2 ,X3 ,R1 , R2 , X4 ≥ 0 Fungsi tujuan r = R1 + R2 = ( 3 – 3 X1 - X2 ) + ( 6 - 4 X1 - 3 X2 + X3 ) = -7 X1 - 4 X2 + X3 + 9(eksplisit) r +7 X1+ 4 X2 - X3 + 0R1 + 0R2 + 0x4= 9(implisit) Tabel Awal VB X1 X2 X3 R1 R2 X4 NK r 7 4 -1 0 0 0 9 R1 3 1 0 1 0 0 3 R2 4 3 -1 0 1 0 6 X4 1 2 0 0 0 1 4
Tabel optimum : setelah 2 iterasi ( periksa ! )
VB X1 X2 X3 R1 R2 X4 NK
r 0 0 0 -1 -1 0 0
X1 1 0 1/5 3/5 -1/5 0 3/5
X2 0 1 -3/5 -4/5 3/5 0 6/5
X4 0 0 1 1 -1 1 1
Karena minimum solusi r = 0, masalah ini memiliki pemecahan ( solusi ) layak. Lanjutkan ke tahap ( Fase ) kedua.
Tahap 2
F Menyingkirkan variabel buatan ( R1 dan R2 )
F Dari tabel optimum tahap 1 didapatkan : X1 + 1/5X3 = 3/5
X2 - 3/5X3 = 6/5
X3 + X4 = 1
Masalah semula ditulis :
Min Z = 4 X1 + X2
Kendala X1 + 1/5X3 = 3/5 ... ( 1 )
X2 - 3/5X3 = 6/5 ... ( 2 )
X3 + X4 = 1
Diktat Program Linear Oleh Abdul Jabar Halaman ke - 13
Maka terdapat 3 persamaan dan 4 variabel sehingga solusi dasar layak didapat dg membuat (4 – 3) = 1 variabel dibuat nol
X3 = 0 -> X1 = 3/5 ; X2 = 6/5 ; X4 = 1 F Fungsi tujuan Z = 4 X1 + X2 = 4 ( 3/5-1/5 X3 ) + (6/5 + 3/5X3 ) = - 1/5 X3 + 18/5 Z +0x1 + 0x2 +1/5 X3 =18/5 Tabel Awal Var msk Tabel optimum Optimalnya Zmin = 17/5, x1 = 2/5, x2 = 9/5 SOAL LATIHAN
1. Selesaikan linear program berikut ini dengan metode Simplex Maksimumkan Z = 400X1 + 300X2
Fungsi kendala/ batasan: 1) 4X1 + 6X2 ≤ 1200
2) 4X1 + 2X2 ≤ 800
3) X1 ≤ 250
4) X2 ≤ 300
5) X1, X2 ≥ 0
2. Selesaikan linear program berikut ini dengan metode Simplex Maksimumkan Z = 2X1 + 3X2 + X3
Dengan fungsi kendala: 1) X1 + X2 + X3 ≤ 9 2) 2X1 + 3X2 ≤ 25 3) X2 + 2X3 ≤ 10 4) X1, X2, X3 ≥ 0 3. Minimumkan Z = 3X1 + 2X2 VB X1 X2 X3 X4 NK Rasio Z 0 0 1/5 0 18/5 X1 1 0 1/5 0 3/5 3 X2 0 1 -3/5 0 6/5 - X4 0 0 1 1 1 1 VB X1 X2 X3 X4 NK Z 0 0 0 -1/ 5 17/5 X1 1 0 0 -1/5 2/5 X2 0 1 0 3/5 9/5 X3 0 0 1 1 1
Diktat Program Linear Oleh Abdul Jabar Halaman ke - 14
Diktat Program Linear Oleh Abdul Jabar Halaman ke - 15
BAB III
PERSOALAN TRANSPORTASI
Metode Transportasi merupakan suatu metode yang digunakan untuk mengatur distribusi dari sumber-sumber yang menyediakan produk yang sama ke tempat-tempat yang membutuhkan secara optimal dengan biaya yang termurah. Alokasi produk ini harus diatur sedemikian rupa karena terdapat perbedaan biaya-biaya alokasi dari satu sumber atau beberapa sumber ke tempat tujuan yang berbeda.
Contoh model transportasi sebagai berikut :
Misalkan suatu produk yang dihasilkan pada tiga pabrik (sumber) harus didistribusikan ke tiga gudang (tujuan) seperti berikut :
Sumber (Pabrik) Tujuan (Gudang)
Cirebon Semarang
Bandung Jakarta
Cilacap Purwokerto
3.1 MASALAH TRANSPORTASI SEIMBANG
Contoh masalah transportasi yang mana jumlah supply dari semua sumber sama dengan jumlah permintaan pada semua tempat tujuan.
Sebuah perusahaan Negara berkepentingan mengangkut pupuk dari tiga pabrik ke tiga pasar. Kapasitas supply ketiga pabrik, permintaan pada ketiga pasar dan biaya transport per unit adalah sebagai berikut : Pasar Penawaran 1 2 3 Pabrik 1 8 5 6 120 2 15 10 12 80 3 3 9 10 80 Permintaan 150 70 60 280
Masalah transportasi diatas dapat gambarkan sebagai suatu model jaringan : Sumber Volume yang diangkut Tujuan (Gudang)
S1 = 120 D1 = 150 S2 = 80 D2 = 70 S3 = 80 D3 = 60 1 2 3 2 1 3
Diktat Program Linear Oleh Abdul Jabar Halaman ke - 16
Masalah ini dapat juga dilihat dalam LP misalkan : Xij : banyaknya unit barang yang di kirim dari
pabrik i (i = 1,2,3) ke pasar j (j = 1,2,3) Dengan fungsi Tujuan :
Z= 8X11 + 5X12 + 6X13 + 15X21 + 10X22 + 12X23 + 3X31 + 9x32 + 10X33 Dengan batasan : X11 + X12 + X13 = 120 X21 + X22 + X23 = 80 X31 + X32 + X33 = 80 X11 + X21 + X31 = 150 X12 + X22 + X32 = 70 X13 + X23 + X33 = 60 3.2 TABEL TRANSPORTASI
Masalah transportasi yang khas dapat ditempatkan dalam suatu bentuk tabel khusus yang dinamakan tabel transportasi.
ke Dari Tujuan Supply 1 2 …….. j …….. n 1 X11 X12 …….. …….. X1n S1 2 X21 X22 …….. X21 …….. X2n S2 . . . . . . . . . . . . . . . . . . . . . . . . I …….. 30 …….. S1 . . . . . . . . . . . . . . . . . . . . . . . . M Xm1 Xm2 …….. Xm1 …….. Sn Demand D1 D2 …….. Dj …….. Dn Si = Dj
Sumber ditulis dalam baris-baris dan tujuan dalam kolom – kolom. Biaya transfer per unit (Cij) di catat pada kotak kecil. Permintaan dari setiap tujuan terdapat pada baris paling bawah, sementara penawaran setiap sumber dicatat pada kolom paling kanan. Dan kotak pojok kanan bawah menunjukkan kenyataan bahwa penawaran sama dengan permintaan. Variabel Xij menunjukkan jumlah barang yang diangkut dari sumber i ke tujuan j (yang akan dicari).
Berikut solusi penyelesaian masalah transportasi, yang dimulai dari mencari solusi awal (dasar). Ada tiga metode dalam penyelesaian solusi awal :
1. Metode North West Corner (NWC) => dari pojok kiri atas ke pojok kanan bawah Kelemahan : tidak memperhitungkan besarnya biaya sehingga kurang efisien.
2. Metode biaya terkecil (Least Cost)=> mencari dan memenuhi yang biayanya terkecil dulu. Lebih efisien dibanding metode NWC.
3. Aproksimasi Vogel C11 C21 Ci1 C12 C22 Ci2 C11 10 Cij C1n Cin Cm1 Cm2 Cm1 Cmn
Diktat Program Linear Oleh Abdul Jabar Halaman ke - 17
da beberapa cara menentukan solusi optimum 1. Metode Stepping Stone
2. Metode Modified Distribution (MODI) 3. Masalah Transportasi Tak Seimbang 4. Degenerasi
5. Solusi Optimum Ganda 6. Rute Terlarang
3.3 METODE NORTH WEST CORNER (Mencari Solusi Awal)
1. Mulai pada pojok kiri atas dan alokasikan sebanyak mungkin pada X11 tanpa menyimpang
dari kendala penawaran atau permintaan (artinya X11 di tetapkan sama dengan yang terkecil
diantara nilai S1 dan D1.
2. Ini akan menghabiskan penawaran pada sumber 1 dan atau permintaan pada tujuan 1. Akibatnya, tak ada lagi barang yang dapat dialokasikan ke kolom atau baris yang telah dihabiskan dan kemudian baris atau kolom itu dihilangkan. Kemudian alokasikan sebanyak mungkin ke kotak di dekatnya pada baris atau kolom yang tak dihilangkan. Jika baik kolom maupun baris telah dihabiskan, pindahlah secara diagonal ke kotak berikutnya.
3. Lanjutkan dengan cara yang sama sampai semua penawaran telah dihabiskan dan keperluan permintaan telah di penuhi.
ke Dari 1 2 3 Supply 1 120 120 2 30 50 80 3 20 60 80 Demand 150 70 60 280 3.4 STEPPING STONE
Suatu metode / teknik dalam masalah transportasi untuk mencari optimal solution (least Cost ) dengan cara trial dan error dari kolom – kolom yang masing-masing kosong yang memiliki biaya yang rendah pada contoh :
ke Dari 1 2 3 Supply 1 120 120 2 30 50 80 3 20 60 80 Demand 150 70 60 280
Alokasi Barang ini memiliki total cost (TC) 8 15 3 5 10 9 6 12 10 8 15 3 5 10 9 6 12 10
Diktat Program Linear Oleh Abdul Jabar Halaman ke - 18
TC = 8 (120) + 15 (30) + 10 (50) + 9 (20) + 10 (60) = 2690 (Apakah ini sudah minimum?) Jika IP ≥ 0, maka pemecahan sudah minimum.
Jika tidak, maka pemecahan dilanjutkan hingga semua IP ≥ 0. IP = Indeks Perbaikan = Nilai Zij-cij
LANGKAH-LANGKAH :
(1) Membuat jalur/lintasan mulai dari kotak non basis yang akan dihitung IP-nya.
(2) Dari suatu kotak nonbasis, ditarik garis lurus ke kotak basis terdekat dengan syarat kotak yang dihubungi mempunyai partner pada kolom/baris yang sama agar garis bisa terus bersambung sampai kembali ke kotak semula.
(3) Awal perjalanan diberi kode *.
(4) Menghitung nilai IP-nya. Dimulai dengan tanda - lalu + dan seterusnya berganti-ganti. Yang diperhitungkan adalah biaya (c).
ke Dari 1 2 3 Supply 1 120 2 2 120 2 30 50 1 80 3 -11 20 60 80 Demand 150 70 60 280
Ternyata nilai IP-nya masih ada yang negatif atau< nol, maka pemecahan belum optimum. Nilai Z1 masih belum minimum dan bisa dikecilkan lagi.
(5) Memilih kotak yang harus masuk basis atau keluar basis.
Kriteria: Kotak dengan nilai IP paling negatif harus masuk basis lebih dulu. Kalau sama besar, pilih sembarang aja.
Dalam kasus ini, kotak (3,1) harus masuk basis karena IP-nya paling negatif (-11). Cara menentukan kotak yang harus keluar basis:
(a) Dari cara mencari IP31, perhatikan biaya dengan tanda - yaitu c32 dan c21.
(b) Kita cari kotak yang memiliki nilai variabel terkecil, dalam hal ini adalah 20. Kita pilih x32 yang keluar
Ingat kotak yang masuk basis adalah kotak (3,1) dengan variabel x31.
Maka: nilai x21 sama dengan nilai minimum yang baru kita pilih.
x’31 = x32 = 20→ diisikan ke kotak (3,1)
Nilai variabel lain yang terlibat pembentukan jalur didapat dengan aturan: Tanda biaya -⇒ nilai variabel baru = nilai variabel lama – nilai minimum. Tanda biaya +⇒ nilai variabel baru = nilai variabel lama + nilai minimum. Sehingga,
TC = 25 (30) + 40 (15) + 15 (10) + 30 (35) = 2450 3.5 Metode VAM (Vogel Aprosimasi Metode)
Metode ini sudah lebih akurat dibanding dengan metode terdahulu (Stepping Stone) 8 15 3 5 10 9 6 12 10
Diktat Program Linear Oleh Abdul Jabar Halaman ke - 19
Adapun langkah-langkahnya :
1. Buatlah table / bagan kebutuhan VS kapasitas.
Sumber K L M Kapasitas Produksi Index Baris A 15 20 10 40 5 B 10 15 25 60 5 C 20 30 40 50 10 Kebutuhan 30 45 75 Xam = 40 Index Kolom 5 5 15
2. Buat selisih dua harga terkecil dan terkecil kedua untuk setiap baris dan kolom
Baris A : 15 – 10 = 5 Baris B : 15 – 10 = 5 Baris C : 30 – 20 = 10 Kolom K : 15 – 10 = 5 Kolom L : 20 – 15 = 5 Kolom M : 25 – 15 = 15
3. Cari nilai terbesar dari nilai – nilai pada langkah – langkah 2
4. Karena nilai terbesar adalah 15 pada kolom 3 maka cari biaya terkecil dari nilai pada kolom ke 3 dan diberi kotak biaya terkecilnya
Biaya terkecilnya adalah 10 à kapasitas : 40
Kebutuhan : 75
5. Hapus Baris A karena sudah terpakai habis
Sumber K L M Kapasitas Index
B 10 15 25 60 5
C 20 30 40 50 10
Kebutuhan 30 45 35 Xbl = 45
Index 10 15 15
6. Ulangi Langkah 2 dengan melihat table di atas
Baris B = 15 – 10 = 5
Baris C = 30 – 20 = 10
Kolom K = 20 – 10 = 10
Kolom L = 30 – 15 = 15
Kolom M = 40 – 25 = 15
7. Index terbesar adalah 15 pada kolom L & M
Karena index sama maka cari yang biaya terkecil à Kolom L
8. Biaya = 15 menghubungkan kapasitas 60
Cari yang terkecil untuk dialokasikan
Kebutuhan 45
9. Hapus Kolom L (Karna sudah habis terpakai )
Sehingga : K M Kapasitas Index B 10 25 15 15 C 20 40 50 20 30 35 Xck = 30 Index 10 15 Baris B = 25 – 10 = 15
Baris C = 40 – 20 = 20 à Index terbesar maka biaya terkecil adalah 20 yang menghubungkan menghubungkan kapasitas 50
Diktat Program Linear Oleh Abdul Jabar Halaman ke - 20
Cari yang terkecil untuk dialokasikan
Kebutuhan 30 Hapus kolom K M kapasitas B 25 15 C 40 20 XBM = 15 XCM = 20 TC = 40 (10) + 45 (15) + 30 (20) + 15 (25) + 20 (40) = 2850 1 2 3 SUPPLY INDEKS BARIS 1 8 5 6 120 1 2 15 10 12 80 2 3 3 9 10 80 6 DEMAND 150 70 60 X31 = 80 INDEKS KOLOM 5 4 4 Z = 3.80 +... 1. Tentukan indeks 2. Pilih indeks terbesar 3. Pilih biaya terkecil 4. Pilih barang yang terkecil
5. Hapus baris atau kolom yang barangnya diambil
1 2 3 SUPPLY INDEKS BARIS 1 8 5 6 120 1 2 15 10 12 80 2 DEMAND 70 70 60 X11 = 70 INDEKS KOLOM 7 5 6 Z = 3.80 + 8.70 +... 2 3 SUPPLY INDEKS BARIS 1 5 6 50 1 2 10 12 80 2 DEMAND 70 60 X13 = 50 INDEKS KOLOM 5 6 Z = 3.80 + 8.70 + 6.50 + ... 2 3 SUPPLY INDEKS BARIS 2 10 12 80 2 DEMAND 70 10 X23 = 10 INDEKS KOLOM 10 12 Z = 3.80 + 8.70 + 6.50 + 12.10 + ... 2 SUPPLY INDEKS BARIS 2 10 70 10 DEMAND 70 X22 = 70 INDEKS KOLOM 10 Z = 3.80 + 8.70 + 6.50 + 12.10 + 10.70 = 1920 Proses VAM dapat diringkas sebagai berikut :
Diktat Program Linear Oleh Abdul Jabar Halaman ke - 21
1. Hitung Opportunity Cost untuk setiap baris dan kolom. Opportunity cost untuk setiap baris I dihitung dengan mengurangkan nilai cij terkecil pada baris itu dari nilai cij satu tingkat lebih besar pada baris yang sama. Opportunity cost kolom diperoleh dengan cara serupa.
2. Pilih baris atau kolom dengan opportunity cost terbesar (jika terdapat nilai kembar pilih secara sembarang). Alokasikan sebanyak mungkin ke kotak dengan nilai cij minimum (biaya paling kecil) pada baris atau kolom yang dipilih. Untuk Cij terkecil. Xij = Minimum [Si,Dj). 3. Sesuaikan penawaran dan permintaan untuk menunjukkan alokasi yang sudah dilakukan.
Hilangkan semua baris dan kolom dimana penawaran dan permintaan telah habis.
4. Jika semua penawaran dan permintaan belum dipenuhi, kembali ke langkah 1 dan hitung lagi opportunity cost yang baru.
Diktat Program Linear Oleh Abdul Jabar Halaman ke - 22
3.6 METODE MODI ( MODIFIED DISTRIBUTION )
Metode ini adalah mirip dengan stepping stone hanya saja dalam mencari biaya minimal menggunakan cara yang lebih pasti.
Perbaikan Contoh berikut :
A = 20 B = 5 C = 14 Kapasitas W = 0 (50) (40) 90 H = 15 -20 (60) 60 P = 5 (10) (40) 50 Kebutuhan 50 110 40 200
Langkah penyelesaian MODI
1. Lakukan pengisian awal (Nort West Corner)
2. Memberi bobot dari setiap baris dan setiap kolom. Ri + Kj = Cij ( Pada kotak-kotak yang terisi)
Ri = Index Baris
Kj = Index Kolom
Cij = Biaya di angkut atau satuan barang dari I ke j
3. Menentukan index perbaikan dengan mengikuti Cij – Ri – Kj (Pada kotak-kotak yang masih kosong)
4. Menentukan titik awal perubahan
- Bahwa perubahan dilakukan bila masih ada index perbaikan yang negative
- Bila ada beberapa index perbaikan yang negative maka titik awal perubahan di mulai pada perbaikan yang paling negative
5. Hitung TC untuk masing-masing perubahan dan perubahan berhenti bila tidak ada index perbaikan yang negative
Pada contoh tersebut maka : Langkah 2 RW + KA = CWA atau 0 + KA = 20 à KA = 20 RW + KB = CWB atau 0 + KB = 5 à KB = 5 RH + KB = CHB atau RH + 5 = 20 à RH = 15 RP + KB = CPB atau Rp + 5 = 10 à RP = 5 RP + KC = CPC atau 5 + KC = 19 à KC = 14 TC = 50 (20) + 40 (5) + 60 (20) + 10 (10) + 40 (19) = 3260 Langkah 3
Kotak Kosong Cij – Ri – Kj Nilai 1 Perbaikan
HA 15 - 15 – 20 - 20 PA 25 - 5 – 20 0 WC 8 - 0 - 14 - 6 HC 10 - 15 - 14 -19 20 15 5 8 20 25 10 10 19
Diktat Program Linear Oleh Abdul Jabar Halaman ke - 23
Langkah 4 memulai pengisian kotak HA
A = 0 B = 5 C = 14 Kapasitas W = 0 90 90 H = 15 50 10 -19 60 P = 5 10 40 50 Kebutuhan 50 110 40 200 TC 2 = 90 (5) + 50(15 + 10 (20) + 10(10) + 40(19) = 2260
Index perbaikan Cij – Ri – Kj hanya untuk kotak yang kosong
Kotak Cij – Ri – Kj Index Perbaikan
WA 20 – 0 – 0 20
WC 8 – 0 – 14 -6
HC 10 – 15 – 14 - 19
PA 25 – 5 – 0 20
Titik awal perbaikan dimulai pada kotak HC dimana kotak HC memiliki tetangga terdekat (membentuk segi empat dengan tiga kotak lainnya yang terisi)
TC = 90 (5) + 50(15) + 10(10) + 20(10) + 30(19) = 2070
Karena index perbaikan masih ada yang negative maka :
A = 19 B = 5 C = 14 Kapasitas W = 0 90 -6 90 H = -4 50 10 60 P = 5 20 30 50 Kebutuhan 50 110 40 200
1. Penentuan index baris dan kolom yang baru Ri + Kj = Cij à hanya untuk kotak yang terisi RW + KB = 5 à 0 + KB = 5 KB = 5
RP + KC = 19 à 5 + KC = 19 KC = 14 RH + KC = 10 à 10 + 14 = -4
RH + KA = 15 à -4 + KA = 15 à KA = 19 2. Index Perbaikan
Kotak Cij – Ri – Kj Index Perbaikan
WA 20 – 0 – 0 20 20 15 5 8 20 25 10 10 19 20 15 5 8 20 25 10 10 19
Diktat Program Linear Oleh Abdul Jabar Halaman ke - 24 WC 8 – 0 – 14 -6 HB 20 – 15 – 5 0 PA 25 – 5 – 0 20 A = 13 B = 5 C = 8 Kapasitas W = 0 60 30 90 H = 2 50 10 60 P = 5 50 50 Kebutuhan 50 110 40 200 TC = 60 (5) + 30(8) + 50(15) + 10(10) + 50(10) = 1890
1. Karena masih ada yang negative – 6 maka : RW = 0 2. Tentukan lagi index baris dan kolom baru
Ri + kj = Cij RW + KB = 5 à 0 + KB = 5 KB = 5 Rp + KB = 10 à Rp + 5 = 10 à KB = 5 RW + KC = 8 à 0 + Kc = 8 à KC = 8 RH + KC = 10 à RH + 8 = 10 RH = 2 RH + KA = 15 à 2 + KA = 15 à KA = 13
3. Kotak Cij – Ri – Kj Index Perbaikan
WA 20 – 0 – 19 1
HB 20 – (-4) – 5 19
PA 25 – 5 – 19 1
PC 19 – 5 – 14 0
Sudah OPTIMAL sebab tidak ada lagi index perbaikan yang negatif SOAL LATIHAN
1. Berikut tabel transportasi Ke Dari Gudang A C1 = Gudang B C2= Gudang C C3= Kapasitas Pabrik Pabrik 1 R1= Rp 3200 Rp 3300 Rp 3400 106 Pabrik 2 R2= Rp 3600 Rp 4200 Rp 3800 132 Pabrik 3 R3= Rp 3400 Rp 3700 Rp 4000 127 Kebutuhan Gudang 122 152 91 365 Ke Dari Gudang A C1 = 3200 Gudang B C2= 3800 Gudang C C3=4100 Kapasitas Pabrik Pabrik 1 R1= 0 Rp 3200 (106) Rp 3300 -500 Rp 3400 -700 106 Pabrik 2 R2= 400 Rp 3600 (16) Rp 4200 (116) Rp 3800 -700 132 Pabrik 3 R3= -100 Rp 3400 300 Rp 3700 (36) Rp 4000 (91) 127 20 15 5 8 20 25 10 10 19
Diktat Program Linear Oleh Abdul Jabar Halaman ke - 25
Kebutuhan
Gudang 122 152 91 365
Selesaikan dengan metode: a. NWC
b. Biaya terkecil c. MODI
2. Produksi pabrik A, B, C adalah sebagai berikut:
Pabrik Kapasitas produksi tiap bulan
A B C 150 ton 40 ton 80 ton Jumlah 270 ton
Gudang pabrik tersebut mempunyai kapasitas sebagai berikut: Gudang Kebutuhan produksi tiap bulan
H I J 110 ton 70 ton 90 ton Jumlah 270 ton
Biaya untuk mendistribusikan barang dari pabrik ke gudang : Ke
Dari
Biaya tiap ton (Rp)
Gudang H Gudang I Gudang J
Pabrik A 27000 23000 31000
Pabrik B 10000 45000 40000
Pabrik C 30000 54000 35000
a. Buat tabel awal transportasi
b. Selesaikan dengan metode biaya terkecil dan optimalkan dengan metodeMODI c. Selesaikan dengan metode VAM
K1 = 8 K2 = 7 K3 = 14 Kapasitas B1 = 0 (80) (20) 8 100 B2 = 2 -1 (90) 4 90 B3 = -4 (5) -5 (75) 80 Kebutuhan 85 110 75 270 K1 = 8 K2 = 7 K3 = 6 Kapasitas B1 = 0 (5) (20) (75) 100 B2 = 2 -1 (90) -4 90 B3 = -4 (80) -5 -8 80 Kebutuhan 85 110 75 270 Z = 1760 Bi + Kj = cij IPij = Bi + Kj – cij 8 11 7 6 9 4 8 12 10 8 11 7 6 9 4 8 12 10
Diktat Program Linear Oleh Abdul Jabar Halaman ke - 27
BAB IV PENUGASAN
Tujuan dari Metode Penugasan adalah bagaimana menempatkan tenaga ahli pada bidang yang telah ditentukan agar biaya lebih meinimum. Penempatan karyawan tidak boleh asal dilakukan saja, sebab kalau cara penempatannya berbeda akan membawa konsekuensi hasil atau pengorbanan yang berbeda pula. Karyawan yang kita alokasikan secara optimal, artinya kalau memakan biaya / pengorbanan kita usahakan sekecil-kecilnya dan menghasilkan manfaat kita usahakan sebesar-besarnya.
Cara pengalokasian karyawan dapat dilakukan dengam menggunakan algoritma. Biasanya yang digunakan sebagai ukuran untuk menentukan efisiensi dan tidaknya adalah uang. Metode algoritma yang digunakan disini sering juga disebut sebagai Hungarian Methode.
Algoritma dalam penyelesaian Penugasan ada dua cara : A. Algoritma dengan Tujuan Meminimumkan B. Algoritma dengan Tujuan Memaksimalkan 4.1 Algoritma dengan Tujuan Meminimumkan
Dalam model ini tujuan kita meminimumkan pengorbanan biasanya dalam bentuk biaya untuk menyelesaikan suatu pekerjaan oleh seorang karyawan.
Dalam penempatan karyawan yang paling cocok adalah satu pekerjaan ditangani satu orang karyawan.
Contoh :
Suatu Penugasan memiliki 4 orang karyawan yang akan ditugaskan untuk menyelesaikan 4 macam tugas. Satu karyawan harus mengerjakan satu macam pekerjaan. Dan biaya penyelesaikan pekerjaan itu oleh tiap karyawan seperti terlihat pada table berikut :
Untuk melakukan alokasi penugasan karyawan yang optimal dengan langkah-langkah sebagai berikut :
1. Membuat Tabel Opportunity Cost dengan mengurangi elemen tiap baris dengan elemen terkecil dari baris itu. Sehingga Menghasilkan Tabel berikut :
2. Membuat Total Opportunity Cost Matrik
- Dari Tabel Opportunity Cost disetiap kolom harus memiliki paling sedikit 1 elemen benilai nol.
- Ternyata pada kolom ketiga belum ada elemen bernilai nol, maka harus kita dibuat agar memiliki nilai nol dengan cara : Mengurangi elemen pada kolom tersebut dengan nilai paling kecil di kolom tersebut.
Setelah semua memiliki nilai nol disetiap kolom, maka diperoleh table TotalOpportunity
Cost Matrix sebagai berikut :
Pekerja Karywan I II III IV
Dalam Rupiah A B C D 20 15 10 25 28 13 21 20 25 13 20 23 24 11 30 20 Pekerja Karywan I II III IV Dalam Rupiah A B C D 0 4 0 5 8 2 11 0 5 2 10 3 4 0 20 0
Diktat Program Linear Oleh Abdul Jabar Halaman ke - 28
3. Menarik Garis untuk meliput angka nol
Setelah semua baris dari kolom memiliki angka nol, maka tariklah garis seminimum mungkin, baik vertical maupun horizontal yang bisa menghubungkan angka nol.
Apakah penugasan sudah optimal? Belum optimal karena jumlah garis yang dibuat itu masih lebih kecil dibanding dengan jumlah baris atau kolom yang belum terliput garis.
Untuk merubah table diatas dilakukan langkah sebagai berikut :
• Pilih angka terkecil diantara semua angka yang belum terliput dengan garis dan kurangkan semua angka yang belum terliput garis dengan angka terkecil tersebut.
• Angka yang terliput dengan garis vertical dan horizontal, tambahkan dengan angka terkecil yang belum terliput dengan garis, sehingga menghasilkan table Perubahan Total Opportunity Cost Matrix sebagai berikut :
Tabel diatas sudah optimal, karena garis yang dibuat sudah 4 garis, sama dengan jumlah baris atau jumlah kolom.
Setelah itu letakkan karyawan pada salah satu pekerjaan yang nilainya pada Total
Opportunity Cost = 0 (Cari Biaya Terendah) tiap kolom atau baris, dan satu pekerjaan bisa
diisi oleh satu orang saja dan tambahkan semua biaya agar diperoleh biaya keseluruhan sebagai berikut :
Karyawan Tugas yang ditempati Biaya yang dikeluarkan
A III Rp. 25
B IV Rp. 11
C I Rp. 10.
D II Rp. 20
Jumlah Rp. 66
Biaya yang tercantum pada kolom ke 3 merupakan biaya yang diambil dari Tabel Biaya Awal Penugasan.
Jumlah biaya Rp. 66 merupakan biaya termurah dibanding dengan semua alternative lain. Pekerja Karywan I II III IV Dalam Rupiah A B C D 0 4 0 5 8 2 11 0 3 0 8 1 4 0 20 0 Pekerja Karywan I II III IV Dalam Rupiah A B C D 0 4 0 5 8 2 11 0 3 0 8 1 4 0 20 0 Pekerja Karywan I II III IV Dalam Rupiah A B C D 0 7 0 8 5 2 8 0 0 0 5 1 1 0 17 0
Diktat Program Linear Oleh Abdul Jabar Halaman ke - 29
4.2 Algoritma dengan Tujuan Memaksimalkan
Dalam model ini tujuan kita Memaksimalkan keuntungan, bila kita menganggap bahwa pekerjaan dalam menempatkan karyawan menguntungkan bagi karyawan.
Dalam penempatan karyawan yang paling cocok adalah satu pekerjaan ditangani satu orang karyawan.
Contoh :
Suatu Penugasan memiliki 4 orang karyawan yang akan ditugaskan untuk menyelesaikan 4 macam tugas. Satu karyawan harus mengerjakan satu macam pekerjaan. Dan biaya penyelesaikan pekerjaan itu oleh tiap karyawan seperti terlihat pada table berikut :
Untuk melakukan alokasi penugasan karyawan yang optimal dengan yang menguntungkan perusahaan maka langkah-langkah penugasan sebagai berikut :
1. Membuat Tabel Opportunity Loss Matrik dengan mencari elemen terbesar dibaris itu dan mengurangkan dengan nilai elemen tiap baris.. Sehingga Menghasilkan Tabel berikut :
2. Membuat Total Opportunity Loss Matrik
a. Dari Tabel Opportunity Loss Matrik disetiap kolom harus memiliki paling sedikit 1
elemen benilai nol (Langkah sama dengan algoritma meminimumkan)
b. Ternyata pada kolom ketiga belum ada elemen bernilai nol, maka harus kita dibuat agar memiliki nilai nol dengan cara : Mengurangi elemen pada kolom tersebut dengan nilai paling kecil di kolom tersebut.
Setelah semua memiliki nilai nol disetiap kolom, maka diperoleh table TotalOpportunity
Loss Matrix sebagai berikut :
3. Menarik Garis untuk meliput angka nol
Setelah semua baris dari kolom memiliki angka nol, maka tariklah garis seminimum mungkin, baik vertical maupun horizontal yang bisa menghubungkan angka nol.
Pekerja Karywan I II III IV
Dalam Rupiah A B C D 20 28 16 26 24 20 18 30 20 18 14 16 16 30 16 32 Pekerja Karywan I II III IV Dalam Rupiah A B C D 4 2 2 6 0 10 0 2 4 12 4 16 8 0 2 0 Pekerja Karywan I II III IV Dalam Rupiah A B C D 4 2 2 6 0 10 0 2 0 8 0 12 8 0 2 0 Pekerja Karywan I II III IV Dalam Rupiah A B C D 4 2 2 6 0 10 0 2 0 8 0 12 8 0 2 0
Diktat Program Linear Oleh Abdul Jabar Halaman ke - 30
Apakah penugasan sudah optimal? Belum optimal karena jumlah garis yang dibuat itu masih lebih kecil dibanding dengan jumlah baris atau kolom yang belum terliput garis.
Untuk merubah table diatas dilakukan langkah sebagai berikut :
• Pilih angka terkecil diantara semua angka yang belum terliput dengan garis dan kurangkan semua angka yang belum terliput garis dengan angka terkecil tersebut.
• Angka yang terliput dengan garis vertical dan horizontal, tambahkan dengan angka terkecil yang belum terliput dengan garis, sehingga menghasilkan table Perubahan Total Opportunity Cost Matrix sebagai berikut :
Tabel diatas sudah optimal, karena garis yang dibuat sudah 4 garis, sama dengan jumlah baris atau jumlah kolom.
Setelah itu letakkan karyawan pada salah satu pekerjaan yang nilainya pada Total
Opportunity Cost = 0 (Cari Biaya Terendah) tiap kolom atau baris, dan satu pekerjaan bisa
diisi oleh satu orang saja dan tambahkan semua biaya agar diperoleh biaya keseluruhan sebagai berikut :
Karyawan Tugas yang ditempati Biaya yang dikeluarkan
A II Rp. 24
B I Rp. 28
C III Rp. 14
D IV Rp. 32
Jumlah Rp.96
Biaya yang tercantum pada kolom ke 3 merupakan biaya yang diambil dari Tabel Biaya Awal Penugasan.
Jumlah biaya Rp. 96 merupakan biaya termurah dibanding dengan semua alternative lain. SOAL LATIHAN
1. Sebuah perusahaan pengecoran logam mempunyai empat jenis mesin yang diberi nama M1, M2, M3 dan M4. Setiap mesin mempunyai kapasitas yang berbeda dalam pengoperasiannya. Dalam minggu mendatang perusahaan mendapatkan pesanan untuk menyelesaikan empat jenis pekerjaan (job) yaitu J1, J2, J3 dan J4. Biaya pengoperasian setiap pekerjaan oleh keempat mesin dapat dilihat dalam tabel berikut:
Mesin Job M1 M2 M3 M4 J1 210 150 180 130 J2 140 160 200 190 J3 150 175 220 200 J4 200 115 160 190
Masalahnya adalah bagaimana menugaskan keempat mesin untuk menyelesaikan keempat jenis pekerjaan agar total biaya pekerjaan minimum!
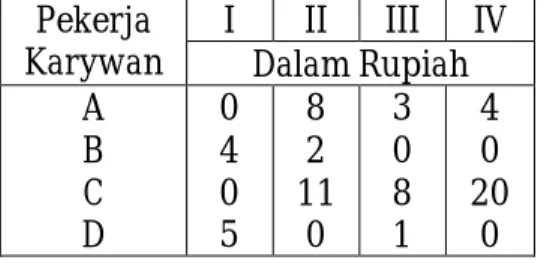
2. Seorang pengusaha konveksi mempunyai 4 orang karyawati yangmemproduksi 4 jenis produk. Jumlah produk yang dihasilkan masing-masingkaryawan tiap bulannya dapat dilihat pada tabel berikut: Pekerja Karywan I II III IV Dalam Rupiah A B C D 4 0 2 4 0 8 0 0 0 6 0 10 10 0 4 0
Diktat Program Linear Oleh Abdul Jabar Halaman ke - 31
Produk
Karyawati Celana panjang Rok Hem Baju safari
Ulfah 6 7 10 9
Salma 2 8 7 8
Rana 8 9 5 12
Nabila 7 11 12 3
Diktat Program Linear Oleh Abdul Jabar Halaman ke - 32
DAFTAR PUSTAKA
Taha,H. Operation Research An Introduction, Edisi 4, Macmillan,New York Bronson, R.Theory and Problem of Operation Research ,McGraw-Hill, Singapore.
Pangestu,S., Asri,M. dan Handoko, H. 2000.Dasar-DasarOperation Research, Yogyakarta. Aminudin.2005. Prinsip-Prinsip Riset Operasi, Erlangga.