BAB II. Konsep Dasar

(1)

Algoritma pewarnaan titik pada graf dengan sisi kabur untuk pengaturan lampu lalu lintas 5

BAB II

Konsep Dasar

2.1 Definisi Graf

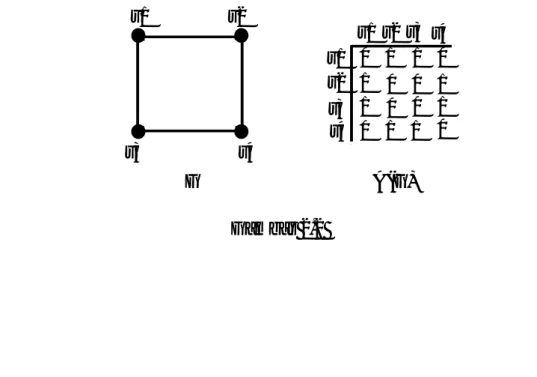
Graf G = (VG ,EG) terdiri dari himpunan tidak kosong VG , disebut himpunan

titik, dan himpunan EG, disebut himpunan sisi, yang beranggotakan pasangan tak

terurut dari anggota berbeda di VG. Sebagai contoh, graf G = (VG, EG) dengan VG =

{v1 , v2 , v3} dan EG = {v1v2, v1v3 } digambarkan pada gambar 2.1.

Jika u, v

∈

VG dan uv

∈

EG, maka u dan v disebut ujung-ujung dari uv.

Dengan demikian, pada graf G di atas, sisi v1v2 mempunyai ujung v1 dan v2, sisi v1v3

mempunyai ujung v1 dan v3.

Titik v dikatakan terkait oleh sisi e jika titik tersebut merupakan ujung dari sisi e. Dua buah sisi dikatakan saling terkait jika keduanya memiliki salah satu ujung yang sama. Graf sederhana adalah graf yang tidak ada dua sisi yang memiliki sepasang ujung yang sama. Untuk selanjutnya, setiap graf yang dimaksud dalam tugas akhir ini adalah graf sederhana.

Graf dinamakan demikian dikarenakan graf dapat direpresentasikan secara grafis. Untuk graf G, setiap u V

∈

G digambarkan dengan titik dan setiap uv E

∈

G,

digambarkan dengan garis yang menghubungkan titik u dengan titik v. Tidak ada cara yang unik dalam menggambarkan graf. Posisi titik dan garis dapat digambar secara bebas.

(2)

Algoritma pewarnaan titik pada graf dengan sisi kabur untuk pengaturan lampu lalu lintas 6 v1 v2 v3 Gambar 2.1. Graf G.

Dua buah titik yang berbeda dikatakan bertetangga jika dua titik tersebut dihubungkan oleh suatu sisi. Pada gambar diatas, v1 bertetangga dengan v2 dan v3; v2

bertetangga dengan v1, dan v3 bertetangga dengan v1. Pada graf sederhana, derajat dari

titik v didefinisikan sebagai banyaknya tetangga dari titik v.

Matriks ketetanggaan A(G)=[aij] dari G dengan n = |VG| dan VG = {v1, ...,vn}

adalah suatu matriks berukuran n x n dengan:

1, jika ; 0 , jika ; i j G i j G v v E ij v v E

a

∈ ∉

⎧⎪

= ⎨

⎪⎩

Gambar 2.2 memperlihatkan suatu graf beserta matriks ketetanggaannya.

v1 v2 v3 v4 v1 v1 v2 v2 v3 v3 v4 v4 1 0 1 1 1 0 0 0 0 1 0 0 1 0 1 1 G A(G) Gambar 2.2

(3)

Algoritma pewarnaan titik pada graf dengan sisi kabur untuk pengaturan lampu lalu lintas

7

2.2 Himpunan Kabur (Fuzzy Set)

Teori himpunan kabur merupakan suatu teori tentang konsep penilaian yang batasannya tidak begitu jelas atau memiliki elastisitas. Dengan nilai/derajat elastisitas ini himpunan kabur mempertegas sesuatu yang kabur, misalkan terdapat kalimat atau pernyataan ‘setengah baya’. Pertanyaan yang muncul, “Berapa kriteria umur yang dapat dikatakan setengah baya ?”. Dapat ditentukan bahwa orang yang disebut ‘setengah baya’ mempunyai kriteria usia berkisar antara 35-55 tahun. Bagaimana dengan yang berusia 34 tahun. Dapatkah dikatakan ‘setengah baya’?. Crisp set atau sistem jangkauan menjawab dengan tegas bahwa 34 tahun tidak termasuk ‘setengah baya’ (bernilai 0), namun himpunan kabur (fuzzy set) dapat menyatakan dengan leluasa bahwa usia 34 tahun juga termasuk setengah baya dengan derajat tertentu.

Himpunan kabur adalah sekumpulan obyek x dengan masing-masing obyek memiliki nilai keanggotaan (membership function), disimbolkan dengan μ( )x . Nilai ini dipetakan ke dalam range [0,1]. Jika Χ adalah sekumpulan obyek, maka himpunan kabur A pada X adalah himpunan dengan sepasang anggota.

{( , _A( )) } A= x μ x x∈ Χ

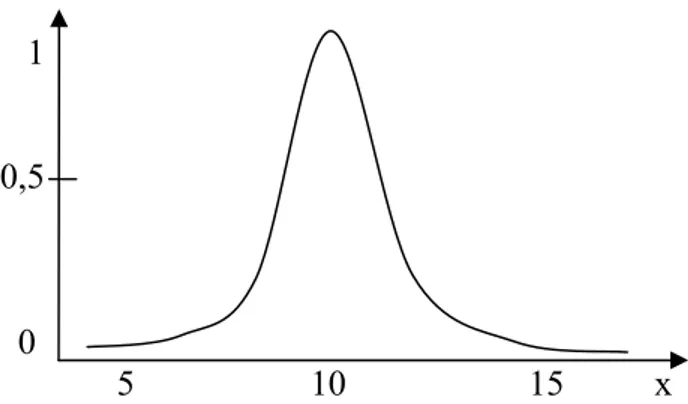
Sebagai contoh, jika ingin didefinisikan himpunan bilangan yang mendekati 10, maka dapat dituliskan dengan menggunakan himpunan kabur sebagai berikut :

2 1

{( , _A( )) _A( ) (1 ( 10) ) , } A= x μ x μ x = + −x − x X∈ .

(4)

8 Grafik yang mewakili nilai μ_A( )x adalah :

1 0,5 0 5 10 15 x

Gambar 2.3. Grafik kabur untuk bilangan yang mendekati 10

2.2.1 Operasi Himpunan Kabur

Misalkan A dan B himpunan kabur pada semesta pembicaraan X.  Himpunan kabur A dan B dikatakan sama ( A=B ) jika

( ) ( ), A x B x x X μ =μ ∀ ∈  A termuat di B (A⊆B) jika ( ) ( ), A x B x x X μ ≤μ ∀ ∈

 Gabungan (union) dari himpunan kabur A dan B, dinotasikan dengan A∪B, didefinisikan sebagai A B∪ ={( ,x μ_{A B}_∪ ( ))x x X∈ } dengan

( ) ( ( ) ( )), A B x A x B x x X

μ _∪ = μ ∨μ ∀ ∈

 Irisan (intersection) dari himpunan kabur A dan B, dinotasikan dengan A B∩ , didefinisikan sebagai A B∩ ={( ,x μ_{A B}_∩ ( ))x x X∈ } dengan

( ) ( ( ) ( )), A B x A x B x x X

μ _∩ = μ ∧μ ∀ ∈

 Komplemen dari himpunan kabur A, dinotasikan A , didefinisikan sebagai {( , _A( )) }

(5)

Algoritma pewarnaan titik pada graf dengan sisi kabur untuk pengaturan lampu lalu lintas 9 ( ) 1 _A( ), A x x x X μ = −μ ∀ ∈

 Produk (product) dari himpunan kabur A dan B, dinotasikan dengan AB, didefinisikan sebagai AB={( ,x μ_AB( ))x x X∈ } dengan

( ) ( ) ( ), AB x A x B x x X

μ =μ μ ∀ ∈

Contoh :

Misalkan X ={1, 2,3, 4,5, 6}.

Misalkan pula μ_A(3) 0.8, = μ_A(6) 0.6= , (3) 0.7, (6) 0.5μ_B = μ_B = , maka :

μ_{A B}_∪ (3) 0.8= μ_{A B}_∩ (6) 0.5=

μ_A(1) 1, (3) 0.2= μ_A = μ_AB(3) 0.56, (6) 0.3= μ_AB =

2.2.2 Fungsi Keanggotaan

Fungsi keanggotaan (membership function) yang sering digunakan terdiri dari beberapa jenis, yaitu :

1. Fungsi-S (S-function)

Aturan dari fungsi-S ini adalah :

2 2 0 jik 2[( ) /( )] jika ( ; , , ) 1 2[( ) /( )] jika 1 jik a a x a x a c a a x b S x a b c x a c a b x c x c < ⎧ ⎪ ₋ ₋ _≤ ⎪ = ⎨ ₋ ₋ ₋ _{≤ ≤}≤ ⎪ ⎪ _> ⎩ dengan b = (a+c)/2

(6)

10 Gambar grafik fungsi keanggotaannya adalah :

1

S

0

a b c x

Gambar 2.5. Grafik fungsi keanggotaan S

Contoh penerapan dari fungsi S :

Χ adalah himpunan yang terletak antara 0 sampai 120, dimana x mewakili usia. A adalah himpunan kabur yang dianggap mempunyai usia tua.

2 1 0 0 40 ( ) {1 [( 40) / 5] } 40 120 A x x x x μ _{= ⎨}⎧ ₋ ₋ ≤ ≤ + − ≤ ≤ ⎩

Di sini terlihat bahwa untuk usia yang melebihi usia 40, nilai anggotanya terus naik dan pada usia 45 akan mempunyai nilai 0,5. Jadi pada usia 45 merupakan titik penyeberangan dan pada usia selanjutnya, nilai keanggotaan akan terus naik menuju nilai 1. Jika digambarkan nilai fungsi >0 di atas, maka bentuknya akan mendekati bentuk fungsi S.

(7)

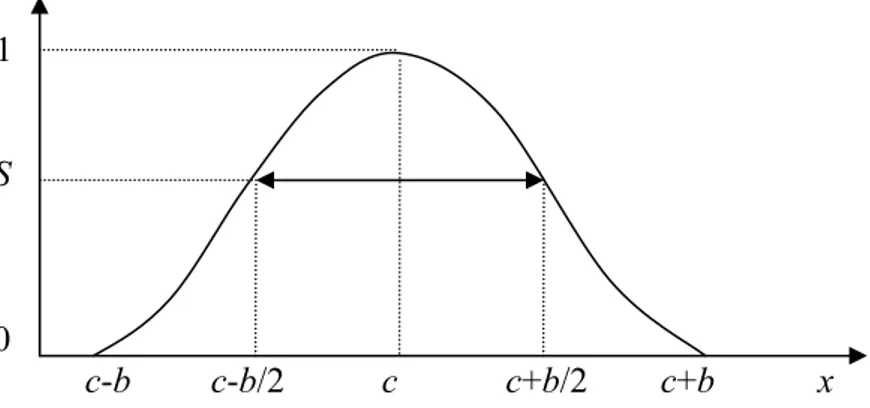
11 2. Fungsi-π (π-function)

Aturan fungsi-π diperoleh dari modifikasi aturan fungsi-S, sebagai berikut : ( ; , / 2, ) jika ( ; , ) 1 ( ; , / 2, ) jika S x c b c b c x c x b c S x c c b c b x c π _{= ⎨}⎧ − − ≤ − + + ⎩ ≥

Gambar grafik fungsi keanggotaannya adalah : 1 S 0 c-b c-b/2 c c+b/2 c+b x

Gambar 2.6. Grafik fungsi keanggotaan π

Contoh penerapan fungsi π :

Misalkan X adalah himpunan yang beranggotakan bilangan yang terletak antara 70 sampai 110. A adalah himpunan kabur yang diasumsikan sebagai bilangan yang mendekati nilai 90. Carilah nilai dari masing-masing nilai himpunan X. Misalkan fungsi keanggotaan adalah μ_A( )x , maka setiap anggota himpunan A dapat ditulis sebagai berikut :

{( , _A( )) |

A= x μ x x X∈ dengan μ_A( ) {1 [1/100( - 90)2]}-1x = + x .

Di sini terlihat bahwa bilangan 90 memiliki nilai tertinggi yaitu 1, sedangkan nilai keanggotaan yang lain sesuai dengan fungsi keanggotaannya. Di sini juga terlihat

(8)

12 bahwa nilai-nilai di atas jika digambarkan akan menghasilkan bentuk mendekati bentuk fungsi π.

3. Fungsi keanggotaan segitiga (Triangular membership function) Aturan untuk bentuk segitiga ini adalah :

0 jika , ( ; , , ) ( ) /( ) jika ( ) /( ) jika x a x c x a b c x a b a a x b c x c b b x c < > ⎧ ⎪ Τ =_⎨ − − ≤ ≤ ⎪ − − ≤ ≤ ⎩

Gambar grafik fungsi keanggotaannya adalah :

1

0 a b c

Gambar 2.7. Grafik fungsi keanggotaan segitiga

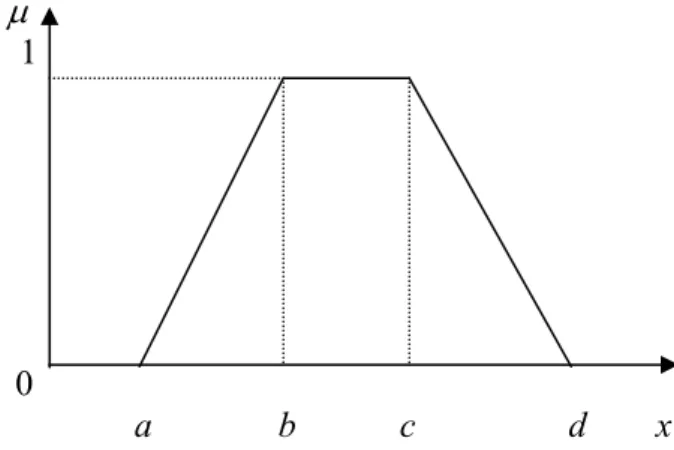
4. Fungsi keanggotaan trapesium (Trapezoidal membership function) Aturan untuk bentuk trapesium ini adalah :

0 jika , 1 jika ( ; , , , ) ( ) /( ) jika ( ) /( ) jika x a x d b x c x a b c d x a b a a x b d x d c c x d < < ⎧ ⎪ _{≤ ≤} ⎪ Ζ _{= ⎨} − − ≤ ≤ ⎪ ⎪ − − ≤ ≤ ⎩

(9)

13 Gambar grafik fungsi keanggotaannya adalah :

μ 1

0

a b c d x

Gambar 2.8. Grafik fungsi keanggotaan trapesium

2.2.3 Variabel Linguistik

Variabel linguistik adalah variabel yang bernilai kata/kalimat, bukan angka. Sebagai alasan menggunakan kata/kalimat daripada angka karena peranan linguistik kurang spesisifik dibandingkan angka, namun informasi yang disampaikan lebih informatif. Variabel linguistik ini merupakan konsep penting dalam logika kabur dan memegang peranan penting dalam beberapa aplikasi.

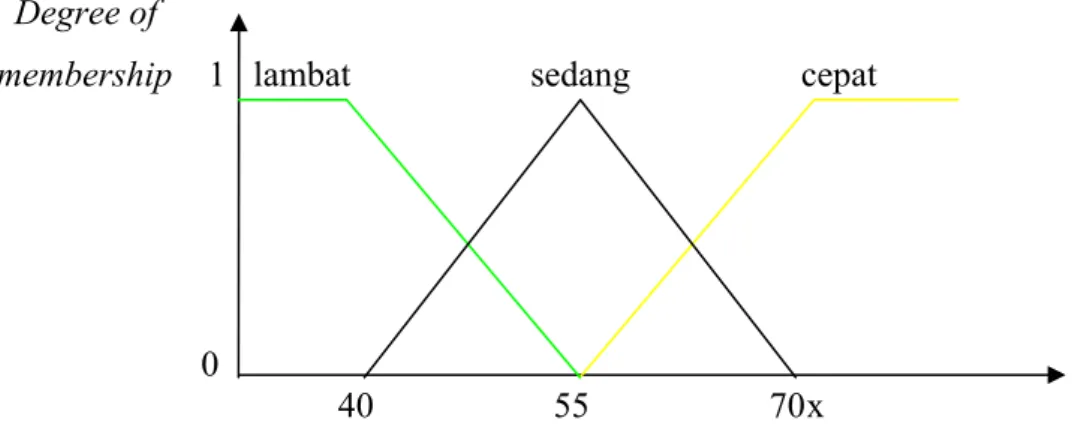
Jika “kecepatan” adalah variabel linguistik, maka nilai linguistik untuk variabel kecepatan adalah, misalnya “lambat”, “sedang”, “cepat”. Hal ini sesuai dengan kebiasaan manusia sehari-hari dalam menilai sesuatu, misalnya : “Ia mengendarai mobil dengan cepat”, tanpa memberikan nilai berapa kecepatannya.

Konsep tentang variabel linguistik ini diperkenalkan oleh Lofti Zadeh. Variabel linguistik menurut Zadeh dikarakteristikkan oleh :

(10)

Algoritma pewarnaan titik pada graf dengan sisi kabur untuk pengaturan lampu lalu lintas 14 dengan : X = nama variabel.

T(x) atau T = semesta pembicaraan untuk x atau disebut juga nilai linguistik dari x .

U = jangkauan dari setiap nilai kabur untuk x yang dihubungkan dengan variabel dasar U.

M = aturan semantik yang menghubungkan setiap dengan artinya.

Χ

Sebagai contoh, jika X = “kecepatan”, dengan U[0, 100] dan T(kecepatan) = {lambat, sedang, cepat}, maka M untuk setiap X, M( )x adalah M(lambat), M(sedang), M(cepat), dengan :

M(lambat) = himpunan kaburnya “kecepatan dibawah 40 km/jam” dengan fungsi keanggotaan μ lambat.

M(sedang) = himpunan kaburnya “kecepatan mendekati 55 km/jam” dengan fungsi keangotaan μ sedang.

M(cepat) = himpunan kaburnya “kecepatan diatas 70 km/jam” dengan fungsi keanggotaan μ cepat.

(11)

15 Gambar grafik fungsi keanggotaannya sebagai berikut :

Degree of

membership 1 lambat sedang cepat

0

40 55 70 x

Gambar 2.4. Grafik fungsi keanggotaan kecepatan

2.3 Graf Kabur (Fuzzy Graph)

Graf ( ,G= V Eμ) terdiri dari himpunan tidak kosong V, disebut himpunan titik, dan himpunan E_μ, disebut himpunan sisi kabur, yang dapat dikarakteristikkan oleh matriks μ =(μij i j V),∈ dengan ({ , }) ij E i j μ =μ ∀i j V i, ∈ , ≠ j dan : E V V I

μ × → adalah fungsi keanggotaan.

Dari definisi diatas, μ_ij∈I merepresentasikan tingkat intensitas sisi {i,j}, . Di sini, fuzzy graph dapat pula dilambangkan dengan

, dengan

i j V∈ i≠ j G=( , )V μ .

Himpunan I tersusun secara linear, dengan demikian ekspresi "μ_ij≺μ_{i j}_{' '}" dapat dikatakan ”tingkat intensitas sisi {i,j} lebih kecil dari tingkat intensitas sisi {i’,j’}”.

Graf G=( , )V E dapat dipandang sebagai graf kabur G=( ,( )V μ_{ij i j V}_,_∈ ) dengan 1 jika , 0 jika , ij i j E i j E μ _{= ⎨}⎧ ∈ ∉ ⎩

(12)

16 Untuk ilustrasi, perhatikan graf kabur G=( , )V E dengan V = {v1, v2, v3, v4},

nilai fungsi keanggotaan 1 1 1 4 3 2

{ , , }

I = , dan tingkat intensitas sisi dinyatakan pada tabel 2.1. v1 v2 v3 v4 v1 0 1/2 1/4 1/4 v2 1/2 0 1/3 1/3 v3 1/4 1/3 0 1/2 v4 1/4 1/3 1/2 0 Tabel 2.1

a. Matriks ketetanggaan dengan tingkat intensitas sisi G 1 2 v1 v2 v3 v4 v1 0 1 0 0 v2 1 0 0 0 v3 0 0 0 1 v4 0 0 1 0 Tabel 2.2

Selanjutnya, dari matriks ketetanggaan ini dapat digambarkan dalam bentuk graf sebagai berikut : v1 Gambar 2.9. 1 2 μ = v2 v3 v4

(13)

17 b. Matriks ketetanggaan G dengan tingkat intensitas sisi 1

3 v1 v2 v3 v4 v1 0 1 0 0 v2 1 0 1 1 v3 0 1 0 1 v4 0 1 1 0 Tabel 2.3

Selanjutnya, dari matriks ketetanggaan ini dapat digambarkan dalam bentuk graf sebagai berikut : v1 v2 Gambar 2.10. 1 3 μ =

c. Matriks ketetanggaan dengan tingkat intensitas sisi G 1 4 v1 v2 v3 v4 v1 0 1 1 1 v2 1 0 1 1 v3 1 1 0 1 v4 1 1 1 0 Tabel 2.4

Selanjutnya, dari matriks ketetanggaan ini dapat digambarkan dalam bentuk graf sebagai berikut :

v3

(14)

Algoritma pewarnaan titik pada graf dengan sisi kabur untuk pengaturan lampu lalu lintas 18 v1 v2 Gambar 2.11. 1 4 μ =

2.4 Pewarnaan Titik

Misal G = (VG, EG) adalah suatu graf. Pewarnaan titik pada graf G adalah

suatu fungsi dari VG ke himpunan bilangan asli. Suatu pewarnaan titik pada graf G

dikatakan k-pewarnaan titik sejati jika titik-titik pada VG dapat dipetakan ke

himpunan k bilangan asli pertama dan memenuhi setiap dua titik yang bertetangga memperoleh warna berbeda.

Bilangan kromatik χ(G) merupakan bilangan asli terkecil k sehingga terdapat k-pewarnaan titik sejati. Suatu graf yang mempunyai bilangan kromatik k disebut graf k-kromatik. Gambar di bawah menunjukkan suatu graf 3-kromatik, karena titik-titik pada graf tersebut dapat diwarnai dengan 3 warna namun tidak dapat diwarnai dengan 2 warna. 1 1 2 2 3 3

Gambar 2.12. graf 3-kromatik

v3

(15)

19

2.5 Pewarnaan Titik Graf Fuzzy

Dalam pewarnaan titik graf fuzzy, konsep pewarnaan titik yang dilakukan sama dengan konsep pewarnaan titik pada graf biasa.

Sebagai contoh, misalkan terdapat suatu sistem lalu lintas sebagai berikut :

A

B D

Gambar 2.13. C

Sistem tersebut dapat dimodelkan dengan suatu graf kabur G=( ,V E_μ) dengan V = {AC, BC, DA, DB, DC} dan fungsi keanggotaan tingkat intensitas sisi di antara lintasan ini dituliskan sebagai berikut :

{ , , , , }

I = n l m h t .

n = null (satu lintasan dengan lintasan lainnya memiliki keterkaitan yang erat

saat tingkat kemacetan sangat tinggi).

l = low (satu lintasan dengan lintasan lainnya memiliki keterkaitan yang erat

saat tingkat kemacetan tinggi).

m = medium (satu lintasan dengan lintasan lainnya memiliki keterkaitan

yang erat saat tingkat kemacetan sedang).

h = high (satu lintasan dengan lintasan lainnya memiliki keterkaitan yang

(16)

20

t = total (satu lintasan dengan lintasan lainnya tidak saling terkait dalam

kondisi tingkat kemacetan sangat rendah)

AC BC DA DB DC AC 0 m n h m BC m 0 n n l DA n n 0 n n DB h n n 0 n DC m l n n 0 Tabel 2.5

Dari matriks ketetanggaan ini, dapat digambarkan dalam bentuk graf untuk setiap tingkat intensitas sisi sebagai berikut :

1. Matriks ketetanggaan G dengan tingkat intensitas sisi h

AC BC DA DB DC AC 0 0 0 1 0 BC 0 0 0 0 0 DA 0 0 0 0 0 DB 1 0 0 0 0 DC 0 0 0 0 0 Tabel 2.6

Selanjutnya, dari matriks ketetanggaan ini dapat digambarkan dalam bentuk pewarnaan graf sebagai berikut :

AC BC DC DB DA 1 1 1 1 1 Gambar 2.14. μ =h

(17)

21 2. Matriks ketetanggaan G dengan tingkat intensitas sisi m

AC BC DC DB DA 1 1 1 Gambar 2.15. μ =m

3. Matriks ketetanggaan G dengan tingkat intensitas sisi l

(18)

Algoritma pewarnaan titik pada graf dengan sisi kabur untuk pengaturan lampu lalu lintas 22 AC BC DC DB DA 1 3 1 1 3 Gambar 2.16. μ=l

Lengkapnya, akan diperoleh hasil sebagai berikut :

μ Eμ χμ AC BC DA DB DC n {AC,BC};{AC,DA};{AC,DB};{AC,DC};{BC,DA}; {BC,DB};{BC,DC};{DA,DB};{DA,DC};{DB,DC} 5 1 2 3 4 5 l {AC,BC};{AC,DB};{AC,DC};{BC,DC} 3 1 2 1 2 3 m {AC,BC};{AC,DB};{AC,DC} 2 1 2 1 2 2 h {AC,DB} 2 1 1 1 2 1 t _∅ 1 1 1 1 1 1 Tabel 2.9 Gambar 2.17. μ=n Gambar 2.18. μ= t BC DA DB DC AC BC DA DC DB AC 1 1 1 1 1 1 1 1 3 2 4 5 2 3 4 5

(19)

23

n

Dari tabel 2.9 diperoleh bilangan kromatik G , yaitu :

( ) {(1, ), (2, )(3, ), (4, ), (5, )}G t h l n

χ =

2.6 Algoritma Pewarnaan Titik

Salah satu metode pewarnaan titik adalah metode pewarnaan terurut SC (Sequential Coloring). Metode pewarnaan tersebut adalah sebagai berikut:

 Beri suatu urutan untuk titik-titik di G, misalkan urutan a0, a1, ..., an-1.

 Beri a0 warna terkecil, yaitu f(a0) = 1.

 Jika a1,…,ai-1 (i ≥ 1) telah menerima warna, maka untuk ai diberikan warna

terkecil yang tidak muncul pada tetangga ai.

Pada tahun 1979 Brelaz menemukan algoritma DSATUR (Degree of Saturation). Algoritma DSATUR merupakan algoritma pewarnaan terurut dengan membangun urutan titik-titik secara dinamis. Derajat saturasi dari suatu titik x yang dinotasikan dengan degs(x) adalah banyaknya warna berbeda yang sudah muncul pada

tetangga x. Langkah-langkah konstruksi pewarnaan f untuk titik-titik dari graf G dengan menggunakan algoritma DSATUR adalah sebagai berikut:

Pilih salah satu titik yang memiliki derajat terbesar. Titik tersebut diberi warna terkecil yaitu 1.

 Titik yang diwarnai selanjutnya ialah salah satu titik yang memiliki degs(x)

(20)

24 Selanjutnya diberikan beberapa definisi yang akan digunakan pada teorema berikutnya.

Definisi 3.1 Pewarnaan f1, f2, dari G = (V, E) dikatakan ekivalen jika f1 dan f2

mempartisi himpunan titik V berturut-turut menjadi U1, ..., Uk dan W1, ..., Wk dengan

|Ui| = |Wi| untuk i = 1, ..., k.

Definisi 3.2 Suatu pewarnaan f dari titik a0,…, an-1 dari graf G disebut ketat terhadap

urutan yang diberikan, jika :

f(ai) ≤ colors(i-1) + 1 untuk semua i = 0,1,…,n-1

dengan colors(j) untuk j = 0,1,...,n-2 merupakan banyaknya warna yang berbeda pada titik a0,…, aj, dan colors(-1) = 0.

Kemudian untuk mengkonstruksi suatu pewarnaan f untuk graf G yang menggunakan warna sebanyak bilangan kromatik χ(G), Brown memperkenalkan suatu algoritma. Algoritma ini menggunakan metode pewarnaan terurut dan penelusuran kembali (backtracking). Untuk efisiensi algoritma, cabang-cabang yang tidak diperlukan dari pohon pencarian dihindari dengan menggunakan teorema berikut.

Teorema 3.1 (Klotz[5]) Misal f adalah pewarnaan dari graf G, maka terdapat suatu

(21)

25

Bukti :

 Misal f(a0) = k1 > 1. Jika tidak ada titik yang mendapat warna 1, maka

ganti k1 dengan 1. Jika ada, maka tukar warna k1 dengan 1.

 Misal f telah ketat untuk semua titik a0,…, ai-1, i ≥ 1 dan misalkan

colors(i-1) = l.

 Jika f(ai) = k > l+1 dan tidak ada titik yang mempunyai warna l+1, maka

ganti warna k dengan l+1. Jika f(ai) = k > l+1 dan ada titik yang

mempunyai warna l+1, maka tukar warna k dengan l+1. ⁯

Konsep Algoritma Backtracking oleh Brown

Konsep algoritma backtracking yang dikemukakan oleh Brown berdasarkan 2 tahap, yaitu maju dan mundur.

Tahap Maju: Semua titik diwarnai satu per satu berdasarkan warna yang

mungkin hingga tidak ada lagi titik yang tidak memiliki warna.

Tahap Mundur: Pilih satu titik yang sudah diwarnai. Kemudian warnai titik

tersebut dengan warna lain yang berbeda dengan warna sebelumnya. Selanjutnya, titik-titik lain diwarnai kembali mengikuti langkah seperti pada tahap maju.

Backtrack: Apabila masih mungkin ditemukan pewarnaan pada graf G

yang lebih sedikit dari pewarnaan sebelumnya maka akan dilakukan suatu pewarnaan titik kembali. Proses ini dilakukan terus menerus dan berhenti apabila titik awal pewarnaan pada tahap maju tidak bisa diwarnai dengan warna yang lain.

(22)

26 Algoritma asli dari Brown dikembangkan lagi oleh Brelaz. Titik-titik dari graf disimpan dalam suatu array, misalkan A. Pertama, titik-titik tersebut diurutkan berdasarkan derajat yang tidak naik. Urutan ini lalu berubah secara dinamis. Misal A[0],…,A[i-1] telah mendapat warna dan misalkan banyaknya warna yang berbeda pada titik-titik ini adalah colors(i-1) = li. Himpunan warna bebas dari suatu titik x =

A[i], dinotasikan dengan U = freeColors(x), adalah himpunan bagian dari warna {1,2,…, li+1} yang tidak muncul pada tetangga x. Jika suatu batas atas, dinotasikan

dengan optColorNumber (χ(G)≤optColorNumber), telah didapat dari suatu pewarnaan f, maka semua warna ≥ optColorNumber dibuang dari U. Titik yang diwarnai selanjutnya adalah seperti pada DSATUR, yaitu titik yang memiliki derajat saturasi terbesar. Titik ini diwarnai dengan warna terkecil di U. Jika U kosong, maka suatu penelusuran kembali (backtrack) dilakukan. Algoritma ini disebut BSC (Backtracking Sequential Coloring) yang dapat mengkonstruksi suatu pewarnaan dari graf G dengan menggunakan warna sebanyak bilangan kromatik χ(G).

Algoritma BSC(Backtracking Sequential Coloring) [input]

n //banyak titik

A[i] , I = 0,1,…….,n-1 //array pengurutan derajat titik secara descending

[Procedure]

for i:=1 to n do //derajat saturasi setiap titik = 0 F[i]:=0;

(23)

27

start := 0; //index awal

optColorNumber := n + 1; //jumlah warna optimal.

v := A[0]; //titik yang akan diwarnai

colors(-1) := 0; //colors(j) = banyaknya warna di A[0],...,A[j] U := [1]; //variabel untuk himpunan warna bebas(terurut) freeColors[v] := U; //array untuk himpunan warna bebas dari v while (start>=0) do //setiap titik diwarnai pada loop dibawah ini back:=false;

for i:= start to n-1 do

if i>start then //cari titik yang belum diwarnai dan mempunyai derajat saturasi terbesar

v:=GetDSaturOne; // GetDSaturOne adalah fungsi untuk mencek derajat saturasi titik

U:=GetUOne; //GetUOne adalah fungsi untuk mencek freecolors titik

if U<>[] then //proses dijalankan jika U ≠ ∅ C:=MinValue(U); //warna bebas yang dipilih

F[v]:=C; //pewarnaan untuk titik v freeColors[v]:=U-[C];

l:=colors[i-1];

colors[i]:= max(C,l);

else //U = ∅ dilakukan penelusuran kembali,

mundur satu posisi start:=i-1;

(24)

28 back:=true;

break; //keluar dari loop for // akhir loop for

if back then

if start>=0 then

v:=A[start]; //titik awal yang baru

F[v]:=0; //hapus warna v

U:=freeColors[v];

else //loop diatas dilalui tanpa berhenti for i:=1 to n do

Fopt[i]:=F[i]; //menyimpan pewarnaan yang optimal pada saat ini

optColorNumber:=colors[n-1];

for i:=0 to n-1 do

if F[A[i]]=optColorNumber then // i = indeks terkecil dimana F[A[i]]=optColorNumber break;

start:=i-1; if start<0 then

break; //keluar dari loop while for j:=start to n-1 do

(25)

29 for i:=0 to start do

v:=A[i];

U:=freeColors[v];

for j:=optColorNumber to MaxVertex do

U:=U-[j]; //semua warna ≥ optColorNumber dihilangkan dari U

freeColors[v]:=U;

// disini v= A[start]; U=freecolors(v) // akhir dari loop while

[Output]

Fopt[n+1]:=fmax(Fopt); //Bilangan Kromatik Result:=Fopt;

(26)

30 Untuk ilustrasi dari algoritma tersebut, perhatikan contoh dibawah ini :

1. Misalkan graf yang akan diwarnai adalah sebagai berikut 1 2 3 4 5 6 7 8 9 10 11 Gambar 2.19

2. Untuk mewarnai graf pada gambar 2.9 dengan menggunakan algoritma BSC, langkah pertama yang dilakukan adalah menyusun derajat titik pada graf tersebut secara descending dalam array A. Sehingga, didapatkan

6 2 10 11 1 3 4 5 7 8 9

A:=[v , v , v , v , v , v , v , v , v , v , v ].

3. Selanjutnya, pilih salah satu titik yang memiliki derajat terbesar. Jika terdapat lebih dari satu, maka pilih titik dengan label terkecil. Cek freecolors U yang mungkin diberikan pada titik tersebut, kemudian warnai titik tersebut dengan warna terkecil yang terdapat pada freecolors v. Kemudian hapus warna yang digunakan untuk mewarnai titik tersebut dari freecolors v.

4. Pilih titik dengan derajat saturasi terbesar. Jika terdapat lebih dari satu, maka pilih titik dengan derajat titik terbesar. Jika terdapat lebih dari satu, maka pilih titik dengan label terkecil. Cek freecolors U yang mungkin diberikan pada titik tersebut, kemudian warnai titik tersebut dengan warna terkecil yang terdapat

(27)

31 pada freecolors v dan tidak dimiliki oleh tetangga dari titik tersebut. Kemudian hapus warna yang digunakan untuk mewarnai titik tersebut dari freecolors v. 5. Langkah 4 dilakukan terus hingga semua titik pada graf diwarnai. Sebagai

gambaran dari langkah 3 dan 4, perhatikan gambar 2.20.

Gambar 2.20

6. Dari langkah 5 diperoleh hasil sebagai berikut

1 2 3 4 5 6 7 8 9 10 11 freeColors(v6) =[] freeColors(v3) =[] freeColors(v₂) =[3] freeColors(v10) = [3] freeColors(v5) = [] freeColors(v1) = [4] freeColors(v₇) = [4] freeColors(v11) = [4] freeColors(v4) = [4] freeColors(v₉) = [] freeColors(v₈) = [3,4,5] Gambar 2.21

(28)

32 8. Titik yang memiliki warna 4 dihapus . Kemudian hapus warna yang

digunakan titik .

9

( )v

8

v

9. Hapus semua warna 4 dari freecolors v dan U. ≥

10. Kemudian warnai kembali dengan warna yang tersedia pada freecolors vv₈ 8.

Selanjutnya v9 diwarnai kembali dengan terlebih dahulu melakukan cek ulang

terhadap freecolors v9. Jika v9 tidak memiliki freecolors yang tersedia, maka

hapus warna titik v9 dan warna titik sebelumnya berdasarkan urutan mundur

dari A (dalam contoh ini kita hapus warna v8).

11. Kemudian warnai kembali dengan warna yang tersedia pada freecolors vv₈ 8.

Jika v8 tidak memiliki freecolors yang tersedia, maka hapus warna titik v8 dan

v7.

12. Semua warna titik akan dihapus berdasar urutan mundur dari A jika titik tersebut tidak memiliki freecolors v yang tersedia (pada contoh ini, proses berhenti hingga v10).

13. Kemudian warnai kembali v₁₀ dengan warna yang tersedia pada freecolors v10.

Setelah v10 diwarnai, lakukan kembali langkah 4 hingga semua titik diwarnai.

(29)

33

Gambar 2.22

15. Dari langkah 14 diperoleh hasil sebagai berikut 1 2 3 4 5 6 7 8 9 10 11 freeColors(v6) =[] freeColors(v3) =[] freeColors(v₂) =[3] freeColors(v10) = [] freeColors(v5) = [] freeColors(v1) = [] freeColors(v₇) = [] freeColors(v11) = [] freeColors(v4) = [] freeColors(v₉) = [] freeColors(v₈) = [] Gambar 2.23

16. Hasil yang diperoleh disimpan pada Fopt (Fopt = 3).

17. Selanjutnya, lakukan cara yang sama pada langkah 8 hingga 13. Algoritma BSC berhenti apabila semua titik memiliki freecolors = [].

18. Hasil yang diperoleh adalah hasil dari Fopt terakhir (pada contoh ini hasil yang diperoleh adalah 3).