PE N EN TU A N R U T E KU N JU N GA N WI SA TA PA D A DESTINASI KOTA MEDAN, KABUPATEN LANGKAT DAN
KABUPATEN DELI SERDANG MENGGUNAKAN M E T O D E B R A N C H A N D B O U N D
SKRIPSI
DESY LOINA BANGUN 160803026
PROGRAM STUDI MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SUMATERA UTARA
MEDAN 2021
PE N EN TU A N R U T E KU N JU N GA N WI SA TA PA D A DESTINASI KOTA MEDAN, KABUPATEN LANGKAT DAN
KABUPATEN DELI SERDANG MENGGUNAKAN M E T O D E B R A N C H A N D B O U N D
SKRIPSI
Diajukan untuk melengkapi tugas dan memenuhi syarat mencapai gelar Sarjana Sains
DESY LOINA BANGUN 160803026
PROGRAM STUDI MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SUMATERA UTARA
MEDAN 2021
PERNYATAAN ORISINALITAS
PE N EN TU A N R U T E KU N JU N GA N WI SA TA PA D A DESTINASI KOTA MEDAN, KABUPATEN LANGKAT DAN
KABUPATEN DELI SERDANG MENGGUNAKAN M E T O D E B R A N C H A N D B O U N D
SKRIPSI
Saya menyatakan bahwa skripsi ini adalah hasil karya sendiri, kecuali beberapa kutipan dan ringkasan yang masing-masing disebutkan sumbernya.
Medan, 12 Agustus 2021
Desy Loina Bangun
160803026
PENENTUAN RUTE KUNJUNGAN WISATA PADA DESTINASI KOTA MEDAN, KABUPATEN LANGKAT
DAN KABUPATEN DELI SERDANG MENGGUNAKAN METODE BRANCH AND BOUND
ABSTRAK
Travelling Salesman Problem merupakan pencarian sebuah rute oleh seorang salesman untuk mengunjungi beberapa daerah yang ditentukan. Rute perjalanan dimulai dari simpul awal dan kembali ke simpul awal tersebut sehingga total jarak perjalanan menjadi optimal. Setiap simpul dikunjungi tepat hanya satu kali. Penelitian ini membahas sebuah permasalahan TSP, khususnya dalam penggunaan algoritma Branch and Bound pada penentuan rute objek wisata di daerah Kota Medan, Kabupaten Langkat dan Kabupaten Deli Serdang. Penentuan lokasi objek wisata dicari melalui internet, dan data dari setiap jarak objek wisata tersebut diambil melalui Google Maps. Proses pengolahan data dilakukan dengan cara menggunakan mekanisme algoritma Branch and Bound serta perhitungannya dikerjakan secara manual. Dari proses yang telah dilakukan, maka rute optimal yang diperoleh yaitu melalui jalur Merdeka walk – The Le Hu Garden – Park Zoo and Resort – Velangkani - Arung jeram sungai binge - Taman air percut – Taman buah Lubuk Pakam – 3D art magic eye museum – Merdeka walk. Total jarak tempuh yang dilalui menggunakan algoritma Branch and Bound adalah 187.7 kilometer dalam sekali tempuh.
Kata kunci: Branch and Bound, Graf, Objek Wisata, Travelling Salesman Problem
DETERMINATION OF THE ROUTE OF THE TOURIST VISIT IN MEDAN CITY DESTINATION, LANGKAT REGENCY AND DELI SERDANG
REGENCY USES BRANCH AND BOUND METHODS
ABSTRACT
Traveling Salesman Problem is the search for a route by a salesman to visit some designated area. The journey starts from the initial node and returns to that initial node so that the total distance traveled is the minimum. Each node is visited exactly once. This study examined a problem of TSP, especially in the use of Branch and Bound algorithms in determining the route of tourist attractions in Medan city, Langkat regency and Deli Serdang regency. Data retrieval is done by looking at the location of tourist attractions that are worth visiting on the internet and then doing a distance search using Google Maps. The process of data processing is carried out by means of Branch and Bound algorithm mechanisms and calculations are done manually. From the process that has been done, the shortest route obtained is through merdeka walk – The Le Hu Garden – Park Zoo and Resort – Velangkani - Binge river rafting - Taman Sungai holiday – Taman Buah Lubuk Pakam – 3D art magic eye museum – Merdeka walk. The total distance traveled using the Branch and Bound algorithm is 187.7 kilometers in one go.
Keyword: Branch and Bound, Graph, Tourist Visit, Travelling Salesman Problem
PENGHARGAAN
Puji dan syukur penulis panjatkan kepada Tuhan Yang Maha Esa atas berkat- Nya sehingga skripsi dengan judul “Penentuan Rute Kunjungan Wisata pada Destinasi Kota Medan, Kabupaten Langkat dan Kabupaten Deli Serdang Menggunakan Metode Branch and Bound” dapat diselesaikan dengan baik. Banyak pihak yang membantu penulis dalam menyelesaikan skripsi ini, penulis menyampaikan ucapan terimakasih kepada:
1. Bapak Drs. Parapat Gultom, MSIE, Ph.D selaku dosen pembimbing yang senantiasa membimbing dan mengarahkan penulis dalam penyelesaian skripsi ini.
2. Ibu Dr. Esther Sorta Mauli Nababan, M.Sc dan Ibu Dr. Mardiningsih, M.Si selaku dosen pembanding yang banyak memberikan saran dan masukkan dalam penyelesaian skripsi ini.
3. Bapak Dr. Suyanto, M.Kom selaku Ketua Departemen Matematika dan Bapak Drs. Rosman Siregar, M.Si. selaku Sekretaris Departemen Matematika FMIPA USU.
4. Ibu Dr. Nursahara Pasaribu, M.Sc sebagai Dekan Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Sumatera Utara.
5. Semua Dosen di Departemen Matematika FMIPA USU atas segala ilmu dan bimbingan selama di perkuliahan dan juga staf/pegawai FMIPA USU.
6. Kedua orangtua penulis Bapak Firnando Bangun dan Ibu Salimah br Sitepu, saudara penulis Dio Pranta Bangun dan Della Melinda Bangun yang mendoakan, memberikan dukungan moral dan materil dalam perkuliahan dan penulisan skripsi ini.
7. Teman-teman terkasih: Dina, Lidya, Yolanda, Rika, Melisa, Herti, Ita, Shella, Dayan, Okta, Yemima, Cici, Flora, Deswari serta rekan-rekan matematika stambuk 2016 yang selalu membantu.
8. Rekan-rekan stambuk 2017, 2018, dan 2019 atas segala bentuk dukungannya.
Terimakasih penulis ucapkan kepada seluruh pihak yang telah membantu penulis dalam penyelesaian skripsi ini. Penulis menyadari skripsi ini masih jauh dari kata sempurna, untuk itu kritik dan saran yang membangun dari semua pihak yang sangat penulis harapkan demi penyempurnaan pembuatan skripsi ini. Akhir kata penulis berharap skripsi ini dapat bermanfaat bagi semua pihak dan Tuhan senantiasa menyertai kita.
Medan,12 Agustus 2021
Desy Loina Bangun
DAFTAR ISI
PENGESAHAN SKRIPSI i
ABSTRAK ii
ABSTRACT iii
PENGHARGAAN iv
DAFTAR ISI vi
DAFTAR TABEL viii
DAFTAR GAMBAR ix
DAFTAR LAMPIRAN xi
BAB 1 PENDAHULUAN 1
1.1 Latar Belakang 1
1.2 Perumusan Masalah 3
1.3 Batasan Masalah 3
1.4 Tujuan Penelitian 4
1.5 Manfaat Penelitian 4
BAB 2 TINJAUAN PUSTAKA 6
2.1 Travelling Salesman Problem 6
2.2 Graf 7
2.2.1 Pengertian Graf 7
2.2.2 Jenis-jenis Graf 9
2.2.3 Terminologi Graf 11
2.2.4 Graf Sederhana Khusus 15
2.2.5 Sirkuit Euler dan Sirkuit Hamilton 16
2.2.6 Representasi Graf 17
2.3 Optimisasi 18
2.3.1 Definisi Optimisasi 18
2.3.2 Macam-macam Permasalahan Optimisasi 19
2.3.3 Permasalahan Rute Terpendek 19
2.3.4 Penyelesaian Optimisasi 20
2.4 Branch and Bound 21
BAB 3 METODOLOGI PENELITIAN 25
BAB 4 PEMBAHASAN DAN HASIL 27
4.1 Deskripsi Permasalahan 27
4.2 Pengumpulan Data 27
4.3 Pengolahan Data 28
BAB 5 KESIMPULAN DAN SARAN 65
5.1 Kesimpulan 65
5.2 Saran 66
DAFTAR PUSTAKA 67
LAMPIRAN 68
DAFTAR TABEL
Nomor Tabel
Judul Halaman
4.1 Data Jarak Objek Wisata 26
DAFTAR GAMBAR
Nomor Gambar
Judul Halaman
2.1 Ilustrasi Masalahan TSP 6
2.2 Contoh Graf G 8
2.3 Sisi Ganda dan Loop 8
2.4 Contoh Graf G dan Subgraf G’ 9
2.5 Graf Sederhana 9
2.6 Graf Tak Sederhana 10
2.7 Graf Berarah dan Berbobot 10
2.8 Graf Tidak Berarah dan Berbobot 10
2.9 Graf Berarah dan Tidak Berbobot 11
2.10 Graf Tidak Berarah dan Graf Tidak Berbobot 11
2.11 Graf Bertetangga 12
2.12 Graf Bersisian 12
2.13 Simpul Terpencil 13
2.14 Graf Kosong 13
2.15 Derajat 13
2.16 Lintasan 14
2.17 Siklus atau Sirkuit 14
2.18 Graf Terhubung dan Tak-terbuhung 15
2.19 Graf Lengkap 15
2.20 Graf Lingkaran 15
2.21 Graf Teratur 16
2.22 Himpunan 𝑉1 dan 𝑉2 16
2.23 Graf Bipartit 16
2.24 Contoh Graf ABCD 17
2.25 Sirkuit Hamilton 17
2.26 Graf 𝐺 dan Matriks Berhubungan Langsung 18 2.27 Graf 𝐺 dan Matriks Senarai Ketetanggan 18
2.28 Graf 𝐴𝐵𝐶𝐷𝐸𝐹𝐺 19
2.29 4.1 4.2
Breadth First Search Representasi Graf Sirkuit Hamilton
20 63 63
DAFTAR LAMPIRAN
Nomor Lampiran
Judul Halaman
1 Jarak Merdeka Walk ke Sungai Binge 63
2 Jarak Merdeka Walk ke Park Zoo and Resort 63 3 Jarak Merdeka Walk ke 3D Art Magic Eye Museum 64 4 Jarak Merdeka Walk ke Taman Buah Lubuk Pakam 64 5 Jarak Merdeka Walk ke The Le Hu Garden 65
6 Jarak Merdeka Walk ke Velangkanni 65
7 Jarak Merdeka Walk ke Taman Air Percut 66 8 Jarak Sungai Binge ke Central Park Zoo 66 9 Jarak Sungai Binge ke 3D Art Magic Eye Museum 67 10 Jarak Sungai Binge ke Taman Buah Lubuk Pakam 67 11 Jarak Sungai Binge ke The Le Hu Garden 68 12 Jarak Sungai Binge ke Taman Air Percut 68
13 Jarak Sungai Binge ke Velangkanni 69
14 Park Zoo ke 3D Art Magic Eye Museum 69
15 Park Zoo ke Taman Buah Lubuk Pakam 70
16 Park Zoo ke The Le Hu Garden 70
17 Park Zoo ke Taman Air Percut 71
18 Park Zoo ke Velangkanni 71
19 3D Art Magic Eye Museum ke Taman Buah Lubuk Pakam
72
20 3D Art Magic Eye Museum ke The Le Hu Garden 72 21 3D Art Magic Eye Museum ke Taman Air Percut 73 22 3D Art Magic Eye Museum ke Velangkanni 73 23 Buah Lubuk Pakam ke The Le Hu Garden 74 24 Taman Buah Lubuk Pakam ke Taman Air Percut 74
25 Taman Buah Lubuk Pakam ke Velangkanni 75 26 The Le Hu Garden ke Taman Air Percut 75
27 The Le Hu Garden ke Velangkanni 76
28 Taman Air Percut ke Velangkanni 76
BAB 1 PENDAHULUAN
1.1 Latar Belakang
Pada masa kini transportasi merupakan suatu permasalahan yang sering kali dihadapi oleh setiap orang. Salah satunya adalah rute atau jarak yang harus dilalui seseorang untuk menempuh atau mengunjungi beberapa daerah dan tiap daerah itu harus dikunjungi tepat satu kali dan kembali kedaerah semula.
Permasalahan diatas biasanya dikenal sebagai Travelling Salesman Problem (TSP), Travelling Salesman Problem merupakan pencarian sebuah rute dari seorang salesman yang dimulai dari simpul awal, mengunjungi beberapa daerah yang ditentukan dan kembali ke simpul awal tersebut sedemikian sehingga total perjalanan adalah minimum dan setiap simpul dikunjungi tepat hanya satu kali.
Nugroho, Suyitno dan Arifudin (2016) dalam penelitiannya yang berjudul Perbandingan Algoritma Branch and Bound dan Algoritma Genetika untuk Mengatasi Travelling Salesman Problem (TSP) menyatakan bahwa dalam lingkup pencarian rute yang optimal, tidak dapat dikatakan secara langsung algoritma mana yang paling optimum untuk keseluruhan kasus, karena belum tentu suatu algoritma yang memiliki optimasi paling tinggi untuk suatu kasus bakal memilki optimasi paling tinggi pula untuk kasus lain. Optimasi yang mencakup efisiensi waktu proses kerja algoritma, waktu tempuh yang diperlukan untuk mencapai tujuan akhir dan jarak tempuh yang paling optimal selalu tergantung dari setiap kondisi permasalahan yang ada. Pemilihan algoritma yang paling optimum selalu menjadi permasalahan dalam pengoptimalan suatu rute karena setiap algoritma memiliki kelebihan dan kekurangannya masing- masing.
Masalah rute yang optimal secara umum dijelaskan menggunakan konsep graf, dapat berupa graf berarah atau tidak berarah. Graf yang digunakan untuk menyelesaikan rute optimal yaitu graf yang memiliki bobot atau nilai disetiap sisinya.
Bobot pada sisi graf dapat menyatakan jarak antara dua simpul dan asumsi yang digunakan adalah semua bobot bernilai positif.
Graf dapat digunakan pada berbagai objek diskrit, terutama graf sering digunakan untuk memodelkan berbagai persoalan untuk memudahkan penyelesaian
pada berbagai macam persoalan-persoalan yang sulit diselesaikan dengan perhitungan dan pertimbangan biasa. Tahun 1796 seorang matimatikawan Swiss, L. Euler adalah orang pertama yang menemukan jawaban pada masalah jembatan koningsberg dimana harus melalui ketujuh buah jembatan, masing-masing tepat satu kali dan kembali lagi ke tempat semula. Euler memodelkan masalah ini kedalam graf. Daratan (titik-titik yang dihubungkan oleh jembatan) dinyatakan sebagai simpul dan jembatan dinyatakan sebagai garis-garis yang disebut sisi. Apabila sebuah graf dapat dilalui setiap sisinya masing-masing satu kali dan kembali lagi ke tempat semula, maka graf tersebut dikatakan memiliki sirkuit euler.
Ada beberapa algoritma yang dapat digunakan untuk menyelesaikan masalah Travelling Salesman Problem (TSP), diantaranya adalah algoritma Genetic, algoritma Dijkstra, algoritma Branch and Bound dan masih banyak lagi algoritma lain yang dapat menyelesaikan permasalahan tersebut. Berdasarkan literatur sebelumnya, permasalahan Travelling Salesman Problem (TSP) akan diselesaikan dengan algoritma Branch and Bound,
Algoritma Branch and Bound adalah suatu prosedur yang paling umum untuk mencari solusi optimal pada masalah optimasi kombinatorial seperti masalah penjadwalan. Dalam algoritma Branch and Bound terdapat tiga bagian utama yaitu:
ekspresi batas bawah (lower bound), srategi pencarian dan pencabangan. (Sutanto, 2011)
Kota Medan, Kabupaten Langkat dan Kabupaten Deli Serdang sangat populer dengan keragaman budaya yang ditawarkan oleh kota identik dengan suku Batak ini.
Daerah tersebut juga merupakan daerah yang masih banyak menyimpan berbagai jenis objek wisata seperti wisata alam, wisata rohani, wisata budaya, wisata pertanian serta masih banyak lagi jenis objek wisata yang dapat ditemukan pada daerah tersebut. Ada beberapa objek wisata di daerah Kota Medan, Kabupaten Langkat dan Kabupaten Deli Serdang yang banyak sekali dikunjungi para wisatawan, antara lain : Merdeka Walk, Arung Jeram Sungai Binge, Park Zoo and Resort, Magic eye 3D Art Museum, Taman Buah Lubuk Pakam, The Le Hu Garden, Taman Air Precut, Velangkani, dan masih banyak objek wisata lainnya yang menjadi daya pikat dan daya tarik tersendiri bagi para wisatawan yang datang.
Berdasarkan latar belakang diatas, penulis akan mengimplementasikan penggunaan algoritma Branch and Bound dalam proses pengoptimasian terhadap penyelesaian Travelling Salesman Problem. Oleh Karena itu, penulis memilihh judul
“Penentuan Rute Kunjungan Wisata pada Destinasi Kota Medan, Kabupaten Langkat dan Kabupaten Deli serdang Menggunakan Metode Branch and Bound ”.
1.2 Perumusan Masalah
Masalahnya adalah belum ada rute yang pasti untuk mengunjungi objek wisata yang berada didaerah Kota Medan, Kabupaten Langkat dan Kabupaten Deli Serdang, sehingga dibutuhkan penentuan rute untuk memaksimalkan perjalanan wisata para wisatawan. Rute tersebut dapat dijadikan sebagai paket perjalanan wisata. Untuk meningkatkan poin positif daerah wisata tersebut, dilakukan dengan menentukan jalur perjalanan wisata yang menghubungkan antar objek-objek wisata pada Kota Medan, Kabupaten Langkat dan Kabupaten Deli Serdang. oleh sebab itu, perlu ditentukan rute untuk mengunjunginya.
Dapat diasumsikan bahwa semua destinasi objek wisata merupakan suatu kota atau wilayah dan wisatawan diasumsikan sebagai salesman. Salesman tersebut harus mengunjungi beberapa wilayah dan wilayah tersebut dikunjungi tepat satu kali dan kembali ke tempat semula, penentuan rute dengan model kasus tersebut dinamakan Travelling salesman problem (TSP). Dari destinasi yang ditentukan tersebut terdapat beberapa lintasan yang bisa dilalui dari simpul awal objek wisata yang ditentukna menuju objek wisata berikutnya, maka perlu diperoleh rute alternatif yang tepat dengan menetapkan metode algoritma Branch and Bound.
1.3 Batasan Masalah
Dalam hal ini penulis membuat beberapa batasan masalah agar hasil pembahasan memberikan hasil yang sesuai dengan permasalahan, diantaranya adalah:
1. Permasalahan yang dibahas hanya Travelling Salesman Problem (TSP).
2. Tempat awal dan akhir dari perjalanan tersebut adalah Merdeka Walk di kota Medan.
3. Daerah wisata yang menjadi simpul yaitu Merdeka walk, arung jeram sungai binge, park zoo and resort, 3D art magic eye museum, taman buah Lubuk Pakam, the le hu garden, taman air precut dan velangkani.
4. Hanya menghitung rute yang optimal dengan melewati tepat satu simpul daerah-daerah yang dilalui.
5. Kendala biaya dan waktu tidak dijadikan sebagai parameter.
6. Kumpulan data diperoleh dari aplikasi Google Maps. Variabel yang diambil hanya jarak tempuh setiap wilayah dimaana 8 daerah atau simpul yang akan dilewati.
1.4 Tujuan Penelitian
Adapun tujuan dari penelitian ini adalah menetapkan rute kunjungan ke destinasi wisata di Kota Medan, Kabupaten Langkat dan Kabupaten Deli Serdang dengan menggunakan metode Branch and Bound.
1.5 Manfaat Penelitian
Manfaat dari penelitian ini adalah sebagai berikut:
1. Bagi wisatawan
Hasil dari penelitian ini diharapkan dapat berguna untuk bahan masukan dan informasi bagi wisatawan yang berkunjung ke daerah Kota Medan, Kabupaten Langkat dan Kabupaten Deli Serdang sebagai acuan rute perjalanan wisata yang ada pada daerah destinasi tersebut.
2. Bagi penulis
Bagi penulis penelitian ini diharapkan dapat memberikan pengalaman dan menambah pengetahuan, serta sebagai penerapan ilmu yang telah diperoleh selama masa kuliah.
3. Bagi pembaca
Bagi pembaca penelitian ini diharapkan dapat memberikan informasi yang bermanfaat dan sebagai bahan referensi dalam penelitian-penelitian selanjutnya.
4. Bagi universitas
Bagi universitas penelitian ini dapat menjadi bahan acuan dan referensi bagi mahasiwa/i dalam melakukan penelitian dengan topik yang sama. Dan terutama bagi penelitian dalam permasalahan Travelling Salesman Problem (TSP) yang menggunakan algoritma Branch and Bound.
BAB 2
TINJAUAN PUSTAKA
2.1 Travelling Salesman Problem
Mahmudi (2008), Travelling Salesman Problem (TSP) adalah masalah rute yang memiliki biaya paling murah untuk dilalui n salesman (n>1) yang harus mengunjungi sejumlah m daerah (m>1), tiap daerah harus dikunjungi tepat satu kali kemudian kembali lagi ke tempat semula. Jarak dalam menentukan rute terpendek, terdapat parameter yang perlu ditentukan sebelumnya yaitu jarak antara simpul awal ke alamat penumpang (simpul tujuan) dan jarak antara alamat penumpang satu dan penumpang lainnya.
Permasalahan Travelling Salesman Problem (TSP) dapat diselesaikan dengan menganggapnya sebagai masalah penugasan dengan bekerja dan pekerjaan sama-sama menyatakan kota-kota yang hendak dikunjungi. Biaya tiap pasang kota adalah jarak yang hendak diminimumkan. Supaya tidak langsung kembali ke kota yang sama maka biaya 𝑐𝑖𝑖= 𝑀 untuk semua i. Misalkan perjalanan dimulai dari kota-1. Jika pasangan kota penyelesaian masalah penugasan meliputi semua kota sebelum kembali ke kota- 1, berarti penyelesaian masalah penugasan adalah penyelesaian masalah Travelling Salesman Problem. Akan tetapi jika sebelum mengunjungi semua kota ia sudah kembali ke kota-1, maka terjadi subtour. Dalam keadaan ini masalah penugasan harus dipecah menjadi 2 bagian dengan menggunakan pendekatan Branch and Bound dengan memutuskan salah satu jalur subtour.
TSP dapat digambarkan seperti gambar dibawah ini:
Gambar 2.1 ilustrasi masalahan TSP
Dalam kehidupan sehari-hari TSP dapat diaplikasikan untuk menyelesaikan kasus lain, diantaranya:
1. Tukang pos mengambil surat di kotak pos pada n lokasi di berbagai sudut kota 2. Lengan robot mengencangkan n buah mur pada beberapa buah peralatan mesin
dalam sebuah jalur perakitan
3. Mobil pengangkut sampah mengambil sampah pada tempat-tempat pembuangan sampah yang berada pada n buah lokasi diberbagai sudut kota 4. Petugas bank melakukan pengisian uang pada sejumlah mesin ATM di n buah
lokasi
Dalam kasus penentuan rute formulasi model TSP dapat ditulis sebagai berikut : Jarak perjalanan dari simpul 𝑖 ke simpul 𝑗 direpresentasikan oleh 𝐶𝑖𝑗. Selanjutnya didefinisikan variable keputusan 𝑋𝑖𝑗 yang mempresentasikan ada tidaknya perjalanan dari simpul 𝑖 ke 𝑗 dalam suatu rute sebagai berikut :
𝑋𝑖𝑗 = {1, 𝑗𝑖𝑘𝑎 𝑡𝑒𝑟𝑑𝑎𝑝𝑎𝑡 𝑝𝑒𝑟𝑗𝑎𝑙𝑎𝑛𝑎𝑛 𝑘𝑒𝑛𝑑𝑎𝑟𝑎𝑎𝑛 𝑑𝑎𝑟𝑖 𝑖 𝑘𝑒 𝑗 0, 𝑗𝑖𝑘𝑎 𝑡𝑖𝑑𝑎𝑘 𝑎𝑑𝑎 𝑝𝑒𝑟𝑗𝑎𝑙𝑎𝑛𝑎𝑛 𝑘𝑒𝑛𝑑𝑎𝑟𝑎𝑎𝑛 𝑑𝑎𝑟𝑖 𝑖 𝑘𝑒 𝑗
(1) Jika Z merupakan fungsi tujuan TSP, maka fungsi tujuan Z dirumuskan dengan meminimumkan:
Z = ∑ ∑ 𝐶𝑖𝑗𝑋𝑖𝑗
𝑛
𝑗=1 𝑛
𝑖=1
(2)
Dengan batasan kendala,
∑𝑋𝑖𝑗= 1
𝑛
𝑖=1
∑𝑋𝑖𝑗= 1
𝑛
𝑗=1
𝑋𝑖𝑗= 1, apabila ada perjalanan salesman dari simpul 𝑖 menuju simpul 𝑗 𝑋𝑖𝑗= 0, apabila tidak ada perjalanan salesman dari simpul 𝑖 menuju simpul 𝑗 𝐶𝑖𝑗menyatakan jarak dari simpul 𝑖 menuju simpul 𝑗
Travelling Salesman Problem (TSP) dapat digambarkan sebagai permasalahan graf. Setiap tempat dilambangkan sebagai simpul (vertex), sedangkan sisinya (edge) adalah jarak antar tempat.
2.2 Graf
2.2.1 Pengertian Graf
Wilson, R. J dan Watkhins, J. J (1990) Suatu graf G terdiri dari himpunan yang tidak
kosong dari elemen-elemen yang disebut simpul (vertex), dan suatu daftar pasangan simpul disebut sisi (edge). Himpunan simpul (vertex) dari suatu graf G di notasikan sebagai V dan daftar himpunan sisi (edge) dari graf tersebut dinotasikan sebagai E.
Oleh sebab itu, suatu graf G dapat dinotasika sebagai: 𝐺 = (𝑉, 𝐸) Dimana: V = himpunan tidak kosong dari simpul-simpul
= {𝑣1, 𝑣2, 𝑣3, … , 𝑣𝑛}
E = himpunan sisi yang menghubungkan sepasang simpul
= {𝑒1, 𝑒2, 𝑒3, … , 𝑒𝑛}
Gambar 2.2 Contoh Graf G
Gambar 2.2 menunjukkan graf G dengan 𝑉 = {𝐴, 𝐵, 𝐶, 𝐷, 𝐸, 𝐹} dan 𝐸 = {𝑒1, 𝑒2, 𝑒3, 𝑒4, 𝑒5, 𝑒6, 𝑒7, 𝑒8, 𝑒9, 𝑒10}
Dua sisi atau lebih yang menghungkan pasangan simpul yang sama disebut sisi ganda dan sebuah sisi yang menghungkan sebuah simpul ke dirinya sendiri disebut loop.
Gambar 2.3 Sisi Ganda dan Loop
Misal G suatu graf dengan himpunan simpul V dan himpunan sisi E. Suatu subgraf G’ adalah suatu himpunan pasangan berurut (V’,E’), dimana V’ merupakan himpunan bagian dari V dan E’ merupakan himpunan bagian dari E’. Dengan kata lain subgraf G adalah suatu graf yang semua simpulnya anggota V dan semua sisinya anggota E.
Jika suatu graf terhubung seperti pada gambar 2.3, dengan 𝑉 = {1,2,3,4} dan
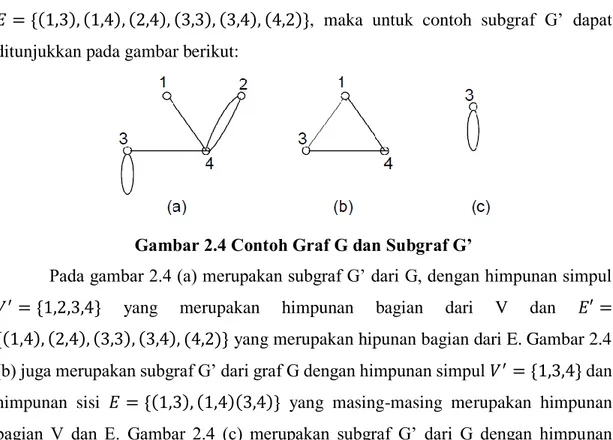
𝐸 = {(1,3), (1,4), (2,4), (3,3), (3,4), (4,2)}, maka untuk contoh subgraf G’ dapat ditunjukkan pada gambar berikut:
Gambar 2.4 Contoh Graf G dan Subgraf G’
Pada gambar 2.4 (a) merupakan subgraf G’ dari G, dengan himpunan simpul 𝑉′ = {1,2,3,4} yang merupakan himpunan bagian dari V dan 𝐸′ = {(1,4), (2,4), (3,3), (3,4), (4,2)} yang merupakan hipunan bagian dari E. Gambar 2.4 (b) juga merupakan subgraf G’ dari graf G dengan himpunan simpul 𝑉′= {1,3,4} dan himpunan sisi 𝐸 = {(1,3), (1,4)(3,4)} yang masing-masing merupakan himpunan bagian V dan E. Gambar 2.4 (c) merupakan subgraf G’ dari G dengan himpunan simpul 𝑉′= {3} dan himpunan sisi 𝐸 = {3,3} yang masing-masing merupakan hmpunan bagian V dan E
2.2.2 Jenis-jenis Graf
Berdasarkan keberadaan loop dan sisi ganda, graf dapat digolongkan menjadi dua jenis sebagai berikut:
1. Graf sederhana (simple graf)
Graf sederhana merupakan graf yang tidak mengandung gelang maupun sisi ganda
Gambar 2.5 Graf Sederhana 2. Graf tak sederhana (unsimple graf)
Graf tak sederhana adalah graf yang mengandung sisi ganda atau gelang. Sisi ganda yang menghubungkan sepasang simpul bisa lebih dari dua buah.
Sedangkan graf semu adalah graf yang mengandung gelang (loop).
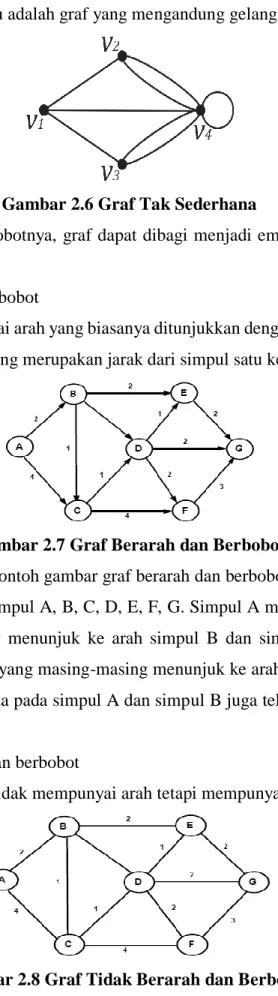
Gambar 2.6 Graf Tak Sederhana
Menurut arah dan bobotnya, graf dapat dibagi menjadi empat bagian, antara lain sebagai berikut:
1. Graf berarah dan berbobot
Setiap sisi mempunyai arah yang biasanya ditunjukkan dengan anak panah dan mempunyai bobot yang merupakan jarak dari simpul satu ke simpul lainnya.
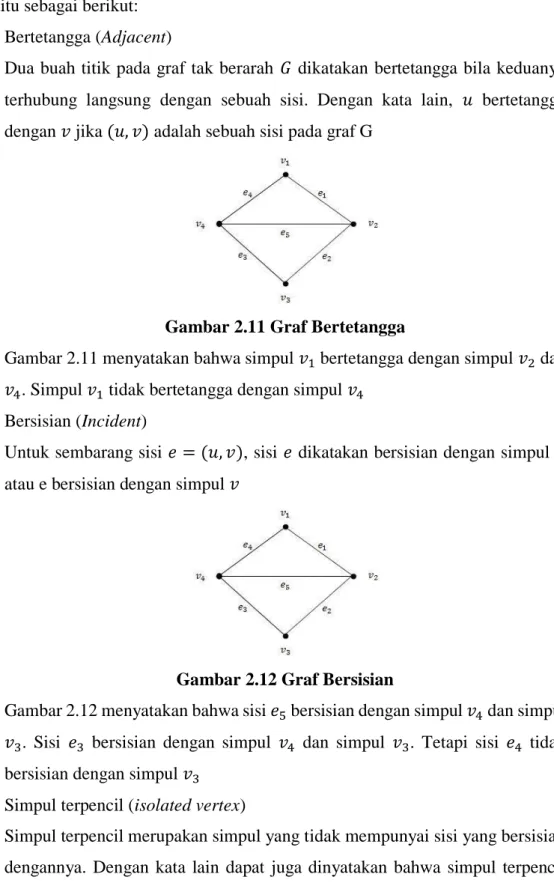
Gambar 2.7 Graf Berarah dan Berbobot
Gambar 2.7 adalah contoh gambar graf berarah dan berbobot yang terdiri dari tujuh simpul yaitu simpul A, B, C, D, E, F, G. Simpul A mempunyai dua sisi yang masing-masing menunjuk ke arah simpul B dan simpul C. Simpul B mempunyai tiga sisi yang masing-masing menunjuk ke arah simpul C, simpul D dan simpul E. Serta pada simpul A dan simpul B juga telah terdapat bobot, yaitu 2.
2. Graf tidak berarah dan berbobot
Setiap sisinya yang tidak mempunyai arah tetapi mempunyai bobot
Gambar 2.8 Graf Tidak Berarah dan Berbobot
Gambar 2.8 adalah contoh graf tidak berarah dan berbobot. Graf tersebut terdiri dari tujuh simpul yaitu simpul A, B, C, D, E, F, G. Simpul A mempunyai sisi yang masing-masing berhubungan dengan simpul B dan C, tetapi masing- masing dari sisi tersebut tidak mempunyai arah. Sisi yang menghungkan simpul A ke simpul B mempunyai bobot yang telah diketahui, yaitu 2. Begitu pula dengan sisi-sisi lainnya.
3. Graf berarah dan tidak berbobot
Setiap sisi mempunyai arah tetapi tidak mempunyai bobot
Gambar 2.9 Graf Berarah dan Tidak Berbobot
Gambar 2.9 merupakan contoh graf berarah dan tidak berbobot. Graf tersebut memiliki tujuh simpul yaitu simpul A, B, C, D, E, F, G. Simpul A mempunyai dua sisi yang masing-masing menunjuk ke arah simpul B dan simpul C, tetapi pada masing-masing sisi tersebut tidak diketahui bobotnya. Begitu pula dengan sisi-sisi lainnya.
4. Graf tidak berarah dan tidak berbobot
Setiap sisi tidak mempunyai arah dan tidak berbobot.
Gambar 2.10 Graf Tidak Berarah dan Graf Tidak Berbobot
2.2.3 Terminologi Graf
Munir (2005) Dalam pembahasan mengenai graf biasanya sering menggunakan terminologi (istilah) yang berkaitan dengan graf. Terminologi yang berkaitan dengan
graf yaitu sebagai berikut:
1. Bertetangga (Adjacent)
Dua buah titik pada graf tak berarah 𝐺 dikatakan bertetangga bila keduanya terhubung langsung dengan sebuah sisi. Dengan kata lain, 𝑢 bertetangga dengan 𝑣 jika (𝑢, 𝑣) adalah sebuah sisi pada graf G
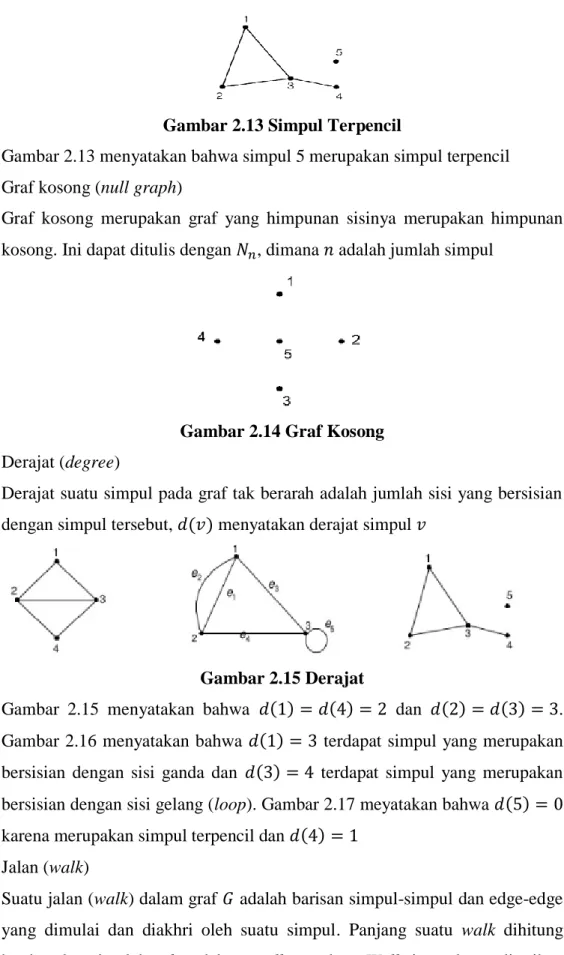
Gambar 2.11 Graf Bertetangga
Gambar 2.11 menyatakan bahwa simpul 𝑣1 bertetangga dengan simpul 𝑣2 dan 𝑣4. Simpul 𝑣1 tidak bertetangga dengan simpul 𝑣4
2. Bersisian (Incident)
Untuk sembarang sisi 𝑒 = (𝑢, 𝑣), sisi 𝑒 dikatakan bersisian dengan simpul 𝑢 atau e bersisian dengan simpul 𝑣
Gambar 2.12 Graf Bersisian
Gambar 2.12 menyatakan bahwa sisi 𝑒5 bersisian dengan simpul 𝑣4 dan simpul 𝑣3. Sisi 𝑒3 bersisian dengan simpul 𝑣4 dan simpul 𝑣3. Tetapi sisi 𝑒4 tidak bersisian dengan simpul 𝑣3
3. Simpul terpencil (isolated vertex)
Simpul terpencil merupakan simpul yang tidak mempunyai sisi yang bersisian dengannya. Dengan kata lain dapat juga dinyatakan bahwa simpul terpencil adalah simpul yang tidak satupun bertetangga dengan simpul-simpul lainnya
Gambar 2.13 Simpul Terpencil
Gambar 2.13 menyatakan bahwa simpul 5 merupakan simpul terpencil 4. Graf kosong (null graph)
Graf kosong merupakan graf yang himpunan sisinya merupakan himpunan kosong. Ini dapat ditulis dengan 𝑁𝑛, dimana 𝑛 adalah jumlah simpul
Gambar 2.14 Graf Kosong 5. Derajat (degree)
Derajat suatu simpul pada graf tak berarah adalah jumlah sisi yang bersisian dengan simpul tersebut, 𝑑(𝑣) menyatakan derajat simpul 𝑣
Gambar 2.15 Derajat
Gambar 2.15 menyatakan bahwa 𝑑(1) = 𝑑(4) = 2 dan 𝑑(2) = 𝑑(3) = 3.
Gambar 2.16 menyatakan bahwa 𝑑(1) = 3 terdapat simpul yang merupakan bersisian dengan sisi ganda dan 𝑑(3) = 4 terdapat simpul yang merupakan bersisian dengan sisi gelang (loop). Gambar 2.17 meyatakan bahwa 𝑑(5) = 0 karena merupakan simpul terpencil dan 𝑑(4) = 1
6. Jalan (walk)
Suatu jalan (walk) dalam graf 𝐺 adalah barisan simpul-simpul dan edge-edge yang dimulai dan diakhri oleh suatu simpul. Panjang suatu walk dihitung berdasarkan jumlah edge dalam walk tersebut. Walk juga dapat diartikan sebagai suatu perjalanan (dalam sebuah graf) dari simpul satu ke simpul lain
yang terhubung dengan suatu sisi.
7. Lintasan (path)
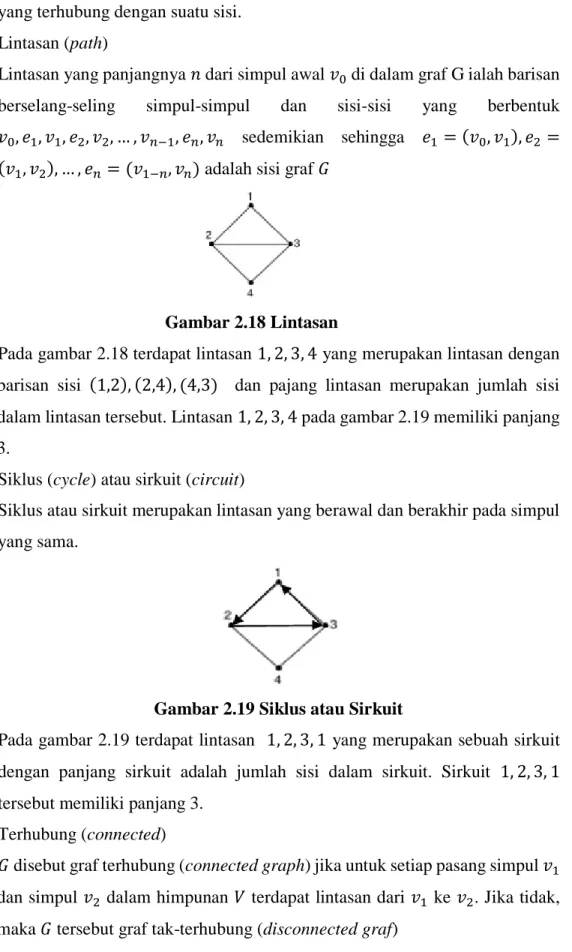
Lintasan yang panjangnya 𝑛 dari simpul awal 𝑣0 di dalam graf G ialah barisan berselang-seling simpul-simpul dan sisi-sisi yang berbentuk 𝑣0, 𝑒1, 𝑣1, 𝑒2, 𝑣2, … , 𝑣𝑛−1, 𝑒𝑛, 𝑣𝑛 sedemikian sehingga 𝑒1 = (𝑣0, 𝑣1), 𝑒2 = (𝑣1, 𝑣2), … , 𝑒𝑛 = (𝑣1−𝑛, 𝑣𝑛) adalah sisi graf 𝐺
Gambar 2.18 Lintasan
Pada gambar 2.18 terdapat lintasan 1, 2, 3, 4 yang merupakan lintasan dengan barisan sisi (1,2), (2,4), (4,3) dan pajang lintasan merupakan jumlah sisi dalam lintasan tersebut. Lintasan 1, 2, 3, 4 pada gambar 2.19 memiliki panjang 3.
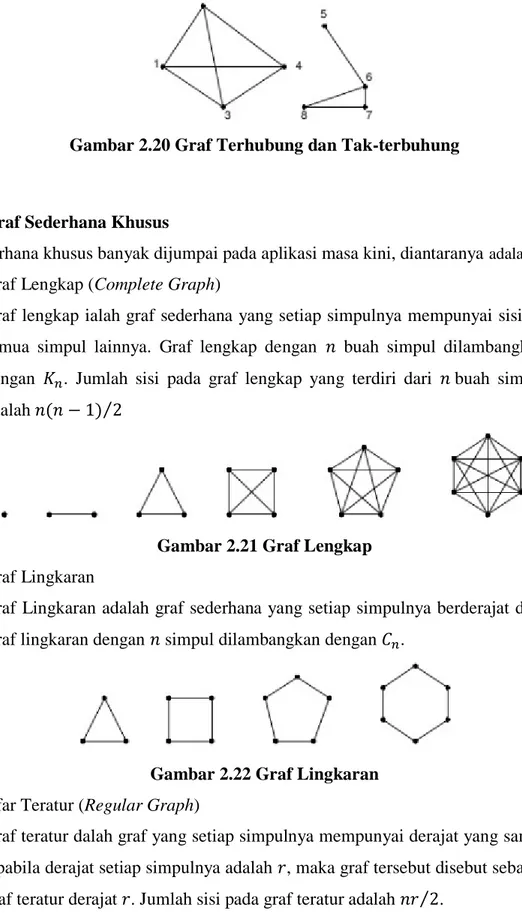
8. Siklus (cycle) atau sirkuit (circuit)
Siklus atau sirkuit merupakan lintasan yang berawal dan berakhir pada simpul yang sama.
Gambar 2.19 Siklus atau Sirkuit
Pada gambar 2.19 terdapat lintasan 1, 2, 3, 1 yang merupakan sebuah sirkuit dengan panjang sirkuit adalah jumlah sisi dalam sirkuit. Sirkuit 1, 2, 3, 1 tersebut memiliki panjang 3.
9. Terhubung (connected)
𝐺 disebut graf terhubung (connected graph) jika untuk setiap pasang simpul 𝑣1 dan simpul 𝑣2 dalam himpunan 𝑉 terdapat lintasan dari 𝑣1 ke 𝑣2. Jika tidak, maka 𝐺 tersebut graf tak-terhubung (disconnected graf)
Gambar 2.20 Graf Terhubung dan Tak-terbuhung
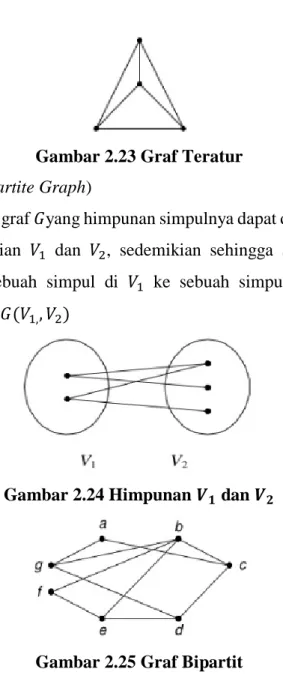
2.2.4 Graf Sederhana Khusus
Graf sederhana khusus banyak dijumpai pada aplikasi masa kini, diantaranya adalah:
1. Graf Lengkap (Complete Graph)
Graf lengkap ialah graf sederhana yang setiap simpulnya mempunyai sisi ke semua simpul lainnya. Graf lengkap dengan 𝑛 buah simpul dilambangkan dengan 𝐾𝑛. Jumlah sisi pada graf lengkap yang terdiri dari 𝑛 buah simpul adalah 𝑛(𝑛 − 1) 2⁄
Gambar 2.21 Graf Lengkap 2. Graf Lingkaran
Graf Lingkaran adalah graf sederhana yang setiap simpulnya berderajat dua.
Graf lingkaran dengan 𝑛 simpul dilambangkan dengan 𝐶𝑛.
Gambar 2.22 Graf Lingkaran 3. Gfar Teratur (Regular Graph)
Graf teratur dalah graf yang setiap simpulnya mempunyai derajat yang sama.
Apabila derajat setiap simpulnya adalah 𝑟, maka graf tersebut disebut sebagai graf teratur derajat 𝑟. Jumlah sisi pada graf teratur adalah 𝑛𝑟 2⁄ .
Gambar 2.23 Graf Teratur 4. Graf Bipartite (Bipartite Graph)
Graf Bipartite ialah graf 𝐺yang himpunan simpulnya dapat dipisahkan menjadi dua himpunan bagian 𝑉1 dan 𝑉2, sedemikian sehingga setiap sisi pada 𝐺 menghubungkan sebuah simpul di 𝑉1 ke sebuah simpul di 𝑉2 dan dapat dinyatakan sebagai 𝐺(𝑉1,, 𝑉2)
Gambar 2.24 Himpunan 𝑽𝟏 dan 𝑽𝟐
Gambar 2.25 Graf Bipartit
Gambar 2.25 dikatakan graf bipartit karena simpul-simpulnya dapat dibagi menjadi 𝑉1= {𝑎, 𝑏, 𝑑} dan 𝑉2 = {𝑐, 𝑒, 𝑓, 𝑔}
2.2.5 Sirkuit Euler dan Sirkuit Hamilton
Dalam sirkuit euler, semua sisi harus dilalui tepat satu kali, sedangkan semua titiknya boleh dikunjungi lebih dari satu kali. Sebaliknya, dalam sirkuit hamilton semua simpul harus dikunjungi tepat satu kali kecuali simpul awal (sekaligus menjadi simpul akhir) yang dilalui dua kali dan tidak harus melalui semua sisinya. Dalam sirkuit euler, yang dipentingkan adalah sisinya. Sedangkan dalam sirkuit hamilton, yang di pentingkan adalah kunjungan pada simpulnya.
Graf 𝐺 adalah sirkuit euler bila dan hanya bila setiap titiknya memiliki derajat genap. Sebaliknya, tidak ada implikasi dua arah yang menjelaskan syarat tentang adanya sirkuit hamilton. Penerapan sirkuit hamilton yang sering dijumpai adalah masalah penjaja keliling (Travelling Salesman Problem). Diketahui beberapa kota beserta dengan jalan dan jarak kota. Seseorang hendak berkeliling mengunjungi setiap kota tepat satu kali, dimulai dan diakhiri dengan kota yang sama. Masalahnya adalah jalur mana yang harus dilalui agar total jarak perjalanannya seoptimal mungkin.
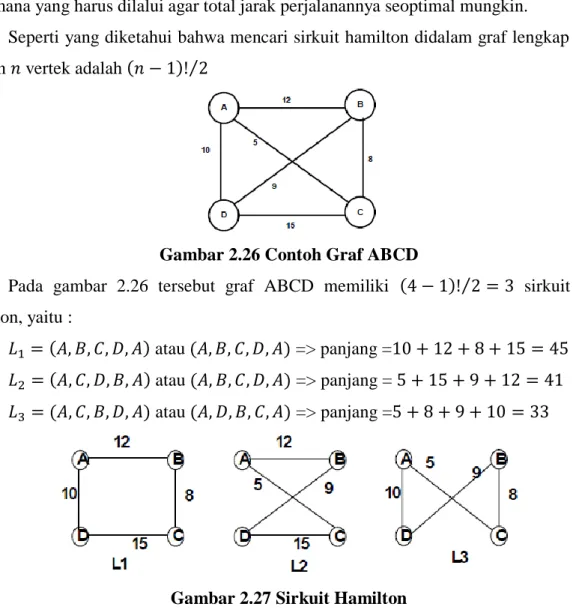
Seperti yang diketahui bahwa mencari sirkuit hamilton didalam graf lengkap dengan 𝑛 vertek adalah (𝑛 − 1)! 2⁄
Gambar 2.26 Contoh Graf ABCD
Pada gambar 2.26 tersebut graf ABCD memiliki (4 − 1)! 2⁄ = 3 sirkuit hamilton, yaitu :
1. 𝐿1 = (𝐴, 𝐵, 𝐶, 𝐷, 𝐴) atau (𝐴, 𝐵, 𝐶, 𝐷, 𝐴) => panjang =10 + 12 + 8 + 15 = 45 2. 𝐿2 = (𝐴, 𝐶, 𝐷, 𝐵, 𝐴) atau (𝐴, 𝐵, 𝐶, 𝐷, 𝐴) => panjang = 5 + 15 + 9 + 12 = 41 3. 𝐿3 = (𝐴, 𝐶, 𝐵, 𝐷, 𝐴) atau (𝐴, 𝐷, 𝐵, 𝐶, 𝐴) => panjang =5 + 8 + 9 + 10 = 33
Gambar 2.27 Sirkuit Hamilton
2.2.6 Representasi Graf
Beberapa representasi yang mungkin untuk graf, diantaranya adalah:
1. Matriks Berhubungan Langsung (Adjacency Matrix)
Misalkan 𝐺 sebuah graf dengan 𝑣(𝐺) = {𝑣1, 𝑣2, 𝑣3, … , 𝑣𝑛. Matriks
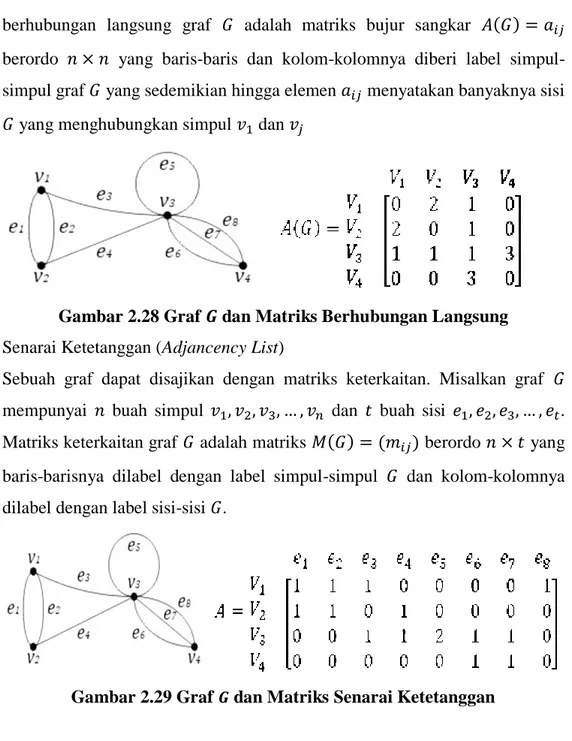
berhubungan langsung graf 𝐺 adalah matriks bujur sangkar 𝐴(𝐺) = 𝑎𝑖𝑗 berordo 𝑛 × 𝑛 yang baris-baris dan kolom-kolomnya diberi label simpul- simpul graf 𝐺 yang sedemikian hingga elemen 𝑎𝑖𝑗 menyatakan banyaknya sisi 𝐺 yang menghubungkan simpul 𝑣1 dan 𝑣𝑗
Gambar 2.28 Graf 𝑮 dan Matriks Berhubungan Langsung 2. Senarai Ketetanggan (Adjancency List)
Sebuah graf dapat disajikan dengan matriks keterkaitan. Misalkan graf 𝐺 mempunyai 𝑛 buah simpul 𝑣1, 𝑣2, 𝑣3, … , 𝑣𝑛 dan 𝑡 buah sisi 𝑒1, 𝑒2, 𝑒3, … , 𝑒𝑡. Matriks keterkaitan graf 𝐺 adalah matriks 𝑀(𝐺) = (𝑚𝑖𝑗) berordo 𝑛 × 𝑡 yang baris-barisnya dilabel dengan label simpul-simpul 𝐺 dan kolom-kolomnya dilabel dengan label sisi-sisi 𝐺.
Gambar 2.29 Graf 𝑮 dan Matriks Senarai Ketetanggan
2.3 Optimisasi
2.3.1 Definisi Optimisasi
Optimisasi adalah suatu proses untuk mencari hasil yang optimal atau nilai efektif yang dapat dicapai. Dalam disiplin matematika, optimisasi merujuk pada studi permasalahan yang mencoba untuk mencari nilai minimal atau maksimal dari suatu fungsi rill. (Wardy, 2007)
2.3.2 Macam-macam Permasalahan Optimisasi
Permasalahan yang berkaitan dengan optimisasi sangat kompleks dalam kehidupan sehari-hari. Nilai optimal yang didapat dalam optimisasi dapat berupa besaran panjang, waktu, jarak dan lain-lain. Berikut ini adalah termasuk beberapa persoalan optimisasi:
1. Menentukan lintasan terpendek dari suatu tempat ke tempat yang lain.
2. Menentukan jumlah pekerja seminial mungkin untuk melakukan suatu proses produksi agar pengeluaran biaya pekerja dapat diminimalkan dan hasil produksi tetap maksimal.
3. Mengatur rute kendaraan umum agar semua lokasi dapat dijangkau.
4. Mengatur routing jaringan kabel telepon agar biaya pemasangan kabel tidak terlalu besar dan penggunaanya tidak boros.
Selain beberapa contoh diatas, masih banyak persoalan lainnya yang terdapat dalam berbagai bidang.
2.3.3 Permasalahan Rute Terpendek
Permasalahan rute terpendek merupakan masalah yang berkaitan dengan penentuan sisi-sisi dalam sebuah jaringan yang membentuk rute terdekat antara sumber dan tujuan. Tujuan dari permasalahan rute terpendek adalah mencari rute yang memiliki jarak terdekat antara simpul asal dan simpul tujuan.
Gambar 2.30 Graf 𝑨𝑩𝑪𝑫𝑬𝑭𝑮
Pada gambar 2.30, misalkan dari kota 𝐴 ingin menuju kota 𝐺. Untuk menuju kota 𝐺, dapat dipilih beberapa rute yang tersedia yaitu:
1. 𝐴 → 𝐵 → 𝐶 → 𝐷 → 𝐸 → 𝐺 2. 𝐴 → 𝐵 → 𝐶 → 𝐷 → 𝐹 → 𝐺 3. 𝐴 → 𝐵 → 𝐶 → 𝐷 → 𝐺
4. 𝐴 → 𝐵 → 𝐶 → 𝐹 → 𝐺 5. 𝐴 → 𝐵 → 𝐷 → 𝐸 → 𝐺 6. 𝐴 → 𝐵 → 𝐷 → 𝐹 → 𝐺 7. 𝐴 → 𝐵 → 𝐷 → 𝐺 8. 𝐴 → 𝐵 → 𝐸 → 𝐺 9. 𝐴 → 𝐶 → 𝐷 → 𝐸 → 𝐺 10. 𝐴 → 𝐶 → 𝐷 → 𝐹 → 𝐺 11. 𝐴 → 𝐶 → 𝐷 → 𝐺 12. 𝐴 → 𝐶 → 𝐹 → 𝐺
Berdasarkan data diatas, dapat dihitung rute terendek dengan cara mencari jarak antar rute-rute tersebut. Apabila jarak antar rute belum diketahui, jarak dapat dihitung berdasarkan koordinat simpul-simpul tersebut, kemudian menghitung jarak terpendek yang dapat dilalui.
2.3.4 Penyelesaian Optimisasi
(Mutakhiroh, 2007) Secara umum, penyelesaian masalah rute terpendek dapat dilakukan dengan menggunakan dua metode, yaitu metode konvensional dan metode heuristik. Metode konvensional dihitung dengan menggunakan perhitungan matematis biasa, sedangkan metode heuristik dihitung dengan menggunakan sistem pendekatan.
1. Metode Konvensional
Metode konvensional adalah metode yang menggunakan perhitungan matematika eksak. Ada beberapa metode konvensional yang biasa digunakan untuk melakukan pencarian rute terpendek, antara lain: algoritma djikstra, algoritma floyd-warshall, dan algoritma bellman-ford dan lain-lain.
2. Metode Heuristik
Metode heuristik adalah suatu metode yang mengguakan sistem pendekatandalam melakukan pencarian optimasi. Ada beberapa algoritma dalam metode heuristik yang biasa digunakan dalam masalah optimasi, antara lain: Algoritma genetika, logika fuzzy, jaringan syaraf tiruan, tabu search, simulated annealing, dan lain-lain.
2.4 Branch and Bound
Pemecahan masalah optimasi Travelling Salesman Problem merupakan pekerjaan yang membutuhkan algoritma yang efisien. Algoritma Branch and Bound adalah salah satu algoritma untuk memecahkan masalah Travelling Salesman Problem. Algoritma Branch and Bound mencari sejumlah solusi yang lengkap untuk masalah optimasi dengan hasil yang terbaik. Walaupun begitu, penggunaan satu-satu secara eksplisit tidak mungkin dilakukan dalam kaitan penambahan sejumlah solusi yang potensial.
(Mulyono, 2007) teknik Branch and Bound dapat diterapkan dengan baik untuk masalah pure maupun mixed integer programming. Metode Branch and Bound adalah salah satu metode untuk menghasilkan penyelesaian optimal program linear yang menghasilkan variabel-variabel keputusan bilangan bulat. Sesuai dengan namanya metode ini membatasi penyelesaian optimum yang akan menghasilkan bilangan pecahan dengan cara membuat cabang atas atau bawah bagi masing-masing variabel keputusan yang bernilai pecahan agar bernilai bulat sehingga setiap pembatasan menghasilkan cabang baru (Widi Hartono, 2014)
Kelebihan dari metode Branch and Bound adalah mampu menyelesaikan permasalahan program integer sehingga keuntungan dari metode ini adalah cara yang efisien untuk mendapatkan jawaban layak (fisibel), sedangkan kekurangan metode ini akan mencari semua jawaban pada setiap titik sehingga persoalan yang besar akan memerlukan memori yang cukup banyak dan waktu yang cukup lama.
Metode Branch and Bound merupakan suatu metode pencarian solusi yang ditransformasikan dalam bentuk pohon percabangan dan pembatasan. Metode ini mula-mula dipakai oleh A. H. Land dan A. G. Doig pada tahun 1960. Algoritma Branch and Bound adalah suatu yang membagi (devine) dan menaklukkan (conquer) sehingga mengurangi masalah asli untuk satu rangkaian lebih kecil dari sub persoalan kemudian secara berulang memecahkan masalah masing-masing sub persoalan tersebut. Ada tiga komponen dalam algoritma Branch and Bound, yaitu sebagai berikut:
1. Fungsi pembatas (bounding) adalah fungsi yang disediakan ruang subspace dari ruang solusi dengan batas rendah untuk nilai solusi terbaik yang diperoleh dalam subspace. Metode dalam bounding ada dua, yaitu sebagai berikut:
1. Metode upper bounding merupakan metode untuk menentukan suatu
batas atas untuk solusi optimum.
2. Metode lower bounding merupakan metode untuk menentukan suatu batas bawah dari fungsi objektif.
3. Strategi pencarian merupakan suatu strategi untuk menyeleksi tiap-tiap simpul yang dihasilkan dan mendapatkan simpul yang optimum.
4. Metode percabangan (brancing) merupakan suatu metode yang diaplikasikan jika subspace setelah diperiksa tidak dapat dibatalkan.
Pembentukan pohon ruang status pada algoritma ini dibangun secara dinamis dengan skema Breadth First Search (BFS) ditambah least cost search. Breadth First Search (BFS) merupakan metode yang menguji semua keadaan dalam pohon pelacakan dalam waktu yang sama. BFS murni simpul berikutnya yang akan diekspansi berdasarkan urutan pembangkitnya. Perhitungan secara kuantitatif akan mempercepat pencarian suatu jawaban, oleh karena itu setiap simpul diberi nilai.
Berdasarkan nilai dari simpul yang dieksplorasi, maka bisa diambil keputusan untuk melakukan eksplorasi berikutnya. Dengan kata lain bahwa simpul yang dieksplorasi berikutnya tidak lagi berdasarkan urutan pembangkitnya (seperti pada BFS murni) tetapi berdasarkan nilai simpul yang paling kecil (least search cost). Nilai ada setiap simpul 𝑖 menyatakan tafsiran biaya termurah atau lintasan minimum dari simpul 𝑖 ke simpul tujuan (simpul solusi).
Gambar 2.31 Breadth First Search
Untuk permasaahan yang simultan, sistem digambarkan dengan matriks 𝑀 dengan ukuran 𝑛 × 𝑛. Dalam hal ini simpul anak beserta nilai batasnya dimasukkan kedalam sebuah antrian untuk dipilih simpul mana yang akan diekplorasi. Simpul yang akan dieksplorasi berikutnya adalah simpul dengan nilai batas terkecil. Nilai batas didapatkan dari hasil reduksi baris dan kolom pada matriks 𝑀.
Matriks tereduksi adalah matriks yang tiap kolom dan tiap barisnya
mengandung paling sedikit satu buah angka 0 dan elemen-elemen lainnya bernilai non- negatif. Untuk mendapatkan matriks tereduksi, maka tiap baris atau kolom yang belum mengandung angka 0 dikurangi dengan nilai terkecil pada baris atau kolom tersebut.
Semua angka yang digunakan untuk mengurangi tiap baris atau kolom tersebut kemudian dijumlahkan. Hasil penjumlahan inilah yang kemudian dijadikan sebagai 𝑐̂(𝑟𝑜𝑜𝑡) atau nilai ongkos dari simpul awal/akar. Hal ini juga berarti bahwa solusi pada persoalan Ttravelling Salesman Problem (TSP) tersebut paling tidak memiliki bobot minimum sebesar nilai 𝑐̂(𝑟𝑜𝑜𝑡) yang diperoleh tersebut.
Langkah-langkah penggunaan algoritma Branch and Bound pada Travelling Salesman Problem sebagai berikut:
1. Melakukan reduksi matriks
Matriks tereduksi adalah matriks yang tiap kolom atau tiap barisnya mengandung paling sedikit satu buah angka 0 dan elemen-elemen lainnnya bernilai non negatif. Untuk mendapatkan matriks tereduksi, maka tiap baris atau kolom yang belum mengandung angka 0 dikurangi dengan nilai terkecil pada baris atau kolom tersebut.
2. Menentukan nilai simpul awal/akar
Semua angka yang digunakan untuk mengurangi atau mereduksi tiap baris atau kolom tersebut kemudian dijumlahkan. Hasil dari penjumlahan inilah yang kemudian dijadikan sebagai ĉ(𝑟𝑜𝑜𝑡) atau nilai ongkos dari simpul awal/akar.
Hal ini juga berarti bahwa solusi pada persoalan TSP tersebut paling tidak memiliki bobot minimum sebesar nilai ĉ(𝑟𝑜𝑜𝑡) yang diperoleh tersebut.
3. Membangkitkan pohon ruang status
Setelah dihasilkan nilai batas simpul akar, maka dapat dibangkitkan pohon ruang status yang masih berisi satu buah simpul yang berbobot sama dengan nilai batas simpul akar atau ĉ(𝑟𝑜𝑜𝑡)
4. Menentukan matriks berikutnya dari matriks yang telah tereduksi
Selanjutnya, misal 𝐴 adalah matriks tereduksi untuk simpul 𝑅, dan misalkan 𝑆 adalah anak dari simpul 𝑅 sehingga sisi (𝑅, 𝑆) pada pohon ruang status berkorespondensi dengan sisi (𝑖, 𝑗), maka dilakukan langkah-langkah sebagai berikut:
1. Mengubah semua nilai pada baris 𝑖 dan kolom 𝑗 menjadi ∞
2. Mengubah 𝐴(𝑗, 1) mnejadi ∞ 3. Mereduksi kembali matriks 𝐴
4. Memperoleh nilai 𝑟 yang merupakan total semua pengurang dari matriks yang telah direduksi sebelumnya, sehingga dapat ditentukan nilai batas dari simpul S sebagai berikut :
ĉ(𝑆) = ĉ(𝑅) + 𝐴(𝑖, 𝑗) + 𝑟 dimana,
𝑐̂(𝑆) = bobot perjalanan minimum yang melalui simpul S (simpul di pohon ruang status)
𝑐̂(𝑅) = bobot perjalanan minimum yang melalui simpul R,
𝐴(i, j) = bobot sisi (i,j) pada graf G yang berkoresponden dengan sisi (R,S) pada pohon ruang status.
r = jumlah semua pengurang pada proses memperoleh matriks tereduksi pada simpul S
BAB 3
METODOLOGI PENELITIAN
Rancangan penelitian yang akan digunakan adalah penelitian studi kasus dengan langkah-langkah sebagai berikut:
1. Studi Literatur
Langkah pertama yang dilakukan dalam penelitian ini berupa studi literatur dengan mencari refrensi teori buku, jural, artikel dan penelitian terdahulu yang relevan dengan kasus graf, Travelling Salesman Problem (TSP), dan Branch and Bound. Beberapa literatur yang dikumpulkan dapat digunakan sebagai pedoman dalam penyelesaian penelitian ini.
2. Pengumpulan Data
Kumpulan data dalam penelitian ini diperoleh dari aplikasi Google Maps.
Variabel yang diambil merupakan jarak tempuh antar lokasi objek wisata yang terletak didaerah Kota Medan, Kabupaten Langkat dan Kabupaten Deli Serdang. Objek Wisata tersebut antara lain: Merdeka Walk, Arung Jeram Sungai Binge, Park Zoo and Resort Pancur Batu, 3D Art Magic Eye Museum, Taman Buah Lubuk Pakam, The Le Hu Garden, Taman Air Percut dan Velankanni. Data yang diambil diasumsikan dalam keadaan lalu lintas yang normal.
Proses pengumpulan data jarak tempuh yang melalui aplikasi Google Maps dalam penelitian ini diambil dari satu simpul ke simpul lain, oleh sebab itu terdapat delapan data jarak tempuh yang akan dicari solusi optimalnya.
Dalam hal ini diasumsikan menggunakan kendaraan mobil pada perhitungan jarak tempuh dengan aplikasi Google Maps.
3. Pengolahan Data
Data variabel yang berupa jarak tempuh akan diinput ke dalam bentuk tabel dan direpresentasikan dalam bentuk matriks, sehingga akan mempermudah dalam melakukan pengolahan data secara manual. Data tersebut akan diolah menggunakan algoritma Branch and Bound. Untuk penyelesaian kasus dengan ketentuan 𝑛 > 10, maka algoritma tersebut tidak efektif jika dikerjakan tanpa bantuan software. Oleh karena data jarak dalam penelitian ini termasuk
kedalam ketentuan 𝑛 < 10 maka algoritma tersebut masih efektif jika dikerjakan secara manual. Pengolahan data tersebut dilakukan dengan mereduksi matriks yang telah direpresentasikan sebelumnya, sehingga dapat dilanjutkan ke tahap berikutnya untuk memperoleh hasil yang optimal.
4. Membuat kesimpulan dan saran
Akan dilihat dari penentuan rute menggunakan algoritma Branch and Bound secara manual.
BAB 4
PEMBAHASAN DAN HASIL
4.1 Deskripsi Permasalahan
Permasalahan yang dibahas dalam tugas akhir ini adalah Travelling Salesman Problem (TSP). Masalah yang muncul dari TSP berhubungan dengan rute perjalanan untuk mengantarkan atau menjual barang pada beberapa kota dengan jarak perjalanan seminimal mungkin. Uraian persoalannya adalah diberikan sejumlah kota dan jarak antar kota. Tentukan rute optimal yang harus dilalui oleh salesman bila salesman tersebut berangkat dari sebuah kota asal dan menyinggahi setiap kota tepat satu kali, dan kembali ke kota asal keberangkatan dengan pencarian yang relatif singkat.
Penyelesaian TSP tersebut dilakukan dengan menggunakan algoritma Branch and Bound.
4.2 Pengumpulan Data
Pengumpulan data diperoleh langsung dari aplikasi google maps. Pada TSP ini menggunakan graf lengkap berbobot yaitu setiap simpul mempunyai sisi atau jarak ke simpul yang lain. Graf ini terdiri dari 8 simpul yang mewakili banyaknya objek wisata pada daerah Kota Medan, Kabupaten Langkat dan Kabupaten Deli Serdang. Berikut ini merupakan matriks jarak antar objek wisata yang akan dicari, dimana jarak tersebut akan dioptimalkan dengan satuan Kilometer (Km).
Tabel 4.1 Data Jarak Objek Wisata
Jarak A B C D E F G H
A 0 27.2 22.6 21.9 33.1 14.2 19 12.4
B 27.2 0 35.3 52.2 59.6 41.4 43.4 25.7
C 22.6 35.3 0 46.9 40.1 21.2 41 15
D 21.9 52.2 46.9 0 12.4 27.7 25.8 32.7
E 33.1 59.6 40.1 12.4 0 29.8 33.9 35.3
F 14.2 41.4 21.2 27.7 29.8 0 30.6 18.6
G 19 43.4 41 25.8 33.9 30.6 0 30.5
H 12.4 25.7 15 32.7 35.3 18.6 30.5 0
Keterangan Simpul:
A : Merdeka Walk
B : Arung Jeram Sungai Binge C : Park Zoo and Resort Pancur Batu D : 3D Art Magic Eye Museum E : Taman Buah Lubuk Pakam F : The Le Hu Garden
G : Taman Air Percut H : Velangkani
4.3 Pengolahan Data
Titik tujuan dari tiap penumpang akan diasosiasikan sebagai simpul dan titik awal sebagai akar. Peta yang menggambarkan lokasi dari simpul awal dan simpul-simpul akan di representasikan dalam bentuk graf. Pemberian nilai ongkos akan dilakukan dengan matriks jarak antar simpul yang dibentuk dari graf 𝐺. Langkah-langkah penggunaan algoritma Branch and Bound pada Travelling Salesman Problem sebagai berikut:
1. Melakukan reduksi matriks
Matriks tereduksi adalah matriks yang tiap kolom atau tiap barisnya mengandung paling sedikit satu buah angka 0 dan elemen-elemen lainnnya bernilai non negatif. Untuk mendapatkan matriks tereduksi, maka tiap baris atau kolom yang belum mengandung angka 0 dikurangi dengan nilai terkecil pada baris atau kolom tersebut.
[
∞ 27.2 22.6 21.9 33.1 14.2 19 12.4 27.2 ∞ 35.3 52.2 59.6 41.4 43.4 25.7 22.6 35.3 ∞ 46.9 40.1 21.2 41 15 21.9 52.2 46.9 ∞ 12.4 27.7 25.8 32.7 33.1 59.6 40.1 12.4 ∞ 29.8 33.9 35.3 14.2 41.4 21.2 27.7 29.8 ∞ 30.6 18.6 19 43.4 41 25.8 33.9 30.6 ∞ 30.5 12.4 25.7 15 32.7 35.3 18.6 30.5 ∞ ]
Matriks diatas merupakan matriks simetris karena jarak 𝑖 ke 𝑗 sama dengan jarak 𝑗 ke 𝑖. Dalam penyederhanaan matriks diatas dilakukan dengan cara mereduksi matriks tersebut.
Reduksi baris:
[
∞ 14.8 10.2 9.5 20.7 1.8 6.6 0 1.5 ∞ 9.6 26.5 33.9 15.7 17.7 0
7.6 20.3 ∞ 31.9 25.1 6.2 26 0
9.5 39.8 34.5 ∞ 0 15.3 13.4 20.3 20.7 47.2 27.7 0 ∞ 17.4 21.5 22.9
0 27.2 7 13.5 15.6 ∞ 16.4 4.4
0 24.4 22 6.8 14.9 11.6 ∞ 11.5
0 13.3 2.6 20.3 22.9 6.2 18.1 ∞ ]
Matriks diatas dihasilkan dari pengurangan tiap baris dengan nilai terkecil pada elemen baris tersebut. Baris ke-1 dikurangkan dengan 12.4, baris ke-2 dikurangkan dengan 25.7, baris ke-3 dikarangkan dengan 15, baris ke-4 dikurangkan dengan 12.4, baris ke-5 dikurangkan dengan 12.4, baris ke-6 dikurangkan dengan 14.2, baris ke-7 dikurangkan dengan 19, baris ke-8 dikurangkan dengan 12.4.
Reduksi kolom:
[
∞ 1.5 7.6 9.5 20.7 0 0 0
1.5 ∞ 7 26.5 33.9 13.9 11.1 0
7.6 7 ∞ 31.9 25.1 4.4 19.4 0
9.5 26.5 31.9 ∞ 0 13.5 6.8 20.3
20.7 33.9 25.1 0 ∞ 15.6 14.9 22.9 0 13.9 4.4 13.5 15.6 ∞ 9.8 4.4 0 11.1 19.4 6.8 14.9 9.8 ∞ 11.5
0 0 0 20.3 22.9 4.4 11.5 ∞ ]
Matriks diatas dihasilkan dari pengurangan tiap kolom dengan nilai terkecil seluruh elemen pada kolom setelah dilakukan reduksi baris. Kolom ke-2 dikurangkan dengan 13.3, kolom ke-3 dikurangkan dengan 2.6, kolom ke-6 dikurangkan dengan 1.8, dan kolom ke-7 dikurangkan dengan 6.6.
2. Menentukan nilai simpul awal/akar
Semua angka yang digunakan untuk mengurangi atau mereduksi tiap baris atau kolom tersebut kemudian dijumlahkan. Hasil dari penjumlahan inilah yang kemudian dijadikan sebagai ĉ(𝑟𝑜𝑜𝑡) atau nilai ongkos dari simpul awal/akar.
Hal ini juga berarti bahwa solusi pada persoalan TSP tersebut paling tidak memiliki bobot minimum sebesar nilai ĉ(𝑟𝑜𝑜𝑡) yang diperoleh tersebut.
Selanjutnya, proses reduksi tersebut akan menghasilkan nilai batas simpul akar ĉ(𝑟𝑜𝑜𝑡), yang didapat dari penjumlahan semua elemen pengurang pada reduksi baris dan reduksi kolom tersebut. jadi, diperoleh:
ĉ(𝑟𝑜𝑜𝑡) = 12.4 + 25.7 + 15 + 12.4 + 12.4 + 14.2 + 19 + 12.4 + 13.3 + 2.6 + 1.8 + 6.6
ĉ(𝑟𝑜𝑜𝑡) = 147.8
3. Membangkitkan pohon ruang status
Setelah dihasilkan nilai batas simpul akar, maka dapat dibangkitkan pohon ruang status yang masih berisi satu buah simpul yang berbobot sama dengan nilai batas simpul akar atau ĉ(𝑟𝑜𝑜𝑡)
Dengan demikian dapat dibangkitkan pohon ruang status:
Berikut merupakan pohon ruang status yang masih berisi satu buah simpul dengan bobot 147.8.
4. Menentukan matriks beriikutnya dari matriks yang telah tereduksi
Selanjutnya, misal 𝐴 adalah matriks tereduksi untuk simpul 𝑅, dan misalkan 𝑆 adalah anak dari simpul 𝑅 sehingga sisi (𝑅, 𝑆) pada pohon ruang status berkorespondensi dengan sisi (𝑖, 𝑗), maka dilakukan langkah-langkah sebagai berikut:
1. Mengubah semua nilai pada baris 𝑖 dan kolom 𝑗 menjadi ∞ 1. Simpul 2, lintasan (1,2)
[
∞ ∞ ∞ ∞ ∞ ∞ ∞ ∞
1.5 ∞ 7 26.5 33.9 13.9 11.1 0
7.6 ∞ ∞ 31.9 25.1 4.4 19.4 0
9.5 ∞ 31.9 ∞ 0 13.5 6.8 20.3
20.7 ∞ 25.1 0 ∞ 15.6 14.9 22.9
0 ∞ 4.4 13.5 15.6 ∞ 9.8 4.4
0 ∞ 19.4 6.8 14.9 9.8 ∞ 11.5
0 ∞ 0 20.3 22.9 4.4 11.5 ∞ ]
2. Mengubah 𝐴(𝑗, 1) mnejadi ∞
[
∞ ∞ ∞ ∞ ∞ ∞ ∞ ∞
∞ ∞ 7 26.5 33.9 13.9 11.1 0
7.6 ∞ ∞ 31.9 25.1 4.4 19.4 0
9.5 ∞ 31.9 ∞ 0 13.5 6.8 20.3
20.7 ∞ 25.1 0 ∞ 15.6 14.9 22.9
0 ∞ 4.4 13.5 15.6 ∞ 9.8 4.4
0 ∞ 19.4 6.8 14.9 9.8 ∞ 11.5
0 ∞ 0 20.3 22.9 4.4 11.5 ∞ ]
3. Mereduksi kembali matriks 𝐴
[
∞ ∞ ∞ ∞ ∞ ∞ ∞ ∞
∞ ∞ 7 26.5 33.9 9.5 5.8 0
7.6 ∞ ∞ 31.9 25.1 0 12.6 0
9.5 ∞ 31.9 ∞ 0 9.1 0 20.3
20.7 ∞ 25.1 0 ∞ 11.2 8.1 22.9
0 ∞ 4.4 13.5 15.6 ∞ 3 4.4
0 ∞ 19.4 6.8 14.9 5.4 ∞ 11.5
0 ∞ 0 20.3 22.9 0 4.7 ∞ ]
Matriks diatas diperoleh dari pengurangan kolom ke-6 dengan 4.4 dan kolom ke-7 dengan 6.8
4. Memperoleh nilai 𝑟 yang merupakan total semua pengurang dari matriks yang telah direduksi sebelumnya, sehingga dapat ditentukan nilai batas dari simpul S sebagai berikut :
ĉ(𝑆) = ĉ(𝑅) + 𝐴(𝑖, 𝑗) + 𝑟 dimana,
𝑐̂(𝑆) = bobot perjalanan minimum yang melalui simpul S (simpul di pohon ruang status)
𝑐̂(𝑅) = bobot perjalanan minimum yang melalui simpul R, yang dalam hal ini R adalah orang tua dari S
𝐴(i, j) = bobot sisi (i,j) pada graf G yang berkoresponden dengan sisi (R,S) pada pohon ruang status.
r = jumlah semua pengurang pada proses memperoleh matriks tereduksi pada simpul S
sehingga 𝑟 = 4.4 + 6.8 = 11.2. Maka diperoleh ĉ(2) dari rumus : ĉ(𝑆) = ĉ(𝑅) + 𝐴(𝑖, 𝑗) + 𝑟
ĉ(2) = 147.8 + 1.5 + 11.2 = 160.5
Selanjutnya menghitung simpul lain pada pohon ruang status yang baru dengan langkah-langkah yang telah dijelaskan diatas:
5. Simpul 3; lintasan (1,3)
[
∞ ∞ ∞ ∞ ∞ ∞ ∞ ∞
1.5 ∞ ∞ 26.5 33.9 13.9 11.1 0
∞ 7 ∞ 31.9 25.1 4.4 19.4 0
9.5 26.5 ∞ ∞ 0 13.5 6.8 20.3
20.7 33.9 ∞ 0 ∞ 15.6 14.9 22.9
0 13.9 ∞ 13.5 15.6 ∞ 9.8 4.4
0 11.1 ∞ 6.8 14.9 9.8 ∞ 11.5
0 0 ∞ 20.3 22.9 4.4 11.5 ∞ ]
=
[
∞ ∞ ∞ ∞ ∞ ∞ ∞ ∞
1.5 ∞ ∞ 26.5 33.9 9.5 4.3 0
∞ 7 ∞ 31.9 25.1 0 12.6 0
9.5 26.5 ∞ ∞ 0 9.1 0 20.3
20.7 33.9 ∞ 0 ∞ 11.2 8.1 22.9
0 13.9 ∞ 13.5 15.6 ∞ 3 4.4
0 11.1 ∞ 6.8 14.9 5.4 ∞ 11.5
0 0 ∞ 20.3 22.9 0 4.7 ∞ ]
Matriks diatas diperoleh dari pengurangan kolom ke-6 dengan 4.4 dan kolom ke-7 dengan 6.8, sehingga 𝑟 = 4.4 + 6.8 = 11.2. Maka diperoleh ĉ(3):
ĉ(𝑆) = ĉ(𝑅) + 𝐴(𝑖, 𝑗) + 𝑟
ĉ(3) = 147.8 + 7.6 + 11.2 = 166.6
6. Simpul 4; lintasan(1,4)
[
∞ ∞ ∞ ∞ ∞ ∞ ∞ ∞
1.5 ∞ 7 ∞ 33.9 13.9 11.1 0
7.6 7 ∞ ∞ 25.1 4.4 19.4 0
∞ 26.5 31.9 ∞ 0 13.5 6.8 20.3
20.7 33.9 25.1 ∞ ∞ 15.6 14.9 22.9
0 13.9 4.4 ∞ 15.6 ∞ 9.8 4.4
0 11.1 19.4 ∞ 14.9 9.8 ∞ 11.5
0 0 0 ∞ 22.9 4.4 11.5 ∞ ]
=
[
∞ ∞ ∞ ∞ ∞ ∞ ∞ ∞
1.5 ∞ 7 ∞ 33.9 9.5 4.3 0
7.6 7 ∞ ∞ 25.1 0 12.6 0
∞ 26.5 31.9 ∞ 0 9.1 0 20.3
20.7 33.9 25.1 ∞ ∞ 11.2 8.1 22.9
0 13.9 4.4 ∞ 15.6 ∞ 3 4.4
0 11.1 19.4 ∞ 14.9 5.4 ∞ 11.5
0 0 0 ∞ 22.9 0 4.7 ∞ ]
Matriks diatas diperoleh dari pengurangan kolom ke-6 dengan 4.4 dan kolom ke-7 dengan 6.8, sehingga 𝑟 = 4.4 + 6.8 = 11.2. Maka diperoleh ĉ(4):
ĉ(𝑆) = ĉ(𝑅) + 𝐴(𝑖, 𝑗) + 𝑟
ĉ(4) = 147.8 + 9.5 + 11.2 = 168.5
7. Simpul 5; lintasan (1,5)
[
∞ ∞ ∞ ∞ ∞ ∞ ∞ ∞
1.5 ∞ 7 26.5 ∞ 13.9 11.1 0
7.6 7 ∞ 31.9 ∞ 4.4 19.4 0
9.5 26.5 31.9 ∞ ∞ 13.5 6.8 20.3
∞ 33.9 25.1 0 ∞ 15.6 14.9 22.9
0 13.9 4.4 13.5 ∞ ∞ 9.8 4.4
0 11.1 19.4 6.8 ∞ 9.8 ∞ 11.5
0 0 0 20.3 ∞ 4.4 11.5 ∞ ]
=
[
∞ ∞ ∞ ∞ ∞ ∞ ∞ ∞
1.5 ∞ 7 26.5 ∞ 9.5 4.3 0
7.6 7 ∞ 31.9 ∞ 0 12.6 0
9.5 26.5 31.9 ∞ ∞ 9.1 0 20.3
∞ 33.9 25.1 0 ∞ 11.2 8.1 22.9
0 13.9 4.4 13.5 ∞ ∞ 3 4.4
0 11.1 19.4 6.8 ∞ 5.4 ∞ 11.5
0 0 0 20.3 ∞ 0 4.7 ∞ ]
Matriks diatas diperoleh dari pengurangan kolom ke-6 dengan 4.4 dan kolom ke-7 dengan 6.8, sehingga 𝑟 = 4.4 + 6.8 = 11.2. Maka diperoleh ĉ(5):
ĉ(𝑆) = ĉ(𝑅) + 𝐴(𝑖, 𝑗) + 𝑟
ĉ(5) = 147.8 + 20.7 + 11.2 = 179.7
8. Simpul 6; lintasan (1,6)
[
∞ ∞ ∞ ∞ ∞ ∞ ∞ ∞
1.5 ∞ 7 26.5 33.9 ∞ 11.1 0
7.6 7 ∞ 31.9 25.1 ∞ 19.4 0
9.5 26.5 31.9 ∞ 0 ∞ 6.8 20.3
20.7 33.9 25.1 0 ∞ ∞ 14.9 22.9
∞ 13.9 4.4 13.5 15.6 ∞ 9.8 4.4
0 11.1 19.4 6.8 14.9 ∞ ∞ 11.5
0 0 0 20.3 22.9 ∞ 11.5 ∞ ]
=
[
∞ ∞ ∞ ∞ ∞ ∞ ∞ ∞
1.5 ∞ 7 26.5 33.9 ∞ 11.1 0
7.6 7 ∞ 31.9 25.1 ∞ 19.4 0
9.5 26.5 31.9 ∞ 0 ∞ 6.8 20.3
20.7 33.9 25.1 0 ∞ ∞ 14.9 22.9
∞ 9.5 0 9.1 11.2 ∞ 5.4 0
0 11.1 19.4 6.8 14.9 ∞ ∞ 11.5
0 0 0 20.3 22.9 ∞ 11.5 ∞ ]
[
∞ ∞ ∞ ∞ ∞ ∞ ∞ ∞
1.5 ∞ 7 26.5 33.9 ∞ 5.7 0
7.6 7 ∞ 31.9 25.1 ∞ 14 0
9.5 26.5 31.9 ∞ 0 ∞ 1.4 20.3
20.7 33.9 25.1 0 ∞ ∞ 9.5 22.9
∞ 9.5 0 9.1 11.2 ∞ 0 0
0 11.1 19.4 6.8 14.9 ∞ ∞ 11.5
0 0 0 20.3 22.9 ∞ 6.1 ∞ ]
Matriks diatas diperoleh dari pengurangan baris ke-6 dengan 4.4 dan kolom ke-7 dengan 5.4, sehingga 𝑟 = 4.4 + 5.4 = 9.8. Maka diperoleh ĉ(6):
ĉ(𝑆) = ĉ(𝑅) + 𝐴(𝑖, 𝑗) + 𝑟
ĉ(6) = 147.8 + 0 + 9.8 = 157.6
9. Simpul 7; lintasan (1.7)
[
∞ ∞ ∞ ∞ ∞ ∞ ∞ ∞
1.5 ∞ 7 26.5 33.9 13.9 ∞ 0
7.6 7 ∞ 31.9 25.1 4.4 ∞ 0
9.5 26.5 31.9 ∞ 0 13.5 ∞ 20.3
20.7 33.9 25.1 0 ∞ 15.6 ∞ 22.9
0 13.9 4.4 13.5 15.6 ∞ ∞ 4.4
∞ 11.1 19.4 6.8 14.9 9.8 ∞ 11.5
0 0 0 20.3 22.9 4.4 ∞ ∞ ]
=
[
∞ ∞ ∞ ∞ ∞ ∞ ∞ ∞
1.5 ∞ 7 26.5 33.9 13.9 ∞ 0
7.6 7 ∞ 31.9 25.1 4.4 ∞ 0
9.5 26.5 31.9 ∞ 0 13.5 ∞ 20.3
20.7 33.9 25.1 0 ∞ 15.6 ∞ 22.9
0 13.9 4.4 13.5 15.6 ∞ ∞ 4.4
∞ 4.3 12.6 0 8.1 3 ∞ 4.7
0 0 0 20.3 22.9 4.4 ∞ ∞ ]
=
[
∞ ∞ ∞ ∞ ∞ ∞ ∞ ∞
1.5 ∞ 7 26.5 33.9 10.9 ∞ 0
7.6 7 ∞ 31.9 25.1 1.4 ∞ 0
9.5 26.5 31.9 ∞ 0 10.5 ∞ 20.3
20.7 33.9 25.1 0 ∞ 12.6 ∞ 22.9
0 13.9 4.4 13.5 15.6 ∞ ∞ 4.4
∞ 4.3 12.6 0 8.1 0 ∞ 4.7
0 0 0 20.3 22.9 1.4 ∞ ∞ ]
Matriks diatas diperoleh dari pengurangan baris ke-7 dengan 6.8 dan kolom ke-6 dengan 3, sehingga 𝑟 = 6.8 + 3 = 9.8. Maka diperoleh ĉ(7):
ĉ(𝑆) = ĉ(𝑅) + 𝐴(𝑖, 𝑗) + 𝑟
ĉ(7) = 147.8 + 0 + 9.8 = 157.6
10. Simpul 8; lintasan (1,8)
[
∞ ∞ ∞ ∞ ∞ ∞ ∞ ∞
1.5 ∞ 7 26.5 33.9 13.9 11.1 ∞
7.6 7 ∞ 31.9 25.1 4.4 19.4 ∞
9.5 26.5 31.9 ∞ 0 13.5 6.8 ∞
20.7 33.9 25.1 0 ∞ 15.6 14.9 ∞
0 13.9 4.4 13.5 15.6 ∞ 9.8 ∞
0 11.1 19.4 6.8 14.9 9.8 ∞ ∞
∞ 0 0 20.3 22.9 4.4 11.5 ∞]
=
[
∞ ∞ ∞ ∞ ∞ ∞ ∞ ∞
0 ∞ 5.5 25 32.4 12.4 9.6 ∞
3.2 2.6 ∞ 27.5 20.7 0 15 ∞
9.5 26.5 31.9 ∞ 0 13.5 6.8 ∞
20.7 33.9 25.1 0 ∞ 15.6 14.9 ∞
0 13.9 4.4 13.5 15.6 ∞ 9.8 ∞
0 11.1 19.4 6.8 14.9 9.8 ∞ ∞
∞ 0 0 20.3 22.9 4.4 11.5 ∞]
=
[
∞ ∞ ∞ ∞ ∞ ∞ ∞ ∞
0 ∞ 5.5 25 32.4 12.4 2.8 ∞
3.2 2.6 ∞ 27.5 20.7 0 8.2 ∞
9.5 26.5 31.9 ∞ 0 13.5 0 ∞
20.7 33.9 25.1 0 ∞ 15.6 8.1 ∞
0 13.9 4.4 13.5 15.6 ∞ 3 ∞
0 11.1 19.4 6.8 14.9 9.8 ∞ ∞
∞ 0 0 20.3 22.9 4.4 4.7 ∞]
Matriks diatas diperoleh dari pengurangan baris ke-2 dengan 1.5, baris ke-3 dengan 4.4 dan kolom ke-7 dengan 6.8, sehingga 𝑟 = 1.5 + 4.4 + 6.8 =