BAB I
PENDAHULUAN
A. Latar Belakang Masalah
Salah satu persoalan nasional dalam menghadapi masa depan adalah
masalah peningkatan kemampuan pembangunan (Development capability)1.
Kemampuan pembangunan yang telah kita miliki sekarang ini perlu kita
tingkatkan agar kita tetap bisa mengatasi masalah-masalah pembangunan yang
akan datang. Faktor utama yang mendorong peningkatan kemampuan
pembangunan adalah faktor dibidang pendidikan, sehingga pendidikan
merupakan bagian integral dalam pembangunan.2 Pembangunan diarahkan dan
bertujuan untuk mengembangkan sumber daya manusia (SDM) yang berkualitas,
yang satu dengan yang lainnya saling berkaitan dan berlangsung secara bersamaan.
dan proses pendidikan itu sendiri sudah tentu tidak dapat dipisahkan dengan semua
upaya yang harus dilakukan untuk mengembangkan sumber daya manusia yang
berkualitas.
Matematika sebagai salah satu cabang ilmu pengetahuan, besar
peranannya dalam mencetak SDM yang berkualitas. Matematika merupakan ilmu
yang esensial bagi manusia sebagai dasar untuk bekerja seumur hidup dalam abad
globalisasi seperti sekarang ini.
Menurut Marris Kline : Matematika memberikan bahasa, proses dan teori,
yang memberikan ilmu suatu bentuk dan kekuasaan. Perhitungan matematika
menjadi dasar bagi disiplin ilmu teknik. Metode matematis memberikan
inspirasi kepada pemikiran di bidang sosial dan ekonomi. Disamping itu, pemikiran
matematis memberikan warna kepada kegiatan seni lukis, arsitektur dan musik.
Bahkan jatuh bangunnya suatu negara, dewasa ini tergantung dari kemajuan
1 Mochtar Buchori, “ Pendidikan Dalam Pembangunan “, ( Yogyakarta, Tiara Wacana Yogya, 1994 ) hal 12
dibidang matematika.3
Oleh karena itu penguasaan tingkat pemahaman terhadap matematika sangat
diperlukan bagi semua siswa selaku penerus masa depan bangsa. Alur pikir dalam
matematika sangat membantu seseorang dalam mengkaji permasalahan, sehingga
mampu membentuk pola pikir yang konsisten dan tersetruktur.4 Mengingat akan
pentingnya peranan matematika, maka sudah sepantasnya jika matematika
diajarkan mulai di sekolah tingkatan dasar sampai di perguruan tinggi.
Matematika sebagai salah satu ilmu dasar, baik aspek terapan maupun aspek
penalaran mempunyai peranan penting dalam upaya penguasaan ilmu dan
tekhnologi. Didalam matematika, penalaran mendapat tempat dan peranan khusus
dalam pengembangan dan penerapan matematika. Karena ciri utama matematika
ialah metode dalam penalaran (reasoning).5 Pengembangan kemampuan
penalaran inilah yang akan membantu siswa meningkatkan kemampuan penalaran
dalam matematika, sehingga kemampuan penalaran siswa merupakan aspek
yang sangat penting. Kemampuan penalaran ini sangat membantu dalam
menyelesaikan masalah-masalah lain, baik masalah matematika maupun
masalah kehidupan sehari-hari. Bahkan menurut Krulik dan Rudnik,
kemampuan penalaran merupakan aspek kunci dalam mengembangkan
kemampuan berfikir kritis maupun kreatif bagi siswa.6
3 Herman Hudoyo, ” Strategi Mengajar Belajar Matematika “, ( Malang, IKIP Malang, 1990 ) hal 62
4 ibid, hal 64
5 Subanji, “Pembelajaran Dengan Pohon matematika Sebagai Upaya meningkatkan Kreatifitas
siswa“, Makalah disampaikan pada workshop pembelajaran matematika kontemporer oleh HMPS TMT STAIN Tulungagung, 12- 14 juli 2007
6 Subanji, “Pembelajaran Sistem Persamaan Linear Secara Bermakna Untuk Mengembangkan
Salah satu alasan kegagalan prestasi siswa untuk menunjukkan
kemampuan yang sebenarnya ialah siswa kadang-kadang salah mengartikan
persoalan yang diberikan oleh guru. Sebagian besar fakta tentang perkembangan
kognitif didasarkan pada jawaban siswa atas pertanyaan-pertanyaan
diberikan penguji. Siswa sering menginterpretasikan sebuah jawaban yang dia
anggap akan kebenarannya, namun dinilai salah oleh perspektif penguji atau guru.
Matematika memang timbul karena pemikirian manusia yang
berhubungan dengan ide, proses, dan penalaran.7 Wujud dari matematika adalah
bahasa yang sangat simbolis. Bahasa matematika banyak yang menggunakan
simbul-simbul dan istilah-istilah yang telah disepakati bersama. Oleh karena itu maka
perlu adanya pemahaman tentang simbul-simbul dan istilah-istilah matematika
yang merupakan prasyarat utama untuk memahami bahasa matematika.8
Jean Piaget berpendapat bahwa proses berfikir manusia sebagai suatu
perkembangan yang bertahap dan berpikir konkrit ke abstrak berurutan melalui
empat periode. Menurut Jean Piaget periode-periode itu adalah: periode
sensomotorik (0 sampai 2 tahun), periode praoprasional (2 tahun sampai 7 tahun),
periode operasi konkrit (7 tahun sampai 12 tahun), dan periode operasi formal (12
tahun dan seterusnya).9
Berdasarkan apa yang telah dikemukakan oleh Jean Piaget maka peneliti akan
meneliti pada periode operasi formal. Karena pada periode ini anak dapat
7 Erman Suherman, Tatang Herman dkk, “Strategi Pembelajaran Matamatika Kontemporer“, (Bandung, Universitas Pendidikan Indonesia, 2003) hal 7
8 Herman Hudoyo, “ Strategi Mengajar Belajar Matematika “, (Malang, IKIP Malang, 1990) hal 64
mengemukakan alasan tentang hipotesis dan kemungkinan abstrak, demikian pula
tentang realitas dan fisik yang konkret. Mereka mencari secara sistematis
penyelesaian persoalan.10 Teori-teori yang telah diberikan guru yang masih sangat
abstrak dapat menjadi realita dalam pikiran operasi formal. Siswa yang termasuk
dalam kategori periode formal yang akan diteliti adalah siswa kelas VIII MTs PSM
Jeli, Karangrejo, Tulungagung, dengan materi bangun datar, karena materi ini
membutuhkan penguasaan penalaran matematika.
Matematika dipelajari karena mempunyai tujuan atau obyektif yang harus
dinyatakan dengan jelas, sehingga tidak ada penafsiran yang berbeda. Menurut
Marger obyektif didefinisikan sebagai suatu pernyataan hasil yang dikehendaki,
yaitu suatu pernyataan yang menunjukkan sebagai apa pelajar itu bila pelajar itu
telah menyelesaikan dengan sukses proses pengalaman belajarnya.11 Dengan
demikian, obyektif ini harus dinyatakan sebagai bentuk klasiflkasi tingkah laku
siswa yang melukiskan hasil yang dikehendaki dari pada proses pendidikan, atau
sering kita gunakan istilah Taksonomi Pendidikan. Menurut Bloom pembagian utama obyektif pendidikan didalam taksonomi ada tiga bidang tingkah laku yaitu:
Kognitif, Afektif dan Psikomotorik.12
Dalam penelitian ini peneliti lebih menekankan pada aspek kognitif yang
meliputi ingatan, pengembangan kemampuan dan ketrampilan intelektual.
Sedangkan prosesnyapun melibatkan berfikir kritis dan pemecahan masalah.
Orang yang mampu mengatur dan mengarahkan aktivitas mentalnya sendiri di
10 ibid, hal 42
11 Herman Hudoyo, “Pengembangan Kurikukulum Matematika dan Pelaksanaanya didepan
bidang kognitif, akan jauh lebih efektif dalam mempergunakan konsep matematika
yang pernah dipelajarinya. Sedangkan aspek afektif dan psikomotorik ini kurang
diperlukan didalam pendidikan matematika.13
Pada aspek kognitif ini terdiri dari: Pengetahuan ( knowledge ), Pemahaman
(comprehension), Penerapan atau Aplikasi (aplication), Analisis (analysis),
Sintesis (synthesis), Evaluasi (evaluation). Karena nantinya yang akan diteliti adalah tahap operasi formal yaitu siswa MTs kelas VIII, maka peneliti hanya mengambil
pada tahapan Analisis, Sintesis dan Evaluasi. Karena tahap mengenal, pemahaman
dan aplikasi lebih sesuai untuk periode operasi konkrit yaitu usia dibawah 12 tahun.
Analisis adalah kemampuan untuk memilah sebuah struktur informasi
kedalam komponen-komponen sedemikian sehingga hierarki dan keterkaitan
antar idea dalam informasi tersebut menjadi tampak jelas.14 Sintesis adalah
kemampuan untukmengkombinasikan elemen-elemen untuk membentuk
sebuah struktur yang unik atau sistem. Dalam matematika, sintesis melibatkan
pengkombinasian dan pengorganisasian konsep-konsep dan prinsip-prinsip
matematika untuk mengkreasikanya menjadi struktur matematika yang lain
dan berbeda dari yang sebelumnya. Salah satunya adalah memformulasikan
teorema-teorema matematika dan mengembangkan struktur-struktur
matematika.15 Evaluasi adalah kegiatan membuat penilaian (judgement )
berkenaan dengan nilai sebuah idea, kreasi, cara, atau metode.16
13 ibid, hal 39
14 Erman Suherman, Tatang Herman dkk, “Strategi Pembelajaran Matamatika Kontemporer“, (Bandung, Universitas Pendidikan Indonesia, 2003) hal 224
B. Fokus Penelitian
Berdasarkan latar belakang diatas serta demi terwujudnya
pembahasan yang sesuai dengan harapan, maka penulis memaparkan
permasalahan yang menjadi fokus penelitian yang dapat dirumuskan sebagai
berikut:
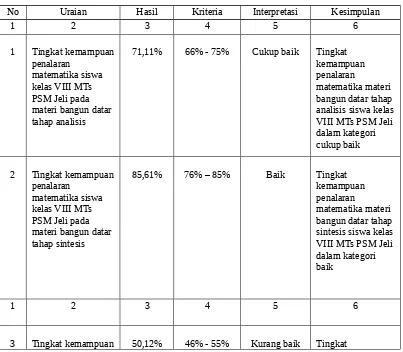
a. Bagaimanakah tingkat kemampuan penalaran matematika siswa kelas VIII
MTs PSM Jeli, tentang pokok bahasan bangun datar pada tahap Analisis ?
b. Bagaimanakah tingkat kemampuan penalaran matematika siswa kelas VIII
MTs PSM Jeli, tentang pokok bahasan bangun datar pada tahap Sintesis ?
c. Bagaimanakah tingkat kemampuan penalaran matematika siswa kelas
VIII MTS PSM Jeli, tentang pokok bahasan bangun datar pada tahap
Evaluasi ?
d. Bagaimanakah tingkat kemampuan penalaran matematika siswa kelas VIII
MTs PSM Jeli, pada pokok bahasan bangun datar ?
C. Tujuan dan Kegunaan Penelitian 1. Tujuan I'enelitian
a. Untuk mengetahui tingkat kemampuan penalaran matcmatika siswa kelas
VIII MTs PSM Jeli, pada pokok bahasan bangun datar pada tahap Analisis.
b. Untuk mengetahui tingkat kemampuan penalaran matematika siswa kelas
VIII MTs PSM Jeli, pada pokok bahasan bangun datar pada tahap Sintesis.
c. Untuk mengetahui tingkat kemampuan penalaran matematika siswa kelas
Evaluasi.
d. Untuk mengetahui tingkat kemampuan penalaran matematika siswa kelas
VIII MTs PSM Jeli, pada pokok bahasan bangun datar.
2. Kegunaan Penelitian a. Secara Teoritis
Peneliti berharap penelitian ini nantinya dapat memberikan gambaran
bahwa tingkat kemampuan penalaran matematika pada periode operasi
formal ini perlu sekali untuk terus ditingkatkan. Oleh karena itu memerlukan
cara atau metode khusus untuk lebih meningkatkan kemampuan
penalaran siswa, sehingga penalaran siswa akan menjadi lebih baik.
b. Secara Praktis
1) Bagi institusi pendidikan sebagai bahan pertimbangan dalam
mengambil kebijakan yang berkenaan dengan pembelajaran
matematika.
2) Bagi guru adalah sebagai bahan rujukan yang dapat diambil manfaat
dan ide dasar dari pembahasan ini, agar dapat lebih meningkatkan
proses pembelajaran sehingga sesuai dengan kemampuan penalaran
yang dimiliki siswa dalam pelajaran matematika.
3) Sebagai bekal pengetahuan bagi siswa agar lebih meningkatkan
kemampuan penalaran matematika untuk menyelesaikan soal-soal
matematika khususnya materi bangun datar, sehingga siswa dapat
membentuk sikap logis, kritis, cermat dan kreatif.
pentingnya penalaran matematika.
D. Penegasan Istilah
1. Penegasan konseptual
Analisis Kemampuan Penalaran Matematika Siswa Kelas VIII MTs
PSM Jeli pada pokok bahasan bangun datar adalah penelaahan fakta terhadap
tingkat kemampuan penalaran matematika siswa kelas VIII MTs PSM Jeli dalam
pembelajaran matematika pada pokok bahasan bangun datar.
2. I'enegasan Operasional
Analisis Kemampuan Penalaran Matematika Siswa Kelas VIII MTs
PSM Jeli pada pokok bahasan bangun datar dalam penelitian ini adalah
pengukuran terhadap aspek kognitif yaitu pada tingkat kemampuan penalaran
matematika siswa kelas VIII MTs PSM Jeli pada pokok bahasan bangun datar
dengan mengukur pada tahap Analisis, Sintesis dan Evaluasi yang diukur
melalui soal-soal tes untuk memperoleh skor atau nilai tentang tingkat
kemampuan penalaran matematika pokok bahasan bangun datar. Untuk benar
setiap soalnya (2,5) dan salah (0), dengan kriteria semakin tinggi skor yang
diperoleh akan semakin tinggi pula tingkat kemampuan penalaran matematika
siswa tersebut.
E. SISTEMATIKA PEMBAHASAN
Kajian terhadap masalah pokok yang disebutkan diatas,dibagi atau
BAB 1 : PENDAHULUAN
1 latar Belakang Masalah
2 Perumusan masalah
3 Tujuan dan Kegunaan Penelitian
4 Penegasan Istilah
5 Sistematika Pembahasan
BAB II : LANDASAN TEORI
1. Hakekat Matematika dan Belajar Matematika
2. Taksonomi Pendidikan
3. Penalaran Dalam Matematika
4. Materi Bangun Datar di MTs
5. Asumsi Penelitian
BAB III : METODE PENELITIAN
1. Pola Penelitian
2. Populasi
3. Variabel, Data, dan Sumber Data
4. Metode dan Instrumen Pengumpulan Data
5. Prosedur Penelitian
6. Tehnik Analisis Data
BAB IV : LAPORAN HASIL PENELITIAN
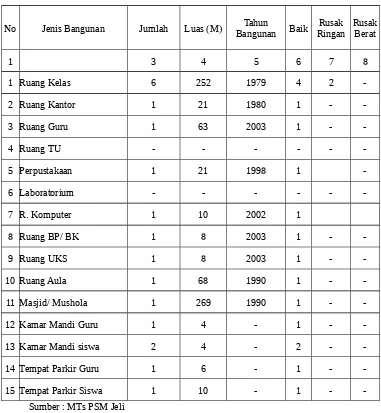
1. Diskripsi singkat Tentang Keadaan Obyek Penelitian
2. Penyajian dan Analisis Data
1. Kesimpulan
2. Saran-saran
BAB II
LANDASAN TEORI
A. Hakekat Matematika dan Belajar Matematika 1. Definisi Matematika
Seperti kata Abraham S Lunchins dan Edith N Lunchins “Apakah
matematika itu ? “, dapat dijawab secara berbeda-beda tergantung pada
bila mana pertanyaan itu dijawab, dimana dijawab, siapa yang menjawab,
dan apa sajakah yang termasuk dipandang dalam matematika.17
Istilah mathematics (Inggris), mathematik (Jerman), mathematique
(Perancis), matematico (Itali), matematiceski (Rusia), atau mathematick/wiskunde (belanda), berasal dari perkataan lain
mathematica, yang mulanya dari perkataan yunani, mathematike, yang berarti “relating to learning“. Perkataan itu mempunyai akar kata
mathema yang artinya pengetahuan atau ilmu (knowledge, science). Perkataan mathematike berhubungan sangat erat dengan sebuah kata lainnya yang serupa, yaitu mathanein yang mengandung arti belajar.18
Jadi berdasarkan etimologis. Perkataan matematika berarti “Ilmu
pengetahuan yang diperoleh dengan bernalar“. Hal ini dimaksudkan
bukan berarti ilmu lain diperoleh tidak melalui penalaran, akan tetapi
dalam matematika lebih menekankan aktivitas dalam dunia rasio
(penalaran), sedangkan dalam ilmu lain lebih menekankan hasil observasi
atau eksperimen disamping penalaran.19
Akan tetapi pengertian matematika secara istilah belumlah dapat disepakati
secara pasti. Banyak pengertian yang dikemukakan oleh para ahli dan para
matematikawan yang semua itu sesuai dengan sudut pandangnya masing-masing.
Sehingga pemaknaannya sangat luas dan fleksibel.
Misalnya James dan James mengatakan bahwa matematika adalah ilmu
17 Erman Suherman, Tatang Herman dkk, “Strategi Pembelajaran Matamatika Kontemporer“, (Bandung, Universitas Pendidikan Indonesia, 2003) hal 15
tentang logika mengenai bentuk susunan, besaran, dan konsep-konsep yang saling
berhubungan antara satu dengan yang lainya.20
Tokoh lain yaitu W.W. Sawyer mengatakan "Mathematic is the clasification and study of all possible pattern” (Matematika adalah penggolongan dan penelaahan tentang semua pola yang mungkin).21
O.G. Sutton mengemukakan matematika adalah suatu penelaahan tentang
pola-pola dari ide-ide, yang dilakukan dengan suatu tekhnik khusus yang telah
dikembangkan secara tinggi, yang dipercayai akan kebenarannya. 22
Herman Hudoyo mengatakan bahwa hakekat matematika adalah berkenaan
dengan ide ide, struktur, dan hubungannya yang di atur menurut urutan yang
logis.23
Reys dkk mengemukakan bahwa matematika adalah telaahan tentang pola
dan hubungan suatu jalan atau pola berpikir, suatu seni, suatu bahasa, dan suatu
alat.24
Johnson dan Rising dalam bukunya mengatakan bahwa matematika
adalah pola pikir, pola mengorganisasikan, pembuktian yang logis,
matematika itu adalah bahasa yang menggunakan istilah yang
didefinisikan dengan cermat, jelas, dan akurat, representasinya dengan
20 Russeffendi, “Pengajaran Matematika Modern dan Masa Kini untuk PGSD Seri ke-2 “, (Bandung, Tarsito, 1990) , hal 1
21 The Liang Gie, “Filsafat Matematika Bagian Kedua “, (Yogyakarta, Yayasan Studi Ilmu dan Tekhnologi, 1993) hal 5
22 ibid, hal 30
23 Herman Hudoyo, “Pengembangan Kurikukulum Matematika dan Pelaksanaanya didepan
Kelas“, (Surabaya, Usaha Nasional, 1979) hal 96
simbol dan padat, lebih berupa bahasa symbol mengenai ide.25
Sedangkan Kline mengatakan bahwa matematika bukanlah pengetahuan
menyendiri yng dapat sempurna karena dirinya sendiri, tetapi adanya
matematika itu untuk membantu manusia dalam memahami dan menguasai
permasalahan sosial, ekonomi dan alam.26
Pengertian matematika sebagai ilmu adalah salah satu cabang ilmu yang
tersusun secara sistematis dan eksak. Pengertian eksak tersebut tidak berarti eksak
secara mutlak, akan tetapi matematika sebagai ilmu lebih eksak daripada ilmu-ilmu
sosial dan lebih eksak dari pada ilmu-ilmu fisik, oleh karena sifatnya yang
eksak ini maka matematika sering disebut sebagai ilmu pasti.27
Di Indonesia pernah digunakan ilmu pasti untuk matematika. Dalam
kurikulum sekolah digunakan berbagai istilah cabang matematika, seperti : Ilmu
ukur, Aljabar, Geometri, Trigonometri, dll. Hal ini berakibat antara lain matematika
seolah-olah terkotak-kotak yang saling tidak berhubungan. Penggunaan kata ilmu
pasti menimbulkan kesan bahwa pelajaran matematika merupakan pelajaran
tentang perhitungan-perhitungan yang memberikan hasil yang pasti dan tunggal.
Hal tersebut dapat menimbulkan suatu miskonsepsi yang pada waktunya harus
dapat ditiadakan. Justru kemungkinan ketidak tunggalan hasil tersebut dapat
dimanfaatkan dalam pembelajaran matematika yang menekankan kepada
mengaktifkan siswa atau “ student active learning “.28
25 Erman Suherman, Tatang Herman dkk, “Strategi Pembelajaran Matamatika Kontemprer“, (Bandung, Universitas Pendidikan Indonesia) hal 62
26 Ismail, “Kapita Selekta Pendidikan Matematika “, (Jakarta : Universitas Terbuka, 1998), hal 14 27 ibid, hal 25
Seperti di katakan diawal, bahwa pendefinisian matematika berfokus
pada tinjauan dan sudut pandang pembuat definisi, sehingga tidak ada kata
sepakat mengenai apa itu arti matematika secara terminologi, akan tetapi
walaupun demikian dapat terlihat ciri khusus atau karakteristik pengertian
matematika secara umum, sebagaimana di katakan R. Soejadi:
a. Memiliki objek kajian abstrak
b. Bertumpu pada kesepakatan
c. Berpola pikir deduktif
d. Mempunyai simbol yang kosong dari arti
e. Memperhatikan semesta pembicaraan
f. Konsisten dalam sistemnya 29
Berikut ini uraian dari masing-masing karakteristik tersebut diatas.
a. Memiliki objek kajian abstrak.
Dalam matematika objek dasar yang dipelajari adalah abstrak, sering
juga disebut objek mental. Objek-ojek itu merupakan objek pikiran. Objek
dasar itu meliputi : fakta, konsep, operasi maupun relasi, dan prinsip. Fakta
(abstrak) berupa konvensi-konvensi yang diungkap dengan symbol tertentu.
Konsep adalah ide abstrak yang dapat digunakan untuk mengklasifikasikan
sekumpulan objek. Operasi (abstrak) adalah pengerjaan hitung, pengerjaan
aljabar dan pengerjaan matematika yang lain. Prinsip (abstrak) adalah objek
29 R.Soejadi, “Kiat Pendidikan Matematika Di Indonesia Konstatasi Keadaan Masa Kini Menuju
matematika yang kompleks. Prinsip dapat berupa dari beberapa fakta,
beberapa konsep, yang dikaitkan oleh suatu relasi ataupun operasi. Secara
sederhana dapat dikatakan prinsip adalah hubungan antara berbagai objek
dasar matematika.Prinsip dapat berupa aksioma, teorema, sifat, dan
sebagainya.
b. Bertumpu pada kesepakatan.
Dalam matematika kesepakatan merupakan tumpuan yang amat penting.
Kesepakatan yang amat mendasar adalah aksioma dan konsep primitif.
Aksioma diperlukan untuk menghindarkan berputar-putar dalam
pembuktian. Sedangkan konsep primitif diperlukan untuk menghindarkan
berputar-putar pada pendefinisian.
c. Berpola pikir deduktif.
Dalam matematika sebagai "ilmu" hanya diterima pola pikir deduktif.
Pola pikir deduktif secara sederhana dapat dikatakan pemikiran yang
berpangkal dari hal yang bersifat umum diterapkan atau diarahkan kepada hal
yang bersifat khusus.
d. Mempunyai simbol yang kosong dari arti.
Dalam matematika banyak sekali simbol-simbol yang digunakan, baik
berupa huruf ataupun bukan huruf. Huruf-huru yang digunakan dalam
model persamaan x + y = z belum tentu bermakna atau berarti bilangan , demikian juga tanda “ + “ belum tentu berarti operasi tambah untuk dua
mengakibatkan terbentuknya model tersebut. Jadi semacam huruf dan tanda
dalam model x + y = z masih kosong dari arti, terserah kepada yang akan
memanfaatkan model tersebut.
e. Memperhatikan semesta pembicaraan.
Terkait dengan penjelasan tentang kosongnya arti dari simbol-simbol dan
tanda-tanda dalam matematika diatas menunjukkan dengan jelas bahwa
menggunakan matematika diperlukan kejelasan dalam lingkup apa model itu
dipakai. Bila lingkup pembicaraannya bilangan, maka simbol-simbol
diartikan bilangan. Namun bila lingkup pembicaraannya transformasi,
maka simbol-simbol itu diartikan transformasi. Lingkup pembicaraan inilah
yang disebut dengan semesta pembicaraan.
f. Konsisten dalam sistemnya.
Dalam matematika terdapat banyak sistem yang berkaitan satu sama
lain, tetapi ada pula sistem yang dapat dipandang terlepas satu sama lain.
Kontradiksi antara sistem tersebut tetap bernilai benar pada sistem dan
strukturnya sendiri. Misalnya dikenal system –sistem aljabar, system
Geometri. Sisteem aljabar dan system geometri tersebut dipandang lepas
satu sama lain. Dalam masing-masing dan strukturnya itu berlaku ketaat
azasan. Ini juga dikatakan bahwa dalam setiap system dan strukturnya
tersebut tidak boleh terdapat kontradiksi. Suatu teorema ataupun suatu
definisi harus menggunakan istilah atau konsep yang telah ditetapkan
kebenarannya. Kalau telah ditetapkan bahwa a + b = x dan x + y = p, maka
a + b + y haruslah p.
Kebenaran merupakan hal yang amat penting dalam ilmu pengetahuan
maupun luar ilmu pengetahuan. Dalam kehidupan sehari – hari juga dikenal
kebenaran dan tidak kebenaran. Tindakan seseorang sering digolongkan pada ‘
benar ‘ dan ‘ tidak benar ‘, meskipun perkembangan terakhir ini dimungkinkan
penggolongan itu tidak hanya dikotomoi seperti itu. Sesuatu nyang dinilai benar
ataupun salah umumnya dapat dinyatakan dalam bentuk pernyataan atau
statement.30
Dalam keilmuan dikenal dengan tiga jenis kebenaran yaitu,
a. Kebenaran konsistensi, adalah kebenaran suatu pernyataan yang didasarkan
kepada kebenaran – kebenaran yang telah diterima terlebih dahulu
sebelumnya. Contoh pada dasarnya kebenaran yang ada dalam matematika
adalah kebenaran konsistensi. Kebenaran suatu teorema dalam matematika
dibuktikan dengan menggunakan kebenaran – kebenaran pernyataan –
pernyataan terdahulu yang telah diterima sebagai benar
b. Kebenaran Korelasional, adalah kebenaran suatu pernyataan yang
didasarkan kepada ‘ kecocokannya ‘ dengan realitas atau kenyataan yang
ada. Contoh : Ada pernyataan : “ Logam kalao dipanaskan memuai “.
Kebenaran pernyataan ini diyakini melalui kecocokannya dengan realitas
suatu logam jika benar- benar di panaskan.
c. Kebenaran Pragmatik, adalah kebenaran suatu pernyataan yang didasarkan
atas manfaat atau kegunaan dari intensi pernyataan itu. Contoh : tentang
logam yang dipanaskan diatas, dapat juga dilihat sebagai kebenaran
pragmatik, karena pernyataan itu dapat dimanfaatkan, misalnya dalam
pemasangan rel kereta api.31
2. Matematika Sekolah
Beberapa uraian diatas tersebut adalah tentang matematika sebagai
ilmu, sedang matematika yang diajarkan di sekolah mulai pra sekolah sampai SMU
sering disebut dengan matematika sekolah. Berikut ini penulis akan membahas
tentang matematika sekolah (school mathematic). Definisi matematika sekolah adalah unsur-unsur atau bagian-bagian dari matematika yang dipilih
berdasarkan kepada kepentingan kependidikan dan perkembangan
IPTEK.32 Hal ini menunjukkan bahwa matematika sekolah tidak sepenuhnya
sama dengan matematika sebagai ilmu. Adapun perbedannya terletak pada :
a. Cara penyajiannya. Penyajian dalam buku matematika di sekolah tidak
selalu di awali dengan teorema ataupun definisi. Disesuaikan dengan
perkembangan intelektual peserta didik.
b. Pola pikirnya. Dalam matematika sekolah meski tetap diharapkan mampu
berfikir deduktif, namun pada proses pembelajarannya dapat
menggunakan pola pikir induktif.
31 Lapis,”Matematika – 1“, (Surabaya, Lapis, 2008) hal 5
32 R.Soejadi, “Kiat Pendidikan Matematika Di Indonesia Konstatasi Keadaan Masa Kini Menuju
c. Keterbatasan semestanya. Dalam matematika di SD terlihat secara
bertahap di perkenalkan bilangan bulat positif, kemudian lebih atas lagi
diperkenalkan pecahan dan bilangan negatif. Jadi semestanya sempit
kemudian meluas.
d. Tingkat keabstrakannya. Diawal pendidikan tingkat abstraksi rendah, semakin
tinggi pendidikan semakin tinggi pula tingkat abstraksinya.33
Terkait dengan fungsi dan tujuan matematika diajarkan di sekolah dalam
hal ini MTs, matematika berfungsi untuk mengembangkan kemampuan
berhitung, mengukur, menurunkan, dan menggunakan rumus matematika yang
diperlukan dalam kehidupan sehari-hari melalui materi pengukuran dan geometri,
aljabar dan trigonometri. Selain itu matematika sekolah berfungsi untuk
mengembangkan kemampuan mengkomunikasikan gagasan dengan bahasa
melalui model matematika yang dapat berupa kalimat dan persamaan matematika,
diagram, grafik atau tabel.34
Sedangkan tujuan matematika diajarkan disekolah menengah termasuk
di dalamnya adalah MTs yaitu :
a. Melatih cara berpikir dan bernalar dalam menarik kesimpulan, misalnya
melalui kegiatan penyelidikan, eksplorasi, eksperimen, menunjukkan
kesamaan, perbedaan, konsisten dan inkonsisten.
b. Mengembangkan aktifitas kreatif yang melibatkan imajinasi, intuisi, dan
33 ibid, hal 37 - 42
penemuan dengan mengembangkan pemikiran divergen, orisinil, rasa
ingin tahu, membuat prediksi dan dugaan serta mencoba-coba.
c. Mengembangkan kemampuan memecahkan masalah.
d. Mengembangkan kemampuan menyampaikan informasi atau
mengkomunikasikan gagasan antara lain melalui pembicaraan lisan, catatan,
grafik, peta, dan diagram dalam menjelaskan gagasan- gagasan.35
3. Proses Belajar Mengajar Matematika
Dalam dunia pendidikan kita mengenal dua istilah kata kerja yang sangat
mendasar yaitu "belajar" dan "mengajar". Definisi tentang belajar sebenarnya
banyak orang yang telah mendefinisikannya. Akan tetapi pemaknaan dari
belajar itu sendiri tiap orang tidaklah sama, karena masing-masing orang
memaknai belajar dari perspektif yang berbeda.
Berikut ini beberapa kutipan tentang pengertian belajar menurut sebagian
ahli :
a. Menurut Dr. Mustofa Fahmi memberikan pengertian bahwa
sesungguhnya belajar adalah (ungkapan yang menunjuk) aktifitas (yang
menghasilkan) perubahan-perubahan atau tingkah laku.36
b. Menurut Cronbach "learning is shown by achange in behavior as aresult of experience"} Jadi menurutnya belajar yang sebaik-baiknya adalah dengan mengalami dan dalam mengalami manusia menggunakan panca
indranya.37
35 ibid, hal 6
c. Menurut Drs. Syaiful Bahri Djamaroh belajar adalah proses perubahan
prilaku berkat pengalaman dan latihan.38
d. W.S. Winkel mengemukakan belajar adalah sebagai proses pembentukan
tingkah laku secara terorganisir.39
e. Menurut Herman Hudoyo, belajar adalah kegiatan bagi setiaporang yang
mengakibatkan suatu perubahan tingkah laku, karena terbentuknya
pengetahuan, keterampilan, kebiasaan, kegemaran, dan sikap seseorang
terbentuk.40
Dari beberapa gambaran definisi di atas penulis menyimpulkan bahwa
belajar merupakan proses perubahan tingkah laku baik aspek jasmani maupun
rohani yang itu didahului atau disertai usaha oleh yang bersangkutan. Selain itu
ada beberapa hal unsur penting sebagai ciri khas pengertian tentang belajar
yaitu:
a. Adanya usaha atau aktifitas yang di sengaja sehingga menghasilkan suatu
perubahan perilaku, dimana perubahan tersebut ada dua kemungkinan yaitu
mengarah pada hal positif dan pada hal negatif.
b. Perubahan prilaku yang terjadi menyangkut berbagai aspek.
c. Perubahan tersebut terjadi melalui pengalaman atau latihan. Dalam hal ini
Ngalim Purwanto mengatakan perubahan yang di sebabkan pertumbuhan
38 Syaiful Bahri Djamaroh, “Strategi belajar Mengajar “, (Jakarta, Rineka Cipta, Cetakan ke-2, 2002) hal 11
39 W.S Winkel, ‘ Psikologi Pengajaran “, (Jakarta, Gramedia, 1996) hal 53
atau kematangan tidak di anggap sebagai hasil belajar.
d. Perubahan relatif bersifat konstan.41
Adapun pengertian mengajar juga banyak ahli yang memberi
pemaknaan, di antaranya adalah sebagai berikut :
a. Pror. Dr. S. Nasution, M.A mengartikan mengajar adalah menanamkan
pengetahuan pada anak.42
b. Nana Sudjana berpendapat mengajar adalah mengatur dan
mengorganisasikan lingkungan yang ada di sekitar siswa sehingga dapat
mendorong dan menumbuhkan siswa melakukan kegiatan belajar.43
c. Herman Hudoyo berpendapat mengajar adalah suatu kegiatan dimana
pengajar menyampaikan pengetahuan atau pengalamanya yang dimiliki
kepada peserta didik dengan tujuan agar pengetahuan yang disampaikan
dapat dipahami peserta didik.44
Dari tiga pengertian mengajar tersebut, dapat diketahui gambaran
tentang maksud mengajar, yaitu adanya pemahaman bahwa dalam mengajar
guru sebagai pemberi informasi sehingga peserta didik hanyalah sebagai
objek. Ada juga pemahaman bahwa dalam mengajar guru hanya sebagai
fasilitator, peracik lingkungan belajar sehingga siswa lebih aktif sebagai subyek
belajar.
41 Ngalim Purwanto, “Psikologi Pendidikan “, ( Bandung, Rosda Karya, 1990 ) hal 85 42 Mustaqim, “Psikologi Pendidikan “, ( Yogyakarta, Pustaka Pelajar, 2001) hal 91
43 Nana Sudjana, “CBSA Dalam Proses Belajar Mengaja “, (Bandung, Sinar Baru, 1989) hal 7 44 Herman hudoyo, “Mengajar Belajar Matematika “, (Jakarta, Departemen Pendidikan Dan
Setelah mengetahui maksud belajar dan mengajar, selanjutnya penulis akan
menguraikan tentang apa yang dimaksud dengan proses belajar mengajar
matematika. Sebagaimana pembahasan sebelumnya matematika berkenaan
dengan ide-ide terstruktur yang sangat hirarkis, sehingga untuk mempelajari suatu
konsep tertentu haruslah menguasai konsep-konsep sebelumnya.45 Misalnya saja
untuk mempelajari konsep "B" haruslah paham dan menguasai konsep
sebelumnya yaitu konsep "A", tidak mungkin seorang siswa mampu memahami
konsep "B" sebelum mampu memahami konsep "A". Jadi kalau misalnya
untuk memahami konsep perkalian, haruslah terlebih dahulu memahami konsep
penjumlahan. Karena konsep perkalian di dasarkan pada konsep penjumlahan.
Misal lain untuk memahami tentang bilangan pecahan harus dipahami terlebih
dahulu tentang bilangan asli, karena bilangan pecahan didasarkan pada bilangan
asli.
Seperti yang telah di kemukakan, bahwa belajar berkenaan dengan
proses perubahan tingkah laku dan dalam mengajar guru sebagai fasilitator maka
dalam proses belajar mengajar matematika guru merupakan mediator, peracik
lingkungan bagaimana agar siswa mampu menerima, Mengatur dan
mengolah informasisecara sistematis dalam mata pelajaran matematika sesuai
kehierarkisan matematika.
Dalam proses mengajar yang sering disebut juga prosedur mengajar, disitu
guru diharuskan melakukan kegiatan atau perbuatan-perbuatan yang berbentuk
membawa anak didik kearah tujuan yang akan dicapai. Dengan pengertian lain
kegiatan guru dan kegiatan murid dapat sejalan atau searah. Apa yang dilakukan
oleh guru akan mendapat respon dari murid, dan sebaliknya apa yang dilakukan
murid akan mendapat sambutan dari guru, atau dengan kata lain bahwa antara
kegiatan guru dan kegiatan murid terjadi hubungan iteraksi yang disebut
"komunikasi Interaksi".46
Dalam proses belajar mengajar selalu ditekankan pada pengertian interaksi
yaitu hubungan aktif dua arah, antara guru dan murid, hubungan antara guru dan
murid harus diikat oleh tujuan pendidikan. Guru berusaha untuk membantu
murid dalam mencapai tujuan pendidikan. Guru harus memilih bahan atau
materi pendidikan yang sesuai dengan tujuan yang akan dicapai.47 Disamping
memilih bahan yang sesuai, guru selanjutnya memilih metode yang paling tepat
dan sesuai dalam penyampaian bahan pertimbangan faktor situasional serta yang
diperkirakan dapat memperlacar jalanya proses belajar mengajar. Setelah proses
belajar mengajar dilakukan, maka langkah selanjutnya yang harus disertakan oleh
guru adalah evaluasi.
Oleh sebab itu seorang guru hendaknya mempunyai rumusan tentang
tujuan atau obyektif pembelajaran yang jelas, sehingga tidak ada Penafsiran
yang berbeda. Obyektif hendaknya dinyatakan sebagai bentuk klasifikasi
tingkah laku siswa yang melukiskan tentang hasil proses pembelajaran yang
telah dilaksanakan, atau dalam dunia pendidikan sering digunakan istilah
"Taksonomi Pendidikan".48
46 ibid, hal 8
47 Herman Hudoyo, “Pengembangan Kurikukulum Matematika dan Pelaksanaanya didepan
B. Taksonomi Pendidikan
Agar interaksi antara guru dan murid dapat lebih jelas, maka kita sering
gunakan istilah "Taksonomi Pendidikan". Menurut Herman Hudoyo yang dimaksud dengan taksonomi pendidikan adalah suatu bentuk klasifikasi tingkah laku
siswa yang melukiskan hasil yang dikehendaki dari pada proses pandidikan.49
Dari pengertian tentang Taksonomi Pendidikan, maka seorang guru perlu
menguasai taksonomi tujuan pendidikan, karena hal ini sangat membantu
proses belajar mengajar. Dengan taksonomi kita mengenal perumusan tujuan
pembelajaran dan memilih metode mengajar, sehingga tingkah laku siswa yang
nyata sebagai hasil belajar dapat dilihat serta diukur dengan istrumen evaluasi yang
tepat.50
Menurut Benyamin Bloom dalam bukunya Herman Hudoyo, pembagian
Obyektif pendidikan dalam taksonomi ada tiga hal bidang tingkah laku, yaitu :
1. Bidang Kognitif
2. Bidang Affektif
3. Bidang Psikomotorik. 51
Keterangan lebih lanjut adalah sebagai berikut :
1. Bidang Kognitif
Bidang ini berhubungan dengan kemampuan individu mengenai dunia
49 ibid, hal 7
50 Erman Suherman, Tatang Herman dkk, “Strategi Pembelajaran Matamatika Kontemporer“, (Bandung, Universitas Pendidikan Indonesia, 2003) hal 223
51 Herman Hudoyo, “Pengembangan Kurikukulum Matematika dan Pelaksanaanya didepan
sekitarnya yang meliputi perkembangan intelektual atau mental. Perubahan yang
terjadi pada bidang ini tergantung pada tingkat kedalaman belajar yang
dialami, dengan pengertian bahwa dengan perubahan yang terjadi dalam
bidang ini seseorang siswa diharapkan akan mampu melaksanakan pemecahan
terhadap masalah-masalah yang dihadapinya sesuai dengan disiplin ilmu
atau bidang ilmu yang dipelajarinya.
Dalam bidang kognitif ini terdiri dari beberapa klasifikasi lagi, yaitu :
Pengetahuan (Knowledge), Pemahaman (comprehension), penerapan atau Aplikasi (aplication), Analisis (analysis), Sintesis (synthesis), Evaluasi
(evaluation).52 Dari beberapa klasifikasi tersebut sebagian hanya cocok untuk
diterapkan di Sekolah Dasar (yaitu pada tataran mengetahui, pemahaman, dan
aplikasi). Sedangkan untuk tataran analisis, sintesis dan evaluasi baru dapat
diterapkan pada tingkatan SLTP, SLTA dan Perguruan Tinggi secara bertahap.
2. Bidang Afektif
Bidang ini meliputi sikap, emosi, nilai tingkah laku dari siswa, yang
direfleksikan dengan perasaan tertarik atau senang. Perubahan yang terjadi pada
bidang ini seorang siswa diharapkan akan lebih peka terhadap nilai atau etika
yang berlaku dalam bidang ilmunya. Jika perubahan yang terjadi cukup
mendasar, maka siswa tidak hanya menerima saja melainkan juga akan mampu
menanggapi dan mampu berperan sesuai dengan bidang ilmunya. Misalnya : “
Siswa akan tertarik pada logika dengan menunjukkan tingkah laku bahwa pada saat
saat tenggangnya ia memilih buku- buku mengenai logika untuk dipelajari”.
Obyektif yang dirumuskanini melukiskan sikap siswa yang tertarik kepada topik
logika. 53
3. Bidang Psikomotorik
Dalam bidang ini akan memperoleh ketrampilan yang bermacam-macam
berdasarkan kepentingannya. Dalam bidang ini banyak terjadi proses peniruan
tingkah laku gurunya, kemudian secara bertahap mampu mengunakan tingkah
laku itu secara tepat dan bertujuan. Misalnya : Siswa mampu mengetik 300
huruf dalam tempo 5 menit.
Dengan adanya taksonomi pendidikan, dapat membantu mempermudah
perumusan obyektif secara lebih jelas. Namun demikian obyektif pendidikan
dalam bidang studi matematika lebih cenderung kepada bidang kognitif,
sedangkan afektif dan psikomotorik hanya untuk memberikan dukungan saja.54
C. Penalaran Matematika 1. Penalaran
Menurut R.G Soekadijo penalaran diartikan sebagai proses berfikir dengan
bertolak dari pengamatan indera atau observasi empirik berdasarkan sejumlah
proposisi yang diketahui atau dianggap benar, orang lalu menyimpulkan
sebuah proposi baru yang sebelumnya tidak diketahui.55
Suriasumantri mengemukakan bahwa penalaran adalah suatu proses
berfikir dalam menarik sesuatu kesimpulan yang berupa pengetahuan.
53 Herman Hudoyo, “Pengembangan Kurikukulum Matematika dan Pelaksanaanya didepan
Kelas“, (Surabaya, Usaha Nasional, 1979) hal 39 54 ibid, hal 39
Penalaran ini menghasilkan pengetahuan yang dikaitkan dengan kegiatan
berfikir yang mempunyai karakteristik tertentu dalam menemukan
kebenaran. 56
Sebagaimana yang ditulis Suriasumanrtri bahwa sebagai suatu
kegiatan berfikir maka penalaran mempunyai ciri-ciri tertentu, yaitu adanya
pola berfikir yang biasa disebut logika, dan bersifat analitik dari proses
berfikirnya.57
a. Adanya suatu pola berfikir yang secara luas dapat disebut logika. Dalam
hal ini maka dapat dikatakan bahwa tiap bentuk penalaran mempunyai
bentuk logikanya sendiri. Atau dapat disimpulkan bahwa kegiatan
penalaran merupakan proses berfikir logis, dimana berfikir logis disini harus
diartikan sebagai kegiatan berfikir menurut suatu pola tertentu.
b. Sifat analitik dari proses berfikirnya. Penalaran merupakan kegiatan
berfikir yang menyadarkan diri kepada suatu analisis, dan kerangka
berfikir yang dipergunakan untuk analisis tersebut adalah logika penalaran
yang bersangkutan. Artinya penalaran ilmiah merupakan suatu kegiatan analisis
yang mempergunakan logika ilmiah, dan demikian juga penalaran lainnya
yang mempergunakan logika tersendiri pula
Kegiatan penalaran haruslah diisi dengan materi pengetahuan yang
berasal dari suatu sumber kebenaran. Adapun pengetahuan yang
dipergunakan dalam penalaran pada dasamya bersumber pada rasio dan fakta.
56 Jujun S. Suria Sumantri, “Filsafat Ilmu Sebuah Penganta “, ( Jakarta, Pustaka Sinar Harapan, 2002) hal 42
Dengan demikian sesuai dengan beberapa pengertian yang telah
dikemukakan diatas, yang kami maksud penalaran dalam penelitian ini adalah
proses berfikir logis dan analitis untuk menemukan pernyataan baru dengan
diketahuinya pernyataan pangkal yang nilai kebenarannya telah disepakati.
2. Penalaran Matematika
Penalaran dalam matematika yang dimaksud dalam penulisan ini, secara
terinci didaftar pada interm handbook Test of Reasoning In Mathematich yang selanjutnya disingkat dengan TRIM. 58
Secara garis besar ketrampilan yang diperlukan untuk menyelesaikan
pertanyaan-pertanyaan yang ada pada TRIM adalah sebagai berikut:
1. Kemampuan untuk memahami dan menafsirkan materi matematika.
2. Kemampuan untuk mentranslasikan antara bentuk soal (kalimat) dengan
bentuk verbal, simbol, tabel, dan diagram.
3. Kemampuan untuk menerapkan keterampilan matematika yang lalu untuk
menyelesaikan maslah yang disajikan dalam situasi yang baru.
4. Kemampuan untuk menganalisa masalah matematika dan menentukan
hubungan antara suatu bagian dengan bagian yang lain.59
D. Materi Bangun Datar di MTs Kelas VIII
Dalam materi bangun datar yang dipelajari di tingkat MTs kelas VIII
dikenal dengan metode global dan metode keunsuran. Metode global ini bersifat
58 Tri Dyah Prastiti, “Pengaruh Tingkat Kemampuan Penalaran dan Pembelajaran yang Melalui
Pendekatan Masalah Terhadap Kemampuan Menyelesaikan Soal Cerita Matematika Siswa Kelas V SDN Banjaran Kodya Kediri “, (Tesis S2 tidak diterbitkan, IKIP Malang, 1997) hal 27
induktif yang dimulai dengan pengamatan atas benda secara utuh kemudian
diikuti oleh pengamatan dan pengenalan atas bagian-bagiannya. Kemudian untuk
metode keunsuran lebih cenderung bersifat deduktif, berawal dari unsur-unsur ke
benda secara utuh.
Dalam Garis-garis Besar Program Pengajaran (GBPP) bidang studi
matematika untuk MTs terdapat materi pokok bahasan bangun datar yang
meliputi : jajargenjang, belah ketupat, layang-Iayang, dan trapesium.
1. Jajargenjang
A D
B C a. Pengertian Jajargenjang
Jajargenjang adalah segi empat dengan sisi-sisi yang berhadapan sejajar
dan sama panjang serta sudut-sudut yang berhadapan sama besar.60
b. Sifat-sifat jajargenjang
> Sisi-sisi yang berhadapan sama panjang dan sejajar.
AB = CD dan AB // CD
AD = BC dan AB // CD
> Sudut-sudut yang berhadapan sama sama besar.
60 Cholik, Sugijono, Subroto, “Matematika Untuk SLTP Kelas II “, (Jakarta, Erlangga, 2000) hal 70
O
< ABC = < CDA
< BAD = < DCB
> Jumlah besar sudut-sudut yang berdekatan adalah 180°
Karena AB // CD dan < A dengan < D maupun < B dengan < C
merupakan sudut dalam sepihak, maka :
< A + < D = 180°
< B + < C = 180°
Karena AD // BC dan < A dengan < B maupun < C dengan < D
merupakan sudut dalam sepihak, maka :
< A + < B = 180°
< C + < D = 180°
> Kedua diagonalnya saling membagi dua sama panjang
OA = OC dan OB = OD
c. Luas jajargenjang
Rumus luas jajargenjang dengan alas a, tinggi t, dan luas L, maka selalu berlaku :
L = a x t
2. Belahketupat
A
B D
a. Pengertian Belahketupat
Belahketupat adalah segiempat dengan sisi yang berhadapan sejajar,
keempat sisinya sama panjang dan sudut-sudut yang berhadapan sama
besar.61
b. Sifat-sifat belahketupat
> Semua sisi pada setiap belahketupat sama panjang.
ABC kongruen dengan ADC, maka :
AB = AD ……….. 1
BC = CD ……… 2
ABC sama kaki, maka :
AB = BC ……… 3
ADC sama kaki, maka :
CD = AD ……… 4
Dari persamaan – persamaan diatas disimpulkan hal berikut ini :
AB = BC ……… 3
BC = CD ……… 2
CD = AD ……… 4
Jadi dapat disimpulkan : AB = BC = CD = AD
> Kedua diagonalnya mempakan sumbu simetri
Segitiga ABC sama kaki engan AB = BC, maka BO merupakan sumbu
simetri. Segitiga ADC sama kaki dengan AD = DC , maka OD
merupakan sumbu simetri.
Karena < BOC dan < COD saling berpelurus, maka BD adalah garis lurus
yang merupakan sumbu simetri belah ketupat.
Sgitiga sama kaki ABC kongruen dengan segitiga sama kaki ADC, maka
AC merupakan sumbu simetri belah ketupat.
> Sudut-sudut yang berhadapan sama besar dan dibagi dua sama besar
oleh diagonal-diagonalnya.
Belah ketupat ABCD dibalik menurut sumbu simetri BD, maka < A = < C,
dan jika dibalik menurut sumbu simetri AC maka < B = < D
> Kedua diagonalnya saling membagi dua sama panjang dan saling
berpotongan tegak lurus.
Belah ketupat ABCD diputar setengah putaran pada O,
< AOB = < AOD = ½ x 180° = 90˚
c. Luas belah ketupat
Luas belah ketupat ABCD = Luas ABCD + BDC
= ½ x BD x AO + ½ x BD x OC
= ½ x BD x ( AO + AC )
= ½ x BD x AC
3. layang-layang A
C
a. Pengertian Layang-layang
Layang-layang adalah segiempat yang masing-masing pasang sisinya
sama panjang dan sepasang sudut yang berhadapan sama besar.62
b. Sifat-sifat layang-layang
> Masing-masing sepasang sisinya sama panjang.
ABD sama kaki, maka AB = AD ; BCD sama kaki, maka BC = CD
> Sepasang sudut yang berhadapan sama besar
ABD sama kaki, maka < ABD = < ADB
BCD sama kaki, maka < CBD = < CDB
< ABD + < CBD = < ADB + < CDB
jadi < ABC = < ADC
> Salah satu diagonalnya merupakan sumbu simetri
Segitiga ABD sama kaki dengan AB = AD, maka
AO merupakan sumbu simetri. Segitiga BCD sama
kaki dengan BC = CD, maka OC merupakan sumbu
simetri. Karena < AOD dan < DOC saling
berpelurus, maka AC adalah garis lurus yang
merupakan sumbu simetri layang – layang.
> Salah satu diagonalnya membagi dua sama panjang diagonal lain dan
tegak lurus dengan diagonal itu.
Layang – laying ABCD dibalik menurut sumbu simetri AC, OB = OD
< AOB = < AOD = 90
c. Luas layang – layang
Luas layang – layang ABCD = Luas ABD + BDC
= ½ x BD x AO + ½ BD x OC
= ½ x BD x ( AO + OC )
= ½ x BD X AC
4. Trapesium
D b C
A a B
a. Pengertian Trapesium
Trapesium adalah segiempat dengan tepat sepasang sisi yang berhadapan
sejajar.63
b. Sifat-sifat Trapesium
Jumlah sudut yang berdekatan diantara dua sisi sejajar adalah 180°.
Pada trapesium ABCD, AB sejajar dengan CD, maka < A dengan < d adalah
sudut dalam sepihak, sehingga < A + < D = 180°. < B dengan < C juga sudut
63 ibid, hal 91
dalam sepihak, sehingga < B + < C = 180°.
c. Luas Trapesium
Luas Trapesium ABCD = Luas ABD + Luas BCD
= ½ x a x t + ½ x b x t
= ( ½ x a + ½ x b ) x t
= ½ ( a + b ) x t
Ket : a dan b merupakan sisi sejajar dan t adalah tinggi.
E. Asumsi Penelitian.
a. Seandainya soal test sudah memenuhi prasyarat validitas dan realibilitas serta
mengacu pada GBPP kelas VIII dan mengambil pokok bahasan yang telah
guru ajarkan.
b. Seandainya siswa mempunyai kesiapan yang sama dalam hal materi yang
diajukan, karena mengikuti pelajaran matematika yang diajarkan oleh guru
yang sama.
c. Seandainya siswa mempunyai kesiapan fisik dan psikis yang sama.
d. Jawaban yang diberikan siswa merupakan kemampuan yang
sesungguhnya karena pada saat test dilaksanakan diawasi oleh peneliti dan
BAB III
METODE PENELITIAN
Metode penelitian adalah cara-cara berfikir dan berbuat yang dipersiapkan dengan
baik-baik untuk mengadakan penelitian dan untuk mencapai suatu tujuan penelitian.64
Sedangkan menurut Arief Furchan, metode penelitian adalah strategi umum yang
dianut dalam pengumpulan dan analisis data yang diperlukan guna menjawab persoalan
yang dihadapi.65
Dengan demikian metode penelitian dapat diartikan sebagai suatu bahasan
yang membahas secara tehnik tentang metode-metode yang digunakan dalam sebuah
penelitian.
A. Pola Penelitian
Agar peneliti dapat memperoleh gambaran yang lebih jelas mengenai
langkah-langkah yang harus diambil dan ditempuh serta gambaran mengenai
masalah-masalah yang dihadapi serta cara mengatasi permasalahan tersebut
haruslah menggunakan pola penelitian yang tepat.
Ditinjau dari jenis permasalahan yang dibahas pada penelitian ini
penulis menggunakan jenis penelitian deskriptif. Penelitian deskriptif adalah
penelitian yang berusaha mendiskripsikan suatu gejala, peristiwa, kejadian yang
64 Sukardi, “ metodologi Penelitian Pendidikan Kompetensi dan praktiknya “, ( Jakarta, Bumi Aksara, 2003) hal 4
terjadi pada saat sekarang, dengan perkataan lain, penelitian deskriptif mengambil
masalah atau memusatkan perhatian kepada masalah-masalah aktual sebagaimana
adanya pada saat penelitian dilaksanakan.66
B. Lokasi Penelitian
Penelitian ini dilaksanakan di Kelas VIII B MTs PSM Jeli Karangrejo.
Lokasi ini dipilih dengan pertimbangan sebagai berikut:
1. Penelitian terkait dengan penalaran matetika siswa sangat dibutuhkan
sekolah ini dalam rangka mengetahui tingkat kemampuan penalaran
matematika siswa.
2. Di sekolah ini belum pernah diadakan penelitian terkait dengan kemampuan
penalaran matematika siswa.
C. Kehadiran Peneliti
Sesuai dengan pendekatan dan jenis penelitian yaitu jenis penelitian
kualitatif, maka kehadiran peneliti di lapangan sangat diperlukan untuk
mengetahui data terkait kemampuan penalaran siswa secara akurat. Dan
alkhamdulilah ketepatan dalam hal ini peneliti adalah guru mata pelajaran
matematika dilokasi penelian tersebut, sehingga peneliti lebih jelas terhadap
keaadaan siswa terkait dengan pola pikir dan penalaran siswa dan mendapatkan
data yang akurat.
65 Arief Furchan, “Pengantar Penelitian dalam Pendidikan “, ( Surabaya, Usaha Nasional, 1983 ) hal 50
D. Populasi
Populasi berasal dari bahasa inggris “ population “ yang berarti jumlah penduduk.67
Menurut Sudjana populasi adalah : totalitas semua nilai yang mungkin hasil
menghitung ataupun pengukuran mengenai karakteristiktertentu dari semua
anggota kumpulan yang jelas dan lengkap yang ingin dipelajari.68
Menurut Sugiyono populasi adalah wilayah generalisasi yang terdiri atas
obyek/subyek yang mempunyai kualitas dan karakteristik tertentu yang
ditetapkan oleh peneliti untuk dipelajari dan kemudian ditarik kesimpulan.69
Jadi intinya populasi adalah keseluruhan obyek yang akan diteliti.70
Dalam penelitian ini populasi yang diambil adalah siswa kelas VIII MTs PSM
Jeli Tulungagung dan mengambil sample kelas VIII B yang berjumlah 38 siswa.
E. Variabel, Data ,dan Sumberdata
1. Variabel
Kata variabel tidak ada dalam perbendaharaan Indonesia, karena variabel
berasal dari bahasa inggris yang berarti faktor tak tetap atau berubah – ubah.
Namun bahasa Indonesia kontemporer telah terbiasa menggunakan kata
variabel ini, pengertian yang lebih tepat disebut bervariasi. Dengan demikian
67 Gulo, “ Metodologi Penelitian “, ( Jakarta, Gramedia Widia sarana Indonesia, 2002 ) hal 76 68 Sudjana,” Metoda Statistika “, ( Bandung, Tarsita, 2005 ) hal 6
variabel adalah fenomena yang bervariasi dalam bentuk kualitas, kuantitas dll.71
Menurut gempur santoso variabel adalah karakteristik atau keadaan atau
kondisi pada suatu obyek yang mempunyai variasi nilai.72
Sedangkan Nana Sudjana mengatakan bahwa "Variabel adalah segala
sesuatu yang akan menjadi obyek pengamatan penelitian".73
Dalam penelitian ini menggunakan satu variabel yaitu:
Kemampuan Penalaran Matematika siswa kelas VIII MTs PSM Jeli pada pokok
bahasan bangun datar (X), yang kemudian dipilah lagi menjadi tiga sub variabel
dengan mengukur pada aspek kognitif meliputi:
a. Tingkat kemampuan penalaran Matematika siswa kelas VIII MTs PSM Jeli
materi bangun datar pada tahap Analisis (X1).
b. Tingkat kemampuan penalaran Matematika siswa kelas VIII MTs PSM Jeli
materi bangun datar pada tahap Sintesis (X2).
c. Tingkat kemampuan penalaran Matematika siswa kelas VIII MTs PSM Jeli
materi bangun datar pada tahap Evaluasi (X3).
2. Data dan Sumber data
Data ( tunggal datum ) adalah bahan keterangan tentang suatu objek
penelitian yang diperoleh dilokasi penelitian.74
Menurut Suharsimi pengertian data adalah segala fakta dan angka
yang dapat dijadikan bahan untuk menyusun suatu informasi, sedangkan
71 Burhan Bungin, “ Metodologi Penelitian Kuantitatif “, ( Jakarta, Prenada Media, 2004 ) hal 59 72 Gempur Santoso,” Metodologi Penelitian “, ( Jakarta, Prestasi pustaka, 2005) hal 22
73 Nana sudjana, Ibrahim, “ Penelitian dan Penilaian Pendidikan “, ( Bandung, Sinar Baru, 1989 ) hal 64
informasi adalah hasil pengolahan data yang dipakai untuk suatu keperluan.
Sedangkan sumber data peneliti adalah subyek dari mana data dapat
diperoleh.75
Menurut Marzuki mengemukakan pendapatnya bahwa sumber data
penelitian digolongkan sebagai berikut : Data primer adalah data yang
diperoleh langsung dari sumbernya, diamati dan dicatat untuk pertama
kalinya.76 Data sekunder yaitu data yang bukan diusahakan sendiri
pengumpulannya oleh peneliti atau data yang diperoleh dari sumber ke dua.
misalnya dari biro statistik, keterangan-keterangan atau publikasi lainnya.77
a. Sumber data primer yaitu orang yang merespon atau menjawab
pertanyaan-pertanyaan peneliti, baik pertanyaan tertulis atau lisan.78
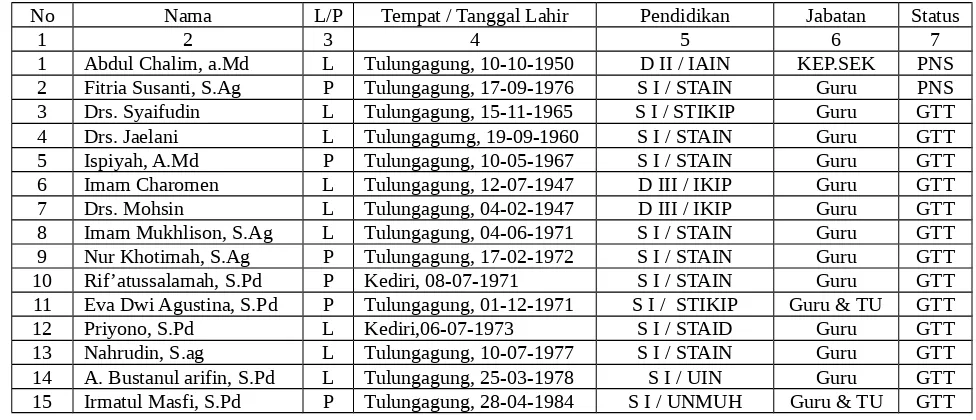
Responden dalam penelitian ini adalah guru, kepala sekolah, dan siswa
kelas VIII MTs PSM Jeli, Karangrejo,Tulungagung.
b. Sumber data sekunder yaitu segala sesuatu yang dari padanya bisa
memberikan data atau informasi yang bukan berasal dari manusia.79 Dalam
penelitian ini adalah dokumentasi, bisa berupa hasil dari tes pada
penelitian.
F. Metode dan Instrumen Pengumpulan Data.
75 Sumardi suryabrata,” Metodologi penelitian “, ( Jakarta, Raja grafindo persada, 1983 ) hal 96 76 Marzuki.” Metodologi Riset “, ( Jogyakarta, Prasetya Widya Pratama, 2002 ) hal 55
1. Metode Pengumpulan data
Dalam pengumpulan data, metode merupakan suatu hal yang mutlak
kebenaranya, sebab ilmiah atau tidaknya suatu tulisan tergantung pada pokok
pikiran yang dikemukakan dan disimpulkan yang dilandasi oleh faktor-faktor yang
didapat secara obyektif dan berhasil lolos dari berbagai hasil pengujian.80
Dalam usaha memperoleh data-data yang penulis perlukan dalam penelitian,
maka penulis menggunakan beberapa metode pengumpulan data. Metode
pengumpulan data adalah cara yang dapat digunakan peneliti dalam
mengumpulkan data.81 Agar dalam penelitian nantinya diperoleh informasi dan
data-data yang sesuai dengan topik yang diteliti, maka peneliti menggunakan
beberapa metode, antara lain :
a. Metode observasi
Metode Observasi adalah metode pengumpulan data dengan mengadakan
pengamatan langsung terhadap suatu obyek dalam suatu periode tertentu dan
mengadakan pencatatan secara sistematis tentang hal-hal yang diamati.82
Metode ini dilakukan dalam penelitian untuk memperoleh data-data yang
berkaitan dengan pelaksanaan pembelajaran baik di ruang kelas maupun diluar
kelas.
b. Metode Interview
Metode interview yaitu suatu cara pengumpulan data dengan jalan
80 Gempur Santoso,” Metodologi Penelitian Kuantitatif dan kualitatif “, ( Jakarta, Prestasi pustaka, 2005) hal 70
mengajukan pertanyaan secara lisan kepada sumber data, dan sumber data
juga memberikan jawaban secara lisan pula.83
Metode ini digunakan untuk memperoleh data dari pihak sekolah
tentang sejarah berdirinya sekolah dan data lain yang relevan dari pihak
sekolah.
c. Metode Test
Metode test adalah serentetan pertanyaan atau latihan serta alat lain yang
digunakan untuk mengukur keterampilan, pengetahuan inteligensi,
kemampuan atau bakat yang dimiliki oleh individu atau kelompok..84
Dengan metode inilah peneliti mendapatkan data atau hasil berupa
nilai dari test yang diadakan pada waktu penelitian, kemudian nilai yang
didapat tersebut diolah dan disajikan dalam bentuk prosentase tentang
tingkat kemampuan penalaran matematika siswa kelas VIII MTs PSM Jeli
Tulungagung.
d.. Metode Dokumentasi
Metode dokumentasi adalah cara pengumpulan data dengan bersumber
pada tulisan.85. Atau dapat dikatakan dokumentasi adalah data-data penting
tentang kegiatan yang berkaitan dengan keadaan dan operasional dari
obyek penelitian, misalnya arsip-arsip.
2. Instrumen Pengumpulan Data
Menurut Suryabrata instrumen yaitu alat yang digunakan untuk
83 Ibid, hal 51
pengambilan data.86 Sedangkan menurut Arief Furchan istrumen ialah seorang
peneliti harus memiliki alat yang dapat mengukur ciri-ciri seperti kecerdasan,
hasil belajar, kepribadian, motivasi, sikap, bakat minat dan sebagainya..87
Berdasarkan beberapa pengertian diatas, peneliti memilih dan
menggunakan instrumen antara lain :
a. Pedoman Observasi, yaitu alat bantu yang digunakan peneliti ketika
mengumpulkan data melalui pengamatan dan pencatatan secara sistematis
terhadap fenomena yang diselidiki.
b Pedoman Interview, yaitu alat bantu yang digunakan peneliti dalam
mengumpulkan data yang berupa daftar pertanyaan yang digunakan
peneliti dalam mengadakan wawancara dengan responden.
c. Pedoman test tertulis, yaitu alat bantu yang berupa soal-soal test tertulis
yang digunakan untuk memperoleh nilai sebagai alat ukur dalam
penelitian. Test tersebut nantinya oleh peneliti akan dimodiflkasi dan
diklasifikasikan menjadi tiga bagian sesuai dengan aspek yang nantinya
akan diteliti, yaitu soal tentang bangun datar yang termasuk pada tahap
analisis, sintesis dan evaluasi
d.. Pedoman dokumentasi, yaitu alat bantu yang digunakan peneliti untuk
mengumpulkan data-data dan arsip dokumentasi maupun buku
kepustakaan yang berkaitan dengan variabel.
86 Sumardi suryabrata,” Metodologi penelitian “, ( Jakarta, Raja grafindo persada, 1983 ) hal 78 87 Arief Furchan, “ Pengantar Penelitian dalam Pendidikan “, ( Surabaya, Usaha Nasional, 1983 )
G. Tekhnik Analisis Data
Dalam penelitian ini peneliti menggunakan tekhnik analisis data
kualitatif dan kuantitatif.
Untuk data kualitatif dianalisis dengan tekhnik analisis deskriptif
induktif yaitu proses pemikiran untuk mengambil pengertian-pengertian atau
kesimpulan yang bersifat umum, berdasarkan atas data atau fakta yang konkrit
yang bersifat khusus.
Sedangkan untuk data kuantitatif atau data yang dapat diwujudkan
dengan angka yang didapat dari lapangan tekhnik analisis disajikan dalam bentuk
prosentase.
Dengan rumus :
100%
XmXo Px
Keterangan :
Px : Persentase Variabel X
Xo : Jumlah skor X yang diperoleh
Xm : Jumlah skor Maximal yaitu N x SmN : Jumlah Frekuensi
Sm : Skor Maximal88
Tabel 3.1 Interpretasi Tingkat Kemampuan Penalaran Matematika 89
No Presentase Kriteria
1.
difokuskan pada “Penguasaan Siswa terhadap konsep luas bangun datar segi
empat”. Untuk mengecek keabsahan data dalam penelitian ini digunakan
triangulasi, ketekunan pengamatan, dan berdiskusi dengan teman sejawat, guru
mata pelajaran Matematika serta konsultasi dengan pembimbing.
Triangulasi adalah teknik pemeriksaan keabsahan data yang
memanfaatkan sesuatu yang lain di luar data itu untuk keperluan pengecekan/
sebagai pembanding terhadap data itu. Triangulasi metode dan triangulasi
sumber diperlukan untuk mengecek data tentang pemahaman siswa terhadap
konsep luas bangun datar segi empat yang diperoleh dari pembelajaran berbasis
kontekstual. Metode yang digunakan dalam triangulasi adalah metode
obsevarsi, wawancara dan catatan lapangan. Sedangkan triangulasi sumber yaitu
dengan membandingkan data hasil pengamatan pada waktu proses belajar
dengan data hasil wawancara dengan siswa.
pengamatan dengan teliti mengerjakan lembar kerja siswa, berdialog antara
siswa dan guru, menemukan konsep luas bangun datar segi empat.
Diskusi dengan teman sejawat adalah mendiskusikan proses dan hasil
penelitian dengan cara mengespos hasil sementara hasil akhir yang diperoleh
dalam bentuk diskusi dengan rekan-rekan sejawat.
Konsultasi dengan pembimbing guna untuk meminta saran tentang
keabsahan data yang diperoleh.
I. Prosedur Penelitian
Untuk memperoleh hasil-hasil yang akan didapat dari penelitian ini,
penulis memakai prosedur atau sistem tahapan-tahapan, sehingga penelitian
nantinya akan lebih terarah dan terfokus serta tercapai hasil kevalidan yang
maksimal. Adapun keterangan dari prosedur penelitian ini penulis jalaskan
sebagai berikut:
1. Persiapan Penelitian
Dalam tahapan ini peneliti melakukan langkah-langkah sebagai berikut:
a. Mengajukan surat permohonan ijin penelitian kepada pihak sekolah, yang
dalam hal ini adalah MTs PSM Jeli, Karangrejo, Tulungagung.
b. Berkonsultasi dengan kepala sekolah dan juga guru bidang studi
matematika MTs PSM Jeli Tulungagung dalam rangka observasi untuk
mengetahui bagaimana aktivitas dan kondisi dari tempat atau obyek
2. Mengadakan Studi Pendahuluan
Dalam tahapan ini peneliti melakukan kegiatan bertanya kepada orang
yang dianggap sebagai objek penelitian yang nantinya dapat digunakan sebagai
bahan atau informasi awal penelitian. Yang pada akhirnya dapat ditentukan
dan disesuaikan antara materi yang ada pada objek penelitian dengan judul
penelitian sesuai dengan rancangan penelitian yang akan peneliti lakukan.
3. Mengumpulkan Data
Dalam tahapan ini peneliti melakukan pengumpulan data yang ada
dilapangan baik berupa dokumen maupun pengamatan langsung pada objek
penelitian, sehingga dengan mengetahui data-data yang terkumpul peneliti dapat
melakukan tes kemampuan penalaran matematika pada materi bangun datar