PELABELAN GRAF SIKLUS SEDERHANA
UNTUK MENGKONSTRUKSI VERTEX-MAGIC GRAPH
MAKALAH
Disusun untuk Melengkapi salah satu Tugas Mata Kuliah Seminar Pendidikan Matematika Semester Genap Tahun Akademik 2006/2007
Disusun oleh :
J A E N U D I N
NIM. 040521
JURUSAN PENDIDIKAN MATEMATIKA
FAKULTAS PENDIDIKAN MATEMATIKA DAN ILMU PENGETAHUAN ALAM
UNIVERSITAS PENDIDIKAN INDONESIA
i KATA PENGANTAR
Bismillahirrahmanirrahim
Segala puji hanya diperuntukkan bagi Allah SWT yang telah menurunkan Al-Qur’an sebagai petunjuk bagi orang yang bertaqwa, Sang Maha Pencipta yang Maha Sempurna dalam setiap penciptaan-Nya. Hanya karena-Nya penyusun dapat menyelesaikan penyusunan makalah ini. Semoga shalawat serta salam tercurahlimpahkan kepada pemimpin alam, Nabi Muhammad SAW yang telah membawa manusia dari gelapnya kehidupan jahiliyah kepada jalan yang lurus yang diridhai Allah SWT.
Masalah dalam makalah yang berjudul "Pelabelan Graf Siklus Sederhana untuk Mengkonstruksi Vertex-Magic Graph" ini adalah pelabelan sisi dan simpul sebuah graf siklus untuk memperoleh vertex-magic graph (graf simpul ajaib). Vertex-magic graph adalah graf siklus dengan v simpul dan e sisi yang diberi label dari 1 hingga (v + e), demikian sehingga apabila setiap label simpul dan sisi yang insiden pada simpul tersebut dijumlahkan akan diperoleh jumlah yang sama. Jumlah yang sama tersebut dinamakan magic number (bilangan ajaib). Untuk mengkonstruksi sebuah vertex-magic graph dapat dilakukan dengan beberapa teknik. Salah satunya adalah pelabelan graf siklus berdasarkan magic number maksimum dan minimum. Selain itu, bisa juga dilakukan berdasarkan penempatan bilangan ganjil atau bilangan genap sebagai label simpulnya.
Dalam kesempatan ini penyusun mengucapkan terima kasih yang tak terhingga kepada Bapak Drs. H. Yaya S. Kusumah, M.Sc., Ph.D. selaku pembimbing yang telah mengarahkan penyusun untuk menyelesaikan penulisan makalah ini. Juga kepada semua pihak yang telah memberikan bantuan kepada penyusun. Semoga segala amal baik yang telah diberikan kepada penyusun dibalas Allah SWT dengan pahala yang berlipat ganda.
Penyusun sangat menyadari bahwa penyusunan makalah ini masih jauh dari sempurna. Untuk itu, penyusun sangat berharap kepada pembaca untuk dapat
ii memberikan kritik dan saran yang membangun untuk perbaikan penyusunan makalah di masa mendatang.
Hanya kepada Allah SWT penyusun berserah diri dan memohon perlindungan.
Bandung, Maret 2007 Penyusun,
iii DAFTAR ISI LEMBAR PENGESAHAN ... i KATA PENGANTAR ... ii DAFTAR ISI ... iv DAFTAR TABEL ... vi
DAFTAR GAMBAR ... vii
BAB I PENDAHULUAN 1.1 Latar Belakang Masalah ... 1
1.2 Rumusan dan Batasan Masalah ... 2
1.3 Tujuan Penulisan ... 2
1.4 Manfaat Penulisan ... 3
BAB II KONSEP DASAR TEORI GRAF 2.1 Sejarah Singkat Teori Graf ... 4
2.2 Pengertian Graf ... 5
2.3 Graf Sederhana ... 6
2.4 Graf Terhubung ... 7
2.5 Graf Siklus ... 8
BAB III VERTEX-MAGIC GRAPH 3.1 Pengertian Vertex-Magic Graph ... 9
3.2 Batas Bawah Magic Number ... 10
3.3 Batas Atas Magic Number ... 15
3.4 Pelabelan Graf Siklus dengan Banyak Simpul Ganjil dan Magic Number Maksimum ... 18
3.5 Pelabelan Graf Siklus dengan Banyak Simpul Ganjil dan Magic Number Minimum ... 21
iv 3.6 Pelabelan Graf Siklus dengan Banyak Simpul Ganjil
dan Bilangan Ganjil sebagai Label Simpul ... 24 3.7 Pelabelan Graf Siklus dengan Banyak Simpul Ganjil
dan Bilangan Genap sebagai Label Simpul ... 27 BAB IV KESIMPULAN DAN SARAN
4.1 Kesimpulan ... 30 4.2 Saran ... 31 DAFTAR PUSTAKA ... 32
v DAFTAR TABEL
Tabel 3.1 Aturan Pelabelan Sisi Graf Siklus dengan Banyak Simpul Ganjil dan Magic Number Maksimum ... 20 Tabel 3.2 Aturan Pelabelan Sisi Graf Siklus dengan Banyak Simpul Ganjil
dan Magic Number Minimum ... 23 Tabel 3.3 Aturan Pelabelan Sisi Graf Siklus dengan Banyak Simpul Ganjil
dan Bilangan Ganjil sebagai Label Simpul ... 25 Tabel 3.4 Aturan Pelabelan Sisi Graf Siklus dengan Banyak Simpul Ganjil
vi DAFTAR GAMBAR
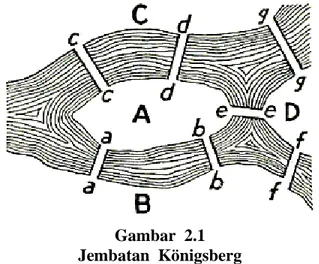
Gambar 2.1 Jembatan Königsberg ... 4
Gambar 2.2 Graf dengan Empat Simpul dan Tiga Sisi ... 6
Gambar 2.3 Sisi Rangkap dan Loop ... 6
Gambar 2.4 Graf Terhubung ... 8
Gambar 2.5 Graf Siklus ... 8
Gambar 3.1 Vertex-Magic Graph dan Edge-Magic Graph ... 10
Gambar 3.2 Label Graf Siklus dengan Banyak Simpul Ganjil dan Magic Number Maksimum ... 19
Gambar 3.3 Graf Siklus dengan 3 Simpul dan Magic Number 12 ... 21
Gambar 3.4 Graf Siklus dengan 5 Simpul dan Magic Number 19 ... 21
Gambar 3.5 Label Graf Siklus dengan Banyak Simpul Ganjil dan Magic Number Minimum ... 22
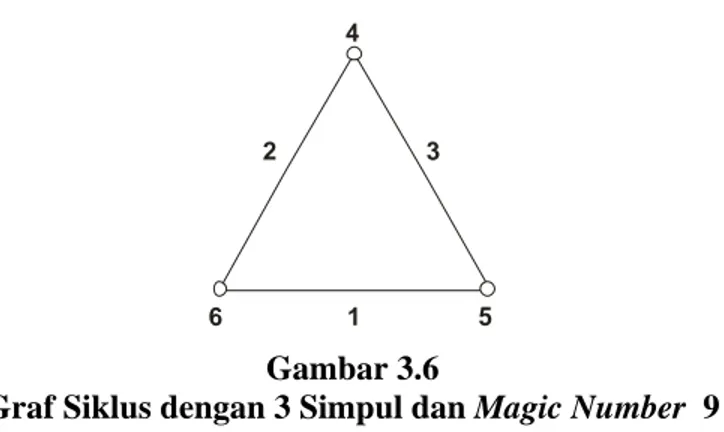
Gambar 3.6 Graf Siklus dengan 3 Simpul dan Magic Number 9 ... 23
Gambar 3.7 Graf Siklus dengan 5 Simpul dan Magic Number 14 ... 24
Gambar 3.8 Label Graf Siklus dengan Banyak Simpul Ganjil dan Bilangan Ganjil sebagai Label Simpul ... 25
Gambar 3.9 Graf Siklus dengan 3 Simpul dan Magic Number 11 ... 26
Gambar 3.10 Graf Siklus dengan 5 Simpul dan Magic Number 17 ... 26
Gambar 3.11 Label Graf Siklus dengan Banyak Simpul Ganjil dan Bilangan Genap sebagai Label Simpul ... 27
Gambar 3.12 Graf Siklus dengan 3 Simpul dan Magic Number 10 ... 28
1
BAB I PENDAHULUAN
1.5 Latar Belakang Masalah
Teori graf adalah salah satu cabang matematika yang cukup penting untuk dipelajari dan dikembangkan. Teori graf mempunyai berbagai terapan dalam berbagai bidang ilmu pengetahuan, diantaranya dalam model jaringan transportasi, sistem komunikasi, silsilah keluarga, desain arsitektur, dan masih banyak lagi terapan lainnya (Sutarno, dkk, 2003: 71-74)
Pada awalnya teori graf diperkenalkan oleh Leonhard Euler sebagai solusi permasalahan mungkin tidaknya melewati ketujuh jembatan di kota Königsberg (sekarang dikenal sebagai Kaliningrad, Rusia) dan kembali ke tempat semula tepat satu kali. Kemudian Leonhard Euler memodelkan permasalahan tersebut ke dalam model matematika berupa bagan yang terdiri dari titik dan garis. Titik merepresentasikan kota yang dihubungkan jembatan dan garis sebagai jembatan yang menghubungkan kota. Model ini kemudian dikenal sebagai teori graf.
Teori graf masih terus berkembang selaras dengan pemikiran-pemikiran para ahli yang mengembangkannya. Salah satu masalah cukup terkenal dalam teori graf adalah Konjektur Empat Warna (Four Color Conjecture),yaitu masalah pewarnaan peta dengan menggunakan empat macam warna sehingga setiap negara yang berbatasan mempunyai warna yang berbeda.
Selain itu, masalah yang cukup menarik dalam teori graf adalah pelabelan graf. Suatu graf siklus dengan e sisi dan v simpul dapat berikan label pada simpul dan sisi mulai 1 sampai (v + e) sehingga apabila label-label pada sisi yang saling ajasen dan label simpul yang insiden dengan sisi-sisi tersebut dijumlahkan, akan menghasilkan jumlah yang sama. Jumlah ini kemudian disebut sebagai bilangan ajaib(magic number) dan graf tersebut dikenal sebagai graf simpul ajaib( vertex-magic graph). Untuk selanjutnya istilah bilangan ajaib disebut magic number saja dan graf simpul ajaib disebut vertex-magic graph saja. Masalah yang cukup
2 menarik dari pelabelan graf tersebut adalah bagaimana cara memberikan label simpul atau sisi sehingga diperoleh vertex-magic graph. Selain itu, berapakah magic number minimum dan maksimum dari pelabelan suatu vertex-magic graph?
Penyusun tertarik dengan masalah pelabelan graf siklus sederhana yang mempunyai banyak simpul ganjil untuk mengkonstruksi vertex-magic graph. Untuk itu penyusun memberikan judul pada makalah ini dengan: "Pelabelan Graf Siklus Sederhana untuk Mengkonstruksi Vertex-Magic Graph".
1.6 Rumusan dan Batasan Masalah
Masalah dalam makalah ini dapat dirumuskan sebagai berikut:
a. Bagaimana pelabelan pada graf siklus sederhana yang banyak simpulnya ganjil sehingga diperoleh vertex-magic graph?
b. Berapakah magic number maksimum dan minimum dari suatu vertex-magic graph?
Makalah ini dibatasi hanya pada permasalahan pelabelan graf untuk mendapatkan vertex-magic graph pada graf siklus sederhana yang banyak simpulnya ganjil saja. Permasalahan pelabelan graf untuk mendapatkan vertex-magic graph pada graf siklus yang lebih kompleks lagi dapat kita kembangkan untuk penelitian atau penulisan berikutnya.
1.7 Tujuan Penulisan
Tujuan penulisan makalah ini adalah sebagai berikut:
a. Memperoleh gambaran umum tentang pelabelan graf siklus sederhana yang banyak simpulnya ganjil sehingga diperoleh sebuah vertex-magic graph
b. Memperoleh gambaran umum tentang magic number maksimum dan minimum dari suatu graf siklus sederhana dengan banyak simpul ganjil yang termasuk vertex-magic graph
3 1.8 Manfaat Penulisan
Penyusunan makalah ini diharapkan dapat memberikan manfaat sebagai berikut:
a. Menambah pengetahuan pembaca mengenai teori graf khususnya tentang pelabelan graf. Karena masalah dalam makalah ini tidak diperkenalkan pada materi perkuliahan matematika diskrit.
b. Sebagai pengetahuan dasar untuk memahami lebih lanjut mengenai teori graf khususnya pelabelan graf.
4
BAB II
KONSEP DASAR TEORI GRAF
2.6 Sejarah Singkat dan Perkembangan Teori Graf
Teori graf pertama kali diperkenalkan oleh Leonhard Euler pada tahun 1736 sebagai upaya pemecahan masalah jembatan Königsberg. Masalah jembatan Königsberg adalah mungkin tidaknya melewati ketujuh jembatan yang ada di kota Königsberg masing-masing tepat satu kali dan kembali lagi ke tempat semula. Untuk memecahkan masalah tersebut, Euler memisalkan daratan yang dihubungkan jembatan dengan titik (vertex) dan jembatan dinyatakan dengan garis atau sisi (edge). Dengan menggunakan model tersebut, Euler berkesimpulan bahwa tidak mungkin seseorang dapat melalui ketujuh jembatan tersebut masing-masing satu kali dan kembali lagi ke tempat semula (Sutarno, dkk, 2005: 65; Munir, 2003: 291; Cunningham, 2004: 1).
Pada tahun 1847, G.R. Kirchoff (Sutarno, dkk, 2003: 58) mengembangkan teori pohon yang digunakan dalam permasalahan listrik. Konsep pohon ini kemudian digunakan oleh A. Cayley untuk menjelaskan masalah kimia yaitu hidrokarbon pada tahun 1857.
Gambar 2.1 Jembatan Königsberg
5 Salah satu masalah yang cukup terkenal dalam teori graf adalah Konjektur Empat Warna(The Four Color Conjecture) yang diajukan oleh Francis Guthrie sekitar tahun 1850 (Cunningham, 2004: 1). Masalah dalam Konjektur Empat Warna(The Four Color Conjecture) adalah mewarnai sebuah peta dengan empat macam warna sedemikian hingga tiap negara yang berbatasan memiliki warna yang berbeda.
Kemudian pada tahun 1859, Sir W. R. Hamilton menemukan sebuah permainan dari kayu berbentuk dodecahedron beraturan yakni berupa polihedron dengan 12 muka dan 20 titik. Tiap muka berbentuk sebuah pentagon beraturan dan tiap pojoknya dibentuk oleh tiga sisi berbeda. Tiap pojok dodecahedron tersebut dipasangkan dengan sebuah kota terkenal seperti London, New York, Paris, dan lainnya. Masalah dalam permainan tersebut adalah mencari suatu rute melalui sisi-sisi dodecahedron sehingga tiap kota dilalui tepat satu kali (Sutarno, dkk, 2005: 65-66).
Pada tahun 1920-an König mengumpulkan hasil-hasil penelitian para ahli matematika tentang teori graf termasuk hasil pemikirannya sendiri untuk kemudian disusun menjadi sebuah buku yang diterbitkan pada tahun 1936. Buku tersebut dianggap sebagai referensi pertama tentang teori graf (Sutarno, dkk, 2005: 66).
Banyak para ahli yang kemudian tertarik dengan teori graf ini, baik untuk pengembangan teori graf murni maupun terapan. Para ahli tersebut diantaranya adalah Claude Berge, Oysten Ore, Paul Erdos, William Tutte, dan Frank Harary (Sutarno, dkk, 200: 66).
2.7 Pengertian Graf
Sebuah graf G adalah himpunan terhingga tak kosong yang memuat objek-objek yang disebut simpul (titik/vertex) dan himpunan pasangan tak urut antara simpul-simpul yang berlainan, yang disebut sisi (rusuk/edge). Himpunan simpul dari graf G ditulis dengan V(G), sedangkan himpunan sisi dari graf G dinyatakan dengan E(G) (Kusumah, 1998: 8-9).
6 Sebuah simpul dikatakan insiden dengan sebuah sisi jika simpul ini merupakan ujung sisi tersebut atau menempel pada sisi tersebut. Jika sebuah sisi menghubungkan dua buah simpul, maka kedua simpul tersebut dikatakan ajasen. Apabila dua buah sisi insiden pada sebuah simpul, maka kita katakan bahwa kedua sisi tersebut saling ajasen.
Perhatikan Gambar 2.2 di bawah ini. Dapat dilihat bahwa sisi e1 ajasen
dengan sisi e2, sisi e1 insiden pada simpul v2 dan simpul v1, simpul v1 ajasen
dengan simpul v2, simpul v2 ajasen dengan simpul v3 dan simpul v4.
v1 v4 v2 v3 e1 e2 e3 Gambar 2.2
Graf dengan Empat Simpul dan Tiga Sisi
2.8 Graf Sederhana
Dua buah sisi yang menghubungkan dua simpul yang sama disebut sebagai sisi rangkap/ganda. Perhatikan Gambar 2.3 di bawah ini. e1 dan e2
merupakan contoh sisi rangkap/ganda karena baik e1 maupun e2 sama-sama
menghubungkan simpul v1 dan v2. Apabila sebuah sisi menghubungkan suatu
simpul dengan simpul itu sendiri, maka sisi tersebut disebut sebagai loop. Contoh loop bisa dilihat pada Gambar 2.3 di bawah ini, yakni sisi e4 yang
menghubungkan simpul v3 dengan simpul itu sendiri.
v1 v3 v2 e1 e3 e2 e4 Gambar 2.3 Sisi Rangkap dan Loop
7 Sebuah graf yang tidak mengandung loop dan sisi rangkap disebut graf sederhana.
2.9 Graf Terhubung
Berikut ini akan kita bahas beberapa istilah untuk menjelaskan graf terhubung. Pertama-tama kita harus memahami jalan, yakni sebuah urutan tak nol w = v0e1v1e2v2...ekvk yang suku-sukunya bergantian antara simpul dan sisi
sedemikian hingga vi-1 dan vi merupakan simpul-simpul ujung sisi ei untuk
1 < i < k. Dengan kata lain w adalah sebuah jalan dari vo ke vk. vo disebut simpul
awal dan vk disebut simpul akhir, sedangkan v1, v2,..., vk -1 disebut simpul internal
(Sutarno, dkk, 2005: 92).
Apabila semua sisi pada sebuah jalan berlainan, maka disebut jejak. Sedangkan apabila semua simpul v1, v2, v3,..., vk dalam suatu jalan berbeda, maka
jalan tersebut dinamakan lintasan. Selanjutnya jejak yang mempunyai simpul awal dan simpul akhirnya sama disebut jejak tertutup. Sebuah siklus akan terbentuk dari jejak tertutup apabila simpul awal dan simpul internal pada sebuah jejak tertutup tersebut berlainan.
Selain konsep yang telah dijelaskan di atas, masih ada konsep yang harus kita bahas untuk menjelaskan graf terhubung, yaitu graf bagian. Graf K disebut graf bagian dari graf G, dinyatakan dengan K ⊆ G, apabila himpunan semua simpul di K merupakan himpunan bagian dari himpunan simpul di G dan himpunan sisi di K juga merupakan himpunan bagian dari himpunan sisi di G.
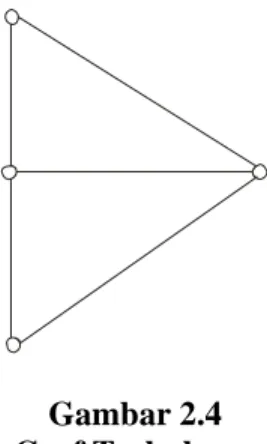
Jika sebuah graf hanya terdiri dari satu bagian, maka graf tersebut disebut graf terhubung. Dalam graf terhubung, untuk setiap pasang sisi sembarang vi dan vjpada graf tersebut, terdapat suatu lintasan unik dari simpul vi dan vj. Gambar 2.4 di bawah ini merupakan contoh graf terhubung.
8 Gambar 2.4
Graf Terhubung
2.10 Graf Siklus
Graf G disebut graf siklus jika graf tersebut merupakan graf terhubung yang setiap simpulnya ajasen pada dua buah simpul yang berbeda. Dengan kata lain dalam sebuah graf siklus termuat sebuah siklus melalui semua simpulnya. Contoh graf siklus dapat dilihat dalam Gambar 2.5 berikut ini.
Gambar 2.5 Graf Siklus
9
BAB III
VERTEX-MAGIC GRAPH
3.8 Pengertian Vertex-Magic Graph
Sebuah sisi atau simpul dari suatu graf dapat diberi label dengan menggunakan bilangan. Label tersebut bisa dipilih sesuai dengan kehendak kita. Namun bisa juga dibatasi bilangan tersebut berdasarkan banyaknya simpul dan sisi.
Salah satu masalah yang sangat menarik dari pelabelan graf berdasarkan banyaknya simpul dan sisi adalah bagaimana mengkonstruksi sebuah graf yang termasuk vertex-magic graph.
Definisi (Cunningham, 2004: 2)
Jika sebuah graf G dengan v simpul dan e sisi diberi label 1 hingga (v + e) demikian sehingga apabila setiap label simpul dan sisi yang insiden pada simpul tersebut dijumlahkan menghasilkan jumlah yang sama, maka graf G disebut vertex-magic graph. Sedangkan jumlah yang sama tersebut disebut magic number.
Jika graf G dengan v simpul dan e sisi diberi label 1 hingga (v + e) demikian sehingga apabila setiap label sisi dan dua buah simpul yang ajasen pada sisi tersebut dijumlahkan menghasilkan jumlah yang sama, maka graf G disebut edge-magic graph.
Apabila diperhatikan, dari kedua definisi di atas akan diperoleh hubungan antara vertex-magic graph dan edge-magic graph. Hubungan tersebut adalah edge-magic graph dapat dibentuk dari vertex-magic graph. Salah satu cara untuk membentuk graf tersebut adalah dengan merotasikan label-label pada vertex-magic graph searah perputaran jarum jam dengan urutan yang tetap. Perhatikan Gambar 3.1 (a) dan Gambar 3.1 (b). Gambar 3.1 (a) merupakan vertex-magic
10 graph dengan magic number 10, sedangkan Gambar 3.1 (b) merupakan edge-magic graph yang dibentuk dari vertex-magic graph pada Gambar 3.1 (a).
1 4 6 3 5 2 6 1 3 2 4 5 (a) (b) Gambar 3.1
Vertex-Magic Graph dan Edge-Magic Graph
Untuk selanjutnya masalah yang dibahas adalah masalah vertex-magic graph saja. Meskipun demikian, kita bisa memperoleh edge-magic graph dengan menggunakan cara yang telah dijelaskan di atas.
Sebuah magic number bisa diperoleh dengan menjumlahkan label simpul dan label sisi yang insiden pada simpul tersebut. Magic number bergantung pada label simpul dan sisi yang diberikan. Hal ini akan memberikan dampak bahwa magic number akan berbeda untuk pelabelan yang satu dengan pelabelan yang lainnya. Namun apakah magic number ini mempunyai batas-batas tertentu? Berikut kita bahas.
3.9 Batas Bawah Magic Number
Untuk mendapatkan suatu vertex-magic graph kita tidak mungkin untuk mencoba-coba setiap bilangan sebagai magic number. Namun akan lebih mudah apabila kita mempunyai range (daerah) magic number. Range (daerah) untuk magic number bisa kita peroleh berdasarkan pada banyaknya simpul dan sisi pada graf tersebut.
11 Lemma 1 (Cunningham, 2004: 3)
Jika G adalah sebuah vertex-magic graph dengan v simpuldan e sisi, maka: k v v e v e v = + + + + sum 2 ) 1 )( ( E
dengan k adalah sebuah magic number dan Esum adalah jumlah seluruh label
sisi graf G.
Bukti lemma di atas adalah sebagai berikut:
Misalkan: V adalah jumlah seluruh label simpul graf G, maka:
Esum + V = 1 + 2 + 3 + ... + (v + e)
=
(
v+e)(
1+v+e)
2 {jumlah (v + e) suku pertama deret aritmetika}
=
(
)(
)
2 1 + + +e v e vKarena setiap sisi insiden pada dua simpul yang berbeda, maka setiap label sisi akan dijumlahkan dengan kedua label simpul yang ajasen pada sisi tersebut. Akibatnya diperoleh:
2Esum + V = vk
(
)(
)
2 1 + + +e v e v + Esum = vk(
)(
)
v e v e v 2 1 + + + + v sum E = k Teorema 1 (Cunningham, 2004: 3)Misalkan G sebuah graf dengan v simpul dan e sisi.Jika G adalah vertex-magic graph,maka magic number k terbatas sehingga berlaku:
v e v e v e e e k v e v e v e e 2 ) )( 1 ( ) 1 ( 2 ) )( 1 ( ) 1 ( + + + + + ≤ ≤ + + + + + +
Bukti teorema ini bisa dikonstruksi dari Lemma 1. Pembuktiannya adalah sebagai berikut:
12 Dari Lemma 1 kita peroleh:
Esum = vk -
(
)(
)
2 1 + + +e v e vEsum minimum akan diperoleh apabila 1 hingga e ditempatkan sebagai
label sisi. Sehingga diperoleh:
Esum ≥ 1 + 2 + 3 + ... + e = e
(
1+e)
2 =(
)
2 1 + e eSedangkan Esum maksimum akan diperoleh apabila (e + 1) hingga (v + e)
ditempatkan sebagai label sisi. Sehingga diperoleh:
Esum ≤ (v + 1) + (v + 2) + ... +(v + e) =
∑
= + e i i v 1 =∑
∑
= = + e i e i v 1 1 1 =(
)
2 1 + +ee veDengan demikian diperoleh bahwa:
(
)
2 1 + e e ≤Esum≤(
)
2 1 + +ee ve(
)
2 1 + e e ≤vk -(
)(
)
2 1 + + +e v e v ≤(
)
2 1 + +ee ve(
)
2 1 + e e +(
)(
)
2 1 + + +e v e v ≤vk≤(
)
2 1 + +ee ve +(
)(
)
2 1 + + +e v e v(
) (
)(
)
v e v e v e e 2 1 1 + + + + + ≤k≤(
) (
)(
)
v e v e v e e e 2 1 1 + + + + + +Berdasarkan teorema di atas diperoleh bahwa magic number terbatas pada interval ⎢⎣⎡
(
+) (
+ +)(
+ +)
+(
+) (
+ +)(
+ +)
⎥⎦⎤ v e v e v e e e v e v e v e e 2 1 1 , 2 1 1 . Dengan demikian kita bisa memilih suatu bilangan untuk dijadikan magic number pada13 interval tersebut. Misalnya kita akan mengkonstruksi sebuah vertex-magic graph dengan 5 buah simpul dan 5 buah sisi, maka magic number graf tersebut akan terletak pada interval
[
14 ,19]
.Contoh 1
Misalkan G adalah graf siklus yang termasuk vertex-magic graph dengan V(G) = {a, b, d, f} dan E(G) = {p, q, r, s}. Tentukan interval untuk magic number yang mungkin.
Graf G memiliki empat buah simpul dan empat buah sisi. Maka berdasarkan Teorema 1, magic number graf G terletak pada interval [11,5; 15,5]
Apabila kita perhatikan sebuah graf siklus, maka kita peroleh bahwa banyaknya simpul dan bayaknya sisi pada graf tersebut adalah sama. Hal ini akan berpengaruh pada penentuan magic number baik untuk graf siklus sederhana dengan banyak simpulnya ganjil maupun genap. Akibat-akibat tersebut diperlihatkan dalam Akibat 1 berikut.
Akibat 1 (Cunningham, 2004: 4)
Misalkan G adalah sebuah graf siklus dengan v simpul. Jika G adalah sebuah vertex-magic graph,makaberlaku:
ganjil jika , 2 3 2 5 v k v+ ≤ , dan genap jika , 2 2 5 v k v+ ≤
Pembuktian Akibat 1 di atas adalah sebagai berikut:
Dari uraian sebelumnya, diketahui bahwa banyak simpul dan sisi pada graf siklus adalah sama. Artinya diperoleh hubungan:
14 Substitusikan persamaan di atas pada Teorema 1, sehingga diperoleh: k ≥
(
) (
)
v v v v v 2 2 1 2 1 + + + = 2 1 1 2v+ v+ = 2 3 2 5 + vJika v ganjil, maka (v + 1) habis dibagi 2. Jadi magic number minimum untuk graf siklus dengan banyak simpulnya ganjil adalah
2 3 2 5 +
v .
Bagaimana bila v genap? (v + 1) tidak habis dibagi 2 dan k haruslah merupakan bilangan bulat. Akibatnya label 1 hingga v tidak bisa digunakan untuk pelabelan sisi untuk memperoleh magic number yang minimum pada graf siklus dengan banyak simpul genap.
Namun dengan menambahkan 2 v
pada salah satu label sisi, akan diperoleh magic number minimum yang merupakan bilangan bulat. Akibatnya
2 v
harus ditambahkan pula pada Esum, sehingga diperoleh: Esum = (1 + 2 + ... + v) + 2 v =
(
)
2 2 1 v v v + + Akibatnya: k = v v 1 sum 2 + +E ≥(
)
v v v v v 2 1 1 2 + + + + = 2 2 1 2v+ +v+ = 2 2 5 + v15 Jadi magic number minimum untuk graf siklus dengan banyak simpulnya genap adalah 2
2 5 +
v . Perhatikan contoh 1 dan contoh 2 untuk melihat bagaimana penerapan Akibat 1.
Contoh 2
Misalkan G adalah graf siklus dengan banyak simpulnya 9 buah. Jika G merupakan vertex-magic graph, tentukan magic number minimum untuk graf G.
Esum terkecil akan diperoleh apabila sisi-sisi graf G diberi label 1 hingga 9.
Berdasarkan Akibat 1, maka magic number minimum untuk graf G adalah
( )
24 2 3 9 2 5 + = . Contoh 3Misalkan G adalah graf siklus dengan banyak sisinya 4 buah. Bagaimana kombinasi pelabelan simpul graf G untuk memperoleh vertex-magic graph dengan magic number minimum?
Dimulai dengan menempatkan 1 hingga 4 sebagai label sisi graf G, maka diperoleh Esum = 1 + 2 + 3 + 4 = 10. Perhatikan bahwa Esum tidak habis dibagi
dengan 4, sehingga Esum harus ditambah 2 agar bisa habis dibagi 4, karena
bilangan terdekat setelah 10 yang habis dibagi 4 adalah 12. Akibatnya Esum =
1 + 2 + 3 + 6. Jadi salah satu kombinasi pelabelan sisi graf G adalah {1, 2, 3, 6} agar diperoleh magic number yang minimum.
3.10 Batas Atas Magic Number
Pada uraian sebelumnya kita telah mengupas masalah batas bawah magic number suatu vertex-magic graph. Karena suatu vertex-magic graph diberi label dari 1 hingga (v + e), maka vertex-magic graph akan mempunyai magic number maksimum. Bagaimana mengatur kombinasi label yang mungkin sehingga diperoleh magic number maksimum? Berikut penjelasannya.
16 Akibat 2 (Cunningham, 2004: 6)
Misalkan G adalah graf dengan v simpul. Jika G merupakan graf vertex-magic graph,maka magic number k terbatas sehingga berlaku:
ganjil jika , 2 3 2 7 v v k≤ + , dan genap jika , 1 2 7 v v k≤ +
Hampir serupa dengan pembuktian Akibat 1, Akibat 2 dapat dibuktikan sebagai berikut:
Magic number akan maksimum apabila kita menempatkan (v + 1) hingga 2v sebagai label sisi. Akibatnya diperoleh:
Esum =
∑
= + v i i v 1 =∑
∑
= = + v i v i i v 1 1 =(
)
2 1 2 +vv+ v =(
)
2 1 3v+ vPerhatikan juga bahwa: k = v v 1 sum 2 + +E , maka k ≤
(
)
v v v v 2 1 3 1 2 + + + =(
)
v v v v 2 1 3 1 2 + + + = 2 1 1 3v+ +v+ = 2 3 2 7 + v17 Seperti pada masalah batas bawah magic number, apabila v ganjil, yakni banyak simpul graf G ganjil, maka (v + 1) habis dibagi 2. Jadi magic number maksimum yang mungkin untuk suatu graf siklus G dengan banyak simpul ganjil adalah
2 3 2 7 +
v . Bagaimana magic number maksimum untuk graf siklus G apabila banyak simpulnya genap?
Apabila v genap, maka (v + 1) tidak habis dibagi 2. Karena tidak boleh ada label sisi yang lebih dari 2v, maka salah satu alternatif untuk mendapatkan magic number maksimum adalah dengan mengurangkan label sisi tersebut dengan
2 v
. Akibatnya Esum harus dikurangi pula dengan
2 v , sehingga diperoleh: Esum =
(
)
2 2 1 3v v v − + =( )
2 3v v = 2 3 2 v Akibatnya: k = v v 1 sum 2 + +E ≤ v v v 2 3 1 2 2 + + = 2 3 1 2v+ + v = 1 2 7 + vJadi magic number maksimum yang mungkin untuk graf siklus G dengan banyak simpul genap adalah 1
2 7 +
v . Perhatikan Contoh 3 dan Contoh 4 berikut untuk melihat bagaimana penerapan Akibat 2.
18 Contoh 4
Misalkan G graf siklus dengan banyak sisinya 7 buah. Jika graf G termasuk vertex-magic graph, tentukan magic number maksimum graf G.
Magic number akan maksimum apabila bilangan 8 hingga 14 kita tempatkan sebagai label sisi. Berdasarkan Akibat 2, maka magic number maksimum graf G tersebut adalah
( )
26 2 3 7 2 7 + = . Contoh 5Misalkan G adalah graf siklus dengan banyak simpul 4 buah. Bagaimanakah pelabelan sisi graf G agar termasuk vertex-magic graph yang mempunyai magic number maksimum?
Karena bilangan 5 hingga 8 ditempatkan sebagai label sisi graf G agar diperoleh magic number maksimum, maka Esum = 5 + 6 + 7 + 8 = 26. Namun Esum tersebut tidak habis dibagi 4. Kelipatan 4 terbesar yang lebih kecil dari
26 adalah 24. Jadi Esum dikurangi 2, maka salah satu label sisi graf G harus
dikurangi 2. Salah satu pelabelan sisi graf G dengan magic number maksimum adalah {3, 6, 7, 8}.
Untuk selanjutnya, fokus pembahasan dibatasi hanya pada pelabelan graf siklus yang banyak simpulnya ganjil saja. Pelabelan graf siklus yang mempunyai banyak simpul genap tidak akan dibahas. Selain itu, pelabelan graf siklus yang dimaksud dalam makalah ini adalah pelabelan graf siklus untuk mengkonstruksi vertex-magic graph.
3.11 Pelabelan Graf Siklus dengan Banyak Simpul Ganjil dan Magic
Number Maksimum
Pada uraian di atas telah dibahas batas atas dan batas bawah suatu magic number dari graf siklus yang termasuk vertex-magic graph, baik untuk graf siklus yang mempunyai banyak simpul ganjil maupun yang genap. Sedangkan pada uraian berikutnya kita akan membahas pemberian label graf siklus yang mempunyai banyak simpul ganjil saja. Graf siklus yang mempunyai banyak
19 simpul ganjil mempunyai batas bawah magic number
2 3 2 5 +
≥ v
k dan batas atas
magic number 2 3 2 7 + ≤ v k .
Magic number maksimum akan diperoleh apabila kita menempatkan (v+1) hingga 2v sebagai label sisi graf tersebut. Dengan kata lain kita menempatkan 1 hingga v sebagai label simpul.
Teorema 2 (Cunningham, 2004: 8)
Misalkan G adalah sebuah graf siklus dengan v simpul dan v ganjil. Terdapat pelabelan vertex-magic graph dengan bilangan 1 hingga v diletakkan pada simpul dan sebuah magic number
2 3 2 7 +
v sebagai batas atas untuk magic number. 1 2v 2 3 4 5 6 v (3/2)v +½ (3/2) - (½)v 2 - 1v (3/2) - (3/2)v 2 - 2v Gambar 3.2
Label Graf Siklus dengan Banyak Simpul Ganjil dan Magic Number Maksimum
Teorema 2 di atas menegaskan bahwa pada graf siklus dengan banyak simpulnya ganjil terdapat suatu pelabelan untuk magic number maksimum dengan bilangan 1 hingga v ditempatkan sebagai label simpul. Teorema tersebut dapat kita buktikan sebagai berikut:
Simpul graf G diberi label 1 hingga v secara berurutan searah perputaran jarum jam (Gambar 3.2). Sebuah sisi kita sebut di sebelah kanan suatu simpul apabila sisi ini ajasen dengan simpul tersebut dan sisi ini mempunyai orientasi
20 negatif (berlawanan arah dengan perputaran jarum jam) terhadap simpul tersebut. Selain itu, sebuah sisi disebut berada di sebelah kiri suatu simpul apabila sisi ini ajasen dengan simpul tersebut dan sisi ini mempunyai orientasi positif (searah perputaran jarum jam) terhadap simpul tersebut. Aturan ini akan sangat penting untuk diingat, sebab akan berpengaruh pada penentuan label suatu sisi graf G yang akan bergantung pada letak suatu simpul graf G.
Pelabelan graf G dimulai dengan memberikan label simpul dengan 1 hingga v. Kemudian dilanjutkan dengan pemberian label sisi yang terletak di sebelah kanan simpul yang berlabel 1. Label sisi dimulai dengan 2v yang kemudian berkurang sesuai dengan label simpul yang bersesuaian. Pelabelan sisi graf G mengikuti aturan yang tertera dalam tabel berikut:
Tabel 3.1
Aturan Pelabelan Sisi Graf Siklus
dengan Banyak Simpul Ganjil dan Magic Number Maksimum Deskripsi kasus Label simpul Label sisi kiri Label sisi
kanan Setiap simpul yang
berlainan dimulai dengan 1 2i + 1 i = 0, ... , 2 1 − v v+ 2−i 1 2 3 2v – i
Setiap simpul yang berlainan dimulai dengan 2 2i + 2 i = 0, ... , 1 2 1 − − v 2v – i v−2−i 1 2 3
Sumber: Cunningham, vertex-magic
Pada kasus pertama, graf G mempunyai magic number berikut:
(
)
(
)
2 3 2 7 2 2 1 2 3 1 2 ⎟+ − = + ⎠ ⎞ ⎜ ⎝ ⎛ + − + + v i v i v i .Sedangkan pada kasus kedua, graf G mempunyai magic number di bawah ini:
(
) (
)
2 3 2 7 2 1 2 3 2 2 2 ⎟= + ⎠ ⎞ ⎜ ⎝ ⎛ − − + − + + v i v i v i .21 Gambar 3.3 dan Gambar 3.4 berikut ini memperlihatkan bagaimana pelabelan graf siklus yang mempunyai banyak simpul ganjil dengan magic number maksimum. 4 2 3 5 6 1 Gambar 3.3
Graf Siklus dengan 3 Simpul dan Magic Number 12
2 1 3 4 5 8 6 9 10 7 Gambar 3.4
Graf Siklus dengan 5 Simpul dan Magic Number 19
3.12 Pelabelan Graf Siklus dengan Banyak Simpul Ganjil dan Magic
Number Minimum
Bagaimana pelabelan graf siklus yang mempunyai banyak simpul ganjil dan Magic Number minimum? Magic Number minimum akan diperoleh manakala kita menempatkan (v + 1) hingga 2v sebagai label simpul. Dengan kata lain kita akan mengatur label-label sisi sedemikian hingga kita peroleh vertex-magic graph dengan magic number minimum.
22 Teorema 3 (Cunningham, 2004: 10)
Misalkan G adalah sebuah graf siklus dengan v simpuldan v ganjil. Terdapat pelabelan pada vertex-magic graph dengan (v + 1) hingga 2v ditempatkan pada simpul dan magic number
2 3 2 5 +
v adalah batas bawah untuk magic number. v + 1 2v v + 2 v + 3 v + 4 v + 5 v + 6 v (½)v +(½) (½) - (½)v v - 1 (½) - (3/2)v v - 2 Gambar 3.5
Label Graf Siklus dengan Banyak Simpul Ganjil dan Magic Number Minimum
Ide yang sama seperti pada pelabelan graf siklus dengan magic number maksimum di atas, dapat kita gunakan untuk menentukan pelabelan graf siklus dengan magic number minimum. Untuk mendapatkan magic number minimum kita harus menempatkan angka (v + 1) hingga 2v sebagai label simpul. Dengan kata kata lain kita hanyalah membuat kombinasi label untuk sisi dengan bilangan 1 hingga v.
Sisi yang pertama kali diberi label adalah sisi yang berada di sebelah kanan simpul yang mempunyai label (v + 1). Label yang diberikan pada sisi tersebut adalah v. Kemudian sisi yang lainnya diberi label berdasarkan label simpul yang bersesuaian. Pemberian label sisi ini mengikuti aturan yang tertera dalam tabel berikut ini:
23 Tabel 3.2
Aturan Pelabelan Sisi Graf Siklus
dengan Banyak Simpul Ganjil dan Magic Number Minimum Deskripsi kasus Label simpul Label sisi kiri Label sisi
kanan Setiap simpul yang
berlainan dimulai dengan (v + 1) v + 2i + 1 i = 0, ... , 2 1 − v 2 2 2 1 2 i v − + v – i
Setiap simpul yang berlainan dimulai dengan (v + 2) v + 2i + 2 i = 0, ... , 1 2 1− − v v – i 2 2 2 1 2 i v − −
Sumber: Cunningham, vertex-magic
Pada kasus pertama, graf G mempunyai magic number berikut:
(
)
(
)
2 3 2 5 2 2 2 1 2 1 2 ⎟+ − = + ⎠ ⎞ ⎜ ⎝ ⎛ + − + + + i v i v i v vSedangkan pada kasus kedua, graf G mempunyai magic number yang sama seperti pada kasus pertama, yaitu:
(
) (
)
2 3 2 5 2 2 2 1 2 2 2 ⎟= + ⎠ ⎞ ⎜ ⎝ ⎛ − − + − + + + i v i v i v vGambar 3.6 dan Gambar 3.7 berikut ini memperlihatkan bagaimana pelabelan graf siklus yang mempunyai banyak simpul ganjil dan magic number maksimum. 1 5 6 2 3 4 Gambar 3.6
24 7 6 8 9 10 3 1 4 5 2 Gambar 3.7
Graf Siklus dengan 5 Simpul dan Magic Number 14
Selain dengan mengatur penempatan label 1 hingga v sebagai label sisi atau sebagai label simpul, kita juga bisa menempatkan bilangan ganjil atau bilangan genap antara 1 hingga 2v sebagai label simpul. Bagaimana pelabelan tersebut dan bagaimana magic number yang diperoleh? Berikut akan disajikan uraiannya.
3.13 Pelabelan Graf Siklus dengan Banyak Simpul Ganjil dan Bilangan Ganjil sebagai Label Simpul
Selain dengan menggunakan cara pelabelan seperti di atas, kita bisa menempatkan bilangan ganjil mulai dari 1 hingga (2v – 1) sebagai label simpul. Dengan kata lain kita akan mengatur penempatan bilangan genap antara 2 hingga 2v sebagai label sisi.
Teorema 4 (Cunningham, 2004: 16)
MisalkanG adalah sebuah graf siklus dengan v simpuldan v ganjil. Terdapat sebuah pelabelan pada vertex-magic graph dengan bilangan ganjil antara 1 hingga (2v – 1)ditempatkan padasimpuldan magic number 3v + 2
25 1 3 5 7 9 11 2 - 1v v+ 1 2v v - 1 2 - 2v v - 3 2 - 4v Gambar 3.8
Label Graf Siklus dengan Banyak Simpul Ganjil dan Bilangan Ganjil sebagai Label Simpul
Pada pelabelan kali ini, kita akan menempatkan bilangan ganjil antara 1 hingga (2v – 1) secara berurutan sebagai label simpul graf G searah perputaran jarum jam. Kita akan mengatur penempatan bilangan genap antara 2 hingga 2v sebagai label sisi graf G sehingga kita peroleh sebuah vertex-magic graph. Dimulai dengan menempatkan 2v sebagai label sisi di sebelah kanan simpul yang berlabel 1, kemudian memberikan label berikutnya searah perputaran jarum jam pada sisi yang lain sesuai dengan label simpul yang bersesuaian. Pemberian label sisi dengan angka genap di atas mengikuti aturan pelabelan pada tabel berikut ini:
Tabel 3.3
Aturan Pelabelan Sisi Graf Siklus dengan Banyak Simpul Ganjil dan Bilangan Ganjil sebagai Label Simpul
Deskripsi kasus Label simpul Label sisi kiri Label sisi kanan Setiap simpul yang
berlainan dimulai dengan 1 4i + 1 i = 0, ... , 2 1 − v v + 1 – 2i 2v – 2i Setiap simpul yang
berlainan dimulai dengan 3 4i + 3 i = 0, ... , 1 2 1 − − v 2v – 2i v – 1 – 2i
26 Pada kasus pertama, kita memperoleh magic number berikut ini:
(
4i+1) (
+ v+1−2i) (
+ 2v−2i)
=3v+2Sedangkan pada kasus kedua, diperoleh magic number yang sama seperti pada kasus pertama, yaitu:
(
4i+3) (
+ 2v−2i) (
+ v−1+2i)
=3v+2Perhatikan Gambar 3.9 dan Gambar 3.10 untuk melihat pelabelan graf siklus dengan bilangan ganjil sebagai label simpulnya.
2 3
5
4 6
1
Gambar 3.9
Graf Siklus dengan 3 Simpul dan Magic Number 11
3 1 5 7 9 6 2 8 10 4 Gambar 3.10
Graf Siklus dengan 5 Simpul dan Magic Number 17
Pada uraian di atas kita telah melihat pelabelan graf siklus dengan menempatkan bilangan ganjil sebagai label simpul sehingga diperoleh vertex-magic graph dengan melakukan pengaturan bilangan genap sebagai label sisinya. Bagaimana apabila bilangan genap ditempatkan sebagai label simpul? Bagaimana dengan magic number yang diperoleh? Berikut ini disajikan uraiannya.
27 3.14 Pelabelan Graf Siklus dengan Banyak Simpul Ganjil dan Bilangan
Genap sebagai Label Simpul
Pada uraian di atas kita telah membahas pelabelan graf siklus dengan menempatkan bilangan ganjil sebagai label simpul. Pada pelabelan kali terakhir ini, kita akan membahas bagaimana pelabelan graf siklus dengan menempatkan bilangan genap sebagai label simpulnya. Dengan kata lain, kita akan mengatur penempatan bilangan ganjil antara 1 hingga (2v – 1) sebagai label sisi supaya diperoleh vertex-magic graph.
Teorema 5 (Cunningham, 2004: 18)
Misalkan G adalah sebuah graf siklus dengan v simpul dan v ganjil. Terdapat sebuah pelabelan vertex-magic graph dengan bilangan genapantara 2hingga 2v ditempatkan pada simpuldan magic number 3v + 1.
2 4 6 8 10 12 2v 2 - 1v v - 2 2 - 3v v - 4 2 - 5v v Gambar 3.11
Label Graf Siklus dengan Banyak Simpul Ganjil dan Bilangan Genap sebagai Label Simpul
Teknik yang serupa seperti pada pelabelan graf siklus dengan bilangan ganjil sebagai label simpul, dapat kita gunakan untuk melakukan pelabelan graf dengan bilangan genap sebagai label sisinya. Bilangan genap antara 2 hingga 2v ditempatkan secara berurutan searah perputaran jarum jam sebagai label sisi. Kemudian kita mengatur kombinasi bilangan ganjil antara 1 hingga (2v – 1) sebagai label sisi. Dimulai dengan memberikan label (2v – 1) pada sisi yang
28 berada di sebelah kanan simpul yang berlabel 2, kemudian memberikan label pada sisi yang lainnya yang terus berkurang hingga 1 berdasarkan label simpul yang bersesuaian. Aturan pemberian label pada sisi graf tersebut tertera dalam tabel berikut:
Tabel 3.4
Aturan Pelabelan Sisi Graf Siklus dengan Banyak Simpul Ganjil dan Bilangan Genap sebagai Label Simpul
Deskripsi kasus Label simpul Label sisi kiri Label sisi kanan Setiap simpul yang
berlainan dimulai dengan 2 4i + 2 i = 0, ... , 2 1 − v v – 2i 2v – 1 – 2i Setiap simpul yang
berlainan dimulai dengan 4 4i + 4 i = 0, ... , 1 2 1 − − v 2v – 1 – 2i v – 2i – 2
Sumber: Cunningham, vertex-magic
Pada kasus pertama, magic number graf tersebut adalah:
(
4i+2) (
+ v−2i) (
+ 2v−1−2i)
=3v+1Sedangkan pada kasus kedua kita memperoleh magic number berikut:
(
4i+4) (
+ 2v−1−2i) (
+ v−2i−2)
=3v+1Untuk melihat pelabelan graf siklus dengan bilangan genap sebagai label simpulnya, perhatikan Gambar 3.12 dan Gambar 3.13 berikut ini.
1 4
6
3 5
2
Gambar 3.12
29 4 2 6 8 10 5 1 7 9 3 Gambar 3.13
Graf Siklus dengan 5 Simpul dan Magic Number 16
Demikian uraian pelabelan graf siklus untuk mengkonstruksi vertex-magic graph. Uraian di atas hanyalah beberapa teknik pelabelan graf, masih banyak lagi teknik-teknik yang lainnya yang tidak dibahas dalam makalah ini.
3.15 Temuan
Berdasarkan uraian yang telah dijelaskan sebelumnya, dapat digeneralisasi sebagai berikut:
Konjektur
Sebuah graf G dengan v simpul dan e sisi dapat diberi label k hingga (k + v + e) demikian sehingga apabila setiap label simpul dan sisi yang insiden pada simpul tersebut dijumlahkan menghasilkan jumlah yang sama, maka graf G disebut vertex-magic graph. Sedangkan jumlah yang sama tersebut disebut magic number.
Sebuah graf G dengan v simpul dan e sisi dapat diberi label k hingga (k + v + e) demikian sehingga apabila setiap label sisi dan dua buah simpul yang ajasen pada sisi tersebut dijumlahkan menghasilkan jumlah yang sama, maka graf G disebut edge-magic graph.
30 Demikian uraian pelabelan graf siklus untuk mengkonstruksi vertex-magic graph. Uraian di atas hanyalah beberapa teknik pelabelan graf, masih banyak lagi teknik-teknik yang lainnya yang tidak dibahas dalam makalah ini.
31
BAB IV
KESIMPULAN DAN SARAN
4.3 Kesimpulan
Berdasarkan uraian pada bagian sebelumnya, kita dapat menyimpulkan beberapa hal berikut:
a. Untuk mengkonstruksi sebuah vertex-magic graph, sebuah graf siklus yang banyak simpulnya ganjil dapat diberi label berdasarkan magic number maksimum atau minimum.
b. Untuk mengkonstruksi sebuah vertex-magic graph, graf siklus yang banyak simpulnya ganjil dapat diberi label dengan bilangan genap atau ganjil sebagai label simpulnya.
c. Magic number yang diperoleh, akan bergantung pada teknik pelabelan graf siklus yang dilakukan, yaitu:
i. Untuk pelabelan graf siklus berdasarkan magic number maksimum, maka diperoleh magic number
2 3 2 7 +
v ;
ii. Untuk pelabelan graf siklus berdasarkan magic number minimum, maka diperoleh magic number
2 3 2 5 +
v ;
iii. Untuk pelabelan graf siklus berdasarkan bilangan ganjil sebagai label simpulnya, maka diperoleh magic number 3v + 2;
iv. Untuk pelabelan graf siklus berdasarkan bilangan genap sebagai label simpulnya, maka diperoleh magic number 3v + 1.
32 4.4 Saran
Dalam kesempatan ini, penyusun ingin memberikan beberapa saran kepada pembaca sebagai berikut:
a. Dalam makalah ini hanya dibahas tentang pelabelan graf siklus sederhana yang banyak simpulnya ganjil berdasarkan magic number maksimum atau minimum dan penempatan bilangan ganjil atau bilangan genap sebagai label simpul. Masih banyak teknik pelabelan graf siklus sederhana dengan banyak simpul ganjil yang tidak tercakup dalam makalah ini. Oleh karena itu, pembaca disarankan agar tidak terpaku pada teknik yang dijelaskan pada makalah ini saja.
b. Makalah ini hanya membahas teknik pelabelan graf siklus sederhana untuk mengkonstruksi vertex-magic graph yang banyak simpulnya ganjil saja. Oleh karena itu, pembaca disarankan untuk mempelajari teknik pelabelan graf siklus yang banyak simpulnya genap. Teknik pelabelan ini sedikit berbeda dengan teknik pelabelan graf siklus yang banyak simpulnya ganjil.
c. Dalam makalah ini hanya dibahas teknik pelabelan untuk graf siklus sederhana saja, jenis graf lainnya seperti graf bipartit, graf euler, dan graf hamilton memerlukan teknik pelabelan yang berbeda. Pembaca dapat memfokuskan penelitiannya pada teknik pelabelan graf tersebut.
33 DAFTAR PUSTAKA
Cunningham, D. 2004. Vertex-Magic. [Online]. Tersedia:
http://math.furman.edu/~woodard/fuejum/content/2004/paper1_2004.pdf. [30 September 2006]
Munir, R. 2003. Matematika Diskrit. Bandung: Informatika.
Kusumah, Y. S. 1998. Matematika Diskrit. Bandung: IKIP Bandung Press Sutarno, H, Nanang Priatna, dan Nurjanah. 2005. Matematika Diskrit. Malang:
34 BIOGRAFI
JAENUDIN, lahir di Garut pada tanggal 18 Desember 1985. Menyelesaikan pendidikan Sekolah Dasar di SDN Tenjolaut (1992 – 1998), kemudian melanjutkan ke SMPN 1 Bungbulang (1998 – 2001). Lulus dari SMAN 1 Bungbulang pada tahun 2004, mendapat kesempatan belajar ke Universitas Pendidikan Indonesia (UPI) dengan mengambil Jurusan Pendidikan Matematika. Setelah empat tahun belajar di UPI, lulus tahun 2008 dengan yudisium
Cum Laude. Saat ini aktif mengajar di sebuah lembaga yang melayani pendidikan
bagi anak-anak SD dan SMP. Selain aktif sebagai konsultan pendidikan, juga aktif dalam bidang webmaster, pemrograman Macromedia Flash, serta database. Saat ini, sedang menunggu kesempatan untuk melanjutkan studi ke jenjang yang lebih tinggi.