INTERSECTIONS JOURNAL
Jurnal Pendidikan Matematika dan MatematikaFakultas Keguruan dan Ilmu Pendidikan Universitas Cokroaminoto Yogyakarta
Volume 1 September 2017 ISSN :
-Diterbitkan Oleh :
Fakultas Keguruan dan Ilmu Pendidikan Universitas Cokroaminoto Yogyakarta
Penanggung Jawab :
Dekan Fakultas Keguruan dan Ilmu Pendidikan Universitas Cokroaminoto Yogyakarta
Dewan Redaksi :
Drs. Triwahyu Budiutomo, M.Pd, M.T. Joko Wahono, S.Pd., M.A.P.
Redaktur Pelaksana :
Yenny Anggreini Sarumaha, S.Pd., M.Sc. Toto Hermawan, S.Pd., M.Sc.
Sekretaria Redaksi : Yudiantiwi Laksmi Dewi, S.E.
Bendahara :
Maratu Shalikhah, S.Pd., M.Pd. Prihastini Oktasari Putri, S.Pd., M.Pd.
Anggota :
Aji Permana Putra, S.Pd., M.Pd. Ika Septi Hidayati, S.Pd.
Mitra Bestari :
Prof. Dr. Rusgianto Heri Santoso, M.Pd. ( Universitas Negeri Yogyakarta ) Prof. Dr. Husaini Usman, M.Pd., M.T. ( Universitas Negeri Yogyakarta )
Prof. Dr.Sudji Munaji, M.Pd. ( Universitas Negeri Yogyakarta ) Prof. Dr. Yoyon Suryono, MS. ( Universitas Negeri Yogyakarta )
Alamat Redakasi:
Program Studi Pendidikan Matematika
Fakultas Keguruan dan Ilmu Pendidikan Universitas Cokroaminoto Yogyakarta Alamat: Gambiran, Umbulharjo Yogyakarta, 55161 Telepon: 0274 – 372274
PENGANTAR REDAKSI
Puji syukur alhamdulillah penulis panjatkan kehadirat Allah SWT, yang telah melimpahkan rahmat serta hidayah-Nya sehingga dapat menyelesaikan Intersections Journal Volume 1 Nomor 1 September 2017 terbit dengan menyajikan tulisan-tulisan tentang Pendidikan Matematika dan Matematika Murni. Journal ini terdapat 6 (tujuh) tulisan yang di buat oleh para ahli di bidang mereka.
Journal ini ditujukan bagi peserta didik, mahasiswa, guru dan dosen pada umumnya. Banyak pihak yang telah membantu dalam penulisan journal baik langsung maupun tidak langsung. Pada kesempatan ini tim redaksi menyampaikan ucapan terima kasih kepada Universitas Cokroaminoto Yogyakarta dan juga pengirim naskah hasil penelitiannya. Tim redaksi banyak mengucapkan terimakasih sehingga jurnal ini dapat di baca oleh berbagai pihak sehingga dapat bermanfaat bagi para pembaca.
Namun demikian, tentunya masih banyak kekurangan yang memerlukan penyempurnaan pada cetakan selanjutnya. Tim redaksi mengharapkan kritik dan saran yang membangun demi penyempurnaan jurnal ini. Di harapkan jurnal ini dapat menambah pengetahuan dan wawasan bagi peserta didik, mahasiswa, guru, dan dosen sehingga dapat menerapkan tugas dan perannya secara kompeten dan professional.
Daftar Isi
Hal
Dewan Redaksi ……… i
Pengantar Redaksi ………... ii
Daftar isi ……….. iii
1 Implementasi Model Pembelajaran TS-TS (Two Stay-Two Stray) untuk Meningkatkan Kemampuan Komunikasi Matematis
(Maratu Shalikhah) 1
2 Metode Pembuktian Matematika
(Toto Hermawan) 12
3 Perubahan Pembelajaran yang Berpusat pada Guru ke Berpusat pada Siswa
(Yenny Anggreini Sarumaha) 21
4 Upaya Meningkatkan Motivasi Belajar Matematika Melalui Model Pembelajaran Kooperatif Tipe Numbered Head Toghether (NHT) Pada Siswa Kelas VIII SMP Negeri 1 Alian
(Prihastini Oktasari Putri) 31
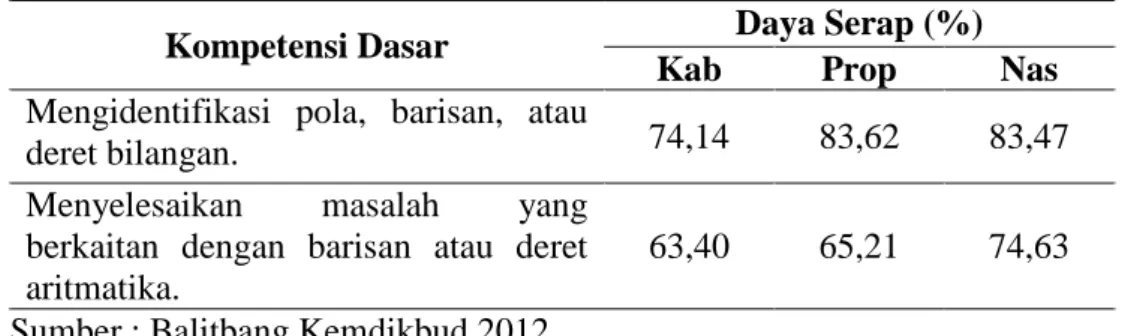
5 Efektifitas Model Pembelajaran Kooperatif Jigsaw II Dan Pembelajaran Langsung Pada Materi Barisan dan Deret Ditinjau Kepribadian Siswa SMK Kelas X Di Kabupaten Klaten
(Luthfiana Mirati ) 39
6 Meningkatkan Minat Belajar Matematika Tentang FPB Dan KPK Melalui Strategi Pembelajaran Ekspositori Bagi Siswa Kelas IV SD Negeri Prembulan Galur Kulon Progo Tahun Ajaran 2015/2016
IMPLEMENTASI MODEL PEMBELAJARAN TS-TS (TWO STAY-TWO STRAY) UNTUK MENINGKATKAN KEMAMPUAN KOMUNIKASI MATEMATIS SISWA
Maratu Shalikhah
Abstrak
Penelitian ini bertujuan untuk: (1) meningkatkan kemampuan komunikasi matematis siswa kelas XI IPA 1 SMA Negeri 1 Pleret Bantul dengan menerapkan model pembelajaran TS-TS; (2) mengetahui respon siswa terhadap pembelajaran matematika dengan model TS-TS.
Penelitian ini merupakan penelitian tindakan kelas. Subjek penelitian ini adalah siswa kelas XI IPA 1 SMA Negeri 1 Pleret Bantul tahun ajaran 2014/2015 dengan banyak siswa 29 orang. Tahapan penelitian ini yaitu perencanaan, pelaksanaan, pengamatan, dan refleksi. Tindakan dilaksanakan dalam 2 siklus. Masing-masing siklus terdiri dari 5 pertemuan. Instrumen yang digunakan untuk mengumpulkan data adalah tes kemampuan komunikasi matematis, angket respon siswa, lembar observasi, dan catatan lapangan.Hasil penelitian menunjukkan bahwa: (1) Kemampuan komunikasi matematis siswa kelas XI IPA 1 SMA N 1 Pleret Bantul meningkat setelah mengikuti pembelajaran dengan model TS-TS; (2) Siswa kelas XI IPA 1 SMA N 1 Pleret Bantul memberikan respon positif terhadap pelaksanaan pembelajaran matematika dengan model TS-TS. Banyaknya siswa yang mengalami peningkatan kategori jumlah skor tes kemampuan komunikasi matematis pada siklus I untuk indikator pertama sebesar 48,28% dan pada siklus II meningkat menjadi 93,10%. Untuk indikator ke dua sebesar 41,38% dan pada siklus II meningkat menjadi 75,86%. Untuk indikator ke tiga sebesar 37,93% dan pada siklus II meningkat menjadi 79,31%. Untuk persentase jumlah skor respon siswa siklus I sebesar 78,55% dan pada siklus II meningkat menjadi 82,86%.
Kata kunci:model, pembelajaran,TS-TS (Two Stay-Two Stray), komunikasi, matematis, Pendahuluan
Matematika merupakan disiplin ilmu yang wajib dipelajari oleh siswa mulai dari tingkat sekolah dasar sampai tingkat sekolah menengah bahkan sampai ke perguruan tinggi. Hal ini karena matematika sangat dibutuhkan dan sangat berguna dalam kehidupan sehari-hari. Oleh karena itu setiap sekolah wajib menyelenggarakan pembelajaran matematika sesuai dengan tujuan pembelajaran matematika.
Dalam Standar Isi Kurikulum Satuan Tingkat Pendidikan (Depdiknas, 2006: 388) dijelaskan bahwa pembelajaran matematika bertujuan agar peserta didik memiliki kemampuan: (1) memahami konsep matematika, menjelaskan keterkaitan antar konsep, dan mengaplikasikan konsep atau algoritma secara luwes, akurat, efisien, dan tepat dalam
pemecahan masalah; (2)
menggunakan penalaran pada pola dan sifat, melakukan manipulasi
Volume I , Intersections Journal matematika dalam membuat generalisasi, menyusun bukti atau menjelaskan gagasan dan pernyataan matematika; (3) memecahkan masalah yang meliputi kemampuan memahami masalah, merancang model matematika, menyelesaikan model dan menafsirkan solusi yang diperoleh; (4) mengkomunikasikan gagasan dengan simbol, tabel, diagram, atau media lain untuk memperjelas keadaan atau masalah; (5) memiliki sikap menghargai kegunaan matematika dalam kehidupan, yaitu memiliki rasa ingin tahu, perhatian dan minat dalam mempelajari matematika, serta sikap ulet dan percaya diri dalam pemecahan masalah; (6) Menalar secara logis dan kritis serta mengembangkan aktivitas kreatif dalam memecahkan masalah dan mengkomunikasikan ide.
Berdasarkan tujuan
pembelajaran matematika yang tercantum dalam Standar Isi Kurikulum Tingkat Satuan Pendidikan tersebut maka
kemampuan berkomunikasi
khususnya kemampuan komunikasi matematis merupakan salah satu tujuan pembelajaran yang sangat penting. Kemampuan komunikasi matematis memiliki peran sentral dalam pembelajaran matematika. Terkait dengan peran kemampuan komunikasi matematis, Huinker & Laughlin (Bistari, 2010: 14) mengungkapkan bahwa salah satu
tujuan yang ingin dicapai dalam pembelajaran matematika adalah memberikan kesempatan seluas-luasnya kepada siswa untuk
mengembangkan dan
mengintegrasikan keterampilan berkomunikasi.
Berdasarkan pengamatan di kelas XI IPA 1 SMA N 1 Pleret Bantul dijumpai bahwa dalam pembelajaran matematika banyak siswa yang belum memiliki inisiatif maju mengerjakan soal tanpa ditunjuk terlebih dahulu oleh guru. Ketika ada teman yang diminta maju mengerjakan soal, siswa lain hanya pasif dan banyak dari mereka memilih diam jika jawaban yang tertulis di papan tulis berbeda
dengan jawaban mereka.
Kebanyakan dari mereka tidak
berani menyanggah atau
berpendapat mengenai langkah-langkah atau proses penyelesaian soal yang dikerjakan. Ketika dihadapkan pada suatu soal uraian, siswa tidak terbiasa menuliskan apa yang diketahui dan apa yang ditanyakan dari soal sebelum menyelesaikannya, sehingga siswa sering salah dalam menafsirkan maksud dari soal tersebut. Selain itu dalam menyelesaikan soal uraian siswa cenderung kurang rinci dalam menuliskan langkah-langkah penyelesaiannya. Dari pengamatan tersebut maka dapat diketahui bahwa kemampuan komunikasi matematis siswa kelas XI IPA 1 masih perlu ditingkatkan.
ISSN : xxxxxxxxxxx Peneliti memberikan satu soal
untuk mengukur kemampuan komunikasi matematis siswa. Soal tersebut adalah: “Dalam kegiatan melambungkan sebuah dadu, jika A adalah kejadian munculnya bilangan ganjil dan B adalah kejadian munculnya bilangan prima, gambarlah diagram Venn yang menunjukkan hubungan dari himpunan 𝐴, himpunan 𝐵, dan semesta himpunan dengan jelas dan tepat. Kemudian tentukan peluang kejadian munculnya bilangan ganjil atau prima.”
Dari jawaban siswa dapat dilihat bahwa siswa tidak menyatakan himpunan semestanya. Selain itu siswa juga masih kurang runtut dalam hal penyelesaian soal, yaitu langsung menggunakan rumus tanpa menuliskan terlebih dahulu cara menghitung peluang dari masing-masing kejadian 𝐴 dan kejadian 𝐵 seperti pada jawaban yang diharapkan oleh peneliti. Hal ini menunjukkan kurangnya kemampuan komunikasi matematis tertulis siswa kelas XI IPA 1.
Permasalahan tersebut mendorong peneliti untuk melakukan penelitian terhadap kemampuan komunikasi matematis siswa kelas XI IPA 1 SMA N 1 Pleret Bantul. Salah satu strategi pembelajaran yang diharapkan dapat
meningkatkan kemampuan
komunikasi matematis siswa adalah model pembelajaran TS-TS (Two Stay-Two Stray). Model
pembelajaran ini merupakan salah satu model pembelajaran kooperatif. Dalam model pembelajaran kooperatif terdapat empat prinsip yang harus tercermin di dalamnya. Empat prinsip tersebut adalah: 1) saling ketergantungan positif; 2) tanggung jawab perseorangan; 3) tatap muka; 4) komunikasi antar anggota; dan 5) evaluasi proses kelompok (Wina Sanjaya, 2009: 246).
Peneliti memilih model TS-TS karena merupakan salah satu tipe pembelajaran kooperatif yang memberikan kesempatan kepada kelompok membagikan hasil dan informasi kepada kelompok lain. Dalam proses pembelajaran dengan model TS-TS, siswa akan melakukan komunikasi satu sama lain. Siswa akan lebih banyak melakukan kegiatan komunikasi secara langsung. Dengan demikian proses pembelajaran matematika di sekolah yang menerapkan model
TS-TS diharapkan dapat
meningkatkan kemampuan
komunikasi matematis siswa
A. Metode Penelitian
Jenis penelitian ini merupakan Penelitian Tindakan Kelas (PTK) yang dilaksanakan dalam 2 siklus. Setiap siklusnya dilaksanakan selama 9 jam pelajaran atau 5 kali pertemuan (4 pertemuan untuk pelaksanaan tindakan dan 1 pertemuan untuk tes siklus). Setiap siklus terdiri dari 4 tahap yaitu
Volume I , Intersections Journal perencanaan (planning), tindakan (acting), pengamatan (observing), dan refleksi (reflecting). Subjek dalam penelitian ini adalah siswa kelas XI IPA 1 SMA N 1 Pleret Bantul tahun ajaran 2014/2015 dengan banyak siswa 29 orang. Sedangkan untuk objek penelitian ini adalah keseluruhan proses dan hasil pembelajaran matematika untuk meningkatkan kemampuan komunikasi matematis siswa kelas XI IPA 1 SMA N 1 Pleret Bantul melalui implementasi model pembelajaran TS-TS. Waktu penelitian dilaksanakan pada semester genap tahun ajaran 2014/2015 pada bulan Januari-Februari 2015 di kelas XI IPA 1 SMA N 1 Pleret Bantul. Dalam penelitian ini siswa dikelompokkan ke dalam tujuh kelompok dengan alur bertamunya dapat dilihat pada gambar 1 berikut.
Gambar 1. Alur bertamu antar kelompok
Instrumen yang digunakan peneliti untuk mengambil data adalah soal tes kemampuan komunikasi matematis, lembar angket respon siswa, dan lembar observasi keterlaksanaan pembelajaran.
Pengkategorian untuk hasil tes komunikasi matematis dan angket respon siswa adalah berdasarkan tabel 1 berikut.
Tabel 1. Pengkategorian Hasil Tes Komunikasi Matematis
dan Respon Siswa Persentase Skor yang Diperoleh (P) Kategori 85% ≤ P ≤ 100 % Sangat Baik 70% ≤ P ≤ 84,99 % Baik 55% ≤ P ≤ 69,99% Cukup 40 % ≤ P ≤ 54,99% Kurang 0% ≤ P ≤ 39,99% Sangat Kurang
Indikator yang digunakan untuk menilai keberhasilan tindakan pada penelitian ini adalah sebagai berikut:
1. Pemberian tindakan pada siklus I dikatakan berhasil meningkatkan
kemampuan komunikasi
matematis jika siswa yang mengalami peningkatan kategori dari sebelum pemberian tindakan sampai akhir siklus I setiap indikator ada sebanyak minimal 65%. Dengan demikian, pemberian tindakan pada siklus I dikatakan belum berhasil meningkatkan kemampuan komunikasi matematis jika terdapat suatu indikator, dimana
siswa yang mengalami
ISSN : xxxxxxxxxxx sebelum pemberian tindakan
sampai akhir siklus I pada indikator tersebut kurang dari 65%.
2. Hasil persentase jumlah skor angket respon siswa terhadap pembelajaran matematika dengan menggunakan model TS-TS pada siklus I mencapai kategori baik.
Jika penelitian belum mencapai indikator keberhasilan pada siklus I maka penelitian dilanjutkan ke siklus II dengan indikator keberhasilan sebagai berikut:
1. Pemberian tindakan pada siklus
II dikatakan berhasil
meningkatkan kemampuan
komunikasi matematis jika siswa yang mengalami peningkatan kategori dari akhir siklus I sampai akhir siklus II setiap indikator ada sebanyak minimal 75% siswa. Dengan demikian, pemberian tindakan pada siklus II dikatakan belum berhasil
meningkatkan kemampuan
komunikasi matematis jika terdapat suatu indikator, dimana
siswa yang mengalami
peningkatan kategori dari akhir siklus I sampai akhir siklus II pada indikator tersebut kurang dari 75%.
2. Hasil persentase jumlah skor angket respon siswa terhadap pembelajaran matematika dengan menggunakan model TS-TS pada siklus II mencapai kategori baik.
B. Hasil Penelitian dan Pembahasan
Hasil analisis tes kemampuan komunikasi matematis pada siklus I disajikan dalam tabel 2 berikut.
Tabel 2. Persentase Jumlah Skor untuk Setiap Indikator Kemampuan Komunikasi Matematis dari Hasil Tes Siklus I
No. Indikator Persen
tase Kategori 1. Menggunakan simbol, rumus matematis, tabel, diagram, ilustrasi, atau media lain dengan jelas dan tepat. 56,89 Cukup 2. Memberikan alasan rasional terhadap suatu pernyataan matematika. 67,59 Cukup 3. Menjelaskan langkah-langkah hasil kerja atau hasil dari penyelesaian masalah matematika dengan logis, sistematis, jelas, dan tepat.
38,62 Sangat Kurang
Dalam Tabel 2 dapat diketahui bahwa kemampuan komunikasi matematis siswa kelas XI IPA 1 SMA N 1 Pleret Bantul pada pembelajaran siklus I masih belum
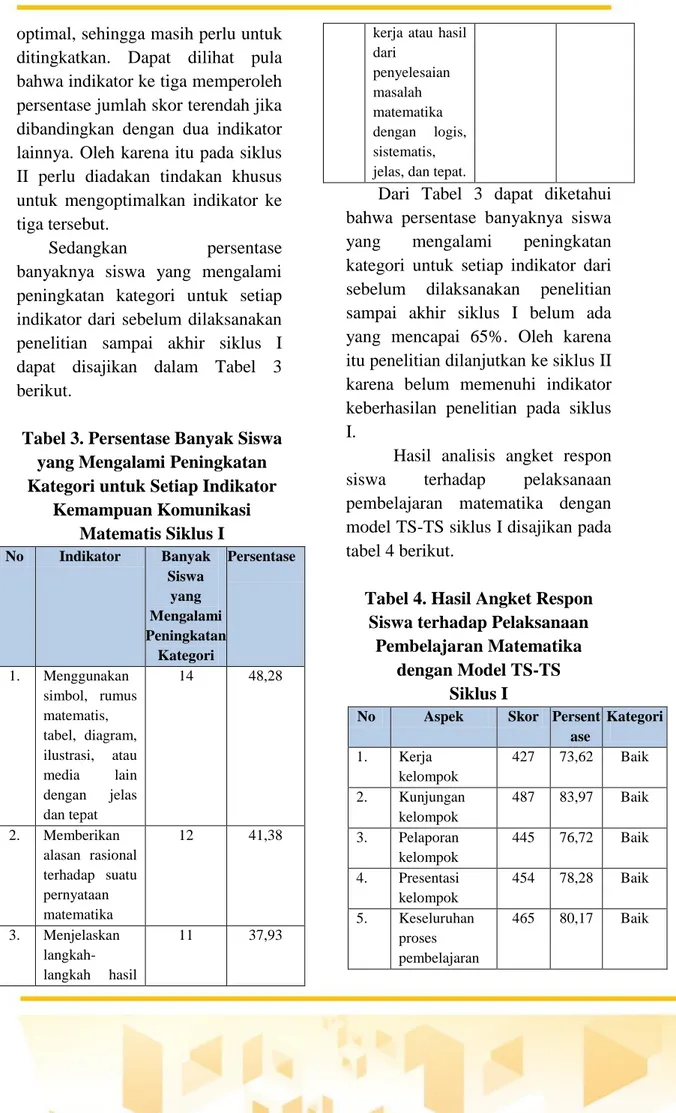
Volume I , Intersections Journal optimal, sehingga masih perlu untuk ditingkatkan. Dapat dilihat pula bahwa indikator ke tiga memperoleh persentase jumlah skor terendah jika dibandingkan dengan dua indikator lainnya. Oleh karena itu pada siklus II perlu diadakan tindakan khusus untuk mengoptimalkan indikator ke tiga tersebut.
Sedangkan persentase
banyaknya siswa yang mengalami peningkatan kategori untuk setiap indikator dari sebelum dilaksanakan penelitian sampai akhir siklus I dapat disajikan dalam Tabel 3 berikut.
Tabel 3.Persentase Banyak Siswa yang Mengalami Peningkatan Kategori untuk Setiap Indikator
Kemampuan Komunikasi Matematis Siklus I No Indikator Banyak Siswa yang Mengalami Peningkatan Kategori Persentase 1. Menggunakan simbol, rumus matematis, tabel, diagram, ilustrasi, atau media lain dengan jelas dan tepat 14 48,28 2. Memberikan alasan rasional terhadap suatu pernyataan matematika 12 41,38 3. Menjelaskan langkah-langkah hasil 11 37,93
kerja atau hasil dari penyelesaian masalah matematika dengan logis, sistematis, jelas, dan tepat.
Dari Tabel 3 dapat diketahui bahwa persentase banyaknya siswa yang mengalami peningkatan kategori untuk setiap indikator dari sebelum dilaksanakan penelitian sampai akhir siklus I belum ada yang mencapai 65%. Oleh karena itu penelitian dilanjutkan ke siklus II karena belum memenuhi indikator keberhasilan penelitian pada siklus I.
Hasil analisis angket respon siswa terhadap pelaksanaan pembelajaran matematika dengan model TS-TS siklus I disajikan pada tabel 4 berikut.
Tabel 4. Hasil Angket Respon Siswa terhadap Pelaksanaan
Pembelajaran Matematika dengan Model TS-TS
Siklus I
No Aspek Skor Persent
ase Kategori 1. Kerja kelompok 427 73,62 Baik 2. Kunjungan kelompok 487 83,97 Baik 3. Pelaporan kelompok 445 76,72 Baik 4. Presentasi kelompok 454 78,28 Baik 5. Keseluruhan proses pembelajaran 465 80,17 Baik
ISSN : xxxxxxxxxxx
Total Skor Angket Respon Siswa Siklus I
2278 78,55 Baik
Dari tabel 4 dapat diketahui bahwa persentase respon siswa terhadap pelaksanaan pembelajaran matematika dengan model TS-TS siklus I untuk semua aspeknya berada pada kategori baik.
Sesuai hasil penelitian pada siklus I, secara umum pelaksanaan pembelajaran dengan model TS-TS (Two Stay-Two Stray) di kelas XI IPA 1 SMA N 1 Pleret Bantul sudah berjalan baik namun belum seluruhnya optimal dan belum mencapai indikator keberhasilan disebabkan beberapa hal. Berikut adalah beberapa permasalahan yang muncul:
1) Pengaturan waktu untuk setiap sesi pembelajaran kurang baik. 2) Beberapa siswa dalam anggota
kelompok belajar masih sering menggunakan kesempatan diskusi untuk bercanda dengan teman lainnya. Ada juga yang mengganggu anggota kelompok lain saat berdiskusi. Perhatian
siswa saat mengikuti
pembelajaran belum begitu fokus.
3) Masih banyak siswa yang kurang bertanggung jawab dalam menjalankan perannya sebagai siswa tamu maupun siswa tuan rumah.
4) Untuk indikator pertama
kemampuan komunikasi
matematis yaitu menggunakan
simbol, rumus matematis, tabel, diagram, ilustrasi, atau media lain dengan jelas dan tepat masih dalam kategori sedang. Untuk indikator ke dua kemampuan komunikasi matematis yaitu memberikan alasan rasional terhadap suatu pernyataan matematika dalam kategori tinggi. Tetapi dalam kenyataannya siswa masih merasa kesulitan dalam merangkai kalimat untuk menyatakan alasan terhadap suatu pernyataan matematika. Sedangkan untuk indikator ke tiga yaitu menjelaskan langkah-langkah hasil kerja atau hasil dari penyelesaian masalah matematika dengan logis, sistematis, jelas, dan tepat masih dalam kategori sedang. Siswa hanya menyelesaikan soal secara langsung tanpa menuliskan penjelasan mengenai langkah-langkah dalam menyelesaikan soal tersebut.
Oleh karena itu, untuk mengatasi beberapa permasalahan yang muncul pada siklus I, direkomendasikan pada siklus II untuk diberikan perlakuan yang berbeda guna menyempurnakan tindakan. Berikut adalah beberapa rekomendasi yang dilakukan:
1) Menggunakan waktu secara efektif dengan cara mengatur kelancaran setiap sesi proses pembelajaran. Selain itu sebelum pembelajaran dimulai
Volume I , Intersections Journal siswa diminta menempatkan diri pada kelompok masing-masing. LKS juga telah dibagikan sebelum pembelajaran dimulai. 2) Pada siklus II, untuk mengatasi
siswa yang terlihat ramai, tidak ikut diskusi dan tidak ikut mengerjakan LKS di dalam kelompok belajarnya, ataupun yang mengganggu teman yang lain akan langsung ditunjuk untuk maju menampilkan hasil diskusi.
3) Guru menjelaskan ulang mengenai tugas atau peran siswa beserta langkah-langkah dalam model pembelajaran TS-TS. 4) Peneliti membenahi dan
memodifikasi LKS siklus II dengan memberikan tambahan petunjuk dalam langkah-langkah penyelesaian soal. Siswa dilatih untuk menjelaskan langkah-langkah hasil kerja atau hasil dari penyelesaian masalah matematika dengan logis, sistematis, jelas, dan tepat.
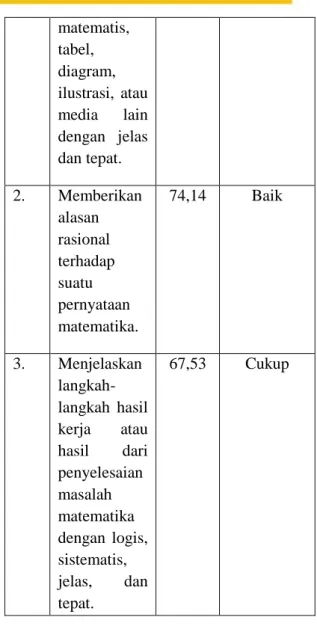
Setelah dilaksanakan pembelajaran siklus II, berikut tabel hasil tes kemampuan komunikasi matematis.
Tabel 5. Persentase Jumlah Skor untuk Setiap Indikator Kemampuan Komunikasi Matematis dari Hasil Tes Siklus II No. Indikator Perse
ntase Kategori 1. Menggunaka n simbol, rumus 93,10 Sangat Baik matematis, tabel, diagram, ilustrasi, atau media lain dengan jelas dan tepat. 2. Memberikan alasan rasional terhadap suatu pernyataan matematika. 74,14 Baik 3. Menjelaskan langkah-langkah hasil kerja atau hasil dari penyelesaian masalah matematika dengan logis, sistematis, jelas, dan tepat. 67,53 Cukup Sedangkan persentase banyaknya siswa yang mengalami peningkatan kategori persentase
jumlah skor kemampuan
komunikasi matematis untuk setiap indikator dari siklus I sampai akhir siklus II dapat disajikan dalam Tabel 6 berikut.
Tabel 6.Persentase Banyak Siswa yang Mengalami Peningkatan
Kategori Skor Kemampuan Komunikasi Matematis Siklus II
ISSN : xxxxxxxxxxx No Indikator Banyak Siswa yang Mengalami Peningkatan Kategori Persen tase 1. Menggunakan simbol, rumus matematis, tabel, diagram, ilustrasi, atau media lain dengan jelas dan tepat 27 93,10 2. Memberikan alasan rasional terhadap suatu pernyataan matematika 22 75,86 3. Menjelaskan langkah-langkah hasil kerja atau
hasil dari
penyelesaian masalah
matematika dengan logis, sistematis, jelas, dan tepat.
23 79,31
Dari Tabel 6 dapat diketahui bahwa persentase banyaknya siswa yang mengalami peningkatan kategori persentase jumlah skor kemampuan komunikasi matemati untuk setiap indikator dari siklus I sampai akhir siklus II telah mencapai lebih dari 75%. Hal ini menunjukkan bahwa indikator keberhasilan penelitian pada siklus II telah terpenuhi.
Hasil analisis angket respon siswa terhadap pelaksanaan pembelajaran matematika dengan model TS-TS siklus II disajikan pada tabel 7 berikut.
Tabel 7. Hasil Angket Respon Siswa terhadap Pelaksanaan
Pembelajaran Matematika dengan Model TS-TS Siklus II No Aspek Sko r Persentas e Katego ri 1. Kerja Kelompok 446 76,89 Baik 2. Kunjunga n kelompok 508 87,59 Baik 3. Pelaporan kelompok 475 81,89 Baik 4. Presentasi kelompok 483 83,28 Baik 5. Keseluruh an proses pembelaja ran 491 84,66 Baik Total Skor Angket Respon Siswa Siklus I 240 3 82,86 Baik
Dari tabel 7 tersebut dapat diketahui bahwa persentase respon siswa terhadap pelaksanaan pembelajaran matematika dengan model TS-TS siklus I untuk semua aspeknya berada pada kategori baik.
Berdasarkan deskripsi hasil pelaksanaan penelitian tindakan kelas pada siklus I, kemampuan komunikasi matematis siswa belum optimal. Hal tersebut dapat diketahui dari hasil kerja kelompok untuk menyelesaikan LKS, bahwa siswa belum mampu sepenuhnya mengerjakan sesuai dengan indikator kemampuan komunikasi matematis yang telah ditentukan.
Volume I , Intersections Journal Pada aktivitas kerja kelompok yang merupakan bagian dari tahapan model pembelajaran TS-TS (Agus Suprijono, 2009: 93-94), banyak siswa pasif dan tidak mau ikut berpartisipasi dalam mengerjakan LKS. Padahal menurut Wina Sanjaya (2009: 246) partisipasi dan komunikasi merupakan prinsip dari model pembelajaran kooperatif. Dengan berkomunikasi dan bertukar ide diharapkan siswa mampu mengoptimalkan kemampuan komunikasi matematis. Hal ini juga sesuai dengan pendapat Robert E. Slavin (1995: 5) yang menyatakan bahwa “cooperative learning methods share the idea that students work together to learn and are responsible for their teammates
learning as well as their own”.
Dalam kerja kelompok ini siswa belum mampu dan masih
merasa kesulitan dalam
menggunakan simbol, rumus matematis, tabel, diagram, ilustrasi, atau media lain dengan benar. Seperti dalam mengerjakan LKS 1, siswa merasa kesulitan dalam menggambarkan fungsi ke dalam bentuk diagram Venn. Ketika diminta menggambarkan contoh lain mengenai fungsi yang injektif, surjektif, dan bijektif kedalam bentuk diagram Venn, masih banyak siswa yang bingung dan menanyakan kepada guru. Guru memberikan arahan dan bimbingan agar siswa mampu untuk menggunakan simbol, rumus
matematis, tabel, diagram, ilustrasi, atau media lain dengan benar.
Siswa juga mengalami kesulitan dalam memberikan alasan rasional terhadap suatu pernyataan matematika. Misalnya pada LKS 1, siswa masih kesulitan dalam menuliskan alasan mengenai mengapa relasi pada soal tersebut disebut fungsi. Begitu juga pada LKS 2, siswa menyelesaikan soal tersebut secara langsung tanpa mengungkapkan alasannya. Sebagian besar siswa masih belum percaya diri untuk menyampaikan ide atau gagasannya terkait alasan secara tertulis, namun guru memaklumi hal ini dan selalu berusaha memotivasi siswa untuk bisa lebih percaya diri dalam menyampaikan ide atau gagasannya. Pada tahap kunjungan kelompok yang merupakan tahapan dalam pembelajaran dengan model TS-TS (Agus Suprijono, 2012: 93), kurang sekali interaksi dari siswa tamu dan siswa tuan rumah sehingga menyebabkan siswa tamu tidak dapat menjelaskan langkah-langkah penyelesaian yang digunakan ke kelompok asalnya. Hal ini dapat mengakibatkan salah satu indikator kemampuan komunikasi matematis yaitu menjelaskan langkah-langkah hasil kerja atau hasil dari penyelesaian masalah matematika dengan logis, sistematis, jelas, dan tepat menjadi kurang optimal. Sesuai dengan pendapat Anita Lie (2004: 61) bahwa model
ISSN : xxxxxxxxxxx pembelajaran TS-TS memberikan
kesempatan kepada kelompok untuk membagikan hasil dan informasi kepada kelompok lain. Dalam aktivitas ini siswa dituntut untuk mampu menjelaskan menjelaskan langkah-langkah hasil kerja atau hasil dari penyelesaian masalah matematika dengan logis, sistematis, jelas, dan tepat. Gambar 2 berikut merupakan diagram peningkatan persentase kemampuan komunikasi matematis setiap indikator dari siklus I sampai dengan siklus II.
Gambar 2 . Diagram Persentase Indikator Kemampuan
Komunikasi Matematis Siswa Dari diagram di atas dapat diketahui bahwa indikator ke tiga yaitu menjelaskan langkah-langkah hasil kerja atau hasil dari penyelesaian masalah matematika dengan logis, sistematis, jelas, dan tepat memperoleh persentase yang paling kecil dibandingkan
persentase indikator kemampuan komunikasi matematis yang lain. Kecilnya persentase untuk indikator ke tiga mungkin disebabkan karena siswa belum terbiasa menjelaskan
langkah-langkah dalam
menyelesaikan suatu masalah dalam LKS. Siswa terbiasa mengerjakan soal secara langsung sehingga kurang begitu memahami makna dari langkah-langkah penyelesaian soal tersebut.
Pada pembelajaran siklus II, peneliti memberikan LKS yang didalamnya terdapat petunjuk mengenai langkah penyelesaian soal dan contoh dalam menyelesaikan soal. Petunjuk dan contoh tersebut diharapkan dapat membantu siswa dalam mengoptimalkan kemampuan komunikasi matematisnya.
Kegiatan pembelajaran pada siklus II berjalan lebih lancar daripada siklus I. Siswa mulai aktif dalam berdiskusi dan berinteraksi untuk bertukar ide satu sama lain. Siswa sudah mulai mampu menggunakan menggunakan simbol, rumus matematis, tabel, diagram, ilustrasi, atau media lain dengan benar. Setelah siswa diberi LKS dengan tambahan petunjuk mengenai langkah-langkah penyelesaian soal beserta contoh penyelesaian soal, kemampuan siswa dalam memberikan alasan rasional terhadap suatu pernyataan matematika dan kemampuan dalam menjelaskan langkah-langkah hasil kerja atau hasil dari penyelesaian Persentase Kemampuan Komunikasi
Volume I , Intersections Journal masalah matematika menjadi lebih baik.
Kunjungan kelompok pada pembelajaran siklus II pada umumnya berjalan dengan tertib dan lancar. Hal ini karena guru telah menegaskan tugas dari siswa tamu dan siswa tuan rumah dalam tahapan kunjungan kelompok. Siswa tuan rumah menjelaskan kepada siswa tamu mengenai langkah-langkah penyelesaian soal yang sebelumnya telah didiskusikan dengan kelompoknya. Dengan penjelasan tersebut siswa tamu dapat memahami langkah-langkah yang digunakan kelompok yang dikunjunginya. Oleh karena itu siswa tamu dapat menjelaskan hasil dari bertamunya tersebut kepada siswa lain dalam kelompoknya ketika tahap pelaporan kelompok. Hal ini telah membantu siswa untuk mengoptimalkan kemampuan komunikasi matematis.
Hal tersebut diperkuat dengan hasil analisis tes akhir siklus II. Dari hasil tes akhir siklus II menunjukkan bahwa kemampuan komunikasi matematis siswa meningkat jika dibandingkan dengan hasil tes siklus I. Hasil tes siklus II juga menunjukkan bahwa persentase banyaknya siswa yang mengalami peningkatan kategori skor kemampuan komunikasi matematis telah memenuhi indikator keberhasilan dalam penelitian ini.
Berdasarkan hasil yang diperoleh dari tes kemampuan komunikasi
matematis akhir siklus II, peneliti dapat menyimpulkan bahwa kemampuan komunikasi matematis siswa kelas XI IPA 1 SMA N 1 Pleret Bantul dalam pembelajaran matematika dengan model TS-TS mengalami peningkatan.
C. Kesimpulan dan Saran 1. Kesimpulan
Berdasarkan hasil penelitian dan pembahasan pada penelitian tentang implementasi model pembelajaran TS-TS untuk
meningkatkan kemampuan
komunikasi matematis siswa kelas XI IPA 1 SMA N 1 Pleret Bantul, dapat disimpulkan bahwa:
a. Kemampuan komunikasi
matematis siswa kelas XI IPA 1 SMA N 1 Pleret Bantul meningkat setelah diterapkan model pembelajaran TS-TS. Penjabarannya adalah sebagai berikut:
1) Ada peningkatan kemampuan komunikasi matematis siswa kelas XI IPA 1 SMA N 1 Pleret Bantul setelah mengikuti pembelajaran dengan model TS-TS.
2) Persentase banyaknya siswa yang mengalami peningkatan kategori dari sebelum dilaksanakan tindakan sampai dengan akhir siklus I untuk indikator pertama yaitu kemampuan menggunakan simbol, rumus matematis, tabel, diagram, ilustrasi, atau
ISSN : xxxxxxxxxxx media lain dengan jelas dan
tepat sebesar 48,28%, untuk indikator ke dua yaitu kemampuan memberikan alasan rasional terhadap suatu pernyataan matematika pada sebesar 41,38%, dan untuk indikator ke tiga yaitu kemampuan menjelaskan langkah-langkah hasil kerja atau hasil dari penyelesaian masalah matematika dengan logis, sistematis, jelas, dan tepat sebesar 37,93%. Sedangkan persentase banyaknya siswa yang mengalami peningkatan kategori dari akhir siklus I sampai dengan akhir siklus II untuk indikator pertama sebesar 93,10%, untuk indikator ke dua sebesar 75,86% dan untuk indikator ke tiga sebesar 79,31%. b. Siswa memberikan respon positif
terhadap pelaksanaan
pembelajaran matematika dengan model TS-TS. Persentase jumlah skor respon siswa kelas XI IPA 1 SMA N 1 Pleret Bantul terhadap pelaksanaan pembelajaran dengan model TS-TS siklus I berada dalam kategori baik yaitu 78,55%. Sedangkan untuk siklus II persentase jumlah skor respon siswa kelas XI IPA 1 SMA N 1 Pleret Bantul terhadap pelaksanaan pembelajaran dengan model TS-TS sebesar 82,86% atau dalam kategori baik.
2. Saran
Beberapa saran yang perlu dipertimbangkan dalam pelaksanaan pembelajaran dengan model TS-TS untuk meningkatkan kemampuan komunikasi matematis siswa antara lain:
a. Alokasi waktu kerja kelompok dan kunjungan kelompok perlu ditegaskan kepada siswa agar setiap tahap pembelajaran dapat terlaksana dengan baik dan tidak mengalami kekurangan waktu diakhir pembelajaran.
b. Tugas dan peran masing-masing siswa perlu ditegaskan agar siswa dapat bertanggung jawab menjalankan tugas dan perannya baik sebagai siswa tamu maupun sebagai siswa tuan rumah. c. LKS yang dibuat sebaiknya
disertai petunjuk mengenai langkah-langkah penyelesaian soal, hal ini bertujuan untuk memfasilitasi siswa untuk mengoptimalkan kemampuan komunikasi matematisnya.
D. Daftar Pustaka
Agus Suprijono. (2009). Cooperative Learning Teori dan Aplikasi PAIKEM. Yogyakarta: Pustaka Pelajar.
Anita Lie. (2004). Cooperative Learning: Mempraktikkan Cooperative Learning di Ruang-Ruang Kelas. Jakarta: PT Grasindo.
Volume I , Intersections Journal
Bistari. (2010). Pengembangan Kemandirian Belajar Berbasis Nilai untuk Meningkatkan Komunikasi Matematik. Jurnal Pendidikan Matematika (Nomor 1 tahun 2010). Hlm. 12 Depdiknas. (2006). Peraturan Pemerintah No.22 Tahun 2006 tentang Standar Kompetensi dan Kompetensi Dasar. Jakarta: Depdiknas
Slavin, R.E. (1995). Cooperative Learning: Theory, Research, and Practice. Massachusetts: Allyn and Bacon Publisher.
Wina Sanjaya. (2009). Strategi Pembelajaran Berorientasi Standar Proses Pendidikan. Jakarta: Kencana Prenada
METODE PEMBUKTIAN MATEMATIKA
Toto Hermawan
ABSTRAK
Persepsi bahwa matematika identik dengan angka-angka dan operasi hitung (tambah, kali, bagi,kurang, pangkat, dll) tidak selamanya benar. Matematika berhubungan juga dengan penalaran karena matematika merupakan hasil abstraksi (pemikiran) manusia terhadap objek-objek sekitar.Di dalam matematika, bukti adalah serangkaian argumen logis yang menjelaskan kebenaran suatu pernyataan. Argumen-argumen ini dapat berasal dari premis pernyataan itu sendiri, teorema-teorema lainnya, definisi, dan akhirnya dapat berasal dari postulat dimana sistem matematika tersebut berasal. Yang dimaksud logis di sini, adalah semua langkah pada setiap argumen harus dijustifikasi oleh langkah sebelumnya. Jadi kebenaran semua premis pada setiap deduksi sudah dibuktikan atau diberikan sebagai asumsi. Pada tulisan sederhana ini dibahas sekilas tentang bukti dalam matematika dan beberapa metoda pembuktiannya.
Kata kunci:Abstraksi, Argumen Logis, Bandwidth, Postulat, Teorema, Difinisi, Dan Pembuktian.
PENDAHULUAN
Matematika sebagai ilmu dasar (basic science) . Teori-teori yang ada di dalam matematika digunakan sebagai landasan untuk pengembangan ilmu terapan dan teknologi. Selain itu, Matematika sebagai ilmu pengetahuan dengan penalaran deduktif mengandalkan logika dalam meyakinkan akan kebenaran suatu pernyataan. Faktor intuisi dan pola berpikir induktif banyak berperan pada proses awal dalam merumuskan suatu konjektur (conjecture) yaitu dugaan awal dalam matematika. Proses penemuan dalam matematika dimulai dengan pencarian pola dan struktur, contoh
kasus dan objek matematika lainnya. Selanjutnya, semua informasi dan fakta yang terkumpul secara individual ini dibangun suatu koherensi untuk kemudian disusun suatu konjektur. Setelah konjektur dapat dibuktikan kebenarannya atau ketidakbenaranya maka selanjutnya ia menjadi suatu teorema.
Pernyataan-pernyataan
matematika seperti definisi, teorema dan pernyataan lainnya pada umumnya berbentuk kalimat logika, dapat berupa implikasi, biimplikasi, negasi, atau berupa kalimat berkuantor. Operator logika seperti and, or, not, xor juga sering termuat dalam suatu pernyataan matematika.
Daftar Pustaka
Jadi membuktikan kebenaran suatu teorema tidak lain adalah membuktikan kebenaran suatu kalimat logika.
Materi logika sudah diberikan sejak diSMA. Namun selama ini, sebagian siswa atau guru masih menganggap logika sebagai materi hapalan, khususnya menghapal tabel kebenaran. Belum tahu mengapa dan untuk apa logika dipelajari. Tanpa menguasai logika maka sulit untuk terbentuknya apa yang disebut dengan logically thinking. Apa yang terbentuk pada siswa, mahasiswa, guru atau bahkan dosen selama ini lebih dominan pada algorithm thinking atau berpikir secara algoritma. Cara berpikir algoritmis dalam belajar matematika ini lebih ditekankan pada memahami langkah-langkah dalam menyelesaikan suatu soal, tanpa melihat lebih dalam mengapa langkah-langkah tersebut dapat dilakukan. Bila pendekatan ini mendominasi dalam pembelajaran matematika, misalnya di sekolah menengah maka akibatnya siswa akan menjadi ”robot matematika”. Mereka mampu dan cepat menyelesaikan soal yang mirip (similar) dengan contoh sebelumnya, tetapi tidak berkutik bilamana soal tersebut dimodifikasi sedikit, sehingga tidak tampak secara kasat mata kemiripannya dengan soal yang sudah ada, walaupun sesungguhnya materinya tetap sama.
Pada tahap awal, pekerjaan memahami bukti bukanlah sesuatu
yang menarik karena kita lebih banyak bergelut dengan simbol dan pernyataan logika ketimbang berhadapan dengan angka-angka yang biasanya dianggap sebagai karakter matematika. Kenyataan inilah menjadikan salah satu alasan orang malas untuk memahami bukti dalam matematika. Alasan lainnya adalah pekerjaan membuktikan lebih sulit dan tidak penting. Padahal banyak manfaat yang dapat diperoleh pada pengalaman membuktikan ini, salah satunya adalah melatih logically thinking dalam belajar matematika.
Secara rinci mengenai bukti dalam matematika meliputi what is proof, why do we prove, what do we prove, dan how do we prove. Dari pernyataan diatas paling tidak terdapat enam motivasi mengapa orang membuktikan, yaitu to establish a fact with certainty, to gain understanding, to communicate an idea to others, for the challenge, to create something beautiful, to construct a large mathematical theory.
To establish a fact with certainty merupakan motivasi paling dasar mengapa orang perlu membuktikan suatu pernyataan matematika, yaitu untuk meyakinkan bahwa apa yang selama ini dianggap benar adalah memang benar. Tidak dapat dipungkiri selama ini banyak kebenaran fakta di dalam matematika hanya dipercaya begitu saja tanpa adanya kecurigaan terhadap
ISSN : xxxxxxxxxxx kebenaran tersebut, tidak berusaha
membuktikan sendiri, termasuk fakta-fakta yang sangat sederhana. Kita hanya menggunakan fakta tersebut karena sudah ada dalam buku (it was in the text), atau karena sudah pernah disampaikan oleh guru kita.
Banyak pembuktian yang tidak hanya membuktikan suatu fakta tetapi juga memberikan penjelasan tentang fakta tersebut. Disinilah, pembuktian teorema berfungsi untuk mendapatkan pemahaman (to gain understanding).
PERNYATAAN DALAM
MATEMATIKA DAN
PEMBUKTIAN-NYA Definisi
adalah kesepakatan bersama mengenai pengertian atau batasan suatu istilah. Misalnya bilangan prima adalah bilangan lebih besar dari 1 yang tidak mempunyai faktor selain dari 1 dan dirinya sendiri.
Teorema
adalah pernyataan yang
kebenarannya dapat
dibuktikan. Teorema dapat berupa kalimat berkuantor yang memuat konektivitas dengan satu atau beberapa premis dan satu konklusi. Teorema Pythagoras: Jika ABC segitiga siku-siku dengan sudut siku-siku di B
maka berlaku AB2 + BC2 = AC2.
Proposisi merupakan teorema kecil dimana tingkat signi_kansinya lebih rendah dari Teorema.
Contoh:
“perkalian antara dua bilangan ganjil menghasilkan sebuah bilangan ganjil”. Fakta kadang digunakan
untuk menyatakan Teorema atau Proposisi tetapi kebenarannya dapat dipahami langsung dan mudah. Contoh: “2 adalah satu-satunya bilangan genap yang sekaligus prima”.
Pembuktian (proof )
adalah serangkaian argumen logis yang menjelaskan kebenaran suatu pernyataan.
Aksioma atau postulat adalah pernyataan yang menjadi asumsi dasar dalam penyusunan suatu konsep dalam matematika. Aksioma biasa digunakan untuk membangun de_nisi, atau
untuk membuktikan
Teorema. Contoh:
“melalui dua titik berlainan dapat dibuat sebuah garis” Lemma
adalah teorema “ kecil “ yang biasanya digunakan untuk membuktikan Teorema. Akibat (collorary) merupakan fakta yang diturunkan
Daftar Pustaka
langsung dari Teorema dimana kebenarannya dapat dibuktikan dari Teorema langsung.
Contoh:
“jika salah satu sisi pada segitiga siku-siku adalah ganjil maka terdapat satu lagi sisinya yang juga ganjil”. (Akibat dari teorema Pythagoras).
Konjektur adalah pernyataan
yang diduga benar
berdasarkan data empiris (evidence), argumen heuristik, atau intuisi para ahli; tetapi belum berdasarkan argumen valid. Bila konjektur dapat dibuktikan dengan argmen yang valid maka ia berubah menjadi Teorema atau proposisi. SKEMA PERNYATAAN DALAM MATEMATIKA METODE PEMBUKTIAN MATEMATIKA
Definisi memainkan peranan penting di dalam matematika. Topik-topik baru matematika selalu diawali
dengan membuat definisi baru. Sebagai contoh, teori fungsi kompleks diawali dengan mendefinisikan bilangan imajiner i, yaitu i2 = -1. Berangkat dari definisi
dihasilkan sejumlah teorema beserta akibat-akibatnya. Teorema-teorema inilah yang perlu dibuktikan. Pada kasus sederhana, kadangkala teorema pada suatu buku ditetapkan sebagai definisi pada buku yang lain, begitu juga sebaliknya. Selanjutnya, untuk memahami materi selanjutnya dibutuhkan prasyarat pengetahuan logika matematika.
1. Pembuktian Langsung
Bukti langsung ini biasanya diterapkan untuk membuktikan teorema yang berbentuk implikasi pq. Di sini p sebagai hipotesis digunakan sebagai fakta yang diketahui atau sebagai asumsi.
Selanjutnya, dengan
menggunakan p kita harus menunjukkan berlaku q. Secara logika pembuktian langsung ini
ekuivalen dengan
membuktikan bahwa
pernyataan pq benar dimana diketahui p benar.
Contoh
“ Jika diketahui n adalah ganjil, maka buktikan bahwa n2 adalah ganjil.”
Bukti :
Diketahui n adalah ganjil,
artinya terdapat suatu bilangan bulat k sehingga n = 2k + 1.
ISSN : xxxxxxxxxxx Akan ditunjukkan bahwa n2
ganjil. n2 = (2k + 1)2 = 4k2 + 4k + 1 = 2(2k2 + 2k) +1. Perhatikan bahwa n2 = 2(2k2 + 2k) +1. Karena k adalah bilangan bulat, maka (2k2 + 2k) juga pasti bilangan bulat, sehingga n2
adalah ganjil.
2. Pembuktian tak langsung Kita tahu bahwa nilai kebenaran suatu implikasi pq ekuivalen dengan nilai kebenaran kontraposisinya ~q~ p. Jadi pekerjaan membuktikan kebenaran pernyataan implikasi dibuktikan lewat kontraposisinya. Contoh
“Buktikan, jika x2 bilangan ganjil maka x bilangan ganjil. “
Bukti.
Pernyataan ini sangat sulit dibuktikan secara langsung. Mari kita coba saja. Karena x2 ganjil maka dapat ditulis x = 2m + 1 untuk suatu bilangan asli m. Selanjutnya
2 1
x m tidak dapat disimpulkan apakah ia ganjil atau tidak. Sehingga bukti langsung tidak dapat digunakan. Kontraposisi dari pernyataan ini adalah
”Jika x genap maka x2
genap”.
Selanjutnya diterapkan bukti
langsung pada
kontraposisinya. Diketahui x genap, jadi dapat ditulis x=2n untuk suatu bilangan bulat n. Selanjutnya,
x2 = (2n)2 = 2 (2n2) = 2m yang merupakan bilangan genap.
3. Bukti Kosong
Bila hipotesis p pada implikasi pq sudah bernilai salah maka implikasi pq selalu benar apapun nilai kebenaran dari q. Jadi jika kita dapat menunjukkan bahwa p salah maka kita telah berhasil membuktikan kebenaran
pq.
Contoh
Didalam teori himpunan kita mengenal definisi berikut : Diberikan dua himpunan A dan B. Himpunan A dikatakan himpunan bagian dari B, ditulis AB jika pernyataan berikut dipenuhi : ”jika xA maka xB”. Suatu himpunan dikatakan himpunan kosong jika ia tidak mempunyai anggota.
“Buktikan, himpunan
kosong merupakan himpunan bagian dari himpunan
apapun.” Bukti.
Misalkan A
suatu himpunan kosong dan B himpunan sebarang. Kita akan cDaftar Pustaka
tunjukkan bahwa pernyataan ”jika xA maka xB” bernilai benar. Karena A himpunan kosong maka pernyataan p yaitu xA selalu bernilai salah karena tidak mungkin ada x yang menjadi anggota himpunan kosong. Karena p salah maka terbuktilah kebenaran pernyataan ” xA maka xB”, yaitu AB. Karena B sebarang maka bukti selesai. 4. Bukti Trivial
Bila pada implikasi pq, dapat ditunjukkan bahwa q benar maka implikasi ini selalu bernilai benar apapun nilai kebenaran dari p. Jadi jika kita dapat menunjukkan bahwa q benar maka kita telah berhasil membuktikan kebenaran
pq
Contoh :
Buktikan kebenaran _Jika “penguin dapat terbang maka 3 + 2 = 5”
Salah maka benar jawabannya Benar
5. Bukti dengan kontradiksi Prosedur: a. Identifikasilah konklusi sebuah proposisi. b. Andaikan konklusi tersebut salah.Temukan kontradiksi. c. Simpulkan bahwa pengandaian salah. d. Proposisi terbukti. Contoh “ Buktikan bahwa 2 bilangan irrasiona “ Bukti : Diasumsikan 2
rasional dan kemudian ditunjukkan bahwa akan terjadi kontradiksi. Sehingga
2 irasional.
Andaikan 2rasional. Maka 2dapat ditulis sebagai hasil bagi dua
bilangan bulat b a
sedemikian
hingga a dan b relatif prima.
Jika b a = 2 maka ( 2 ) b a = 2 dan a2 = 2b2 Karena 2b2 bilangan
bulat genap, maka a2 adalah genap, demikian pula a. Mengapa?
Karena a genap, maka a dapat ditulis sebagai a = 2c, c bilangan bulat. Didapat a2 = 4c2. Padahal a2 = 2b2, maka b2 = 2c2 , sehingga b2 genap, akibatnya b genap.
Karena a dan b keduanya genap, tentu mempunyai faktor persekutuan 2.
Maka didapat keadaan yang kontradiksi dengan pengandaian. Sehingga pengandaian 2 bilangan rasional tidak benar. Jadi
2 irasional. 6. Bukti ketunggalan
ISSN : xxxxxxxxxxx
Dalam membuktikan
ketunggalan, pertama harus ditunjukkan eksistensi suatu objek.
Contoh :
“Buktikan sistem persamaan 2x + y = 4 dan x - 2y = - 3 mempunyai penyelesaian tunggal. “
Buktikan
eksistensi penyelesaiannya. Dengan eliminasi misalnya, diperoleh (x=1; y=2) adalah penyelesaian. Ambil (x1, y1) sebarang penyelesaian maka haruslah memenuhi 2x1 + y1 = 4
dan x1 - 2y1 = - 3. Dengan cara
yang sama akan diperoleh x1 = x
dan y1=y. Terbukti
penyelesaiannya tunggal.
7. Bukti dengan counter example Untuk membuktikan suatu konjektur terkadang kita membutuhkan penjabaran yang cukup panjang dan sulit. Tapi bila kita dapat menemukan satu saja kasus yang tidak memenuhi konjektur tersebut maka selesailah urusannya.
Contoh :
Diberikan ruang matrik (X,d) dan 𝐴, 𝐵 ∈ 𝑋 , Buktikan A B A B tidak belaku ? Bukti: counter example (2, 3) A maka A[2, 3] (3, 4) B maka B[3, 4] {3} A B Tetapi A B 3 A B tetapi 3 A B
8. Bukti dengan induksi matematika
Misalkan 𝑃(𝑛) pernyata-an tentpernyata-ang 𝑛 dimana 𝑛 berjalan pada himpunan bil asli N atau subsetnya. Kebenaran 𝑃(𝑛) bergantung dari nilai 𝑛 yang diberikan.
PRINSIP INDUKSI: Bila S himpunan bagian dari N dengan sifat-sifat:
(i)1 ∈ 𝑆 (ii) 𝑘 ∈ 𝑆 → 𝑘 + 1 ∈ 𝑆 Maka haruslah S=N. Metode Induksi Matematika : Misalkan diberikan fungsi proposisi 𝑃(𝑛), 𝑛 ∈ 𝑁. Bila (i)P(1) Benar (ii) 𝑃(𝑘) → 𝑃(𝑘 + 1) Benar
Maka P(n) TRUE untuk setiap 𝑛 ∈ 𝑁 Contoh : Buktikan 1 + 2 + 3 + ⋯ + 𝑛 = 𝑛 2(𝑛 + 1) berlaku untuk setiap 𝑛 ∈ 𝑁. BUKTI: (i) P(1): 1 = 1 2(1 + 1) Benar (ii) Diketahui P(k) Benar, yaitu 1 +
2 + 3 + ⋯ + 𝑘 = 𝑘 2(𝑘 + 1) Diperhatikan P(k+1): 1 + 2 + 3 + ⋯ + 𝑘 ⏟ 𝑘 2(𝑘+1) + (𝑘 + 1)
Daftar Pustaka
= 𝑘
2(𝑘 + 1) + (𝑘 + 1) = 𝑘 + 1
2 (𝑘 + 2)
yakni P(k+1) Benar . Jadi P(n) berlaku untuk setiap 𝑛 ∈ 𝑁.
9. Bukti dua arah
Suatu pernyataan berupa bi-implikasi, pq. Ada dua kemungkinan bi-implikasi bernilai benar pq yaitu p benar dan q benar, atau p salah dan q salah. Dalam prakteknya, pernyataan ini terdiri dari pqdan q p.
Membuktikan kebenaran bi-implikasi pq berarti membuktikan kebenaran kedua implikasi pqdan q p.
Selanjutnya dapat
menggunakan bukti langsung, taklangsung atau mungkin dengan kontradiksi.
Contoh
Diberikan ruang metrik (X,d) dan barisan { }xn X . Barisan
{ }xn memiliki titik cluster
xX jika dan hanya jika terdapat subbarisan { } k n n x x di mana k n n x x . Bukti
()Diketahui merupakan titik cluster dari { }xn , maka untuk setiap kN bola terbuka B x( , )1
k memuat tak hingga banyak elemen
dari { }xn , Sehingga untuk setiap kN dapat dipilih
1 ( , ) { } k n n x B x x k . Akan dibuktikan{ } k n x konvergen ke x . Diperhatikan bahwa untuk setiap kN berlaku 1 ( , ) k n x B x k dengan kata lain d x x( , n) 1 k . Diambil sebarang
0, berdasar-kan Archimedes maka terdapat NN, untuk kN berlaku 1 1 k N . Dengan demikian untuk setiapkN berlaku 1 1 ( , ) k n d x x k N . Jadi untuk sebarang
0 terdapat NN , untuk setiap kN berlaku ( , nk) d x x . Kesimpulan: { } k n x konvergen ke x. ()Diketahui terdapatsub-barisan { } k n n x x di mana k n n x x . Dengan demikian untuk sebarang
0 terdapat NN , untuk kN berlaku ( , ) k n d x x . Hal ini berarti berlaku1 ( , ) k n x B x k untuk semua
ISSN : xxxxxxxxxxx
0
, bola terbuka B x( , ) memuat tak hingga banyak elemen dari {xnk}, dengan kata lain merupakan titikcluster dari { } k n x . Kesimpulan: karena { } k n n x x maka x juga merupakan titik cluster dari {xnk}.
KESIMPULAN
Persepsi bahwa matematika identik dengan angka-angka dan operasi hitung (tambah, kali, bagi,kurang, pangkat, dll) tidak selamanya benar. Matematika berhubungan juga dengan penalaran karena matematika merupakan hasil abstraksi (pemikiran) manusia terhadap objek-objek sekitar. Produk utama matematika berupa pernyataan-pernyataan berupa definisi, teorema, akibat, keonjektur, dll. Angka dan operasi aritmatika yang menyertainya merupakan produk turunan matematika. Dalam matematika kebenaran pernyataan perlu dibuktikan.
PENUTUP
Belajar matematika dengan cara memahami bukti tidaklah mudah. Dibutuhkan waktu untuk
memahami matematika sebagai bahasa logika. Juga, dibutuhkan wawasan matematika yang luas untuk belajar membuktikan fakta-fakta yang lebih rumit. Di dalam bukti termuat nilai-nilai strategis yang dapat melatih kita berpikir secara logis. Keindahan matematika juga banyak terdapat pada harmonisasi penalaran-penalaran dalam bukti. Dengan memahami bukti kita dapat mengikuti alur berpikir para ahli yang pertama kali menemukannya, yang berdampak pada kekaguman terhadap para inventor matematika dan pada akhirnya menyenangi matematika itu sendiri. Berlatih memahami bukti merupakan modal utama untuk dapat melakukan riset matematika. DAFTAR PUSTAKA
1. Bartle, Robert G and D.R. Sherbet, 1994. Introduction to real analysis, second edition, John Willey & sons, New York.
2. Royden, HL.1998. Real Analysis 3rd ed, Macmillan Publishing Company, New York
3. Sukirman.2006.Pengantar teori Bilangan. yogyakarta: Hanggar Kreator
ISSN : xxxxxxxxxxx Perubahan Pembelajaran yang Berpusat pada Guru ke Berpusat pada Siswa
Yenny Anggreini Sarumaha
Fakultas Keguruan Ilmu Pendidikan, Universitas Cokroaminoto Yogyakarta [email protected]
Abstrak
Kajian ini bertujuan untuk memaparkan dan menggali lebih dalam perubahan pembelajaran yang berpusat pada guru ke berpusat pada siswa. Dilengkapi dengan beberapa hasil-hasil penelitian yang telah dilakukan, kajian ini menjelaskan bagaimana seyogyanya pembelajaran yang berpusat pada guru dilaksanakan di kelas. Guru dituntut harus lebih kreatif dan aktif memfasilitasi siswa belajar, salah satunya dengan merancang aktivitas yang mendorong siswa untuk mengkonstruksi pengetahuan yang mereka miliki. Sedangkan siswa dihadapkan pada kontrak didaktis yang baru, diantaranya keharusan berfikir untuk diri sendiri, untuk menjelaskan dan mengklarifikasi solusi yang mereka miliki, untuk mencoba dan memahami pemahaman siswa lain, untuk bertanya tentang penjelasan yang tidak mereka pahami, dan untuk berargumen apabila mereka tidak setuju.
Kata kunci: pembelajaran berpusat pada siswa, students centered, belajar bermakna.
I. Pendahuluan
Paradigma pembelajaran matematika telah berubah dari hanya sekedar transfer ilmu dari guru ke siswa ke konstruksi pengetahuan oleh siswa sebagai pebelajar aktif. Guru tidak lagi sebagai orang yang maha tahu dan maha benar tentang berbagai hal mengenai materi yang diajarkannya. Sebaliknya, saat ini guru dituntut untuk belajar dari siswa, bagaimana mereka menyelesaikan tugas-tugas yang diberikan, bagaimana mereka bereaksi atas tugas yang diberikan
dan bagaimana interaksi mereka dengan teman maupun guru dalam menghadapi masalah yang diberikan. Jawaban-jawaban dari pertanyaan inilah yang diharapkan nantinya akan memberikan masukan dalam perbaikan pembelajaran ke depan. Sehingga metode, model ataupun pendekatan yang digunakan oleh guru dalam proses pembelajaran akan berkembang dengan lebih baik lagi.
Perubahan paradigma ini tidak bisa dilakukan dengan instan. Perlu
Daftar Pustaka
proses dan pengalaman-pengalaman yang diperuntukkan agar dapat membatu terjadinya perubahan yang dimaksud. Beberapa perubahan yang harus diperhatikan dalam mendorong terlaksananya pembelajaran yang berpusat pada guru adalah pengorganisasian kelas, pengelolaan waktu, pemanfaatan alat peraga, penggunaan konteks, dan peran guru
dalam pembelajaran.
Keseluruhannya tidak mutlak dapat berubah seklaigus dalam waktu yang cepat. Guru dapat membuat beberpa perubahan sederhana untuk mengubah iklim kelas yang terbiasa dengan metode guru sebagai tokoh utama.
Pada kenyataannya di lapangan, masih banyak guru-guru yang tetap mengguanakan teacher centered sebagai metode dalam pembelajaran. Beberapa alasan yang diberikan misalnya karena mereka telah terbiasa dengan metode tersebut sehingga tidak dapat mengubahnya, pembelajaran yang berpusat pada siswa menghabiskan waktu yang terlalu banyak untuk membahas satu materi tertentu, dan mereka belum memiliki gambaran bagaimana
pelaksanaan pembelajaran yang berpusat pada siswa serta dampak ke depannya bagu guru dan siswa tersebut. Hal ini lah yang menjadi sumber keingintahuan penulis bagaimana sebenarnya pembelajaran yang berpusat pada guru itu dilaksanakan dan apa maknanya bagi guru dan siswa. Pada kesempatan kali ini, penulis ingin mengkaji perubahan pembelajaran yang berpusat pada guru ke pembelajaran yang berpusat pada siswa.
II. Isi
Dalam kurun waktu sepuluh tahun terakhir, dunia pendidikan terutama pendidikan matematika mengalami perubahan paradigma yang ditandai dengan beralihnya makna pembelajaran dari transfer ilmu menjadi konstruksi pengetahuan (Gravemeijer, 2010). Perubahan paradigma yang bisa kita sebut dengan reformasi pendidikan matematika ini menuntut adanya budaya kelas atau norma di dalam kelas yang sangat berbeda dengan budaya sebelumnya. Guru dalam hal ini, diminta untuk membangun norma di mana diskusi kelas
ISSN : xxxxxxxxxxx termasuk di dalamnya pendugaan,
penjelasan, dan pengklarifikasian memegang peranan penting. Dengan kata lain, reformasi dalam pendidikan matematika bertujuan untuk mengganti pola pengajaran teaching by telling dengan students constructing atau penemuan kembali (Gravemeijer, 2004). Implikasinya
adalah perubahan penekanan dari semulanya pada apa yang guru lakukan menjadi penekanan pada apa yang siswa lakukan. Sejalan dengan hal tersebut, terjadi perubahan dari pembelajaran yang berpusat pada guru (teacher centered) ke pembelajaran yang berpusat pada siswa (student centered).
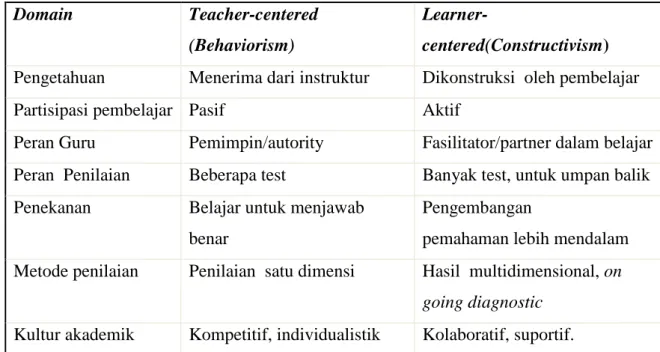
Tabel 1. Perbedaan teacher centered dan students centered.
Domain Teacher-centered
(Behaviorism)
Learner-centered(Constructivism) Pengetahuan Menerima dari instruktur Dikonstruksi oleh pembelajar
Partisipasi pembelajar Pasif Aktif
Peran Guru Pemimpin/autority Fasilitator/partner dalam belajar Peran Penilaian Beberapa test Banyak test, untuk umpan balik Penekanan Belajar untuk menjawab
benar
Pengembangan
pemahaman lebih mendalam Metode penilaian Penilaian satu dimensi Hasil multidimensional, on
going diagnostic Kultur akademik Kompetitif, individualistik Kolaboratif, suportif. Sumber : Schuman, L (1996). Perspective on instruction.
Dari Tabel 1 dapat dilihat bahwa perubahan paradigma menjadi berpusat pada guru menuntut adanya keaktifan dari siswa dalam mengikuti proses pembelajaran di kelas. Hal ini tentunya tidak lepas dari
aktivitas atau masalah yang diangkat oleh guru dalam pembelajaran dan norma-norma yang ada di kelas, terutama norma matematika sosial. Peranan guru tidak lagi sebagai sumber dari segalanya, sumber
Daftar Pustaka
dari ilmu pengetahuan. Guru dalam hal ini, dituntut harus lebih kreatif dan aktif memfasilitasi siswa belajar, salah satunya dengan merancang aktivitas yang mendorong siswa untuk mengkonstruksi pengetahuan yang mereka miliki. Selain itu, perlu diperhatikan bentuk umpan balik dari jawaban yang diberikan siswa, bagaimana guru membimbing siswa untuk menemukan kembali konsep matematika yang ada lewat masalah atau aktivitas yang disajikan.
Paradigma baru ini, ditandai dengan diterimanya pendekatan,
metode, dan model
pembelajaran baru yang
inovatif, munculnya kesadaran bahwa informasi atau pengetahuan dapat diakses lewat berbagai cara dan media oleh peserta didik, mulai diterapkannya teknologi pembelajaran berbasis teknologi informasi (TI), perubahan orientasi pendidikan tidak hanya pada pengembangan sumber daya manusia (human resources development) tetapi juga pada pengembangan kapabilitas manusia (human capability development), diperkenalkannya e-learning, dependence ke independence, individual ke team work oriented, dan large group ke small class (Das Salirawati, 2010).
Gambar 1. Keefektifan Model Pembelajaran Sumber: Edgar Dale. Audio Visual Methods in Teaching.
ISSN : xxxxxxxxxxx Gambar 1 menunjukkan dua
kelompok model pembelajaran yaitu pembelajaran pasif dan pembelajaran aktif. Gambaran tersebut juga menunjukkan bahwa kelompok pembelajaran aktif cenderung membuat siswa lebih cepat dan taham lama dalam mengingat (retention rate of knowledge) materi pembelajaran. Model pembelajaran aktif ini merupakan salah satu alternatif pembelajaran yang dapat
mendukung siswa dalam
mengkonstruksi pengetahuan.
Selain itu, terdapat beberapa model pembelajaran yang dapat digunakan, diantaranya diskusi kelompok kecil, role play and simulation, studi kasus, metode penemuan, self directed learning, collaborative learning, contextual instruction, project bases learning, problem based learning,inquiry, and solution based learning.
Implementasi perubahan paradigma pembelajaran yang berpusat pada siswa jelas memerlukan usaha yang lebih. Gravemeijer (2004) menyatakan bahwa apa yang diperlukan untuk reformasi
pendidikan matematika adalah sebuah bentuk dari desain instruksional yang mendukung berbagai instruksi guna membantu siswa mengembangkan cara berfikir mereka menjadi lebih baik dan matang dalam hal penalaran. Pada kenyataannya, siswa belum terbiasa berfikir sendiri dan berbagi pemikiran mereka dengan guru dan teman sekelas. Hal ini disebabkan masih melekatnya norma sosial di kelas pada diri siswa di mana guru selalu benar (Cobb & Yackel, 1996). Brosseau (1996) dalam Gravemeijer (2010) menyatakan secara implisit adanya kontrak didaktis. Pembelajaran yang berpusat pada siswa menghendaki adanya kontrak didaktis yang baru, diantaranya keharusan berfikir untuk diri sendiri,
untuk menjelaskan dan
mengklarifikasi solusi yang mereka miliki, untuk mencoba dan memahami pemahaman siswa lain, untuk bertanya tentang penjelasan yang tidak mereka pahami, dan untuk berargumen apabila mereka tidak setuju. Kontrak didaktis inilah yang hendaknya dinegosiasikan
Daftar Pustaka
dengan siswa. Namun,
pelaksanaannya merupakan suatu proses pembiasaan diri siswa dalam kurun waktu tertentu.
Dalam kelas matematika, norma-norma yang ada dikembangkan menjadi norma matematika sosial yang berisi cara-cara yang diharapkan dalam mengajak siswa aktif dalam diskusi matematika. Cara-cara ini tentunya memberi pengaruh pada kemampuan matematika siswa. (Kilpatrick, Swafford, dan Findell, 2001). Frye (2013) dalam penelitiannya mengungkapkan bahwa dia dan siswa di kelas menerapkan norma yang disebut persistensi dalam pembelajaran matematika. Mereka mendefinisikan persistensi sebagai bekerja untuk mengidentifikasi tahapan penyelesaian, menemukan solusi penyelesaian, bekerja dengan solusi yang mungkin untuk mengekspor metode lain yang bisa digunakan dalam menyelesaikan masalah, dan mengembangkan
masalah yang ada guna
memunculkan permasalahan baru. Pertanyaan kunci yang membantu
siswa mengkonstruksi pemahaman mereka (Frye, 2013) diantaranya: konsep matematika apa yang bisa digunakan dalam menyelesaikan permasalahan, strategi mana yang paling efisien, dan kesalahan apa yang saya buat sehingga teman-teman dapat belajar dari kesalahan tersebut. Guru dalam hal ini dituntut untuk mendorong siswa menjadi ingin tahu tentang ide teman lain dan pemahaman yang mereka miliki karena tiap siswa memiliki tanggung jawab dalam mengembangkan pemahaman dan berpartisipasi serta mendukung pemahaman teman mereka.
Belajar Bermakna
Belajar bermakna (meaningful learning) adalah pembelajaran dimana suatu konsep atau pengetahuan yang dipelajari dipahami sepenuhnya oleh individu dan kaitan pengetahuan ini dengan pengetahuan yang telah ada sebelumnya dalam fikirannya. Ausubel (1963) menyatakan pembelajaran bermakna adalah suatu
ISSN : xxxxxxxxxxx proses pembelajaran dimana siswa
lebih mudah memahami dan mempelajari pelajaran karena guru mampu memberi kemudahan bagi siswa untuk mengaitkan pengalaman atau pengetahuan yang sudah ada dalam pikirannya dengan materi baru. Kebalikan dari meaningful learning adalah rote learning. Rote learning adalah kemampuan mengingat sesutu tanpa adanya pemahman secara menyeluruh dan tidak mengetahui kaitan informasi baru dengan pengetahuan yang telah ada sebelumnya.
Misalkan terdapat 5 konsep yang dipelajari dalam satu semester yang dinomori 1-5. Siswa yang menggunakan rote learning dalam mempelajarinya, memahami kelima konsep tersebut sebagai pengetahuan yang tidak berkaitan. Hal ini merupakan kebalikan dari meaningful learning dimana tiap pengetahuan memiliki kaitan satu dengan yang lainnya. Rote learning dan meaningful learning dapat diilustrasikan melalui gambar berikut
Gambar 2. Perbedaan rote learning dan meaningful learning
Faktor-faktor utama yang mempengaruhi belajar bermakna menurut Ausubel adalah struktur kognitif yang ada, stabilitas dan
kejelasan pengetahuan dalam suatu bidang studi tertentu dan pada waktu tertentu. Seseorang belajar dengan mengasosiasikan fenomena baru ke