DISTRIBUSI SKEW-NORMAL SKRIPSI

(1)

UNIVERSITAS INDONESIA

DISTRIBUSI

SKEW

-NORMAL

SKRIPSI

RIYANTO D SETYAWAN 0706261884

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM PROGRAM STUDI SARJANA MATEMATIKA

DEPOK JULI 2011

(2)

UNIVERSITAS INDONESIA

DISTRIBUSI

SKEW

-NORMAL

SKRIPSI

Diajukan sebagai salah satu syarat untuk memperoleh gelar sarjana sains

RIYANTO D SETYAWAN 0706261884

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM PROGRAM STUDI SARJANA MATEMATIKA

DEPOK JULI 2011

(3)

iii

Skripsi ini adalah hasil karya sendiri,

dan semua sumber baik yang dikutip maupun dirujuk telah saya nyatakan dengan benar.

Nama : Riyanto D Setyawan

NPM : 0706261884

Tanda Tangan :

Tanggal : 12 Juli 2011

(4)

HALAMAN PENGESAHAN

Skripsi ini diajukan oleh

NPM : 0706261884

Program Studi : Sarjana Matematika Judul Skripsi : Distribusi Skew-Normal

Telah berhasil dipertahankan di hadapan Dewan Penguji dan diterima sebagai bagian persyaratan yang diperlukan untuk memperoleh gelar Sarjana Sains pada Program Studi S1 Matematika, Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Indonesia

DEWAN PENGUJI

Pembimbing : Dra. Ida Fithriani, M.Si. ( )

Penguji : Dra. Netty Sunandi, M.Si. ( )

Penguji : Dra. Rianti Setiadi, M.Si. ( )

Penguji : Fevi Novkaniza, M.Si. ( )

Ditetapkan di : Depok Tanggal : 17 Juni 2011

(5)

v

Puji syukur yang tak terkira saya panjatkan kepada Tuhan Yesus, karena atas berkat dan rahmat-Nya, saya dapat menyelesaikan skripsi ini. Penulisan skripsi ini dilakukan dalam rangka memenuhi salah satu syarat untuk mencapai gelar Sarjana Sains Jurusan Matematika pada Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Indonesia.

Saya menyadari bahwa, tanpa bantuan dan bimbingan dari berbagai pihak, dari masa perkuliahan sampai pada penyusunan skripsi ini, sangatlah sulit bagi saya untuk menyelesaikan skripsi ini. Oleh karena itu, saya mengucapkan terima kasih kepada:

(1) Tuhan Yesus, tentunya Dia yang menguatkan, memampukan, dan terus memberikan berkatnya kepada saya sehingga saya dapat menyelesaikan skripsi ini dengan sebaik-baiknya;

(2) Dra. Ida Fithriani, selaku dosen pembimbing akademik dan pembimbing skripsi yang telah menyediakan waktu, tenaga, dan pikiran untuk mengarahkan saya dalam penyusunan skripsi ini, juga yang telah memberikan perhatian dan arahannya selama masa empat tahun kuliah; (3) Karyawan dan karyawati Tata Usaha dan Perpustakaan Departemen

Matematika Universitas Indonesia, yang telah turut mendukung saya baik secara langsung maupun tidak langsung;

(4) Pak Hengki Tasman, Bu Cecil, dan pihak Sekolah Tirtamarta BPK Penabur, yang telah mengizinkan saya mengalokasikan waktu lebih untuk mengerjakan skripsi, serta memberikan dukungan moral kepada saya; (5) Bu Emmy, Kak Bertha, dan staf-staf Kumon Bandung Cinere yang juga

telah mengizinkan saya mengalokasikan waktu lebih untuk mengerjakan skripsi saya, dan juga memberikan dukungan moral;

(6) Orang tua dan keluarga saya yang telah memberikan bantuan dukungan material dan moral;

(7) Sahabat-sahabat yang telah banyak membantu dan mendukung saya dalam menyelesaikan skripsi ini, Farah, Winda, Syahrul, Riski, Ferdy, Widita,

(6)

Widiyani, Lois, dan Nora;

(8) Teman-teman angkatan 2007 yang juga mengerjakan skripsi dan mengusahakan kelulusan di semester genap 2010/2011, Shafa, Paramitha, Sisca, Farah, Winda, Syahrul, Risky, Ferdy, Lois, Anggun, Adi, Gamar, Anjar, Arif, Bowo, Isna, Widya, Shafira, Adit, Danar;

(9) Erik, Karina, Prita, Prisia, Trixie, Ninay, Daud, Alice, dan teman-teman pengurus Komisi Pemuda GKI Pondok Indah dan panitia retret Komisi Pemuda, yang telah memberikan kelonggaran serta dukungan kepada saya untuk mengerjakan skripsi ini;

(10) Teman-teman dan senior-senior dari angkatan 2005-2009 yang juga telah memberikan dukungan dalam pengerjaan skripsi ini;

Akhir kata, saya berharap Tuhan berkenan membalas segala kebaikan semua pihak yang telah membantu. Semoga skripsi ini membawa manfaat bagi pengembangan ilmu.

Penulis

2011

(7)

vii

HALAMAN PERNYATAAN PERSETUJUAN PUBLIKASI TUGAS AKHIR UNTUK KEPENTINGAN AKADEMIS

Sebagai sivitas akademik Universitas Indonesia, saya yang bertanda tangan di bawah ini:

NPM : 0706261884

Program Studi : Sarjana Matematika

Departemen : Matematika

Fakultas : Matematika dan Ilmu Pengetahuan Alam Jenis karya : Skripsi

demi pengembangan ilmu pengetahuan, menyetujui untuk memberikan kepada Universitas Indonesia Hak Bebas Royalti Noneksklusif (Non-exclusive Royalty Free Right) atas karya ilmiah saya yang berjudul:

Distribusi Skew-Normal

beserta perangkat yang ada (jika diperlukan). Dengan Hak Bebas Royalti Noneksklusif ini Universitas Indonesia berhak menyimpan,

mengalihmedia/format-kan, mengelola dalam bentuk pangkalan data (database), merawat, dan memublikasikan tugas akhir saya selama tetap mencantumkan nama saya sebagai penulis/pencipta dan sebagai pemilik Hak Cipta.

Demikian pernyataan ini saya buat dengan sebenarnya.

Dibuat di : Depok Pada tanggal : 12 Juli 2011

Yang menyatakan

(Riyanto D Setyawan)

(8)

Nama : Riyanto D Setyawan Program Studi : Matematika

Judul : Distribusi Skew-Normal

Distribusi normal merupakan salah satu distribusi probabilitas data, yang banyak digunakan dalam berbagai bidang karena sifat ideal yang dimilikinya, yaitu distribusi probabilitas data-datanya terpusat di sekitar mean dan distribusi

probabilitas data lainnya tersebar secara merata. Namun ada kasus-kasus tertentu di mana distribusi normal sebaiknya tidak digunakan karena akan menghasilkan analisis yang kurang sesuai, terutama ketika data memiliki kemencengan yang kuat dan mempunyai heavy-tail. Pada tugas akhir ini diperkenalkan distribusi probabilitas yang dapat memfasilitasi kemencengan data, yaitu distribusi skew -normal. Distribusi skew-normal merupakan bentuk perluasan dari distribusi normal dengan memasukkan parameter kemencengan. Tugas akhir ini

memberikan penjelasan mengenai karakteristik-karakteristik dari distribusi skew -normal univariat dan perluasannya dengan memasukkan parameter location dan

scale, serta distribusi skew-normal secara umum dalam bentuk multivariat. Karakteristik-karakteristik yang dimaksud adalah fungsi kepadatan probabilitas, fungsi distribusi, mean, variansi, fungsi pembangkit momen, dan sifat-sifatnya. Kata Kunci : distribusi normal, kemencengan, distribusi skew-normal,

parameter location dan scale, fungsi kepadatan probabilitas, fungsi distribusi, fungsi pembangkit momen, mean, kovariansi, variansi.

xiii+204 halaman; 3 gambar; 2 tabel Daftar Pustaka : 20 (1961-2008)

(9)

ix Universitas Indonesia ABSTRACT

Name : Riyanto D. Setyawan Program Study : Mathematics

Title : Skew-Normal Distribution

The normal distribution is one of the probability distribution of data, which are widely used in various fields because of the nature of the ideal, namely the

probability distribution of data centers around the distribution of average data and other probability is spread evenly. But there are certain cases where the normal distribution should not be used because it will produce less precise analysis, especially when the data has a strong skewness and heavy-tail. This final project will introduce a probability distribution which can facilitate the skewness of data, i.e skew-normal distribution. The skew-normal distribution is an extend form of normal distribution, allowing a skewness parameter. This final project will give an explanation about the chararteristics of the univariate skew-normal distribution and its extend to the location and scale family, and skew-normal distribution in general in multivariate form. The characteristics are probability density function, distribution function, mean, covariance, variance, moment generating function, and the properties of the distribution.

Key Words : normal distribution, skewness, skew-normal distribution, location and scale parameter, probability density function, distribution function, moment generating function, mean, covariance, variance.

xiii+204 pages ; 3 pictures; 2 tables Bibliography : 20 (1961-2008)

(10)

HALAMAN PERNYATAAN ORISINALITAS... iii

HALAMAN PENGESAHAN... iv

KATA PENGANTAR ...v

HALAMAN PERNYATAAN PERSETUJUAN PUBLIKASI ... vii

ABSTRAK ... viii

ABSTRACT ... ix

DAFTAR ISI ...x

DAFTAR GAMBAR ... xii

DAFTAR LAMPIRAN ... xiii

BAB 1 PENDAHULUAN ...1

1.1 Latar Belakang ... 1

1.2 Permasalahan ... 3

1.3 Tujuan Penulisan ... 3

BAB 2 LANDASAN TEORI ...4

2.1 Percobaan Acak dan Ruang Sampel ... 4

2.2 Fungsi Himpunan Probabilitas ... 4

2.3 Variabel Acak ... 5

2.4 Fungsi Kepadatan Probabilitas ... 5

2.5 Fungsi Distribusi ... 6

2.6 Ekspektasi dari Variabel Acak ... 7

2.7 Variansi ... 9

2.8 Fungsi Pembangkit Momen ... 10

2.9 Aturan Leibnitz ... 11

2.10 Kemencengan ... 12

2.11 Distribusi Normal ... 13

2.12 Fungsi T-Owen ... 16

2.13 Distribusi Folded-Normal ... 19

2.14 Bentuk Khusus dari Distribusi Half-Normal ... 25

2.15 Distribusi Gamma dan Distribusi Chi-Square ... 28

2.16 Distribusi Bivariat ... 32

2.16.1 Fungsi Kepadatan Probabilitas ... 32

2.16.2 Fungsi Distribusi ... 33

2.16.3 Fungsi Kepadatan Probabilitas Marjinal ... 34

2.16.4 Mean ... 35

2.16.5 Variansi dan Kovariansi ... 36

2.16.6 Koefisien Korelasi... 36

2.16.7 Variabel-variabel Acak yang Saling Bebas ... 37

2.17 Hubungan Independensi Variabel Acak Normal Standar dan Half-Normal ... 39

2.18 Sifat Ketertutupan ... 43

2.19 Parameter Location dan Scale ... 43

2.20 Matriks dan Sifat-sifat Matriks ... 44

2.20.1 Notasi Matriks dan Terminologi ... 44

2.20.2 Operasi-operasi Matriks ... 45

2.20.3 Transpos dari Matriks ... 46

2.20.4 Sifat-sifat dari Operasi-operasi Matriks ... 47

2.20.5 Matriks-matriks Nol ... 47

2.20.6 Matriks-matriks Identitas ... 48

2.20.7 Invers dari Matriks ... 48

2.20.8 Matriks-matriks Diagonal, Segitiga, dan Simetris ... 49

(11)

xi Universitas Indonesia

2.20.9 Matriks Definit Positif ... 51

2.20.10 Pangkat dari Matriks ... 52

2.20.11 Fungsi Determinan dan Sifat-sifatnya ... 53

2.20.12 Ruang Berdimensi-n Euclidean ... 54

2.20.13 Ruang-ruang Vektor Riil ... 55

2.20.14 Kebebasan Linier ... 56

2.20.15 Hasil Kali Dalam ... 57

2.20.16 Keortogonalan ... 58

2.20.17 Nilai Eigen dan Vektor Eigen ... 59

2.20.18 Diagonalisasi ... 59

2.20.19 Diagonalisasi Ortogonal ... 60

2.20.20 Matriks Akar Kuadrat. ... 61

2.20.21 Vektor Acak ... 61

2.20.22 Turunan Terhadap Vektor ... 63

2.21 Distribusi Normal Multivariat ... 64

2.22 Notasi Integral ... 71

2.23 Distribusi Nonsentral-t ... 71

BAB 3 VARIABEL ACAK YANG BERDISTRIBUSI SKEW-NORMAL UNIVARIAT ...72

3.1 Fungsi Kepadatan Probabilitas ... 73

3.2 Fungsi Distribusi ... 79

3.3 Fungsi Pembangkit Momen ... 82

3.4 Sifat-sifat dari Variabel Acak yang Berdistribusi Skew-Normal ... 89

3.5 Mean dan Variansi ... 112

3.6 Perluasan: Famili Location-Scale ... 114

3.6.2 Fungsi Distribusi ... 115

3.6.3 Fungsi Pembangkit Momen ... 119

3.6.4 Mean dan Variansi ... 120

3.7 Perbandingan Grafik Normal dan Skew-Normal ... 123

3.8 Contoh ... 125

BAB 4 VEKTOR ACAK YANG BERDISTRIBUSI SKEW-NORMAL MULTIVARIAT ...127

4.1 Distribusi Skew-Normal Multivariat ... 127

4.1.3 Matriks Mean dan Kovariansi ... 158

4.2 Distribusi Skew-Normal Bivariat ... 163

4.2.3 Mean, Kovariansi, dan Variansi ... 172

4.3 Contoh ... 180 BAB 5 PENUTUP...183 5.1 Kesimpulan ... 183 5.2 Saran ... 187 DAFTAR PUSTAKA ...188

(12)

xii Universitas Indonesia DAFTAR GAMBAR

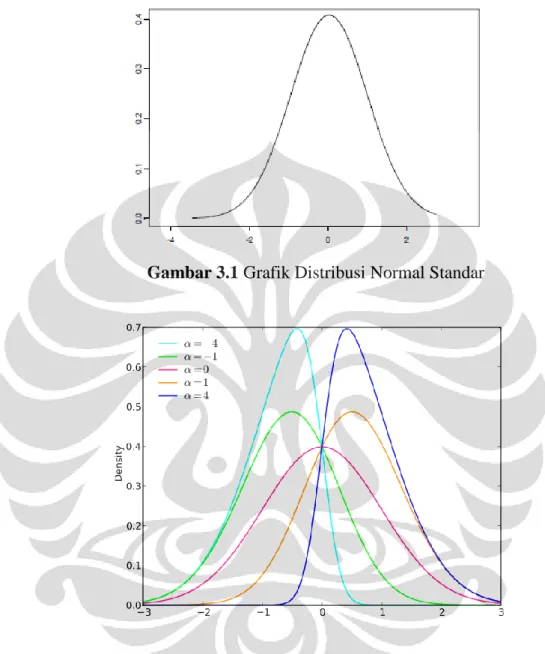
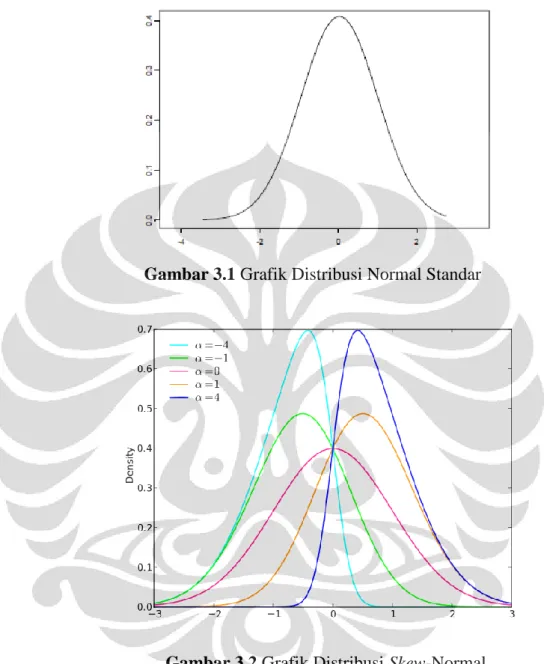
Gambar 2.1 Grafik Distribusi Half-Normal... ...25 Gambar 3.1 Grafik Distribusi Normal Standar...124 Gambar 3.2 Grafik Distribusi Skew-Normal Univariat...124

(13)

xiii Universitas Indonesia DAFTAR LAMPIRAN

Lampiran 1 Indeks dan Parameter Kemencengan...190

Lampiran 2 Matriks Ω dan Sifat-sifatnya...196

Lampiran 3 Tabel Nilai Probabilitas Distribusi Normal Standar...199

Lampiran 4 Tabel Nilai Fungsi T-Owen...200

(14)

1.1 Latar Belakang

Distribusi probabilitas data adalah penyebaran probabilitas data terkait dengan suatu kejadian tertentu. Distribusi probabilitas sangat terkait dengan variabel acak. Misalkan dcari suatu percobaan acak diperoleh suatu ruang sampel. Variabel acak adalah fungsi yang memetakan setiap elemen dari ruang sampel ke satu dan hanya satu bilangan riil [Hogg-Craig, 1995]. Setiap variabel acak

memiliki ruang nilai, yaitu daerah hasil dari variabel acak, yang merupakan subhimpunan dari bilangan riil. Berdasarkan ruang nilainya, ada dua jenis variabel acak, yaitu variabel acak yang berdistribusi probabilitas diskret dan variabel acak yang berdistribusi probabilitas kontinu. Variabel acak yang berdistribusi

probabilitas diskret adalah variabel acak yang memiliki ruang nilai yang terhitung. Contoh: variabel acak yang berdistribusi binomial, Poisson, dan hipergeometrik. Sedangkan variabel acak yang berdistribusi probabilitas kontinu adalah variabel acak yang memiliki ruang nilai yang tidak terhitung. Contoh: variabel acak yang berdistribusi normal, normal bivariat, Gamma, beta, F, dan Chi-square.

Di dalam berbagai aplikasi di dunia nyata, terdapat suatu distribusi probabilitas data yang sudah dikenal luas dan sering digunakan, yaitu distribusi normal. Distribusi normal memiliki karakteristik yang penting, yaitu distribusi probabilitas datanya terpusat di sekitar mean, dan probabilitas data-data lainnya tersebar secara merata. Grafik fungsi kepadatannya berbentuk lonceng ( bell-shaped).

Karakteristik yang dimiliki distribusi normal tersebut dianggap ideal. Oleh karena itu, distribusi probabilitas ini sering digunakan untuk melakukan analisis data dalam berbagai jenis aplikasi. Namun, hal ini dapat menjadi tidak realistis, karena dalam kehidupan nyata tidak semua data berdistribusi normal. Oleh karena itu, pada banyak kasus di mana data tidak berdistribusi normal, tidak disarankan untuk melakukan analisis data dengan menggunakan distribusi normal, karena

(15)

Universitas Indonesia

hasil analisis data akan kurang atau tidak sesuai, khususnya untuk data dengan kemencengan yang kuat dan mempunyai heavy-tail.

Kemencengan merupakan ukuran ketidaksimetrisan dari suatu distribusi probabilitas data. Jika kemencengan suatu distribusi bernilai 0, berarti distribusi tersebut simetris. Distribusi normal memiliki kemencengan bernilai 0 dan bukan merupakan distribusi probabilitas yang mempunyai heavy-tail.

Untuk dapat mengetahui apakah data berdistribusi normal atau tidak, terkait dengan kemencengannya, perlu dilakukan pengujian hipotesis. Data yang memiliki kemencengan yang signifikan, atau berarti kemencengannya melebihi batas tertentu pada pengujian hipotesis, data tersebut merupakan data yang tidak berdistribusi normal.

Pada kasus di mana data tidak berdistribusi normal, seringkali pada kenyataannya banyak orang tetap mengasumsikan bahwa data tersebut

berdistribusi normal, atau hampir normal, jika kemencengan dianggap masih bisa ditolerir, atau dengan metode transformasi, mengusahakan agar data tersebut dapat dianalisis dengan menggunakan distribusi normal. Metode demikian merupakan metode yang kurang tepat, dan menjadi tidak realistis. Seharusnya, seperti telah disebutkan sebelumnya, tidak disarankan untuk tetap melakukan analisis dengan menggunakan distribusi normal.

Jadi, diperlukan distribusi probabilitas yang lain, yang dapat memfasilitasi kemencengan distribusi probabilitas data. Beberapa distribusi probabilitas data yang dikenal dapat memfasilitasi kemencengan distribusi probabilitas data adalah distribusi F, Chi-square, log-normal, dan Weibull.

Jika dilihat bentuk grafik fungsi kepadatan dari distribusi-distribusi probabilitas tersebut, memang distribusi-distribusi probabilitas tersebut dapat memfasilitasi masalah kemencengan data. Namun, distribusi-distribusi yang menjadi contoh tersebut hanya bisa digunakan untuk ruang nilai nonnegatif atau positif. Jadi, ruang nilai negatif tidak difasilitasi oleh variabel-variabel acak tersebut. Selain distribusi F, Chi-square, log-normal, Weibull, terdapat distribusi-distribusi probabilitas lain yang juga dapat memfasilitasi kemencengan data. Namun, distribusi-distribusi probababilitas tersebut kurang atau tidak dapat

(16)

memfasilitasi data yang memiliki bentuk distribusi probabilitas terpusat di sekitar mean tetapi kurang atau tidak simetris.

Dalam tugas akhir ini, akan diperkenalkan dan dibahas suatu distribusi probabilitas data yang merupakan perluasan dari distribusi normal, yang dapat memfasilitasi kemencengan data saja, tetapi tidak terkait dengan data yang mempunyai heavy-tail, dan data yang berdistribusi probabilitas terpusat di sekitar mean tetapi kurang atau tidak simetris. Distribusi probabilitas data tersebut adalah distribusi skew-normal. Distribusi skew-normal ini dibangun dengan

menggunakan distribusi normal standar. Pada pembahasan selanjutnya akan terlihat bahwa variabel acak ini memiliki suatu parameter yang disebut parameter kemencengan. Parameter ini menentukan kemencengan dari distribusi probabilitas data. Jika parameter ini bernilai nol, maka variabel acak berdistribusi normal standar, yang simetris.

1.2 Permasalahan

Bagaimana karakteristik dari distribusi skew-normal?

1.3 Tujuan Penulisan

Mempelajari karakteristik-karakteristik distribusi skew-normal.

(17)

4 Universitas Indonesia

2.1 Percobaan Acak dan Ruang Sampel

Misalkan terdapat suatu percobaan, hasilnya tidak dapat diprediksi dengan pasti. Percobaan acak adalah suatu percobaan yang dilakukan berulang kali dan di dalam kondisi yang sama. Ruang sampel adalah koleksi dari semua hasil yang mungkin dari suatu percobaan acak.

2.2 Fungsi Himpunan Probabilitas

Misalkan C menyatakan himpunan dari semua hasil yang mungkin dari suatu percobaan acak, atau disebut ruang sampel.

Definisi 2.1.

Jika P(C) didefinisikan untuk suatu tipe subhimpunan dari ruang C, dan jika (a) P(C) ≥ 0

(b) P C( ₁C₂C₃ )P C( ₁)P C( ₂)P C( ₃) , di mana himpunan himpunan Ci, i = 1, 2, 3, . . ., adalah saling lepas, yaitu CiCj   , i j

(c) P(C) = 1,

maka P disebut fungsi himpunan probabilitas dari hasil percobaan acak.

Untuk setiap subhimpunan C dari C, bilangan P(C) disebut probabilitas bahwa hasil dari percobaan acak adalah elemen dari himpunan C, atau

probabilitas kejadian C.

Suatu fungsi himpunan probabilitas memberitahukan bagaimana probabilitas didistribusikan terhadap berbagai subhimpunan C dari suatu ruang sampel C. Dalam hal ini disebut distribusi probabilitas.

(18)

Beberapa sifat dari suatu fungsi himpunan probabilitas adalah: 1. Untuk setiap C_C, P(C) = 1 – P(C*).

2. Probabilitas dari himpunan kosong adalah nol; yaitu, P( ) 0.

3. Jika C1 dan C2 adalah subhimpunan-subhimpunan dari C sedemikian sehingga

1 2

C C , maka P(C1) ≤ P(C2).

4. Untuk setiap CC, 0 ≤ P(C) ≤ 1.

5. Jika C1 dan C2 adalah subhimpunan-subhimpunan dari C, maka

1 2 1 2 1 2

( ) ( ) ( ) ( )

P C C P C P C P C C .

2.3 Variabel Acak

Berikut ini diberikan definisi dari variabel acak.

Definisi 2.2.

Perhatikan suatu percobaan acak dengan ruang sampel _C. Suatu fungsi X, yang memetakan setiap elemen cC satu dan hanya satu bilangan riil X(c) = x, disebut variabel acak [Hogg-Craig 5thed.; 1995].

Ruang nilai dari variabel acak X adalah himpunan dari bilangan-bilangan riil

A = {x |x = X(c), cC}.

2.4 Fungsi Kepadatan Probabilitas

Misalkan X menyatakan suatu variabel acak dengan ruang nilai satu dimensi A. Misalkan A berisi nilai-nilai bilangan yang terhitung. Ruang A yang demikian disebut himpunan diskret dari nilai-nilai.

Hal yang serupa berlaku juga untuk variabel acak kontinu, tetapi A berisi nilai-nilai bilangan yang tidak terhitung.

(19)

Untuk kasus diskret, misalkan X menyatakan variabel acak dengan ruang satu dimensi A, yang memuat titik-titik bilangan yang terhitung. Misalkan f(x) adalah suatu fungsi sedemikian sehingga f(x) ≥ 0, x , dan



f x( ) 1

A

.

Ketika suatu fungsi himpunan probabilitas P(A), A A, dapat dinyatakan dalam bentuk

( ) Pr( ) ( )

A

P A  XA 



f x , (2.1)

maka X disebut sebagai variabel acak tipe diskret dan f(x) disebut sebagai fungsi kepadatan probabilitas (f.k.p) dari X.

Untuk kasus kontinu, misalkan X menyatakan variabel acak dengan ruang satu dimensi A, yang memuat suatu interval atau gabungan dari interval-interval. Misalkan f(x) adalah suatu fungsi sedemikian sehingga f(x) ≥ 0, x , dan

( ) 1

f x dx



A .

Ketika suatu fungsi himpunan probabilitas P(A), A_A, dapat dinyatakan dalam bentuk

( ) Pr( ) ( )

A

P A  XA 



f x dx, (2.2) maka X disebut variabel acak tipe kontinu dan f(x) disebut fungsi kepadatan probabilitas (f.k.p) dari X.

2.5 Fungsi Distribusi

Misalkan variabel acak X mempunyai fungsi himpunan probabilitas P(A), di mana A adalah himpunan satu dimensi.

Ambil bilangan rill x dan perhatikan himpunan A yang merupakan himpunan yang tidak terbatas dari – ∞ sampai x, termasuk titik x itu sendiri. Untuk setiap himpunan A yang demikian, diperoleh P(A) = Pr(XA) = Pr(X ≤ x). Probabilitas ini bergantung pada nilai x; yaitu, probabilitas ini adalah fungsi dari

x. Fungsi nilai ini dinyatakan dengan

F(x) = Pr (X ≤ x). (2.3)

(20)

Fungsi F(x) dikenal dengan sebutan fungsi distribusi, atau fungsi distribusi kumulatif (f.d.k) dari variabel acak X. Karena F(x) = Pr (X ≤ x), maka dengan f(x) adalah f.k.p, diperoleh:

Untuk X variabel acak diskret:

( ) ( )

w x

F x f w







. (2.4)

Untuk X variabel acak kontinu:

( ) x ( )

F x f w dw





_

, sehingga F' x( ) f x( ). (2.5) Berikut diberikan sifat-sifat dari suatu fungsi distribusi.

1. 0 F(x)  1.

2. F(x) merupakan fungsi tidak turun. 3. F(∞) = 1 dan F(– ∞) = 0.

4. F(x) kontinu kanan.

2.6 Ekspektasi dari Variabel Acak

Misalkan X adalah suatu variabel acak yang mempunyai f.k.p. f(x) sedemikian sehingga dimiliki kekonvergenan absolut; dalam kasus diskret,

| | ( )



x

x f x konvergen ke suatu batas berhingga,

atau, dalam kasus kontinu, | | ( )x f x dx

 



konvergen ke suatu batas berhingga. Ekspektasi dari suatu variabel acak adalah

( )



( )

x

E X xf x , dalam kasus diskret, (2.6)

atau

( ) ( )

E X 



_ xf x dx, dalam kasus kontinu. (2.7) Ekspektasi E(X) disebut juga sebagai ekspektasi matematika dari X atau nilai harapan dari X.

(21)

Perhatikan suatu fungsi dari variabel acak X dengan ruang nilai A. Misalkan fungsi ini adalah Y = u(X). Misalkan X merupakan variabel acak yang bertipe kontinu dan y = u(x) merupakan fungsi kontinu naik dari X dengan invers fungsinya x = w(y), yang juga merupakan fungsi naik. Jadi, Y adalah suatu variabel acak dan fungsi distribusinya adalah

G(y) = Pr(Y ≤ y) = Pr[u(X) ≤ y] = Pr[X ≤ w(y)] ( ) ( ) w y f x dx  



di mana f(x) adalah f.k.p dari X.

Dengan salah satu bentuk dari Teorema Dasar Kalkulus,

g(y) = G'(y) = f[w(y)]w'(y) , yB, (2.8) = 0 , lainnya,

di mana

B = {y | y = u(x), xA}.

Dengan definisi, nilai harapan dari Y adalah

( ) ( )

E Y  yg y dy





_

. (2.9)

Dengan menggunakan teknik perubahan variabel dari integrasi melalui y = u(x) atau, secara ekivalen, x = w(y). Karena

( ) 0 dx w' y dy   , (2.10) diperoleh ( ) ( ) E Y  yg y dy  

_

( ) [ ( )] 1 [ ( )] u x g u x dx w' u x   

_

 u x f x dx( ) ( )  

_

. (2.11)

Hal ini benar secara umum dan juga tidak ada perbedaan apakah X variabel acak bertipe diskret atau kontinu dan Y = u(X) tidak harus merupakan fungsi naik dari

X. Jadi, jika Y = u(X) mempunyai ekspektasi, dapat diperoleh dari (2.11) bahwa

(22)

[ ( )] ( ) ( )

E u X  u x f x dx





_

, (2.12)

untuk kasus kontinu, dan

[ ( )] ( ) ( )

x

E u X 



u x f x , (2.13)

untuk kasus diskret.

Berikut ini diberikan beberapa sifat dari ekspektasi matematika: 1. Jika k adalah sebuah konstanta, maka E(k) = k.

2. Jika k adalah sebuah konstanta dan V adalah suatu variabel acak, maka

E(kV) = kE(V).

3. Jika k1, k2, ..., km adalah konstanta-konstanta dan V1, V2, ..., Vm adalah

variabel-variabel acak, maka E(k1V1 + k2V2 + ... + kmVm) =

k1E(V1) + k2E(V2) + ... kmE(Vm).

2.7 Variansi

Misalkan X adalah suatu variabel acak yang mempunyai f.k.p f(x). Variansi dari suatu variabel acak X adalah suatu ekspektasi matematika dari (X – μ)2, dengan μ = E(X). Var(X) = E[(X - μ)2] = E(X2 – 2μX + μ2) = E(X2) – E(2μX) + E(μ2) = E(X2) – 2μE(X) + E(μ2) = E(X2) – 2μE(X) + μ2 = E(X2) – 2μ.μ. + μ2 = E(X2) – 2μ2 + μ2 = E(X2) – μ2 = E(X2) – [E(X)]2. (2.14)

(23)

E e 



e f x , (2.16)

jika X adalah variabel acak tipe diskret.

Ekspektasi matematika ini dikenal dengan sebutan fungsi pembangkit momen (f.p.m.) dari variabel acak X (atau dari distribusi) dan dinyatakan dengan

M(t) atau MX(t).

 

( ) tX

X

M t E e . (2.17)

Jika t = 0, diperoleh MX(0) = 1. Tidak semua distribusi memiliki f.p.m,

tetapi jika f.p.m. ada, fungsi ini unik dan menentukan distribusi dari variabel acak. Jadi, jika dua variabel acak memiliki f.p.m. yang sama, berarti keduanya memiliki distribusi yang sama.

Momen ke-k dari distribusi dari variabel acak X dinotasikan dengan ( )

(0)

k X

M , di mana M_X( )k (0)E X

 

k . E(X) dan E(X2) merupakan momen pertama dan kedua dari suatu distribusi, yang dinyatakan sebagai

( ) 'X(0) E X M ,

 

2 (0) '' X E X M . (2.18)

Jadi, mean dan variansi dari variabel acak X adalah

( ) '_X(0)

E X M , (2.19)

2

Var(X)M_X''(0) M'_X(0)_ . (2.20)

(24)

2.9 Aturan Leibnitz

Aturan Leibnitz.

Misalkan f(x, t) merupakan suatu fungsi kontinu dan mempunyai turunan  f / t yang kontinu pada domain dari bidang-xt yang di dalamnya termasuk persegi

axb, t1tt2. Maka untuk t1tt2, ( , ) ( , ) b b a a d f f x t dx f x t dx dt t   



. (2.21)

Dengan kata lain, diferensiasi dan integrasi dapat ditukar.

Bukti: Misalkan ( ) b ( , ) a f g t x t dx t   



, untuk t1tt2.

Karena f / t kontinu, maka g(t) kontinu untuk t1tt2.

Untuk t1t3t2, diperoleh 3 3 1 1 ( ) ( , ) t t b t t a f g t dt x t dxdt t   



 

3 1 ( , ) b t a t f x t dtdx t   

 

b



( , )₃ ( , )₁



a f x t f x t dx 

_

 b ( , )₃ b ( , )₁ a f x t dx a f x t dx 

_



_

F t( )₃ F t( )₁ , (2.22)

dengan F(t) didefinisikan sebagai ( ) b ( , )

a

F t 



f x t dx.

Jika dimisalkan t3 merupakan variabel t, berarti t1tt2 dan diperoleh

1 1

( ) ( ) t ( )

t

F t F t 



g u du. (2.23)

Kedua sisi dari (2.23) kemudian dapat diturunkan terhadap t. Dengan Teorema Dasar Kalkulus, diperoleh



1



1 ( ) ( ) ( ) t t d g u du d F t F t dt dt  



(25)

Universitas Indonesia ( ) ( ) b ( , ) a f F' t g t x t dx t    



(2.24) b ( , ) b ( , ) a a d f f x t dx f x t dx dt t   



.

Jadi, terbukti bahwa jika f(x, t) merupakan suatu fungsi kontinu dan mempunyai turunan  f / t yang kontinu pada domain dari bidang-xt yang di dalamnya termasuk persegi axb, t1tt2, maka untuk t1tt2,

( , ) ( , ) b b a a d f f x t dx f x t dx dt t   



. 2.10 Kemencengan

Misalkan X adalah suatu variabel acak. E(X) = μ disebut momen pertama dan E(X2) momen kedua dari distribusi dari variabel acak X. Secara umum, E(Xk) disebut momen ke-k dari X dan E[(X – μ)k] disebut momen tengah ke-k dari X. Momen tengah ketiga yang distandardisasi yang dinyatakan oleh





3 3 3 E X     _     , (2.25)

disebut kemencengan dari distribusi dari variabel acak X.

Kemencengan mengukur ketidaksimetrisan dari suatu distribusi. Jika kemencengan bernilai 0 berarti distribusi tersebut simetris. Jika kemencengan bernilai negatif, berarti distribusi probabilitas datanya menceng negatif, atau disebut juga menceng kiri (mempunyai tail kiri yang lebih panjang). Jika kemencengan bernilai positif, berarti distribusi probabilitas datanya menceng positif, atau disebut juga menceng kanan (mempunyai tail kanan yang lebih panjang). Dalam kasus distribusi yang tidak simetris, derajat ketidaksimetrisan disebut kemencengan. Formula untuk kemencengan ini adalah

3 3



 atau dapat juga 33

2   , (2.26) di mana 3 3 1 ( ) i i i f x x N  



 , (2.27)

(26)

dan 3 2 3 1 2 ( ) i i i f x x N  _  _ 



 . (2.28)

Definisi kemencengan yang seringkali digunakan adalah definisi menurut Karl Pearson, yaitu mean modus kemencengan standar deviasi   . (2.29) 2.11 Distribusi Normal Perhatikan integral 2 exp 2 y I  dy     _ _  



.

Integral ini ada karena integran (fungsi yang diintegralkan) merupakan fungsi yang kontinu positif yang terbatas oleh suatu fungsi yang dapat diintegralkan, yaitu





2 0 exp exp | | 1 , 2    _ _          y y y , dan





exp |y| 1 dy 2e      



.

Untuk menghitung nilai integral I, ingat bahwa I > 0 dan I2 dapat ditulis sebagai 2 2 2 exp 2 y z I   dydz       _ _  

 

.

Integral ini dapat dihitung dengan mengubahnya ke koordinat polar. Jika

y = rcos dan z = rsin, diperoleh

2 2 2 /2 0 0     

_{ }

r I e rdrd 2 0 2    



d  .

(27)

Dari hasil tersebut, diperoleh I  2 dan

2_{/ 2} 1 1 2 y e dy   _  



.

Jika diperkenalkan suatu variabel baru dari integrasi, sebut x, dengan menulis

, 0   x a  y b b , Integral / 2I  menjadi 2 2 1 ( ) exp 1 2 2 x a dy b b    _   _    



.

Karena b > 0, hal ini mengakibatkan 2 2 1 ( ) ( ) exp , 2 2 x a f x x b b      _ _        (2.30)

memenuhi kondisi-kondisi untuk menjadi suatu f.k.p. dari variabel acak kontinu. Variabel acak bertipe kontinu yang mempunyai f.k.p. dengan bentuk f(x) disebut mempunyai distribusi normal, dan sebarang f(x) dari bentuk ini disebut f.k.p. normal.

merupakan

f.k.p. normal dengan parameter a pada (2.30) disubstitusikan dengan a + b2t, maka integral tersebut bernilai 1.

(28)

Mean µ dan variansi ζ2 dari distribusi normal akan dicari melalui M(t) dengan menggunakan (2.18), (2.19), dan (2.20). 2 2 2 2 ( ) exp ( ) ( )( ) 2 b t M' t  _at _ a b t M t a b t   dan 2 2 2 2 2 2 2 ( ) exp ( ) exp 2 2 b t b t M'' t  _at _ a b t  _at _b     2 2 2 ( )( ) ( ) M t a b t M t b    .

Maka, mean distribusi normal adalah

µ = M'(0)

= M(0).a

= a, (2.33)

dan variansinya adalah

ζ2

= M''(0) - µ2

= M(0)b2 + M(0)a2 – a2

= b2 + M(0)a2 – a2 = b2. (2.34) Jadi, bentuk f.k.p normal adalah

2 2 1 ( ) ( ) exp , 2 2 x f x  x        _ _        , (2.35)

Suatu bentuk yang menunjukkan secara eksplisit nilai-nilai dari µ dan ζ2. f.p.m. M(t) dapat ditulis sebagai

2 2 ( ) exp 2 t M t  _t _  . (2.36)

Untuk penghitungan probabilitas Pr(Xx), digunakan standardisasi ke distribusi normal standar N(0, 1), yaitu dengan mendefinisikan

X Z     , (2.37) sehingga





Pr X x Pr X  x          _  _   Pr Z x       _  _  . (2.38)

(29)

Nilai-nilai probabilitas Pr(Zz) dengan z x 

 

 diberikan pada bagian Lampiran 3.

2.12 Fungsi T-Owen

Fungsi T-Owen memiliki bentuk





2 2 2 0 1 exp 1 1 2 ( , ) 2 1 h x T h dx x    _ _       



, h > – ∞, α < + ∞. (2.39) Sifat-sifat dari fungsi T-Owen adalah:

1. T(h, α) merupakan fungsi turun dari h. Bukti:

Ambil sebarang h h₁, ₂ di mana h1 < h2.

Karena h1 < h2 maka, h12h22 dan

2 2

1 2

1 1

2h 2h

   .



2 2 2 2 1 2 1 1 exp 1 exp 1 2h x 2h x _ _ _ _ _          dan









2 2 2 2 1 2 1 1 1 1 exp 1 exp 1 2 2h x 2 2h x _ _ _ _ _         . Karena 1 + x 2 > 0, maka

















2 2 2 2 1 2 2 2 1 1 exp 1 exp 1 1 2 1 2 2 1 2 1 h x h x x x    _ _   _ _         _ __  _ _                   .

Sesuai dengan sifat fungsi yang dapat diintegralkan, diperoleh

















2 2 2 2 1 2 2 2 0 0 1 1 exp 1 exp 1 1 2 1 2 2 1 2 1 h x h x dx dx x x      _ _   _ _           _                     



, atau

(30)

















2 2 2 2 1 2 2 2 0 0 1 1 exp 1 exp 1 1 2 1 2 2 1 2 1 h x h x dx dx x x     _ _  _ _        _    



. Berarti diperoleh T(h1, α) > T(h2, α).



 T h( , ) .

Jadi, terbukti bahwa – T(h, α) = T(h, – α).

(31)

3. T(– h, α) = T(h, α). (2.41)

Bukti:

Fungsi T-Owen adalah





2 2 2 0 1 exp 1 1 2 ( , ) 2 1 h x T h dx x    _ _       



, h > – ∞, α < + ∞. Jika h disubstitusi dengan – h, diperoleh





2 2 2 0 1 exp 1 1 2 ( , ) 2 1 h x T h dx x    _ _        



T h( , )

Jadi, terbukti bahwa T(– h, α) = T(h, α).

4. 2T(h, 1) = Φ(h)Φ(– h). (2.42) Bukti:





2 2 2 0 1 exp 1 1 2 ( , ) , , 2 1 h x T h dx h x     _ _            



. Dari [Owen, 1956], diperoleh persamaan

1 1 1 ( , ) ( ) ( ) ( ) ( ) , 2 2 T h h h h h T h           _{ } _  . Jadi, untuk α = 1, 1 1 ( ,1) ( ) ( ) ( ) ( ) ( ,1) 2 2 T h   h   h   h  h T h 2T(h,1) = (h) – (h)(h) 2T(h,1) = (h)[1 – (h)] 2T(h,1) = (h)(– h).

Jadi, terbukti bahwa 2T(h,1) = (h)(– h).

Nilai-nilai dari fungsi T-Owen disajikan pada bagian Lampiran 4.

(32)

2.13 Distribusi Folded-Normal

Misalkan X adalah variabel acak yang berdistribusi normal N(μ, ζ2). Perhatikan f.k.p dari X, yaitu

2 2 ( ) /2 1 ( ) , 2 x f x e   x           (2.43)

di mana μ dan ζ2 adalah mean dan variansinya secara berurutan. Misalkan Y = |X|.

A = {x | – ∞ < x < ∞}.

B = {y | 0 ≤ y < ∞}.

y = |x| bukan merupakan transformasi satu-satu.

Ambil A1 dan A2 di mana A1, A2A, A1A2 = A, dan A1A2 = .

A1 = {x | –  < x < 0}.

A2 = {x | 0 ≤ x < }.

Pemetaannya dengan transformasi y = |x| adalah:

A1 = {x | –  < x < 0} → {y | 0 < y < }.

A2 = {x | 0 ≤ x < } → {y | 0 ≤ y < }.

Hasil pemetaan yang diperoleh berbeda, letak perbedaannya yaitu pada y = 0. Maka dari itu, ruang nilai akan didefinisikan kembali untuk mengatasi permasalahan ini.

Didefinisikan kembali untuk x = 0, y = 0. Jadi, ruang nilai-ruang nilai yang baru adalah:

2 2 2 2 1 ( ) ( ) ( ) exp exp , 0 2 2 2 0 , lainnya. y y g y   y               _ _ _ _ __          (2.44)

Variabel acak yang mempunyai f.k.p tersebut dinamakan dengan variabel acak yang berdistribusi folded-normal.

Distribusi half-normal adalah bentuk khusus dari distribusi folded-normal, yaitu ketika μ = 0.

(34)

2 2 2 2 1 ( ) exp exp 2 2 2 y y g y           _ _ _ _ __       2 2 1 2 exp 2 2 y        _ _ __     2 2 2 exp 2 2 y       _ _  .

Jadi, variabel acak yang berdistribusi half-normal mempunyai f.k.p 2 2 2 ( ) exp , 0 2 2 0 , lainnya. y g y y       _ _     (2.45)

Fungsi distribusi dari variabel acak Y adalah 2 2 0 2 ( ) exp 2 2 y y G y dy       _ _  



2 2 0 2 exp 2 2 y y dy       _ _  



, (2.46)





2 2 2 2 0 2 ( ) exp exp 2 2 2 Y y t t M t   dy          _ _  _ _     



_ _ ₂ 2 2 2 2 2 exp exp 2 t 2 2 t p dp             _ _ _ _  



  . (2.48) Misalkan: p = – s; dp = – ds. Batas integrasinya:

2 2 1 2 (0) 2 2 '' Y E Y M    _{ }   . (2.53)

Dengan menggunakan persamaan (2.14), diperoleh

 

₂





2 Var( )Y E Y  E Y( ) 2 2 2 2       _{ } _   2 2 4 2      2 2 2     2 2 1      _  _  . (2.54)

Jadi, mean dan variansi dari variabel acak Y adalah 2 ( ) E Y    , 2 2 Var( )Y  1     _  _  .

Berikut ini diberikan gambar grafik dari distribusi half-normal, yaitu

(38)

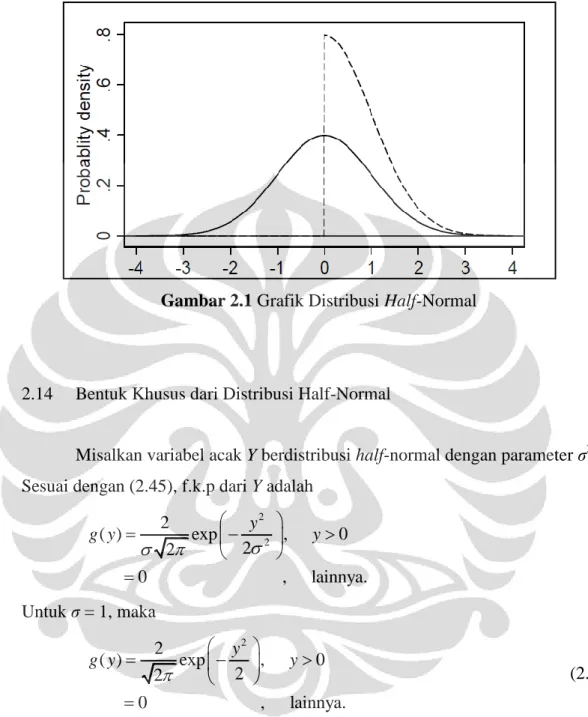
Gambar 2.1 Grafik Distribusi Half-Normal

2.14 Bentuk Khusus dari Distribusi Half-Normal

Misalkan variabel acak Y berdistribusi half-normal dengan parameter ζ2. Sesuai dengan (2.45), f.k.p dari Y adalah

2 2 2 ( ) exp , 0 2 2 0 , lainnya. y g y y       _ _     Untuk ζ = 1, maka 2 2 ( ) exp , 0 2 2 0 , lainnya. y g y y     _ _     (2.55)

Akan ditunjukkan bahwa jika Z ~ N(0, 1), maka |Z| dan Y pada saat ζ = 1 berdistribusi identik.

Misalkan Z ~ N(0, 1), dan f.k.p dari variabel acak Z adalah

2 2 1 ( ) , 2 z h z e z        . Misalkan W = |Z|. A = {z | – ∞ < z <∞}.

Dengan transformasi w = |z| diperoleh

B = {w | 0 ≤ w < ∞}.

(39)

Karena A = {z | – ∞ < z < ∞}dan B = {w | 0 ≤ w < ∞}, maka, w = |z| bukan transformasi satu-satu.

Ambil A1 dan A2 di mana A1, A2A, A1A2 = A, dan A1A2 = .

A1 = {z | –  < z < 0}.

A2 = {z | 0 ≤ z < }.

Pemetaannya dengan transformasi w = |z| adalah:

A1 = {z | –  < z < 0} → {w | 0 < w < }.

A2 = {z | 0 ≤ z < } → {w | 0 ≤ w < }.

Hasil pemetaan yang diperoleh berbeda, letak perbedaannya yaitu pada w = 0. Maka dari itu, ruang nilai akan didefinisikan kembali untuk mengatasi

permasalahan ini.

Didefinisikan kembali untuk z = 0, w = 0. Jadi, ruang nilai-ruang nilai yang baru adalah:

A = {z | –  < z < , z 0}. B = {w | 0 < w < }. Inversnya adalah: z = – w ; z = w, dz = – dw ; dz = dw, Jacobian-nya: J1 = – 1 ; J2 = 1, | J1| = 1 ; | J2| = 1. Misalkan B_B. A3 = {z | z = – w, wB} A1. A4 = {z | z = w, wB} A2. Kemudian diperoleh 3 4 Pr(WB)Pr(ZA)Pr(ZA) 3 4 ( ) ( ) A A h z dz h z dz 







( ) | ₁| ( ) | ₂| B B h w J dw h w J dw 



 



(40)

.

Jadi, f.k.p dari variabel acak W adalah

2 2 2 ( ) , 0 2 0 , lainnya. w k w e w      (2.56)

Karena f.k.p W = |Z| dan f.k.p Y sama, maka distribusi Y dan W = |Z| identik. Jadi,dapat dikatakan bahwa |Z| berdistribusi half-normal dengan ζ = 1. f.p.m dari variabel acak Y dapat dicari dengan menggunakan (2.49), yaitu

2 2 2 2 2 1 ( ) 2 exp exp 2 2 2 t Y t s M t   ds          _ _ _ _  



  . Untuk ζ = 1, maka 2 2 1 ( ) 2 exp exp 2 2 2 t Y t s M t ds        _{ } _ _  



  . (2.57) 2 2 exp ( ) 2 t t    _{ }   . (2.58)

Dengan menggunakan persamaan (2.52) dan (2.54), diperoleh mean dan variansi dari variabel acak Y untuk ζ = 1, yaitu

2 2 ( ) 2 E Y     , (2.59) 2 Var( ) 1Y    . (2.60)

(41)

2.15 Distribusi Gamma dan Distribusi Chi-Square

Perhatikan bentuk integral 1 0 y y e dy  _{ }



.

Integral tersebut ada untuk α > 0, dan nilai integral tersebut positif. Integral tersebut disebut fungsi gamma dari α, dan ditulis

1 0

( ) y e dyy

 

_

.

Jika α = 1, jelas bahwa 0

(1)  e dyy 1

 



 .

Jika α > 1, dengan menggunakan integral parsial diperoleh bahwa 2

0

( ) ( 1) y e dyy ( 1) ( 1)

  



    .

Jika α adalah bilangan bulat positif yang lebih dari 1, maka Γ(α) = (α – 1)( α – 2)...(3)2(1)Γ(1) = (α – 1)! Karena Γ(1) = 1, hal ini berarti 0! = 1.

Misalkan: x y   , di mana β > 0. 1 dy dx   . Batas integrasinya:

Jika y = 0, maka x = 0; jika x = ∞, maka y = ∞. Jadi, diperoleh 1 / 0 1 ( ) x e x dx         _     _{ } _{ }    



1 / 1 0 1 x x e dx        _     _{ }  



1 / 1 0 1 x x e dx        _     _{ }  



1 / 0 x x e dx       _ 



(42)

1 / 0 1 ( ) _ x e xdx   _ _  

_

,

atau, ekivalen dengan 1 / 0 1 1 ( ) x x e dx     _ _  



1 / 0 1 1 ( ) x x e dx        _  



1 / 0 1 1 ( ) x x e dx     _ _  



.

Karena α > 0, β > 0, dan Γ(x) > 0, diperoleh bahwa 1 / 1 ( ) , 0 ( ) 0 , lainnya x f x _ x e  x           (2.61)

adalah f.k.p dari variabel acak yang bertipe kontinu. Suatu variabel acak X yang mempunyai f.k.p dengan bentuk demikian disebut mempunyai distribusi gamma dengan parameter α dan β, atau dinyatakan dengan X ~ Γ(α, β); dan sebarang f(x) yang demikian disebut dengan f.k.p gamma.