kel and persamaan bdang rata

Makalah Geometri Analitik

BIDANG RATA

D

I

S

U

S

U

N

OLEH :

KELOMPOK VII

 Fitri Lambok Sinaga (4133311035)

 Gustin Maya Sari (4133311017)

 Irene Lasro Sitohang (4133311007)

 Reynold Pasaribu (4133311030)

JURUSAN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS NEGERI MEDAN

2014

Puji syukur penulis panjatkan kehadirat Tuhan Yang Maha Esa, karena berkat limpahan rahmat dan karunianya penulis dapat menyusun makalah ini dengan baik. Dalam makalah ini penulis akan membahas mengenai ” Bidang Rata ”.

Penulis menyadari bahwa masih banyak kekurangan dan keterbatasan penyajian data dalam makalah ini. Oleh karena itu, penulis mengharapkan kritik dan saran yang membangun dari semua pembaca, khususnya Dosen pembimbing demi kesempurnaan makalah ini. Semoga makalah ini dapat menambah pengetahuan pembaca dan menjadi bahan pembelajaran selanjutnya.

Demikian makalah ini penulis susun, apabila ada kekurangan ataupun kesalahan dalam isi makalah ini, penulis mohon maaf yang sebesar-besarnya. Akhir kata semoga makalah ini dapat memberikan manfaat bagi kita semua.

Medan , Desember 2014

Penulis

Kata Pengantar... i

Daftar Isi... ii

BAB I PENDAHULUAN... 1

1.1 Latar Belakang... 1.2 Rumusan Masalah... 1.3 Tujuan...

BAB II PEMBAHASAN...

A. Persamaan Parameter Bidang Rata... B. Persamaan Umum Bidang Rata... C. Vektor Normal Suatu Bidang... D. Bentuk Normal Bidang Rata... E. Sudut Antara Dua Bidang... F. Jarak Titik Ke Bidang Rata... G. Jarak Dua Bidang Yang Sejajar... H. Jaringan Bidang Rata...

BAB III PENUTUP...

a. Kesimpulan... b. Saran...

BAB I

1.1 Latar Belakang

Kata “ geometri ” berasal dari bahasa Yunani yang berarti “ ukuran bumi “. Maksudnya mencakup segala sesuatu yang ada di bumi. Geometri adalah ilmu yang membahas tentang hubungan antara titik, garis, sudut, bidang dan bangun-bangun ruang. Mempelajari geometri penting karena geometri telah menjadi alat utama untuk mengajar seni berpikir. Dengan berjalannya waktu, geometri telah berkembang menjadi pengetahuan yang disusun secara menarik dan logis. Geometri terutama terdiri dari serangkaian pernyataan tentang titik - titik, garis - garis, dan bidang - bidang, dan juga planar (proyeksi bidang) dan benda – benda padat. Geometri dimulai dari istilah istilah yang tidak terdefinisikan, definisi definisi, aksioma -aksioma, postulat - postulat dan selanjutnya teorema - teorema. Berdasarkan sejarah, geometri telah mempunyai banyak penerapan yang sangat penting, misalnya dalam mensurvei tanah, pembangunan jembatan, pembangunan stasiun luar angkasa dan lain sebagainya.

Garis dan bidang merupakan salah satu contoh dari istilah tak terdefinisikan yang menjadi pijakan awal dari geometri, sehingga konsep garis dan bidang sering digunakan dalam geometri. Misalnya adalah perpotongan dari dua bidang akan menghasilkan sebuah garis yang terletak pada dua bidang yang saling berpotongan. Kubus, balok dan lain sebagainya merupakan kumpulan dari bidang – bidang. Dari contoh di atas dapat dipahami bahwa garis dan bidang merupakan faktor dasar geometri, tentunya dengan tidak melupakan bahwa titik juga merupakan dasar dari geometri. Sebuah bidang dapat dianggap sebagai kumpulan titik yang jumlahnya tak terhingga yang membentuk permukaan rata yang melebar ke segala arah sampai tak terhingga.

1.2 Rumusan Masalah

Adapun rumusan masalah dalam penulisan makalah bidang rata adalah :

 Bagaimanakah bentuk persamaan parameter bidang rata ?

 Bagaimanakah bentuk persamaan umum bidang rata ?

 Bagaimanakah bentuk normal bidang rata ?

 Bagaimanakah hubungan sudut antara dua bilangan ?

 Bagaimanakah mencari jarak titik kebidang rata ?

 Bagaimanakah mencari jarak dua bidang rata yang sejajar ?

 Apakah yang termasuk dalam jaringan bidang rata ?

Adapun tujuan dari penulisan makalah ini yaitu :

Mengetahui bentuk persamaan parameter bidang rata.

Mengetahui bentuk persamaan umum bidang rata.

Mengetahui bentuk normal bidang rata.

Mengetahui hubungan sudut antara dua bidang.

Mengetahui dan memahami cara mencari jarak titik kebidang rata.

Mengetahui dan memahami cara mencari jarak dua bidang rata yang sejajar.

Mengetahui dan memahami cakupan dalam jaringan bidang rata

BAB II

PEMBAHASAN

A. Persamaan Parameter Bidang Rata

Suatu bidang rata akan tertentu bila diketahui tiga buah titik yang tak kolinier (tidak segaris) yang terletak pada bidang rata tersebut. Misalkan diketahui tiga titik pada bidang rata V.

´

PQ=

_[

x2−x1, y2−y1, z2−z1

]

´

PR=[x3−x1, y3−y1, z3−z1]

Untuk setiap titik sembarang X (x, y, z) pada bidang rata V berlaku :

PX = λPQ + µPR (-∞ < λ < ∞, -∞ < µ < ∞)

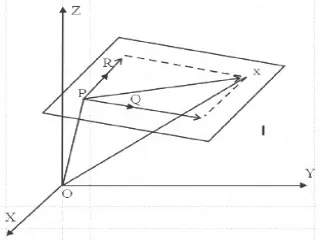
Perhatikan gambar 1.1 tampak bahwa OX = OP + PX atau

[x, y, z] = [x1, y1, z1] + λ[x2 - x1, y2 - y1, z2 - z1] + µ[x3 - x1, y3 - y1, z3-z1]…... (1)

Adalah persamaan bentuk vektor bidang rata yang melalui tiga buah titik. Kedua vektor

´

PQ dan _PR´ _{disebut juga vektor – vrektor arah bidang (setiap dua vector yang tidak} segaris pada bidang merupakan vector-vektor arah bidang tersebut).

Gambar 1.1

Suatu bidang yang melalui titik P(x1, y1, z1) dan diketahui vektor – vektor arahnya

´

a=

_[

x_a, y_a, z_a

_]

dan b´=[x_b, y_b, z_b] mempunyai persamaan dalam bentuk vektor :

[x, y, z] = [x1, y1, z1] + λ[xa, ya, za] + µ[xb, yb, zb]…... (2) dengan (-∞ < λ < ∞, -∞ < µ < ∞). Dari persamaan (2) dapat ditulis menjadi tiga persamaan :

x = x1 + λxa + µxb ………... (3)

y = y1 + λya + µyb…….………...… (4)

z = z1 + λza + µzb ……...………. (5)

Yang disebut sebagai persamaaan bidang rata.

Tentukan persamaan bentuk vektor bidang rata yang melalui (1, 2, 2), (2, 4, 5) dan (1, 2, 6) dan tentukan persamaan parameternya.

Penyelesaian :

Persamaan bentuk vektor bidang rata :

[x, y, z] = [x1, y1, z1] + λ[x2 - x1, y2 - y1, z2 - z1] + µ[x3 - x1, y3 - y1, z3-z1]

Persamaan bidang rata dapat ditulis dalam bentuk lain. Jika λ dan µ pada persamaan (3) dan (4) dieliminasi, maka diperoleh :

λ=yb

(

x−x1

)

−xb(y−y1)

c dan µ=xa

(

y−y1

)

−ya(x−x1)

c , misalkan xa yb – ya xb = c Kemudian λ dan µ disubstitusikan ke persamaan (5), maka diperoleh :

(ya zb – za yb)(x – x1) + (za xb – xa zb)(y – y1) + c(z - z1) = 0 ...(6)

Ambil : ya zb – za yb =

|

y_yaza bzb

|

= A

za xb – xa zb =

|

z_zaxa bxb

|

= B

xa yb – ya xb =

|

x_xaya byb

|

= C

Maka persamaan (6) menjadi : A(x – x1) + B(y – y1) + C(z – z1) = 0

Jadi persamaan linier (umum) bidang rata adalah A(x – x1) + B(y – y1) + C(z – z1) = 0...(7)

 Contoh 1.2 :

Diketahui bidang rata yang melalui titik – titik (1, 2, 2) , (2, 4, 5) dan (1, 2, 6). Tentukan persamaan liniernya.

Penyelesaian :

[x, y, z] = [1, 2, 2] + λ[2-1, 4-2, 5-2] + µ[1-1, 2-2, 6-2]

[x, y, z] = [x1, y1, z1] + λ[xa, ya, za] + µ[xb, yb, zb]

[x, y, z] = [1, 2, 2] + λ [1, 2, 3] + µ [0, 0, 4]

Vektor normal diperoleh dari [1, 2, 3] x [0, 0 , 4] = [8, -4, 0]

Jadi persamaan linier bidang rata yang melalui ketiga titik tersebut adalah :

A(x – x1) + B(y – y1) + C(z – z1) = 0

8(x – 1) – 4(y – 2) + 0 (z – 2) = 0

8x – 8 – 4y + 8 = 0

8x – 4y = 0

C. Vektor Normal Suatu Bidang

Vektor normal adalah vektor yang tegak lurus terhadap bidang datar. Bidang ax + by + cz + d = 0 dan bidang px + qy + rz + s = 0 dikatakan tegak lurus bila normalnya n1 = [a, b, c ] dan n2 = [p, q, r] adalah vektor – vektor orthogonal (tegak lurus), yakni n1.n2 = 0. Maka kedua bidang dikatakan tegak lurus.

Perkalian titik (dot product) dua buah vektor akan menghasilkan sebuah skalar. Jenis perkalian ini bersifat komutatif.

´

A .B´=

(

axi^+ay^j+azk^

)

.(bxi^+by^j+bzk^)

Hasil suatu perkalian silang (cross product) dua buah vektor adalah juga sebuah vektor. Perkalian silang bersifat tidak komutatif.

´

a xb´ merupakan vektor yang tegak lurus pada bidang rata yang di bentuk oleh a´ dan

´

b , yaitu V : Ax + By + Cz + D = 0.

n = [A, B, C] disebut sebagai vektor normal dari bidang rata V = 0

Dari persamaan (7) diatas, suatu bidang rata yang melalui (x1, y1, z1) dengan vektor normal [A, B, C] berbentuk :

A(x – x1) + B(y – y1) + C(z – z1) = 0...(8)

Hal – hal khusus yang perlu diperhatikan dari bidang rata V : Ax + By + Cz + D = 0 diantaranya :

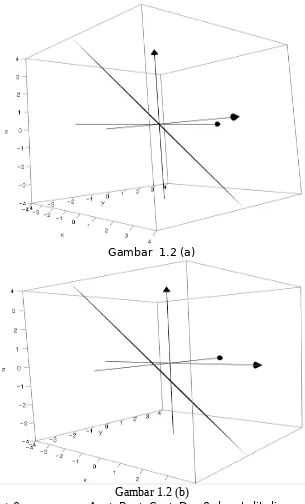
Gambar 1.2 (a)

Gambar 1.2 (b)

 Apabila D ≠ 0 persamaan Ax + By + Cz + D = 0 dapat ditulis menjadi Ax/ -D + By/ -D + Cz/ -D = 1 dan sebut berturut-turut A/ -D = 1/p, B/ -D=1/ q, C/-D =1/ r, didapat persamaan :

x/p + y/q + z/r = 1 yang mana memotong sumbu X di (p, 0, 0 ) sumbu Y di ( 0, q ,0 ) sumbu Z di ( 0, 0, r )...(10)

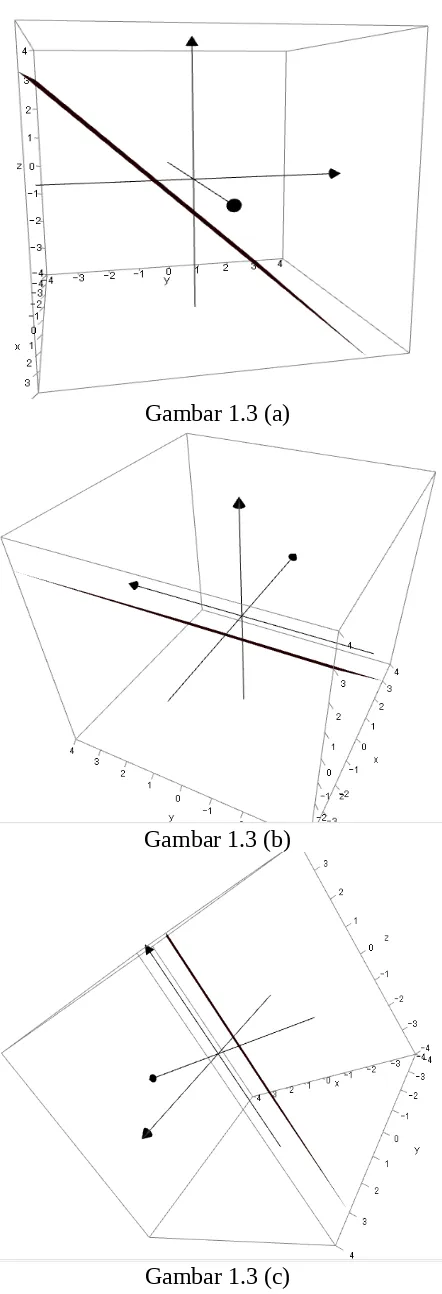
Gambar 1.3 (a)

Gambar 1.3 (b)

Gambar 1.3 (c)

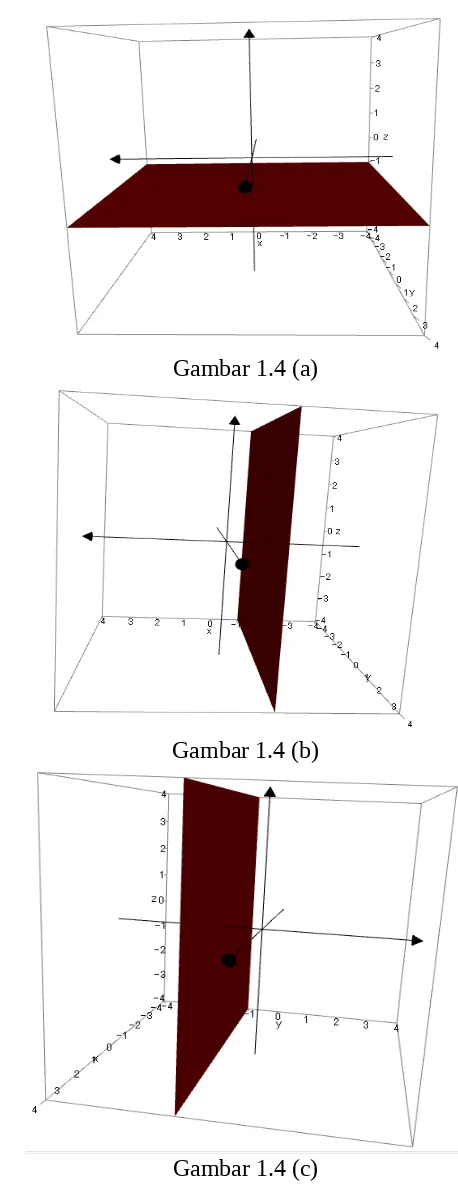
Gambar 1.4 (a)

Gambar 1.4 (b)

Gambar 1.4 (c)

 Contoh 1.3 :

Tentukan titik – titik bidang rata 3x – 4y + 2z + 8 = 0 dengan ketiga sumbu.

Penyelesaian :

3x – 0 + 0 + 8 = 0 ↔ x = -2 ₃2

Titik potong dengan sumbu-Y, x = 0, z = 0

0 – 4y + 0 + 8 = 0 ↔ y = 2

Titik potong dengan sumbu-Z, y = 0, x = 0

0 – 0 + 2z + 8 = 0 ↔ z = -4

Jadi titik potong bidang rata dengan ketiga sumbu adalah

A(-2 ₃2 , 0, 0), B(0, 2, 0), dan C(0, 0, -4)

D. Bentuk Normal Bidang Rata

Misalkan vektor normal bidang V : Ax + By + Cz +D = 0 adalah n = [A, B, C], dan α , β , γ berturut – turut sudut antara n dengan sumbu koordinat (yang arahnya ditentukan oleh vektor i, j, k).

Gambar 1.5

Ternyata bahwa :

cosα= ´n´i

|n´|

|

´_i

_|

=

cosβ= ´n´j

yaitu vektor satuan yang searah dengan n, juga berarti :

cos2_α persamaan normal Hesse dari bidang V = 0.

Untuk mengubah bentuk V : Ax + By + Cz +D = 0 ke bentuk normal maka dari persamaan (13) diperoleh :

|n´| = ( xcosα+ycosβ+zcosγ¿ = - D... (16).

Dimana selalu menghendaki −_|D

Bentuk bidang rata V: Ax + By + Cz +D = 0

6x + 3y -2z -6 = 0

D = - 6 adalah negatif, sedangkan |n´| =

_√

62

+32

+(−2)2 = 7

Jadi persamaan normalnya adalah 6₇ x+3

7 y− 2

7z−6=0

E. Sudut Antara Dua Bidang

Sudut antara dua bidang rata sama dengan sudut antara vektor – vektor normalnya.

Misalkan V₁:A₁x+B₁y+C₁z+D₁=0dan

V₂:A₂x+B₂y+C₂z+D₂=0

Maka sudut antara bidang V1 dan bidang V2 adalah sudut antara normal- normalnya. Jika

|

n´₁

_|

=

_[

A₁, B₁,C₁

]

dan

|

n´₂

_|

=

_[

A₂, B₂,C₂

]

maka

Dua bidang H1 dan bidang H2 dikatakan saling tegak lurus, berarti n´₁ tegak lurus n´₂

Jadi α = cos-1 11

√

156

F. Jarak Titik Ke Bidang Rata

Perhatikanlah bidang V₁:xcosα+ycosβ+zcosγ=p , jarak dari P (x1, y1, z1) ke bidang V₁ ditentukan dengan cara berikut :

= 28

√

49= 28

7 =¿ 4

G. Jarak Dua Bidang Yang Sejajar

Untuk mencari jarak dua bidang sejajar V2, ambil sembarang titik pada V2, lalu menghitung jarak titik tersebut V1.

 Contoh 1.7 :

Diketahui V1 = x + y + z – 2 = 0 dan V2 = x + y + z – 5 = 0. Jika R pada V2, hitunglah jarak tersebut ke V1.

Penyelesaian :

Misal ambil R pada V2 : x = 0, y = 0, dan z = 5 didapat R(0, 0, 5) . Maka jarak titik R ke V1 adalah

d=

|

1.0+1.0+1.5−2

√

12+12+12

|

= 3

√

3 =

√

3

H. Jaringan Bidang Rata

Jika persamaan bidang rata A1x + B1y + C1z + D1 = 0 dinyatakan secara lambang sebagai V1 = 0 dan A2x + B2y + C2z + D2 = 0 sebagai V2 = 0 ,maka V1 + Vƛ 2 = 0. Jika V1dan V2 sejajar ,maka berkas bidang V1 + Vƛ 2 = 0 merupakan himpunan bidang-bidang yang sejajar V1 = 0 dan V2 = 0 (gambar 1.7), dapat ditulis menjadi :

A1x + B1y + C1z = k1 k = parameter

Gambar 1.7

 Contoh 1.8 :

Penyelesaian :

V dapat dinyatakan sebagai V1 + Vƛ 2 = 0 atau

2x + 3y + z + 12 + (x – 4y + z – 10 ) = 0 yang melalui titik (1,2,3) ƛ

 2.1 + 3.2 + 3 + 12 + (1 – 4.2 + 3 – 10 ) = 0 => = ƛ ƛ 23

14 Jadi bidang persamaan V adalah :

2x + 3y + z + 12 + 23

14 (x – 4y + z – 10 ) = 0 atau

51x – 50y + 37z – 62 = 0

BAB III

PENUTUP

Dari hasil pembahasan tentang bidang rata, maka dapat ditarik beberapa kesimpulan diantaranya :

 Bentuk umum (linier) persamaan bidang rata yaitu A(x – x1) + B(y – y1) + C(z – z1) = 0

 Bentuk dari persamaan jarak titik ke bidang rata yaitu

d=

|

A x1+B y1+C z1+D

√

A2+B2+C2

|

.

 Sebuah bidang dapat dikontruksikan dengan cara:

 Melalui tiga buah titik yang tidak segaris.

 Melalui sebuah garis dan sebuah titik diluar garis.

 Melalui dua buah garis yang sebidang atau dua buah garis yang berpotongan dan dua buah garis yang sejajar

 Perbedaan perkalian titik (dot product) dengan perkalian silang ( cross product) yaitu kalau perkalian titik (dot product), dua buah vektor akan menghasilkan sebuah skalar. Jenis perkalian ini bersifat komutatif. Sedangkan perkalian silang (cross product), dua buah vektor adalah juga sebuah vektor. Perkalian silang bersifat tidak komutatif.

 Bentuk persamaan dari sudut yang dibentuk antara dua bidang rata yaitu

cosα= n´1n´2

DAFTAR PUSTAKA

Athma Putri Rosyadi, alfiani. 2012. Analytic Geometry. Malang : Ikip Budi Utomo

Sriwasito, putut. 2007. Bidang dan Garis. Semarang : Universitas Diponegoro

Tim dosen matematika. 2014. Geometri Analitik. Medan : Universitas Negeri Medan

http://lms.unhas.ac.id/claroline/backends/download diakses pada 17 oktober 2014

http://elearning.gunadarma.ac.id/docmodul/matematika_lanjut/bab1-vektor di r3 dan ilmu ukur analitik_ruang.pdf diakses pada 17 oktober 2014

http://toermoedy.files.wordpress.com/2010/11/bab-viii-bidang-rata-dan-garis-lurus.pdf diakses pada 19 oktober 2014

http://intanramadhanisa.blogspot.com/2012/12/persamaan-bidang-datar.html diakses pada 19 oktober 2014

http://sharetogetherbyreynold.blogspot.com/2012/10/persamaan-parameter-bidang-rata.html diakses pada 01 november 2014

http://ediskm.staff.gunadarma.ac.id/Downloads/files/36140/vektor+dan+bidang+rata.ppt diakses pada 07 november 2014