Matematika SMP 002

BAB I

BILANGAN BULAT DAN PECAHAN I. OPERASI BILANGAN BULAT

A. Penjumlahan dan Pengurangan  Sifat Komutatif (Pertukaran)

a + b = b + a Misalnya:

1. 87 + 76 = 76 + 87 2. 214 + 428 = 428 + 214 3. 5 + 78 = 78 + 5

 Sifat Asosiatif (Pengelompokan) (a + b) + c = a + (b + c)

Misalnya:

1. 7 + (8 + 5) = (7 + 8) + 5 2. (3 x 2) x 7 = 3 x (2 x 7)  Sifat identitas

a + 0 = 0 + a = a Misalnya:

4 + 0 = 0 + 4 = 4 B. Perkalian

 Sifat Komutatif (Pertukaran) a x b = b x a

Misalnya: 3 x 4 = 4 x 3

 Sifat Asosiatif (Pengelompokan) (a x b) x c = a x (b x c)

Misalnya:

(2 x 3) x 4 = 2 x (3 x 4)  Sifat Identitas

a x 1 = 1 x a = a Misalnya:

5 x 1 = 1 x 5 = 5

 Sifat Distributif (Penyebaran) a x (b x c) = (a x b) x (a x c) Misalnya:

3 x (2 x 4) = (3 x 2) x (3 x 4) C. Pembagian

Pada pembagian bilangan bulat, berlaku : (a + b) : c = (a : c) + (b : c), c ≠ 0

(a – b) : c = (a : c) – (b : c) Misalnya:

Sifat-sifat : am _{x a}n _{= a}m + n

am _{: a}n _{= a}m - n

(am₎n _{= a}m x n

am _{: b}m _{= (a : b)}m

II. FAKTOR PRIMA, FAKTORISASI PRIMA, FPB DAN KPK a. Faktor Prima

Faktor Prima adalah faktor-faktor suatu bilangan yang merupakan bilangan prima. Bilangan Prima adalah bilangan yang hanya dapat dibagi oleh 1 dan bilangan itu sendiri, Misalnya:

Faktor prima dari 36 adalah 2 dan 3 36

2 18 2 9 3 3

b. Faktorisasi Prima

Faktorisasi Prima adalah perkalian beberapa faktor bilangan prima. Misalnya:

50 Faktorisasi Prima = 2 x 5 x 5 = 2 x ₅2 Faktor Prima = 2 dan 5

2 25 5 5

c. Faktor Persekutuan Terbesar (FPB)

Carilah faktor prima dan bilangan dengan pangkat terendah, misalnya: 18 = 2 x 32

24 = 23 _{x 3}

Jadi FPB dari 18 dan 24 = 2 x 3 = 6 d. Kelipatan Persekutuan Terkecil (KPK)

Carilah faktor prima yang ada dan pangkat yang terbesar, misalnya: 18 = 2 x 32

24 = 23 _{x 3}

Jadi KPK dari 18 dan 24 = 23 _{x 3}2 _{= 72}

III. BILANGAN PECAHAN

A. Penjumlahan dan pengurangan

a b +

c b =

a+c

b , b ≠ 0 a

b - c b =

a−c b

Semua sifat berlaku pada penjumlahan dalam pengurangan bilangan bulat, berlaku pada penjumlahan dan pengurangan pecahan.

Misalnya:

5 9 +

2 9 =

7 11 -

5 11 =

2 11

B. Perkalian dan pembagian

a b x

c d =

a x c b x d

b, c dan d = 0

a b :

c d =

a x d b x c a

b invers perkalian dari b

a a.b ≠ 0

Misalnya:

2 3 x

4 5= 8 15 3 2: 2 3 =

3 5x 3 2= 9 10

C. Perpangkatan pecahan

(

a b

)

n =a n bn Misalnya: 1. 3 2

5+4 1 3−2

1

2 adalah …

Jawab : 3 ₅2+41

3−2 1 2=3

12 30+4

10 30−2

15 30=5

7 30

2. Bentuk sederhana dari 43 4×2

4 5:1

2

5 adalah …

Jawab :

43 4×2

4 5:1

2 5

= 19

4 × 14

5 : 7 5

= 19₄ ×14

5 × 7 5

= 91 2

D. Mengurutkan pecahan

Untuk pecahan yang penyebutnya berbeda dapat dibandingkan dengan aturan seperti di bawah ini :

a b<

c

d jika a x d ¿ b x c

3 7<

6

11 sebab 3 x 11 ¿ 7 x 6

BAB II

BENTUK ALJABAR DAN FAKTORISASI BENTUK ALJABAR I. Bentuk Aljabar

Pada bentuk aljabar 3y + 2x + 3 :  3y, 2x dan 3 disebut suku-suku  x dan y disebut peubah/variabel  koefisien dari 3y adalah 3

 koefisien dari 2x adalah 2

 suku yang tidak mengamdung peubah/variabel disebut konstanta. Konstanta dari bentuk aljabar di atas adalah 3

Pada bentuk aljabar dengan 3x2 _{– xy}2 _{– 5 dan 3xy}2 _{+ 2x}2_{y + 3x}2 _{– 1 adalah}

…

 Suku 3x2y sejenis dengan 2x2y  Suku –xy2 _{sejenis dengan 3xy}2

 Suku 3x2 _{tidak sejenis dengan suku x}

II. Operasi Bentuk Aljabar

a. Penjumlahan dan pengurangan

Hanya berlaku bagi variabel yang sama Misalnya:

1) 6a + 7 + 2a – 4 = 6a + 2a + 7 – 4 = (6 + 2)a + (7 – 4) = 8a + 3

2) 2x + 3y + 4 dikurangi 7x – 4y – 2 = (2x – 7x) + (3y – (-4y)) + (4 – (-2)) = (2 – 7)x + (3 + 4)y + (4 + 2)

= -5x + 7y + 6

b. Perkalian dan pembagian Misalnya:

1) (-7x) (-3y) (-2a) = (-7) (-3) (-2) xya = -42 xya

2) 15xy+10y2

= 15xy

5y +

10y2

5y

= 3x + 2y c. Perpangkatan

Misalnya :

[

4a b

]

2

= 42a2

b2 =

16a2 b2

III. Operasi Hitung pada Pecahan Aljabar Suku Tunggal a. Penjumlahan dan pengurangan

Syarat penyebut harus sama Misalnya: k 4+ 2k 3 = 3k 12+ 8k 12= 11 12k 4a

3b− a+3

b =

4a

3b−

3(a+b)

3b =

4a

3b−

3a−9 3b =

a−9 3b

b. Perkalian dan pembagian Misalnya:

9m. n

4k ×

6k . n2

3m2 =

9n3

2m

4xy

7z :

16y2

14x2z=

4xy

7z ×

14x2z

6y2 =

4x3

3y

IV. Perkalian istimewa bentuk aljabar a. (x + a)(x + b) = x2 _{+ (a + b) x + a.b}

(x + a)(x – b) = x2 _{+ (a – b) x – a.b}

Misalnya:

(3p + 2)(3p + 3) = (3p)2 _{+ (2 + 3) . 3p + 2.3}

= 9p2 _{+ 15p + 6}

(p + 2q)(p – 3q) = p2 _{+ (2q – 3q)p – 2q . 3q}

= p2 _{– pq – 6q}2

b. Pengkuadratan bentuk aljabar (a + b)2 _{= a}2 _{+ 2ab + b}2

(a – b)2 _{= a}2 – 2_{ab – b}2

Misalnya:

(3b + 5)2 _{= (3b)}2 _{+ 2.3b.5 + 5}2

= 9b2 + 30b + 25

(5p – 2q)2 _{= (5p)}2 _{– 2.5p.2q + (2q)}2

= 25p2 _{– 20pq + 4q}2

V. Menyederhanakan operasi pecahan aljabar Misalnya:

1 2x−1−

3

x+5=

P

m n

¿x+5−6x−3

2x2+11x+5

¿ −5x+2

2x2+11x+5 1

a−

1

b

1

ab

=

b−a ab

1

ab

=b−a

VI. Faktorisasi Bentuk Aljabar a. ax + bx = x(a + b) b. a2 _{– b}2 _{= (a + b)(a – b)}

c. x2 _{+ bx + c = (x + m)(x + n), dengan aturan m . n = c dan m + n = b}

d. ax2 _{+ bx + c = a(x + p)(x + q), dimana p + q = b dan p . q = ac}

Misalnya:

Faktorkan bentuk-bentuk berikut ini : a. 4a2_{b + 6a}

b. 25x2 + _{- 9y4}

c. x2 _{– 5x - 6}

d. 4x2 _{- 8x + 3}

e. 32 – 50x2

Jawab:

a. 4a2_{b + 6a = 2a (ab + 3)}

b. 25x2 _{– 9y}4 _{= (5x)}2 _{– (3y2)}2

= (5x + 3y2)(5x + 3y2)

c. x2 _{– 5x – 6 = (x + 1)(x – 6) karena -6 . 1 = -6 dan -6 + 1 = -5}

d. 4x2 _{– 8x + 3 = 4}

(

_x+−6

4

)(

x+

−2 4

)

= (2x – 3)(2x – 1) karena -6 + (--2) = -8 dan -6 . (-2) = 4 . 3

e. 32 – 50x2 _{= 2(16 – 25x}2₎

= 2(42 _{– (5x)}2₎

= 2(4 + 5x)(4 – 5x)

CARA LAIN PEMFAKTORAN BENTUK ax2 _{+ bx + c, dimana a ≠ 1}

Langkah-langkah : ax2 _{+ bx + c}

adalah hasil kali a dengan c

adalah dua bilangan jika dikalikan sama dengan p dan bila dijumlahkan sama dengan b

3 -8

Sehingga bentuk aljabar ax2 _{+ bx + c dapat diubah menjadi bentuk ax}2 _{+ mx}

+ nx + c

Selanjutnya gunakan sifat distributif untuk menguraikan atas faktor-faktornya.

Misalnya:

Faktorkan 6x2 _{– 5x – 4}

Jawab:

6x2 _{– 5x – 4 sehingga 6x}2 _{– 5x – 4 = 6x}2 _{+ 3x – 8x = 4}

= (6x2 _{+ 3x) + (-8x – 4)}

24 = 3x (2x + 1) – 4 (2x + 1) = (3x -4)(2x + 1)

BAB III

ARITMETIKA SOSIAL

I. Harga Pembelian, Harga Penjualan, Untung dan Rugi a. Dalam Keadaan Untung

U = untung

P = persentase untung J = harga jual

B = harga beli Misalnya:

Seorang pedagang sepeda membeli sebuah sepeda Rp 750.000,00. Dijual laku Rp 862.500,00. Berapakah persentase keuntungannya? Jawab:

U = J – B

= 862.500 – 750.000 = 112.500

P=U

B×100 ¿112.500

750.000×100

= 15%

U = J –

B

U= P

100+P× J J=100+P

100 × U B=

100

100+P× J B=

100

P ×U U=

P

100× B

J=100+P

100 × B

P=U

B×100

b. Dalam Keadaan Rugi

R = rugi

q = persentase rugi B = harga beli J = harga jual Misalnya:

1. Harga jual TV 21” Rp 2.100.000. Dengan harga tersebut pedagang rugi 12 1

2 %. Tentukan harga pembelian TV!

Jawab:

B= 100

100−q× J ¿ 100

100−121 2

×2.100 .000

¿ 2.400.000

Jadi harga pembeliian TV adalah Rp. 2.400.000,00

2. Seorang pedagang membeli 1 lusin pot dengan harga Rp. 168.000,00. Karena rusak dalam perjalanan, maka setiap pot dijual dengan harga Rp. 10.500,00. Tentukan persentase kerugiannya! Jawab:

Harga jual = 12 x 10.500 = 126.000

Rugi = 168.000 – 126.000 = 42.000

Persentase rugi= 42.000

168.000×100

= 25% II. Bunga Tunggal

P=B

M×100 Ma=

100+P

100 × M

P% = persentase bunga 1 thn

B = bungan

M = tabungan/modal

B= P

100× M Ma=

100+P

100 × B

R = B

- J

U= q

100−q× J J=100−q

q × R B=

100

100−q× R B=

100

q × R R= q

100× B

J=100−q

100 × B

q=R

B×100

awal

Ma = modal akhir

Bn = bungan ke-n bulan

M=100

P × B n

12× B

M= 100

100+P× M

Misalnya:

1. Amira menabung di bank dengan bunga tunggal 18% setahun. Setelah satu tahun ia menerima bunga Rp. 54.000,00. Berapa besar tabungan Amira?

Jawab:

M=100

P × B ¿100

18 ×54.000

¿300.000

Jadi tabungan Amira Rp. 300.000,00

2. Setelah 1 tahun menabung dengan bunga tunggal 12% setahun, Adin mengambil semua tabungan beserta bunganya sebesar Rp 1.680.000,00. Tentukan besar tabungan Adin semula!

Jawab:

M= 100

100+P× Ma ¿ 100

100+12×1.680 .000

¿1.500.000

Jadi tabungan Adin semula adalah Rp 1.500.000,00. III. Rabat, Bruto, Netto, Tara

Netto (berat bersih) = Bruto – Tara Persentase Tara = Tara

Broto×100

Persentase Rabat (diskon) = Rabat

Harga Awal×100

Misalnya:

Sebuah toko member diskon sebesar 15% terhadap semua barang. Jika seseorang membeli barang seharga Rp 200.000,00. Berapakah yang harus ia bayar?

Jawab: Cara 1 :

Diskon = 15

100×200.000=30.000

Pembayaran = 200.000 – 30.000 = 170.000 Cara 2 :

BAB IV

PERSAMAAN DAN PERTIDAKSAMAAN LINEAR SATU VARIABEL A. PERSAMAAN LINEAR SATU VARIABEL

Bentuk Umum

ax + b = c, a ≠ 0, x = variabel/peubah

Dalilnya adalah kedua ruas harus diberlakukan sama, misalnya : a + b = c

⇔ a + b – c = c – b ⇔ a = c – b

ax = b ⇔ ax

a = b a

⇔ x = b

a

Untuk menyelesaikan persamaan linear satu variabel dilakukan dengan cara: 1. Menambah atau mengurangi kedua ruas dengan bilangan yang sama. 2. Mengalikan atau membagi kedua ruas dengan bilangan yang sama. Misalnya :

1. Penyelesaian dari 3(2x – 5) = 5 (x – 4) adalah … a. 35

b. 36 c. 37 d. 38

Jawaban : A Pembahasan :

x = 35

2. Penyelesaian dari

2 3x−1=

5

x+4 adalah …

a. 1 b. 2 c. 3 d. 4

Jawaban : A Pembahasan :

2 3x−1=

5

x+4

2(x + 4) = 5(3x – 1) 2x + 8 = 15x – 5 2x – 15x = -8 – 5 -13x = -13

x = 1

3. Penyelesaian ₃2(2x−1)=1

2(3x+5)adalah …

a. -19 b. -11 c. 11 d. 19

Jawaban : A Pembahasan :

2

3(2x−1)= 1

2(3x+5) 6.2

3(2x−1)=6. 1

2(3x+5)

4.(2x – 1) = 3.(3x + 5) 8x – 4 = 9x + 15

8x – 9x = 15 + 4 -x = 19

x = -19

B. PERTIDAKSAMAAN LINEAR SATU VARIABEL Bentuk Umum

ax + b <, >, ≤ , ≥ c misalnya :

a + b < c

⇔ a + b – c < c – b ⇔ a < c – b

ax < b

⇔ ax_a <b

⇔ x < b_a

Cara menentukan penyelesaian pertidaksamaan linear satu variabel: 1. Menambah atau mengurangi kedua ruas dengan bilangan yang sama. 2. Mengalikan atau membagi kedua ruas dengan bilangan yang sama

dengan catatan jika dikalikan atau dibagi dengan bilangan negative tanda pertidaksamaan dibalik.

Misalnya:

1. Tentukan penyelesaian dari 4x – 5 < 6x + 13 Jawab :

4x – 5 < 6x + 13

4x – 5 – 6x < 6x + 13 – 6x (kedua ruas dikurangi 6x) -2x – 5 < 13

-2x – 5 + 5 < 13 + 5 (kedua ruas ditambah 5) -2x < 18

−2x

−2 > 18

−2 (kedua ruas dibagi (-2) pertidaksamaan dibalik )

x > -9

2. Jika x {0, 1, 2, 3, …, 10}, maka penyelesaian dari 3x – 5(x – 1) < -4x + 13 adalah…

Jawab :

3x – 5(x – 1) ≤ -4x + 13 3x – 5x + 5 ≤ -4x + 13 -2x + 5 ≤ -4x + 13 -2x + 4x ≤ 13 – 5 2x ≤ 8

X ≤ 4

Jadi x = {0, 1, 2, 3, 4}

PERUBAHAN TANDA!!

Apabila suatu persamaan dikali/dibagi dengan (-) maka tanda akan berubah.

Misalnya :

4x + 24 < 7x + 7

⇔ 4x – 7x < 7 – 24

⇔ -3x < -17

⇔ 3x > 17

BAB V

PERBANDINGAN

A. GAMBAR BERSKALA

Skala = ukuran pada gambar_{ukuran sebenarnya} Perbandingan gambar

Pgambar Psebenarnya=

lgambar lsebenarnya=

tgambar tsebenarnya

Misalnya :

1. Pada sebuah peta dengan skala 1 : 2.500.000 jarak dua kota pada peta adalah 15 cm. Jarak sesungguhnya kedua kota tersebut adalah …

Jawab :

Jarak sesungguhnya = 15 x 2.500.000 = 375 km

2. Sebuah peta dibuat sehingga jarak yang sesungguhnya 80 km dilukis pada peta dengan jarak 16 cm. Skala peta adalah …

Jawab :

Skala = ukuran pada gambar(peta)

ukuran sebenarnya

= 16

80.000.000

= _500.0001

Jadi skala pada peta adalah 1 : 500.000 B. PERBANDINGAN SENILAI

a

b cd

a b=

c

d ad = bc

Misalnya:

1. Sebuah mobil menempuh jarak 100 km dalam waktu 2 jam. Berapa jarak yang ditempuh mobil jika berjalan selama 5 jam?

Jawab : Lama

perjalanan Jarak tempuh 2

5 100x

2 5=

100

x =2x=5.100

X = 250

Jadi jarak yang ditempuh adalah 250 km. 2. Harga 3 kg gula Rp. 20.250

Harga 16 kg gula yang sejenis adalah … Jawab :

Banyak gula

(kg) Harga (Rp)

3

16 20.250X

Dengan perkalian silang : Cara I :

3x = 16 . 20250 3x = 324000 X = 108000 Cara II :

Harga I kg gula = 20250₃ =6750

Harga 16 kg gula = 16 x 6750 = 108000

3. Pada sebuah percetakan kartu undangan diperoleh data sebagai berikut :

Dengan satu mesin selama 6 jam menghasilkan 4000 lembar kertas. Banyaknya kartu undangan yang dikerjakan dengan 3 mesin selama 4 jam adalah …

Jawab :

Mesin Waktu Hasil

1

3 64 4000X

Maka,

Mesin Waktu Hasil

3 6

Waktunya sama banyak

M

Didapatlah m = 12000

Mesin Waktu Hasil

3 3

Banyaknya mesin sama

6

4 12000X

Didapatlah x = 4

6 x12000=8000

Dengan menggunakan cara lain :

Mesin Waktu Hasil

1 x

3 x 64 4000X

Didapatlah x 12

6 x4000=8000

C. PERBANDINGAN BERBALIK NILAI Komponen I Komponen II a

b cd

a b=

c

d ac = bd

Misalnya:

1. Dengan kecepatan 40 km/jam, jarak kota A dan B dapat ditempuh selama 15 jam. Jika kecepatan perjalanan 50 km/jam berapa waktu yang diperlukan untuk menempuh jarak kota A dan kota B?

Jawab : Kecepatan

(km/jam) Waktu (jam) 40

50 15X

40 50=

x

15

x=15.40

50

= 12

Jadi waktu yang diperlukan 12 jam.

2. Suatu proyek yang direncanakan selesai dalam waktu 24 hari dengan 6 pekerja. Jika proyek ingin diselesaikan dalam 18 hari, berapakah tambahan pekerja yang diperlukan?

Jawab :

6

X 2418

6

x=

18 24

X = 8

Jadi banyaknya tambahan pekerja adalah 8 – 6 = 2 orang D. GRAFIK PERBANDINGAN

komponen II

komponen I grafik perbandingan senilai

komponen II

komponen I

grafik perbandingan berbalik nilai

BAB VI HIMPUNAN A. HIMPUNAN

Himpunan adalah kumpulan benda-benda yang didefinisikan dengan jelas atau kumpulan benda-benda atau obejk yang didefiniskan (diberi batasan) dengan jelas.

Misalnya :

P = himpunan bilangan bulat M = {x|x ≤ 4, bilangan cacah}

Untuk menyatakan suatu benda (objek) yang merupakan anggota himpunan dilambangkan ∈ dan jika bukan anggota dilambangkan ∉ , misalnya jika B = {x|x faktor dari 15} maka 3 ∈ B, 4 ∉ B.

Himpunan terhingga adalah himpunan yang anggotanya tertentu misalnya, P = {1, 2, 3, 4, 5}. Sedangkan himpunan tak terhingga adalah himpunan yang anggotanya tak terbatas jumlahnya, misalnya Q = Himpunan bilangan asli.

Himpunan A merupakan himpunan bagian dari B, bila setiap anggota A menjadi anggota B, ditulis dengan notasi A ∁ B, misalnya A = {1, 2, 3}, B = {1, 2, 3, 4, 5} maka A ∁ B. Jika banyaknya anggota suatu himpunan A adalah n(A), maka banyaknya himpunan bagian dari A adalah 2n(A)_{. Misalnya}

A = {1, 2, 3}; n(A) = 3 maka banyaknya himpunan bagian dari A adalah 23 ₌

8.

Himpunan semesta adalah himpunan yang memuat semua objek yang dibicarakan. Himpunan semesta biasanya menggunakan notasi “S”.

Diagram Venn digunakan untuk menyatakan suatu himpunan atau hubungan antar himpunan. Misalnya:

S = {siswa di sekolahan} A = {siswa di kelasmu}

B = {siswa perempuan di kelasmu}

B. OPERASI ANTAR HIMPUNAN 1. Irisan Himpunan

A irisan B ditulis A ∩ B = {x | x ∩ A dan x ∩ B} Misalnya:

Diketahui A = {x | x bilangan prima kurang dari 10} B = {y | 5 ≤ y ≤ 15, y bilangan ganjil}

Tentukan A ∩ B! Jawab:

A = {2, 3, 5, 7}

B = {5, 7, 9, 11, 13, 15} A ∩ B = {5, 7}

2. Gabungan Himpunan

A gabungan B ditulis A ∪ B = {x | x ∪ A atau x ∪ B} Misalnya:

Jika A = {m, u, r, a, h} dan B = {m, e, r, I, a, h}

Maka A ∪ B = {m, u, r, a, h, e, i} 3. Komplemen Himpunan

Komplemen A ditulis A1 atau Ac = {x | x ∈ S dan x ∉ A} Misalnya:

Jika S = {x | x ≤ 10, x bilangan asli} dan P = {2, 3, 5, 7}

Maka pc _{= {1, 4, 6, 8, 9, 10}}

4. Pengurangan Himpunan

S

A

A – B = A ∩ Bc Misalnya:

Jika S = {1, 2, 3, 4, …, 10} A = {2, 3, 4, 5} dan B = {4, 5, 6, 7} Maka A – B = {2, 3}

C. DIAGRAM VENN pada OPERASI HIMPUNAN

BAB VII

SUDUT DAN GARIS

Sudut biasanya dinyatakan dalam derajat (0_{), menit (‘), dan detik (“)}

Tingkatan untuk satuan sudut adalah : 10 _{= 60’}

1’ = 60” 10 _{= 3600”}

Besar sudut satu putaran penuh adalah 3600_{, besar sudut lurus/setengah}

putaran adalah 1800 _{dan besar sudut siku-siku/seperempat putaran}

adalah 900_.

A. Jenis-jenis sudut

Jenis Sudut Besar Sudut Gambar

Sudut lancip 00 _{< α < 90}0

Sudut siku-siku α = 900

Sudut tumpul 900 _{< α < 180}0

Sudut lurus α = 1800

Sudut reflex 1800 _{< α < 360}0

Hubungan dua sudut Sifat Gambar Dua sudut berpelurus

(suplemen)

α + β = 1800

Dua sudut berpenyiku

(komplemen) α + β = 90

0

C. Sudut-sudut pada dua garis sejajar dipotong sebuah garis

Hubungan dua sudut Sifat Gambar

Dua sudut sehadap Besarnya sama α = β

Dua sudut dalam

berseberangan Kedua sudut samabesar α = β

Dua sudut luar

berseberangan Kedua sudut samabesar α = β

Dua sudut dalam

sepihak α + β = 180

0

Dua sudut luar sepihak α + β = 1800

D. Penjumlahan dan pengurangan sudut Misalnya:

30o _{42’ 55” + 15}o _{27’ 11” = ….}

Jawab : 30o _{42’ 55”}

15

o _{27’ 11” +}

46o _{10’ 6”}

Atau

29o _{32’45” – 12}o_49’50”

Jawab :

29o _{32’45” 28}o _91’105”

12

o _{49’50”+ → 12} o _{49’ 50”+}

16o _{42’ 55”}

E. GARIS

1. Hubungan antara dua garis

- Dua garis sejajar jika kedua garis terletak pada satu bidang datar dan tidak berpotongan.

- Dua garis berpotongan jika dua garis itu mempunyai satu titik persekutuan (titik potong).

- Dua garis berimpit jika semua titik pada garis pertama terletak pada garis kedua atau sebaliknya.

[image:19.612.65.552.76.380.2]

AP : PB = m : n AP = _mm

+nx AB gambar

PB = n

m+nx B

Misalnya:

Diketahui ruas garis AB panjangnya 15 cm, titik P terletak pada AB dengan perbandingan AP:PB = 3:2 maka,

AP = 3₅ x15 = 9 cm AP = 2

5 x15 = 6 cm

3. Sifat-sifat garis sejajar

- Aksioma 1 : “melalui dua titik yang berbeda dapat dibuat tepat satu garis lurus.”

- Aksioma 2 : “melalui sebuah titik di luar suatu garis hanya dapat dibuat tepat satu garis yang sejajar dengan garis tersebut.”

- Teorema 1 : “jika sebuah garis memotong salah satu dari dua garis yang sejajar, maka garis itu juga akan memotong garis yang kedua.”

- Teorema 2 : “jika sebuah garis sejajar dengan dua garis lainnya, maka kedua garis itu sejajar.”

BAB VIII STATISTIKA

1. MEAN ( _X´ ₎

Mean ( _X´ _{) adalah nilai rata-rata, jika terdapat data x1, x2, x3, … xn,}

maka nilai rata-ratanya adalah:

´

X = x1, x2, x3, … xn

n keterangan :

xn = data ke-n

n = banyak data Misalnya :

- Nilai rata-rata data nilai : 8, 6, 4, 4, 8, 7, 6, 8, 9, 7adalah …. Jawab :

= 6.7

- Nilai rata-rata 8 anak adalah 6.8. Jika ditambah nilai 2 anak yang lain, rata-ratanya menjadi 7,24. Jumlah nilai kedua anak yang lain tersebut adalah..

Jawab :

Jumlah nilai 8 anak = 8 x 6.8 = 54.5 Jumlah nilai 10 anak = 10 x 7.24 = 72.4 Jumlah nilai 2 anak = 72.4 – 54.4

= 18 2. MEDIAN

Median adalah nilai tengah dari sekumpulan data yang sudah diurutkan. Dalam mencari median, ada dua kemungkinan:

- Jika banyaknya data ganjil, maka median dari kumpulan data tersebut adalah data yang terletak di tengah-tengah. Misalnya, data yang sudah diurutkan tersebut adalah x1, x2, x3, x4, x5 maka mediannya adalah x3.

- Jika banyaknya data genap, maka median dari kumpulan data tersebut adalah jumlah data yang di tengah dibagi dua. Misalkan data yang sudah diurutkan itu ada 6 yaitu x1, x2, x3, x4, x5, x6 maka mediannya adalah x3 +

x4

2 Contoh :

- Tentukan median dari data 5, 8, 4, 6, 6, 7, 9, 8, 6. Data diurutkan sebagai berikut:

4, 5, 6, 6, 6, 7, 8, 8, 9 Median

Jadi mediannya = 6

- Tentukan median dari data : 8, 6, 8, 4, 5, 7, 4, 6, 8, 6 Jawab :

Data diurutkan sebagai berikut: 4, 4, 5, 6, 6, 6, 7, 8, 8, 8

Median

Jadi mediannya = 6 + 6 = 6 2

3. MODUS

Modus adalah data yang sering muncul, misalnya dari data hasil ulangan Matematika dari 40 anak, maka modusnya adalah 6.

4. QUARTIL

Quartil berarti pengelompokkan empat-empat, membagi data yang telah diurutkan menjadi empat bagian yang sama. Untuk menyatakan quartil digunakan huruf Q.

Q2 = quartil tengah/median

Q3 = quartil atas

Misalnya, tentukan Q1, Q2, Q3 dari data 12, 12, 13, 15, 16, 16, 18, 19, 21,

21, 21, 21, 28 Maka :

Q1 = 13+15

2 = 14

Q2 = 16+18

2 = 17

Q3 = 21+21

2 = 21

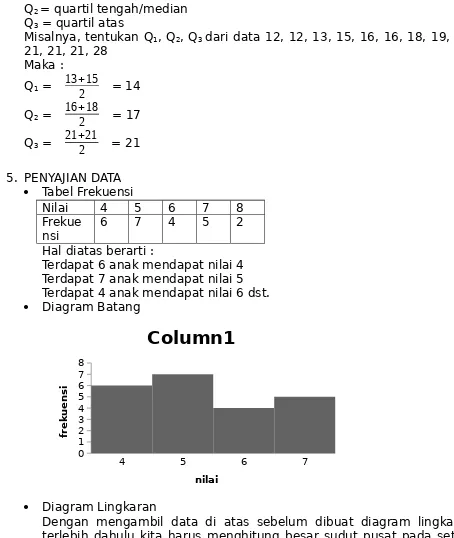
5. PENYAJIAN DATA  Tabel Frekuensi

Nilai 4 5 6 7 8

Frekue

nsi 6 7 4 5 2

Hal diatas berarti :

Terdapat 6 anak mendapat nilai 4 Terdapat 7 anak mendapat nilai 5 Terdapat 4 anak mendapat nilai 6 dst.  Diagram Batang

4 5 6 7

0 1 2 3 4 5 6 7 8

Column1

nilai

fr

e

k

u

e

n

s

i

 Diagram Lingkaran

Dengan mengambil data di atas sebelum dibuat diagram lingkaran terlebih dahulu kita harus menghitung besar sudut pusat pada setiap juring lingkaran sebagai penempatan setiap bagian data.

Nilai Frekuensi Besar sudut pusat

4 6 6

22 x 360o =

5 7 7

[image:22.612.66.520.70.608.2]

6 4 4

22 x 360o =

7 5 5

22 x 360o =

Total 22

Maka diagram lingkarannya adalah :

1st Qtr 2nd Qtr 3rd Qtr 4th Qtr

Contoh soal :

1. Diagram lingkaran di bawah adalah data tentang pekerjaan orang tua murid..

1st Qtr 2nd Qtr 3rd Qtr 4th Qtr

jika banyaknya orang tua murid 48 orang, tentukan banyaknya orang tua murid yang pekerjaannya swasta.

Jawab :

∠ swasta = 360o _{– (45}o _{+ 105}o_{) = 210}o

Banyaknya orang tua siswa yang bekerja di swasta adalah 210

360 x 48 = 28

orang

2. Nilai rata-rata ulangan 12 siswa putra 6,5 sedangkan nilai rata-rata 8 siswa putri 8,0. Tentukan nilai rata-rata gabungan siswa tersebut!

Jawab :

Nilai rata-rata gabungan = jumlahnilai putra_{banyak siswa putra}+jumlah nilai putri +putri

= 12x6,5+8x8,0

12+8

= 142₂₀

1 2 3 4 5

6

8 BAB IX

RELASI DAN FUNGSI A. RELASI

1. Definisi

Relasi adalah hubungan antara dua himpunan yang berbeda. Dua himpunan A ke himpunan B adalah pemasangan anggota-anggota himpunan A dengan anggota-anggota himpunan B. fungsi (pemetaan) → setiap anggota daerah asal (domain) semuanya terpasangkan tepat ke anggota daerah kawan (kodomain).

2. Relasi biasa dinyatakan oleh : a. Diagram panah

b. Grafik Cartesius

c. Himpunan pasangan berurutan Misalnya:

Jika A = {1, 2, 3, 4, 5} dan B = {6, 8}, maka tunjukkan relasi dari A ke B yang menyatakan “faktor dari” dengan ; diagram panah, grafik cartesius, dan himpunan pasangan berurutan.

1 2

3 A

B c b.

c. Himpunan pasangan berurutan {(1,6), (1,8), (2,6), (2, 8), (3,6), (4, 8)}

B. FUNGSI

Fungsi f dari A ke B adalah relasi yang memasangkan setiap anggota A dengan tepat satu anggota B

F : A → B Misalkan

Fungsi linier adalah fungsi yang peuba bebasnya paling tinggi berpangkat satu. Misalnya, Fungsi f : x 3 → x – 1 dengan x → R, maka ini berarti fungsi f pada himpunan R ditentukan oleh f(x) = 3x – 1, dimana x disebut peubah/variabel bebas.

Cara yang mudah untuk menggambar grafik fungsi pada koordinat cartesius yaitu dengan membuat tabel fungsi. Misalnya, bagaimana menggambar fungsi f(x) = 2x – 3 untuk x ∈ R pada bidang cartesius adalah :

X 0 1½

f(x) -3 0

Dari tabel, ini didapatkan dua titik pada bidang cartesius yang memenuhi fungsi tersebut, yaitu (0, -3) dan (1½, 0)

Y f(x) = 2x - 3 1 ½ x

-3

Kemudian, nilai suatu fungsi dapat dihitung dengan menstubtitusikan bilangan ke dalam rumus fungsi. Misalnya, diketahui fungsi f(x) = 4 – 3x, tentukan nilai fungsi f untuk x = 5

Dan jika f(m) = 10 tentukan m! Jawab :

f(x) = 4 – 3m = 10 f(5) = 4 – 3.5 = 4 – 15

f(m) = 4 – 3m = 10 ⇔ -3m = 10 – 4 ⇔ -3m = 6 ⇔ m = -3

Selanjutnya banyak fungsi dari A ke B adalah

b

a misalnya jika A = {a, b, c} dan B = {x | x < 10, x bilangan prima} maka tentukan banyaknya pemetaan dari A ke B, maka N(A) = 3 dan n(B) = 4, maka banyaknya pemetaan dari A ke B = 43 = 64.

BAB X

POLA BILANGAN, BARISAN DAN DERET A. MACAM POLA BILANGAN

1. Pola bilangan ganjil

1 3 5 7 +2 +2 +2 Pola ke n = 2n – 1

2. Pola bilangan persegi

1 4 9 16 12 ₂2 ₃2 ₄2

Pola ke n = n2

1 3 6 10

1₂x2 2x₂3 3x₂4 4₂x5 Pola ke n = n(n+1)

2

4. Pola bilangan persegi panjang

2 6 12 20 1x2 2x3 3x4 4x5 Pola ke n = n(n+1)

5. Pola bilangan segitiga paskal

1 baris 1

1 1 baris 2 1 2 1 baris 3

1 3 3 1 baris 4 1 4 6 4 1 baris 5

Misalnya :

Gambar berikut menunjukkan pola suatu barisan bilangan. Banyaknya garis batang pada pola ke 10 adalah …

Jawab :

Banyaknya garis batang pada pola ke 1 = 3 Banyaknya garis batang pada pola ke 2 = 7 Banyaknya garis batang pada pola ke 3 = 11 Banyaknya garis batang pada pola ke 4 = 15, dst 3, 7, 11, 15, 19, 23, …

+4 +4 +4 +4 +4

Jadi banyaknya garis batang pada pola ke 10 adalah 39 buah. B. BARISAN DAN DERET ARITMETIKA

 Barisan bilangan

Adalah urutan bilangan-bilangan menurut aturan tertentu. Misalnya: a. 5 , 10 , 15 , 20 , …

+5 +5 +5

Suku berikutnya diperoleh dengan menambahkan 5 pada suku sebelumnya.

[image:27.612.87.439.69.352.2]

Suku berikutnya diperoleh dengan mengalikan 3 pada suku sebelumnya.

 Barisan aritmetika

Adalah memiliki ciri selisih atau beda antara dua suku yang berurutan selalu tetap, misalnya:

2 , 5 , 8 , 11 , 14 , … +3 +3 +3 +3

Suku ke 1 suku ke 5

(U1=a) (U5)

Selisih dua suku yang berdekatan = 3 atau beda (b) = 3 Dari contoh di atas dapat diketahui bahwa :

U1 = a = 2 beda → b = U2 – U1

U2 = 5 = U3 – U2

U3 = 8 dan seterusnya = Un – Un – 1

Untuk rumus suku ke n barisan aritmetika adalah …

U

n

= a + (n – 1) b

Jadi rumus suku ke n dari barisan aritmetika 2, 5, 8, 11, 14, … Un = 2 + (n – 1) 3

= 2 + 3n – 3 Un = 3n – 1

 Deret aritmetika

Adalah jumlah dari suku-suku barisan aritmetika. Jumlah n suku pertama deret aritmetika adalah:

Sn =

1₂

n (a + Un)

Sn =

1₂

n (2a + (n – 1)b)

Misalnya:

Diketahui deret aritmetika 3 + 7 + 11 + 15 + 19 + 23 + 27 + 31 + 35 + 39. Tentukan jumlah suku dari deret tersebut!

Jawab:

Banyak suku n = 10 → U10 = 34

a = 3 Sn = 1₂n(a+Un)

= 1

210(3+39)

= 5(42) = 210] Contoh soal!

Sn = 1₂n(a+Un) = 1

250(1+99)

= 1₂50.100=2500

2. Diketahui deret aritmetika dimana suku pertamanya 4 dan bedanya 3

Tentukan :

a) Rumus suku ke n

b) Jumlah 20 suku pertama Jawab :

a) Rumus suku ke n Un = a + (n – 1) b

= 4 + (n – 1) 3 = 3n – 1

b) Jumlah 20 suku pertama Sn = 1

2n(a+Un)

= 1₂20(4+61) = 650

 Barisan geometri

Barisan geometri memili ciri yaitu perbandingan antara dua suku yang berurutan selalu tetap, misalnya :

2, 4 , 8, 16 , 32 , … Suku ke 1 = (a) Suku ke 4 = U4

U₂ U1

=U3

U2 =U4

U2

=2 , jadi rasio r barisan = 2

Untuk menentukan suku ke n digunakan rumus :

U

n

= ar

n-1

Rumus suku ke n barisan di atas : Un = 2 x 2n – 1

Un = 2n

 Deret geometri

Deret geometri adalah jumlah dari suku-suku barisan geometri. Rumus jumlah n suku pertama deret geometri :

Sn = a1−r

n

1−r ,r<1

Sn = a r

n −1

r−1 ,r>1

Misalnya :

Jawab :

1. Jumlah n suku pertama pada deret geometri dicari dengan rumus : Sn = a1−r

n

1−r ,r ≠1 rumus ini digunakan jika r < 1

Sn = a r

n −1

r−1 ,r ≠1 rumus ini digunakan jika r > 1

Dari penjelasan di atas didapat : a = 2, r = 2 ( r > 1), n = 7

Sn = a r

n −1

r−1

S7 = 2(2

7 −1)

2−1

= 2(128−1)

2−1

= 2 . 127 = 254

NB : mencari rumus suku ke n dengan beda yang tidak tetap. 2. Tentukan rumus suku ke n dari barisan bilangan

3 7 13 21 31 … a + b + c 4 6 8 10 … a + 3b

2 2 2 … 2a

Secara umum rumus suku ke n dari barisan bilangan tersebut dapat ditulis:

Un = an2 + bn + c

Selanjutnya untuk menentukan nilai a, b, dan c dilakukan sebagai berikut :

2a = 2 a = 1

a + 3b = 4 1 + 3b = 4 3b = 3

b = 1

a + b + c = 3 1 + 1 + c = 3

c = 1

BAB XI PELUANG

A. Ruang Sampel dan Titik Sampel

Pada suatu percobaan himpunan semua hasil yang mungkin diperoleh disebut ruang sampel. Sebagai contoh percobaan pelemparan sebuah dadu, hasil yang mungkin diperoleh mata dadu 1, 2, 3, 4, 5, atau 6. Jadi dalam hal ini ruang sampelnya adalah S = ruang sampel = {1, 2, 3, 4, 5, 6). Tiap-tiap anggota pada ruang sampel disebut titik sampel.

Cara membuat ruang sampel adalah :

1. Dua uang logam yang sama dilepmar bersama-sama. Susunlah ruang sampelnya!

Jawab:

G A

G (G,

A (A,

G) (A,A) G = gambar A = angka

Ruang sampelnya adalah { GG, GA, AG, AA } yang terdiri dari 4 ruang sampel.

2. Dua buah dadu merah dan biru dilempar bersama-sama. Susunlah ruang sampelnya!

Jawab :

1 2 3 4 5 6

1 (1,

1) (1, 2) (1, 3) (1, 4) (1, 5) (1, 6) 2 (2,

1) (2, 2) (2, 3) (2, 4) (2, 5) (2, 6) 3 (3,

1) (3, 2) (3, 3) (3, 4) (3, 5) (3, 6) 4 (4,

1) (4, 2) (4, 3) (4, 4) (4, 5) (4, 6) 5 (5,

1)

(5, 2)

(5, 3)

(5, 4)

(5, 5)

(5, 6) 6 (6,

1) (6, 2) (6, 3) (6, 4) (6, 6) (6, 6) Banyaknya ruang sampel adalah 36.

3. Jika sebuah dadu dan sebuah uang logam dilempar sekali. Tentukan banyaknya sampel yang ada!

Jawab :

1 2 3 4 5 6

A (A,

1) (A, 2) (A, 3) (A, 4) (A, 5) (A, 6) G (G,

1) (G, 2) (G, 3) (G, 4) (G, 5) (G, 6) Angka = Dadu

Huruf = Uang

Maka banyaknya ruang sampel yang ada adalah 12.

B. Menghitung Peluang

Rumus =

P(A) =

n_n(₍A_S))

n(S) = banyaknya anggota sampel

n(A) = banyaknya kejadian pada percobaan yang bersangkutan p(A) = nilai peluang munculnya kejadian A

1. Sebuah dadu dilempar sekali. Tentukan peluang munculnya mata dadu genap dan mata dadu bilangan prima!

Jawab :

Kejadian muncul mata dadu genap adalah {2, 4, 6} Jadi n (A) = 3

P(A) = ₆3 = 1₂

Kejadian banyak muncul mata dadu bilangan prima adalah {2, 3, 5} Jadi banyaknya kejadian = 3

Peluang muncul mata dadu bilangan prima 3

6 = 1 2

2. Tiga uang logam yang sama dilempar sekali bersama-sama. Tentukan peluang munculnya :

- Dua angka dan satu gambar! - Ketiganya angka!

Jawab :

Ruang sampel = {GGG, AGG, GAG, GGA, AAG, AGA, GAA, AAA} - Peluang munculnya dua angka dan satu gambar = 3₈

- Peluang muncul ketiganya adalah = 1

8

3. Dua dadu yang sama dilempar sekali bersama-sama. Tentukan peluang muncul :

- Mata dadu berjumlah 10 - Mata dadu berjumlah 12 Jawab :

Banyaknya ruang sampel adalah 36

- Peluang muncul mata dadu berjumlah 10 = ₃₆3 = 1

12

- Peluang muncul mata dadu berjumlah 12 = ₃₆1 C. Frekuensi Harapan

Frekuensi harapan kejadian A ditulis E(A) dari n kali percobaan dirumuskan :

E(A) = P(A) x n

Misalnya :

Sebuah dadu dilempar 120 kali. Tentukan frekuensi harapan munculnya mata dadu bilangan prima!

Jawab :

E(prima) = P(Prima) x n = 1₂ x 120

BAB XII

BILANGAN BERPANGKAT DAN BENTUK AKAR A. Pengertian

a pangkat n atau ditulis an diartikan sebagai : an _{= a x a x … x a → sebanyak n factor}

misalnya :

53 _{= 5 x 5 x 5 sebanyak 3 faktor}

(2x3_{) = 2x . 2x . 2x}

B. Pangkat Negatif dan Nol a-n ₌ 1

an

= 1_a x 1_a x … x 1_a dengan syarat a ≠ 0 ↓

Sebanyak n factor Misalnya :

3-4 ₌ 1

34

= 1

3x 1 3x

1 3x

1 3 =

1 81

a0 _{= 1 untuk setiap a bilangan nyata}

C. Bilangan Pecahan Berpangkat  ( a

b¿ n = an

bn syarat b ≠ 0

 ( 1

b¿ n =

1

bn  ( a

b¿ -n = bn an Misalnya : ( 2

3¿ 3 = 23 33 =

8 27

( 1₄¿ -2 ₌ 4

2

12 = 16 ( 3

4¿ 2 = 32

42 = 9 16

D. Bentuk Akar Bilangan Bulat Menjadi Bilangan Berpangkat Pecahan n

√

am

=

_amn

Misalnya : a.

√

4

23 ₌ 2

3 4

b.

√

5 = ₅12 c. 3

√

8 = ₈13 d.

√

273 ₌

27

3 2

E. Akar Kuadrat

Untuk a, b bilangan nyata positif

√

a

= b ↔ a = b

2

Misalnya:

√

16 = 4 ↔ 16 = 42

√

24 = 6 ↔ 36 = 62

√

100 = 10 ↔ 100 = 102

Sifat :

√

a x b

=

√

a

x

√

b

√

a

b

=

√

a

√

b

Misalnya :

√

121x36 =

√

121 x

√

36

= 11 x 6 = 66

√

48 =

√

16 x

√

3 = 4

√

3

√

72 =

√

36 x

√

2 = 6

√

2

√

75 =

√

25 x

√

3 = 5

√

3

F. Operasi pada Bilangan Berpangkat - (a x b)n _{= a}n _{x b}n

- am

an = a

m-n

- am _{x a}n _{= a}m+n

-

(

a

b

)

m

= a m

bm -

(

am

)

n _{= a}m x n

- n

√

m

√

a =

(

_ami

)

1 n =

a

1 mn

-

√

√

2 =

(

₂12

)

1 2 =

-

√

√

√

x =

(

(

_x12

)

1 2

)

1 2 ₌

x

1 8

Misalnya :

1. 34 _{x 3}2 _{= 3}4 + 2 _{= 3}6

2. (3 x 5)2 _{= 3}2 _{x 5}2 _{= 9 x 25 = 225}

3. 4 6

44 = 46 – 4 = 42 = 16 4.

(

8

2

)

3

= 83

23 = 512

8 = 64

5. (33₎2 _{= 3}3 x 2 _{= 3}6

6. 2-3 ₌ 1

23 =

1 8

7. (-4)2 _{= -4 x (-4) = 16}

8. (3a)-3 ₌ 1

(3a)3 =

1

3a x3a x3a =

1 27a3 Contoh Soal!

1. Bentuk sederhana dari

√

75 +

√

12 -

√

48 adalah … Pembahasan :

√

75 +

√

12 -

√

48 =

√

25

√

5 +

√

4

√

3 -

√

16

√

3

= 5

√

3 + 2

√

3 – 4

√

3

= 3

√

3

2. Nilai dari 3

√

√

5y+4 = 2 adalah … Pembahasan :

3

√

√

5y+4 = 2

5(y + 4)⅙ _{= 2}

5y + 4 = 26

5y + 4 = 64 5y = 60 y = 12

3. Diketahui

√

2 = a dan

√

3 = b Nilai dari

√

12 +

√

32 adalah … Pembahasan :

√

12 +

√

32 =

√

4

√

3 +

√

16

√

2

= 2

√

3 + 4

√

2

BAB XIII

SISTEM PERSAMAAN LINIER DUA VARIABEL A. Bentuk Umum

a1x + b1y = c1

a2x + b2y = c2

misalnya : 2x – 3y = 4 X + y = -5 B. Penyelesaian

Pasangan nilai x dan y yang memenuhi semua persamaan dalam sistem tersebut disebut penyelesaian dari sistem persamaan linier dua variabel. - Metode Eliminasi

Misalnya:

Tentukan HP dari 2x – y = 4 dan x + 3y = -5

 Menentukan nilai x, maka ya dieliminasi dengan cara sebagai berikut :

2x – y = 4 |x 3 6x – 3y = 12

x + 3y = -5 |x 1 x + 3y = -5 + 7x = 7

x = 1

 Menentukan nilai y, maka x dieliminasi dengan cara sebagai berikut :

2x – y = 4 |x 1 2x – y = 4

x + 3y = -5 |x 2 2x + 6y = 10 -7y = 14

y = -2 Jadi HP = {(1, -2)}

- Metode Substitusi

Dari contoh di atas, bentuk x + 3y = -5 dapat diubah menjadi : x = -5 – 3y

Nilai x = -5 – 3y disubstitusikan ke persamaan 2x – y = 4 sehingga diperoleh :

-10 – 7y = 4 -7y = 4 + 10 -7y = 14 y = -2

Untuk y = -2 disubstitusikan ke salah satu persamaan. Misalnya ke persamaan 2x – y = 4

2x – (-2) = 4

2x + 2 = 4

2x = 2 x = 1 Jadi HP = {(1, 2)} - Metode Grafik

Untuk menyelesaikan sistem persamaan 2x – y = 4

x + 3y = -5

Kedua persamaan dapat digambar pada grafik kartesius : Garis 2x – y = 4

x 0 2

y -4 0

-5 -4 -3 -2 -1 0 1 2

Garis x + 3y = -5 2 (1,2)

x 0 2

y

-1 ½

0

C. Model Matematika

Adalah terjemahan soal cerita dalam bentuk sistem persamaan linier matematika.

Misalnya :

Jumlah umur Wawan dan Asep 30 tahun. Selisih umur mereka 6 tahun. Jika Wawan lebih tua dari Asep tentukan :

a. Model matematikanya b. Umur masing-masing Jawab :

a. Misal umur Wawan = x dan umur Asep = y Jumlah umur = 30 → x + y = 30

Selisih umur = 6 → x – y = 6 Jadi model matematikanya :

x – y = 6_ + 2x = 36 x = 18 x + y = 30

x – y = 6_ 2y = 24 y = 12

jadi umur Wawan adalah 18 tahun dan Asep adalah 12 tahun.

BAB XIV

TEOREMA PYTHAGORAS A. Rumus Pythagoras

Jika segitiga ABC siku-siku di A, maka berlaku : a2 _{= b}2 _{+ c}2

b2 _{= a}2 _{– c}2

c2 _{= a}2 _{– b}2

B. Tripel Pythagoras

Tripel pythagoras merupakan rangkaian tiga bilangan bulat positif yang ketiganya masing-masing merupakan panjang dari sisi-sisi suatu segitiga siku-siku.

Rumus Tripel Pythagoras

Jika a dan b bilangan bulat positif dan a > b, maka 2ab, a2 _{– b}2_{, a}2 _{+ b}2

merupakan tripel pythagoras. Misalnya:

a b 2ab a2 _–

b2 a

2 ₊

b2 Bentuk_pythagoras tripel

2 1 2 3 5 3, 4, 5

3 2 12 5 13 5, 12, 13

BAB XV

PERSAMAAN GARIS LURUS A. Gradien Garis

Persamaan garis lurus dengan satu variabel adalah ax + b = c Persamaan garis lurus dengan dua variabel adalah y = mx + c

Garis g memotong sumbu x di A (-a, 0) Garis g memotong sumbu y di B (0, b)

Gradien garis g = komponen y garis g_{komponen x garis g} = b

a

Garis g mirng (condong) ke kanan, maka gradien positif Garis yang miring (condong) ke kiri, gradiennya negatif Misalnya:

Gradien garis g adalah garis g condong ke kanan, maka gradien

Gradien garis h adalah garis h condong ke kiri, maka gradien

Garis h adalah negatif.

a. Gradien Garis yang melalui dua titik

Gradien garis yang melalui titik A (x1, y1) dan B (x2, y2) dapat dicari

dengan rumus :

m = y1y2

x1x2

atau y2y1

x2x1 misalnya :

Tetapkan gradien garis yang melalui A(-5, 2) dan B(4, -1)! Jawab :

m = y2 y1

x2x1

= −1−2

4−(−5) = −3

9

= - 1₃

b. Gradien garis yang persamaannya diketahui

Garis yang diketahui persamaannya ay = bx + c mempunyai gradien m = b

a

misalnya :

Tentukan gradien garis dengan persamaan 2x – 3y + 5 = 0! Jawab :

2x - 3y + 5 = 0 3y = 2x + 5 y = ₃2x + 5₃

Gradien garis y = 2

3 x + 5

3 adalah 2 3

Garis m sejajar n garis m tegak lurus garis n

Jika gradien garis m adalah x1 dan gradien garis n adalah x2, maka :

- Agar garis m dan n sejajar harus dipenuhi syarat : x1 – x2

- Agar garis m dan n saling tegak lurus, maka harus dipenuhi syarat : x1.x2 – 1

Misalnya pasangan garis yang sejajar

- Garis h dengan persamaan 3x + 2y – 5 = 0 dengan - Garis I dengan persamaan 3x + 2y + 2 = 0

Misalnya pasangan garis yang saling tegak lurus - Garis m dengan persamaan 5x – y + 8 = 0 dengan - Garis n dengan persamaan x + 5y – 3 = 0

Generally :

a. Garis yang melalui (x1, y1) dan tegak lurus garis ax + by + c = 0,

persamaanya adalah bx – ay = bx1 = ay1

b. Garis yang melalui (x1, y1) dan sejajar garis ax + by + c = 0,

persamaannya adalah ax – by = ax1 – by1

Contoh!

1. Tentukan persamaan garis melalui (-5, 2) dan tegak lurus dengan garis 3x -5y + 2 = 0.

Jawab :

3y + 5x = 3(2) + 5(-5) 3y + 5x = -19

3y + 5x + 19 = 0

2. Tentukan persamaan garis melalui (2,1) dan sejajar dengan garis 2x + 3y -5 = 0.

Jawab :

2x + 3y = 2(2) + 3(1) 2x + 3y = 7

2x + 3y + 7 = 0

C. Persamaan Garis Lurus

- Persamaan garis lurus yang bergradien m dan melalui titik A(x1, y1)

dapat diketahui dengan rumus :

y – y

1

= mx –x

1

- Persamaan garis yang melalui titik A(x1, y1) dan B(x2, y2) dapat

diketahui dengan rumus:

y – y

1

=

x_2−¿x1 y₂−y₁

¿

- Persamaan garis yang bergradien m dan melalui (o, q) dapat diketahui dengan rumus :

y = mx + c

Contoh!

1. Tentukan persamaan garis yang melalui titik A(-3, 5) dan bergradien 2! Jawab :

Persamaan umum : y = mx + c Karena m = 2, maka : y = 2x + c Melalui A(-3,5) ⇔ y = 2x + c

⇔ 5 = 2(-3) + c ⇔ c = 11

Jadi, persamaan garis yang dicari y = 2x + 11

2. Tentukan persamaan garis melalui A(5,2) dan B(-3,4) Jawab :

y – y1 =

x_2−¿x1 y₂−y₁

¿

(x – x1)

y – 2 = 4−2

−3−5 (x – 5)

y – 2 = 2

−8 (x – 5)

-8(y – 2) = 2(x – 5) -8y + 16 = 2x – 10 2x + 8y – 26 = 0 x + 4y – 13 = 0

3. Tentukan persamaan garis melalui (3,5) dan bergradien 2. Jawab :

y = mx + c y = 2x + c

Karena garis melalui (3,5) maka harus dipenuhi : 5 = 2.3 + c

5 = 6 + c C = -1

BAB XVI LINGKARAN

A. Unsur – Unsur Lingkaran

O = pusat lingkaran OA = jari – jari lingkaran AC = diameter

Daerah arsiran I = juring atau sektor lingkaran Daerah arsiran II = tembereng

Garis lengkung BEC = busur lingkaran Garis lurus BC = tali busur

OD = aphotema

Sudut AOB = sudut pusat Sudut ACB = sudut keliling SUDUT PUSAT DAN KELILING

- Sudut pusat = 2 x sudut keliling ATAU sudut keliling = 1₂ x sudut pusat.

- Sudut-sudut keliling yang menghadap busur yang sama adalah sama besar.

- Jumlah sudut pada bangun segi empat di dalam lingkaran yang sehadap adalah sebesar 1800_.

B. Keliling dan Luas lingkaran

Rumus Keliling Lingkaran adalah : K = π d

= 2 π r

Rumus Luas Lingkaran adalah : L = π r2

= 1₄ π d2

Contoh Soal!

Tentukan luas dan keliling daerah arsiran berikut!

Jawab :

Luas = 1

4 π r2

= 1₄ .3,14 . 10 . 10 = 78,5

Keliling = OA + OB + BA = 10 + 10 + 1

4 + 3,14 . 20

= 35,7

C. Hubungan Sudut usat, Panjang Busur dan Luas Juring

Panjang busur AB =

a

360 x keliling

lingkaran

Luas juring = a

360 x

luas lingkaran

Sudut a adalah sudut pusat

Sudut b adalah sudut keliling

Maka berlaku : ao _{= 2b}o

busur AB

busurCD =

sudut a sudut b

= luas juring OAB

Contoh!

Dari gambar di samping, luas juring AOB = 96 cm2 _{dan ∠ AOB}

= 40 ∠ . Jika luas

juring DOC = 84 cm2_{, berapakah besar sudut COD!}

Jawab:

luas juring AOB

∠AOB =

luas juring COD

∠COD x

96 40 =

84

x = 35

Jadi besar ∠ COD = 35o

Atau

Dari gambar di samping diketahui OA = 21 cm ∠ ABC = 600, maka ∠ AOC = 2 x 600 = 1200 Maka Luas daerah AOC = 120

0

3600 x luas lingkaran = 1₃ x 22₇ x 21 x 21 = 462

Jadi luas juring AOC = 462o

D. Segi n Beraturan

Besar sudut pusat segi n adalah 3600

n

Besar tiap-tiap sudut segi n adalah 1800 _- 3600

n atau

n−2x180

n

Jumlah sudut-sudut segi n = 180n - 3600

Misalnya :

Tentukan besar sudut segi n beraturan jika besar sudut pusat segi n tersebut 720!

Jawab :

Besar sudut segi n = 1800 _{– 72}0

= 1080

E. Segi Empat Tali Busur

∠ A + ∠ C = 1800

∠ B + ∠ D = 1800

Misalnya :

Pada gambar di samping, jika ∠ ABC = (4x – 10)0 _dan

Jawab :

∠ B + ∠ D = 1800

4x – 10 + x + 5 = 1800 _{5x – 5 = 180}0

5x = 185 x = 37

F. Sudut Antara Dua Tali Busur

Besar ∠ AEB = 1

2 ( ∠DOC+∠AOB )

Besar ∠ ABC = 1

2 ( ∠AOC+∠DOE )

Misalnya :

Diketahui busur PS = 1400 _{dan busur QR = 60}0

Hitunglah besar sudut QTR! Jawab :

∠ QTR = 1

2 (busur PS + busur QR)

= 1₂ (1400 _{+ 60}0₎

= 1000

G. Garis Singgung

Panjang garis singgung persekutuan luar =

PL =

R−r ¿ ¿ AB2−¿

√¿

Panjang garis singgung persekutuan dalam

PD =

R+r ¿ ¿ AB2−¿

√¿

Misalnya :

Jawab :

Jarak kedua pusat lingkaran = x, maka

x =

R+r ¿ ¿ PD2+¿

√¿

=

√

162+122

=

√

400

= 20

Jadi, jarak kedua pusat lingkaran adalah 20 cm. H. Lingkaran Luar dan Lingkaran Dalam Segitiga

Panjang jari-jari lingkaran dalam

segitiga Panjang jari-jari luar segitiga

r= luas segitiga ABC

1

2keliling segitiga ABC

r= AB . AC . BC

4luas segitiga ABC

Misalnya :

Dalam segitiga siku-siku PQR panjang sisi QR = 15 cm, PQ = 9 cm, dan PR = 12 cm. Tentukan panjang jari-jari lingkaran luarnya!

Jawab :

PQ = 9, PR = 12, QR = 15

Luas ∆ PQR = PQ X PR

2

= 9x₂12 = 54 L = PQ . PR . QR

4luas segitiga PQR

= 9.₄12_.54.15 = 7,5

BAB XVII

1. Kesebangunan

Dua bangun datar dikatakan sebangun yaitu bentuk kedua bangun sesuai dengan bentuk aslinya dengan ukuran diperbesar atau diperkecil, jika : - Sudut-sudut yang bersesuaian sama besar.

- Sisi-sisi yang bersesuaian mempunyai perbandingan yang sama.

Gambar

Pada bangun KLMN dan PQRS :

∠ K = ∠ P

∠ L = ∠ Q ⇒ sudut-sudut yang bersesuaian sama besar

∠ M = ∠ R

∠ N = ∠ S

Bangun KLMN sebangun dengan PQRS jika memenuhi :

KL QR=

LM SR=

MN PS =

NK PQ

Misalnya :

1. Panjang PS adalah … Jawab :

Gambar AB

CD= QR

PS

8 10=

20

PS

BPS = 200 PS = 25

Jadi panjang PS adalah 25 cm.

2. Sebuah foto ditempel pada karton sehingga pada sebelah kiri, kanan dan atas foto masih tersisa karton dengan lebar 6 cm. Jika panjang dan lebar foto berturut-turut 12 cm dan 10 cm, maka lebar karton di bawah foto adalah …

Jawab :

panjang foto lebar foto =

panjang karton lebar karton

12 10=

18+x

10(18 + x) = 12 . 28 180 + 10x = 264 10x = 84

X = 8,4

Jadi lebar karton di sebelah bawah foto adalah 8,4 cm.

Dua segitiga dikatakan sebangun yaitu bentuk kedua bangun sesuai dengan bentuk aslinya dengan ukuran diperbesar atau diperkecil, jika : - Sudut-sudut yang bersesuaian sama besar.

- Sisi-sisi yang bersesuaian memiliki perbandingan yang sama. Misalnya :

Segitiga PQR sebangun dengan segitiga KLM, karena memenuhi syarat :

∠ P = ∠ K GAMBAR ∠ R = ∠ L ∠ Q = ∠ M Dan berlaku PR_KL= PQ

KM= QR ML

Untuk menghitung panjang sisi pada bangun segitiga yang sebangun dapat digunakan rumus berikut :

1. a

b= c d=

p q−p

a a+b=

p q=

c c+d

GAMBAR

2. Jika ∆ ABC siku-siku di B dan BD ⊥ AC, maka berlaku rumus : BC2 _{= CD . CA}

BA2 _{= AD . AC}

BD2 _{= DA . DC}

GAMBAR

3. Jika sudut EBC dan sudut EDC saling berpelurus, maka berlaku rumus :

AB AD=

EB CD=

AE AC

GAMBAR

a b=

c

d x =

p . b+q . a a+b

GAMBAR

Contoh Soal!

1. Pada gambar di samping besarnya x adalah … Jawab :

12 8 =

12+x

18

8(12 + x) = 12 . 18 96 + 8x = 116 8x = 120 x = 15 Jadi, x = 15

2. Diketahui PS = 64 cm dan SR = 36 cm. Tentukan QS, QR dan QP! Jawab :

a. QR2 _{= RS . RP}

QR =

√

36.100

QR = 60 cm b. QS2 _{= SP . SR}

QS =

√

64.36

QS = 48 cm c. QP2 _{= PS . PR}

QP =

√

64.100

QP = 80 cm

3. Pada gambar di bawah ini diketahui sisi AB = 8 cm, AE = 4 cm, ED = 6 cm dan CD = 2 cm. Tentukan panjang sisi EF!

Jawab : a. Cara 1

Buatlah garis DG // CB memotong di EF di H AG = 8 – 2 = 6 cm

DE DA=

EH AG⟺

6 10=

EH

6

EH = 3,6 EF = 2 + 3,6 EF = 5,6 cm

[image:51.612.83.532.72.694.2]

EF = dc . ae_de+ab . de +ae EF=2.4+8.6

6+4

EF = 5,6 cm

4. Diketahui sisi CE = 5 cm, BE = 10 cm dan BD = 6 cm. Tentukan panjang sisi AD!

Jawab :

BD BC=

BE AB

6 15=

10

AB

6 AB = 10 + 15 AB = 25 – 6 AB = 19 cm

2. Kekongruenan

Syarat dua segitiga dikatakan kongruen yaitu bangun-bangun mempunyai bentuk dan ukuran yang sama adalah :

1. Satu sisi dan dua sudut pada sisi itu sama. ∠ A = ∠ P (sudut)

AB = PQ

∠ B = ∠ Q

2. Tiga sisi bersesuain sama besar. KL = DE

KM = DF LM = EF

3. Dua sisi dan dua sudut yang diapit sama. TI = RH

∠ I = ∠ H IK = HS

BANGUN RUANG SISI LENGKUNG, BANGUN RUANG SISI DATAR DAN BANGUN DATAR

BANGUN RUANG SISI LENGKUNG A. TABUNG

Rumus mengitung Tabung - Luas Tabung

L ¿π r2

- Luas Selimut Tabung

L=2π r t

- Luas Alas Tabung L = π r2

Rumus Luas Tabung

L =

2π r2

+

2π r t

L =

2π r(r+t)

Rumus Volume Tabung

V =

π r2

t

Contoh Soal!

1. Sebuah drum berbentuk tabung dengan jari-jari 24 cm dan tinggi 70 cm berisi penuh air. Kemudian air dalam drum tersebut seluruhnya akan ditaruh dalam kaleng-kaleng kecil masing-masing memiliki jari-jari 6 cm dan tinggi 10 cm, sehingga kaleng penuh dengan air. Tentukan banyaknya kaleng kecil yang diperlukan!

Pembahasan:

volume drum volume kaleng=

V₁ V2

= π r 2_t

1

π r2_t 2

= 242.70

62.10

= 112 buah

2. 10 kaleng susu terbuat dari alumunium. Jari-jari kaleng 10 cm dan tingginya 15 cm (π = 3,14). Jika harga 1 m2 _{alumunium Rp. 210.000,}

tentukan biaya pembelian kaleng! Pembahasan :

Luas 10 kaleng susu adalah : 10 L = 10 . 2 π r (r + t)

= 20 . 3,14 . 10 (10 + 15) = 628 . 25

Biaya pembelian kaleng :

15700

10000 x210000=329700

Jadi biaya pembelian bahan kaleng adalah Rp. 329.000

B. KERUCUT

- Selimut kerucut L = πrs

- Alas kerucut L = πr2

Rumus Luas Kerucut

L

= p π

2

+ π r s

= p π (r + s)

Rumus Volum Kerucut

V

=

1₃

π r

2

t

Contoh Soal!

1. Sebuah benda berbentuk kerucut dengan tinggi 3 m dan alasnya berjari-jari 4 m. Untuk membuat tenda digunakan kain dengan harga Rp 5.000 tiap meter persegi. Tentukan besarnya dana yang diperlukan untuk pembelian bahan tenda!

Pembahasan :

Luas tenda = luas selimut kerucut L = π r s

Dana yang diperlukan = 5000 . L = 5000 . π r s

= 5000 . 3,14 . 4 . 5 = 314.000

Jadi dana yang diperlukan untuk membeli bahan tenda adalah Rp. 314.000

2. Sebuah tempat air berbentuk kerucut berdiameter 70 cm dan tingginya 60 cm penuh berisi air. Tentukan Volum tempat tersebut! Pembahasan :

Rumus volum kerucut = 1

3 π r2 t

= 1

3 . 22

7 . 70

2 . 70

2 . 60

= 77.000

C. BOLA

Unsur-unsur bola - Pusat bola

- Jari-jari bola GAMBAR - Diameter bola

Rumus Luas Bola

L = 4 π r

2

Rumus Volum Bola

V =

4₃

π r

3

Contoh Soal!

1. Sebuah benda berbentuk belahan bola padat dengan jari-jari 14 cm. Tentukan luas dan volum benda tersebut!

Pembahasan :

a. Luas benda = 3 x luas lingkaran = 3 π r2

= 3 . 3,14 . 14 . 14 = 1848

Jadi luas benda adalah 1848 cm2

b. Volum benda = 1

2 volum bola

= 1₂ . 3₄ . 22₇ . 14 . 14 . 14 = 5749 1₃ cm3

2. Sebuah bola berada di dalam tabung sehingga bola menyinggung setiap sisi tabung. Jika volum tabung 200 cm3_{, tentukan volum bola}

tersebut! Pembahasan :

Volume tabung volume bola =

3 2

Sehingga Vbola = Vtab x ₃2

= 369 x 2

3 = 264 cm3

[image:55.612.70.540.75.724.2]

A. KUBUS

Ciri-ciri kubus adalah :

- Mempunyai 6 sisi berbentuk persegi. - Mempunyai 8 buah titik sudut.

- Setiap sisi kubus mempunyai 2 buah diagonal sisi, misalnya diagonal sisi CF, EB, BD dsb.

- Mempunyai 4 buah diagonal ruang yaitu HB, DF, EC, dan AG. - Mempunyai 6 bidang diagonal, misalnya ACGE.

Contoh jarring-jaring kubus adalah :

GAMBAR

Untuk sebuah kubus yang panjang rusuknya a cm, maka :

Jumlah panjang rusuknya = 12 a

Panjang diagonal sisi = a

√

2

Panjang diagonal ruang = a

√

3

Luas permukaan kubus = 6a

2

Volume kubus = a

3

(a x a x a)

Contoh Soal!

1. Luas permukaan kubus adalah 150 cm2_{. Tentukan volum kubus!}

Pembahasan : L = 6a2

150 = 6a2

25 = a2

a =

√

25

a = 5

V = a3

= 53

= 125

Jadi volum kubus adalah 125 cm3

Jumlah panjang rusuk balok = 4 (p x l x t) Panjang diagonal ruang balok =

√

p2_{x l}2_{x t}2 Volum balok = p x l x t

Luas permukaan = 2 (pl + pt + lt) Contoh Soal!

1. Perbandingan panjang, lebar dan tingg sebuah balok 5 : 2 : 1. Jika volum balok 270 m3_{. Tentukan ukuran balok!}

Pembahasan : V = p x l x t 270 = 5x . 2x . x 270 = 10x3

27 = x3

X =

√

27

X = 3

2. Sebuah ruangan berbentuk balok berukuran p = 4 m, l = 3 m, dan t = 12 m. Tentukan pipa terpanjang yang dapat masuk ke dalam ruangan tersebut!

Pembahasan :

Misalnya panjang pipa yang dapat masuk ke ruangan adalah r, maka : r =

√

p2

+l2

+t2

=

√

42 +32

+122 =

√

169

= 13 C. PRISMA

Di bawah ini adalah prisma segitiga ABCDEF

Volume prisma = luas alas x tinggi

Luas permukaan = 2 x luas alas + keliling alas x tinggi Contoh Soal!

Sebuah prisma alasnya berbentuk segitiga siku-siku dengan panjang sisi siku-siku masing-masing 6 cm dan 8 cm. jika tinggi prisma 5 cm, tentukan luas permukaan prisma!

Jawab :

Sisi miring alas =

√

62+82 = 10

= 2 x 6x₂8 + (6 + 8 + 10) x 5 = 48 + 120

= 168

Jadi luas permukaan prisma adalah 168 cm2

D. LIMAS

Rumus menghitung Limas adalah : Volum Limas = luas alas x tinggi

Luas Limas = luas alas + jumlah luas sisi atas Contoh Soal!

Sebuah limas alasnya berbentuk persegi dengan panjang sisi 12 cm. Jika tinggi limas 8 cm, tentukan luas permukaan limas!

Pembahasan :

Tinggi segitiga sisi atas =

√

62+82 = 10 (pakai rumus phythagoras)

L = luas alas + jumlah luas sisi atas = 12 . 12 + 4 . 1₂ . 12 . 10

= 144 + 240 = 384

Jadi luas permukaan limas adalah 384 cm2

BANGUN DATAR A. SEGITIGA

Jika AC = b, AB = c dan BC = a, maka : Keliling segitiga ABC = K = a + b + c

Luas segitiga ABC = L =

√

s(s−a) (s−b)(s−c) Dimana S = 1

2keliling

Contoh Soal!

Segitiga ABC siku-siku dengan sisi AB = 15 cm, BC = 20 cm dan AC = 25 cm. Tentukan keliling dan luasnya!

Pembahasan :

a. K = a + b + c = 15 + 20 + 25 = 60 cm

= 1₂ x 15 x 20 = 150 cm2

Atau

L =

30−25 1

2(30−15)(30−20)¿ √¿

=

√

30x15x10x5

=

√

22500

= 150

Jadi luas segitiga = 150 cm2

Rumus-rumus dalam Segitiga N

o Gambar Keterangan rumus

1 ∠ A + ∠ B + ∠ C = 1800

2 ∠ C2 = ∠ A + ∠ B

3 CD ⊥ AB, CD garis tinggi pada sisi AB

EB ⊥ AC, EB garis tinggi pada sisi AC EB : CD = 1

AC :

1

AB

4 Jika ta garis tinggi pada sisi a, maka :

ta = 2

a

√

s(s−a)(s−b)(s−c)

tb = 2_b

√

s(s−a)(s−b)(s−c)

tc = 2

c

√

s(s−a) (s−b)(s−c)

s = 1₂ keliling segitiga

5 CD garis bagi pada ∆ ABC, maka ∠ C1

= ∠ C2

C1 = _bbc

+a

C2 = ac

b+a

6 Bila dc adalah garis sudut C, maka :

dc2 = ab – c1 c2

bila da dan db masing-masing garis bagi

[image:59.612.88.565.252.703.2]

(da)2 = bc – a1a2

(db)2 = ac – b1b2

7 SA : SP = 2 : 1

SB : SQ = 2 : 1 CS : SR = 2 : 1

8 Jika Pa garis berat ke sisi a, maka :

Pa2 = 1₂b

2 +1

2c

2 −1

4a

2

Jika Pb dan Pc masing-masing garis berat ke

sisi b dan c, maka : (Pb)2 = 1

2a

2 +1

2c

2 −1

4b

2

(Pc)2 = 1₂a

2 +1

2b

2 −1

4c

B. SEGIEMPAT

No Nama Gambar _Keliling Rumus _luas

1 Persegi K = 4s L = s2

L = 1

2 D2

2 Persegi

panjang K = 2 x (p + l) L = p x l

3 Belah

ketupat K = 4a L =

1

2 x D1 x

D2

4 Jajar genjang K = 2 x (a + b) L = a x t

5

Layang-layang K = 2 x (a + b) L =

1

2 (D1 x

D2)

6 Trapesium K = a + b + c

+ d L =

1

2 (a +

[image:60.612.84.563.71.272.2]

BAB XIX

PERSAMAAN KUADRAT A. Bentuk Umum

ax2 _{+ bx + c = 0}

Misalnya :

2

x−3+ 1

x+3 = 2, x ≠ 3 dan x ≠ 2

⇔ 2 (x + 3) + 1 (x – 2) = 2 (x – 2)(x + 3) ⇔ 2x + 6 + x – 2 = 2 (x2 _{+ x – 6)}

⇔ 3x + 4 = 2x2 _{+ 2x – 12}

⇔ 2x2 _{– x – 16 = 0}

B. Akar P