Model Pengintegrasian Nilai Pendidikan Karakter

(1)

(2)

1. Menggunakan konsep integral dalam pe-mecahan masalah.

Standar Kompetensi Kompetensi Dasar Nilai Indikator

1.1 Memahami konsep integral tak tentu dan integral tentu.

1.2 Menghitung integral tak tentu dan integral tentu dari fungsi aljabar dan trigonometri yang sederhana. 1.3 Menggunakan integral untuk

meng-hitung luas daerah di bawah kurva dan volume benda putar.

Pada bab ini akan dipelajari:

1. Integral sebagai lawan dari turunan (antiderivatif) 2. Integral tak tentu dan integral tertentu fungsi aljabar 3. Integral tak tentu dan integral tertentu fungsi trigonometri 4. Integral substitusi dan integral parsial

5. Luas daerah di bawah kurva dan volume benda putar

Teliti

Cermat

Teliti dalam menentukan hasil pengintegralan.

Cermat dalam menentukan batas-batas daerah yang akan dihitung luas atau volumenya.

Model Pengintegrasian Nilai Pendidikan Karakter

Integral

Mendefinisikan konsep integral fungsi aljabar

• Menentukan hasil integral tak tentu fungsi aljabar • Menentukan hasil integral

tertentu fungsi aljabar • Menentukan rumus fungsi

jika diketahui turunannya

• Menentukan hasil integral tak tentu fungsi trigono-metri

• Menentukan hasil integral tertentu fungsi trigonometri

• Melakukan pengintegralan dengan metode substitusi • Melakukan pengintegralan

dengan metode parsial

• Menentukan luas daerah yang dibatasi kurva • Menentukan volume benda

putar Mendefinisikan konsep

integral fungsi trigonometri

Menentukan hasil integral dengan metode

peng-integralan

Menggunakan integral untuk menentukan luas daerah dan

volume benda putar

Siswa mampu menentukan integral fungsi aljabar

Siswa mampu menentukan integral fungsi trigonometri

Siswa mampu menentukan hasil integral dengan metode substitusi dan

parsial

Siswa mampu mengguna-kan integral untuk menentukan luas daerah

dan volume benda putar

(3)

v(t) = 0⇔ 5t –

2 1

t2_{= 0}

⇔ ₂1t(10 – t) = 0

⇔ t = 0 atau t = 10

Jadi, benda berhenti setelah 10 detik. 5. Jawaban: b

dy

dx = 4x + 5

y =

∫

(4x + 5) dx = 2x2_{+ 5x + c}

Kurva melalui titik (–3, –3). y = 2x2_{+ 5x + c}

⇔ –3 = 2(–3)2_{+ 5(–3) + c}

⇔ –3 = 2(9) – 15 + c

⇔ –3 = 18 – 15 + c

⇔ –3 = 3 + c

⇔ c = –6

Jadi, persamaan kurva tersebut y = 2x2_{+ 5x – 6.} 6. Jawaban: c

3

1

∫

(3x2_{+ 2x – 1) dx =}

3

2 1 1 1

1

3 2

2 1x 1 1x x

+ +

 

 ₊ ₊ 

 + − 

= 3 2 3

1

x x x

 + − 

 

= (33_{+ 3}2_{– 3) – (1}3_{+ 1}2_{– 1)} = (27 + 9 – 3) – (1 + 1 – 1) = 33 – 1

= 32

7. Jawaban: c

2

1

∫

(x2_–

2

1 x ) dx =

2

1

∫

(x2_{– x}–2_{) dx}

=

2

3 1

1

1 1

3x 1x

−

 

 ₋ 

 − 

=

2 3

1

1 1

3x x

 

 

 + 

= (8

3 + 1 2) – (

1 3 + 1)

= 19₆ – 4₃

= 11

6 A. Pilihan Ganda

1. Jawaban: a

∫

3x−_{x x}4x2 x dx =

∫

( 3x x x –

2

4x x x x ) dx

=

∫

(3 1 2

x− – 4x) dx = 1

2

3 1

− + 1 2 1

x− + – 4

1 1+ x1 + 1 + c

= 1 2

3 1₂

x – 4₂x2_{+ c}

= 6 x – 2x2_{+ c} 2. Jawaban: b

∫

(2x – 3)(3x + 2) dx =

∫

(6x2_{– 5x – 6) dx} = _{2 1}6₊ x2 + 1_– 5

1 1+ x1 + 1 – 6x + c = 6

3x3 – 5

2x2 – 6x + c

= 2x3_–5

2x2 – 6x + c

3. Jawaban: d

f′(x) = 3x2_{+ 6x – 5 dan f(–1) = 8} f(x) =

∫

f′(x) dx

=

∫

(3x2_{+ 6x – 5) dx} = 3 · ₃1x3_{+ 6 ·}1

2x2 – 5x + c

= x3_{+ 3x}2_{– 5x + c}

f(–1) = 8 ⇒ (–1)3_{+ 3(–1)}2_{– 5(–1) + c = 8}

⇔ –1 + 3 + 5 + c = 8

⇔ c = 1

Jadi, f(x) = x3_{+ 3x}2_{– 5x + 1.} 4. Jawaban: c

Percepatan = a(t) = 5 – t

dv(t)

dt = a(t) ⇒ v(t) =

∫

a(t) dt =

∫

(5 – t) dt

= 5t –

2 1

t2_{+ c} Benda bergerak dari keadaan diam maka v(0) = 0 ⇒ c = 0.

Kecepatan benda dirumuskan v(t) = 5t –

2 1

(4)

8. Jawaban: e

9. Jawaban: d

3

Oleh karena tidak ada nilai x yang memenuhi persamaan x2_{+ 3x + 7 = 0 maka penyelesaiannya} a = 2.

Jadi, 1₂a = 1₂ × 2 = 1.

10. Jawaban: b

(5)

A. Pilihan Ganda

1. Jawaban: c

∫

(cos 2x – 2 sin x) dx =

∫

cos 2x dx – 2

∫

sin x dx = 1

2 sin 2x – 2(–cos x) + c

= 1₂ sin 2x + 2 cos x + c 2. Jawaban: d

∫

(3 – 6 sin2_{x) dx =}

∫

_{3(1 – 2 sin}2_{x) dx} = 3

∫

cos 2x dx = 3 · 1₂ sin 2x + c

= 3₂ · 2 sin x cos x + c = 3 sin x cos x + c

3. Jawaban: b

sin a cos b = 1

2(sin (a + b) + sin (a – b))

∫

4 sin 5x cos 3x dx

=

∫

4 · ₂1(sin 8x + sin 2x) dx = 2

∫

(sin 8x + sin 2x) dx = 2(–1

8 cos 8x – 1

2cos 2x) + c

= –1

4 cos 8x – cos 2x + c

4. Jawaban: b

∫

sin (₂1x – π) cos (₂1x – π) dx =

∫

1

2sin 2( 1

2x – π) dx

= ₂1

∫

sin (x – 2π) dx = –1

2 cos (x – 2π) + c

b. 2

2

1 (px

∫

– 4x + 5) dx = 20

⇔ 3 2 2

1

p

3x 2x 5x

 ₋ ₊ 

 

  = 20

⇔(8p₃ – 8 + 10) – (p₃ – 2 + 5) = 20

⇔ 7p₃ – 1 = 20

⇔ 7p₃ = 21

⇔ p = 21 × 3₇ = 9

4. a. f′(x) = 4 – 6x

f(x) =

∫

f′(x) dx =

∫

(4 – 6x) dx = 4x – 3x2_{+ c}

f(3) = –12 ⇒ 4(3) – 3(3)2_{+ c = –12}

⇔ 12 – 27 + c = –12

⇔ c = 3

Jadi, f(x) = –3x2_{+ 4x + 3.}

b. 2

1

−

∫

f(x) dx = 2

1 −

∫

f(x) dx =

2

1 −

∫

(–3x

2_{+ 4x + 3) dx}

= 3 2 2

1

x 2x 3x ₋

− + + 

 

= (–8 + 8 + 6) – (1 + 2 – 3) = 6 – 0 = 6

5. 6

0

∫

f(x) dx = 3

0

∫

f(x) dx + 6

3

∫

f(x) dx

= 3

0

∫

(x + 4) dx + 6

3

∫

(2 – 4x) dx

=

3 2

0

1

2x 4x

 

 

 +  +



2x – 2x2 6 3  

= (9₂ + 12) – (0 + 0)

+ (12 – 72) – (6 – 18)

= (9₂ + 12) – 0 + (–60) – (–12)

= 9₂ – 36

= –31₂1

Jadi, nilai 6

0

∫

f(x) dx = –31₂1.

(6)

5. Jawaban: d

∫

1 cos 2x− dx =

∫

2 sin x2 dx =

∫

2sin x dx = – 2cos x + c 6. Jawaban: e

1 7. Jawaban: d

0

8. Jawaban: b

1

9. Jawaban: b

2

10. Jawaban: e

(7)

b

a

∫

sin 2x dx =

b

a

1 2cos 2x

 



− 

=

b 2

a

1

2(1 2 sin x)

 



− − 

=

b 2

a

1

2 sin x

 



− + 

= (–1

2 + sin2 b) – (– 1

2 + sin2 a)

= sin2_{b – sin}2_a

= (sin b – sin a)(sin b + sin a) = c (sin b + sin a)

= c (sin a + sin b)

Terbukti bahwa b

a

∫

sin 2x dx = c(sin a + sin b).

5. a. f′(x) = 12 cos 2x f(x) = ∫ 12 cos 2x dx

= 12 · 1

2sin 2x + c

= 6 sin 2x + c

f_₁₂π_ = 8

⇔ 6 sin 2_₁₂π_ + c = 8

⇔ 6 sin ₆π + c = 8

⇔ 6 · 1

2 + c = 8

⇔ 3 + c = 8

⇔ c = 5

Diperoleh f(x) = 6 sin 2x + 5.

b. f  _{ }₄π = 6 sin 2  _{ }₄π + 5

= 6 sin ₂π + 5 = 6 · 1 + 5 = 11 b.

∫

(sin 2x – cos 2x)2_dx

=

∫

(sin2_{2x – 2 sin 2x cos 2x + cos}2_{2x) dx} =

∫

(sin2_{2x + cos}2_{2x – 2 sin 2x cos 2x) dx} =

∫

(1 – sin 4x) dx

= x + ₄1 cos 4x + c

3. a. 2 0 π

∫

(cos 2x + sin 3x) dx

= 2

0

1 1

2sin 2x 3cos 3x

π

 

 

 − 

= (1₂ sin π – ₃1 cos 3₂π) – (₂1 sin 0 – 1₃ cos 0)

= (0 – 0) – (0 – 1₃) = ₃1

b. 2

4 π

π

∫

2 cos (₄π – x) dx

= 2

4 2

1sin (4 x)

π

π π

 

 

− − 

= –2 (sin (–₄π) – sin 0)

= –2 (–1₂ 2 – 0) = 2

c. 3 0 π

∫

6 sin x cos x dx

= 3 0 π

∫

3 sin 2x dx

= 3

0

3 2cos 2x

π 

− _

 

= –3₂ (cos 2₃π – cos 0)

= –3

2(– 1 2 – 1)

= –3

2(– 3 2)

= 9

4

4. b

a

∫

cos x dx = c

⇔

b

a sin x

 

 

(8)

A. Pilihan Ganda

1. Jawaban: c

Misalkan u = 2x2_{+ 8x + 1} 2. Jawaban: d

Misalkan u = 2x3_{– 5}

3. Jawaban: c

Misalkan u = 2x3_{+ 4} 4. Jawaban: c

Misalkan u = 3x2_{+ 9x – 1} 5. Jawaban: c

(9)

6. Jawaban: c

1

a∫12x(x

2_{+ 1)}2_{dx = 14}

⇔ 6

1

a∫(x

2_{+ 1)}2_{· 2x dx = 14}

⇔ 6 · 2 3

1 1

3(x + 1) _a

 



  = 14

⇔ 2((1 + 1)3_{– (a}2_{+ 1)}3_{) = 14}

⇔ 8 – (a2_{+ 1)}3_{= 7}

⇔ (a2_{+ 1)}3_{= 1}

⇔ a2_{+ 1 = 1}

⇔ a2_{= 0}

⇔ a = 0

7. Jawaban: c

Misalkan u = sin 2x

du

dx = 2 cos 2x ⇔ 1

2du = cos 2x dx

∫

cos 2x sin 2x dx =

∫

(sin 2x)

1

2_{(cos 2x dx)}

=

∫

u 1 2₍1

2du)

= 1

2

∫

u

1 2_du

= 1₂ · 2₃u 3 2_{+ c} = 1

3u u + c

= 1₃ sin 2x sin 2x + c 8. Jawaban: c

0 π

∫

sin2x cos x dx

= 0 π

∫

(2 sin x cos x) cos x dx

= 2 0 π

∫

cos2_{x sin x dx}

= 2 0 π

∫

(cos x)2_{d(–cos x)}

= –2 0 π

∫

(cos x)2_{d(cos x)}

= –2 · 1 3

3(cos x) ₀

π  

= –2₃ (cos3_π_{– cos}3₀₎

= –2

3(–1 – 1)

= 4

3

9. Jawaban: b

Misalkan u = cos 2x

du

dx = –2 sin 2x ⇔ sin 2x dx = – du

2

∫

cos4_{2x sin 2x dx}

=

∫

u4_(–du

2 )

= –1

2

∫

u

4_du

= –1

2 · 1 5u

5_{+ c}

= – 1

10 cos

5_{2x + c}

10. Jawaban: b

Misalkan u = (x2_{– 2)} _⇒ _{du = 2x dx}

dv = sin x dx ⇒ v =

∫

sin x dx = –cos x

∫

u dv = uv –

∫

v du

∫

(x2_{– 2) sin x dx}

= (x2_{– 2) (–cos x) –}

∫

_{(–cos x) (2x dx)} = –(x2_{– 2) cos x +}

∫

_{2x cos x dx} = (2 – x2_{) cos x + 2}

∫

_{x d(sin x)}

= (2 – x2_{) cos x + 2 (x sin x –}

∫

_{(sin x) dx)} = (2 – x2_{) cos x + 2x sin x – 2 (–cos x) + c} = (2 – x2_{) cos x + 2x sin x + 2 cos x + c} = (4 – x2_{) cos x + 2x sin x + c}

B. Uraian

1. a. Misalkan u = 5 – x

du

dx = –1 ⇔ dx = –du

∫

₅2₋_x dx =

∫

2_u (–du)

= –2

∫

u 1 2 −

du

= –2 · 2u 1 2_{+ c} = –4 5−x + c b. Misalkan u = x2_{– 3}

du

dx = 2x ⇔ 2x dx = du

∫

2x(x2_{– 3)}3_{dx =}

∫

_(x2_{– 3)}3_{· 2x dx} =

∫

u3_du

= 1₄u4_{+ c}

= 1

4(x

(10)

(11)

∫

4x

Jadi, luas daerah:

L = L_I + L_II = 11₃ + 1₃1 = 22₃ satuan luas.

= 0 – (–11₃)

= 11₃ satuan luas

Jadi, luas daerah yang diarsir:

L = L_I + L_II = 11₃ + 1₃1 = 22₃ satuan luas.

1. Jawaban: d

(12)

Luas daerah yang diarsir:

2. Jawaban: a

x + y = 2 ⇔ y = 2 – x Luas daerah yang diarsir:

L =

3. Jawaban: a

Persamaan garis yang melalui titik (2, 0) dan (0, 2)

y 0

L = 4. Jawaban: c

(13)

Y 5. Jawaban: b

L =

6. Jawaban: c

Volume benda putar:

V =π

7. Jawaban: d

Volume benda putar:

V = π

8. Jawaban: c

Batas-batas daerah yang diarsir menurut sumbu Y. Batas atas: y = x3 _⇔ _{x =}y13

Batas bawah: y2_{= x}

Kedua kurva berpotongan di titik (0, 0) dan (1, 1), berarti batas-batas nilai y adalah 0 ≤ y ≤ 1. Volume benda putar:

(14)

B. Uraian

1. a. Daerah yang diarsir dibatasi oleh parabola y = x2_{+ 1 dan sumbu X pada interval 0}_≤_x_≤_2. Luas daerah yang diarsir:

L =

b. Daerah yang diarsir dibagi menjadi dua bagian.

Daerah I dibatasi oleh parabola y = 1

2x

2_dan sumbu X pada interval 0 ≤ x ≤ 2.

Daerah II dibatasi oleh garis y = 4 – x dan sumbu X pada interval 2 ≤ x ≤ 4.

Luas daerah yang diarsir: L = L_I + L_II

c. Daerah yang diarsir dibatasi oleh parabola y = 8 – 2x2_{dan garis y = –x + 2 pada interval} 0 ≤ x ≤ 2.

L =

d. Daerah yang diarsir dibatasi oleh parabola y = –x2_{+ x + 6 dan garis y = 2x + 4.} 9. Jawaban: a

y = x2_{+ 1} _⇔ _x2_{= y – 1} Volume benda putar:

V = π 10. Jawaban: a

Daerah yang diarsir diputar mengelilingi sumbu X.

V_X= π

Daerah yang diarsir diputar mengelilingi sumbu Y.

(15)

Luas daerah yang diarsir: Menentukan L_I.

L_I= –

Luas gabungan daerah II dan III:

L_gab=

Menentukan L_III.

L_III= –

= 1₆ + 2

= 2₆1

Jadi, luas daerah yang diarsir adalah 2₆1 satuan luas.

3. a. Luas daerah yang dimaksud yaitu luas

daerah yang dibatasi kurva y = cos x dan sumbu X pada interval 0 < x < ₂π.

(16)

Luas daerah di antara kurva y = sin x dan

Luas daerah yang dibatasi oleh kurva y = sin x dan y = cos x pada interval 0 < x < π dan sumbu X.

a. Luas daerah D:

L =

b. Daerah D diputar mengelilingi sumbu X, volumenya:

c. Daerah D diputar mengelilingi sumbu Y. y = 3 – x ⇔ x = 3 – y

y = 2x ⇔ x = ₂1y

Volume benda putar yang terjadi:

V_Y= π

a. Jika daerah D diputar mengelilingi sumbu X, volume benda putar yang terjadi adalah:

V_X= π

(17)

1. Jawaban: b

∫

(3x2_{– 4x + 2) dx} = _{2 1}3₊ x2 + 1_– 4

1 1+ x1 + 1 + 2x + c = 3₃x3_–4

2x2 + 2x + c

= x3_{– 2x}2_{+ 2x + c} 2. Jawaban: c

∫

3x3 _x_{dx = 3}

∫

_x 7 2_dx

= 3 · 2₉x 9

2_{+ c =}2

3x4 x + c

3. Jawaban: b

∫

( x – 2)(2 x + 1) dx =

∫

(2x – 3 x – 2) dx =

∫

(2x – 3x

1

2_{– 2) dx}

= x2_{– 3 ·}2

3x

3

2_{– 2x + c} = x2_{– 2x} _x _{– 2x + c} 4. Jawaban: c

∫

(3x – 3

2 x )

2_dx

=

∫

(3x – 2x 1 3 −

)2_dx

=

∫

(9x2_{– 12x} 2 3_{+ 4x}

2 3 −

) dx

= 9 · 1₃x3_{– 12 ·}3

5x

5 3

+ 4 · 3x 1 3

+ c

= 3x3_–36_x3_x2 _{+ 12}3_x_{+ c}

5. Jawaban: c

f(x) =

∫

(2ax2_{+ (a – 1)x) dx} = 2

3ax3 + 1

2(a – 1)x2 + c

f(2) = 24

⇔ ₃2a(2)3₊1

2(a – 1) · 22 + c = 24

⇔ 16₃ a + 2(a – 1) + c = 24

⇔ 16a + 6a – 6 + 3c = 72

⇔ 22a + 3c = 78 . . . . (1)

f(1) = 7

⇔ ₃2a + ₂1(a – 1) + c = 7

⇔ 4a + 3a – 3 + 6c = 42

⇔ 7a + 6c = 45 . . . . (2)

Eliminasi c dari persamaan (1) dan (2). 22a + 3c = 78 ×2 44a + 6c = 156

7a + 6c = 45 × 1 7a + 6c = 45

–––––––––––– – 37a = 111

⇔ a = 3

Jadi, nilai a = 3. 6. Jawaban: b

dy dx = 3x

2_{+ 4x – 5} Persamaan kurva:

y = f(x) =

∫

(3x2_{+ 4x – 5) dx = x}3_{+ 2x}2_{– 5x + c} Kurva melalui titik (1, 2) maka f(1) = 2.

f(1) = 1 + 2 – 5 + c ⇔ 2 = –2 + c ⇔ c = 4 Persamaan kurva: y = x3_{+ 2x}2_{– 5x + 4} V_II= π

4

2

∫

(y – (y – 2) 2_{) dy}

= π 4 2

∫

(5y – y

2_{– 4) dy}

= π

4

2 3

2

5 1

2y 3y 4y

 ₋ 

 

 − 

= π ((40 – 64₃ – 16) – (10 – 8₃ – 8)) = π (22₃ – (–2₃))

= 3₃1π satuan volume

V_Y= V_I + V_II = 2π + 31₃π

(18)

7. Jawaban: d

8. Jawaban: d

b 9. Jawaban: d

3

10. Jawaban: d

∫

sec x cotan2_{x dx =}

∫

1

11. Jawaban: c

∫

8 sin 5x cos 3x dx

12. Jawaban: d

∫

(cos4_{2x – sin}4_{2x) dx}

=

∫

(cos2_{2x + sin}2_2x)(cos2_{2x – sin}2_{2x) dx} =

∫

1 · (cos 2 (2x) dx

=

∫

cos 4x dx = 1₄ sin 4x + c 13. Jawaban: d

1

14. Jawaban: a 2

(19)

---16. Jawaban: b

4

17. Jawaban: d

Misalkan u = 1 + 2x – x2

18. Jawaban: c

1

19. Jawaban: e

Misalkan u = sin 2x

20. Jawaban: a

0 21. Jawaban: b

Turunan Integral 22. Jawaban: a

(20)

23. Jawaban: d

Daerah yang diarsir dibatasi parabola y = (2 – x)2 dan sumbu X pada interval 0 ≤ x ≤ 2.

L =

24. Jawaban: e

y = 2 ⇒ x2_{– 4x – 3 = 2}

⇔ x2_{– 4x – 5 = 0}

⇔ (x + 1)(x – 5) = 0

⇔ x = –1 atau x = 5

Parabola dan garis berpotongan di titik (–1, 2) dan (5, 2).

L =

25. Jawaban: a

L = a

26. Jawaban: c

Daerah I:

27. Jawaban: b

V =π3_∫ 28. Jawaban: c

(21)

29. Jawaban: c

Volume benda putar:

V_y = π

30. Jawaban: d

Volume benda putar:

(22)

b. 4

2 π

π −

∫

(2 sin x + 6 cos x) dx

= _–2 cos x + 6 sin x 4 2 π

π −

 

= –2 cos

4

π + 6 sin

4

π

– (–2 cos (–

2

π

) + 6 sin (–

2

π ))

= –2 (1

2 2) + 6( 1

2 2) – (0 – 6)

= – 2+ 3 2+ 6 = 6 + 2 2

5.

∫

2

4x

2 x− dx

Misalkan u = 2 – x2 _⇔ _{du = –2x dx}

⇔ –2 du = 4x dx

∫

2

4x

2 x− dx =

∫

12

1

u

· (–2) du

= –2 ∫ 1 2

u− du = –2 · 1

2

1 1

− + 1 2 1

u− + + c

= 1 2

2

− _u12_{+ c}

= –4 u + c = –4 _{2 x}₋ 2 _{+ c} 6. a. Misalkan

u = x ⇒ du = dx dv = cos x dx

⇒ v =

∫

cos x dx = sin x

∫

x cos x dx =

∫

u dv = uv –

∫

v du = x sin x –

∫

sin x dx = x sin x + cos x + c

b. Misalkan

u = 3 – 2x ⇒ du = –2 dx dv = sin x dx

⇒ v =

∫

sin x dx = –cos x

∫

(3 – 2x) sin x dx =

∫

u dv

= uv –

∫

v du

= (3 – 2x)(–cos x) –

∫

(–cos x)(–2dx) = –(3 – 2x) cos x – 2

∫

cos x dx = (2x – 3) cos x – 2 sin x + c

Y

X 2

0 ₂ ₄ ₆ ₈ _{x + 4y = 8}

x = 4

Y

X

0 4

y = 8x – 2x2

y = 4x – x2

Y

X –3 –2 –10 1 2 3

y = 9 – x2 9

7.

x + 4y = 8

⇔ 4y – 8 = x

⇔ y = 2 – ₄1x

L = 4

0

∫

y dx

= 4

0

∫

(2 – 1

4x)) dx

=

4 2

0

1 8

2x x

 

 

 − 

= (8 – 2) – (0 – 0) = 6

Jadi, luas daerah tersebut 6 satuan luas.

8. a. Daerah D

b. Luas daerah D yang diarsir

L = 4

0

∫

((8x – 2x2_{) – (4x – x}2_{)) dx}

= 4

0

∫

(4x – x2_{) dx}

=

4

2 3

0

1 3

2x x

 

 

 − 

= (32 – 64

3 ) – 0

= 102₃ satuan luas

(23)

1

0 –1

2

π

2 3_π π

Y

X y = sin x

2π a. Diputar terhadap sumbu X

V_x= π 3

0

∫

y2_dx

= π 3

0

∫

(9 – x2₎2_dx

= π 3

0

∫

(81 – 18x2_{+ x}4_{) dx}

= π 3 1 5 3

5 ₀ 81x 6x x

 

 

 − + 

= π((81(3) – 6(3)3₊1

5(3)

5_{) – 0)}

= π(243 – 162 + 243₅ )

= π(81 + 243₅ )

= π(648

5 )

= 648₅ π satuan volume b. Diputar terhadap sumbu Y

V_y= π 9

0

∫

x2_dy

= π 9

0

∫

(9 – y) dy

= π 2 9

0

1 2 9y y

 

 

 − 

= π((9(9) – 1

2(9)

2_{) – 0)}

= π(81 – 81₂ ) = 81

2 π satuan volume

10.

Volume = π 2

0 sin π

∫

x dx

= π 0 π

∫

12(1 – cos 2x) dx

= π

0

1 1

2x 4sin 2x

π

 

 

 − 

= π((₂π – 1₄sin 2π) – (0 – ₄1 sin 0)) = π(

2

π

– 0) – 0)

(24)

2. Menyelesaikan masalah program linear.

Standar Kompetensi Kompetensi Dasar Nilai Indikator

2.1 Menyelesaikan sistem pertidaksamaan linear dua variabel. 2.2 Merancang model

mate-matika dari masalah program linear. 2.3 Menyelesaikan model

matematika dari masa-lah program linear dan penafsirannya.

Rasa ingin tahu

Menanyakan cara membuat model matematika dari permasalahan sehari-hari.

Pada bab ini akan dipelajari:

1. Sistem pertidaksamaan linear dua variabel dari suatu daerah 2. Daerah penyelesaian sistem pertidaksamaan linear dua variabel 3. Nilai optimum suatu fungsi objektif

4. Model matematika dari masalah program linear 5. Penyelesaian masalah program linear

Model Pengintegrasian Nilai Pendidikan Karakter

• Menentukan daerah penyelesaian sistem pertidaksamaan linear dua variabel

• Menentukan sistem pertidak-samaan linear dua variabel dari suatu daerah penyelesaian • Menyelesaikan sistem persamaan

linear dua variabel

Menentukan nilai optimum fungsi objektif

• Menentukan nilai optimum fungsi objektif menggunakan metode uji titik sudut

• Menentukan nilai optimum fungsi objektif menggunakan metode garis selidik

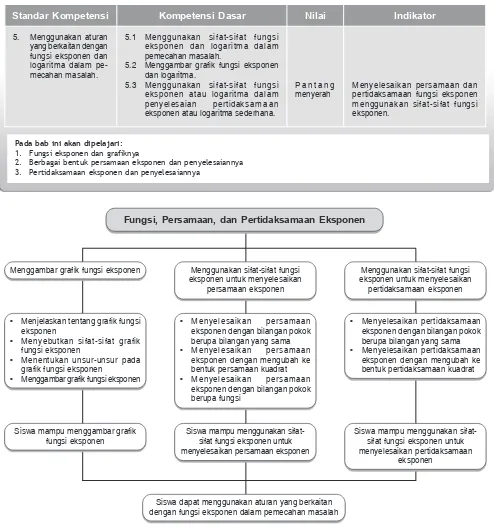
Siswa dapat menyelesaikan masalah program linear

• Menyelesaikan model matematika • Menafsirkan penyelesaian model

matematika

• Merancang dan menyelesaikan model matematika masalah program linear

Menerjemahkan dan menyelesaikan permasalahan menggunakan program linear

Program Linear

Mendeskripsikan dan menyelesaikan sistem pertidaksamaan linear dua

variabel

Siswa mampu menyelesaikan sistem pertidaksamaan linear

Siswa mampu menentukan nilai optimum suatu fungsi

(25)

Y

X 0

3

1

–2 4

9

5

---8 5

x – 2y = –2

3x + 4y = 12 Y

X 4

–6

21 2

–7

Daerah penyelesaian→ –3x + 2y = 21

–2x + 3y = 12

0

A. Pilihlah jawaban yang tepat.

1. Jawaban: b

Garis x + 2y = –12 memotong sumbu X di titik (–12, 0) dan memotong sumbu Y di titik (0, –6). Uji titik (0, 0) ke x + 2y = –12

0 + 2(0) = 0 ≥ –12 (bernilai benar).

Daerah penyelesaian x + 2y = –12 dibatasi garis x + 2y = –12 dan memuat titik (0, 0).

Jadi, grafik himpunan penyelesaian x + 2y ≥ –12 adalah pilihan b.

2. Jawaban: c

Persamaan garis yang melalui titik (–2, 0) dan titik (0, 1):

y 0

1 0

− − =

x 2

0 2

+ +

⇔ y₁ = x₂+2

⇔ x – 2y = –2

⇔ 2y – x = 2

Titik (–1, 0) pada daerah penyelesaian. Uji titik (–1, 0) ke 2y – x:

0 – (–1) = 1 < 2 (benar)

Garis digambar putus-putus sehingga tanda ketidaksamaannya <.

Jadi, PtLDV-nya 2y – x < 2. 3. Jawaban: b

Garis –3x + 2y = 21 melalui titik (0, 21

2)

dan titik (–7, 0). Daerah penyelesaian –3x + 2y ≤ 21 di kanan garis –3x + 2y = 21. Garis –2x + 3y = 12 melalui titik (0, 4) dan titik (–6, 0).

Daerah penyelesaian

–2x + 3y ≥ 12 di kiri garis –2x + 3y = 12.

Daerah penyelesaian x ≤ 0 di kiri sumbu Y dan daerah penyelesaian y ≥ 0 di atas sumbu X. Jadi, daerah penyelesaian dari sistem pertidak-samaan tersebut adalah b.

4. Jawaban: c

1) Persamaan garis yang melalui titik (–2, 0) dan titik (0, 3):

x 2

− +

y 3 = 1

–––––––––– × 6

⇔ –3x + 2y = 6

Titik (1, 1) pada daerah penyelesaian.

Uji titik (1, 1) ke –3x + 2y: –3(1) + 2(1) = –1 < 6

Jadi, PtLDV-nya –3x + 2y ≤ 6.

2) Persamaan garis yang melalui titik (0, 4) dan titik (6, 0):

x 6 +

y

4 = 1 ←(kali 24)

⇔ 4x + 6y = 24 ⇔ 2x + 3y = 12 Titik (1, 1) pada daerah penyelesaian. Uji titik (1, 1) ke 2x + 3y:

2 · 1 + 3 · 1 = 5 < 12

Jadi, PtLDV-nya 2x + 3y ≤ 12.

3) Daerah penyelesaian di kanan sumbu Y maka x ≥ 0.

4) Daerah penyelesaian di atas sumbu X, maka y ≥ 0.

Sistem pertidaksamaannya:

x ≥ 0; y ≥ 0; 2x + 3y ≤ 12; –3x + 2y ≤ 6. 5. Jawaban: d

1) Garis 3x + 4y = 12 melalui titik (4, 0) dan titik (0, 3).

Uji titik (0, 0) ke 3x + 4y ≤ 12: 3(0) + 4(0) ≤ 12 bernilai benar

Daerah penyelesaiannya dibatasi garis 3x + 4y = 12 dan memuat titik (0, 0). 2) Garis x – 2y = –2 melalui titik (–2, 0) dan titik

(0, 1).

Uji titik (0, 0) ke x – 2y ≥ –2: 0 – 2(0) = 0 ≥ –2 bernilai benar

Daerah penyelesaiannya dibatasi garis x – 2y = –2 dan memuat titik (0, 0).

3) Garis 3x + 4y = 12 dan x – 2y = –2 berpotongan

di titik (8

5, 9 5).

4) Daerah penyelesaian yang memenuhi per-tidaksamaan y ≥ 0 di atas sumbu X.

(26)

Daerah yang diarsir berbentuk segitiga dengan panjang alas = 4 – (–2) = 6 dan tinggi = 9

5 – 0 = 9 5. L_segitiga= 1

2 × alas × tinggi = 1

2 × 6 × 9 5

= 27 5

= 52

5 satuan

Jadi, luas daerah yang diarsir 52

5 satuan. 6. Jawaban: c

1) Garis x + 2y = 12 melalui titik (0, 6) dan (12, 0). Daerah penyelesaian x + 2y ≥ 12 dibatasi garis x + 2y = 12 dan tidak memuat titik (0, 0). 2) Garis x – y = –2 melalui titik (0, 2) dan (–2, 0).

Daerah penyelesaian x – y ≥ –2 dibatasi garis x – y = –2 dan memuat titik (0, 0).

3) Garis 2x + y = 24 melalui titik (0, 24) dan (12, 0). Daerah penyelesaian 2x + y ≤ 24 dibatasi garis 2x + y = 24 dan memuat titik (0, 0).

4) Daerah penyelesaian x ≥ 0 di sebelah kanan sumbu X.

5) Daerah penyelesaian y ≥ 0 di atas sumbu X. Daerah penyelesaian sistem pertidaksamaan tersebut.

7. Jawaban: b

1) Garis x + y = 4 melalui titik (0, 4) dan (4, 0). Daerah penyelesaian x + y ≥ 4 dibatasi garis x + y = 4 dan tidak memuat (0, 0).

2) Garis 2x – y – 4 = 0 melalui titik (0, –4) dan (2, 0).

Daerah penyelesaian 2x – y – 4 ≤ 0 dibatasi garis 2x – y – 4 = 0 dan memuat (0, 0). 3) Garis x + 4 = 2y melalui titik (0, 2) dan (–4, 0).

Daerah penyelesaian x + 4 ≥ 2y dibatasi garis x + 4 = 2y dan memuat (0, 0).

8. Jawaban: e

a.

Luas ABC = ₂1 × BC × AD

= 1₂ × 8 × 5 = 20 satuan

b.

Luas ABCD = 1

2 × AB(AD + BC)

= 1

2 × 5(3 + 6)

= 221

2 satuan

c.

Luas ABCD = 1₂ × AC × BD

= 1₂ × 6 × 4 = 12 satuan Y

X x – y = –1 3

–3 –1 0 2 5 A

B –2 D C y = –2

5x + 3y = 19

Y

X A

B

C D

y = 3

y = –2 5x + 3y = 14 3

–2 0 1 4 –2

Y

X 24

6 2

–2 12

I IIIII IV

V

Daerah penyelesaian

→

2x + y = 24

x – y = –2

x + 2y = 12

X Y

0 4

–4

2 4

–4 –2 2

–2 x + y = 4

x + 4 = 2y 2x – y – 4 = 0

Y

X A

B

C D

3x + 2y = 2

3x + 2y = –10 3x – 2y = –2

3x – 2y = – 14

– 4 – 2 0

1

(27)

Y

X

3x + 2y = 4 2x – 3y = –6

2x – 3y = 20

–3 0 1 4 2

–4

–6

3x + 2y = –9 d.

Luas ABCD = 1

2 × AC × BD

= 1

2 × 7 × 4 = 14 satuan

e.

Luas ABCD = AB × BC = 13 × 13

= 13 satuan

Jadi, sistem pertidaksamaan yang daerah penyelesaiannya mempunyai luas 13 satuan adalah pilihan e.

9. Jawaban: b

Daerah penyelesaian x – 2y ≤ –2 dibatasi garis x – 2y = –2 dan tidak memuat titik (0, 0).

Daerah penyelesaian 3x + 4y ≥ –2 dibatasi garis 3x + 4y = 12 dan tidak memuat titik (0, 0). Daerah penyelesaian 5x + 3y ≤ 15 dibatasi garis 5x + 3y = 15 dan memuat titik (0, 0).

Daerah penyelesaian sistem pertidaksamaan di atas adalah:

Y

X A

B

C D

x – y = –6

2x – 5y = –4 2x + 5y = 16

x + y = –2 4 2

–4 –2 0 3 –2

Y

X A

B

C D

2x – 3y = –13

2x – 3y = 0

3x + 2y = 13

3x + 2y = 0 3

2

–2 0 1 3 5

Y

X 5

3

–2 1

3 4

10. Jawaban: b

a.

Daerah penyelesaian berbentuk belah ketupat.

b.

Daerah penyelesaian berbentuk layang-layang.

c.

Daerah penyelesaian berbentuk persegi panjang.

5x + 3y = 15

x – 2y = –2

3x + 4y = 12

Y

X x – 3y = –12

3x + 7y = –12

7x + 3y = 12 3x – y = –12

–4 –3 0 3 4

3

–3 Y

X y = 2 4x + 3y = 14

y = –2

4x + 3y = –6 –3 0 2 5

2

–2

(28)

Daerah yang diarsir merupakan penyelesaian SPtLDV.

2. 1) Persamaan garis yang melalui titik (3, 0) dan titik (0, 1):

y – 0 1– 0 =

x – 3 0 – 3

⇔ y₁ = x 3

3

− −

⇔ –3y = x – 3

⇔ x + 3y= 3

Daerah penyelesaian tidak memuat titik (0,0) maka pertidaksamaannya x + 3y ≥ 3. 2) Persamaan garis yang melalui titik (1, 0) dan

(0, 3)

y 0

3 0

− − =

x 1

0 1

− −

⇔ y₃ = x 1₋−₁

⇔ –y = 3x – 3

⇔ 3x + y = 3

Daerah penyelesaian tidak memuat titik (0,0) maka pertidaksamaannya 3x + y ≥ 3. 3) Persamaan garis melalui titik (5, 0) sejajar

sumbu Y adalah x = 5. Daerah penyelesaian di sebelah kiri x = 5 sehingga pertidaksamaan-nya x ≤ 5.

4) Persamaan garis melalui titik (0, 5) sejajar sumbu X adalah y = 5. Daerah penyelesaian-nya di bawah garis y = 5 maka pertidaksama-annya y ≤ 5.

5) Daerah penyelesaian di atas sumbu X dan di kanan sumbu Y, berarti x ≥ 0 dan y ≥ 0. Jadi, sistem pertidaksamaannya adalah:

x + 3y ≥ 3 x + 3y≥ 3

3x + y ≥ 3 atau 3x + y≥ 3

x≤5 0 ≤ x≤ 5

y≤5 0 ≤ y≤ 5

x≥ 0 y≥ 0

3. a. 1) Garis 3x + 2y = 12 melalui titik (4, 0) dan titik (0, 6).

Daerah penyelesaian 3x + 2y ≤ 12 dibatasi garis 3x + 2y = 12 dan memuat titik (0, 0). 2) Garis x + 2y = 8 melalui titik (8, 0) dan

titik (0, 4).

Daerah penyelesaian x + 2y ≤ 8 dibatasi garis x + 2y = 8 dan memuat titik (0, 0). 3) Garis 4x + y = 4 melalui titik (1, 0) dan

titik (0, 4).

Daerah penyelesaian 4x + y ≥ 4 dibatasi garis 4x + y = 4 dan tidak memuat titik (0, 0).

d.

Daerah penyelesaian berbentuk persegi. e.

Daerah penyelesaian berbentuk trapesium. Jadi, sistem pertidaksamaan yang daerah penyelesaiannya berbentuk persegi panjang adalah pilihan b.

B. Uraian

1. 1) Garis x + y = 1 melalui titik (0, 1) dan titik (1, 0). Daerah penyelesaian x + y ≥ 1 dibatasi garis x + y = 1 dan tidak memuat titik (0, 0). 2) Garis 2x + 3y = 12 melalui titik (0, 4) dan titik (6, 0). Daerah penyelesaian 2x + 3y ≤ 12 di-batasi garis 2x + 3y = 12 dan memuat titik (0, 0). 3) Garis –x + y = 2 melalui titik (0, 2) dan titik (–2, 0). Daerah penyelesaian –x + y ≤ 2 tidak memuat titik (0, 0).

4) Garis x = 1 melalui titik (1, 0) dan titik (1, 2). Daerah penyelesaian x ≤ 1 dibatasi garis x = 1 dan di kiri garis x = 1.

Dari 1), 2), 3), dan 4) diperoleh: Y

X 2x + y = –6

2x – 3y = –6

2x – 3y = 4

y = 2

–3 0 2 5 2

–6

Y

X x – 4y = –16

4x + y = 4 4x + y = –13

–4 –3 0 1 4 3

–1 x – 4y = 1

Y

X –x + y = 2

x + y = 1 2x + 3y = 12 4

2 1

(29)

4) Daerah penyelesaian x ≥ 0 dibatasi garis x = 0 dan di kanan sumbu Y.

Daerah penyelesaian y ≥ 0 dibatasi garis y = 0 dan di atas sumbu X.

5) Daerah penyelesaian sistem pertidak-samaan tersebut adalah:

b. Luas daerah himpunan penyelesaian:

Titik C dapat dicari dengan eliminasi: 3x + 2y= 12

x + 2y = 8 ––––––––– –

2x = 4

⇔ x = 2

y = 3

Diperoleh titik C(2, 3).

Luas daerah penyelesaian adalah luas daerah ABCD.

L = L_I + L_II

= ₂1 × 2 × 4 + ₂1 × 3 × 3

= 4 + 9₂

= 81₂ satuan luas

4.

Y

X

A B

C D

3x + 2y = 12 x + 2y = 8

1 4 8

6 4

4x + y = 4

A(1, 0) B(4, 0) C(2, 3) D(0, 4)

I II

X Y

0 A

B D 2

1 2 –1

–2 –4

–1 _C

1

1) Persamaan garis yang melalui titik A(–4, 1) dan titik B(–1, –2):

A

B A

y y

−

− = B AA

x x

− −

⇔ _{− −}y₂−1₁ = _{− +}x_{1 4}+4

⇔ y₋−₃1 = x₃+4

⇔ y – 1 = –x – 4

⇔ x + y = –3

Daerah penyelesaian di kanan garis x + y = –3 maka pertidaksamaannya x + y ≥ –3. 2) Persamaan garis yang melalui titik B(–1, –2)

dan titik C(2, –1):

B

C B

y y

−

− = C BB

x x

− −

⇔ _{− +}y_{1 2}+2 = x₂+₊1₁

⇔ y + 2 = x₃+1

⇔ 3y + 6 = x + 1

⇔ x – 3y = 5

Daerah penyelesaian di kiri garis x – 3y = 5, maka pertidaksamaannya x – 3y ≤ 5. 3) Persamaan garis yang melalui titik C(2, –1)

dan titik D(0, 2):

C

D C

y y

−

− = D CC

x x

− −

⇔ y₂+₊1₁ = x₀−₋2₂

⇔ y₃+1 = x₋−₂2

⇔ –2y – 2 = 3x – 6

⇔ 3x + 2y = 4

Daerah penyelesaian di kiri garis 3x + 2y = 4, maka pertidaksamaannya 3x + 2y ≤ 4. 4) Persamaan garis yang melalui titik A(–4, 1)

dan titik D(0, 2): A

D A

y y

−

− = D AA

x x

− −

⇔ y₂−₋1₁ = x₀+₊4₄

⇔ y₁−1 = x 4

4

+

⇔ 4(y – 1) = x + 4

⇔ 4y – 4 = x + 4

⇔ x – 4y = –8

(30)

1. Jawaban: b

B merupakan titik potong garis 3x – y = 18 dengan sumbu X.

3x – 0 = 18

⇔ x = 6

Diperoleh titik B(6, 0).

A merupakan titik potong garis x + y = 3 dengan sumbu X.

x + 0 = 3

⇔ y = 3

Diperoleh titik A(3, 0).

F merupakan titik potong garis x + y = 3 dengan sumbu Y.

0 + y = 3

⇔ y = 3

Diperoleh titik F(0, 3).

Uji titik pojok penyelesaian terhadap fungsi objektif f(x, y) = 5x + 6y.

Titik f(x, y) = 5x + 6y

A(3, 0) 15

B(6, 0) 30

C(7, 3) 60

D(5, 6) 61

E(2, 5) 40

F(0, 3) 18

Diperoleh nilai maksimum dan minimumnya adalah 61 dan 15.

2. Jawaban: d

P titik potong x + 2y = 6 dengan x = 1. x + 2y = 6

⇔1 + 2y = 6

⇔ y = 5

2

Diperoleh P(1, 5

2).

Q titik potong x + 2y = 6 dengan x + 2y = 6. x + 2y = 6

⇔4 + 2y = 6

⇔ y = 1

Diperoleh Q(4, 1).

R titik potong 2x + y = 12 dengan x = 4. 2x + y = 12

⇔ 2 · 4 + y = 12

⇔ y = 4

Diperoleh R(4, 4).

S titik potong x – y = –2 dengan 2x + y = 12. x – y = –2

2x + y = 12 ––––––––––– +

3x = 10

⇔ x = 10

3

x – y = –2

⇔ 10₃ – y = –2

⇔ y = 16₃ Y

X A

B

C D 5x – y = 13

3x + 5y = 19

x + 2y = –4 5x – 2y = –20

–4 –2 0 2 3 5

2

–2 –3

Jadi, sistem pertidaksamaannya adalah x + y≥ –3

x – 3y≤ 5 3x + 2y≤ 4 x – 4y≥ –8 5.

Diagonal-diagonal daerah penyelesaian adalah AC dan BD.

Panjang AC = (xC−x )A 2+(yC−y )A 2 = (2 2)+ 2+ − −( 3 5)2

= ₄2_{+ −}_{( 8)}2 = 16+64

= 80 = 4 5

Panjang BD = (xD−x )B2+(yD−y )B 2 = (3+4)2+ −(2 0)2

= ₇2₊₂2 = 49+4 = 53

(31)

Diperoleh S(10₃ , 16₃ ).

T Titik potong garis x = 1 dengan x – y = –2. x – y = –2

⇔ 1 – y = –2

⇔ y = 1

Diperoleh T(1, 3).

Uji titik pojok penyelesaian terhadap fungsi objektif f(x, y) = 3x + 6y.

Daerah penyelesaian di atas mencapai maksimum di titik S.

3. Jawaban: d

Persamaan fungsi objektif: f(x, y) = 7x + 7y. Persamaan garis yang melalui titik (10, 0) dan titik (0, 25) adalah 5x + 2y = 50.

Persamaan garis yang melalui titik (30, 0) dan titik (0, 10) adalah x + 3y = 30.

Persamaan garis yang melalui titik (20, 0) dan titik (0, 15) adalah 3x+ 4y = 60.

Titik B adalah titik potong garis 3x + 4y = 60 dan x + 3y = 30. Koordinat titik B adalah:

3x + 4y = 60 × 1 3x + 4y = 60 x + 3y = 30 × 3 3x + 9y = 90

––––––––––– – 5y = 30

⇔ y = 6

x = 12 Diperoleh titik B(12, 6).

Titik C adalah titik potong garis 3x + 4y = 60 dan 5x + 2y = 50. Koordinat titik C adalah:

3x + 4y = 60 × 1 3x + 4y = 60

5x + 2y = 50 × 2 10x + 4y = 100 ––––––––––––– –

7x = 40

⇔ x = 40

7

y = 75

7

Diperoleh titik koordinat C (40

7 , 75

7 ).

Uji titik pojok.

Nilai minimum fungsi objektif f(x, y) = 7x + 7y adalah 115, sehingga persamaan garis selidik yang me-nyebabkan f(x, y) minimum adalah 7x + 7y = 115.

4. Jawaban: d

Garis 2x – 3y = 12 melalui titik (6, 0) dan (0, –4). Garis x + 2y = 4 melalui titik (4, 0) dan (0, 2). Uji titik (0, 0) ke masing-masing pertidaksamaan:

Pertidaksamaan Uji Titik (0, 0) Penyelesaian

2x – 3y ≤ 12 0 ≤ 12 Memuat (0, 0) x + 2y ≥4 0 ≥ 4 Tidak memuat (0, 0)

Daerah penyelesaian sistem pertidaksamaan:

A titik potong garis x = 2 dan x + 2y = 4. Koordinat titik A adalah (2, 1).

Uji titik pojok ke dalam fungsi objektif f(x, y) = 3y + x.

Jadi, nilai minimum f(x, y) pada daerah penyelesai-an SPtLDV tersebut adalah 4.

5. Jawaban: d

Misalkan: x = banyak pupuk jenis I y = banyak pupuk jenis II

Pupuk Banyak Isi (gram) Harga/bungkus

Jenis I x 300x 40.000

Jenis II y 200y 30.000

Pembatas 40 9.000

Y

X 2x – 3 = 12

x + 2y = 4

x = 2

x = 6

A _B _C

DP

0 2 4 6

–4 2

Titik

A(30, 0) B(12, 6) C(40₇ , 75₇ ) D(0, 25)

f(x, y) = 7x + 7y

210 126 115 175

Titik

A(2, 1) B(4, 0) C(6, 0)

f(x, y) = 3y + x

5 4 6 Titik

P(1, 5₂) Q(4, 1) R(4, 4) S(10₃ , 16₃ ) T(1, 3)

f(x, y) = 3x + 6y

(32)

Y

X x + y = 10 2x + y = 12

12 10 8

2 6 10 0

Jenis Sabun Banyak Harga Laba

A x 4.000 800

B y 3.000 600

Pembatas 500 1.800.000

Y

X A

B C

O 450 500

600 500 Diperoleh model matematika:

x + y ≥ 40

300x + 200y ≥ 9.000 ⇔ 3x + 2y ≥ 90 x ≥ 0

y ≥ 0

Fungsi objektif meminimumkan f(x, y) = 40.000x + 30.000y.

Daerah penyelesaian SPtLDV:

B merupakan perpotongan garis 3x + 2y = 90 dan x + y = 40.

3x + 2y = 90 × 1 3x + 2y = 90

x + y = 40 × 3 3x + 3y = 120

––––––––––– – y = 30 x + y = 40

⇔ x + 30 = 40

⇔ x = 10

Uji titik pojok daerah penyelesaian ke dalam fungsi objektif f(x, y) = 40.000x + 30.000y.

Titik f(x, y) = 40.000x + 30.000y

A(0, 45) 40.000 × 0 + 30.000 × 45 = 1.350.000 B(10, 30) 40.000 × 10 + 30.000 × 30 = 1.300.000 C(40, 0) 40.000 × 40 + 30.000 × 0 = 1.600.000 Nilai f(x, y) minimum adalah 1.300.000.

Jadi, biaya minimum yang dikeluarkan Rp1.300.000,00.

6. Jawaban: e

Misal x = banyak sabun A dan y = banyak sabun B.

Model matematika:

Memaksimumkan f(x, y) = 800x + 600y dengan kendala: x + y≤ 500

4x + 3y≤ 1.800 x≥ 0 y≥ 0

Daerah penyelesaian x + y ≤ 500 di kiri garis x + y = 500.

Daerah penyelesaian 4x + 3y ≤ 1.800 di kiri garis 4x + 3y = 1.800.

Daerah penyelesaian:

B titik potong x + y = 500 dan 4x + 3y = 1.800. Koordinat 3x + 3y = 1.500

4x + 3y = 1.800 ––––––––––––- –

x = 300 y = 200

Koordinat titik B adalah B(300, 200).

Uji titik pojok ke dalam f(x, y) = 800x + 600y.

Titik f(x, y) = 800x + 600y

O(0, 0) 0

A(450, 0) 340.000

B(300, 200) 360.000

C(0, 500) 300.000

Laba maksimum yang dapat diperoleh sebesar Rp360.000,00.

7. Jawaban: e

Garis 2x + y = 12 mempunyai gradien m₁ = –2. Garis x + y = 10 mempunyai gradien m₂ = –1. Persamaan fungsi objektif f(x, y) = ax + 10y mem-punyai gradien m = ₁₀−a.

Fungsi objektif f(x, y) = ax + 10y akan mencapai minimum hanya di titik (2, 8), jika m₁ < m < m₂.

–2 < a

10

− < –1

⇔ –20 < –a < –10

⇔ 10 < a < 20

Jadi, nilai a yang memenuhi 10 < a < 20. Y

X 0

A

B

C 40

45

35 40

(33)

Titik

A(25, 0) B(4, 21) C(0, 28)

f(x, y) = 400.000x + 300.000y

10.000.000 7.900.000 8.400.000

Jenis Banyak Karung Ongkos

Truk x 14 400.000

Kol y 8 300.000

Pembatas 25 224

Y

X A B

C

x + y = 25 7x + 4y = 112

O 16 25

28 25 8. Jawaban: b

Misalkan: x = banyak kapsul yang dibeli y = banyak tablet yang dibeli

Jenis Banyak Kalsium_(gram) Zat Besi_(gram) _SatuanHarga

Kapsul x 5x 2x 1.000

Tablet y 2y 2y 800

Pembatas 60 30

Diperoleh model matematika: 5x + 2y ≥ 60

2x + 2y ≥ 30 ⇔ x + y ≥ 15 x ≥ 0

y ≥ 0

Fungsi objektif:

Meminimumkan f(x, y) = 1.000x + 800y. Daerah penyelesaian SPtLDV.

Titik B merupakan perpotongan garis 5x + 2y = 60 dan x + y = 15.

5x + 2y = 60 × 1 5x + 2y = 60

x + y = 15 × 2 2x + 2y = 30

––––––––––– – 3x = 30

⇔ x = 10 x + y = 15

⇔ 10 + y = 15

⇔ y = 5

Diperoleh koordinat titik B(10, 5).

Uji titik pojok daerah penyelesaian ke fungsi objektif f(x, y) = 1.000x + 800y.

Titik Pojok f(x, y) = 1.000x + 800y

A(0, 30) 1.000 × 0 + 800 × 30 = 24.000 B(10, 5) 1.000 × 10 + 800 × 5 = 14.000 C(15, 0) 1.000 × 15 + 800 × 0 = 15.000 Nilai f(x, y) minimum adalah 14.000.

Jadi, biaya minimum yang harus dikeluarkan untuk memenuhi kebutuhan anak balita tersebut Rp14.000,00.

9. Jawaban: d

Misal: x = banyaknya truk y = banyaknya kol Y

X 0

30

12 15 15

B A

x + y = 15 5x + 2y = 60

Model matematika:

Minimumkan f(x, y) = 400.000x + 300.000y dengan

kendala: x + y≥ 25

14x + 8y≥ 224

⇔ 7x + 4y≥ 112 x≥ 0 y≥ 0

Daerah penyelesaian x + y ≥ 25 di kanan garis x + y = 25 dan tidak memuat titik (0, 0).

Daerah penyelesaian 7x + 4y ≥ 112 di kanan garis 7x + 4y = 112 dan tidak memuat titik (0, 0). Daerah penyelesaian:

B titik potong garis 7x + 4y = 112 dan x + y = 25. 7x + 4y = 112

4x + 4y = 100 ––––––––––– –

3x = 12

⇔ x = 4

y = 21

Koordinat titik B adalah B(4, 21). Uji titik pojok ke dalam fungsi f(x, y) = 400.000x + 300.000y.

Nilai minimum fungsi objektif

f(x, y) = 400.000x + 300.000y adalah Rp7.900.000,00 dengan menyewa 4 truk dan 21 kol.

10. Jawaban: e

x = banyak kandang berisi ayam y = banyak kandang berisi itik

Jenis Banyak _TampungDaya

Kandang berisi ayam x 36 Kandang berisi itik y 24

(34)

Y

X 12

6

0 12 18

A B(9, 3) C

x + y = 12 x + 3y = 18 O

Diperoleh SPtLDV: x + y ≤ 10 36x + 24y ≤ 300 x ≥ 0

y ≥ 0

Jadi, SPtLDV yang memenuhi:

x ≥ 0, y ≥ 0, 36x + 24y ≤ 300, x + y ≤ 10 11. Jawaban: e

Misalkan: x = banyak barang jenis I y = banyak barang jenis II

Barang Banyak Unsur A Unsur B Harga

Jenis I x 1 2 250.000

Jenis II y 3 2 400.000

Pembatas 18 24

Diperoleh model matematika:

Memaksimumkan f(x, y) = 250.000x + 400.000y dengan kendala:

x + 3y ≤ 18

2x + 2y ≤ 24 ⇔ x + y ≤ 12 x ≥ 0

y ≥ 0

Daerah penyelesaian x + 3y ≤ 18 dibatasi garis x + 3y = 18 dan memuat titik (0, 0).

Daerah penyelesaian x + y ≤ 12 dibatasi garis x + y = 12 dan memuat titik (0, 0).

Garis x + 3y = 18 dan x + y = 12 berpotongan di titik B(9, 3).

Uji titik pojok ke f(x, y) = 250.000x + 400.000y

Titik Pojok f(x, y) = 250.000x + 400.000y

O(0, 0) 250.000 × 0 + 400.000 × 0 = 0

A(12, 0) 250.000 × 12 + 400.000 × 0 = 3.000.000 B(9, 3) 250.000 × 9 + 400.000 × 3 = 3.450.000 C(0, 6) 250.000 × 0 + 400.000 × 6 = 2.400.000 Penjualan maksimum Rp3.450.000,00 dicapai di titik B(9, 3) atau x = 9 dan y = 3.

Jadi, agar penjualan mencapai maksimum harus dibuat 9 barang jenis I dan 3 barang jenis II.

12. Jawaban: b

Misal: x = banyak kue jenis A y = banyak kue jenis B

Model matematika:

Memaksimumkan fungsi objektif f(x, y) = 4.000x + 3.000y dengan kendala:

20x + 20y≤ 4.000 60x + 40 y ≤ 9.000

x≥ 0 y≥ 0

Garis 20x + 20y = 4.000 dan 60x + 40y = 9.000 berpotongan di titik B(50, 150).

Uji titik pojok ke fungsi objektif f(x, y) = 4.000x + 3.000y.

Nilai maksimum fungsi objektif f(x, y) = 4.000x + 3.000y adalah 650.000.

Jadi, pendapatan maksimum yang dapat diperoleh pembuat kue Rp650.000,00.

Titik Pojok

O(0, 0) A(150, 0) B(50, 150) C(0, 200)

f(x, y) = 4.000x + 3.000y

4.000 · 0 + 3.000 · 0 = 0 4.000 · 150 + 3.000 · 0 = 600.000 4.000 · 50 + 3.000 · 150 = 650.000 4.000 · 0 + 3.000 · 200 = 600.000 Y

X

20x + 20y = 4.000 60x + 40y = 9.000

B(50, 150) 225

200

150

O _A

C

0 50 150 200 Jenis

Kue

A B Pembatas

Banyak

x y

Kebutuhan Gula (gram)

20 40 4.000

Kebutuhan Tepung (gram)

60 40 9.000

Harga

(35)

Y

X O

A B(200, 300)

P(400, 100)

T Q

500 500

400 y = 3₂x

y = 500 – x f(x, y) = 5.000x + 6.000y

5.000 × 20 + 6.000 × 0 = 100.000 5.000 × 80 + 6.000 × 0 = 400.000 5.000 × 20 + 6.000 × 60 = 460.000 Titik Sudut

A(20, 0) B(80, 0) C(20, 60) 13. Jawaban: e

Misal: x = banyak tablet I yang dikonsumsi y = banyak tablet II yang dikonsumsi

Diperoleh SPtLDV:

5x + 10y ≥ 25 ⇔ x + 2y ≥ 5 3x + y≥ 5

x≥ 0 y≥ 0

Meminimumkan f(x, y) = 4.000x + 8.000y Daerah penyelesaiannya:

Titik B merupakan titik potong antara garis 3x + y = 5 dan x + 2y = 5. Koordinat B(1, 2). Uji titik pojok ke fungsi objektif:

Nilai f(x, y) minimum adalah 20.000.

Jadi, pengeluaran minimum untuk pembelian tablet per hari Rp20.000,00.

14. Jawaban: c

Misal x = banyak soto ayam yang dijual (porsi) y = banyak soto daging yang dijual (porsi) Model matematika:

Memaksimumkan fungsi objektif f(x, y) = 5.000x + 6.000y dengan kendala:

x + y ≤ 80 x≥ 20 y≤ 60 x≥ 0 y≥ 0

Uji titik pojok ke f(x, y) = 5.000x + 6.000y

Penjualan maksimum Rp460.000,00 diperoleh pada saat menjual 20 porsi soto ayam dan 60 porsi soto daging.

Jadi, kantin harus menyediakan soto ayam 20 porsi dan soto daging 60 porsi.

15. Jawaban: e

Daerah yang menyatakan banyak karyawan:

Luas ∆OAB menyatakan banyak karyawan

seluruhnya.

L_∆_OAB = 1

2 × OA × BT = 1

2 × 500 × 300 = 75.000 L_∆_APQ menyatakan banyak karyawan

berpeng-hasilan lebih dari 400 ribu.

L_∆_APQ = 1₂ × AQ × PQ

= 1₂ × 100 × 100 = 5.000

APQ OAB

L L

∆

∆ =

5.000 75.000 =

1 15

Jadi, banyak karyawan yang berpenghasilan di

atas Rp400.000,00 sebanyak 1

15 bagian.

5

O 5

3 5

21

2

A(5, 0) B(1, 2)

3x + y = 5

f(x, y) = 4.000x + 8.000y

4.000 × 5 + 8.000 × 0 = 20.000 4.000 × 1 + 8.000 × 2 = 20.000 4.000 × 0 + 8.000 × 5 = 40.000 Titik Pojok

A(5, 0) B(1, 2) C(0, 5) C(0, 5)

Y X

x + 2y = 5

Jenis

Tablet I Tablet II Pembatas

Banyak

x y

Vitamin A (unit)

5 10 25

Vitamin B (unit)

3 1 5

Harga

4.000 8.000

A B

C (20, 60) 80

60

0 20 80

x = 20

x + y = 80 Y

(36)

Garis 3y – x = 12 dan garis y + 2x = 32 berpotongan di titik (12, 8).

Garis putus-putus pada gambar merupakan garis selidik. Oleh karena memaksimumkan fungsi objektif f(x, y) = 4y + x (koefisien x positif), maka dipilih garis selidik yang paling kanan. Garis selidik yang paling kanan mempunyai persamaan 4y + x = 200.

Jadi, untuk memperoleh hasil maksimum harus memproduksi minyak goreng 24 kemasan 1 liter dan 44 kemasan 2 liter, dan nilai maksimum fungsi objektif adalah 200. 2. a. Misalkan: x = banyaknya minyak goreng

kemasan 1 liter

y = banyaknya minyak goreng kemasan 2 liter

Model matematika permasalahan di atas: x + y≤ 120

x≥ 30 y≥ 50

memaksimumkan f(x, y) = 3.000x + 5.000y b. Daerah penyelesaian x + y ≤ 120 terletak di

sebelah kiri garis x + y = 120 dan memuat titik (0, 0).

Daerah penyelesaian x ≥ 30 adalah daerah di sebelah kanan garis x = 30.

Daerah penyelesaian y ≥ 50 adalah daerah di sebelah atas garis y = 50.

B. Uraian

1. a. Garis 2x + y = 24 melalui titik (12, 0) dan titik (0, 24).

Daerah penyelesaian 2x + y ≤ 24 adalah daerah yang memuat (0, 0).

Garis x + 2y = 12 melalui titik (12, 0) dan titik (0, 6).

Daerah penyelesaian x + 2y ≥ 12 adalah daerah yang tidak memuat (0, 0).

Garis x – y = –2 melalui titik (–2, 0) dan titik (0, 2).

Daerah penyelesaian x – y ≥ –2 adalah daerah yang memuat (0, 0).

Daerah penyelesaian x ≥ 0 daerah sebelah kanan garis x = 0 (sumbu Y).

Daerah penyelesaian y ≥ 0 adalah daerah di atas garis y = 0 (sumbu X).

Garis putus-putus pada gambar di atas merupa-kan garis selidik. Oleh karena memaksimum-kan fungsi f(x) = 7x – 3y (koefisien x positif), dipilih garis selidik yang paling kanan, yaitu persamaan 7x – 3y = 84.

Jadi, nilai maksimumnya adalah 84.

b. Garis 3y – x = 12 melalui titik (0, 4) dan titik (12, 8).

Daerah penyelesaian y – 3x ≥ 4 di kiri garis y – 3x = 4.

Garis y – x = 20 melalui titik (0, 20) dan titik (24, 44).

Daerah penyelesaian y – x ≤ 20 di kanan garis y – x = 20.

Garis y + 2x = 32 melalui titik (0, 32) dan titik (12, 8).

Daerah penyelesaian y + 2x ≥ 32 di kanan garis y + 2x = 32.

Daerah penyelesaian x ≤ 24 di kiri garis x = 24.

Garis y – x = 20 dan garis y + 2x = 32 berpotongan di titik (4, 24).

Y

X 7x – 3y = –21

7x – 3y = 84 x – y = –2

x + 2y = 12 2x + y = 24 A

B C

–3

7x – 3y = 14₃ 7x – 3y = 70₃

–2 24

7 6 2

Y

X x = 24

4y + x = 200

3y – x = 12

4y + x = 72

4y + x = 44 y + 2x = 32

4y + x= 100 44

32

24 20

12 8 4

4 12 24 y – x = 20

Jenis

1 liter 2 liter Pembatas

Banyak

x y 120

x

30 y 50

Laba

(37)

Y

X 0

12

8

3

2 4 9

A(9, 0) B(3, 2)

C(1, 6) D(0, 12)

6x + y = 12 2x + y = 8 x + 3y = 9

f(x, y) = 3.000x + 5.000y

90.000 460.000 540.000 Titik Pojok

A(30, 50) B(70, 50) C(30, 90) Y

X

A B

C

y = 50

x + y = 120 x = 30

0 30 120

120

50

Daerah penyelesaian →

Uji titik pojok ke fungsi f(x, y) = 8.500x + 4.000y

A(9, 0) 8.500(9) + 4.000(0) = 76.500 B(3, 2) 8.500(3) + 4.000(2) = 33.500 C(1, 6) 8.500(1) + 4.000(6) = 32.500 D(0, 12) 8.500(0) + 4.000(12) = 48.000 Nilai minimum f(x, y) = 8.500x + 4.000y adalah 32.500.

Jadi, orang tersebut harus mengeluarkan uang paling sedikit Rp32.500,00 per minggu agar ke-butuhan protein, karbohidrat, dan lemak terpenuhi.

4. a. Misalkan: x = banyak kue isi cokelat y = banyak kue isi keju

Jenis Kue Banyak Tepung Mentega Harga

Isi cokelat x 150 gr 50 gr 7.000

Isi keju y 75 gr 75 gr 5.500

Pembatas 18 kg 12 kg

Model matematika permasalahan di atas: memaksimumkan fungsi F(x, y) = 7.000x + 5.500y dengan kendala:

x + y≤ 180 2x + y ≤ 240 2x + 3y≤ 480

x≥ 0 y≥ 0

Daerah penyelesaian x + y ≤ 180 dibatasi garis x + y = 180 dan memuat titik (0, 0).

Daerah penyelesaian 2x + y ≤ 240 dibatasi garis 2x + y = 240 dan memuat titik (0, 0). Daerah penyelesaian 2x + 3y ≤ 480 dibatasi garis 2x + 3y = 480 dan memuat titik (0, 0). Daerah penyelesaian dari model matematika

tersebut:

c. Uji titik pojok

Agar memperoleh laba maksimum, pabrik tersebut harus membuat 30 botol minyak goreng kemasan 1 liter dan 90 botol minyak goreng kemasan 2 liter.

d. Keuntungan maksimum dapat diperoleh pabrik tersebut jika memproduksi 30 botol minyak kemasan 1 liter dan 50 botol minyak kemasan 2 liter sebesar Rp540.000,00.

3. Misalkan: x = banyak makanan jenis A y = banyak makanan jenis B

Makanan Protein Karbohidrat Lemak Harga

Jenis A (x) 2 6 1 8.500

Jenis B (y) 1 1 3 4.000

Kendala 8 12 9

Model matematika:

Meminimumkan f(x, y) = 8.500x + 4.000y dengan kendala:

(38)

Y

X y = x

x + y = 1.500 x = 500

A

B C 1.500

1.000

500

0 500 1.500 a. Model matematika:

Meminimumkan fungsi objektif f(x, y) = 4.000x + 5.000y dengan kendala:

x≥ 500 y≥ x x + y≤ 1.500

Daerah penyelesaian x ≥ 500 di kanan garis x = 500.

Daerah penyelesaian y ≥ x di kiri garis y = x. Daerah penyelesaian x + y ≤ 1.500 di kiri garis x + y = 1.500.

Garis x + y = 1.500 dan garis x = 500 ber-potongan di titik A(500, 1.000).

Garis y = x dan garis x = 500 berpotongan di titik B(500, 500).

Garis x + y = 1.500 d ngaris y = x berpotongan di titik C(750, 750).

Uji titik pojok ke fungsi objektif f(x, y) = 4.000x + 5.000y

A(500, 1.000) 4.000 · 500 + 5.000 · 1.000 = 7.000.000 B(500, 5.00) 4.000 · 500 + 5.000 · 500 = 4.500.000 C(750, 750) 4.000 · 750 + 5.000 · 750 = 6.750.000

Nilai minimum f(x, y) = 4.000x + 5.000y adalah 4.500.000.

Jadi, biaya minimum yang dikeluarkan LSM untuk melakukan survei Rp4.500.000,00. b. Uji titik pojok ke fungsi objektif

f(x, y) = 2.000x + 1.000y

A(500, 1.000) 2.000 · 500 + 1.000 · 1.000 = 2.000.000 B(500, 5.00) 2.000 · 500 + 1.000 · 500 = 1.500.000 C(750, 750) 2.000 · 750 + 1.000 · 750 = 2.250.000

Nilai maksimum f(x, y) = 2.000x + 1.000y adalah 2.250.000,00.

Jadi, keuntungan maksimum yang diperoleh LSM dari survei Rp2.250.000,00.

Daerah penyelesaian SPtLDV:

Garis 2x + y = 240, 2x + 3y = 480, dan x + y = 180 berpotongan di titik B.

2x + y = 240 x + y = 180 ––––––––––– –

x = 60 y = 120

Diperoleh koordinat titik B(60, 120).

Titik potong garis 2x + 3y = 480 dan x + y = 180.

2x + 3y= 480 × 1 2x + 3y= 480

x + y = 180 × 2 2x + 2y= 360

––––––––––– – y = 120 x = 60 Uji titik pojok ke dalam fungsi objektif F(x, y) = 7.000x + 5.500y.

Jadi, pedagang tersebut harus membuat 60 kue isi cokelat dan 120 kue isi keju agar memperoleh pendapatan maksimum.

b. Pendapatan maksimum yang diperoleh

pedagang Rp1.080.000,00.

5. Misal x = banyak kuesioner yang disebar di daerah pedesaan

y = banyak kuesioner yang disebar di daerah perkotaan

Ongkos dari Biaya

Daerah TV Oke Per Responden Keuntungan

Per Responden

Pedesaan 6.000 4.000 2.000

Perkotaan 6.000 5.000 1.000

Titik

A(120, 0) B(60, 120) C(0, 160)

f(x, y) = 7.000x + 5.500y

840.000 1.080.000 880.000 Y

X 2x + 3y = 480

2x + y = 240 x + y = 180

120 180 240 240

180 160

A B C

(39)

Y

X 2y – 3x = 8

3x – 2y = 18

2x + 3y = 12

2x + 3y = –1 A

B

C D –2 0 4 6

4

1

–3 Barang

A B Pembatas

Banyak

x y

Bahan Baku

20 kg 30 kg 270 kg

Waktu Kerja

2 jam 1 jam 17 jam Y

X 0

4

–8

Y

X 0

4 3

4 2

3x + 4y = 12

2x + y = 4

1. Jawaban: c

Garis –x + 2y = 0 melalui titik (8, 0) dan (0, 4). Daerah penyelesaian –x + 2y ≤ 8 adalah daerah yang dibatasi garis –x + 2y = 8 dan memuat titik (0, 0). Daerah penyelesaian:

Daerah penyelesaian –x + 2y ≤ 8 2. Jawaban: e

Persamaan garis yang melalui titik (–3,5, 0) dan titik (0, 7):

y 0

7 0

− − =

x 3,5 0 3,5

+ +

⇔ ₇y = x_3,5+3,5

⇔ y = 2x + 7

⇔ –2x + y = 7

Daerah penyelesaian memuat (0, 0) maka pertidak-samaannya –2x + y ≤ 7.

3. Jawaban: d

Daerah penyelesaian 2x + y ≥ 4 dibatasi oleh garis 2x + y = 4 dan tidak memuat titik (0, 0).

Daerah penyelesaian 3x + 4y – 6 ≤ 12 dibatasi oleh garis 3x + 4y = 12 dan memuat (0, 0). Daerah penyelesaian SPtLDV:

4. Jawaban: d

Garis x + y = 6 melalui titik (6, 0) dan titik (0, 6). Daerah penyelesaian x + y ≥ 6 tidak memuat titik (0, 0).

Garis –8x + 3y + 12 = 0 melalui titik (1,5, 0) dan (0, 4).

Daerah penyelesaian –8x + 3y + 12 ≥ 0 memuat titik (0, 0).

Garis –3x + 5y = 15 melalui (–5, 0) dan (0, 3). Daerah penyelesaian –3x + 5y ≤ 15 memuat titik (0, 0).

Y

X x + y = 6

–3x + 5y = 15–5 1,5 6

6

3

–4

–8x + 3y + 12 > 0

Daerah penyelesaian

→

Daerah penyelesaiannya:

5. Jawaban: b

Misalkan: x = banyaknya barang A y = banyaknya barang B

Model matematika sesuai dengan permasalahan di atas adalah:

20x + 30y≤ 270 ⇔ 2x + 3y ≤ 27 2x + y≤ 17

x ≥ 0 ; y≥ 0 6. Jawaban: a

a.

Luas ABCD = AB × BC = 13 × 2 13

= 26 satuan

(40)

b.

Luas ABCD = 1

2 × AC × BD

= 1₂ × 6 × 4 = 12 satuan Luas daerah penyelesaian 12 satuan. c.

Luas ABCD = AB × BC

= 20 × 20 = 20 satuan Luas daerah penyelesaian 20 satuan. d.

Luas ABCD = alas × tinggi = 5 × 4 = 20 satuan Luas daerah penyelesaian 20 satuan. e.

Luas ABCD = 1

2 × CD(AD + BC)

= 1

2 × 4(9 + 3) = 24 satuan

Luas daerah penyelesaian 24 satuan. Jadi, sistem pertidaksamaan yang daerah penyelesaiannya mempunyai luas 26 satuan adalah pilihan a.

Y

X A

B C

D x = 9

y = 4

2x + 3y = 12 0 6 9 –4

Y

X 2y – x = 12

2y – x = 2

2x + y = 6 A

2x + y = 16 B

C D

0 2 3 4 6 8

6 4 2

Y

X y = 4

2x + 3y = 12 A

B C

D

0 1 6 4

2x + 3y = 2 –5

Y

X 2y – x = 2

x + y = 7 x = –2

y – 2x = 7

A

B

C

D E

–2 0 4 7 7

3 1 Y

X 3x – 2y = 2

2x + y = 6 y – 2x = 6

3x + 2y = –2 A B

C D –2 0 2

6

2

–1

7. Jawaban: c

Garis y – 2x = 7 melalui titik (0, 7) dan titik (–2, 3). Daerah penyelesaian y – 2x ≤ 7 di kanan garis y – 2x = 7.

Garis 2y – x = 2 melalui titik (0, 1) dan titik (–2, 0). Daerah penyelesaian 2y – x ≥ 2 di kiri garis 2y – x = 2.

Garis x + y = 7 melalui titik (0, 7) dan titik (7, 0). Daerah penyelesaian x + y ≤ 7 di kiri garis x + y = 7. Daerah penyelesaian x ≥ –2 di kanan garis x = –2. Garis 2y – x = 2 dan x + y = 7 berpotongan di titik D(4, 3).

Garis x = –2 dan y – 2x = 7 berpotongan di titik B(–2, 3).

Daerah Penyelesaian:

Luas daerah penyelesaian = Luas ABCD

= Luas ABD + luas BCD = 1

2 × BD × AE + 1

2 × BD × BC

= 1

2 × 6 × 4 + 1

2 × 6 × 3

= 12 + 9 = 21

Jadi, luas daerah penyelesaian sistem pertidak-samaan 21 satuan.

8. Jawaban: c

Misalkan: x = banyak barang A y = banyak barang B

Model matematika sesuai dengan permasalahan di atas adalah memaksimumkan f(x, y) = 4x + 3y dengan kendala: 4x + 3y≤ 180

x + y≤ 50 x + 2y≤ 80

Persamaan garis 4x + 3y = 180 melalui (45, 0) dan (0, 60). Daerah penyelesaian 4x + 3y ≤ 180 dibatasi garis 4x + 3y = 180 dan memaut titik (0, 0). Persamaan garis x + y = 50 melalui (50, 0) dan (0, 50). Daerah penyelesaian x + y ≤ 50 dibatasi garis x + y = 50 dan memuat titik (0, 0).

(41)

Y

X

4x + 3y = 12 y – x = 5

x + 3y = –3

–5 –4 –3 –2 –1 0 1 2 3 4 5 6

5 4 3 2 1

Y

X 0

20

6

2 –2

2

4 5x + y = 20 x – y = –2 Tipe

A B Pembatas

Banyak

x y 125

Luas

100 m2 75 m2 10.000 m2

Keuntungan

6.000.000 4.000.000 Daerah penyelesaian SPtLDV:

B titik potong 4x + 3y = 180 dan x + y = 50. 4x + 3y = 180

3x + 3y = 150 ––––––––––– –

x = 30 y = 20

C titik potong x + y = 50 dan x + 2y = 80 x + y = 50

x + 2y = 80 ––––––––– –

y = 30 x = 20

Diperoleh titik C(20, 30).

Uji titik pojok penyelesaian ke dalam f(x, y).

Agar diperoleh laba maksimum maka harus dibuat 30 barang A dan 20 barang B.

9. Jawaban: b

Misalkan: x = banyak rumah tipe A y = banyak rumah tipe B

Model matematika permasalahan di atas: x + y≤ 125

4x + 3y≤ 400 x≥ 0 y≥ 0

memaksimumkan F(x, y) = 6.000.000x + 4.000.000y 1) Persamaan garis x + y = 125 melalui (125, 0) dan (0, 125). Daerah penyelesaian x + y ≤ 125 dibatasi garis x + y = 125 dan memuat (0, 0). 2) Persamaan garis 4x + 3y = 400 melalui (100,0)

dan (0, 400

3 ). Daerah penyelsaian 4x + 3y ≤ 400

dibatasi garis 4x + 3y = 400 dan memuat titik (0, 0).

3) Daerah penyelesaian x ≥ 0 dan y ≥ 0 adalah daerah pada kuadran I.

Daerah penyelesaian SPtLDV di atas adalah:

B adalah titik potong garis 4x + 3y = 400 dan x + y = 125.

4x + 3y = 400 3x + 3y = 375 –––––––––––– –

x = 25 y = 100

Uji titik pojok penyelesaian ke dalam f(x, y).

Jadi, keuntungan maksimum yang dapat diperoleh Rp600.000.000,00.

10. Jawaban: c

Jadi, himpunan titik yang berada di dalam daerah penyelesaian sistem pertidaksamaan adalah {(–1, 1), (–1, 2), (–1, 3), (–2, 1), (–2, 2), (–3, 1)}. 11. Jawaban: c

a. Titik

O(0, 0) A(100, 0) B(25, 100) C(0, 125)

f(x, y) = 6.000.000x + 4.000.000y

0 600.000.000 550.000.000 500.000.000 Daerah penyelesaian SPtLDV→

Y

X 4x + 3y = 400

A B C

0 100 125

400 3

125

x + y = 125

Titik Pojok