BAB III. Monte Carlo dan metode least-square, maka pada bab ini diantaranya akan

BAB III

METODE LEAST-SQUARE MONTE CARLO

Pada bab sebelumnya telah dijelaskan antara lain mengenai simulasi Monte Carlo dan metode least-square, maka pada bab ini diantaranya akan dibahas penggunaan kedua metode tersebut didalam metode LSM. Pada bab ini, akan dijelaskan bagaimana metode LSM digunakan untuk

mengaproksimasi nilai opsi put Amerika. Metode ini terdiri dari tiga tahap sekuensial, pertama adalah mensimulasikan lintasan dari harga saham, kemudian menghitung matriks payoff opsi, dan yang terakhir adalah menentukan harga opsi. Pada akhir bab ini juga akan dijelaskan contoh sederhana penerapan metode LSM. Namun sebelum contoh penerapan akan diberikan skema sederhana metode LSM ini.

Lebih jelasnya pada bab 3.1 akan dibahas mengenai ekspektasi bersyarat dan ruang Hilbert, bab 3.2 mengenai simulasi lintasan harga

saham, bab 3.3 mengenai perhitungan matriks payoff opsi, bab 3.4 mengenai perhitungan nilai opsi , bab 3.5 berisi skema metode LSM dan bab 3.6

menjelaskan contoh sederhana dari metode LSM.

3.1 Ekspektasi Bersyarat dan Ruang Hilbert

kosong dari semua kemungkinan hasil yang dapat terjadi pada dunia nyata atau dalam suatu eksperimen, dengan elemen Ω dilambangkan ω. Φ adalah σ-aljabar dari subset Ω, yaitu himpunan dan semua subset dari Ω. Elemen dari Φ disebut kejadian.

Probability measure Pm adalah fungsi dari Φ ke bilangan real antara 0

dan 1 yang menyatakan probabilitas masing-masing kejadian. Ruang

probabilitas merupakan ruang terukur dengan measure Pm, yang memenuhi

aksioma probabilitas, yaitu

1. Pm(J) ≥0, untuk setiap J∈Φ 2. Pm(Ω) = 1, dan 3. Pm(J1∪ J2∪…∪ Jn) = 1 ( ) n m i i P J =

∑

.

Ruang probabilitas yang complete adalah setiap subset C dari

himpunan null J0 (Pm(J0) = 0) dengan J0∈Φ adalah terukur (Wikipedia, 2008).

Variabel random X adalah fungsi terukur dari ruang sampel Ω ke ruang terukur lainnya yang disebut state space, X(ω) : Ω→R. Shiryaev (1994)

menyatakan bahwa jika terdapat H yang merupakan ruang variabel random X dengan mean nol dan momen kedua yang terbatas pada ruang probabilitas

(

Ω Φ, ,P_m

)

, dengan inner product <X,Y> = E[X.Y], norm _{X = E X⎡} 2_⎤ ⎣ ⎦ dan fungsi jarak (metric) X Y− , maka H adalah ruang Hilbert.

Pada ruang probabilitas

(

Ω Φ, ,P_m

)

dimisalkan 2 2

(

_{, ,}

)

m

L =L Ω ΦP adalah kelas dari variabel random X yang bernilai real (Φ-measurable), sedemikian sehingga X terbatas, yaitu E X⎡_⎣

( )

2⎤ < ∞_⎦ . Ruang L2 dengan definisi

penjumlahan dan perkalian skalar (skalar real) merupakan ruang vektor real. Untuk setiap X, Y ∈L2_{, didapat}

( )

E X < ∞, _{Var X( )=E X}

( )

2 _{−E X}

( )

2_{< ∞,} dan_{E XY}

(

)

_{≤E X}

( ) ( )

2 12_{E Y}2 12 _{< ∞ , dengan ketidaksamaan terakhir}

berdasarkan ketidaksamaan Cauchy-Schwartz pada fungsi yang square integrable x y, 2 ≤ x x, . ,y y . Sehingga Cov X Y( , )=E XY( )−E X E Y( ) ( ) ada dan terbatas.

Dari struktur square integrable diatas, disimpulkan bahwa L2 dengan inner product X Y| =E XY( )dan norm _X = _{X X|} 12 =_{E X(} 2₎12 _juga merupakan ruang Hilbert.

Selanjutnya akan dijelaskan adanya (existence) ekspektasi bersyarat pada ruang L2 yang telah dijelaskan diatas, ekspektasi bersyarat tersebut akan digunakan dalam metode LSM. Namun sebelum itu akan dijelaskan teorema proyeksi pada ruang Hilbert.

Teorema Proyeksi

Misalkan H adalah ruang Hilbert dan M subruang dari H, dan x sembarang vektor di H. Jika terdapat vektor m0∈M sedemikian sehingga

Kondisi perlu dan cukup bahwa m0∈M menjadi vektor unik yang

meminimumkan x m− untuk m∈M adalah x m− ₀ ⊥M. Jika M complete (barisan Cauchy di M konvergen di M), maka vektor unik yang

meminimumkan x m− untuk m∈M ada. m0 disebut juga proyeksi ortogonal

dari x ke M.

Penjelasan dan bukti teorema diatas dapat dilihat pada (Luenberger, 1969).

Sekarang akan dibahas adanya ekspektasi bersyarat pada ruang Hilbert yang telah dijelaskan Rogers (1997). Misalkan Σ adalah sub σ-aljabar dari Φ, dan misalkan X menyatakan variabel random yang integrable pada

(

Ω Φ, ,P_m

)

. Rogers (1997) menyatakan adanya variabel random E X

[

|Σ ,

]

disebut ekspektasi bersyarat dari X diberikan Σ, yang memiliki sifat-sifat berikut

i) E X

[

|Σ Σ-measurable dan integrable,

]

ii)

∫

=

∫

[

|Σ

]

,

A A

XdP E X dP untuk setiap A∈ Σ.

Selanjutnya akan diaplikasikan teorema proyeksi untuk memastikan adanya ekspektasi bersyarat untuk variabel-variabel random yang square integrable. Diasumsikan X square integrable, yaitu X ∈ 2

(

_{, ,}

)

m

L Ω Φ P dan misalkan 2

(

_{, ,}

)

m

L Ω ΣP menyatakan ruang variabel-variabel random yang memenuhi Σ-measurable dan square integrable. Seperti ditulis sebelumnya

(pada halaman 45), ruang variabel random 2

(

_{, ,}

)

m

L Ω ΣP adalah ruang Hilbert, sehingga untuk Y0 ∈L2

(

Ω Σ, ,P_m

)

merupakan subruang yang complete pada

(

)

2 _{, ,}

m

L Ω Φ P . Maka berdasarkan teorema proyeksi, terdapat elemen Y0 ∈L2

(

Ω Σ, ,P

)

sedemikian sehingga

a) 2

(

(

)

2

)

{

2 2

(

)

}

0 0 inf : , , m

X Y− =E X Y− = x Z− Z L∈ Ω ΣP . b) X Y Z− ₀| =0,untuk semua _{Z L∈} 2

(

_{Ω Σ, ,P}

)

_.

Karena Y0 ∈L2

(

Ω Σ, ,P_m

)

, Y0 adalah Σ-measurable dan square integrable,

sehingga memenuhi kondisi i) diatas. Jika A∈Σ, maka Z I= (fungsi indikator _A dari himpunan A) adalah elemen dari 2

(

_{, ,}

)

m

L Ω ΣP dan poin b) menyatakan bahwa

(

)

(

)

0 ( ) A A A E X Y Z X Y dP XdP YdP = − =

∫

− =

∫

−

∫

.

Dengan merujuk ke ii), maka Y0 adalah E X

[

|Σ . Dengan kata lain,

]

ekspektasi bersyarat dari X diberikan Σ adalah proyeksi ortogonal dari X pada

(

)

2 _{, ,}

m

L Ω ΣP . Jadi Y0 =E X

[

|Σ adalah anggota ruang

]

L2

(

Ω Σ, ,P_m

)

yang

merupakan ruang Hilbert. Karena ekspektasi bersyarat merupakan anggota ruang Hilbert sehingga kita dapat menggunakan teori yang yang berlaku pada ruang Hilbert untuk menentukan aproksimasi fungsi ekspektasi bersyarat yang nanti dijelaskan kembali pada subbab 3.3.

Pada skripsi ini ruang probabilitas

(

Ω Φ, ,P_m

)

dapat dijelaskan sebagai berikut: Ω merupakan himpunan semua kemungkinan proses stokastik harga saham dan suku bunga yang terjadi antara waktu 0 dan T, Ω memiliki elemen ω, yaitu sampel lintasan harga saham dan suku bunga, Φ merupakan σ-aljabar dari semua lintasan harga saham dan suku bunga subset dari Ω, dan Pm merupakan probability measure yang didefinisikan pada Φ. Sehingga

fungsi ekspektasi bersyarat dinyatakan dengan E X

[

|Φ . X yang dimaksud

]

adalah ekspektasi besar payoff P yang didapat ketika kondisi harga saham saat ini S dan suku bunga saat ini r elemen dari Φ, maka dapat juga

dinyatakan dengan E P S r .

[

| ( , )

]

3.2 Simulasi Lintasan Harga Saham

Pada subbab ini akan dijelaskan tahap pertama dalam metode LSM. Tahap pertama adalah mensimulasikan lintasan aset induk dari opsi put Amerika yaitu harga saham.

Setiap opsi memiliki jangka waktu dan jumlah waktu eksekusi yang berbeda. Misalkan suatu opsi dapat dieksekusi pada harga E dengan aset induk S yang memiliki N buah kesempatan waktu eksekusi dengan interval waktu sebesar δ dan simulasi akan dilakukan sebanyak M kali. Simulasi t

dilakukan menggunakan persamaan (2.20) yang telah dibahas di bab dua yaitu

2 2 1 3 2 ( ) ( ).exp 1 , 0,1,..., 1. 2 i i S t₊ =S t ⎡_⎢⎜⎛r D− −σ _⎟⎞dt +σ dt ⎡_⎣ −ρ ε +ρε _⎦⎤_⎥⎤ i = N− ⎝ ⎠ ⎣ ⎦

Nilai short rate r pada persamaan (2.20) tidak lagi nilai yang konstan namun merupakan faktor stokastik pembentuk harga saham. Dengan demikian sebelum kita mensimulasikan lintasan harga saham terlebih dahulu kita simulasikan lintasan untuk short rate, yang sebelumnya telah dibahas pada bab II dengan menggunakan persamaan (2.15) berikut

(

)

2 1 2 1 ( ) ( ). 1 . 2 adt adt adt i i e r t r t e b e a ν − ε − − + − = + − + ,i =0,1,...,N− 1.

Sehingga persamaan (2.20) menjadi

2 2 1 1 3 2 ( ) ( ).exp ( ) 1 , 0,1,..., 1. 2 i i i S t₊ =S t ⎡_⎢⎜⎛r t₊ − −D σ ⎞_⎟dt+σ dt ⎡ −ρ ε +ρε ⎤_⎥⎤ i= N− ⎣ ⎦ ⎝ ⎠ ⎣ ⎦ (3.1)

Harga saham dan short rate akan disimulasikan sebanyak M kali, sehingga harga saham pada lintasan ke-j dan di waktu eksekusi ke-ti disebut S t _j( )_i

dan short rate disebut dengan ( )r t dengan j = 1, 2, …, M dan i = 1, 2, …, N. _{j i} Dari simulasi (2.15) kita akan dapatkan matriks short rate ukuran M x N, yaitu

   Waktu Eksekusi t1 t2 . . . tN Simulasi 1  r t1 1( )  r t1( )2     r t1( )N   2  r t2( )1   r t2( )2     r t2( )N   3  r t3( )1   r t3( )2     r t3( )N   4  r t4( )1   r t4( )2     r t4( )N   .           .           .           M  r t_M( )₁   r t_M( )₂   . . .  r t_M( )_N  

Gambar 3.1. Matriks short rate

Nilai ( )r t akan digunakan untuk mendapatkan ( )_{j i} S t pada _{j i}

persamaan (3.1). Nilai r t didapat dari persamaan (2.15) dengan nilai awal _j( )₁ short rate r t yang sama untuk masing-masing simulasi. Hal ini juga berlaku ( )₀ untuk harga saham pada (3.1), nilai awal harga sahamS t sama untuk ( )₀ masing-masing simulasi. Hasil simulasi (3.1), yaitu harga saham yang didapat di tiap waktu eksekusi disusun sedemikian sehingga kita mendapatkan

   Waktu Eksekusi t1 t2 . . . tN Simulasi 1  S t_{1 1}( )  S t₁( )₂     S t₁( )_N   2  S t2( )1   S t2( )2     S t2( )N   3  S t₃( )₁   S t₃( )₂     S t₃( )_N   4  S t4( )1   S t4( )2     S t4( )N   .           .           .           .           M  S tM( )1 S tM( )2 . . .  S tM( )N  

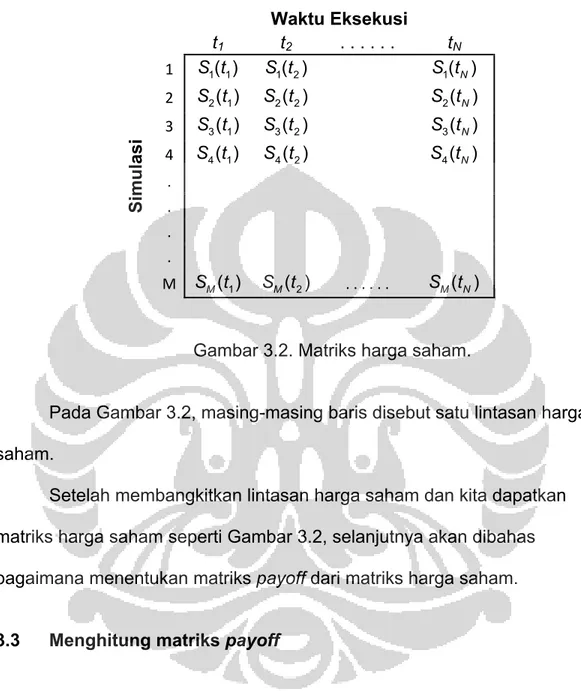
Gambar 3.2. Matriks harga saham.

Pada Gambar 3.2, masing-masing baris disebut satu lintasan harga saham.

Setelah membangkitkan lintasan harga saham dan kita dapatkan matriks harga saham seperti Gambar 3.2, selanjutnya akan dibahas bagaimana menentukan matriks payoff dari matriks harga saham.

3.3 Menghitung matriks payoff

Misalkan ( ( ))F S t_{j i} menyatakan payoff opsi yang didapat jika pada waktu ti opsi dieksekusi pada lintasan j, dimana j = 1, 2, …, M, dan i = 1, 2,

…, N. Maka ( ( ))F S t_{j i} =E S t− _j( )_i dengan E adalah harga eksekusi. ( ( ))F S t_{j i} disebut juga payoff segera.

Misalkan P menyatakan matriks payoff yang berdimensi M x N dengan elemen f . Pada saat T (waktu jatuh tempo opsi), payoff pada masing-_{j i,} masing lintasan adalah nilai maksimum dari nol dan nilai opsi yang sebenarnya pada waktu T, yaitu

(

)

, max 0, ( )

j N j

f = ⎡_⎣ F S T ⎤_{⎦ , 1 ≤ j ≤ M.}

Untuk menentukan keputusan apakah kita harus mengeksekusi segera atau menunda dan mengeksekusi pada waktu mendatang, kita perlu membandingkan dua nilai berikut, yaitu nilai payoff saat ti (payoff segera

( ( ))_{j i}

F S t ) dan nilai ekspektasi payoff dimasa mendatang yang bersyarat harga saham dan short rate saat ti yang dinyatakan dengan E P S t r t⎡_⎣ | _j( ), ( ) ._{i j i} ⎤_⎦

Untuk membandingkan dua nilai tersebut, kita bekerja mundur dimulai dari waktu jatuh tempo opsi T ke waktu ti dimana 0 < i < N pada setiap

lintasan yang in the money. Dalam hal ini hanya digunakan lintasan yang in the money karena keputusan eksekusi hanya relevan ketika opsi dalam kondisi in the money (Longstaff dan Schwartz,2001).

Untuk sembarang waktu ti, 0 < i < N, ekspektasi bersyarat payoff opsi dimasa mendatang pada saat harga saham saat ti sebesar Sj(ti) dan short

rate saat ti sebesar rj(ti),yaitu ⎡E P S t r t⎣ | _j( ), ( )_{i j i} ⎦⎤, seperti yang telah dijelaskan

pada subbab 3.1, ⎡E P S t r t_⎣ | _j( ), ( )_{i j i} ⎤_⎦ merupakan anggota ruang Hilbert L2, sehingga kita dapat mengaproksimasi fungsi tersebut menggunakan teori

yang berlaku pada ruang Hilbert. Misalkan ⎡E P S t r t_⎣ | _j( ), ( )_{i j i} ⎤_⎦ berkaitan dengan sebuah fungsi yang tidak diketahui, kita sebut sebagai g(x).

Teori dalam ruang Hilbert menyatakan bahwa sembarang fungsi g(x) anggota ruang tersebut, dapat dinyatakan sebagai kombinasi linear terhitung dari basis ruang vektornya, sehingga

0 ( ) _{k k}( ) k g x ∞ β φ x = =

∑

(3.2)

dimana

{

φ_k( )x

}

_k∞₌₁merupakan himpunan basis didalam ruang Hilbert. Longstaff dan Schwartz (2001) menyarankan untuk menggunakan monomial

{

}

∞

=1 ( )k

i _k

S t

untuk mengestimasi fungsi g(x) tersebut sebagai himpunan basis sehingga

persamaan (3.2) dapat ditulis sebagai ∞ β = =

∑

0 ( ) ( ) k k i k g x S t . Teorema

aproksimasi Stone-Weierstrass menyatakan bahwa monomial

{

}

∞ =1 ( )k

i _k

S t

membentuk basis ruang L2 _{(Hassani,1999).}

{

}

∞

=1 ( )k

i _k

S t merupakan basis yang tidak ortonormal, tetapi bebas linear. Hassani (1999) menyatakan bahwa jika ingin mendapatkan kombinasi linear yang ortonormal, dapat digunakan proses Gram-Schmidt, sedemikian sehingga didapat polinomial yang ortonormal satu dengan yang lain dan merentang L2.

Secara teori, kita menyatakan g(x) sebagai kombinasi linear atas K suku yang dapat ditulis sebagai berikut

β = =

∑

0 ( ) K ( )k K k i k g x S t .

Aproksimasi dari gK(x) diatas dimisalkan dengan β

∧ ∧ = =

∑

0 ( ) K ( )k K k i k g x S t yang

diselesaikan menggunakan regresi least-square. Dalam skripsi ini dipilih K = 2, sehingga β β β ∧ ∧ ∧ ∧ = + + 2 2( ) 0 1 ( )i 2 ( )i g x S t S t . (3.3)

Oleh karena g x∧₂( ) digunakan untuk mengaproksimasi fungsi ekspektasi payoff opsi mendatang yang bersyarat harga saham saat ti ,Sj(ti), dan short

rate saat ti, rj(ti), jadi ada dua variabel independen yang akan digunakan

untuk menaksir besar ekspektasi payoff mendatang ⎡E P S t r t_⎣ | _j( ), ( )_{i j i} ⎤_⎦, maka merujuk pada sifat regresi polinomial dengan dua variabel yang ditunjukkan persamaan (2.31), maka persamaan (3.3) menjadi

β β β β β β

∧ ∧ ∧ ∧ ∧ ∧ ∧

= + + + 2+ 2+

2( ) 0 1 ( )i 2 ( )i 11 ( )i 22 ( )i 12 ( ) ( )i i

g x S t r t S t r t S t r t . (3.4)

Untuk mendapatkan persamaan (3.4) dengan regresi least-square, digunakan data cross-section pada observasi-observasi yang dihasilkan oleh simulasi lintasan yang in the money yaitu

{

_{g x}( ), ( ), ( )i

(

_{S x r x}i i

)

}

_{. Data tersebut}

digunakan untuk menaksir parameterβ β β β β β₀, , ,_{1 2 11}, ₂₂, ₁₂dengan menyelesaikan { }β ₌₀

∑

₌

(

β +β +β +β +β +β −

( )

)

2 2 2 0 1 2 11 22 12 1 min ( ) ( ) ( ) ( ) ( ) ( ) K k k M i i i i i i i i S t r t S t r t S t r t g x . (3.5)

Cara penaksiran parameter tersebut akan dijelaskan dibawah. _{g x pada}

( )

i

persamaan (3.5) merupakan besar payoff yang diperoleh jika opsi tidak dieksekusi pada waktu ti, yaitu payoff pada suatu waktu yang dimisalkan tn

dimana i < n ≤ N , yang nilainya didiskonto ke waktu ti. Sehingga g x dapat

( )

i

dinyatakan sebagai , , 1 ( ) i n N j i j n t t n i y t f B = + =

∑

(3.6) dengan _, i n t t

B adalah faktor untuk mendiskontokan nilai payoff pada tn ke

waktu ti dan f adalah payoff yang diterima pada waktu t_{j n,} n dan lintasan ke-j

dimana j = 1, 2, .., M. Untuk lebih jelasnya perhatikan gambar berikut. t1 … ti … tn1 tn2 tn3 … tN lintasan 1 g(xi) = y1(ti) f_1,n1 2 g(xi) = y2(ti) f1,n3 : : j g(xi) = yj(ti) fj,n2 : M

Gambar 3.3. Diskonto payoff masa datang jika opsi tidak dieksekusi Pada Gambar 3.3, ti < tn1≤ tn2≤ tn3 ≤ tN.

Untuk menaksir parameterβ β β β β β₀, , ,_{1 2 11}, ₂₂, ₁₂yang telah disebutkan diatas, digunakan cara yang telah dijelaskan pada subbab 2.6. Kita ingat

y X∧ = β∧ .

Variabel X yang dimaksud adalah matriks X berikut

2 2 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 3 3 3 3 3 3 2 2 1 ( ) ( ) ( ) ( ) ( ) ( ) 1 ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) 1 ( ) ( ) : : : : : : 1 ( ) ( ) ( ) ( ) ( ) ( ) ⎡ ⎤ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎣ ⎦ i i i i i i i i i i i i i i i i i i n i n i n i n i n i n i S t r t S t r t S t r t S t r t S t r t S t r t S t r t S t r t S t r t S t r t S t r t S t r t , dengan

(

)

1 ( ) ( )' ( ) ( )' ( ) β∧ − = i i i i i t X t X t X t y t . (3.7) yang kemudian digunakan pada persamaan (3.4) untuk mendapatkan estimasi fungsi ekspektasi payoff opsi g x sebenarnya yaitu ₂( )

⎡ ⎤

= ⎣ ⎦

2( ) j( ) |i j( ), ( )i j i

g x E y t S t r t .

Kembali kepada permasalahan bagaimana membandingkan dua nilai berikut, yaitu nilai payoff saat ti (payoff segera ( ( ))F S t_{j i} ) dan nilai ekspektasi

payoff dimasa mendatang yang bersyarat harga saham dan short rate saat ti

yang dinyatakan dengan E P S t r t⎡_⎣ | j( ), ( ) .i j i ⎤_⎦

Nilai estimasi dari regresi, yaitu y t∧( )_i =X t( ) ( )_i β∧ t_i kemudian digunakan untuk menentukan apakah saat ti memang waktu yang optimal untuk

mengeksekusi opsi. Waktu optimal tersebut ditentukan dengan cara membandingkany t yang merupakan ekspektasi payoff mendatang jika ∧( )_i opsi tidak dieksekusi, dengan nilai payoff segera ( ( ))F S t_{j i} . Jika

∧ ( )_i

y t < ( ( ))F S t_{j i} , maka f diberikan nilai ( ( ))_{j i,} F S t_{j i} dan semua nilai f pada _{j n,} matriks payoff P dengan i < n ≤ N, diberi nilai nol. Hal ini karena opsi hanya bisa dieksekusi paling banyak satu kali sepanjang lintasan atau selama opsi tersebut berlaku. Pada kasus yang lain yaitu y t∧( )_i ≥ ( ( ))F S t_{j i} , maka f diberi _{j i,} nilai nol.

Pemberian nilai f secara matematis dapat dinyatakan sebagai berikut. _{j i,}

(

)

(

)

(

)

~ j , , j ( ) dan 0, jika ( ) ( ) , 0 jika ( ) ( ) j i j n j i i j i j i i F S t f i n N F S t y t f j M F S t y t ∧ ∧ ⎧ _{= < ≤ >} ⎪ =_⎨ ∈ ⎪ _≤ ⎩

Setelah kita dapatkan matriks payoff opsi P langkah selanjutnya adalah menghitung nilai opsi menggunakan matriks tersebut.

3.4 Menghitung nilai opsi

Setelah didapat matriks payoff opsi, selanjutnya estimasi nilai opsi P∧ pada waktu t0 didapat dengan mendiskonto seluruh payoff di tiap-tiap

lintasan ke waktu t0 dan merata-ratakannya dengan pembagi M yaitu

banyaknya lintasan , 0, 1 1 1 . i M N j i t j i P f B M ∧ = = =

∑∑

Tiga langkah sekuensial yang telah dijelaskan diatas selanjutnya akan digunakan dalam implementasi penentuan nilai opsi put Amerika yang akan

penerapan sederhana dari metode LSM ini akan dijelaskan pada subbab-subbab selanjutnya.

3.5 Skema Metode LSM

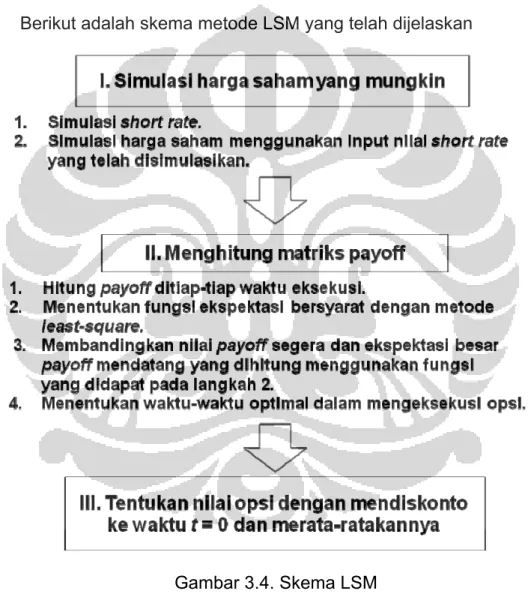
Berikut adalah skema metode LSM yang telah dijelaskan

Gambar 3.4. Skema LSM

3.6 Contoh Penerapan

Pada subbab ini akan diberikan contoh penerapan metode LSM yang telah dijelaskan. Misalkan terdapat sebuah opsi put Amerika dengan aset

induk berupa saham. Diketahui harga saat ini dari saham tersebut yaitu S0 =

$100. Saham ini memiliki volatilitas sebesar 25% dan tingkat hasil dividen sebesar 1,5%. Opsi tersebut dapat dieksekusi pada harga $110 pada saat t1, t2, dan t3, dimana saat t3 adalah masa berakhirnya hak opsi. Sehingga

panjang intervalnya adalah 1/3.

Diketahui pula bahwa tingkat suku bunga bebas risiko saat ini adalah sebesar 3% ,memiliki volatilitas sebesar 3% dan kecepatan mean reversion sebesar 2 dan reversion level 5%. Simulasi akan dilakukan sebanyak 8 kali. Dan koefisien korelasi antara proses Wiener harga saham dW dan short rate dZ dipilih sebesar ρ = -0,5, dengan kata lain dWdZ = -0.5dt.

Berikut ini langkah demi langkah bagaimana metode LSM menentukan harga opsi dari data parameter yang diketahui.

Langkah 1 : Simulasi harga saham

Seperti telah dijelaskan sebelumnya, simulasi harga saham akan

menggunakan persamaan (3.1) dan short rate dengan persamaan (2.15). Dalam hal ini, program yang digunakan adalah Matlab. Dari simulasi tersebut kita dapatkan matriks S berikut

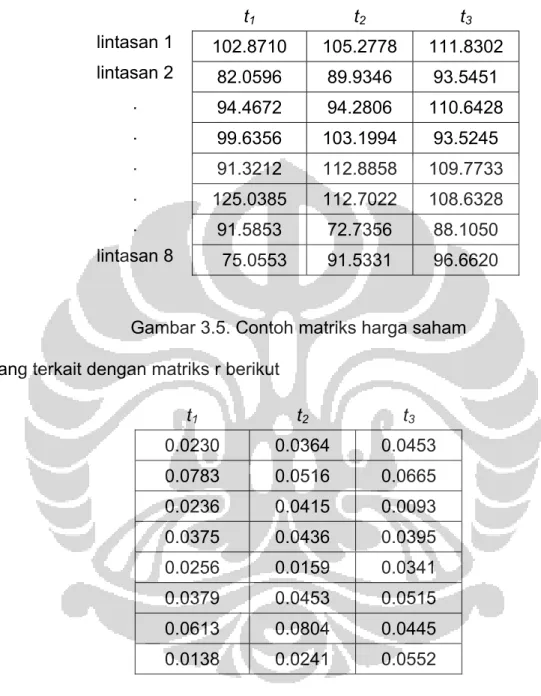
t1 t2 t3 lintasan 1 _{102.8710 105.2778 111.8302} lintasan 2 _{82.0596 89.9346 93.5451} . _{94.4672 94.2806 110.6428} . _{99.6356 103.1994 93.5245} . _{91.3212 112.8858 109.7733} . _{125.0385 112.7022 108.6328} . _{91.5853 72.7356 88.1050} lintasan 8 _{75.0553 91.5331 96.6620}

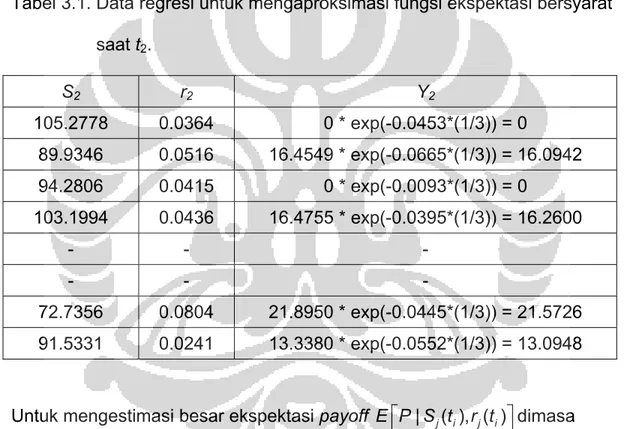
Gambar 3.5. Contoh matriks harga saham yang terkait dengan matriks r berikut

t1 t2 t3 0.0230 0.0364 0.0453 0.0783 0.0516 0.0665 0.0236 0.0415 0.0093 0.0375 0.0436 0.0395 0.0256 0.0159 0.0341 0.0379 0.0453 0.0515 0.0613 0.0804 0.0445 0.0138 0.0241 0.0552

Gambar 3.6. Contoh matriks short rate

Nilai 0.0230 (2,3%) pada baris dan kolom pertama matriks diatas didapat dari perhitungan berikut

(

)

2.2.(1/ 3) 2(1/ 3) 2(1/ 3) 1 2 1 ( ) (3%). (5%) 1 (3%) . 2.2 i e r t e e ε − − − + − = + − + .

Nilai ε2 yang terambil pada perhitungan tersebut adalah -0.6502.

Selanjutnya nilai 0.0230, digunakan untuk mendapatkan nilai 102.8710 pada baris dan kolom pertama matriks harga saham. Yaitu

2 1 1 (0.25) ( ) 100.exp 0.0230 0.015 (1/ 3) 0.25 1/ 3 . 2 i S t₊ = ⎡_⎢⎛_⎜ − − ⎞_⎟ + ε ⎤_⎥ ⎝ ⎠ ⎣ ⎦

Nilai ε1 yang terambil pada perhitungan tersebut adalah 0.1442.

Langkah 2 : Menghitung matriks payoff

Dari matriks S yang diperoleh, kemudian dihitung matriks payoff yang didapat apabila opsi dieksekusi segera dimasing-masing waktu yang ada dengan menggunakan formula ( ( ))F S t_{j i} =E S t− _j( )_i dengan E = $110 adalah harga eksekusi. t1 t2 t3 7.1290 4.7222 0 27.9404 20.0654 16.4549 15.5328 15.7194 0 10.3644 6.8006 16.4755 18.6788 0 0.2267 0 0 1.3672 18.4147 37.2644 21.8950 34.9447 18.4669 13.3380

dibandingkan harga eksekusi (S E). Contohnya nilai 0 pada kolom pertama, $125.0385 > $110. Sehingga pemegang opsi dapat menjual sahamnya dipasar dan payoff opsi yang diterimanya sebesar 0.

Tujuan yang ingin dicapai pada langkah 2 ini adalah untuk

menemukan waktu yang optimal yang memaksimumkan payoff opsi yang kita dapatkan di tiap masing-masing lintasan. Untuk tujuan tersebut, metode LSM bekerja dari belakang (backward), maka perhatikan pada saat t2 dan t3. Jika

opsi put dalam kondisi in the money pada saat t2, pemegang opsi harus

memutuskan apakah mengeksekusi pada saat tersebut atau menunggu hingga t3.

Perlu diingat bahwa pada langkah ini hanya akan digunakan lintasan yang in the money karena membuat fungsi ekspektasi bersyarat dapat diestimasi lebih baik pada waktu-waktu dimana keputusan eksekusi adalah relevan, dan hal ini juga meningkatkan efisiensi algoritma LSM.

Dari Gambar 3.7 yang merujuk pada matriks harga saham pada Gambar 3.5 dapat kita simpulkan bahwa terdapat 6 lintasan yang berada dalam kondisi in the money pada t2. Misalkan S2 menyatakan harga saham

pada t2 dan r2 menyatakan short rate pada t2, kemudian Y2 menyatakan

payoff yang didapat pada t3 yang didiskonto ke t2 apabila opsi tidak

dieksekusi pada t2. Proses diskonto dilakukan menggunakan persamaan

(3.6) berikut , , ( ) i n N j i j n t t y t =

∑

f B .

,

i n

t t

B merupakan faktor diskonto antara waktu tn dan ti yaitue−r t(n−ti) dan fj,n

merupakan payoff yang diterima pada masa datang. Proses ini dilakukan karena nilai dimasa datang dapat dibandingkan dengan nilai saat ini jika dipandang pada waktu yang sama. S2 , r2 dan Y2 diberikan oleh tabel berikut

ini.

Tabel 3.1. Data regresi untuk mengaproksimasi fungsi ekspektasi bersyarat saat t2. S2 r2 Y2 105.2778 0.0364 0 * exp(-0.0453*(1/3)) = 0 89.9346 0.0516 16.4549 * exp(-0.0665*(1/3)) = 16.0942 94.2806 0.0415 0 * exp(-0.0093*(1/3)) = 0 103.1994 0.0436 16.4755 * exp(-0.0395*(1/3)) = 16.2600 - - - - - - 72.7356 0.0804 21.8950 * exp(-0.0445*(1/3)) = 21.5726 91.5331 0.0241 13.3380 * exp(-0.0552*(1/3)) = 13.0948

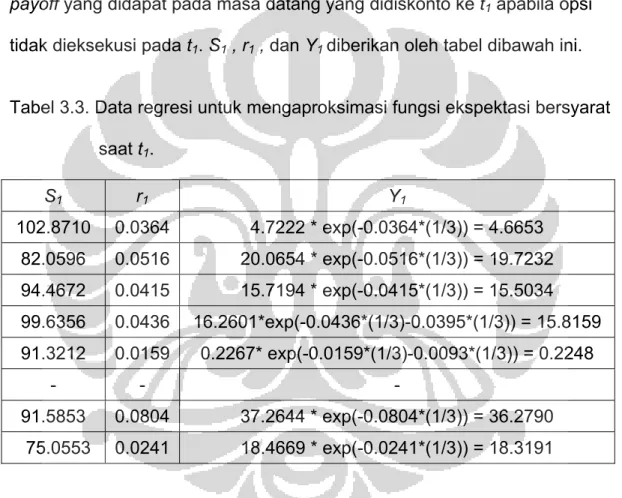
Untuk mengestimasi besar ekspektasi payoff E P S t r t⎡_⎣ | _j( ), ( )_{i j i} ⎤_{⎦ dimasa} datang yang bersyarat atas harga saham dan short rate pada t2, kita

regresikan data pada tabel 3.1 dengan Y2 sebagai variabel tak bebas dan S2,

r2, S22, r22, dan S2r2 sebagai regressor. Matriks X sesuai dengan persamaan

X 2 2 2 2 2 2 1 * 1 105.2778 0.0364 (105.2778) (0.0364) (105.2778)(0.0364) 1 89.9346 0.0516 (89.9346) (0.0516) (89.9346)(0 S r S r S r = 2₂ 2₂ 2 2 2 2 .0516) 1 94.2806 0.0415 (94.2806) (0.0415) (94.2806)(0.0415) 1 103.1994 0.0436 (103.1994) (0.0436) (103.1994)(0.0436) 1 72.7356 0.0804 (72.7356) (0.0804) (72.7356)(0.0804) 1 91.5331 0.0241 (91.5331) (0.0241) (91.5331)(0.0241) ⎡ ⎤ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎣ ⎦

Dari matriks X diatas kemudian dapat dihitung koefisien fungsi ekspektasi bersyarat persamaan (3.4) berikut

β β β β β β

∧ ∧ ∧ ∧ ∧ ∧ ∧

= + + + 2+ 2+

2( ) 0 1 ( )i 2 ( )i 11 ( )i 22 ( )i 12 ( ) ( )i i

g x S t r t S t r t S t r t

dengan menggunakan persamaan (3.7)

(

)

1 ( ) ( )' ( ) ( )' ( ) 8086 -152 -32195 1 -61411 400 i i i i i t X t X t X t y t β∧ − = ⎡ ⎤ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ = ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎣ ⎦

Hasilnya, kita mendapatkan aproksimasi fungsi ekspektasi bersyarat berikut

2 2

2 2 2 2 2 2

8086 - 152 - 32195 - 61411 400

y∧ = S r +S r + S r (3.8)

Persamaan (3.8) merupakan aproksimasi fungsi ekspektasi bersyarat untuk keseluruhan kemungkinan lintasan pada t2 menuju t3 dengan menggunakan

sampel data tabel 3.1 yang hanya sebanyak 6 lintasan. Oleh karena itu, semakin banyak sampel lintasan yang diambil akan semakin akurat hasil yang diperoleh.

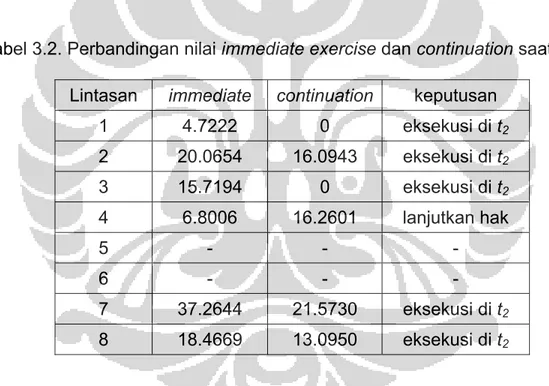
Selanjutnya akan dibandingkan payoff yang didapat jika mengeksekusi pada t2 (immediate exercise), yang ditunjukkan pada kolom kedua tabel 3.2,

dengan nilai ekspektasi payoff (continuation) yang diberikan pada kolom ketiga tabel 3.2. Nilai eksekusi yang dilakukan saat t2 adalah payoff yang

didapat, yaitu 110 – S2 untuk tiap lintasan yang in the money. Sementara itu

nilai masa datang atau kelanjutan didapat dengan mensubstitusi S2 dan r2

pada persamaan (3.8).

Tabel 3.2. Perbandingan nilai immediate exercise dan continuation saat t2.

Lintasan immediate continuation keputusan

1 4.7222 0 eksekusi di t2 2 20.0654 16.0943 eksekusi di t2 3 15.7194 0 eksekusi di t2 4 6.8006 16.2601 lanjutkan hak 5 - - - 6 - - - 7 37.2644 21.5730 eksekusi di t2 8 18.4669 13.0950 eksekusi di t2

Pada lintasan pertama, nilai 4.7222 pada kolom kedua adalah hasil dari $110-$105.2778, sedangkan nilai 0 pada kolom ketiga adalah hasil substitusi S2 = 105.2778 dan r2 = 0.0364 kedalam persamaan (3.8). Pada lintasan

pertama, nilai ekspektasi masa datang sebesar 0, lebih kecil dibandingkan nilai 4.7222 yang didapat apabila opsi dieksekusi pada saat t2, sehingga

Pada lintasan keempat, nilai ekspektasi sebesar 16.2601 lebih besar ketimbang 6.8006 yang didapat apabila opsi dieksekusi di t2, maka keputusan

menunda eksekusi dan mengharapkan payoff masa datang adalah lebih optimal.

Dari tabel 3.2,terlihat bahwa keputusan tidak optimal pada saat t2

hanya terjadi pada lintasan ke-4 saja. Hal ini membuat kita mendapatkan matriks pada Gambar 3.8. Pada matriks tersebut, opsi yang dieksekusi pada saat t2, payoff pada t3 harus bernilai 0, karena opsi hanya dapat dieksekusi

satu kali sepanjang masa opsi berlaku.

t1 t2 t3 - 4.7222 0 - 20.0654 0 - 15.7194 0 - 0 16.2601 - 0 0.2267 - 0 1.3672 - 37.2644 0 - 18.4669 0

Gambar 3.8. Matriks payoff hasil perbandingan t2 dan t3.

Langkah selanjutnya, kita lakukan kembali proses metode LSM langkah kedua yang sama diatas pada waktu t1, untuk menentukan apakah

Dari Gambar 3.7 yang merujuk pada matriks harga saham pada Gambar 3.5 dapat kita simpulkan bahwa terdapat 7 lintasan yang berada dalam kondisi in the money pada t1. Misalkan S1 menyatakan harga saham

pada t1 dan r1 menyatakan short rate pada t1, kemudian Y1 menyatakan

payoff yang didapat pada masa datang yang didiskonto ke t1 apabila opsi

tidak dieksekusi pada t1. S1 , r1 , dan Y1 diberikan oleh tabel dibawah ini.

Tabel 3.3. Data regresi untuk mengaproksimasi fungsi ekspektasi bersyarat saat t1. S1 r1 Y1 102.8710 0.0364 4.7222 * exp(-0.0364*(1/3)) = 4.6653 82.0596 0.0516 20.0654 * exp(-0.0516*(1/3)) = 19.7232 94.4672 0.0415 15.7194 * exp(-0.0415*(1/3)) = 15.5034 99.6356 0.0436 16.2601*exp(-0.0436*(1/3)-0.0395*(1/3)) = 15.8159 91.3212 0.0159 0.2267* exp(-0.0159*(1/3)-0.0093*(1/3)) = 0.2248 - - - 91.5853 0.0804 37.2644 * exp(-0.0804*(1/3)) = 36.2790 75.0553 0.0241 18.4669 * exp(-0.0241*(1/3)) = 18.3191

Dari data pada tabel 3.3, dengan menggunakan persamaan (3.7) didapat koefisien estimasi fungsi fungsi ekspektasi bersyarat seperti berikut.

(

)

1 ( ) ( ) ' ( ) ( ) ' ( ) -5 4 3 1 7 -2 1 2 7 7 β∧ = − ⎡ ⎤ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ = ⎢ ⎥ i i i i i t X t X t X t y t

Hasilnya, kita mendapatkan aproksimasi fungsi ekspektasi bersyarat berikut 2

2 2 2 2 2

543 +17 - 21277 80052 167

y∧ = − S r + r + S r (3.9)

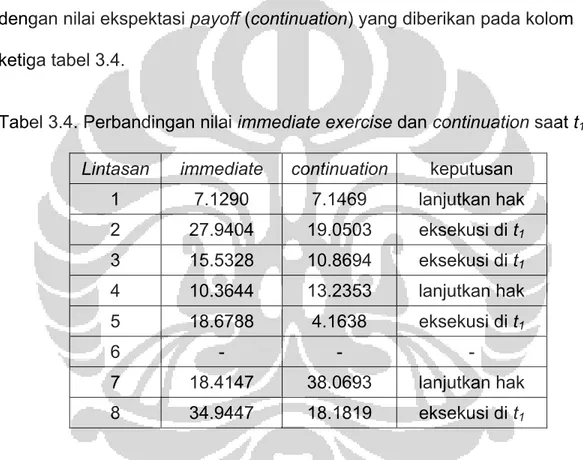
Selanjutnya akan dibandingkan payoff yang didapat jika mengeksekusi pada t1 (immediate exercise), yang ditunjukkan pada kolom kedua tabel 3.4,

dengan nilai ekspektasi payoff (continuation) yang diberikan pada kolom ketiga tabel 3.4.

Tabel 3.4. Perbandingan nilai immediate exercise dan continuation saat t1.

Lintasan immediate continuation keputusan

1 7.1290 7.1469 lanjutkan hak 2 27.9404 19.0503 eksekusi di t1 3 15.5328 10.8694 eksekusi di t1 4 10.3644 13.2353 lanjutkan hak 5 18.6788 4.1638 eksekusi di t1 6 - - - 7 18.4147 38.0693 lanjutkan hak 8 34.9447 18.1819 eksekusi di t1

Dari tabel 3.4, terlihat bahwa, keputusan optimal terjadi pada lintasan ke 2, 3, 5, dan 8. Hal ini membuat kita mendapatkan matriks payoff berikut.

t1 t2 t3 lintasan 1 0 4.7222 0 lintasan 2 27.9404 0 0 . 15.5328 0 0 . 0 0 16.2601 . 18.6788 0 0 . 0 0 1.3672 . 0 37.2644 0 lintasan 8 34.9447 0 0

Gambar 3.9. Matriks payoff.

Pada Gambar 3.9, dilintasan pertama keputusan optimal untuk mengeksekusi opsi terjadi pada t2. Sedangkan untuk lintasan kedua terjadi

pada t1. Untuk lintasan keempat dan keenam, keputusan optimal terjadi pada

saat terakhir opsi berlaku yaitu t3.

Langkah 3 : Menentukan nilai opsi

Dari matriks payoff Gambar 3.9 tersebut, kemudian nilai opsi dapat diperoleh dengan mendiskonto semua payoff ke saat t0 dan

Tabel 3.5. Perhitungan diskonto ditiap-tiap lintasan.

lintasan _{Nilai diskonto}

1 _{4.7222*exp(-0.0364*(1/3)+(-0.0230*(1/3))) = 4.6296} 2 _{27.9404*exp(-0.0783*(1/3)) = 27.2206} 3 _{15.5328*exp(-0.0236*(1/3)) = 15.4111} 4 _{16.2601*exp(-0.0395*(1/3)+(-0.0436*(1/3))+(-0.0375*(1/3))) = 15.6194} 5 _{18.6788 *exp(-0.0256*(1/3)) = 18.5201} 6 _{1.3672*exp(-0.0515*(1/3)+(-0.0453*(1/3))+(-0.0379*(1/3))) = 1.3072} 7 _{37.2644*exp(-0.0804*(1/3)+(-0.0613*(1/3))) = 35.5452} 8 _{34.9447*exp(-0.0138*(1/3)) = 34.7843}

Pada lintasan pertama, opsi dieksekusi pada t2, sehingga nilai 4.7222 dari

matriks payoff (Gambar 3.9) didiskonto ke t0 (saat ini). Diketahui dari matriks

short rate (Gambar 3.6), nilai short rate lintasan pertama pada t2 adalah

0.0364 (3,64%) dan t1 adalah 0.0230 (2.3%). Nilai saat ini dari 4.7222 adalah

0.0364.(1/ 3) ( 0.0230.(1/ 3))

4.7222.e− + − ₌4.6296_. Maka estimasi nilai opsi yang diperoleh adalah

4.6296+27.2206+15.4111+15.6194+18.5201+1.3072+35.5452+34.7843 8 153.0375 8 19.1297 = = =

Dari hasil perhitungan, didapat bahwa estimasi nilai opsi sebesar $19.1297. Artinya, harga wajar menurut hasil perhitungan metode LSM dari sebuah opsi dengan data parameter yang telah diberikan adalah sebesar $19.1297.