5 1. OPERASI BILANGAN REAL (PERSEN)
1. Sebuah celana panjang, setelah dikenakan potongan harga dijual dengan harga Rp. 80.000,00. Jika harga pada labelnya Rp. 120.000,00, maka besar persentase potongan harga tersebut adalah … . . (UN 4, 99)
a. 31
2 % b. 5% c. 33 1
3% d. 40% e. 50%
2. Agar mendapat untung 25%, sebuah rumah harus dijual dengan harga
a. Rp. 37.500.000,00 b. Rp. 38.500.000,00 c. Rp. 40.000.000,00 d. Rp. 42.500.000,00 e. Rp. 45.000.000,00
Rp. 50.000.000,00. Harga pembelian rumah tersebut adalah … . . (UN 5, 00)
3. Jumlah siswa SMK A ada 1.400 orang, terdiri dari jurusan Bangunan, Listrik, Mesin, dan Otomotif. Bila siswa jurusan Bangunan ada 200 siswa, Listrik 250 siswa, Mesin 450 orang, dan sisanya Otomotif, maka persentase jumlah siswa jurusan Otomotif adalah … . . (UN 3, 01)
a. 20,7% b. 35,7% c. 45,7% d. 55,7% e. 65,7%
4. Seorang mendapat hadiah dari suatu undian sebesar Rp. 100.000.000,00 sebelum dipotong pajak undian. Jika pajak undian sebesar 20% dan 25% dari undian yang ia dapatkan disumbangkan kepada suatu yayasan yatim piatu, 15% disumbangkan tabungkan adalah … . . (UN 1, 02)
a. Rp. 32 juta b. Rp. 40 juta c. Rp. 48 juta d. Rp. 60 juta e. Rp. 80 juta kepada panti sosial,.sedangkan sisanya ia tabungkan, maka besar uang yang ia
5. Pada suatu sensus pertanian di suatu desa, dari 100 orang petani ternyata 75% menanam padi dan 48% menanam jagung, petani yang menanam padi dan jagung sebanyak … (UN 2P11, 03)
a. 21 orang b. 22 orang c. 23 orang d. 24 orang e. 25 orang
6. Sebuah baju setelah dikenakan potongan harga dijual dengan harga Rp. 60.000,00. Jika harga pada labelnya Rp. 75.000,00, maka besar persentase potongan tersebut … (UN 2P21, 03)
a. 10% b. 15% c. 17,5% d. 20% e. 25%
7. Seorang pedagang membeli 1 lusin gelas seharga Rp. 45.000,00, dan pedagang tersebut telah menjual 5 gelas seharga Rp. 10.000,00. Jika semua gelas telah terjual dengan harga tersebut, maka persentase kerugian pedagang tersebut adalah … …. (UN 2,08 &10)
6 8. Ayah membeli satu unit rumah seharga Rp. 36.000.000,00 lalu rumah itu dijual dengan
harga Rp. 45.000.000,00. Persentase keuntungan yang diperoleh ayah adalah … (UN 3,09) a. 15% b. 20% c. 25% d. 30% e. 35%
9. Seorang pedagang menjual sepeda dengan harga Rp. 675.000,00. Jika pedagang tersebut mendapat keuntungan 12,5 %, maka harga pembelian sepeda tersebut adalah … (UN 8,11) a. Rp. 550.000 b. Rp. 950.000 c. Rp. 600.000 d. Rp. 662.500 e. Rp. 759.500
2. MENGHITUNG HASIL OPERASI BILANGAN BERPANGKAT 10. Bentuk sederhana dari (2 ) x (2 ) adalah … . (UN 1, 99)
a. 16 b. 8 c. 6 d. e. 1 8
11. Jika a = 27 dan b = 32, maka nilai dari 3(a ̇ )x 4b adalah … (UN 1, 01)
a. −25 b. −16 c. 0 d. 16 e. 25 12. Hasil perkalian (4 ) (2 ) = ⋯ (UN 2, 04)
a. -2a b. - 1 2 c. 1 2 d. 1 2 e. 2 13. Jika a = 27 , b = 4 , c = 3 , maka nilai dari
( . ). adalah….(UN 2, 05)
a. -72 b. -8 c. 0 d. 8 e. 72 14. Diketahui a = 32 dan b = 27.
Nilai dari 4( ) x 6( ) adalah….(UN 1P21, 06) a. -144 b. -48 c. 8 d. 16 e. 48 15.
27 + 64 – 8 adalah……(UN 2P23, 06) a. 33 b. 27 c. 25 d. 24 e. 17 Hasil dari :
16. Nilai dari 2 . 8 . (32) =…..(UN 1P22, 06) a. 2 b. 2 c. 2 d. 2 e. 2
7 17. (x y). (3x y ) 2x y = ⋯ (UN 1P32, 06) a.2 3 b. 8 9 c. 1 1 3 d. 24 e. 48 Jika x = 2 dan y = 3, maka nilai dari :
18. Bentuk sederhana dari ÷ x ( ) adalah…..(UN 1P19, 07) a. b. c. d. e.
19. Bentuk sederhana dari ( ) ÷ x adalah…..(UN 1P52, 07)
a. b. c. d. e. 20. Nilai x yang memenuhi ∶
1
25 = 5 adalah …( 11, 99)
a. 3 b. 1 c. 0 d. −1 e. −3 21. Nilai x yang memenuhi persamaan ∶
25 = 125 adalah …( 13, 00) a. −1 3 b. − 1 4 c. − 1 5 d. − 1 6 e. − 1 7 22. Bentuk sederhana dari ∶
25. X
X adalah … ( 3, 02)
a. 5 x b. 5 x c. 5 x d. 5 x e. 5 x
23. Nilai x yang memenuhi persamaan :
3 = 27 adalah…..(UN 2P19, 07)
a. -9 b. -7 c. 3 d. 4 e. 6
24. Nilai x yang memenuhi persamaan (4) = (32) adalah … (UN 2P19, 10) a. −17 b. −4 c. −1 d. 1 e. 4
25.
Nilai dari (216) + (1
64) − (27) adalah … (UN 6, 11) a. −4 b. −1 c. 6 d. 7 e. 13
8 3. MENYEDERHANAKAN BENTUK AKAR DAN PECAHAN BENTUK AKAR
26. Bentuk sederhana dari: 2 √12 − √8 adalah … (UN 1, 08) a. √3 + √2 b. 2√3 − √2 c. √3 − 1 5√2 d. 2 √3 − √2 e. 2 4 √12 − √8 27. Bentuk sederhana dari:
3 − √5 3 + √5 adalah … . . (UN 1, 09) a. 7 − 3√5 2 b. 7 − 5√3 2 c. 7 + 3√5 2 d. 7 + 5√3 2 e. 3 + 7√5 2
28. Bentuk sederhana dari ∶ 6
√8 + √5 adalah … (Erlangga hl. 41,22)
a. 2√2 + 2√5 b. 2√2 − 2√5 c. 4√2 − √5 d. 4√2 − 2√5 e. 4√2 + 2√5 29. Nilai ∶
6 − √3
√3 adalah … . (Tiga Serangkai hl. 90,17) a. 1 b. √3 c. √3 − 1 d. 2√3 − 1 e. −1 30. Nilai ∶
√3
2 − √3 adalah … . . (Tiga Serangkai hl. 90,18)
a. 2√3 − 3 b. 2√3 + 3 c.1
2 √3 − 1 d. 1
2 √3 + 1 e. 2√3 + 9 31. Bentuk sederhana 4√3 + 3√12 − √27 adalah … . (UN 2, 00)
a. 10√3 b. 9√3 c. 8√3 d. 7√3 e. 6√3
32. Diketahui p = 6 − 3√27 dan q = 4 + √12 bentuk sederhana dari p + q adalah … (UN 1P19, 10)
9 33. Bentuk sederhana dari 5√2 + 3 2√2 − 1 adalah … … . (UN 9, 11)
a. 16 b. 17 c. 17 − √2 d. 17 + √2 e. 32 − 8√2
4. MENGHITUNG NILAI LOGARITMA
34. Jika log 3 = 0,477 dan log 5 = 0,699, maka log 45 adalah … . . (UN 2, 09) a. 0,255 b. 0,653 c. 0,667 d. 1,176 e. 1,653
35. Nilai dari. log 16 −. log 27 +. log 1 = ⋯ … … (UN 3, 00) a. −1 b. 0 c. 1 d. 5 e. 6
36. Nilai dari. log 4 +. log 12 −. log 6 = ⋯ … … (UN 2, 01) a. 8 b. 6 c. 5 d. 4 e. 3
37. Diketahui. log 3 = p dan . log 5 = q, maka . log 45 = ⋯ … … (UN 4, 02) a. p + q b. 2p + q c. 2(p + q) d. p + 2q e. p + q
38. Nilai dari ∶
. log 8 −. log 0,25 +. log 1
27 + . log 1 = ⋯ … … (UN 13P11, 03) a. −2 b. −1 c. 0 d. 1 e. 2
39.
log x = a dan log y = b, log10x
y = ⋯ (UN 11, 04) a.10a b b. 30a 2b c. 10(3a − 2b) d. 10 + 3a − 2b e. 1 + 3a − 2b Jika diketahui :
40. Nilai dari. log 75 −. log 54 −. log 3 + . log 2 adalah … . . (UN 8, 05)
a. −5 b. −1 c. 25
27 d. 1 e. 5
41. Diketahui ∶ log 3 = 0,4771, log 4 = 0,6021, log 5 = 0,6990, maka log 180 = ⋯ (UN 2P21, 06)
a. 2,2477 b. 2,2553 c. 2,3803 d. 2,4772 e. 3,2553
42. Jika . log 2 = a dan . log 5 = b maka nilai . log 200 = ⋯ (UN 10P23, 06). a. a − b b. a + b c. b − a d. 3a − 3b e. 3a + 2b
10 43. Jika. log 3 = a dan . log 2 = b maka nilai . log 12 adalah. . (UN 2P22, 06).
a. 1 2b b. 1 2b + ab c. 2b d. 2b + ab 1 + ab e. 1 + ab 2b + ab
44. Jika log 3 = 0,4771 dan log 5 = 0,6990, maka log √45 = ⋯ (UN 2P32, 06) a. 0,1276 b. 0,2552 c. 0,5104 d. 0,6532 e. 0,8266 45. a. 3 4a b. 3 4a c. 2 3a d. 2 3a c. 4 3a Jika . log 5 = a maka nilai . log 125 = ⋯ (UN 3P19, 07) .
46. Jika log 2 = a dan log 3 = b, maka nilai log 72 = ⋯ (UN 3P52, 07) a. (a + b) b. (3a + b) c. (3a + 2b) d. 2(a + b) e. (2a + 3b) 47. Nilai dari (. log 125 −. log5) ∶ (. log 10 − . log 2) adalah … (UN 4, 08)
a. 2 b. 3 c. 4 d. 12 e. 16
48. Jika diketahui log 2 = 0,301 dan log 3 = 0,477 maka nilai dari log 36 adalah … (UN 2, 09)
a. 1,336 b. 1,346 c. 1,546 d. 1,556 e. 1,566 49. Nilai . log 12 −. log 6 + 2. log 2 adalah … … (UN 4P19, 10)
a. 3 b. 4 c. 5 d. 6 e. 8 50. a. 2a 3 b. 3 2a c. 3 2a d. 2a − 3 c. 3 − 2a Jika . log 7 = a maka . log 49 = ⋯ (UN 10, 11) .
5. MENENTUKAN PERSAMAAN GARIS
51. Persamaan garis yang melalui titik (−1 , 1)dan titik (−2 , 6)adalah … (UN 8,99) a. y = 5x − 4 b. y = 5x + 6 c. y = −5x − 4 d. y = −5x + 4 e. y = −5x − 6 52. Persamaan garis yang melalui titik A (3 , 2)dan tegak lurus garis dengan persamaan
3x + y = −2 adalah … … (UN 10, 00)
a. 3x − 3y − 1 = 0 b. 3x − y + 10 = 0 c. 3x − y − 3 = 0 d. x − 3y + 3 = 0 e. x − 3y − 3 = 0
11 y
(0,4)
53. Persaman garis yang melalui titik potong garis dengan persaman 2x + 5y = 1 dan x − 3y = −5 serta tegak lurus pada garis dengan persaman 2x − y + 5 = 0 adalah … (UN 8, 01)
a. y + x = 0 b. 2y + x = 0 c. y = −2x + 2 d. y + 2x + 2 = 0 e. y = −1 2x + 2 54. Persamaan garis yang melalui garis lurus yang melalui titik (1 , 2)dan tegak lurus
garis y = 2x + 4 adalah … . (UN 27P19, 07)
a. x + y = 3 b. x − y = −1 c. x + 2y = 5 d. x − 2y = −3 e. 2y − x = 3 55. Persaman garis lurus melalui titk A(−1 , 2)dan tegak lurus garis 2x − 3y = 5
adalah … (UN 27P52, 07)
a. 3x + 2y − 7 = 0 b. 3x + 2y − 1 = 0 c. − 3x + 2y − 7 = 0 d. −3x + 2y − 4 = 0 e. − 3x + 2y − 1 = 0
56. Persamaan garis pada gambar di bawah adalah …
b. 2x + 3y = 12 d. − 2x + 3y = 12 e. − 2x + 3y = −12 a. 2x − 3y = 12 c. 2x − 3y = −12 (6,0) x g
12 y
0 9 x
-6
57. Gra ik sistem persamaan linear x + y = 4 dan 6x − 5y = −30 adalah. . (UN 9, 09) a. 6 b. 5 4 4 -5 4 4 6 b. 6 c. 5 4 4 -4 5 -6 5 e. 6 4 4 5
58. Persamaan garis pada gambar di samping adalah … (UN 5P19, 10)
b. − 2x − 3y = 16 d. 2x − 3y = −16 e. 2x + 3y = −18 a. 2x + 3y = 18 c. 2x − 3y = 18
59. Persaman garis lurus yang sejajar x + 4y − 2 = 0 dan melalui titik P (8, −3) adalah … (UN 14, 11)
a. − x + y + 11 = 0 b. x + 4y + 4 = 0 c. x + 4y − 20 = 0 d. 4x − y − 35 = 0 e. 4x − y + 35 = 0
60. Gradien garis dengan persamaan 3x + 7y + 1 = 0 adalah … (UN 11, 11)
a. − 7 b. − 3 c. −3 7 d. 3 7 e. 7 3
13 3- y
2-
-1 2 x 6. MENGGAMBAR DAN MENENTUKAN GRAFIK FUNGSI KUADRAT 61.
b. y = x − 4x c. y = x − 2x d. y = x + 4x e. y = x + 2x − 2
Persamaan parabola dari gra ik pada gambar di samping ini adalah … (UN 8, 02)
a. y = x + 2x − 4
62. Persamaan dari gra ik fungsi kuadrat di samping ini adalah … (UN 7, 04)
b. y = 1 2x + x − 1 1 2 c. y = x − 2x − 3 d. y = x + 2x − 3 e. y = 2x − 4x − 6 a. y = x − x − 1 63. a. y = 2x + 8x b. y = 2x − 8x c. y = −2x + 8x d. y = −2x − 8x e. y = −2x + 6x
Persamaan fungsi dari gra ik di y samping ini adalah … (UN 5, 05) 8
0 x= 2 4 x 64.
c. y = x − x + 3 d. y = x + 4x + 3 e. y = x − 4x + 3
Perhatikan gambar ! (UN 4P19, 07) y a. y = 3x − 4x + 1 b. y = 3x + 4x + 1 3 0 1 3 x Y -1 0 1 3 x -2
14 65. a. y = x − 10x + 16 c. y = x − 10x − 16 d. y = −x + 10x − 16 e. y = −x − 10x + 16
Perhatikan gambar ! (UN 4P52, 07) y b. y = x + 10x + 16 16
0 2 8 x
66. Gra ik fungsi kuadrat f(x) = −x + 6x − 8 adalah. . (UN 5, 09)
a. y c. y e. y 0 2 4 x 8 -4 -2 x -8 -2 0 4 x -8 y 8 y b. d. -4 0 2 x 0 2 4 x -8
67. Perhatikan gambar ! (UN 8P19, 10)
a. y = x + 2x − 3 b. y = x − 4x + 3 c. y = −2x − 4x + 6 d. y = −2x + 4x + 6 e. y = 2x − 8x − 6
Persamaan gra ik fungsi kuadrat pada Y gambar di samping adalah …. 6
15 68.
b. f(x) = x − 4x
e. f(x) = −x + 4x
Persamaan gra ik fungsi kuadrat
yang sesuai dengan gambar di samping adalah … . (UN 6P52, 10) P (-2, 4) a. f(x) = x − 4 c. f(x) = −x + 4 d. f(x) = −x − 4x -4 -2 0
69. Titik balik (titik puncak) grafik fungsi kuadrat y = x2 – 6x – 7 adalah….. (UN 15, 11) a. (3 , 0) b. (-1 , 7) c. (0 , -7) d. (3 , -16) e. (-3 , 16)
70. Diketahui grafik fungsi kuadrat memotong sumbu x di titik (2 , 0) dan (6 , 0) serta melalui titik (4 , -2). Persamaan grafik fungsi kuadrat tersebut adalah……… (UN 16, 11)
a. y = -1/2 x2 + 4x – 10 c. y = 1/2 x2 – 4x + 7 e. y = 2x2 – 16x + 24 b. y = 1/6 x2 – 2/3 x – 2 d. y = 1/2 x2 – 4x + 6
7. MENENTUKAN HIMPUNAN PENYELESAIAN PERTIDAKSAMAAN LINEAR SATU VARIABEL 71. Himpunan penyelesaian pertidaksamaan 8 + 2x ≤ 12 + 6x adalah. . (UN 6, 99)
a. {x/x ≤ −1} b. {x/x ≥ −1} c. {x/x ≤ −3} d. {x/x ≥ −5} e. {x/x ≤ −5} 72.
c. {x/x < −5, ∈ }
Himpunan penyelesaian 4x − 6 > 6 + 4, ∈ ℎ. . (UN 8, 00) a. {x/x > −5, ∈ } d. {x/x < 5, ∈ } b. { x/x > 5, ∈ } e. {x/x ≤ −5, x ∈ R} 73. Himpunan penyelesaian c. {x/x > 4, x ∈ R} < 3 , x ∈ R adalah. . (UN 5, 01) a. {x/x > −4, ∈ } d. {x/x < −4, x ∈ R} b. { x/x < 4, x ∈ R} e. {x/x > −8, ∈ } 74. c. {x/x ≤ 1}
Himpunan penyelesaian dari ∶ 2(x − 3) ≥ 4(2x + 3) adalah. . (UN 5, 04) a. {x/x ≤ −1} d. {x/x ≤ −3}
b. {x/x ≥ 1} e. {x/x ≥ −3}
75. Himpunan penyelesaian
16 c. {x/x ≤ 7, x ∈ R}
a. {x/x ≥ −7, x ∈ R} d. {x/x ≥ 7, x ∈ R} b. {x/x ≤ −7, x ∈ R} e. {x/x ≥ 12, x ∈ R}
76. Himpunan penyelesaian pertidaksamaan: 2(2x − 3) ≤ 3(2x − 6) adalah. . (UN 26P52, 07)
a. x/x ≤ − b. x/x ≥ − c. {x/x ≤ 6} d. {x/x ≥ 6} e. {x/x ≤ 12}
77. Himpunan penyelesaian dari pertidaksamaan linier ∶
c. {x ≥ 1}
(6x − 9) − (10x − 5) ≤ (8x + 12) adalah. . (UN 7, 08)
a. {x ≥ −1} d. {x ≤ 1} b. {x ≤ −1} e. {x = 1}
78. Himpunan penyelesaian pertidaksamaan 4x + 8 ≤ 6x − 10 adalah. . (UN 7, 09) a. {x/x ≤ 9} b. {x/x ≥ 9} c. x/x ≥ d. x/x ≤ e. x/x ≥
79. Himpunan penyelesaian dari pertidaksamaan:
a. x ∈R x ≤ − 3 2 d. {x ∈ R/x ≤ 20} c. x ∈ R/x ≥3 2 (6x − 12) ≥ 2(6x + 2) adalah. . (UN 7P19, 10) b. x ∈ ≥ − e. {x ∈ R/x ≥ 20}
80. Himpunan penyelesaian dari pertidaksamaan:
a. x ∈R
x ≥ 8 d. {x ∈ R/x ≤ 2}
c. {x ∈ R/x ≥ 2}
(2x + 4) ≤ 5(x − 2) adalah. . (UN 18, 11)
b. x ∈ ≤ 8 e. x ∈ ≤ −
8. MENYELESAIKAN MASALAH SISTEM PERSAMAAN LINEAR DUA VARIABEL
81. Harga 2 buah buku dan 3 buah penggaris adalah Rp. 5.400,00 sedangkan harga 3 buah buku dan 4 buah penggaris Rp. 7.700,00. Harga sebuah penggaris adalah. . . (UN 7, 00) a. Rp. 1.500,00 d. Rp. 900,00
17 c. Rp. 1.000,00
b. Rp. 1.200,00 e. Rp. 800,00
82. Harga 2 buah buku dan 3 buah pensil Rp. 8.800,00 jika harga sebuah buku Rp. 600,00 lebih murah daripada harga sebuah pensil, maka harga sebuah buku adalah …
(UN 4, 01)
a. Rp. 1.400,00 c. Rp. 1.900,00 e. Rp. 2.500,00 b. Rp. 1.600,00 d. Rp. 2.000,00
83. Himpunan penyelesaikan dari sistem persamaan linear
c. ({−3 , −4}) 3x+2y = 1 adalah….(UN 5, 02) 2x+3y = -6 a. ({3 , 4}) d. ({2 , −4}) b. ({3 , −4}) e. ({4 , −3})
84. Dari sistem persamaan
c. 3 3x + 5y = 4 Nilai 2x + 3y adalah….(UN 3P11, 03) x – 3y = 6 a. 1 d. 4 b. 2 e. 5
85. Harga 3 buah buku dan 2 buah penggaris Rp. 9.000,00 jika harga sebuah buku Rp. 500,00 lebih mahal dari pada harga sebuah penggaris, maka harga sebuah buku dan 3 buah penggaris adalah. . . (UN 3, 04)
c. Rp. 8.000,00
a. Rp. 6.500,00 d. Rp. 8.500,00 b. Rp. 7.000,00 e. Rp. 9.000,00
86. Himpunan penyelesaian dari persamaan ….(UN 9P21, 06) 2x – 9y – 24 = 0
-3x + 4y + 17 = 0
a. ({2 , −3}) c. ({2 , 3}) e. ({−3 , −2}) b. ({3 , −2}) d. ({3 , 2})
87. Himpunan penyelesaian persamaan 2x − 3y = 16 dan 3x + 5y = 5 adalah …. (UN 3P23, 06)
a. ({5 , −2}) d. ({−5 , 2}) b. ({−5 , −2}) e. ({−4 , 3})
18 c. ({−5 , 2})
88. Jika 2x + y = 4 dan x + 2y = 5 maka nilai dari 2x + 2y adalah … (UN 8P22, 06) a. − 2 b. 1 c. 2 d. 6 e. 8
89. Jika {(x, y)} himpunan penyelesaian sistem persamaan 2 − 3 = 174 + = −1 nilai 15x +y =…..… (UN 5P19, 07)
a. 6 b. 8 c. 10 d. 15 e. 50
90. Abdul membeli 6 buah pensil dan 4 buah penghapus dengan membayar Rp. 11.400,00 dan Budi membayar Rp. 3.600,00 untuk 2 buah pensil dan sebuah penghapus merk yang sama. Harga sebuah pensil tersebut adalah. . . (UN 22P19, 07)
c. Rp. 1.500,00
a. Rp. 1.200,00 d. Rp. 1.600,00 b. Rp. 1.400,00 e. Rp. 1.800,00
91. Nilai f(x, y) = 2x + 2y dari sistem persamaan linier
c. 0 3 + 4 = 2
2 + = 3 adalah … (UN 5P52, 07) a. − 4 d. 2 b. − 2 e. 4
92. Harga 10 pensil dan 4 penggaris adalah Rp. 31.000,00 sedangkan harga 4 pensil dan 10 penggaris adalah Rp. 25.000,00. Harga 1 buah penggaris adalah. . . (UN 22P52, 07)
c. Rp. 2.500,00
a. Rp. 1.500,00 d. Rp. 3.000,00 b. Rp. 2.000,00 e. Rp. 3.500,00
93. Dari sistem persamaan ∶
dari − 2 adalah … (UN 8P52, 09)
2 − 3 = 5
5 + 4 = 24 = dan = merupakan penyelesaiannya, maka nilai
a. 8 b. 6 c. 5 d. 4 e. 2
94. Di koperasi sekolah, Andi membeli 4 buah buku dan 6 buah ballpoint seharga tidak lebih dari Rp. 35.000,00. Sedangkan Rudi membayar tidak lebih dari Rp. 50.000,00 untuk 8 buah buku dan 4 buah ballpoint. Jumlah uang yang harus dibayar oleh Heni, jika Ia membeli 1 buah buku dan 1 buah ballpoint di koperasi
19 a. Rp. 18.000,00
c. Rp. 16.000,00 d. Rp. 14.000,00 e. Rp. 7.500,00
yang sama adalah … …(UN 10, 09)
b. Rp. 16.500,00
95.
c. {(−3 , 1)}
Himpunan penyelesaikan dari sistem persamaan linear 2x + y = 7
3x – y = 8
adalah….. (UN 6P19, 10) a. {(2 , 3)} d. {(3 , −1)}
b. {(3 , 2)} e. {(3 , 1)}
96. Penyelesaian sistem persamaan linier 2x − 5y = −21 dan 3x + 2y = −3 adalah x dan y. Nilai dari 4x + 6y adalah … (UN 8P52, 10)
c. 2
a. − 6 d. 3 b. − 5 e. 6
97. Dian membeli 4 pulpen dan 3 penggaris seharga Rp. 29.000,00. Dery membeli 2 pulpen dan 5 penggaris dengan harga Rp. 32.000,00. Jika Anita akan membeli 2 pulpen dan 1 penggaris, maka ia harus membayar sebesar…….. (UN 19, 11)
a. Rp. 8.500,00 c. Rp. 12.000,00 d. Rp. 13.500,00 b. Rp. 10.000,00 d. Rp. 13.250,00
9. MENULISKAN MODEL MATEMATIKA DARI MASALAH PROGRAM LINEAR
98. Seorang pemborong pengecatan rumah mempunyai perseadiaan 80 kaleng cat putih dan 60 kaleng cat abu. . abu. Pemborong tersebut mendapat tawaran untuk mengecat ruang tamu dan ruang tidur. Setelah dihitung ternyata 1 ruang tamu menghabiskan 2 kaleng cat putih dan 1 kaleng cat abu … abu, sedangkan 1 ruang tidur menghabiskan cat masing − masing warna sebanyak 1 kaleng. Jika banyak ruang tamu dinyatakan dengan x dana ruang tidur dengan y, maka model matematika dari pernyataan di atas adalah … (UN 19, 99) c. 2x + y ≥ 80; x + y ≤ 60; x ≥ 0; y ≥ 0 d. 2x + y ≤ 80; x + y ≥ 60; x ≥ 0; y ≥ 0 e. x + y ≤ 80; 2x + y ≤ 60; x ≥ 0; y ≥ 0 a. 2x + y ≤ 80; x + y ≤ 60; x ≥ 0; y ≥ 0 b. x + y ≤ 80; 2x + y ≥ 60; x ≥ 0; y ≥ 0
20 99. Seorang penjual buah yang menggunakan gerobak mempunyai modal Rp. 1000.000,00.
Ia telah membeli jeruk dengan harga Rp. 4000,00 per kg dan pisang Rp. 1.600,00 per kg. Jika banyak jeruk yang dibeli x kg , banyak pisang y kg sedangkan muatan gerobak tidak dapat melebihi 400 kg maka sistem pertidaksamaan yang memenuhi permasalahan di atas adalah … (UN 21, 00)
c. 5x + 2y ≤ 1250; x + y ≤ 400; x ≥ 0; y ≥ 0 d. 5x + 2y ≤ 1200; x + y ≤ 400; x ≥ 0; y ≥ 0 a. 5x + 4y ≤ 2500; x + y ≤ 400; x ≥ 0; y ≥ 0 b. 5x + 4y ≤ 1250; x + y ≤ 400; x ≥ 0; y ≥ 0
e. 5x + y ≤ 750; x + y ≤ 400; x ≥ 0; y ≥ 0
100. Suatu pesawat udara mempuyai tempat duduk tidak lebih dari 48 orang penumpang. Setiap penumpang kelas utama boleh membawa bagasi 60 kg sedangkan kelas ekonomi 20 kg. Pesawat itu hanya dapat membawa bagasi 1.440 kg, bila x dan y berturut. . turut menyatakan banyaknya penumpang kelas utama dan ekonomi , maka model matematika dari persoalan di atas adalah … (UN 19, 01)
c. x + y ≤ 48; 3x + y ≤ 72; x ≥ 0; y ≥ 0 d. x + y ≥ 48; x + 3y ≥ 72; x ≥ 0; y ≥ 0 e. x + y ≥ 48; x + 3y ≥ 72; x ≥ 0; y ≥ 0 a. x + y ≤ 48; 3x + y ≥ 72; x ≥ 0; y ≥ 0 b. x + y ≤ 48; x + 3y ≤ 72; x ≥ 0; y ≥ 0
101. Seorang pengusaha mebel akan memproduksi meja dan kursi yang menggunakan bahan dari papan kayu dengan ukuran tertentu. Satu meja memerlukan bahan 10 potong dan satu kursi memerlukan 5 potong papan. Papan yang tersedia ada 500 potong. Biaya pembuatan satu meja Rp. 100.000,00 dan biaya pembuatan satu kursi Rp. 40.000,00. Anggaran yang tersedia Rp. 1000.000,00. Model matematika dari persoalan tersebut adalah … (UN 34, 04) c. 2x + y ≤ 100; 2x + 5y ≤ 50; x ≥ 0; y ≥ 0 d. 2x + y ≤ 100; 5x + 2y ≤ 50; x ≥ 0; y ≥ 0 e. 2x + y ≥ 100; 5x + 2y ≥ 50; x ≥ 0; y ≥ 0 a. x + 2y ≤ 100; 5x + 2y ≤ 50; x ≥ 0; y ≥ 0 b. x + 2y ≤ 100; 2x + 5y ≤ 50; x ≥ 0; y ≥ 0
102. Seorang siswa boleh memilih sembarang jurusan, jika jumlah nilai matematika dan isika tidak kurang dari 12 dan nilai masing − masing pelajaran tersebut tidak boleh kurang dari 5. Jika nilai matematika dan isika berturut − turut adalah x dan y maka model matematika yang sesuai adalah … (UN 7P19, 07)
c. x ≤ 5; y ≤ 5; x + y ≥ 12 a. x ≥ 0; y ≥ 0; x + y ≥ 12 b. x ≥ 5; y ≥ 5; x + y ≥ 12 d. x ≥ 0; y ≥ 5; x + y ≤ 12 e. x ≥ 5; y ≤ 5; x + y ≤ 12
21 103. Seorang pengrajin akan membuat 2 macam tas. Setiap minggunya menghasilkan tidak
lebih dari 50 buah tas. Harga bahan tas pertama Rp. 50.000,00 dan bahan tas kedua Rp. 75.000,00. Pengrajin tersebut tidak akan belanja lebih dari Rp. 3.000.000,00 setiap minggu, misalkan jenis tas pertama = x dan jenis kedua = y. Model matematika dari persoalan di atas adalah … (UN 11, 09)
c. x + y ≥ 50 2x + 3y ≤ 120 x ≥ 0, y ≥ 0 a. x + y ≤ 50 d. x + y ≤ 50 2x + 3y ≤ 120 3x + 2y ≤ 120 x ≥ 0, y ≥ 0 x ≥ 0, y ≥ 0 b. x + y ≤ 50 e. x + y ≥ 50 2x + 3y ≥ 120 3x + 2y ≤ 120 x ≥ 0, y ≥ 0 x ≥ 0, y ≥ 0
104. Harga 1 kg pupuk jenis A Rp. 4000,00 dan pupuk jenis B Rp. 2000,00. Jika petani hanya mempunyai modal Rp. 800.000,00 dan gudang hanya mampu menampung 500 kg pupuk (misal pupuk A = x dan pupuk B = y). Model matematika dari permasalahan di
c. x + y ≤ 500; 2x + y ≤ 400; x ≤ 0; y ≤ 0 d. x + y ≥ 500; 2x + y ≥ 400; x ≤ 0; y ≤ 0 e. x + y ≤ 500; 2x + y ≥ 400; x ≥ 0; y ≥ 0 atas adalah … (UN 12P19, 10) (UN 12, 11)
a. x + y ≥ 500; 2x + y ≥ 400; x ≥ 0; y ≥ 0 b. x + y ≤ 500; 2x + y ≤ 400; x ≥ 0; y ≥ 0
105. Daerah yang diarsir pada gambar di samping adalah himpunan penyelesaian dari
c. 3x + 5y ≤ 30; 2x − y ≥ 4; x ≥ 0; y ≥ 0 d. 3x + 5y ≤ 30; 2x − y ≤ 4; x ≥ 0; y ≥ 0 e. 3x + 5y ≥ 30; 2x − y ≤ 4; x ≥ 0; y ≥ 0
sistem pertidaksamaan … . . (UN 20, 01) y a. 5x + 3y ≤ 30; x − 2y ≥ 4; x ≥ 0; y ≥ 0
b. 5x + 3y ≤ 30; x − 2y ≤ 4; x ≥ 0; y ≥ 0 (0,6)
0 (2,0) (10,0) x
22 106. Sistem pertidaksamaan linier untuk daerah yang diarsir pada gambar di samping
c. x ≥ 0; y ≥ 0; x − 4y ≥ 12; 3x + 9y ≥ 45 adalah … . . (UN 17, 05) y a. x ≥ 0; y ≥ 0; x − 4y ≤ 12; 3x + 9y < 45 b. x > 0; > 0; − 4 ≥ 12; 3 + 9 ≥ 45 d. x ≥ 0; y ≥ 0; x − 4y ≤ 12; 3x + 9y ≤ 45 5 e. x ≥ 0; y > 0; − 4 ≥ 12; 3 + 9 ≥ 45 0 12 15 x -3
107. Perhatikan gambar berikut ini.
c. 3x + 2y ≤ 12; x + 2y ≥ 6; x ≥ 0; y ≥ 0 d. 2x + 3y ≥ 12; 2x + y ≤ 6; x ≥ 0; y ≥ 0
Daerah yang diarsir pada gambar tersebut y adalah himpunan penyelesaian sistem 6 pertidaksamaan … . . (UN 8P21, 06) a. 3x + 2y ≥ 12; x + 2y ≤ 6; x ≥ 0; y ≥ 0 b. 3x + 2y ≥ 12; x + 2y ≥ 6; x ≥ 0; y ≥ 0 3
e. 2x + 3y ≤ 12; 2x + y ≥ 6; x ≥ 0; y ≥ 0
4 6 x
108. Perhatikan gambar berikut ini.
d. 2x + 5y ≥ 20; 4x + 3y ≤ 24; x ≥ 0; y ≥ 0
Daerah yang diarsir pada gambar tersebut y adalah himpunan penyelesaian sistem 8 pertidaksamaan … . . (UN 19P23, 06) a. 2x + 5y ≤ 20; 4x + 3y ≥ 24; x ≥ 0; y ≥ 0 b. 2x + 5y ≤ 20; 4x + 3y ≤ 24; x ≥ 0; y ≥ 0 4 c. 2x + 5y ≥ 20; 4x + 3y ≥ 24; x ≥ 0; y ≥ 0 e. 2x + 5y ≤ 40; x + 3y ≥ 24; x ≥ 0; y ≤ 0 6 10 x 109. Daerah terarsir pada gambar di samping
c. x ≥ 2; y ≤ 2; 3x + 4y ≤ 24 merupakan daerah penyelesaian
dari sistem pertidaksamaan . . (UN 10, 08) y a. 2 ≤ x ≤ 6; 0 ≤ y ≤ 2; 3x + 4y ≥ 24 8 b. x ≤ 2; y ≥ 2; 3x + 4y ≤ 24 d. x ≥ 2; 0 ≤ y ≤ 2; 4x + 3y ≤ 24 e. x ≥ 2; 0 ≤ y ≤ 2; 4x + 3y ≥ 24 2 2 6 x
23 110. Apotek "Sehat" akan membuat sediaan Salep yang terdiri dari 2 bahan dasar
yaitu Zinci oxydi dan Acidi salicylici. Berat kedua bahan tidak lebih dari 75 gram. Harga 1 gram Zinci oxydi Rp. 3.000,00 dan 1 gram Acidi salicylici Rp. 1.500,00. Modal yang tersedia tidak lebih dari dari Rp. 150.000,00. Jika x = Zinci oxydi dan y = Acidi salicylici (dalam gram), maka gra ik penyelesaiannya adalah … (UN 11, 08) a. y c. y e. 75 75 100 50 50 75 75 100 x 75 100 x 50 75 x y y b. 75 d. 100 50 75 75 100 x 50 75 x
111. Daerah penyelesaian model matematika yang ditunjukkan sistem pertidaksamaan
c. III 5x + 2y ≤ 20 7x + 10y ≤ 70 2x + 5y ≥ 20 10 (UN 20, 99) adalah daerah yang ditunjukkan oleh … 7
a. I d. IV 4 b. II e. V
0 4 10
2X+5Y=20
5X+2Y=20 7X+10Y=70
112. Daerah yang merupakan penyelesaian dari sistem pertidaksamaan ∶ 3x + 2y ≥ 12; x + 2y ≤ 8; 0 ≤ x ≤ 8; y ≥ 0
c. III
seperti pada gambar di samping adalah daerah … (UN 22,00) a. I d. IV y b. II e. V 6 II III V 4 I I V 0 4 8 x
24 113. Daerah yang merupakan himpunan penyelesaian sistem pertidaksamaan
2y − x ≤ 2
4x + 3y ≤ 12
(UN 23, 04) 4 I − ≤
pada gambar di samping adalah …
a. I d. IV II
b. II e. V IV c. III V III
-2 0 3 x + ≤
10.MENGHITUNG NILAI OPTIMUM DARI PROGRAM LINEAR
114. Nilai minimum fungsi obyektif f(x, y) = 4x + 3y dari sistem pertidaksamaan ∶
x ≥ 0 y ≥ 0 2x + y ≥ 11 x + 2y ≥ 10 (UN 21, 99) a. 15 d. 33 b. 22 e. 40 c. 25
115. Daerah yang diarsir pada gambar di samping adalah himpunan penyelesaian dari untuk 5x + 4y dari daerah penyelesaian
c. 24 e. 16
sistem pertidaksamaan. Nilai maksimum y tersebut adalah … . . (UN 21, 01)
a. 40 (0,6)
b. 28
d. 20 (0,4) (4,2)
0 (4,0) (8,0)
116. Daerah yang diarsir adalah daerah himpunan penyelesaian
permasalahan program linear. Nilai maksimum y E (2,5) dari fungsi tujuan Z = 2x + 5y adalah … (UN 14P11, 03) a. 6 b. 7 c. 10 A (0,2) (5,1) d. 15 D e. 29 B (1,1) 0 C (3,0)
25 117. Nilai minimum fungsi obyektif Z = 3x + 4y yang memenuhi
sistem pertidaksamaan ∶ 2x + 3y ≥ 12 5x + 2y ≥ 19 (UN 22, 04) x ≥ 0, y ≥ 0 a. 38 d. 17 b. 32 e. 15 c. 18 118.
pada daerah penyelesaian gambar di samping
Perhatikan gambar berikut ini. y Nilai maksimum dari Z = 3x + 5y 12 adalah … (UN 18P23, 06) a. 24 d. 42 8 b. 32 e. 48 c. 40 8 16 x 119.
pada daerah penyelesaian gambar di samping Perhatikan gambar berikut ini. y Nilai maksimum dari Z = 3x + 5y (0,5) adalah … (UN 7P22, 06) a. 25 d. 9 (0,3) , b. 21 e. 0 c. 18 (5,0) (8,0) x 120.
penyelesaian suatu sistem pertidaksamaan. Perhatikan gambar berikut ini. y
Daerah yang diarsir pada gambar y = x di samping merupakan daerah himpunan
Nilai minimum untuk f(x, y) = 7x − 14y
adalah … (UN 7P32, 06)
a. − 14 d. 2 b. − 12 e. 4
c. − 7
26 121.
Setelah diterjemahkan ke dalam model
Perhatikan gambar berikut ini! y (6,14)
matematika, penyelesaian suatu permasalahan (11,10) program linear ditunjukkan oleh daerah yang (1,8)
diarsir. Nilai maksimum untuk Z = 4x + 2y adalah … (UN 21P52, 07) a. 20 d. 64 b. 48 e. 68 (10,4) c. 52 (3,2) 0 x 122. fungsi obyektif f(x, y) = 4x + y c. 43
Daerah yang diarsir pada gambar y di samping adalah penyelesaian suatu
program linier. Nilai maksimum untuk 12 adalah … (UN 9, 08)
a. 36 d. 52 8 b. 38 e. 54 5
3
4 6 9 11 x
123. Pak Daud membeli es krim jenis I dengan harga per buah Rp. 500,00 dan es krim jenis II dengan harga Rp. 400,00 per buah. Lemari es yang dipunyai pak Daud untuk menyimpan es krim tersebut tidak dapat memuat lebih dari 300 buah dan uang yang dipunyai pak Daud hanya Rp. 140.000,00. Jika es krim tersebut dijual kembali dengan mengambil untung masing − masing jenis Rp. 100,00 per buah maka banyak es krim jenis I dan II yang harus dibeli pak Daud agar jika terjual seluruhnya mendapat untung sebesar~besarnya, masing − masing adalah … (UN 23, 00)
c. 100 buah dan 200 buah d. 75 buah dan 225 buah e. 50 buah dan 250 buah
a. 200 buah dan 100 buah b. 150 buah dan 150 buah
124. Seorang pemilik kios ingin mengisi kiosnya dengan bibit pohon jeruk paling sedikit 100 pohon, dan pohon mangga paling sedikit 150 pohon, kios tersebut dapat memuat 400 bibit pohon. Keuntungan bibit pohon jeruk @ Rp. 2000, dan
c. Rp. 450.000, −
pohon mangga @Rp. 1000, Jika banyaknya bibit pohon jeruk tidak boleh lebih dari 150, maka keuntungan maksimum yang didapat adalah …
(UN 30P22, 06)
a. Rp. 350.000 , − d. Rp. 550.000, − b. Rp. 400.000, − e. Rp. 650.000, −
27 y 10 5 5 5 15 x 125. Seorang pengusaha busana muslim wanita akan membuat dua jenis busana.
Bahan yang tersedia berupa 12 m kain bermotif dan 9 m kain polos. Busana jenis I membutuhkan 2 m kain bermotif dan 1 m kain polos, dan busana jenis II membutuhkan 1,5 m kain bermotif dan 1,5 m kain polos. Jika semua busana itu dapat terjual habis, dengan harga busana jenis I Rp. 82.500,00 dan busana jenis II
c. Rp. 547.500,00
Rp. 75.000,00, maka jumlah penerimaan maksimum adalah …(UN 30P32, 06) a. Rp. 450.000,00 d. Rp. 555.000,00
b. Rp. 495.000,00 e. Rp. 900.000,00
126.
penyelesaian program linier.
Nilai maksimum dari fungsi objektif
Perhatikan gambar di samping, daerah yang diarsir merupakan himpunan
f(x, y) = 2x + 5y adalah … (UN 11P19, 10) (UN 13, 11)
a. 15 d. 26 b. 20 e. 30
c. 25
127.
dari program linier.
Nilai maksimum f(x, y) = 8x + 2y
Pada gambar di samping, daerah yang diarsir adalah penyelesaian
adalah … (UN 10P52, 10) a. 4 d. 14 b. 8 e. 16 c. 9
11. MENENTUKAN HASIL OPERASI MATRIKS 128. Diketahui A = 3 1
2 4 , B =
0 1
−1 2 , dan X matriks berordo (2x2)yang memenuhi persamaan 2A − B + X = 0, maka X sama dengan … (UN 14, 02)
a. 6 −1 −5 6 c. 6 −1 −5 −6 y 4 2 y = 1 2 3 I II
28 b. 6 −1 5 −6 d. −6 −1 −5 −6 e. −6 1 5 6 129. Diketahui A = 2 1 0 −1 dan B = −1 1 0 2 Nilai A − 2B = ⋯ (UN 9P11, 03) a. 4 1 0 5 c. 0 −1 0 −5 b. 4 −1 0 −5 d. 0 3 0 3 e. 0 −1 0 3 130. Matriks X yang memenuhi persamaan 5 6
7 8 − X = 3 −4 7 −9 adalah … (UN 6P19, 07) a. −2 −10 0 −17 c. −2 2 0 1 b. 2 2 14 −1 d. 2 10 0 17 e. 8 10 0 1
131. Nilai x, y dan z dari 4x 2x + y
z x + 2z = 8 6 5 12 berturut − turut adalah … (UN 6P52, 07) c. − 2, 2, dan − 5 a. 2, 2, dan 5 d. 5, 2, dan 2 b. 2, −2, dan 7 e. 2, 5, dan 2 132. matriks A = 5 3 6 2 1 1 , B = 2 3 1 4 0 2 , dan C = 5 0 3 2 0 1
maka bentuk sederhana dari (A + B) − (A − C) adalah (UN 14, 09) Jika diketahui : a. 0 3 3 0 1 0 c. 7 3 4 6 0 3 b. 2 6 4 4 1 2 d. 7 6 7 6 1 3 e. 12 6 10 8 1 4 133. A = 4 −2 1 3 , B = −3 2 1 4 , dan C = 1 4 −3 2 . Maka 2A − B + C = ⋯ (UN 10P19, 10) Diketahui : a. 12 −2 2 −4 c. 12 −2 −2 4
29 b. 12 2 −2 −4 d. 12 −2 −2 −4 e. 12 2 2 −4 134. matriks A = 2 −1 3 1 4 −2 dan B = −1 3 1 2 3 −2 maka AB = ⋯ (UN 40, 99) Diketahui : a. 6 −3 −2 15 c. 6 −2 −3 15 b. 6 −2 −3 7 d. 6 −3 −2 7 e. 15 2 3 6 135. matriks A = 2 −1 3 −4 2 0 dan matriks B = 1 −1 3 −2 −1 2 maka matriks AB = ⋯ (UN 40, 01)
Diketahui : a. −2 2 6 0 c. 2 −3 −3 4 −4 0 b. −4 6 2 0 d. 2 4 −3 −4 −3 0 e. 6 −3 3 14 −7 9 9 5 −3 136. Jika ∶ A = 1 −3 −2 4 , B = −2 0 1 3 , dan C = 3 −1 1 −2
maka A(B − C) = ⋯ (UN 8, 04)
a. −5 −14 10 18 c. 1 −16 −2 22 b. −5 −4 10 6 d. 1 −2 −2 2 e. −7 19 −10 20 137. Diketahui ∶ A = 6 −1 0 2 dan B = −2 4 4 0 : Hasil dari A + B adalah … (UN 5, 05) a. 36 1 0 4 c. 34 5 4 2 b. 34 3 4 2 d. 34 −4 4 4 e. 36 −4 0 4 138. Nilai ∶ dari −2 3 1 −4 x 1 5 2 −3 : adalah … (UN 12, 08)
30 a. −2 15 2 12 c. 13 −13 −19 14 b. 0 −13 −5 3 d. 4 −19 −7 17 e. 2 15 2 −12
139. Diketahui persamaan matriks 4 −2 1 3 . X =
−14
7 . Matriks X yang memenuhi persamaan tersebut adalah … (UN 13, 08)
a. 2 3 c. −2 3 b. 2 −3 d. 3 −2 e. −3 2 140. Diketahui matriks A = 1 2 3 4 dan B = 1 2 2 4 : Matriks A x B adalah … (UN 15, 09) a. 27 54 59 118 c. 59 27 61 133 b. 27 61 133 592 d. 118 27 59 54 e. 61 27 59 133 141. Invers matriks A = 1 2 3 4 adalah A = ⋯ (UN 15, 02) a. 2 −1 c. 1 b. 2 d. −1 2 e. −2 1 − 142. Invers matriks ∶ 1 4 −3 −2 adalah … (UN 10P11, 03) a. − −1 −3 4 2 c. −1 −3 4 2 b. −2 −4 3 1 d. − −2 −4 3 1 e. − −1 −3 4 2 143. Invers matriks B = 3 1 9 2 adalah = ⋯ (UN 12, 06)
31 a. − −1 1 c. 1 3 b. − 1 3 −1 d. −1 3 − e. − 3 −1 144. Invers matriks 5 2 9 4 adalah = ⋯ (UN 7P23, 06) a. 4 2 1 2 c. 2 −4 −1 2 b. −2 4 1 2 d. 2 −1 −4 2 e. 2 −1 −4 2 145. Diketahui A = 4 1
11 3 , maka invers matriks A adalah = ⋯ (UN 11P22, 06) a. 3 11 1 4 c. 3 −1 −11 4 b. 3 1 4 11 d. 4 11 1 3 e. 3 4 1 11 146. Invers matriks ∶ −4 −3 4 2 adalah … (UN 11P32, 06) a. − 2 3 −4 −4 c. 2 3 −4 −4 b. − 2 4 −3 −4 d. − 2 3 −3 −4 e. 2 −4 3 −4 147. Invers matriks 2 3 1 1 adalah = ⋯ (UN 28P19, 07) a. 1 3 1 2 c. 1 −3 −1 2 b. −1 3 1 −2 d. −1 −3 −1 −2 e. 3 2 1 1 148. Jika A = 2 −6 1 −4 , A adalah … (UN 28P52, 07)
32 a. −4 6 1 4 c. 2 −3 − −1 b. 2 −3−1 d. −2− −1 e. 3 −1− 32
149. Invers dari matriks A = 7 5
−4 −3 adalah … (UN 16, 09) a. −3 −5 4 7 c. 3 5 −4 −7 b. −7 −5 4 3 d. 7 5 −4 −3 e. 7 5 4 3 150. Diketahui matriks A = 3 x 5 1 dan B = 3 4 5 y − x :
Jika Matriks A = B, maka nilai x dan y masing − masing adalah … (UN 24, 11) a. 4 dan − 4 c. 2 dan − 3
b. − 2 dan 2 d. 2 dan 3 e. 4 dan 5 151. A = 8 1 2 −3 , B = 1 4 5 0 , dan C = 2 −1 3 4 . Maka 2A − B + 3C = ⋯ (UN 25, 11) Diketahui : a. 9 −4 0 1 c. 17 −3 2 −2 b. 21 −5 8 6 d. 21 −4 8 1 e. 9 1 −10 −18
12. MENENTUKAN HASIL OPERASI VEKTOR
152. Jika diketahui vektor a = 5i − 4j , b = 3i − 3j dan c = i − j maka hasil dari a − b + c adalah … (UN 12, 09)
c. 3i − 2j
a. 3i + 6j d. 6i + 3j b. 9i − 2j e. 9i − 8j
153. Diketahui dua vektor a = 2i − 3j + 4k dan b = 5j + k. Nilai a. b adalah … (UN 34P11, 03)
c. 7
a. − 9 d. 8
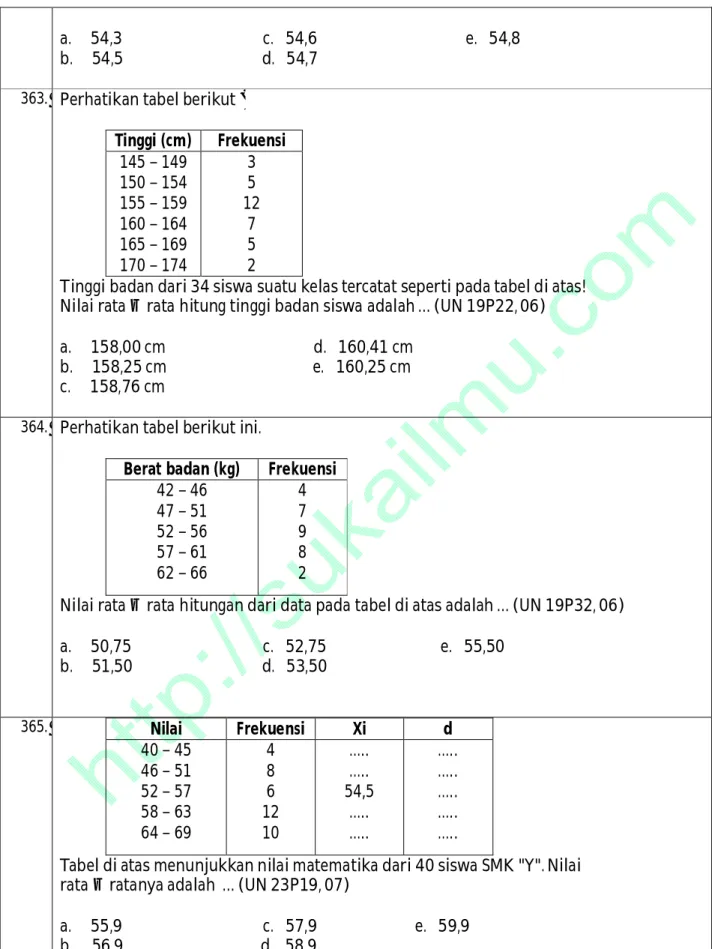
33 154. Diketahui dua vektor a = i + 2j + mk dan b = 2i − 10j + 2k. Nilai a. b = 0
maka nilai m adalah … (UN 29, 05)
c. 6
a. 18 d. 3 b. 9 e. − 16
155. Diketahui titik A (−1, 2, 3) dan B (2, −2, 3). Panjang vektor AB adalah … (UN 8P52, 07)
c. √17 satuan panjang
a. 1 satuan panjang d. √22 satuan panjang b. √10 satuan panjang e. 5 satuan panjang
156. Jika diketahui vektor a = 3i − 2j + 4k dan b = i + 5j − 3k maka vektor 2a + b = ⋯ (UN 23, 11)
c. 5i + 8j − 2k
a. 7i + 3j + k d. 5i − 7j + 7k b. 7i + j + 5k e. 4i + 3j + k
13. MENENTUKAN BESAR SUDUT ANTARA DUA VEKTOR 157. Jika sudut antara ∶
besarnya α = ⋯ (UN 37, 04) c. 90 vektor a = 2 1 −3 dan vektor b = −1 3 −2 adalah α maka a. 45 d. 120 b. 60 e. 150
158. Diketahui vektor a = 2i − 4j − 2k dan vektor b = −i − j − 2k. Besar sudut antara dua vektor adalah … (UN 13P21, 06)
c. 60
a. 30 d. 90 b. 45 e. 120
159. Diketahui vektor a = 3i + 5j − 4k dan b = 8i − 4j + k. Besar sudut yang dibentuk oleh vektor a dan b adalah … (UN 8P19, 07)
c. 45
a. 0 d. 60 b. 35 e. 90
34 160. Vektor a = 3i + j dan b = 2j − 2k. Jika sudut antara kedua vektor adalah α, maka nilai
dari cos α adalah … (UN 15, 08)
a. √5 c. − √5 e. − √5 b. √5 d. √5 161. Diketahui ∶ vektor a = 1 3 −2 dan b = 2 −1 3
jika sudut antara vektor a dan b adalah α, maka
c. 90 nilai α = ⋯ (UN 13, 09) a. 30 d. 120 b. 45 e. 150 162. Diketahui ∶ vektor a = 1 1 0 dan b = 1 0 1
. Besar sudut antara a dan b adalah …
c. 60
(UN 16P19, 10) (UN 17, 11) a. 30 d. 90
b. 45 e. 180
163. Jika vektor a dan b membentuk sudut 30 , |a| = 2√6 dan b = √6 , maka a . b adalah … (UN 12P52, 10)
c. 6√3
a. 2√3 d. 8√3
b. 4√3 e. 10√3
14. MENGHITUNG KELILING BANGUN DATAR
164. Pada gambar di samping tampak suatu lembaran kertas berbentuk persegi panjang yang pada setiap sudutnya terpotong seperempat lingkaran. Keliling sisi lembaran kertas tersebut setelah dipotong adalah … . (UN 18, 02)
d. 48 cm e. 36 cm a. 92 cm b. 80 cm c. 64 cm 14 cm 32 cm
35 165.
Keliling bangun di samping adalah … . (π =22
7 ) … . (UN 33, 02) a. 76,5 cm b. 82 cm 7 cm 10 cm c. 93 cm d. 102 cm 14 cm e. 126 cm 20 cm
166. Gambar di samping adalah gambar trapesium sama kaki . ABCD,.Jika panjang AC = 15 cm, BF = 3 dan DE = 9 cm, maka keliling trapesium ABCD adalah … . (UN 5P11, 03) a. 12 + √10 cm D C b. 18 + 3√10 cm c. 24 + 6√10 cm 9 cm 15 cm d. 29 + 6√10 cm e. 27 + 6√10 cm A E F 3 cm B 167. adalah … (UN 36P11, 03)
Panjang besi beton yang diperlukan untuk membuat ring berdiameter 42 cm, jika π =
a. 1386 cm d. 84 cm
b. 924 cm e. 21 cm
c. 132 cm
168. Diberikan gambar disamping dengan ukurannya, maka keliling bidang yang diarsir adalah … . cm. (UN 5P21, 03) a. 94 b. 75 c. 66 28 d. 61 21 e. 28 28
36 169. Panjang kawat yang dibutuhkan untuk membuat bentuk seperti gambar di samping
e. 92 cm
jika π = , adalah … (UN 36P21, 03) 26
3 3,5 a. 111 cm b. 109 cm c. 97,5 cm 7 7 d. 95 cm 14
170. Perhatikan gambar berikut ini !
d. 72 cm
Keliling daerah yang diarsir adalah … . (UN 9P52, 07) a. 58 cm
b. 65 cm c. 70 cm
e. 86 cm
171. Keliling daerah yang di arsir di samping ini adalah ….
π = (UN 19, 07) a. 50 cm b. 66 cm c. 72 cm d. 94 cm e. 102 cm 14 cm 14 cm 14 cm 14 7 cm 7 cm 7 cm 7 cm 7 cm
37
O
172. Sebuah jendela berbentuk seperti pada gambar di samping mempunyai keliling 20 m. Supaya banyaknya sinar yang masuk sebesar − besarnya , maka panjang dasar jendela (x) adalah … . (UN 37P21, 03)
a. 8 m b. 7,5 m c. 6 m Y d. 5 m e. 21 m
x
173. Seorang atlet mampu mengelilingi lapangan berbentuk persegi panjang sebanyak 8 kali adalah … . (UN 17, 09)
putaran, jarak yang ditempuh adalah 3.200 m. Jika lebar lapangan 50 m maka panjang
a. 50 m c. 100 m e. 175 m b. 75 m d. 150 m
174. Perhatikan gambar berikut ini.
Diketahui ∠POQ = 60 , OP = 18 cm (π = 3,14), maka panjang busur PQ adalah … (UN 14P21, 06) a. 18,84 cm P b. 30,68 cm c. 37,68 cm 600 d. 42,86 cm e. 57,86 cm Q
175. Jika sudut pusat suatu juring 22,5 dan jari − jarinya 14 cm, π =22
7 . Maka panjang busur juring adalah … . (UN 13P32, 06) a. 2,78 cm d. 19,25 cm
b. 3,67 cm e. 38,50 cm c. 5,50 cm
38 176.
pita. Panjang pita yang diperlukan adalah … Sebuah miniatur gapura seperti tampak pada gambar. Di sekeliling gapura akan dihiasi dengan
π = (UN 14P19, 10) a. 248 cm b. 236 cm c. 232 cm d. 215 cm e. 198 cm
177. Perhatikan gambar di samping ini. Keliling bangun yang diarsir adalah …
π = (UN 22, 11) a. 106 cm b. 108 cm c. 118 cm d. 136 cm e. 812 cm
15. MENGHITUNG LUAS BANGUN DATAR
178. Luas daerah yang diarsir pada gambar berikut adalah … . (UN 22, 99)
d. 16.422 cm 144 cm a. 21.336 cm b. 21.024 cm c. 18.828 cm 120 cm e. 10.512 cm 216 cm 5 cm 6 cm 6 cm 31 31 cm 30 cm 31 cm 8 cm 14 cm 8 cm 84 cm 7 cm 7 cm 28 cm 14 cm 24 cm 30 cm 31 cm
39 179. Luas daerah yang diarsir pada gambar di samping adalah … … ….
π =22 7 (UN 15P19, 10) a. 382 cm b. 336 cm 13 cm 13 cm c. 324 cm d. 305 cm 5 cm 5 cm e. 259 cm 24 cm
180. Luas daerah yang diarsir pada gambar di samping adalah … … ….
π = (UN 15P52, 10) a. 56 cm 7cm b. 119 cm c. 196 cm 3 cm 3 cm d. 273 cm e. 315 cm
181. Pada gambar di samping panjang AB = 8 cm, BC = 6 cm, dan EA = 10 cm. Luas bidang ACGE adalah … (UN 19, 02)
a. 100 cm H G b. 130 cm c. 144 cm E F d. 156 cm D e. 169 cm C A B
182. Satu keping paving berbentuk seperti pada gambar di samping. Luas permukaan kepingan paving tersebut adalah … (UN 6, 04)
a. 133 cm b. 266 cm 7 cm c. 287 cm d. 308 cm 7 cm e. 397 cm 7 cm
7 cm 7 cm 7 cm
183. Gambar di samping adalah sebuah lingkaran dengan pusat di titik O, luas juring AOB = 252
3 cm , dan sudut AOB = 60 . Jari − jari lingkaran tersebut 7 cm
40 adalah … (UN 7, 05) a. 49 cm b. 28 cm c. 21 cm d. 14 cm B e. 7 cm
A
184. Perhatikan gambar layang − layang ABCD berikut ini. Jika AD = 17 cm, BD = 16 cm
e. 138
dan BC = 10 cm. Maka luas layang − layang ABCD adalah … cm (UN 12P22, 06) D a. 186 b. 168 c. 148 d. 146 A E C B 185. Perhatikan gambar berikut ini.
Diketahui persegi panjang ABCD, dengan DE ∶ EC = 2 ∶ 1, AD = 16 cm.
d. 384 cm
Jika luas segitiga BCE = 96 cm , maka luas segitiga ABE = ⋯ … … … (UN 12P32, 06) a. 144 cm D E C b. 192 cm c. 288 cm e. 576 cm A B 186. Luas daerah pada gambar berikut adalah … (UN 6P23, 06)
a. 125 cm b. 185 cm c. 225 cm 25 cm d. 245 cm e. 275 cm 14 cm
O
41 187.
Luas daerah yang diarsir adalah … . (UN 10P19, 07)
d. 38,5 cm
Perhatikan gambar berikut ini !
a. 10,5 cm
b. 19,25 cm
c. 29,75 cm
e. 49 cm 7cm
188. Pada gambar berikut luas daerah yang diarsir adalah 385
6 cm , dan sudut AOB = 150 . Jari − jari lingkaran tersebut adalah … … … . π = 22 7 (UN 10P52, 07) A a. 7 cm b. 14 cm c. 21 cm d. 42 cm B e. 220,5 cm
B
189. Suatu taman berbentuk persegi ditanami dengan rumput. Ditengah − tengah taman dibuat kolam seperti tampak seperti tampak pada gambar.
Luas taman yang ditanami rumput
e. 126 m adalah … (UN 18, 09) 28 m a. 745 m b. 658 m c. 581 m 7m 28 m d. 203 m 7 m 190. Luas daerah yang diarsir pada gambar
di samping adalah … … … 12 cm π = (UN 15P19, 10) a. 157 cm 14 cm b. 182 cm c. 287 cm 18 cm d. 364 cm e. 497 cm 7 cm
O
42 191. Komponen elektronika didesain seperti
tampk pada gambar terbuat dari plat besi. 28 mm
Luas bahan yang diperlukan untuk membuat 7 mm
sebuah komponen adalah … … …
π = (UN 15P52, 10) a. 626,5 mm b. 896,0 mm c. 974,0 mm d. 1.024,5 mm e. 1.130,5 mm
16. MENGHITUNG LUAS PERMUKAAN BANGUN RUANG
192. Luas bahan yang diperlukan untuk membuat pipa saluran udara dari pelat seng berdiameter 42 cm dan panjang 2 meter adalah … . (UN 23, 99)
a. 0,132 m d. 2,64 m b. 0,264 m e. 5,28 m c. 1,32 m
193. Luas permukaan sebuah kaleng berbentuk tabung dengan sisi atasnya tanpa tutup seperti pada gambar di samping adalah … .. (UN 23, 01) d. 83.292 cm e. 83.424 cm a. 8.052 cm b. 9.306 cm c. 10.692 cm 60 cm 42 cm
194. Luas permukaan kerucut yang diameter alasnya 14 cm dan tingginya 24 cm adalah … . (UN 20, 02)
a. 570 cm d. 682 cm b. 572 cm e. 704 cm c. 594 cm
195. Luas selimut tabung pada gambar di samping dengan π =22 7 adalah … (UN 11P11, 03) d. 10.500 cm a. 66.000 cm b. 33.000 cm 150 cm c. 16.500 cm e. 5.750 cm 70 cm
43 196. Suatu tabung seperti gambar disamping, π = 3,14, luas permukaan tabung adalah ….
(UN 11P21, 03) d. 565,2 cm e. 282,6 cm a. 847,8 cm b. 722,2 cm c. 643,7 cm 18 cm 10 cm
197. Luas permukaan kerucut dengan diameter alas 14 cm dan panjang garis pelukis 10 cm , π =22
7 adalah … . (UN 30P21, 06) a. 440 cm d. 90 cm b. 374 cm e. 54 cm c. 154 cm
198. Luas permukaan prisma tegak segi empat beraturan dengan rusuk alas 12 cm dan tinggi prisma 4 cm adalah … (UN 14P22, 06)
a. 48 cm d. 480 cm
b. 192 cm e. 620 cm
c. 384 cm
199. Sebuah kotak obat berbentuk balok dengan ukuran panjang 25 cm, lebar10 cm dan tinggi 20 cm. Luas permukaan kotak tersebut adalah … . (UN 12P23, 06)
a. 950 cm d. 2.500 cm b. 1.500 cm e. 5.000 cm c. 1.900 cm
200. Perhatikan gambar berikut. Luas permukaan tabung pada gambar berikut adalah … . (UN 11P19, 07) d. 2,464 cm a. 9.865 cm b. 4.752 cm c. 3.520 cm 40 cm e. 1,760 cm 28 cm
201. Luas selimut sebuah kerucut adalah 44 cm sedangkan jari − jarinya adalah 3,5 cm. Panjang garis pelukis kerucut tersebut adalah … π = (UN 11P52, 07)
44 a. 1 cm d. 3,5 cm b. 2 cm e. 4 cm
c. 3 cm 202.
tegak berbentuk trapesium sama kaki, seperti tampak pada gambar di samping. Luas bahan tersebut adalah … . . (UN 18, 08)
Diketahui sebuah kap lampu dengan H G atap terbuka berbentuk limas segi empat terpancung dengan bidang alas dan bidang E F 16 cm atas berbentuk persegi serta bidang − bidang 16 cm
yang diperlukan untuk membuat kap lampu 25 cm
a. 2.086 cm D C b. 2.146 cm c. 2.208 cm 30 cm d. 2.300 cm A B e. 2.600 cm 30 cm
203. Diketahui prisma segitiga siku − siku ABCD. DEF dengan alas segitiga ABC prisma adalah … . (UN 19, 09)
siku − siku di B. Panjang AB = 8 cm, BC = 6 cm, dan tinngi 10 cm. Luas permukan
a. 100 cm d. 288 cm
b. 220 cm e. 388 cm
c. 240 cm
204. Seorang pemborong akan mengecet ruang kantor yang mempuyai ukuran panjang 10 meter,. .lebar 5 meter dan tinggi 4 meter. Jika biaya pengecatan Rp. 11.000,00/m , maka besar biaya pengecatan adalah. . . (UN 20, 09)
c. Rp. 750.000,00
a. Rp. 2.420.000,00 d. Rp. 480.000,00 b. Rp. 1.320.000,00 e. Rp. 384.000,00
205. Sebuah kaleng tanpa tutup berbentuk tabung dengan ukuran diameter 42 cm dan tinggi 60 cm. Luas permukaan kaleng tersebut adalah … (UN 13P19, 10)
π =22 7
a. 10.692 cm d. 5.346 cm
b. 9.306 cm e. 3.960 cm
c. 6.732 cm
206. Sebuah tabung tertutup berdiameter alas 140 cm
dan tinggi 2 m. Luas permukaan tabung adalah … (UN 21, 11) π =22
45 a. 88.000 cm d. 176.000 cm
b. 103.400 cm e. 308.000 cm c. 118.800 cm
17. MENENTUKAN VOLUME BANGUN RUANG
207. Gambar di samping adalah bujur sangkar dengan sisi 12 dm. Pada setiap sudutnya dipotong bujur sangkar dengan sisi x dm kemudian dibuat kotak tanpa tutup. Nilai x agar volum kotak maksimum adalah … . (UN 29, 02)
d. 4 dm a. 1 dm b. 2 dm c. 3 dm e. 5 dm 12 dm
208. Volume pondasi tiang penyangga yang mempunyai ketentuan seperti gambar berikut adalah … . (UN 32, 99) 20 cm a. 0,09500 m 15 cm b. 0,08000 m c. 0,01800 m d. 0,01575 m 30 cm e. 0,01350 m 15 cm 40 cm
209. Volume limas pada gambar di samping adalah … (UN 33, 00) a. 624 dm b. 576 dm c. 312 dm 13 dm d. 208 dm e. 192 dm 6 dm 8 dm
46 210. Volume limas pada gambar di samping adalah … (UN 14, 04)
T a. 192 cm b. 288 cm c. 312 cm 13 cm d. 576 cm e. 624 cm D C A E B 6 cm 8 cm
211. Sebuah tabung tanpa tutup yang terbuat dari seng tipis dapat memuat zat cair sebanyak 64 cm . Seluruh luas tabung itu akan minimum jika jari − jari tabung sama dengan … . (UN 23P11, 03)
a. √π d. √2π
b. √2π e. 4
c. √π
212. Diketahui prisma ABC. DEF, AB = 8 cm, AC = 6 cm, AB ⊥ AC, dan volum prisma 240 cm . Tinggi prisma tersebut adalah … … (UN 10, 05)
a. 5 cm F b. 10 cm c. 15 cm D d. 20 cm E e. 30 cm C A B 213. Volume sebuah limas 384 cm dan alasnya berbentuk bujur sangkar, sedangkan
tinggi limas 18 cm, maka panjang sisi alasnya = ⋯ (UN 15P21, 06)
a. 4 cm d. 12 cm b. 8 cm e. 14 cm
c. 10 cm
214. Diketahui volume tabung 1.540 cm dengan tinggi 10 cm maka jari − jarinya adalah … . (UN 15P22, 06)
a. 1,4 cm d. 171 cm
b. 7 cm e. 513 cm
c. 14 cm
47 215. Sebuah kerucut berjari − jari 3 cm dan tinggi 5 cm. Limas segi empat beraturan
dengan rusuk alas 2 cm dan tinggi 5 cm. Perbandingan volume kerucut dan limas adalah … . (UN 28P22, 06)
a. π ∶ 3 d. 9π ∶ 4 b. π ∶ 1 e. 13π ∶ 4 c. 2π ∶ 1
216. Perbandingan panjang, lebar dan tinggi balok adalah 4 ∶ 3 ∶ 2. Jika volume balok 81.000 cm , maka luas permukaan balok tersebut adalah … …. (UN 14P23, 06) a. 2.700 cm d. 9.000 cm
b. 5.850 cm e. 11.700 cm c. 6.300 cm
217. Diketahui sebuah limas persegi T. ABCD, dengan panjang BD = 24 cm. Jika volumenya adalah = 1536 cm , maka tinggi limas tersebut adalah … (UN 15P32, 06)
a. 1,78 cm d. 8 cm b. 2,67 cm e. 16 cm
c. 5,33 cm
218. Di dalam sebuah limas yang alasnya bangun persegi terdapat sebuah kerucut yang alasnya terletak pada bidang alas limas dan menyinggung sisi − sisi bidang alas limas. Diketahui π =22
7 . Jika tinggi kerucut sama dengan tinggi limas, maka perbandingan volume kerucut dan volume limas = ⋯ (UN 28P32, 06) a. 11 ∶ 42 d. 33 ∶ 14
b. 11 ∶ 14 e. 42 ∶ 11 c. 14 ∶ 11
219. Sebuah kerucut mempunyai panjang garis pelukis 25 cm dan berdiameter 14 cm. Volume dari kerucut tersebut adalah … . (UN 12P19, 07)
a. 1.232 cm d. 8.983,3 cm b. 3.696 cm e. 14.784 cm c. 4.928 cm
48 220. Pondasi sebuah bangunan berbentuk prisma tegak yang mempunyai ukuran
seperti pada gambar berikut ! Jika tinggi pondasi 30 cm, maka volume pondasi bangunan itu adalah … . . (UN 12P52, 07)
a. 3,6 cm b. 36 cm c. 360 cm d. 3.600 cm e. 36.000 cm 0,3 m 0,4 m
221. Berikut adalah gambar sebuah gasing. Volume gasing adalah … .. (UN 17, 08)
a. 39π cm 3 cm b. 45π cm c. 63π cm d. 72π cm e. 99π cm 9 cm
222. Sebuah prisma tegak ABC. DEF dengan alas siku − siku di titik B. Panjang AB = 5 cm, BC = 12 cm dan AD = 15 cm. Volume prisma tersebut adalah …. (UN 17P19, 10) (UN 20, 11)
a. 135 cm d. 650 cm b. 225 cm e. 725 cm c. 450 cm
223. Alas sebuah prisma berbentuk segitiga samakaki. Panjang sisi alas segitiga 20 cm dan sisi lainnya 26 cm. Jika tinggi prisma 10 cm, maka volume prisma tersebut adalah … . (UN 17P52, 10)
a. 1.300 cm d. 2.400 cm b. 1.500 cm e. 2.600 cm c. 2.100 cm
18. MENENTUKAN PERNYATAAN DAN NILAI KEBENARAN SUATU PERNYATAAN MAJEMUK 224. Dibawah ini yang bukan pernyataan adalah … . .( 9, 02)
a. Jakarta Ibu kota Republik Indonesia
b. Ada bilangan prima yang genap c. Semua bilangan prima ganjil
d. Harga dolar naik semua orang pusing
49 225. Nilai kebenaran dari pernyataan dalam tabel berikut adalah … (UN 14, 99)
→ B B S S B S B S …. …. …. …. a. BBSS b. BBSB c. BSBB d. BSBS e. BSSS
226. Perhatikan tabel berikut ! Nilai kebenaran yang tepat adalah … (UN 16, 00) ~ ∨ B B S S B S B S …. …. …. …. a. BSBB b. BBSB c. BSSB d. SBSB e. BBSS
227. Jika diketahui pernyataan bernilai benar dan pernyataan bernilai salah, maka dari pernyataan berikut yang bernilai benar adalah … . (UN 23, 09) a. → c. ∨ e. ⇔
b. ∼ → ∼ d. ∧
228. Perhatikan tabel berikut ! Nilai kebenaran pada kolom ketiga pada tabel berikut adalah … (UN 18P19, 10) {( → ) ∧∼ } → ~ B B S S B S B S …. …. …. …. a. SSSS b. BBBB c. BBSS d. SSBB e. BSBS
229. Jika diketahui pernyataan p bernilai salah dan q bernilai benar, maka pernyataan berikut yang bernilai benar adalah……. (UN 4, 11)
a. ~ → ~ c. ( ↔ ) ∨ e. ∼ ( ↔ ) ∧ b. ∧ ( → ) d. ( ∨ ) →
19. MENENTUKAN NEGASI PERNYATAAN MAJEMUK
230. Negasi dari pernyataan" ℎ , ℎ . " adalah ….
(UN 14, 01)
a. Jika upah buruh tidak naik, maka harga barang naik b. Jika harga barang naik maka, upah buruh naik
c. Upah buruh naik dan harga barang tidak naik
d. Upah buruh naik dan harga barang naik
50 231. Negasi (ingkaran) dari pernyataan
"Jika Dani belajar maka ia akan pintar".adalah … . (UN 16P21, 06)
e. Dani belajar dan ia tidak akan pintar
a. Jika Dani tidak belajar maka ia tidak akan pintar b. Dani tidak belajar dan ia tidak akan pintar c. Dani belajar dan ia akan pintar
d. Jika Dani belajar maka ia tidak akan pintar
232. Negasi dari pernyataan" . "
adalah … . (UN 17P23, 06)
a. Jika Nita bukan seorang perawat maka Nita tidak bekerja di RS
b. Jika Nita tidak bekerja di RS maka Nita bukan seorang perawat c. Jika Nita bekerja di RS maka Nita seorang perawat
d. Nita bukan perawat dan bekerja di RS
e. Nita seorang perawat dan tidak bekerja di RS
233. Negasi dari pernyataanJika hari ini hujan, maka saya tidak akan datang.adalah …. (UN 16P22, 06)
a. Hari ini hujan dan saya datang
b. Jika hari ini tidak hujan maka saya datang
c. Jika hari ini tidak hujan maka saya tidak datang
d. Hari ini tidak hujan dan saya tidak datang
e. Saya tidak datang dan hari ini hujan
234. Negasi dari pernyataan" ℎ , ℎ . "
adalah … . (UN 16P32, 06)
e. Harga barang naik jika hanya jika harga BBM naik. a. Jika harga BBM tidak naik, maka harga barang naik
b. Jika harga barang naik, maka harga BBM naik c. Harga BBM naik dan harga barang tidak naik
d. Harga BBM naik dan harga barang naik
235. Negasi dari implikasi ∶
" , ℎ. "
adalah … . (UN 24P52, 07)
e. Berat badannya bertambah atau pemberian gizi pada balita cukup
a. Balita tidak diberi gizi cukup dan berat badannya tidak bertambah
b. Balita tidak diberi gizi cukup tetapi berat badannya bertambah c. Balita diberi gizi cukup tetapi berat badannya tidak bertambah
d. Jika berat badannya tidak bertambah, maka balita tidak diberi gizi cukup