commit to user
MODEL NILAI TUKAR DOLAR KANADA
TERHADAP RUPIAH MENGGUNAKAN
MARKOV
SWITCHING GARCH
oleh
YUNITA EKASARI NIM. M0108072
SKRIPSI
ditulis dan diajukan untuk memenuhi sebagian persyaratan memperoleh gelar Sarjana Sains Matematika
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SEBELAS MARET SURAKARTA
commit to user
ABSTRAK
Yunita Ekasari, 2012. MODEL NILAI TUKAR DOLAR KANADA TER-HADAP RUPIAH MENGGUNAKAN MARKOV SWITCHING GARCH. Fa-kultas Matematika dan Ilmu Pengetahuan Alam, Universitas Sebelas Maret.
Dolar Kanada merupakan salah satu dari mata uang komoditas yang aktif diperdagangkan di pasar valuta asing. Data nilai tukar dolar Kanada terhadap rupiah periode 1 Februari 2002 sampai 29 Februari 2012 memiliki sifat heteroske-dastisitas dan juga terdapat perubahan struktur. Model GARCH mampu me-modelkan adanya heterokedastisitas dengan baik namun tidak memperhitungkan adanya perubahan struktur. Perubahan struktur merupakan suatu perubahan pola yang terjadi pada data runtun waktu. Markov Switching (MS) merupakan alternatif pemodelan data runtun waktu yang mengalami perubahan struktur. Dalam MS, perubahan struktur model yang terjadi tidak dianggap sebagai suatu hasil peristiwa deterministik tetapi sebagai suatu hasil variabel random tak tera-mati. Dalam literatur sering disebutstate. Banyaknyastate diasumsikan ada dua yaitu state nol untuk volatilitas rendah dan state satu untuk volatilitas tinggi.
Tujuan skripsi ini adalah menentukan model runtun waktu yang sesuai un-tuk nilai un-tukar dolar Kanada terhadap rupiah. Data nilai un-tukar dolar Kanada terhadap rupiah dimodelkan dengan melibatkan Markov Switching pada model
GARCH atau sering disebut MS-GARCH. Hasil penelitian menunjukkan model untuk meramalkan data nilai tukar dolar Kanada terhadap rupiah periode 1 Fe-bruari 2002 sampai 29 FeFe-bruari 2012 untukstate nol adalahARMA(1,0) sebagai model rata-rata bersyarat dan GARCH(1,0) sebagai model variansi bersyarat. Sedangkan untuk state satu ARMA(1,0) sebagai model rata-rata bersyarat dan
GARCH(1,1) sebagai model variansi bersyarat.
commit to user
Yunita Ekasari, 2012. EXCHANGE RATE MODEL OF CANADIAN DO LLAR TO RUPIAH USING MARKOV SWITCHING GARCH. Faculty of Ma-thematics and Natural Sciences, Sebelas Maret University.
Canadian dollar is one of commodity currencies traded actively in foreign currency market. The data of Canadian dollar exchange rate to rupiah during February 1, 2002 to February 29 2012 period have heteroscedasticity property and a structural change, too. GARCH can model the presence of heteroscedasticity correctly but does not take into account the presence of structural change. The structural change is a pattern change occurring in the data time series. Markov switching(M S) is an alternative of time series data modeling having structural change. In Markov Switching, change of model structural that occured is not considered as a result of deterministic event but a result of random anobserved variable. In literature, it is called state. It is assumed that there are two number of states : state zero for low volatility and state one for high volatility.
The purpose of this final project is to determine an appropriate time series model for exchange rate of Canadian dolar to rupiah. The data is modeled by involving Markov Switching in GARCH model or frequently called MS-GARCH. The result of research shows that a model to forecast the exchange rate of Cana-dian dolar to rupiah during February 1, 2002 to February 29 2012 period for state zero is ARMA(1,0) as conditional mean and GARCH(1,0) as conditional variance model, while state one is ARMA(1,0) as conditional mean and GARCH(1,1) as conditional variance model.
commit to user
MOTO
Tidak ada simpul yang tidak dapat diurai, tidak ada masalah yang tidak dapat
diselesaikan asalkan kita mempunyai kesabaran
Keberuntungan adalah sesuatu yang terjadi ketika kesempatan bertemu dengan
commit to user
PERSEMBAHAN
commit to user
KATA PENGANTAR
Puji syukur penulis panjatkan kepada Allah SWT, yang telah melimpahkan rahmat dan karunia-Nya, sehingga penulis dapat menyelesaikan skripsi ini. Selain itu, penulis juga mengucapkan terimakasih kepada semua pihak yang telah mem-bantu dalam penyusunan skripsi ini, khususnya kepada Bapak Drs. Sugiyanto, M.Si. selaku Dosen Pembimbing I dan Bapak Drs. Pangadi, M.Si. selaku Dosen Pembimbing II atas kesabarannya membimbing dan memotivasi penulis dalam penyusunan skripsi ini.
Semoga skripsi ini dapat bermanfaat bagi pembaca.
commit to user
Daftar Isi
PENGESAHAN . . . iii
ABSTRAK . . . iii
ABSTRACT . . . iv
MOTO . . . v
PERSEMBAHAN . . . vi
KATA PENGANTAR . . . vii
DAFTAR ISI . . . . x
DAFTAR TABEL . . . . xi
DAFTAR GAMBAR . . . . xii
DAFTAR NOTASI . . . xiii
DAFTAR NOTASI . . . xiv
I PENDAHULUAN 1 1.1 Latar Belakang Masalah . . . 1
1.2 Perumusan Masalah . . . 3
1.3 Batasan Masalah . . . 3
1.4 Tujuan Penelitian . . . 3
1.5 Manfaat Penelitian . . . 4
II LANDASAN TEORI 5 2.1 Tinjauan Pustaka . . . 5
2.1.1 Model Runtun Waktu dan Stasioneritas . . . 7
2.1.2 ACF dan PACF . . . 7
commit to user
2.1.4 Model ARMA . . . 8
2.1.5 Estimasi Model ARMA . . . 9
2.1.6 Uji Autokorelasi Residu . . . 11
2.1.7 Uji Heterokedastisitas . . . 12
2.1.8 Uji Perubahan Struktur . . . 12
2.1.9 Model GARCH . . . 13
2.1.10 Kriteria Informasi . . . 17
2.1.11 Model Markov Switching . . . 17
2.1.12 Model Markov Switching GARCH . . . 19
2.1.13 Probabilitas Transisi . . . 20
2.1.14 Spesifikasi model rata-rata bersyarat dan variansi bersyarat 21 2.1.15 Fungsi Likelihood MS-GARCH . . . 23
2.1.16 Algoritma EM untuk Fungsi Likelihood MS GARCH . . . 25
2.2 Kerangka Pemikiran . . . 26
III METODE PENELITIAN 28 IV PEMBAHASAN 30 4.1 Deskripsi Data . . . 30
4.2 Log Return . . . 31
4.3 Pengujian Karakteristik Log Return . . . 32
4.4 Pembentukan Model Stasioner . . . 33
4.4.1 Identifikasi Model . . . 33
4.4.2 Estimasi Parameter Model ARMA . . . 34
4.4.3 Pemeriksaan Diagnostik ModelARMA(1,0) . . . 34
4.4.3.1 Uji Autokorelasi . . . 35
4.4.3.2 Homokesdastisitas Variansi . . . 35
4.4.4 Uji Efek Heteroskedastisitas . . . 36
4.4.4.1 Uji Korelasi Kuadrat Residu . . . 36
4.4.4.2 Uji Lagrange Multiplier . . . 37
commit to user
4.4.6 Model GARCH . . . 38
4.4.7 Model Markov Switching GARCH . . . 39
4.4.8 Peramalan . . . 40
4.4.8.1 Peramalan Volatilitas . . . 40
4.4.8.2 Peramalan Rata-Rata Bersyarat . . . 41
4.4.9 Validasi Model . . . 42
V PENUTUP 44 5.1 Kesimpulan . . . 44
5.2 Saran . . . 44
commit to user
Daftar Tabel
2.1 Ciri-ciri ACF dan PACF model ARMA(p, q) . . . 9
4.1 Hasil Estimasi Model ARMA pada Data Log Return . . . 34
4.2 Uji Breusch-Godfrey Residu Model ARMA(1,0) . . . 35
4.3 Uji Lagrange Multiplier Residu ModelARMA(1,0) . . . 37
4.4 Uji Chow Break Point Berdasarkan Model ARMA(1,0) . . . 38
4.5 Uji Lagrange Multiplier Residu ModelARMA(1,0) . . . 39
4.6 Hasil ramalan volatilitas log return enam periode ke depan . . . 40
4.7 Hasil Ramalan Log Return Enam Periode ke Depan dengan Inte-rval Konfidensi 95% . . . 41
4.8 Hasil Ramalan Nilai Tukar Dolar Kanada terhadap Rupiah Enam Periode ke Depan dengan Interval Konfidensi 95% . . . 42
4.9 Peramalan Nilai Tukar Dolar Kanada terhadap Rupiah . . . 42
commit to user
Daftar Gambar
4.1 Plot Nilai Tukar Dolar Kanada terhadap Rupiah . . . 30 4.2 Plot ACF dan PACF Nilai Tukar Dolar Kanada terhadap Rupiah 31 4.3 Plot Log Return Nilai Tukar Dolar Kanada terhadap Rupiah . . . 31 4.4 Histogram dan Statistik Deskriptif Log Return Nilai Tukar Dolar
Kanada terhadap Rupiah . . . 32 4.5 Plot Absolut Log Return dan Kuadrat Log Return Nilai Tukar
Dolar Kanada terhadap Rupiah . . . 32 4.6 Plot ACF dan PACF Log Return Nilai Tukar Dolar Kanada
commit to user
DAFTAR NOTASI
Pt : data pada waktu ke-t
rt : log return pada waktu ke-t
T : jumlah observasi
E() : harga harapan
γk : autokovariansi pada lag-k
ρk : autokorelasi pada lag-k
ϕkk : autokovariansi parsial
ϕ : parameter autoregressive
θ : parameter rata-rata bergerak
p : orde parameter autoregressive
q : orde parameter rata-rata bergerak
µ : rata-rata
σ2 : variansi
x : variabel bebas
S∗ : jumlah kuadrat residu
εt : residu rata-rata bersyarat pada waktu t
ut : deret white noise berdistribusi normal dengan variansi satu
Ψt : himpunan semua observasi samapai waktu ke-t
α : parameter GARCH
β : parameter GARCH
st : state
f() : fungsi densitas probabilitas
α : parameter GARCH
pij : probabilitas transisi state i akan diikuti state j
commit to user
Ij(st) : fungsi indikator bernilai nol atau bernilai satu
φjt : probabilitasstate j waktut berdasarkan informasi Ψt
lt : fungsi loglikelihood pada waktu ke-t
Θ : vektor parameter MS-GARCH
χ2 : statistik uji Breuch-Godfrey
ξ∗ : statistik uji Lagrange Multiplier Q : statistik uji Ljung Box
F : statistik uji Chow Break Point
H0 : hipotesis nol
commit to user
Bab I
PENDAHULUAN
1.1
Latar Belakang Masalah
Globalisasi dalam bidang ekonomi menyebabkan hampir semua negara di dunia menganut sistem perekonomian terbuka. Perekonomian terbuka meng-gambarkan suatu kondisi dimana antar negara melakukan suatu hubungan, baik secara ekonomi melalui perdagangan internasional maupun politik. Perdagang-an internasional mengakibatkPerdagang-an munculnya masalah baru yakni perbedaPerdagang-an mata uang antar negara-negara yang bersangkutan. Harga suatu mata uang terhadap mata uang yang lainnya disebut nilai tukar (kurs). Nilai tukar merupakan alat untuk mengukur kondisi perekonomian suatu negara.
Sejak 14 Agustus 1997, Indonesia menganut sistem nilai tukar mengambang bebas (free floating exchange rate system). Nilai tukar rupiah dibiarkan secara bebas bergerak berdasarkan mekanisme pasar. Akibatnya nilai tukar rupiah ter-hadap mata uang asing sangat berfluktuasi. Salah satu mata uang yang dapat mempengaruhi pergerakan perekonomian dunia adalah dolar Kanada yang me-rupakan salah satu dari commodity currency yang aktif diperdagangkan di pasar valuta asing (Haruko [9]). Fluktuasi nilai tukar memberikan dampak yang besar terhadap perekonomian sehingga diperlukan manajemen nilai tukar yang baik, yang menjadikan nilai tukar stabil. Fluktuasi nilai tukar dolar Kanada terhadap rupiah dapat diprediksi menggunakan analisis runtun waktu karena merupakan himpunan observasi terurut.
commit to user
ke waktu sehingga variansi dari eror berubah setiap waktu (heteroskedastisitas). Hal ini mengakibatkan asumsi homoskedastisitas tidak terpenuhi. Berdasarkan kenyataan tersebut, diperlukan model yang dapat menggambarkan pergerakan variansi eror.
Engle [5] memperkenalkan model Autoregressive Conditional Heteroscedas-ticity (ARCH) untuk memodelkan variansi eror. Model ARCH dalam penera-pannya memiliki kelemahan yaitu ketika diperoleh orde ARCH yang besar me-nyebabkan presisi estimator berkurang. Bollerslev [2] memperkenalkan model
Generalized Autoregressive Conditional Heteroscedasticity (GARCH) yang me-rupakan generalisasi dari model ARCH. Namun, baik model ARCH maupun
GARCH tidak memperhitungkan perubahan struktur serta tidak dapat mende-teksi pergeseran volatilitas.
Hamilton [7] memperkenalkan Markov Switching(MS) sebagai alternatif pemodelan data time series yang mengalami perubahan struktur. Perubahan struktur merupakan suatu perubahan pola yang terjadi pada data runtun waktu. Dalam Markov Switching, perubahan struktur yang terjadi tidak dianggap seba-gai suatu hasil peristiwa deterministik tetapi sebaseba-gai suatu hasil variabel random tak teramati(unobservable) dan dalam literatur sering disebut state atau regime. Hamilton [7] melibatkanMarkov Switching pada modelAutoregressive dan meng-hasilkan model yang dapat menjelaskan perubahan struktur dengan baik, namun belum bisa menjelaskan adanya pergeseran volatilitas. Selanjutnya, Hamilton dan Susmel [8] melibatkan Markov Switching pada model ARCH, dikenal de-ngan model MS-ARCH. Model ini mampu menjelaskan perubahan struktur dan mendeteksi pergeseran volatilitas pada data. Gray [6] memperkenalkan model
commit to user
dolar Kanada terhadap rupiah periode 1 Februari 2002 sampai 29 Februari 2012 dengan rata-rata bersyarat modelAutoregressive.
1.2
Perumusan Masalah
Berdasarkan latar belakang masalah dapat disusun perumusan masalah sebagai berikut.
1. Bagaimana menurunkan ulang model nilai tukar dolar Kanada terhadap rupiah menggunakan MS-GARCH.
2. Bagaimana ramalan nilai tukar dolar Kanada terhadap rupiah menggunakan
MS-GARCH untuk periode 1 Maret samapi dengan 8 Maret 2012.
1.3
Batasan Masalah
Batasan masalah pada penulisan skripsi ini diberikan untuk membatasi ru-ang lingkup pembahasan masalah yaitu data yru-ang digunakan adalah data harian nilai tukar jual dolar Kanada terhadap rupiah yang diambil pada hari Senin-Jumat dan selain hari libur nasional periode 1 Februari 2002 sampai 29 Februari 2012. Model yang digunakan adalah MS-GARCH dengan asumsi terdapat dua
state yaitu state nol untuk volatilitas rendah dan state satu untuk volatilitas tinggi.
1.4
Tujuan Penelitian
Berdasarkan perumusan masalah, tujuan dari penelitian ini adalah sebagai berikut.
1. Menurunkan ulang model nilai tukar dolar Kanada terhadap rupiah meng-gunakan MS-GARCH.
2. Menentukan ramalan nilai tukar dolar Kanada terhadap rupiah menggunakan
commit to user
1.5
Manfaat Penelitian
Hasil dari penelitian ini diharapkan dapat menambah pengetahuan, khu-susnya dalam pengembangan model variansi eror yang melibatkan perubahan
commit to user
Bab II
LANDASAN TEORI
2.1
Tinjauan Pustaka
Tinjauan pustaka adalah pembahasan mengenai penelitian-penelitian se-belumnya yang mendasari penelitian penulis. Penelitian tersebut diantaranya, Engle [5], Bollerslev [2], Hamilton [7], Hamilton dan Susmel [8], Gray [6] Mar-cucci [12] dan Klaasen [10].
Pemodelan variansi eror pertama kali diperkenalkan oleh Engle [5] meng-gunakan model ARCH. Engle [5] membandingkan hasil estimasi antara model standar yakni model klasik OLS dengan model ARCH melalui penaksiran mak-simum likelihood. Data yang digunakan adalah data inflasi di U.K.periode 1958 sampai 1977. Hasil penelitian memperlihatkan bahwa model ARCH lebih baik daripada model klasik OLS.
Bollerslev [2] memperkenalkan model GARCH yang merupakan genera-lisasi dari modelARCH dengan mengikutsertakan variansi masa lalu untuk men-jelaskan variansi masa yang akan datang. Model ini diterapkan pada data GNP U.S. periode 1948 sampai 1983. Hasil penelitian menunjukkan modelGARCH(1,1) lebih akurat daripada model ARCH(8).
Hamilton [7] memperkenalkan Markov Switching sebagai alternatif pemo-delan data time series yang mengalami perubahan struktural. Model Markov Switching dikombinasikan dengan modelAutoregressive dan diterapkan pada da-ta GNP U.S. periode 1952 sampai 1984. Hasil penelitian masih belum men-deskripsikan volatilitas data.
commit to user
[8] menggunakan dua sampai empat state dengan distribusi dari Gaussian dan
Student t. Hasil penelitian memperlihatkan model MS-ARCH mampu menje-laskan pergeseran volatilitas dengan baik. Model ini memperlihatkan state yang terbentuk ada tiga dan distribusi Student t lebih baik daripadaGaussian.
Gray [6] memperkenalkan model MS-GARCH yang diterapkan pada data suku bungaU.S.periode Januari 1970 sampai April 1994. Gray [6] menggunakan
path-independent switching GARCH, dimana setiap conditional variance hanya bergantung pada informasi di masa lalu. ModelMS-GARCH lebih mudah dalam menaksir parameter karena melibatkan parameter yang lebih sederhana.
Marcucci [12] menggunakan model standar GARCH dan Markov Regime Switching GARCH pada data indeks saham S and P100 periode 1 Januari 1988 sampai 15 Oktober 2003. Masing-masing model menggunakan tiga distribusi yang berbeda yaitu Normal, Student t dan Genaralised Error Distribution (GED). Hasil penelitian menunjukkan model Markov Regime Switching GARCH dengan distribusi normal lebih baik dibandingkan model lainnya.
Klaasen [10] menerapkan model GARCH dan MS-GARCH pada data ni-lai tukar dolar Amerika terhadap GBP, mark Jerman dan yen Jepang periode 3 Januari 1978 sampai 23 Juli 1997. Hasil penelitian menunjukkan modelGARCH
menghasilkan ramalan yang terlalu tinggi pada beberapa periode dan dapat dia-tasi menggunakan model MS-GARCH.
Penelitian-penelitian tersebut membuat penulis tertarik untuk menerapkan model Markov Switching GARCH pada data nilai tukar dolar Kanada terhadap rupiah. Penulis menggunakan model Autoregressive pada model rata-rata bersya-ratnya dan menggunakan identifikasi model untuk menentukan ordeMS-GARCH. Beberapa hal yang mendasari penelitian penulis diantaranya pengertian menge-nai model runtun waktu dan stasioneritas, ACF dan PACF, log return, model
commit to user
2.1.1
Model Runtun Waktu dan Stasioneritas
Pemodelan runtun waktu digunakan untuk meramalkan data periode waktu ke depan. Menurut Makridakis et al [11], peramalan kuantitatif dapat diterap-kan apabila memenuhi tiga kondisi, yaitu tersedia informasi tentang masa lalu, informasi tersebut dapat dibentuk menjadi data numerik, dan dapat diasumsi-kan bahwa aspek pola data di masa lalu adiasumsi-kan terus berlanjut di masa mendatang. Asumsi yang diperlukan untuk menentukan model adalah data dalam keadaan stasioner.
Stasioneritas berarti tidak terdapat pertumbuhan dan penurunan pada da-ta. Fluktuasi data berada di sekitar suatu nilai rata-rata yang konstan, tidak tergantung pada waktu dan tidak memperlihatkan perubahan variansi yang sig-nifikan dari waktu ke waktu. Selain dari plot data, kestasioneran dapat dilihat dari plot ACF.
2.1.2
ACF
dan
PACF
Autocorrelation Function(ACF) merupakan fungsi yang menunjukkan be-sarnya korelasi antara pengamatan pada waktu ke-t dengan pengamatan waktu sebelumnya. Sedangkan Partial Autocorrelation Function( PACF) adalah fungsi yang menunjukkan besarnya korelasi parsial antara pengamatan pada waktu ke-t
dengan pengamatan waktu sebelumnya.
Menurut Cryer [4], prosesYtdikatakan stasioner apabilaE(Yt) =µ, V ar(Yt) =
σ2 adalah konstan dan
Cov(Yt, Yt+k) =E(Yt−µ, Yt+k−µ) =γk, (2.1)
dengan Cov(Yt, Yk) adalah fungsi dari selisih waktu |t − k|. Korelasi antara
(Yt, Yt+k) adalah
ρk =Corr(Yt, Yt+k) =
Cov(Yt, Yt+k)
√
V ar(Yt)
√
V ar(Yt+k)
= γk
γ0
commit to user
Jika suatu runtun waktu stasioner, maka estimasi nilai ACF turun secara cepat mendekati nol dengan semakin bertambahnya lag (selisih waktu). Sedang-kan jika estimasiACF turun secara perlahan mendekati nol atau nilai yang keluar dari interval konfidensi membentuk pola tertentu maka runtun waktu tidak sta-sioner.
Autokorelasi parsial antaraYt dan Yt+k adalah korelasi antara Yt dan Yt+k
setelah hubungan linearnya dengan Yt+1, Yt+2, ..., Yt+k−1 diabaikan. Autokorelasi
parsial antara Yt dan Yt+k dinotasikan dengan
ϕkk=Corr[Yt, Yt+k|Yt+1, Yt+2, ..., Yt+k−1] =
ρk−∑kj=1−1ϕk−1,jρk−j
1−∑k−1
j=1 ϕk−1,jρk−j
, (2.4) denganϕkk disebut fungsi autokorelasi parsial atau PACF.
2.1.3
Log
Return
Return diinterpretasikan sebagai hasil yang diperoleh dari suatu investasi. Studi mengenai ekonomi dan finansial lebih dititikberatkan padareturn daripada nilai sebenarnya. Menurut Tsay [13], log return dirumuskan sebagai berikut
rt=ln(
Pt
Pt−1
) (2.5)
dengan rt adalah log return pada waktu ke t dan Pt adalah nilai tukar dolar
Kanada terhadap rupiah pada waktu ke t. Setelah data stasioner selanjutnya data dimodelkan dengan ARMA.
2.1.4
Model
ARMA
meng-commit to user
lalunya. Menurut Cryer [4], ARMAmengandung dua komponen yaitu model AR (Autoregressive) danMA (Moving Average) denganpadalah orde model ARdan
q adalah orde model MA.
Menurut Tsay [13], modelAR(p) dinotasikan sebagai berikut
rt =ϕ1rt−1+ϕ2rt−2+...+ϕprt−p+εt (2.6)
dengan ϕ1, ϕ2, ..., ϕp adalah parameter model AR dan εt adalah eror model AR.
Sedangkan modelMA(q) dinotasikan
rt=εt−θ1εt−1−θ2εt−2−...−θqεt−q (2.7)
dengan θ1, θ2, ..., θq adalah parameter model AR dan εt adalah eror model MA.
ModelARMA(p, q) merupakan gabungan dari modelAR(p) danMA(q) sehingga dapat dituliskan sebagai berikut
rt−ϕ1rt−1−ϕ2rt−2−...−ϕprt−p =εt−θ1εt−1−θ2εt−2−...−θqεt−q
rt =ϕ1rt−1+ϕ2rt−2+...+ϕprt−p+εt−θ1εt−1−θ2εt−2−...−θqεt−q.
(2.8)
Menurut Bollerslev [2], ACF dan PACF digunakan sebagai alat untuk mengidentifikasi model ARMA(p, q).
Tabel 2.1. Ciri-ciri ACF dan PACF model ARMA(p, q)
Model ACF PACF
AR(p) Turun secara eksponensial Terpotong setelahlag p
MA(q) Terpotong setelahlag q Turun secara eksponensial
ARMA(p, q) Terpotong setelahlag (q−p) Terpotong setelah lag (q−p)
Pada model ARMA (p, q) terdapat parameterϕ1, ϕ2, ..., ϕp dan θ1, θ2, ..., θq
yang tidak diketahui sehingga perlu diestimasi.
2.1.5
Estimasi Model
ARMA
me-commit to user
minimumkan jumlah kuadrat residu. Jumlah kuadrat residu dinotasikan sebagai
S∗(ϕ, θ) =
n
∑
t=1
ε2t (2.9)
denganεtadalah eror modelARMA. FungsiS∗akan mempunyai suatu nilaiϕbdan b
θ yang minimum jika menyamakan turunan parsial pertama fungsi S∗ terhadap ϕ danθ dengan nol sehingga didapatkan estimasi akhir parameterϕbdan θb. Nilai fungsi S∗ pada persamaan (2.9) akan minimum jika turunan parsial kedua dari
fungsi S∗ terhadap ϕ ataupun θ memenuhi
(S∗)φφ.(S∗)θθ −[(S∗)φθ]2 >0
(S∗)φφ >0,(S∗)θθ >0.
Misal dipunyai model ARMA(1,1) sebagai berikut
rt−ϕ1rt−1 =εt−θ1εt−1. (2.10)
Dari persamaan (2.10) diperoleh nilai residual
εt=rt−ϕ1rt−1+θ1εt−1
Estimasi dari θbdapat dicari dengan menyamakan ∂S∗(φ,θ)
∂θ dengan nol, sehingga
diperoleh persamaan sebagai berikut
commit to user
Estimasi dari ϕb dapat dicari dengan menyamakan ∂S∗(φ,θ)
∂φ dengan nol, sehingga
diperoleh persamaan sebagai berikut
∂∑nt=1(rt−ϕ1rt−1+θ1εt−1)2
2.1.6
Uji Autokorelasi Residu
Model stasioner yang baik akan memenuhi asumsi bahwa tidak ada auto-korelasi dalam residu yang dihasilkan. Hal ini dapat dilihat dari plot ACF dan
PACF. Apabila tidak ada nilai yang signifikan berbeda dengan nol berarti sudah tidak ada autokorelasi dalam residu dan mengindikasikan bahwa model sudah cukup baik. Bentuk plot ACF danPACF merupakan indikasi awal adanya auto-korelasi. Uji statistik perlu dilakukan untuk meyakinkan indikasi awal. Menurut Cryer [4], autokorelasi pada residu model rata-rata dapat diperiksa melalui uji
Ljung-Box. Hipotesisnya adalah
H0 : tidak terdapat autokorelasi di dalam residu model rata-rata
H1 : terdapat autokorelasi di dalam residu model rata-rata
Statistik uji Ljung-Box dirumuskan sebagai
Q=T(T −2)
dengan T merupakan ukuran sampel, k adalah jumlah lag yang diuji, dan ρbk
commit to user
tabelχ2
k. H0 ditolak jika nilai Q lebih besar dari nilai χ2k.
Setelah dilakukan uji autokorelasi residu, kemudian menguji efek heteroke-dastisitas dalam residu menggunakan ujiLagrange Multiplier.
2.1.7
Uji Heterokedastisitas
Menurut Bollerslev [2], efek heteroskedastisitas dapat diperiksa melalui uji
Lagrange Multiplier yang dilakukan pada residu modelconditional mean. Prinsip dalam uji Lagrange Multiplayer adalah dengan meregresikan kuadrat residu εt
denganlag nya sendiri. Uji hipotesisnya adalah
H0 : tidak terdapat efek ARCH sampai lag-k
H1 : terdapat efek ARCH sampai lag-k
Statistik uji dirumuskan sebagai
ξ=T R2,
denganT merupakan ukuran sampel danR2 adalah adalah koefisien determinasi.
Statistik uji ξ dibandingkan dengan nilai tabel χ2
k. H0 ditolak jika nilai ξ lebih
besar dari nilai χ2 k.
Jika terdapat efek heteroskedastisitas maka digunakan model yang dapat menggambarkan pergerakan variansi eror.
2.1.8
Uji Perubahan Struktur
da-commit to user
H0 : tidak terdapat perubahan struktur pada data
H1 : terdapat perubahan struktur pada data
Statistik uji dirumuskan sebagai
F = RSS1/k
RSS2/(n1+n2−2k)
,
denganRSS1 adalah residual kuadrat dari model dengan keseluruhan data
diku-rangi residual kuadarat dari model dengan data tiap sub sampel, RSS2 adalah
residual kuadarat dari model dengan data tiap sub sampel, k adalah banyaknya parameter, n1 adalah jumlah observasi sebelum terjadinya perubahan struktur,
n2 adalah jumlah observasi sebelum terjadinya perubahan struktur . H0 ditolak
jika nilai F lebih besar dariF tabel dengan derajat bebas (k, n1+n2−2k).
2.1.9
Model
GARCH
Bollerslev [2] memperkenalkan modelGARCH untuk menggambarkan per-gerakan variansi eror. Model GARCH merupakan pengembangan dari model
ARCH [5]. Model GARCH mengikutsertakan variansi masa lalu untuk menje-laskan variansi masa yang akan datang, sehingga dapat diperoleh estimasi yang akurat untuk variansi. Conditional variance (σt) digunakan sebagai fungsi dari
eror dimasa lalu. Diberikan ψt adalah himpunan semua informasi untuk εt dari
waktu lampau sampai dengan waktu t. εt adalah eror model ARMA dan dapat
dimodelkan sebagai
εt=utσt
denganutadalah proseswhite noiseberdistribusi normal dengan mean nol dan
commit to user
dan p ≥ 0, q ≥ 0, α0 ≥ 0, αi ≥ 0 untuk i = 1,2, ..., q dan βj ≥ 0 untuk
j = 1,2, ..., p. Jika p = 0 maka model GARCH tereduksi menjadi model
AR-CH(q). Jadi model ARCH adalah bentuk khusus dari model GARCH.
Menurut Bollerslev [2], parameter dari model GARCH(p, q) dapat dies-timasi menggunakan metode Berndt Hall Hall Hausman (BHHH). Metode ini ditemukan oleh Berndt et al yang dinyatakan sebagai
ρ(i+1) =ρ(i)+λi[
MetodeBHHH menggunakan turunan pertama fungsi loglikelihood untuk meng-estimasi parameter model. Persamaan regresi yang dimiliki adalah
rt =x
′
tµ+εt,
rt =µ0+µ1xt+εt, t= 1,2, ..., T,
denganεtadalah eror dari model regresi danxtadalah variabel eksogen (variabel
bebas), dengan
Oleh karena itu, dimiliki vektor parameter Θ yang dinyatakan sebagai Θ = [µ0, µ1, α1, α2, ..., αq, β1, β2, ..., βp]t= [µt, φt]t,
denganµt= [µ
0, µ1] dan φt = [α0, α1, α2, ..., αq, β1, β2, ..., βp].
Menggunakan asumsi normalitas, fungsi densitas probabilitas dari εt|ψt−1
adalah
f(ε|ψ ) = √1 e−
commit to user
Fungsi log likelihood untuk observasi ke-t adalah
lt =logf(εt|ψt−1) = log(
Vektor parameter variansi yaitu φ diestimasi menggunakan turunan per-tama dari fungsi log likelihood pada persamaan (2.14) terhadap parameter φ, yaitu
σt2 −1. Menggunakan metode BHHH diperoleh
bentuk iterasi estimasi parameter variansi yang dirumuskan sebagai
φ(i+1) =φ(i)+λ
Iterasi pada persamaan (2.15) dapat ditulis ke dalam bentuk matriks sebagai
commit to user
T ×1.
Mengestimasi parameter rata-rata yaituµ, menggunakan turunan pertama dari fungsilikelihood pada persamaan (4.3) terhadap parameter µ, yaitu
∂lt
t −1 maka persamaan (2.16) menjadi
∂lt
Iterasi untuk estimasi parameter rata-rata adalah
µ(i+1) =µ(i)+λi[(
Persamaan (2.17) dapat ditulis ke dalam notasi matriks sebagai
µ(i+1) =µ(i)+λi[BB′)]−1B
′ C,
denganB untuk model GARCH(p, q) adalah
B =
commit to user
2.1.10
Kriteria Informasi
Kriteria informasi digunakan untuk pemilihan model terbaik yang dipilih berdasarkan Akaike Info Criterion (AIC) dan Schwarz Criterion (SC). Kedua kriteria tersebut dirumuskan sebagai berikut
AIC =−2l
T + 2
k T,
SC =−2l
T +k
log(T)
T ,
denganl adalah fungsi log likelihood, k adalah jumlah parameter yang diestimasi danT adalah jumlah observasi. Model yang dipilih untuk meramalkan data ada-lah model dengan AIC dan SC terkecil.
Model GARCH mampu menjelaskan variansi eror dengan baik, namun ti-dak memperhitungkan perubahan struktural.
2.1.11
Model
Markov Switching
Model Markov Switching merupakan alternatif pemodelan data runtun waktu yang mengalami perubahan struktur. Dalam Markov Switching, peru-bahan struktur model yang terjadi tidak dianggap sebagai suatu hasil peristiwa deterministik tetapi sebagai suatu hasil variabel random tak teramati dan dalam literatur sering disebut state. Sebagai contoh model berikut,
zt=µ0+ϕ1zt−1+εt
yang bersesuaian dengan runtun waktu padati, ti+1,..., ti+m. Sementara
zt=µ1+ϕ2zt−1+εt
yang bersesuaian dengan runtun waktu pada tj, tj+1,..., tj+m. Kasus ini
meng-gambarkan adanya pergeseran model antara model pertama dan model kedua yang terjadi pada runtun waktu yang sama pada waktu yang berbeda. Secara umum, kedua model tersebut dapat dituliskan sebagai
commit to user
dimana st bernilai nol atau bernilai satu, yang merepresentasikan periode state
yang berbeda. st bernilai nol bersesuaian dengan model pada periode ti,ti+1,...,
ti+msedangkanstbernilai satu bersesuaian dengan model pada periodetj,tj+1,...,
tj+m.
Hamilton [7] menggunakan ordo pertamamarkov chain untuk memodelkan
state. Jika probabilitas st sama dengan nilai tertentu sebesar j, untuk jϵ{0,1}
yang dependen terhadap nilai masa lalunya hanya berdasarkan nilai st−1 yang
terkini(most recent value)maka probabilitas transisinya dapat dituliskan sebagai berikut
P[st=j|st−1 =i, st−2 =k, ...] = P[st=j|st−1 =i] = pij
pij adalah probabilitas transisi bahwa state i akan diikuti oleh state j untuk
i, jϵ{0,1}dengan asumsi probabilitas perubahansthanya tergantungst−1. Proses
ordo pertama markov chain dapat dituliskan sebagai berikut
P[st = 0|st−1 = 0] =p00
P[st = 1|st−1 = 0] =p01
P[st = 1|st−1 = 1] =p11 P[st = 0|st−1 = 1] =p10
dan dapat dituliskan dalam bentuk matriks P yaitu
P =
p00 p01
p10 p11
.
Penjumlahan seluruh probabilitas untuk tiap st−1 adalah 1.
1
∑
j=0
pij = 1,
untuk setiap bilangan i= 0,1.
commit to user
2.1.12
Model
Markov Switching GARCH
Model Markov Switching GARCH dapat dituliskan sebagai berikut
rt=µst +εt
dengan µst mewakili model rata-rata bersyarat untuk setiap state. Distribusi
probabilitas yang mendasarirtpada setiapstate adalah distribusi normal ([6] dan
[12]) dengan nilai parameter yang berbeda untuk setiap state, dapat dituliskan sebagai berikut
yang berakibat pola erornya menjadi
εt|Ψt−1 ∼ dengan Ψt−1adalah informasi atau data yang dihimpun sampai pada waktut−1.
Fungsi densitas bersyarat darirt berdasarkan variabel random st yang bernilaij
adalah
Nilai probabilitas untuk sebuah state sebagai variabel random yang tidak tera-mati dinotasikan dengan
P(st=j|Ψt−1) = pjt,untukj = 0,1. (2.21)
commit to user
Fungsi densitas darirtdidapatkan dengan menjumlahkan persamaan (2.22) untuk
semua kemungkinan nilai j
f(rt|Ψt−1) = 2
∑
j=1
P(rt, st =j|Ψt−1). (2.23)
Setelah memperoleh nilai densitas dari rt, maka dapat dicari nilai probabilitas
bersyarat dari st dengan cara membagi persamaan (2.22) untuk setiap nilai j
dengan persamaan (2.23) sehingga menghasilkan persamaan
P(st=j|rt,Ψt−1) =
P(rt, st=j|Ψt−1)
f(rt|Ψt−1)
. (2.24)
2.1.13
Probabilitas Transisi
Komponen penting yang membentuk modelMarkov Switching adalah vari-abelst yang berperan sebagai indikator state yang berlaku pada saat t. Variabel
st tidak akan bisa diobservasi oleh peneliti, namun dalam model Markov
Swi-tching variabel ini akan ditentukan probabilitasnya untuk masing-masing state
pada saat t. Terdapat dua perhitungan untuk menentukan probabilitas terjadi-nya state pada saatt, yaitu ex ante probability ([6]) dan filtered probability ([7]).
Ex ante probability merupakan terjadinya state pada saat t berdasarkan informasi Ψt−1, yakni P(st = j|Ψt−1) = pjt, ∑1j=0pjt = 1 seperti pada (2.18).
Probabilitas ini merupakan probabilitas marjinal dari probabilitas gabungan an-tara st dan st−1, yakni
Mengacu pada struktur markov chain, probabilitas pjt hanya bergantung pada
state yang terjadi saat t−1, sehingga (2.25) akan menjadi
pjt = 1
∑
j=0
P(st=j|st−1 =k,Ψt−1)P(st−1 =k|Ψt−1). (2.26)
proba-commit to user
yakni φjt = P(st = j|Ψt). φjt dapat dituliskan kembali sebagai fungsi dari ex
ante probability, sebagai berikut
P(st =j|Ψt) =P(st=j|Ψt,Ψt−1)
=P(st=j|rt,Ψt−1)
= f(rt, st=j|Ψt−1
f(rt,Ψt−1)
(2.27)
dimana f(rt,Ψt−1) berbentuk distribusi normal mixture seperti pada (2.18)
se-hingga
P(st=j|Ψt) =
f(rt, st=j|Ψt−1P(st =j|Ψt−1)
∑1
j=0f(rt|st=j,Ψt−1)P(st=j|Ψt−1)
(2.28) dengan demikian, sesuai (2.26) dan (2.28) dapat dilihat bahwa pjt danφjt dapat
dihitung secara rekursif diantara keduanya.
2.1.14
Spesifikasi model rata-rata bersyarat dan variansi
bersyarat
Pada penelitian ini menggunakan model umumARMAsebagai model rata-rata bersyarat ([6]). Berikut model rata-rata-rata-rata bersyarat yang digunakan :
rt=µst +εt (2.29)
denganµst adalah rata-rata bersyarat untuk setiapstate.
Rata-rata bersyarat untukMS-GARCH pada penelitian ini mengacu pada ([6]) yakniGARCH(1,1) dengan parameter mengikuti prosesswitching
σt2 =α0+α1ε2t−1+β1σ
2
t−1 (2.30)
Untuk menghindari ketergantungan komponen ε2
t−1 dan σ2t−1 dalam (2.30)
meng-commit to user
Untuk mendeskripsikanσ2
t−1akan dihitungE[r
2
t|Ψt−1] berdasarkanGARCH
tanpa melibatkan perubahan state yakni:
E[rt2|Ψt−1] =E[(µt+εt) dan untuk masing-masing state
E[r2t|St= 0,Ψt−1] =µ0t+σ02t,
E[r2t|St= 1,Ψt−2] =µ1t+σ12t.
(2.35)
Melalui cara yang sama dengan (2.31), formulaE[r2
commit to user
switching regime dapat dihitung
E[r2t|Ψt−1] =
sehingga dengan substitusi (2.35) pada (2.36) maka diperoleh
E[r2t|Ψt−1] =
t−1 dapat dicari melalui substitusi (2.31) dan (2.37) yakni
σ2t−1 =E[r2t−1|Ψt−2]−[E[rt2−1|Ψt−2]]2,
=p0t−1(µ20t−1+σ20t−1) + (1−p1t−1)(µ21t−1+σ12t−1)
−[p0t−1µ0t−1+ (1−p1t−1)µ1t−1],
(2.38)
sesuai dengan (2.32) dan (2.38), maka komponen ε2
t−1 dan σt2−1 pada (2.30)
ti-dak akan tergantung pada kombinasistate sebelumnya yakni (st, st−1, st−2, ..., s1)
sehingga pada tahap penyusunan fungsi likelihood tidak menimbulkan kesulitan dalam optimasinya.
2.1.15
Fungsi
Likelihood MS-GARCH
Untuk menentukan fungsilikelihood pada MS-GARCH, pertama kali yang dilakukan adalah meninjau distribusi dari return rt untuk setiap state, yakni
commit to user
pada (2.26), pjt untuk state nol adalah
p0t=P(st= 0|Ψt−1) =
dan untuk state satu
p1t=P(st= 1|Ψt−1) = 1−P(st= 0|Ψt−1) = 1−p0t.
Fungsi likelihood untuk Markov Switching GARCH yakni:
L(Θ|rt,Ψt−1) =
Fungsilikelihood ini dibentuk dari distribusimixture normal dengan asumsi bah-wa setiap datanya telah diketahui masuk ke state 0 atau 1. Artinya, ketika diketahui bahwa suatu data adalah anggota state 0, maka nilai f(rt|Ψt−1) akan
bernilai nol pada state 1, demikian juga sebaliknya ([7]). Berdasarkan distibusi
mixture normal, loglikelihood pada (2.41) akan menjadi :
lnL(Θ|rt,Ψt−1) = ΣTt=1ln[Σ1j=0f(rt|st=j,Ψt−1)pjt]
= ΣTt=1ln[f(rt|st= 0,Ψt−1)p0t+f(rt|st= 1,Ψt−1)p1t]
= ΣTt=1ln[f(rt|st= 0,Ψt−1)p0t+f(rt|st= 1,Ψt−1)(1−p0t)].
(2.42) Namun karena setiap data tidak diketahui akan masuk kestate yang mana, maka optimisasi log likelihood tidak dapat dilakukan dengan metode numerik standar.
commit to user
2.1.16
Algoritma EM untuk Fungsi
Likelihood MS
GARCH
State (st) adalah variabel yang unobservable, sehingga dapat dianggap
sebagai missing. Bila didefinisikan variabel acak st akan bernilai j adalah pjt
maka dapat dibuat fungsi untuk st sebagai berikut:
f(st) = P(st=j|Ψt−1) =
dimanaIj(st) adalah fungsi indikator bernilai 0 dan 1, yakni :
Ij(st) = Fungsi indikator ini menentukan observasi mana yang akan masuk ke masing-masingstate. Algoritma EM akan melibatkan st ini dalam fungsilikelihood pada
iterasinya. Bila fungsi indikator (2.44) diterapkan pada distribusi probabilitas dari rt maka :
Sedangkan bila (2.44) diterapkan pada joint distribusi st dan rt maka
f(rt|st =j,Ψt−1) = T
∏
t=0
f(rt|st=j,Ψt−1)Itst. (2.46)
Bila diasumsikan bahwa diketahui observasi yang menjadi anggota masing-masing state, maka akan terdapat pasangan observasi (rt, st) pada setiap data
ke t, dan fungsi likelihood (2.40) akan dimaksimumkan berdasarkan distribusi bersama anatara st dan rt, yakni : atau dalam log likelihood dapat dituliskan lagi sebagai :
commit to user
Estimasi parameter untuk setiapstate dapat dilakukan mengacu pada optimisasi untuk (2.48).
Karena tidak ada petunjuk tetang observasi yang bersesuaian dengan sta-te nol atau satu maka fungsi indikator pada (2.44) tidak akan bisa digunak-an. Untuk mengatasi hal ini fungsi indikator diganti dengan ekspektasinya yakni
E[Ij(st)|Ψt−1]:
E[Ij(st)|Ψt] = Σ1It(st)=0Ij(st)P(st=j|Ψt)
= 1.P(st =j|Ψt−1) + 0.P(st=j|Ψt)
=P(st=j|Ψt)
(2.49)
dan mengacu pada filtered probability seperti pada maka didapatkan ekspektasi dari fungsi indikator adalah :
E[Ij(st)|Ψt] =P(st=j|Ψt) = φjt =
pjtf(rt|st=j)
∑1
j=0pjtf(rt|st =j)
(2.50) yang akan digunakan untuk menyusun algoritma EM.
Berdasarkan (2.49), makacomplete data likelihood (2.48) akan menjadi:
Q=E[lnL(Θ|rt, st,Ψt−1)|rt,Ψt−1]
=EΣT
t=1Σ1j=0Ij(st)[ln(pjtf(rt|st=j,Ψt−1))]
= ΣT
t=1Σ1j=0E[Ij(st)Ψt−1][ln(pjtf(rt|st=j,Ψt−1))]
= ΣT
t=1Σ1j=0P(st =jΨt−1)[ln(pjtf(rt|st =j,Ψt−1))]
Fungsi Q tersebut akan dimaksimumkan menggunakan metode Sequential Qua-dratic Programming.
2.2
Kerangka Pemikiran
sedangk-commit to user
heteroskedastisitas.Hal ini menyebabkan model ARMA tidak relevan untuk di-gunakan. Sehingga dapat digunakan model GARCH yang untuk memodelkan heterokesdastisitas, namun model GARCH tidak memperhitungkan perubahan struktural.
Model Markov Switching adalah alternatif pemodelan data runtun waktu yang mengalami perubahan struktural. Pada model Markov Switching perubah-an struktural merupakperubah-an hasil variabel rperubah-andom tak teramati (state). Data runtun waktu nilai tukar Dolar Kanada memiliki heteroskedastisitas dan mengalami pe-rubahan struktural dapat dimodelkan dengan melibatkan Markov Switching pa-da prosesGARCH. ModelGARCH untuk melihat kedinamisan volatilitas dalam suatu state. Sedangkan modelMarkov Switching akan menentukan perpindahan
commit to user
Bab III
METODE PENELITIAN
Metode yang digunakan dalam penelitian ini adalah penerapan model de-ngan menggunakan data harian nilai tukar jual dolar Kanada terhadap rupiah yang diambil pada hari Senin-Jumat dan selain hari libur nasional periode 1 Februari 2002 sampai 29 Februari 2012. Data ini diperoleh dari website Bank Indonesia yaituwww.bi.go.id [1].
Langkah-langkah analisis data dalam penelitian ini diuraikan sebagai berikut.
1. Membuat plot data untuk melihat kestasioneran data dalam mean dan
variansi.
2. Melakukan transformasi logreturn apabila data belum stasioner baik dalam rata-rata maupun variansi.
3. Membuat plot ACF dan PACF dari fungsi log return. Jika data stasioner maka dimodelkan dengan menggunakan proses ARMA. Jika data masih belum stasioner kembali ke langkah dua.
4. Mengestimasi parameter model ARMA.
5. Memeriksa autokorelasi dalam kuadrat residu model ARMA, jika memiliki autokorelasi maka terdapat efek heteroskedastisitas. Efek heteroskedastisi-tas juga dapat diuji dengan ujiLagrange Multiplier.
6. Memeriksa adanya perubahan struktur. 7. Membentuk model GARCH
heteros-commit to user
(b) menentukan model terbaik dari model GARCH yang telah diperoleh dengan melihat nilaiAIC dan SC yang terkecil,
(c) mengestimasi secara bersama parameter model ARMAdan GARCH, (d) menguji kecocokan model dengan memeriksa efek heteroskedastisitas,
autokorelasi dan asumsi distribusi dari residu terstandar. 8. Membentuk model Markov Switching GARCH
(a) menentukan probabilitas terjadinya masing-masing state pada setiap waktu,
(b) menentukan probabilitas transisi dan matrik transisi antar state. 9. Mencari nilai estimasi parameter model GARCH yang melibatkan
peru-bahan state dengan metodeMaximum Likelihood (MLE).
(a) menentukan fungsi likelihood berdasarkan fungsi densitas return yang melibatkan probabilitas masing-masingstate dan probabilitas transisi, (b) menerapkan algoritma EM untuk mengestimasi parameterMS-GARCH. 10. Melakukan peramalan
(a) menentukan banyaknya ramalan sepanjang f periode yang akan dila-kukan,
(b) menentukan probabilitas terjadinya masing-masing state pada waktu
t+f melalui proses markov chain,
(c) meramalkan nilai logreturn menggunakan model ARMA untuk men-cari nilai ramalan kurs jual dolar Kanada terhadap rupiah,
(d) meramalkan volatilitas log return menggunakan model MS-GARCH
commit to user
Bab IV
PEMBAHASAN
4.1
Deskripsi Data
Pada penelitian ini, data yang digunakan adalah data harian nilai tukar jual dolar Kanada terhadap rupiah. Data diambil pada hari Senin-Jumat dan selain hari libur nasional mulai 1 Februari 2002 sampai 29 Februari 2012. Data ini berjumlah 2466 observasi yang diperoleh dari website Bank Indonesia ([1]).
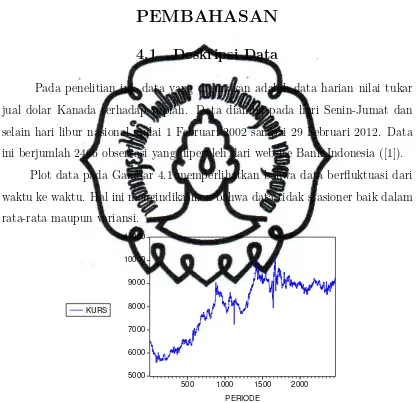
Plot data pada Gambar 4.1 memperlihatkan bahwa data berfluktuasi dari waktu ke waktu. Hal ini mengindikasikan bahwa data tidak stasioner baik dalam rata-rata maupun variansi.
5000 6000 7000 8000 9000 10000 11000
500 1000 1500 2000
KURS
PERIODE
Gambar 4.1. Plot Nilai Tukar Dolar Kanada terhadap Rupiah
Indikasi bahwa data tidak stasioner dapat diperkuat menggunakan plot
ACF dan PACF yang ditunjukkan pada Gambar 4.2.
commit to user
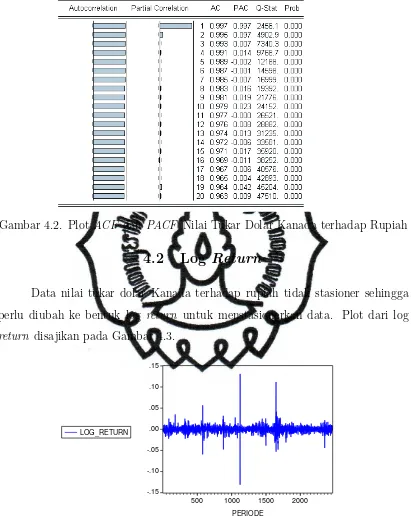
Gambar 4.2. Plot ACF dan PACF Nilai Tukar Dolar Kanada terhadap Rupiah
4.2
Log
Return
Data nilai tukar dolar Kanada terhadap rupiah tidak stasioner sehingga perlu diubah ke bentuk log return untuk menstasionerkan data. Plot dari log
return disajikan pada Gambar 4.3.
-.15 -.10 -.05 .00 .05 .10 .15
500 1000 1500 2000
LOG_RETURN
PERIODE
commit to user
4.3
Pengujian Karakteristik Log
Return
Karakteristik data log return dalam pembentukan model heteroskedastisi-tas adalah adanyavolatility clustering. Volatility clustering dapat dilihat dari plot data absolut log return, kuadrat log return dan bentuk kurtosis dari distribusi data log return yang leptokurtik.
0 200 400 600 800 1,000 1,200
-0.10 -0.05 0.00 0.05 0.10
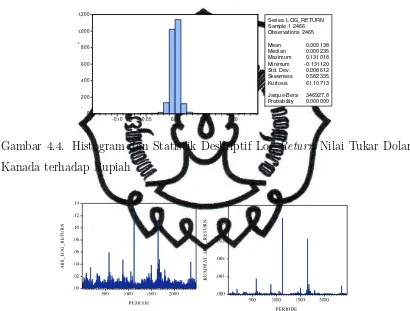
Series: LOG_RETURN Sample 1 2466 Observations 2465 Mean 0.000138 Median 0.000235 Maximum 0.131018 Minimum -0.131120 Std. Dev. 0.008612 Skewness 0.582335 Kurtosis 61.10713 Jarque-Bera 346927.8 Probability 0.000000
Gambar 4.4. Histogram dan Statistik Deskriptif Log Return Nilai Tukar Dolar Kanada terhadap Rupiah
Gambar 4.5. Plot Absolut Log Return dan Kuadrat Log Return Nilai Tukar Dolar Kanada terhadap Rupiah
Berdasarkan Gambar 4.4, diperoleh kurtosis yaitu 61,10713. Nilai kurtosis-nya lebih besar dari 3 sehingga dapat disimpulkan kurtosiskurtosis-nya berupa leptokurtik. Kurtosis yang berbentuk leptokurtik mengindikasikan volatility clustering. Ada-nya volatility clustering juga diperkuat dengan berkumpulnya sekelompok aset
commit to user
4.4
Pembentukan Model Stasioner
4.4.1
Identifikasi Model
Autokorelasi dalam data logreturn dapat dilihat dari plot ACF danPACF
yang ditunjukkan pada Gambar 4.6.
Gambar 4.6. PlotACF dan PACF LogReturn Nilai Tukar Dolar Kanada terha-dap Rupiah
Plot ACF dan PACF dapat digunakan untuk identifikasi model ARMA.
Gambar 4.6 menunjukkan nilai ACF meluruh menuju nol kemudian terputus setelah lag pertama dan nilai PACF meluruh menuju nol kemudian terputus se-telah lag pertama sehingga memungkinkan model yang sesuai adalahARMA(1,0),
ARMA(0,1)dan ARMA(1,1). Estimasi model ARMAuntuk log return mengha-silkan model ARMA(1,1) dengan koefisien yang tidak signifikan sehingga model
ARMA(1,1) tidak dapat digunakan untuk memodelkan data log return. Model
ARMA yang sesuai untuk memodelkan data log return adalah ARMA(1,0) dan
commit to user
4.4.2
Estimasi Parameter Model
ARMA
Hasil uji pada identifikasi model awal menghasilkan modelARMA(1,0) dan
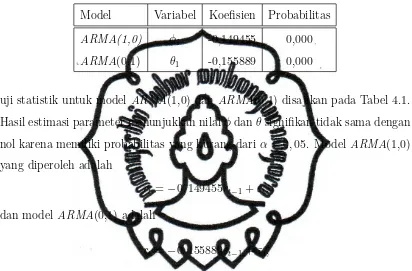
ARMA(0,1) adalah model yang tepat untuk memodelkan data log return. Hasil Tabel 4.1. Hasil Estimasi ModelARMA pada Data Log Return
Model Variabel Koefisien Probabilitas
ARMA(1,0) ϕ1 -0,149455 0,000
ARMA(0,1) θ1 -0,155889 0,000
uji statistik untuk modelARMA(1,0) dan ARMA(0,1) disajikan pada Tabel 4.1. Hasil estimasi parameter menunjukkan nilaiϕdanθsignifikan tidak sama dengan nol karena memiliki probabilitas yang kurang dariα = 0,05. Model ARMA(1,0) yang diperoleh adalah
rt=−0,149455rt−1 +εt,
dan model ARMA(0,1) adalah
rt=−0,155889εt−1+εt,
dengan rt adalah log return pada waktu t dan εt adalah residu yang dihasilkan
model pada waktu t. Pada penelitian ini akan menggunakan model ARMA(1,0) sebagai model conditional mean mengacu pada Gray([6]).
4.4.3
Pemeriksaan Diagnostik Model
ARMA
(1,0)
commit to user
4.4.3.1 Uji Autokorelasi
Model ratarata bersyarat dikatakan baik jika residu yang dihasilkan sudah tidak memiliki autokorelasi. Autokorelasi residu dapat dideteksi menggunakan uji statistik Breusch-Godfrey dengan hipotesis
H0 : tidak terdapat autokorelasi di dalam residu model rata-rata bersyarat
H1 : terdapat autokorelasi di dalam residu model rata-rata bersyarat.
Tabel 4.2. Uji Breusch-Godfrey Residu Model ARMA(1,0) Koefisien Probabilitas Uji Breusch-Godfrey 0,4231
ARMA(1,0) 1,529553 0,5650 Residu pada lag-1 -1,534067 0,5639 Residu pada lag-2 0,198099 0,6185 Residu pada lag-3 -0,060538 0,3344 Residu pada lag-4 0,019380 0,3792 Residu pada lag-5 -0,004950 0,8066
Statistik uji Breusch-Godfrey untuk residu sampai lag-10 pada model AR-MA(1,0) disajikan pada Tabel 4.2. UjiBreusch-Godfrey untuk modelARMA(1,0) memberikan nilai probabilitas 0,4613 yang lebih besar dari tingkat signifikansi
α = 0,05 sehingga H0 tidak ditolak. Jadi dapat disimpulkan bahwa di dalam
residu model ARMA(1,0) tidak memiliki autokorelasi.
4.4.3.2 Homokesdastisitas Variansi
commit to user
-.15 -.10 -.05 .00 .05 .10 .15
500 1000 1500 2000
RESID_AR
PERIODE
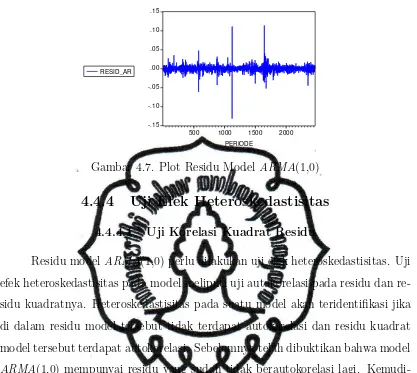
Gambar 4.7. Plot Residu Model ARMA(1,0)
4.4.4
Uji Efek Heteroskedastisitas
4.4.4.1 Uji Korelasi Kuadrat Residu
Residu modelARMA(1,0) perlu dilakukan uji efek heteroskedastisitas. Uji efek heteroskedastisitas pada model meliputi uji autokorelasi pada residu dan re-sidu kuadratnya. Heteroskedastisitas pada suatu model akan teridentifikasi jika di dalam residu model tersebut tidak terdapat autokorelasi dan residu kuadrat model tersebut terdapat autokorelasi. Sebelumnya telah dibuktikan bahwa model
commit to user
Bardasarkan Gambar 4.8 memperlihatkan bahwa ada nilai yang berbeda signifikan dengan nol yang berarti terdapat autokorelasi di dalam kuadrat residu modelARMA(1,0). Hal ini diperkuat dengan uji Ljung-Box Q statistik sampai lag-20 yang memberikan probabilitas lebih kecil dari α maka dapat disimpulkan bahwa di dalam kuadrat residu modelARMA(1,0) terdapat autokorelasi. Adanya autokorelasi di dalam residu modelARMA(1,0) dapat disimpulkan residu model
ARMA(1,0) terdapat efek heteroskedastisitas.
4.4.4.2 Uji Lagrange Multiplier
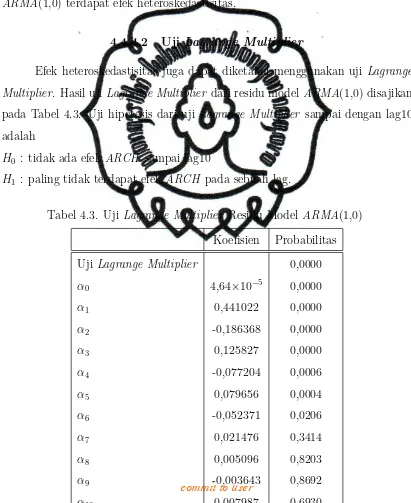
Efek heteroskedastisitas juga dapat diketahui menggunakan uji Lagrange Multiplier. Hasil uji Lagrange Multiplier dari residu modelARMA(1,0) disajikan pada Tabel 4.3. Uji hipotesis dari uji Lagrange Multiplier sampai dengan lag10 adalah
H0 : tidak ada efek ARCH sampai lag10
H1 : paling tidak terdapat efek ARCH pada sebuah lag.
Tabel 4.3. Uji Lagrange Multiplier Residu ModelARMA(1,0) Koefisien Probabilitas Uji Lagrange Multiplier 0,0000
α0 4,64×10−5 0,0000
α1 0,441022 0,0000
α2 -0,186368 0,0000
α3 0,125827 0,0000
α4 -0,077204 0,0006
α5 0,079656 0,0004
α6 -0,052371 0,0206
α7 0,021476 0,3414
α8 0,005096 0,8203
α9 -0,003643 0,8692
commit to user
Tabel 4.3 memperlihatkan bahwa statistik uji sampai lag-10 untuk residu model ARMA(1,0) menghasilkan nilai probabilitas 0,000000. Nilai ini lebih kecil dari α = 0,05 sehingga H0 ditolak. Jadi dapat disimpulkan bahwa pada residu
model ARMA(1,0) terdapat efek ARCH atau efek heteroskedastisitas.
4.4.5
Uji Perubahan Struktur
Pengujian perubahan struktur perlu dilakukan untuk mengetahui ada ti-daknya perubahan struktur pada data nilai tukar dolar Kanada terhadap rupiah. Hipotesis untuk menguji ada tidaknya perubahan struktur adalah sebagai berikut :
H0 : tidak terdapat perubahan struktur pada data nilai tukar dolar Kanada
ter-hadap rupiah
H1 : terdapat perubahan struktur pada data nilai tukar dolar Kanada terhadap
rupiah
Tabel 4.4. Uji Chow Break Point Berdasarkan ModelARMA(1,0)
Break F Probabilitas
1624 8,865309 0,002935
Tabel 4.4 menghasilkan nilai probabilitas 0,002935. Nilai ini lebih kecil da-ri α = 0,05 sehingga H0 ditolak. Jadi dapat disimpulkan terdapat perubahan
struktur pada data nilai tukar dolar Kanada terhadap rupiah.
4.4.6
Model
GARCH
commit to user
Tabel 4.5. Uji Lagrange Multiplier Residu ModelARMA(1,0) Parameter GARCH(1,1) GARCH(1,2)
α0 1,10×10−5 1,45×10−5
prob α0 0,0000 0,0000
α1 0,185615 0,231897
prob α0 4,64E-05 0,0000
β1 0,671527 0.238028
prob β1 0,0000 0,0001
β2 - 0.336637
prob β2 - 0,0000
AIC -6,912568 -6,914858
SC -6,905495 -6,905427
Model yang dipilih adalah model yang memilikiAIC dan SC terkecil. Oleh karena itu, untuk memodelkan heteroskedastisitas dari residu model ARMA(1,0) menggunakan model GARCH(1,1). Model yang diperoleh adalah
σ2t = 1,10×10−5+ 0,185615ε2t−1+ 0,671527σt2−1.
4.4.7
Model
Markov Switching GARCH
Data return nilai tukar dolar Kanada mengindikasikan adanya perbedaan antara state volatilitas tinggi dan volatilitas rendah. Model GARCH konvensio-nal tidak mampu mendeteksi adanya perubahan state dari volatilitas tinggi ke rendah atau sebaliknya sehingga diperlukan model MS-GARCH. Sesuai dengan identifikasi model, rata-rata bersyarat yang digunakan adalah ARMA(1,0) dan variansi bersyarat yang digunakan adalah GARCH(1,1). Hasil estimasi parame-ter MS-GARCH sebagai berikut
rt=
commit to user
Matriks transisi P memberikan penjelasan bahwa probabilitas terjadinya periode volatilitas rendah diikuti periode volatilitas rendah sebesarp00=0,8532020,
sehingga probabilitas periode volatilitas tinggi diikuti periode volatilitas rendah sebesar 1-p00= 0,1467980. Hal ini berarti nilai tukar dolar Kanada terhadap
rupi-ah akan mengalami volatilitas tinggi setiap 1/(p01)= 7 hari. Sedangkan
probabi-litas terjadinya periode volatiprobabi-litas tinggi diikuti periode volatiprobabi-litas tinggi sebesar
p11= 0,9894466, sehingga probabilitas periode volatilitas tinggi diikuti periode
volatilitas rendah sebesar 1-p11= 0,0105534. Hal ini berarti nilai tukar dolar
Ka-nada terhadap rupiah akan mengalami volatilitas rendah setiap 1/(p10)=95 hari.
4.4.8
Peramalan
4.4.8.1 Peramalan Volatilitas
Ramalan volatilitas log return dari waktu t menggunakan model MS-GARCH dihitung berdasarkan persamaan variansi bersyarat
σt2 =
Hasil ramalan volatilitas log return untuk enam periode ke depan, yaitu periode 2467 sampai 2472 dapat dilihat pada Tabel 4.6.
commit to user
4.4.8.2 Peramalan Rata-Rata Bersyarat
Ramalan nilai log return dihitung berdasarkan persamaan rata-rata ber-syarat yang dirumuskan sebagai
rt=
−0,00145400,untuk state nol 0,00022500,untuk state satu.
Karena terdapat heteroskedastisitas di dalam residu ARMA(1,0), diasum-sikan bahwa
εt+s∼N(0, σ2t+s)
Sehingga interval konfidensi 95% untuk pengamatan berikutnya adalah
b
rt+s±1,96σt+s.
Tabel 4.7. Hasil Ramalan Log Return Enam Periode ke Depan dengan Interval Konfidensi 95%
Periode Nilai ramalan Batas bawah Batas atas 2466 0,00011239 -0.015146583 0.0153714 2467 0,00011239 -0,015030909 0,0152557 2468 0,00011239 -0,014954076 0,0151788 2469 0,00011239 -0,014954067 0,0151788 2470 0,00011239 -0,014954067 0,0151788 2471 0,00011239 -0,014954067 0,0151788
Logreturn bukan data yang sebenarnya, sehingga bentuk logreturn harus diubah ke dalam bentuk semula untuk melihat hasil ramalan nilai tukar dolar Kanada terhadap rupiah. Persamaan untuk data pada periode t yaitu
Pt=Pt−1e
rt.
commit to user
pada hari Senin-Jumat dan selain hari libur nasional. Hasil ramalan nilai tukar dolar Kanada terhadap rupiah untuk periode ke 2367 sampai 2372 atau tanggal 1 Maret sampai 8 Maret 2012 yang disajikan pada Tabel 4.8.
Tabel 4.8. Hasil Ramalan Nilai Tukar Dolar Kanada terhadap Rupiah Enam Periode ke Depan dengan Interval Konfidensi 95%
Periode Data asli Nilai ramalan Batas bawah Batas atas 2466 9234,86 9192.61 9053,41 9333,96 2467 9248,43 9192,61 9055,47 9333,93 2468 9290,57 9193,65 9055,47 9333,93 2469 9278,06 9194,70 9056,82 9334,64 2470 9255,28 9195,71 9058,15 9335,36 2471 9236,92 9196,75 9059,07 9336,51
4.4.9
Validasi Model
Ramalan nilai tukar dolar Kanada terhadap rupiah untuk enam periode ke depan, yaitu pada tanggal 1 Maret sampai 8 Maret 2012 menggunakan model
ARMA,GARCH dan MS-GARCH disajikan pada Tabel 4.9.
Tabel 4.9. Peramalan Nilai Tukar Dolar Kanada terhadap Rupiah
Periode 1 Mar 2 Mar 5 Mar 6 Mar 7 Mar 8 Mar Data Asli 9248,43 9290,57 9278,06 9255,28 9236,92 9234,86 RamalanARMA 9191,62 9191,62 9191,62 9191,62 9191,62 9191,62 RamalanGARCH 9192,22 9192.21 9192.21 9192.21 9192.21 9192.21 RamalanMS-GARCH 9192,61 9192,61 9193,65 9194,70 9195,71 9196,75
Tabel 4.10. MSE Peramalan Nilai Tukar Dolar Kanada terhadap Rupiah Model ARMA GARCH MS-GARCH
commit to user
Tabel 4.9 menghasilkan ramalan nilai tukar dolar Kanada terhadap rupiah menggunakanMS-GARCH yang paling mendekati data aslinya. Hal ini diperkuat denganMSE dari peramalan modelMS-GARCH lebih kecil apabila dibandingkan
commit to user
Bab V
PENUTUP
5.1
Kesimpulan
Berdasarkan pembahasan diperoleh kesimpulan sebagai berikut.
1. Model untuk meramalkan data nilai tukar dolar Kanada terhadap rupiah periode 1 Februari 2002 sampai 29 Februari 2012 adalah ARMA(1,0) se-bagai model rata-rata bersyarat dan GARCH(1,0) sebagai model variansi bersyarat untuk state nol dan ARMA(1,0) sebagai model rata-rata bersya-rat danGARCH(1,1) sebagai model variansi bersyarat untuk state satu. 2. Hasil ramalan nilai tukar dolar Kanada terhadap rupiah untuk enam
pe-riode kedepan dari tanggal 1 Maret sampai 8 Maret 2012 berturut-turut 9192,61, 9192,61, 9193,65, 9194,70, 9195,71, 9196,75.
5.2
Saran
commit to user
DAFTAR PUSTAKA
[1] BI,Kurs uang kertas asing mata uang dolar kanada, www.bi.go.id, 1 Februari 2012.
[2] Bollerslev, Tim, Generalized autoregressive conditional heteroskedasticity, Econometrics 31 (1986), 307–327.
[3] Chow, G.C,Tests of equality between sets of coefficient in two linear regres-sion, Econometrica 28 (1960), no. 3, 591–605.
[4] Cryer, J. D,Time series analysis, PWS Publisherrs Duxbury Press, Boston, 1986.
[5] Engle, R. F, Autoregressive conditional heteroscedasticity with estimates of the variance of United Kingdom inflation, Econometrics50(1982), 987–1006. [6] Gray, S. F,Modeling the conditional distribution of interest rates as a
regime-switching process, Econometrics 42 (1996), 27–62.
[7] Hamilton, J. D, A new aproach to the economic analysis of nonstationary time series and the business cycle, Econometrics 57 (1989), 357–384.
[8] Hamilton, J. D and R. Susmel, Autoregressive conditional heterocedasticity and changes in regime, Econometrics 64 (1994), 307–333.
[9] Haruko, K, Change in the relationship between currency and commodity, Bank of Japan, 2012.
commit to user
[11] Makridakis, S., S.C. Wheelwright, and V.E. McGee, Metode dan aplikasi peramalan, 2 ed., Erlangga, Jakarta, 1995.
[12] Marcucci, J, Forecasting stock market volatility with regime-switching GAR-CH models, University of California, San Diego, 2005.