Distribusi weibull : sifat-sifat dan aplikasinya dalam analisis data waktu hidup dan pengendalian mutu - USD Repository

i

DISTRIBUSI WEIBULL: SIFAT-SIFAT DAN APLIKASINYA DALAM ANALISIS DATA WAKTU HIDUP DAN PENGENDALIAN MUTU

Skripsi

Diajukan untuk Memenuhi Salah Satu Syarat Memperoleh Gelar Sarjana Program Studi Matematika

Oleh:

Cecilia Novianti Salsinha NIM: 083114015

PROGRAM STUDI MATEMATIKA JURUSAN MATEMATIKA FAKULTAS SAINS DAN TEKNOLOGI

UNIVERSITAS SANATA DHARMA YOGYAKARTA

ii

WEIBULL DISTRIBUTION: CHARACTERISTICS AND ITS APPLICATIONS IN LIFETIME DATA ANALYSIS AND

QUALITY CONTROL

Thesis

Presented as Partial Fulfillment of the Requirements to Obtain the Sarjana Sains Degree in Mathematics

By:

Cecilia Novianti Salsinha Student Number: 083114015

MATHEMATICS STUDY PROGRAM, MATHEMATICS DEPARTMENT FACULTY OF SCIENCE AND TECHNOLOGY

SANATA DHARMA UNIVERSITY YOGYAKARTA

v

HALAMAN PERSEMBAHAN

!

"#$% " # & "'(

MOTTO

)

*

+

,

)

-

.

*

)

vii ABSTRAK

Distribusi Weibull merupakan salah satu distribusi probabilitas kontinu. Sama halnya dengan distribusi lainnya, distribusi Weibull pun dicirikan dengan Mean, Variansi dan Fungsi Pembangkit Momen. Kelebihan distribusi ini dibandingkan dengan distribusi lainnya adalah fleksibilitasnya, yaitu distribusi ini dapat berubah menjadi distribusi lain seperti distribusi eksponensial tergantung pada nilai parameter distribusi yang dipilih yaitu parameter skala dan parameter bentuk. Jika dilihat dari grafik distribusinya maka akan tampak sangat jelas fleksibilitas tersebut.

Salah satu aplikasi dari distribusi Weibull yaitu dapat digunakan dalam analisis data waktu hidup. Distribusi ini merupakan distribusi yang paling baik jika dibandingkan dengan distribusi lainnya seperti distribusi Eksponensial yang mengasumsikan tingkat kegagalan komponen konstan. Distribusi Weibull cukup mendeskripsikan waktu kegagalan dari komponen ketika tingkat kegagalan dari komponen tersebut meningkat atau menurun seiring dengan bertambahnya waktu. Selain dalam analisis data waktu hidup, distribusi ini juga dapat digunakan dalam pengendalian proses statistik. Oleh karena tidak semua data berdistribusi normal maka grafik pengendali Shewhart tidak dapat digunakan. Salah satu cara menyelesaikan masalah tersebut adalah data dianalisis dengan grafik pengendali Weibull dengan memanfaatkan kuantil-kuantil yaitu 0,00135, 0,5 dan 0,99865. Kuantil 0,00135 adalah kuantil bawah yang digunakan untuk membentuk Batas Pengendali Bawah, Garis Tengah adalah median dari data yaitu 0,5 yang menggantikan rata-rata dan untuk membentuk Batas Pengendali Atas digunakan kuantil atas yaitu 0,99865.

viii ABSTRACT

Weibull distribution is one of the continous probability density function. Similar to other distributions, Weibull distribution also characterized by mean, variance and moment generating function. The goodness of this distribution compared to other distributions is its flexibility, that is the distribution can be transformed into other distribution such as exponential distribution depends on the parameter selected. The flexibility obviously can be seen from the graph.

One of the applications of Weibull distribution is the distribution can be used in a lifetime data analysis. This distribution is the best distribution compared to other distributions such as Exponential distribution, which assumes a constant failure rate of component. Weibull distribution is sufficient to describe a failure of the component when the failure rate is increases or decreases in time. In addition to the lifetime data analysis, this distribution can also be used in statistical process control. Because not all of data follows normal distribution so Shewhart control chart can’t be applied. To solve this problem we can use Weibull control chart to analyze the data by using 0,00135, 0,5 and 0,99865 as quantiles. 0,00135 quantile is the lower quantile used to construct Lower Specification Limit, the Center Line is the median of data that is 0,5 which replaces mean and to construct Upper Specification Limit, upper quantile that is 0,99865 quantile is used.

ix

x

KATA PENGANTAR

Puji dan syukur penulis haturkan ke hadirat Tuhan Yang Maha Kuasa atas segala berkat dan penyertaanNya sehingga penulis dapat menyelesaikan skripsi ini dengan baik.

Skripsi yang berjudul “Distribusi Weibull: Sifat-Sifat dan Aplikasinya Dalam Analisis Data Waktu Hidup dan Pengendalian Mutu” ini adalah salah satu syarat untuk memperoleh gelar sarjana Matematika pada Fakultas Sains dan Teknologi. Dalam penulisan skripsi ini, tentunya penulis telah menerima bantuan baik secara moril maupun materil dari berbagai pihak. Oleh karena itu penulis ingin menyampaikan ucapan terima kasih kepada:

1. Bapak Ir. Ig. Aris Dwiatmoko,M.Sc selaku dosen pembimbing yang dengan penuh kesabaran telah memberikan bimbingan, nasihat dan arahan kepada penulis.

2. Ibu Lusia Krismiyati Budiasih, S.Si., M.Si. selaku Ketua Program Studi Matematika beserta Ibu Ch. Enny Murwaningtyas, S.Si., M.Si yang telah memberikan banyak bimbingan dalam hal akademik dan perkuliahan. 3. Seluruh bapak dan ibu dosen yang telah memberikan banyak ilmu

pengetahuan kepada penulis selama menjalani perkuliahan di Universitas Sanata Dharma.

4. Mas Susilo selaku laboran yang telah banyak membantu penulis dalam perkuliahan, terutama dalam penulisan skripsi ini.

5. Perpustakaan Universitas Sanata Dharma dan staf sekretariat Fakultas Sains dan Teknologi yang telah memberikan fasilitas dan kemudahan pembelajaran, serta administrasi bagi penulis selama masa perkuliahan. 6. Ayahanda yang penulis banggakan dan Ibundaku tercinta serta

xi

memberikan dukungan dan pengorbanan sehingga penulis dapat menyelesaikan studi dengan baik.

7. Kakak Oktovianus Koa atas perhatian dan kasih sayangnya serta telah memberikan dukungan, nasihat dan semangat kepada penulis dalam perkuliahan terlebih dalam penyusunan skripsi ini.

8. Teman-teman angkatan 2008 Program Studi Matematika yaitu Yudith, Hilary, Amel, Marcel, Fenny, Ethus, Moyo dan Widi yang telah memberikan dukungan dan semangat dalam perkuliahan terlebih dalam penyusunan skripsi ini.

9. Teman-teman Kos Putri Aulia: K Merlyn Kris, Kakatua, Awo, Sende, Elpir, Wiwi, Tere, Asri dan Tesa serta Pipot yang selalu memberikan semangat dan dukungan dalam perkuliahan dan dalam penyelesaian skripsi ini.

10.Teman-teman KKN XLII Kelompok 33: Ermen, Ulin, Susan, Adel, Arum, Abet dan Aben.

11.Semua pihak yang tidak dapat disebutkan satu persatu yang telah banyak memberikan bantuan, dorongan dan motivasi sehingga skripsi ini dapat terselesaikan.

Penulis menyadari bahwa skripsi ini masih jauh dari kesempurnaan, maka saran dan kritik yang konstruktif dari semua pihak sangat diharapkan demi penyempurnaan selanjutnya. Semoga skripsi ini dapat bermanfaat bagi semua pihak, khususnya bagi penulis dan para pembaca pada umumnya.

Yogyakarta, April 2012 Penulis

xii DAFTAR ISI

Halaman

HALAMAN JUDUL ... i

HALAMAN JUDUL DALAM BAHASA INGGRIS ... ii

HALAMAN PERSETUJUAN PEMBIMBING ... iii

HALAMAN PENGESAHAN ... iv

HALAMAN PERSEMBAHAN ... v

HALAMAN PERNYATAAN KEASLIAN KARYA ... vi

HALAMAN ABSTRAK ... vii

HALAMAN ABSTRACT ... viii

LEMBAR PERNYATAAN PERSETUJUAN PUBLIKASI... ix

KATA PENGANTAR ... x

DAFTAR ISI ... xii

DAFTAR TABEL ... xvii

DAFTAR GAMBAR ... xviii

BAB I PENDAHULUAN A.Latar Belakang Masalah... 1

B.Rumusan Masalah ... 4

C.Pembatasan Masalah ... 4

D.Tujuan Penulisan ... 5

xiii

F. Metode Penulisan ... 5

G.Sistematika Penulisan ... 6

BAB II LANDASAN TEORI A.Distribusi Probabilitas ... 10

1. Variabel Random ... 10

2. Fungsi Probabilitas ... 11

a. Distribusi Probabilitas Diskret ... 11

b. Distribusi Probabilitas Kontinu ... 12

3. Fungsi Distribusi Kumulatif ... 12

4. Karakteristik Distribusi Probabilitas... 13

a. Mean ... 13

b. Variansi ... 13

c. Momen ... 14

d. Fungsi Pembangkit Momen ... 14

B. Distribusi Eksponensial ... 15

1. Fungsi Probabilitas ... 15

2. Sifat-sifat Distribusi Eksponensial ... 15

xiv

b. Mean ... 16

c. Variansi ... 17

C. Distribusi Gamma ... 18

1. Fungsi Probabilitas ... 18

2. Sifat-sifat Distribusi Gamma ... 19

a. Fungsi Pembangkit Momen ... 19

b. Mean ... 20

c. Variansi ... 21

D. Teorema Nilai Rata-rata Untuk Turunan ... 23

E. Deret Taylor ... 25

F. Metode Maksimum Likelihood ... 29

G.Pengendalian Proses Statistik ... 31

1. Grafik Pengendali ... 32

2. Analisis Kemampuan Proses ... 34

BAB III DISTRIBUSI WEIBULL A. Fungsi Probabilitas ... 39

B. Grafik Distribusi ... 41

xv

D. Sifat-sifat Distribusi Weibull ... 45

1. Mean ... 45

2. Variansi ... 46

3. Fungsi Pembangkit Momen ... 48

E. Kertas Peluang Weibull ... 52

1. Grafik Probabilitas Weibull ... 52

2. Skala Dalam Kertas Peluang Weibull ... 55

a. Kertas Peluang Weibull Jenis Pertama (1 cycle ) ... 59

b. Kertas Peluang Weibull Jenis Kedua (2 cycle ) ... 60

c. Kertas Peluang Weibull Jenis Ketiga (3 cycle ) ... 61

F. Pendugaan Parameter Distribusi ... 61

BAB IV APLIKASI DISTRIBUSI WEIBULL A. Aplikasi Dalam Analisis Data Waktu Hidup ... 68

1. Reliabilitas ... 68

b. Sistem Seri ... 70

c. Sistem Paralel ... 73

2. Distribusi Waktu Kegagalan ... 76

xvi

B. Aplikasi Dalam Pengendalian Mutu ... 89

1. Grafik Pengendali ... 89

2. Perbandingan Kemampuan Proses ... 91

BAB V PENUTUP A. Kesimpulan ... 100

B. Saran ... 101

DAFTAR PUSTAKA ... 102

xvii

DAFTAR TABEL

xviii

DAFTAR GAMBAR

Halaman

Gambar 2.1 ... 23

Gambar 2.2 ... 41

Gambar 2.3 ... 33

Gambar 2.4 ... 37

Gambar 2.5 ... 37

Gambar 3.1 ... 42

Gambar 3.2 ... 43

Gambar 3.3 ... 58

Gambar 3.4 ... 59

Gambar 3.5 ... 60

Gambar 3.6 ... 61

Gambar 3.7 ... 62

Gambar 3.8 ... 66

Gambar 4.1 ... 71

Gambar 4.2 ... 74

Gambar 4.3 ... 81

Gambar 4.4 ... 86

Gambar 4.5 ... 87

Gambar 4.6 ... 88

Gambar 4.7 ... 88

xix

BAB I PENDAHULUAN

A. Latar Belakang Masalah

Distribusi Weibull dikembangkan antara tahun 1922 dan 1943. Distribusi ini menggunakan nama seorang ahli mesin dari Swedia, Waloddi Weibull. Hal ini disebabkan karena dialah yang mempublikasikan distribusi ini sehingga dikenal oleh dunia internasional. Awalnya distribusi ini digunakan oleh Rosin, Rammler dan Sperling pada tahun 1933 dalam proses penghancuran material padat. Selanjutnya pada tahun 1939 digunakan oleh Weibull untuk mengukur kekuatan material.

Lebih dari setengah abad distribusi Weibull telah menarik perhatian ahli statistik yang mempelajari teori dan metode dalam berbagai bidang aplikasi statistika. Ratusan bahkan ribuan dokumen menuliskan distribusi ini. Distribusi ini menjadi orientasi dari ahli statistika karena kelebihannya yakni dapat digunakan dalam berbagai bidang mulai dari da-ta uji hidup sampai dada-ta cuaca ada-tau observasi anda-tara lain dalam bidang ekonomi, hidrologi dan biologi.

Distribusi Weibull termasuk dalam keluarga dari distribusi eksponensial. Fungsi densitas dari distribusi eksponensial adalah

dengan adalah parameter distribusi. Distribusi eksponensial merupakan distribusi yang sering digunakan dalam analisis data waktu hidup. Pada umumnya data uji hidup tidak berdistribusi normal sehingga tidak dapat diselesaikan dengan prosedur statistik standar dalam menganalisis data. Dalam penerapan tersebut distribusi eksponensial diasumsikan sebagai distribusi dari waktu kegagalan. Misalkan adalah fungsi densitas dari waktu kegagalan komponen sehingga probabilitas komponen tersebut akan gagal antara sampai + adalah ∙ . Jadi probabilitas komponen tersebut akan gagal pada interval antara 0 sampat t adalah

=

dan fungsi reliabilitas yang memperlihatkan bahwa komponen tersebut bertahan sampai waktu t adalah = 1 −

= 1 − #

Karena distribusi dari waktu kegagalan diasumsikan berdistribusi Eksponensial maka = 1 − # $%

= 1 − 1 − $%

= $

%

dengan adalah tingkat kegagalan dan adalah lamanya komponen tersebut bertahan.

padahal dalam banyak kasus tingkat kegagalan komponen tidak selalu konstan (Johnson, 2005). Dalam beberapa kasus, waktu kegagalan komponen juga mungkin akan sangat panjang sepanjang periode pengujian. Oleh karena itu model eksponensial tidak dapat digunakan, dan sebagai solusi untuk masalah tingkat kegagalan komponen yang tidak konstan digunakan distribusi Weibull.

Secara umum fungsi densitas dari distribusi Weibull adalah

= {

&' _, ( ) * (, + ,+- ,& ,'

(1.1)

Dapat dilihat bahwa jika pada persamaan (1.1) = 1 maka fungsi distribusi di atas menjadi fungsi eksponensial dengan = .. Salah satu kelebihan dari distribusi Weibull adalah dapat digunakan jika tingkat kegagalannya menurun atau meningkat sesuai dengan peningkatan waktu. Sesuai dengan uraian di atas maka penulis ingin mempelajari lebih jauh tentang distribusi Weibull khususnya sifat - sifat dan aplikasinya dalam analisis data waktu hidup (lifetime data) dan pengendalian mutu.

Grafik pengendali yang biasanya digunakan dalam praktik didasarkan pada analisis distribusi normal yaitu dengan rata-rata Shewhart dan kisaran grafik pengendali 3 (standar deviasi). Namun demikian σ tidak semua data berdistribusi normal. Jika data tak berdistribusi normal dan tetap dianalisis dengan grafik pengendali tersebut dengan mengasumsikan bahwa data berdistribusi normal maka error yang besar akan terjadi (Samanta, 2004).

Dalam skripsi ini akan dibahas salah satu distribusi yang memiliki sifat lebih fleksibel yaitu distribusi Weibull. Aplikasi distribusi Weibull yang dibahas adalah grafik pengendali dan analisis data waktu hidup.

B. Rumusan Masalah

Adapun rumusan masalah dalam tulisan ini adalah sebagai berikut : 1. Apa saja sifat – sifat dari distribusi Weibull?

2. Bagaimana aplikasi dari distribusi Weibull dalam analisis data waktu hidup dan pengendalian mutu?

C. Pembatasan Masalah

Adapun beberapa hal yang dibatasi penulis dalam tulisan ini adalah sebagai berikut :

2. Pada mengaplikasikan distribusi Weibull dalam pengendalian mutu, penulis hanya menganalisis grafik pengendali.

3. Tidak semua teorema dalam bidang kalkulus yang digunakan dalam skripsi ini dibuktikan.

4. Dalam mengestimasi parameter distribusi, penulis tidak menjelaskan lebih rinci tentang metode Newton-Raphson.

D. Tujuan Penulisan

Tujuan dari penulisan ini adalah untuk mengetahui sifat-sifat dari distribusi Weibull serta aplikasinya dalam dalam analisis data waktu hidup dan pengendalian mutu.

E. Manfaat Penulisan

Manfaat yang akan diperoleh setelah mempelajari topik ini adalah dapat memahami sifat-sifat distribusi Weibull serta dapat mengaplikasikannya dalam analisis data waktu hidup dan pengendalian mutu.

F. Metode Penulisan

G. Sistematika Penulisan BAB I PENDAHULUAN A. Latar Belakang Masalah B. Rumusan Masalah C. Pembatasan Masalah D. Tujuan Penulisan E. Manfaat Penulisan F. Metode Penulisan G. Sistematika Penulisan BAB II LANDASAN TEORI A. Distribusi Probabilitas

1. Variabel Random 2. Fungsi Probabilitas

a. Distribusi Probabilitas Diskret b. Distribusi Probabilitas Kontinu 3. Fungsi Distribusi Kumulatif

4. Karakteristik Distribusi Probabilitas a. Mean

b. Variansi c. Momen

d. Fungsi Pembangkit Momen B. Distribusi Eksponensial

2. Sifat-sifat Distribusi Eksponensial a. Fungsi Pembangkit Momen b. Mean

c. Variansi C. Distribusi Gamma

1. Fungsi Probabilitas

2. Sifat-sifat Distribusi Gamma a. Fungsi Pembangkit Momen b. Mean

c. Variansi

D. Teorema Nilai Rata-rata Untuk Turunan E. Deret Taylor

F. Metode Maksimum Likelihood G. Pengendalian Proses Statistik

1. Grafik Pengendali

2. Analisis Kemampuan Proses

BAB III DISTRIBUSI WEIBULL A. Fungsi Probabilitas

B. Grafik Distribusi

C. Fungsi Distribusi Kumulatif D. Sifat-sifat Distribusi Weibull

2. Variansi

3. Fungsi Pembangkit Momen E. Kertas Peluang Weibull

1. Grafik Probabilitas Weibull

2. Skala Dalam Kertas Peluang Weibull

a. Kertas peluang Weibull Jenis Pertama (1 cycle log₂ ) b. Kertas peluang Weibull Jenis Kedua (2 cycle log₂ ) c. Kertas peluang Weibull Jenis Ketiga (3 cycle log₂ ) F. Pendugaan Parameter Distribusi

BAB IV APLIKASI DISTRIBUSI WEIBULL A. Aplikasi Dalam Analisis Data Waktu Hidup

1. Reliabilitas a. Sistem Seri b. Sistem Paralel

2. Distribusi Waktu Kegagalan 3. Model Waktu Hidup Weibull B. Aplikasi Dalam Pengendalian Mutu

1. Grafik Pengendali

2. Perbandingan Kemampuan Proses BAB V PENUTUP

BAB II

LANDASAN TEORI

A. Distribusi Probabilitas

1. Variabel Random

Definisi 2.1

Variabel random adalah fungsi bernilai real yang didefinisikan pada

ruang sampel. Variabel random biasanya dinotasikan dengan huruf

kapital seperti X, Y, Z dan sebagainya. Sedangkan huruf kecil misalnya

x, y dan z menyatakan nilai tertentu dari X, Y dan Z.

Contoh 2.1

Dalam percobaan pelemparan dua koin akan diamati hasilnya.

Misalkan X menunjukkan banyaknya angka yang muncul. Tentukan

probabilitas dari masing-masing nilai X.

Penyelesaian

Misalkan A dan G adalah lambang munculnya angka dan gambar

secara berturut-turut; Ruang sampel dari percobaan di atas adalah

= GG, AG, GA, AA . Oleh karena X menunjukkan banyaknya angka

yang muncul maka nilai dari X bergantung pada banyaknya angka

yang muncul. Berdasarkan hasil percobaan di atas maka terdapat 3

Selanjutnya dapat ditentukan probabilitas hasil yang mungkin.

Berdasarkan contoh di atas terdapat empat kejadian yaitu

GG : kejadian muncul gambar semua pada pelemparan dua koin.

AG : kejadian muncul angka pada pelemparan pertama dan gambar

pada pelemparan kedua.

GA : kejadian muncul gambar pada pelemparan pertama dan angka

pada pelemparan kedua.

AA : kejadian muncul angka semua pada pelemparan dua koin.

Oleh karena X adalah variabel random yang menunjukkan banyaknya

angka yang muncul maka dapat dicari hubungan antara variabel

random dan kejadian dalam tabel sebagai berikut.

Tabel 2.1

Tabel hubungan antara variabel random dengan kejadian

Hasil

P 1 = 0,5. Probabilitas dari kemungkinan nilai yang berbeda dari X

P(x) memberikan kemungkinan pada tiap nilai x yang mungkin dari

sebuah variabel random X.

Variabel random dibagi menjadi dua macam yaitu variabel

random diskret dan varibel random kontinu.

Definisi 2.2

Variabel random dikatakan diskret jika nilai-nilainya membentuk

himpunan berhingga (finite) atau tak berhingga terbilang (Countably

infinite). Variabel random yang tidak memenuhi definisi di atas

disebut variabel random kontinu.

2. Fungsi Probabilitas

Fungsi distribusi probabilitas atau sering disebut fungsi probabilitas

dibagi menjadi dua yaitu:

a. Distribusi Probabilitas Diskret

Definisi 2.3

Fungsi probabilitas variabel random diskret X adalah fungsi yang

memetakan himpunan nilai variabel random diskret X ke

himpunan bilangan real yang merupakan nilai probabilitasnya.

Fungsi p(x) disebut fungsi probabilitas diskret bila memenuhi

syarat:

1 0 ≤ ≤ 1

Contoh dari distribusi probabilitas diskret yaitu distribusi

Binomial, distribusi Seragam, distribusi Poisson, distribusi

Bernoulli, dan distribusi Hipergeometrik.

b. Distribusi Probabilitas Kontinu

Definisi 2.4

Fungsi probabilitas variabel random kontinu X adalah fungsi

yang memetakan himpunan nilai variabel random kontinu X ke

himpunan bilangan real yang merupakan nilai probabilitasnya.

Fungsi f(x) disebut fungsi probabilitas variabel random kontinu X

bila memenuhi syarat:

1 ≥ 0

2 = 1

Contohnya distribusi Normal, distribusi Exponential, distribusi

Gamma, distribusi Chi-Square dan distribusi Weibull.

3. Fungsi Distribusi Kumulatif

Definisi 2.5

Fungsi distribusi kumulatif dari variabel random diskret dan kontinu

didefinisikan sebagai berikut.

= ≤ =

! "

∀#$%

, &'() diskret

1 2 2 , bila kontinu

4. Karakteritik Distribusi Probabilitas

Adapun karakteristik dari sebuah distribusi probabilitas adalah sebagai

berikut:

a. Mean

Definisi 2.6

Mean atau ekspektasi matematik (expected value) dari variabel

random diskret dan kontinu adalah sebagai berikut.

: =

! "

∀%

, bila diskret

1 , bila kontinu

9

b. Variansi

Definisi 2.7

Jika X suatu variabel random, maka variansi dari X, ditulis

Var(X) atau V(X), didefinisikan

Var(X) = E(X – E(X))2

Teorema 2.8

Var(X) = E(X2) – (E(X))2

Bukti:

Var(X) = E(X – E(X))2

= E(X2) – 2E(X)E(X) + (E(X))2

= E(X2) – (E(X))2 ∎

c. Momen

Definisi 2.9

Nilai harapan dari < yang menyatakan momen nol ke-r dari

variabel random X adalah

=< = : < (2.1)

Secara umum, r adalah sebarang bilangan real, tetapi untuk

banyak kasus, r adalah bilangan bulat non-negatif.

d. Fungsi Pembangkit Momen

Definisi 2.10

Fungsi pembangkit momen (moment generating function, MGF)

dari X, ditulis MX(t) dari variabel random diskret dan kontinu

didefinisikan sebagai berikut.

>? 2 = : @A?

=

! " @A

∀%

, bila diskret

1 @A _{, bila kontinu}

B. Distribusi Eksponensial

Pada subbab ini akan sedikit dibahas tentang distribusi Eksponensial.

Hal-hal yang berkaitan dengan distribusi Eksponensial antara lain sebagai

berikut.

1. Fungsi Probabilitas

Definisi 2.11

Variabel random X dikatakan berdistribusi Eksponensial apabila

fungsi probabilitasnya sebagai berikut

=

_{B ,CDEFGHHIF}JKLM% , NB,JNB (2.2)

2. Sifat-sifat Distribusi Eksponensial

Sifat-sifat dari distribusi eksponensial antara lain mean, variansi dan

fungsi pembangkit momen. Untuk mendapatkan mean dan variansi

terlebih dahulu akan dicari Fungsi Pembangkit Momen sebagai

berikut.

a. Fungsi Pembangkit Momen

Berdasarkan Definisi 2.10 maka Fungsi pembangkit Momen dari

= O 1 @A _@ J B

= O 1 @ J A B

= O P_{− O − 2 R}@ J A

B

= O P@_{2 − O R}J A

B

= O SB T

A JU

= _{O − 2}O

Jadi, Fungsi Pembangkit Momen dari distribusi eksponensial

adalah

>_? 2 =_{O − 2}O

b. Mean

Mean dapat dicari dengan mencari turunan pertama dari Fungsi

Pembangkit Momen kemudian diaplikasikan pada saat t = 0.

: _{= 2VO − 2W}O

= − X O −1_{O − 2 Y}Z

= _{O − 2}O _Y

Pada s aat t = 0 maka : =T

J adi, m ean dari dist ri busi Eks ponensi al adal ah : = T

J.

c. Vari ansi

Berdasarkan Teorema 2.8, variansi dari sebuah fungsi densitas

adalah sebagai berikut.

[)\ = : Y _{− :} Y

Dari definisi di atas maka nilai dari : Y dan : Y adalah

: Y

= 2X O − 2O YZ

= −O ∙ 2 O − 2 ∙ −1_{O − 2 ^}

=2O O − 2_{O − 2 ^}

Pada saat t = 0 maka : Y = YJ_

J`

=_O2_Y

Nilai dari : 2 _{adalah sebagai berikut.}

: 2 = S1

JU

2

= _O1₂

[)\ = : Y _{− :} Y

=_O1_Y

Jadi, variansi dari distribusi eksponensial adalah

[)\ = _O1_Y

C. Distribusi Gamma

Pada subbab ini akan sedikit dibahas tentang distribusi Gamma. Hal-hal

yang berkaitan dengan distribusi Gamma antara lain sebagai berikut.

1. Fungsi Probabilitas

Definisi 2.12

Variabel random X dikatakan berdistribusi Gamma jika dan hanya jika

fungsi probabilitasnya sebagai berikut

=_ab1 _c b T_{@ d, > 0, a > 0, c > 0}

dimana c merupakan nilai dari fungsi gamma yang didefinisikan

sebagai berikut

Definisi 2.13

Definisi fungsi gamma yaitu

Fungsi gamma ini sangat bermanfaat terutama dalam membantu

mencari mean, variansi dan fungsi pembangkit momen yang

melibatkan integral yang rumit.

2. Sifat-sifat Distribusi Gamma

Sama halnya dengan distribusi Eksponensial, distribusi Gamma pun

mempunyai sifat-sifat antara lain mean, variansi dan fungsi

pembangkit momen yaitu sebagai berikut

a. Fungsi Pembangkit Momen

Berdasarkan Definisi 2.10 maka fungsi pembangkit momen dari

distribusi Gamma adalah sebagai berikut.

>? 2 = : @A?

= 1 @A B

= 1 @A 1

ab _c b T@ d B

= 1_ab1 _c b T_{@ STd AU} B

= 1_ab1 _c b T_{@ T Ad d} B

= _{1 − 2a}1 _b1S1 − 2aa U

b

c b T@ ST Add U

B

Menggunakan fakta bahwa

1 &₎f f T_@ g B

= 1 , ∀) > 0, & > 0

maka, fungsi pembangkit momen dari distribusi gamma adalah

>? 2 = _{1 − 2a}1 _b

b. Mean

Berdasarkan Definisi 2.6 maka mean dari distribusi Gamma

adalah sebagai berikut

: = 1

B

= 1 ab _c b T@ d B

=_ab1 _{c 1} b_{@ d} B

Misalkan h =

d maka = ah

= a h

maka : = T

= _ab1 _{c 1 a}b_hb_@ j _{a h} B

= a_{c 1 h}b_@ j _h B

Berdasarkan Definisi 2.13, maka

: = a_{c Γ c + 1}

= a_{c c Γ c}

= ca

c. Variansi

Berdasarkan Teorema 2.8 maka variansi dari sebuah fungsi

densitas adalah sebagai berikut

Var = : Y _{− :} Y

Dari definisi di atas maka nilai dari : Y dan : Y adalah

: Y _{= 1} Y

B

= 1_ab Y_c b T_{@ d} B

=_ab1 _{c 1} bnT_{@ d} B

Misalkan h =

d maka = ah

maka : Y = T

di _{b B} ah bnT@ j a h

= _ab1 _{c 1 a}bnT_hbnT_@ j _{a h} B

= _aa_bbnY_{c 1 h}bnT_@ j _h B

= a_{c 1 h}Y bnT_@ j _h B

Berdasarkan Definisi 2.13, maka

: Y ₌ aY

c Γ c + 2

= a_{c c + 1 Γ c + 1}Y

= a_{c c + 1 c Γ c}Y

= c c + 1 aY _2.3

Nilai dari : Y adalah sebagai berikut.

: Y _{= ca} Y

= cYaY 2.4

Berdasarkan persamaan (2.3) dan(2.4) di atas maka

Var = : Y _{− :} Y

= rc c + 1 aY_{s − c}Y_aY

= caY

Jadi, Var = caY

D. Teorema Nilai Rata-rata Untuk Turunan

Teorema 2.15: Jika f kontinu pada selang tertutup r), &s

dan terdiferensialkan pada titik-titik dalam dari ), & maka terdapat

paling sedikit satu bilangan t dalam ), & dengan

& − )

& − ) = t

atau sama dengan

& − ) = t & − )

Gambar 2.1 Skema dari fungsi u = − v

Bukti:

Pembuktian teorema di atas didasarkan pada analisis seksama dari fungsi

u = − v , yang diperkenalkan pada Gambar 2.1 Pada gambar

&, & . Oleh karena garis ini mempunyai kemiringan rx g x f s

g f dan

melalui titik ), ) , bentuk kemiringan titik untuk persamaannya

adalah

v − ) = & − )_{& − )} − )

Persamaan ini kemudian menghasilkan rumus untuk u , yaitu:

u = − v = − ) − & − )_{& − )} − )

Jelas bahwa u & = u ) = 0 dan untuk dalam ), &

u = − & − )_{& − )}

Sampailah pada suatu pengamatan penting, jika diketahui bahwa terdapat

suatu bilangan t dalam ), & yang memenuhi u t = 0, maka bukti akan

selesai. Persamaan terakhir mengatakan bahwa

0 = − & − )_{& − )}

yang setara dengan kesimpulan dari teorema tersebut.

Untuk melihat bahwa u t = 0 untuk suatu t dalam ), & ,

alasannya adalah sebagai berikut. Jelas bahwa u kontinu pada r), &s karena

merupakan selisih dua fungsi kontinu. Jadi menurut Teorema Keberadaan

Maks-Min, u harus mencapai baik nilai maksimum maupun nilai minimum

pada r), &s. Jika kedua nilai ini kebetulan adalah 0, maka u secara

identik adalah 0 pada r), &s, akibatnya u = 0 untuk semua dalam

Jika satu nilai maksimum atau nilai minimum berlainan dengan 0,

maka nilai tersebut dicapai pada sebuah titik dalam t, karena u ) =

u & = 0. Sekarang u mempunyai turunan disetiap titik dari ), & ,

sehingga dengan Teorema Titik Kritis, u t = 0. ∎

E. Deret Taylor

Sebuah deret disebut deret Taylor jika deret tersebut dapat

direpresentasikan dalam x-a. Pertanyaan yang berkembang dalam deret

pangkat adalah: Jika diketahui sebuah fungsi f misalnya fungsi sin x,

dapatkah fungsi tersebut direpresentasikan dalam x-a? Dua teorema

berikut akan menjawab pertanyaan tersebut.

Teorema 2.16: Rumus Taylor dengan Suku Sisa (Ekspansi Taylor)

Misalkan f adalah fungsi dimana turunan ke-(n+1)-nya

ynT _{ada untuk setiap x pada selang terbuka I yang mengandung a.}

Jadi, untuk setiap x dalam I,

= ) + ) − ) + _2!) − ) Y_{+ ⋯}

+x|_y!f − ) y_{+ }y}

dimana sisanya (atau kesalahannya) }_y dinyatakan dengan rumus

}y =

ynT _t

dengan c adalah titik diantara x dan a.

Bukti:

Untuk membuktikan teorema tersebut terlebih dahulu akan didefinisikan

fungsi }_y di I dengan

}y = − ) − ) − ) − _2!) − ) Y−

•

3! − ) •

− ⋯ −x_y!| − ) y

Kemudian anggap x dan a sebagai konstanta dan definisikan fungsi baru g

di I dengan

v 2 = − 2 − 2 − 2 − 2 _2!− 2 Y− • 2_3! − 2 •

− ⋯ − y 2 _~!− 2 y − }y − 2 ynT

− 2 ynT

Jelaslah bahwa v = 0 (ingat, x dianggap tetap) dan

v ) = − ) − ) − ) − ) _2!− ) Y− • )_3! − ) •

− ⋯ − x| f_y! f|− }y f |€• f|€•

= }_y − }_y

= 0

Karena a dan x adalah titik-titik di I dengan sifat bahwa v ) = v = 0

maka Teorema Nilai Rata-rata untuk Turunan dapat diterapkan. Dengan

v t = 0. Untuk mendapatkan turunan g, harus diterapkan aturan

perkalian bilangan berulang kali.

v 2 = 0 − 2 − r 2 −1 + − 2 2 s

−_{2! ‚ 2 2 − 2 −1 + − 2}1 Y • _{2 ƒ}

−_{3! ‚}1 • _{2 3 − 2} Y _{−1 + − 2} • ^ _{2 ƒ − ⋯}

−_{~! ‚}1 y _{2 ~ − 2} y T _{−1 + − 2} y ynT _{2 ƒ}

− }y ~ + 1 − 2

y ₋₁

− ) ynT

= −

_{~! − 2}

1

y ynT

_{2 + ~ + 1 }}

y

− 2

y

− )

ynT

Jadi, berdasarkan Teorema Nilai Rata-rata untuk Turunan, terdapat suatu

nilai c di antara x dan a sedemikan sehingga

0 = v t = −

_y!T

− t

y ynT

_{2 + ~ + 1 }}

y „

| f |ۥ

Ini akan menuntun pada

T

y!

− t

y ynT

t = ~ + 1 }

y

„ |

f |ۥ

Teorema 2.17: Teorema Taylor

Misalkan fungsi f yang memiliki turunan ke-berapapun pada suatu selang

) − \, ) + \ .

Deret Taylor

) + ) − ) + _2!) − ) Y₊ • )

3! − ) • + ⋯

mempresentasikan fungsi f pada selang ) − \, ) + \ jika dan hanya jika

lim

y→ }y = 0

dimana }_y adalah suku sisa dalam Rumus Taylor,

}y =

ynT _t

~ + 1 ! − ) ynT

dan c adalah titik pada ) − \, ) + \ .

Bukti:

Untuk membuktikan teorema di atas hanya dibutuhkan Teorema 2.16.

Deret pada Teorema 2.16 adalah sebagai berikut

= ) + ) − ) + _2!) − ) Y_{+ ⋯}

+x|_y!f − ) y_{+ }y}

) + ) − ) + _2!) − ) Y₊ • )

F. Metode Maksimum Likelihood

Salah satu metode penting yang dapat digunakan untuk mencari

penduga parameter selain dengan metode kuadrat terkecil adalah metode

maksimum likelihood. Metode ini diperkenalkan oleh R. A. Fisher pada

tahun 1922. Secara umum prinsip dari metode maksimum likelihood

adalah sebagai berikut. Misalkan adalah variabel random dengan

parameter ˆ yang tidak diketahui. Diambil ~ sampel random yaitu

T, Y, … , y dengan nilai sampelnya adalah T, Y, … , y. Fungsi densitas

bersama dari _T, _Y, … , _y adalah _T, _Y, … , _y; ˆ . Fungsi likelihood

dari sampel tersebut adalah

‹ ˆ; T, Y, … , y = T, Y, … , y; ˆ .

‹ ˆ; T, Y, … , y disingkat menjadi ‹ ˆ . Jika T, Y, … , y merupakan

variabel random berdistribusi diskret dengan fungsi densitas Œ , ˆ maka

fungsi likelihoodnya adalah

‹ ˆ = T = T, … , y = y

= • Ž = Ž y

= • Ž; ˆ y

Ž‡T

Dan dalam kasus kontinu, jika fungsi densitasnya adalah , ˆ maka

fungsi likelihoodnya adalah

‹ ˆ = •yŽ‡T Ž; ˆ (2.7)

Tujuan dari metode maksimum likelihood adalah menentukan penduga

yang memaksimalkan fungsi likelihood. Penduga ini disebut penduga

kemungkinan maksimum. Beberapa langkah yang digunakan untuk

mendapatkan parameter dengan metode maksimum likelihood adalah

sebagai berikut:

1. Mendefinisikan fungsi likelihood, ‹ ˆ

2. Mengoperasikan fungsi likelihood dengan logaritma natural (ln)

3. Mendiferensialkan ln ‹ ˆ terhadap ˆ dan menyamakan derivatifnya

dengan nol.

4. Menyelesaikan derivatif tersebut dalam parameter ˆ dan akan

diperoleh ˆ•.

Berikut ini adalah alasan mengapa fungsi likelihood dioperasikan dengan

logaritma natural (ln). Seperti diketahui bahwa fungsi logaritma natural

adalah fungsi naik sehingga jika _T < _Y maka _T < _Y . Ini berarti

bahwa pada titik tertentu dimana logaritma natural dari fungsi likelihood

mencapai maksimum maka pada titik yang sama pula fungsi likelihood

G. Pengendalian Proses Statistik

Dalam banyak proses produksi, bagaimanapun baiknya dirancang,

akan selalu ada variabilitas hasil produksi karena adanya gangguan atau

sebab-sebab kecil yang pada dasarnya tidak terkendali (untuk selanjutnya

disebut variabilitas dasar). Apabila gangguan dasar suatu proses relatif

kecil maka biasanya dipandang sebagai tingkat yang dapat diterima dari

peranan proses. Dalam kerangka pengendalian kualitas statistik, suatu

proses yang bekerja hanya dengan adanya variasi dari sebab-sebab tak

terduga dikatakan ada dalam pengendalian statistik.

Dalam proses produksi dikenal 3 sumber antara lain: mesin yang

dipasang dengan tidak wajar, kesalahan operator, dan/atau bahan baku

yang cacat. Variabilitas seperti ini umumnya besar apabila dibandingkan

dengan variabilitas dasar dan biasanya merupakan tingkat yang tidak dapat

diterima dari peranan proses. Sumber-sumber variabilitas yang bukan

bagian dari pola sebab tak terduga dinamakan dengan “sebab-sebab

terduga”. Suatu proses yang bekerja dengan adanya sebab-sebab terduga

dikatakan tidak terkendali.

Dalam buku pedoman Western Electric (1956) yang dikutip oleh

Montgomery (2009) mengusulkan sekumpulan aturan pengambilan

keputusan untuk penyidikan pola tak random pada grafik pengendali.

Khususnya, buku tersebut mengusulkan penyimpulan bahwa proses tak

terkendali apabila salah satu:

2. Dua dari tiga titik berurutan jatuh di luar batas peringatan 2-sigma.

3. Empat dari lima titik yang berurutan jatuh pada jarak 1-sigma atau

lebih dari garis tengah.

4. Delapan titik yang berurutan jatuh pada satu sisi dari garis tengah.

Beberapa hal yang berhubungan dengan pengendalian proses

statistik adalah sebagai berikut.

1. Grafik Pengendali

Untuk mengawasi agar proses agar tetap stabil digunakan

beberapa alat untuk mengendalikannya, antara lain histogram, grafik

pareto, dan grafik pengendali. Grafik pengendali (control charts)

adalah yang paling terkenal yang digunakan dalam pengendalian

mutu untuk mengontrol suatu proses berulang. Grafik pengendali

sangat berguna dalam menetapkan standar pencapaian dari sebuah

proses, membantu mencapai standar tersebut dan mempertimbangkan

standar mana yang sudah tercapai.

Secara umum, langkah-langkah utama dalam membuat grafik

pengendali adalah menentukan parameter dari proses yang diinginkan,

memilih statistik uji yang sesuai misalkan w, membuat Garis Tengah

(GT), Batas Pengendali Atas (BPA) dan Batas Pengendali Bawah

(BPB). Untuk lebih jelasnya dapat dilihat pada Gambar 2.2 di bawah

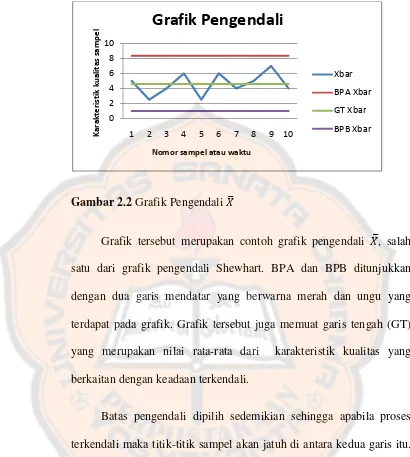
Gambar 2.2 Grafik Pengendali ’

Grafik tersebut merupakan contoh grafik pengendali ’, salah

satu dari grafik pengendali Shewhart. BPA dan BPB ditunjukkan

dengan dua garis mendatar yang berwarna merah dan ungu yang

terdapat pada grafik. Grafik tersebut juga memuat garis tengah (GT)

yang merupakan nilai rata-rata dari karakteristik kualitas yang

berkaitan dengan keadaan terkendali.

Batas pengendali dipilih sedemikian sehingga apabila proses

terkendali maka titik-titik sampel akan jatuh di antara kedua garis itu.

Apabila semua titik-titik berada di dalam batas-batas pengendali maka

proses dianggap terkendali dan tidak perlu diadakan tindakan tertentu.

Namun jika ada titik yang berada di luar batas pengendali maka

diperlukan tindakan penyelidikan dan perbaikan untuk menyingkirkan

penyebab proses tak terkendali tersebut. Merupakan kebiasaan untuk

menghubungkan titik-titik sampel di dalam grafik dengan segmen

titik-titik itu tersusun menurut waktu. Apabila proses itu terkendali

maka semua titik yang digambar harus mempunyai pola yang pada

dasarnya random (Montgomery, 2008).

2. Analisis Kemampuan Proses

Teknik statistik dapat berguna sepanjang putaran produk,

termasuk aktivitas pengembangan sebelum produksi, untuk

kuantifikasi variabilitas proses, analisis variabilitas relatif terhadap

persyaratan atau spesifikasi produk, dan untuk membantu

pengembangan dan produksi dalam menghilangkan atau mengurangi

banyaknya variabilitas ini. Aktivitas umum ini dinamakan analisis

kemampuan proses.

Sudah menjadi kebiasaan mengambil penyebaran 6-sigma

dalam distribusi karakteristik kualitas produk sebagai ukuran

kemampuan proses. Dalam proses produksi, produk atau hasil yang

diperoleh dapat digunakan untuk mengukur mean proses dan batas

toleransi alami. Batas toleransi alami dideskripsikan sebagai jarak 3

standar deviasi dari mean proses. Deskripsi ini juga mengarah pada

batas 3 sigma. Batas toleransi ini dibedakan menjadi 2 yaitu Batas

Toleransi Alami Atas (BTAA) yang jatuh pada = + 3“ dan Batas

Toleransi Alami Bawah (BTAB) yang jatuh pada = − 3“. Gambar

dibawah ini menunjukkan proses karakteristik kualitas yang

Gambar 2.3 Proses Karakteristik Kualitas Dengan Distribusi Normal

Bagi distribusi normal, batas toleransi alami meliputi 99,73% dari

sampel itu, atau dengan cara lain, hanya 0,27% dari hasil proses akan

jatuh diluar batas toleransi alami. Dua hal yang harus diingat yaitu:

a. 0,27% diluar toleransi alami kedengarannya kecil, namun bila

jumlah produksi satu juta berarti nilai ini bersesuaian dengan 2700

benda tak sesuai per juta.

b. Jika distribusi hasil proses tidak normal, maka persen hasil yang

jatuh di luar = ± 3“ dapat berbeda cukup besar dengan 0,27%.

Analisis kemampuan proses dapat didefinisikan sebagai suatu

studi keteknikan guna menaksir kemampuan proses. Taksiran

kemampuan proses mungkin dalam bentuk distribusi probabilitas yang

mempunyai spesifikasi bentuk, nilai tengah (mean) dan penyebaran

berdistribusi normal dengan mean = = 1,0 cm dan standar deviasi

“ = 0,001 cm.

Ada beberapa teknik yang dapat digunakan dalam analisis

kemampuan proses yakni dengan histogram atau grafik probabilitas,

grafik pengendali, dan rancangan percobaan. Pada skripsi ini hanya

akan dibahas analisis kemampuan proses dengan histogram atau grafik

probabilitas.

Distribusi frekuensi dapat berguna dalam menaksir kemampuan

proses. Paling sedikit 50 sampai 100 (atau lebih) observasi harus

tersedia supaya histogram agak stabil sehingga dapat diperoleh

taksiran kemampuan proses yang cukup dapat dipercaya. Keunggulan

pendekatan distribusi ferkuensi untuk menaksir kemampuan proses

adalah bahwa cara itu memberikan kesan visual dan segera tentang

penampilan proses. Cara itu juga dapat menunjukkan dengan segera

apa sebab penampilan proses jelek. Misalkan Gambar 2.4

menunjukkan suatu proses dengan kemampuan yang cukup, tetapi

sasaran proses terletak sangat jelek, sedangkan Gambar 2.5

menunjukkan suatu proses dengan kemampuan kurang sebagai hasil

variabilitas yang besar.

Cara yang baik untuk menyatakan kemampuan proses adalah

melalui Perbandingan Kemampuan Proses (PKP). PKP ini dihitung

dengan memanfaatkan batas spesifikasi yaitu batas yang ditetapkan

dapat diterima atau tidak. Batas spesifikasi ini biasanya digunakan

untuk memenuhi keinginan pelanggan atas produk yang dihasilkan.

Jika data berdistribusi normal atau diasumsikan normal maka

Perbandingan Kemampuan Prosesnya adalah

PKP =BSA − BSB_6“

dengan BSA dan BSB masing-masing adalah Batas Spesifikasi Atas

dan Batas Spesifikasi Bawah. Batas Spesifikasi Atas adalah batas

terbesar dimana suatu proses dapat diterima sedangkan Batas

Spesifikasi Bawah adalah batas terkecil dimana suatu proses dapat

diterima. Persamaan di atas digunakan untuk menyatakan spesifikasi

dua sisi. Untuk spesifikasi satu sisi, PKPnya adalah sebagai berikut

PKP =™š› œ_•• (hanya spesifikasi atas)

atau

PKP =œ ™š™_•• (hanya spesifikasi bawah)

Gambar 2.5 Kemampuan Proses Jelek karena Variabilitas Proses

BAB III

DISTRIBUSI WEIBULL

A. Fungsi Probabilitas

Definisi 3.1

Variabel random X dikatakan berdistribusi Weibull apabila fungsi

probabilitasnya sebagai berikut:

= {

_, , , ,

(3.1)

dimana dan adalah parameter distribusi Weibull.

Fungsi distribusi Weibull di atas merupakan fungsi distribusi

Weibull dengan dua parameter yaitu parameter skala dan parameter

bentuk . Definisi dari masing-masing parameter adalah sebagai berikut.

Definisi 3.2 _{Parameter Skala}

Misalkan { ∙ ; " , " > 0% adalah keluarga dari fungsi densitas dengan parameter ". Parameter " didefinisikan sebagai parameter skala jika dan hanya jika fungsi densitas ; " dapat ditulis sebagai 1 "' ℎ '" untuk setiap fungsi densitas ℎ ∙ .

Contoh 3.1

Diberikan beberapa contoh dari parameter skala sebagai berikut.Pada

; ) = 1 )' *+ ,' _{, ) adalah parameter skala. Pada fungsi distribusi} normal berikut

; - =_/012. exp 6−.₀8₂90:, - disebut parameter skala.

Berdasarkan fungsi distribusi Weibull pada persamaan (3.1),

menunjukkan parameter skala yaitu parameter yang menentukan skala atau

penyebaran statistik dari distribusi probabilitas. Jika parameter skala besar

maka distribusi akan menyebar, sedangkan jika parameter skala kecil maka

distribusi akan lebih terkonsentrasi.

Definisi 3.3 _{Parameter Bentuk}

Parameter bentuk adalah parameter yang menunjukkan bentuk kurva

suatu distribusi.

Misalnya bentuk kurva condong ke kanan (skewness positif), bentuk kurva

condong ke kiri (skewness negatif) dan bentuk kurva yang menyerupai

distribusi normal. Selain dua parameter di atas, terdapat satu parameter

yang disebut sebagai parameter lokasi.

Definisi 3.4 _{Parameter Lokasi}

Misalkan ; ", ) adalah fungsi densitas dari variabel random ;. Parameter " adalah parameter lokasi jika dan hanya jika fungsi densitas

ℎ − ", ) untuk setiap fungsi ℎ ∙ ; ) dan ℎ ∙ ; ) tidak bergantung pada

".

Contoh 3.2

Berikut ini adalah contoh dari parameter lokasi. Pada fungsi distribusi

normal berikut

; <; - = 1

/2>-exp 6− 1

2 8 − <- 9

0

:

< disebut sebagai parameter lokasi.

B. Grafik Distribusi

Grafik dari distribusi Weibull sangat beragam. Dengan memilih

nilai-nilai parameter dan distribusi itu akan mempunyai berbagai macam bentuk. Jika parameter skala yang diubah-ubah dengan

menganggap bahwa parameter bentuk konstan maka akan diperoleh grafik

fungsi densitas dengan nilai > 1. Hal ini juga terjadi jika parameter yang diubah adalah parameter bentuk dengan menganggap bahwa

parameter skala konstan. Grafik di bawah ini adalah contoh grafik fungsi

Gambar 3.1 _G

Grafik distribusi Weibull untuk = 0BC, 1 dan

di atas tampak jelas bahwa dengan nilai yan

entuk grafik yang berbeda-beda pula. Pada sa

3.1) akan berubah menjadi persamaan (2.

ri distribusi eksponensial. Selain itu nilai

eibull akan lebih besar atau sama dengan 1 t

pa yang diubah.

arkan dengan menggunakan MATLAB, denga

hasil yang diperoleh adalah sebagai berikut

Gambar 3.2 _{Grafik distribusi Weibull untuk} = D,C _; = 1

Berikut ini akan ditunjukkan bahwa fungsi probabilitas Weibull memenuhi

sifat-sifat fungsi probabilitas berdasarkan Definisi 2.4_{. Selain nilai}

> 0, nilai FH G = 1.

FH G = FH +._*+ _G

Misalkan I =

GI = +._G

J G

H

= J +._*+ _G H

= J *+K_GI H

= 1

Jadi, nilai FH G = 1

C. Fungsi Distribusi Kumulatif

Berdasarkan Definisi 2.6 _{maka fungsi distribusi kumulatif dari distribusi}

Weibull adalah sebagai berikut:

N = J O GO

= J O

+.

_*

+ P

_GO

Misalkan I = O maka O = 8K9

GI = O +._GO

N = J *+K_GI

= L−*

+K

_M

= L−*

+ P

_Q

= −*

+

_{− −1}

= 1 − *

+

Jadi, fungsi distribusi kumulatif dari distribusi Weibull adalah

D. Sifat-sifat Distribusi Weibull

Beberapa sifat penting dari distribusi Weibull yaitu:

1. Mean

Salah satu konsep penting dalam teori probabilitas adalah tentang

ekspektasi atau sering disebut sebagai mean dari variabel random.

Pada bab ini secara khusus akan dibahas mengenai sifat-sifat dari

salah satu fungsi probabilitas kontinu yaitu fungsi distribusi Weibull.

Menurut Definisi 2.6 _{mean dari fungsi densitas di atas adalah sebagai}

R ; = J W*+K₈I₉._{X GI}

R ; = J `*+KI .

.a GI

R ; = . F b*+K I c GI

Berdasarkan Definisi 2.13 _{maka persamaan di atas dapat diubah}

menjadi

R ; = + 8.+ 19 (3.2)

2. Variansi

Dari fungsi densitas yang terdapat pada persamaan (3.1), maka

menurut Teorema 2.8 _{variansi dari distribusi Weibull adalah sebagai}

berikut.

Var ; = R ;0 _{− R ;} 0

Dari definisi di atas maka nilai dari R ;0 dan R ; 0 adalah

R ;0 _{= J} 0 +._*+ _G

R ;0 _{= J} g._*+ _G

Nilai dari R ; 0 adalah sebagai berikut.

R ; 0 _{= Y} +. _b1_{+ 1cZ}0

R ; 0 ₌ +l _{m 8}._{+ 19Q}0 _(3.4)

Dari persamaan (3.3) dan (3.4) maka

Var ; = R ;0 _{− R ;} 0

= +l 80+ 19 − +l m 8.+ 19Q0

= +0 n b2+ 1c − 6 b1+ 1c:0o

Jadi, Var ; = +

l

p 80+ 19 − m 8.+ 19Q0q

3. Fungsi Pembangkit Momen

Dengan mereduksi variabel Weibull pada persamaan (2.1) akan

diperoleh:

<rs t = R tr = J Ir u H

Iv

Misalkan w = I maka I = w sehingga Gw = I +.GI integral di atas akan menjadi

= J wr*+z_Gw

Integral di atas sulit diselesaikan namun integral di atas biasanya

dikenal dengan fungsi Gamma seperti pada Definisi 2.13_{, sehingga}

akan diperoleh

<rs t = Γ 8r+ 19 (3.5)

Momen nol dari variabel umum Weibull berhubungan dengan

variabel Weibull yang direduksi. Dengan mensubstitusikan ; = | +

}t ke dalam persamaan (2.1) dan menggunakan persamaan (3.5) akan diperoleh:

<rs ; = E ;r = E• | + }t rM

= € b•_{‚c |}ƒ_}r+ƒ_{R t}r+ƒ r

ƒ„

Dengan mensubstitusikan persamaan (3.5) ke dalam bentuk di atas

maka persamaan di atas akan menjadi

Dari persamaan (3.6) dapat diperoleh momen-momen berdasarkan

perubahan nilai r. Empat momen pertama yang diperoleh adalah

sebagai berikut.

<_.s _{; = R ; = | + }Γ. (3.7)}

<₀s _{; = R ;}0 _{= |}0_{+ 2|}Γ}

0+ }0Γ0 (3.8)

<†s ; = R ;† = |†+3|0}Γ.+ 3|}0Γ0+ }†Γ† (3.9)

<‡s ; = R ;‡ = |‡+ 4|†}Γ.+ 6|0}0Γ0+ 4|}†Γ†+ }‡Γ‡ (3.10)

Berdasarkan Definisi 2.10 _{fungsi pembangkit momen (moment}

generating function, MGF) dari variabel random X, ditulis Mx(t),

didefinisikan sebagai

Š‹ O = R *P‹

Ketika Š O ada untuk setiap interval vOv < •, dimana T > 0. Fungsi

Pembangkit Momen dari distribusi Weibull kemudian dapat dicari

dengan menggunakan ekspansi Taylor sebagai berikut.

Dari Teorema 2.18 _{deret Taylor didefinisikan sebagai berikut}

= €

Ž

_|

− |

Ž

•!

H

Ž„

Empat momen pada persamaan (3.7), (3.8), (3.9) dan (3.10) kemudian

Pada saat • = 0 maka berdasarkan persamaan (3.6) diperoleh

<s _{; = R 1 = | } Γ 0 + 1}

<s _{; = 1 (3.11)}

Deret Taylor yang dapat dibentuk dari persamaan (3.7), (3.8), (3.9),

(3.10) dan (3.11) adalah sebagai berikut:

Š O = <s _{; + <}

Berdasarkan hasil ekspansi Taylor di atas maka terlihat bahwa <_rs ;

adalah koefisien dari P’

Dengan mengkombinasikan persamaan (3.5) dan persamaan

E. Kertas Peluang Weibull

1. Grafik Probabilitas Weibull

Grafik probabilitas adalah sebuah teknik grafis untuk menduga

apakah data mengikuti distribusi yang diberikan seperti distribusi

normal atau Weibull. Grafik probabilitas Weibull termasuk jenis

grafik probabilitas yang biasanya digunakan untuk mengestimasi

parameter dan pada distribusi Weibull. Dengan kata lain grafik

Weibull adalah metode pemeriksaan informal untuk memeriksa

asumsi pada model distribusi Weibull dan juga untuk menduga

parameter dari distribusi Weibull. Pada subbab ini akan dijelaskan dan

diilustrasikan metode pembuatan grafik probabilitas Weibull. Ide

dasar dari pembuatan grafik probabilitas Weibull adalah hubungan

antara p-kuantil tp dari probabilitas Weibull dan p untuk 0 < p < 1. p

-kuantil tpdidefinisikan dengan sifat sebagai berikut

“ = N”•O–— = ˜•• ≤ O–— = 1 − *8+š P›œ 9 (3.13)

sehingga akan didapatkan

O

_–

=

•+ .+– M

Jika kedua ruas persamaan di atas dioperasikan dengan logaritma

natural (ln) maka persamaan di atas akan menjadi

•_– = ln•O_–— = ln 8.9 + .ln•−ln 1 − “ M (3.14)

Jadi jika ln•O_–— diplotkan dengan

maka grafik akan berbentuk garis lurus dengan berpotongan pada

| = ln 8.9 dengan kemiringan } = .. Jadi, = . dan = .

¡.

Pembuatan plot grafik Ÿ “ dengan •_– = ln•O_–— biasanya dikerjakan

pada kertas peluang Weibull. Untuk itu perlu dilihat hubungan linear

berikut ini

Ÿ “ = mln•O–— − ln 8._¢9Q (3.16)

dengan kemiringan

£ = (3.17)

dan berpotongan pada

¤ = − ln 8.9 (3.18)

Dari persamaan (3.17) dan (3.18) diperoleh nilai parameter bentuk

= £ dan parameter skala = *¥¦. Pada saat “ tidak diketahui maka

digunakan sampel quantil. Untuk sampel yang lengkap, •_., … , •_Ž, “_¨

diperoleh dengan mengurutkan •_¨ dari yang terkecil hingga yang

terbesar sehingga didapatkan •_. ≤ ⋯ ≤ •_Ž dan dengan

menggunakan “_¨ =.+ ,©

Ž maka pendekatan kuantil “¨ dapat diduga dan

•¨ menunjukkan sampel kuantil ke-ª.

Ide dari pembuatan grafik probabilitas Weibull untuk sampel

yang lengkap adalah membuat grafik Ÿ “_¨ = ln•−ln 1 − “_¨ M

kaitannya dengan variasi dari •_¨ di sekitar O_–«berdasarkan pada

persamaan (3.16) maka dapat dilihat secara kasar terdapat hubungan

yang linear. Kualitas dari hubungan linear ini akan memberikan suatu

indikasi apakah asumsi dari model Weibull layak atau tidak. Untuk

ukuran sampel yang kecil, bentuk linear akan sangat kasar, meskipun

sampel tersebut berdistribusi Weibull. Jadi, deviasi dari linearitas

tidak perlu dipelajari lebih jelas. Pengujian formal merupakan cara

yang lebih baik untuk dilakukan.

Untuk menggambarkan titik ln••_¨ —, Ÿ “_¨ akan

ditempatkan atau diinterpolasikan nilai dari label •_¨ pada absis dan

nilai dari “_¨ pada ordinat, dengan kata lain tidak perlu dilakukan

transformasi ln••_¨ — dan Ÿ “_¨ = ln•−ln 1 − “_¨ M. Beberapa

pengarang menyarankan untuk menggunakan “_¨s= ¨+ ,†

Žg‡ sebagai “¨,

ada juga yang menggunakan ¨

Žg. . Selengkapnya dapat dilihat pada

Tabel 3.1_{. Semua pilihan dari} “_{¨ memberikan nilai antara 0 sampai 1}

atau 0 < p < 1 untuk menghasilkan nilai berhingga dari Ÿ_–«. Untuk

ukuran sampel n yang besar terdapat sedikit perbedaan dalam memilih

Ҭ dan untuk ukuran sampel n yang kecil variabilitas dalam sampel

Tabel 3.1

Kedudukan Grafik (plotting position)

Nama Variabel Tereduksi I¬¨:Ž

2. Skala Dalam Kertas Peluang Weibull

Kertas peluang Weibull ada 3 macam dengan perbedaan

besarnya skala pada absis. Kertas jenis pertama skala pada absis

dimulai dari 1 sampai 10, pada kertas jenis kedua skala dimulai dari 1

sampai 1000. Jika pada observasi terutama data observasi waktu hidup,

misalkan data berada pada skala dari 50 sampai 4000, secara sederhana

unit waktu ke sepersepuluhnya diubah dan kemudian menggunakan

kertas jenis ketiga yang dapat menampung data tersebut dan skalanya

berubah dari 5 sampai 400. Jika skalanya sangat besar maka sebaiknya

digunakan kertas dengan skala yang lebih besar. Skala yang lebih

besar tidak diberikan disini karena skalanya penuh sesak (sangat kecil)

dan karena transformasinya sangat sulit.

Jika •~µ , (dengan kata lain • berdistribusi Weibull dengan

parameter dan ) maka •s= •¶~µ 8 ¶,_¶9 = µ s, s

sehingga ˜ •s ≤ • = ˜ •¶ ≤ • = ˜ 8• ≤ • 9 = 1 − *h+Y · Z i

= 1 − *j+• ·M k = 1 − *b+š ¸·œ ¸c

Jadi, dapat selalu dihasilkan skala dari waktu kegagalan naik atau

turun (tapi biasanya turun) ke dalam jarak yang tepat dengan

transformasi yang tepat. Setelah mengestimasi s, s dengan mudah

dapat mentransformasinya kembali menjadi , menggunakan nilai

dari |, namakan = s dan = | s.

Sebagai contoh, jika sebuah sampel dengan minimum dan

maksimum •_. = 5 dan •_Ž = 800000 secara berturut-turut, akan

membutuhkan 6 orde sehingga dapat menampung semua sampel,

memberikan •s_. = º•_. = 2,24 dan •s_Ž = º•_Ž = /800000 =

894,43 dan sekarang semua sampel yang ditransformasi dapat

ditampung pada interval •1, 1000M atau dengan kata lain pada kertas

peluang Weibull jenis ketiga. Sebaliknya jika diambil •_. = 0,5 dan

•Ž = 800000 secara berturut, transformasi tersebut tidak memenuhi

karena º0,5 = 0,71. Sekarang akan dicoba mengambil nilai | =.

† dan

diperoleh 0,5¼ = 0,794 dan 800000¼ = 92,83. Dengan menyatakan

nilai ini kedalam unit dari .

. akan diperoleh nilai baru 7,94 dan 928,3

yang dapat ditampung dengan kertas peluang Weibull jenis ketiga.

Berikut adalah contoh grafik probabilitas Weibull yang terbentuk.

Contoh 3.3

Untuk memperlihatkan grafik probabilitas Weibull, 1000 sampel

random dibangkitkan dengan Minitab dengan parameter skala (α) yaitu

3 dan parameter bentuk (β) yaitu 2. Sampel random tersebut kemudian

diplotkan sehingga terbentuk grafik probabilitas Weibull sebagai

Gambar 3.3 _{Grafik Probabilitas Weibull}

Dari grafik di atas dapat dilihat bahwa sampel random yang

digambarkan dalam grafik probabilitas Weibull sebagian besar berada

dalam selang pada grafik tersebut. Meskipun terdapat titik yang berada

di luar selang namun jika dilihat dari nilai P-value yang dihasilkan

yaitu 0,069, menunjukkan bahwa sampel random berdistribusi

Weibull. Grafik probabilitas di atas merupakan grafik probabilitas

yang dibentuk pada salah satu jenis kertas peluang Weibull yaitu kertas

peluang Weibull jenis pertama. Berikut ini adalah contoh kertas

a. Kertas peluang Weibull jenis pertama ( 1 cycle log_. )

Gambar 3.4 _{Kertas peluang Weibull jenis pertama}

b. Kertas peluang Weibull jenis kedua ( 2 cycle log_. )

Gambar 3.5 _{Kertas peluang Weibull jenis kedua}

c. Kertas peluang Weibull jenis ketiga ( 3 cycle log_. )

Gambar 3.6 _{Kertas peluang Weibull jenis ketiga}

Sumber: Scholz, F. Weibull Probability Paper (2008)

F. Pendugaan Parameter Distribusi

Distribusi Weibull sangat beragam tergantung pada pemilihan

nilai dan pada persamaan (3.1). Oleh karena itu penting untuk

1 maka distrib

tribusi Weibull tersebut akan menjadi distribu

pada saat = 1 dan = DC maka distribus istribusi normal. Namun demikian nilai ini ada

i pendekatan yang diperoleh dari sampel). Ja

tidak ada ekspektasi dari nilai eksak 3,5 u

g merupakan pendekatan untuk distribusi nor

pemilihan nilai dan yang berbeda dapat di

Grafik distribusi Weibull untuk = 1 = 1

a Gambar 3.7 _{bahwa tampak jelas perubaha}

l menjadi distribusi normal dengan berubahn

emperoleh parameter α dan βdigunakan met

yang diaplikasikan pada fungsi distribusi Weibu

Fungsi probabilitas dari distribusi Weibull adalah sebagai berikut

= +._*+

maka fungsi likelihood dari distribusi Weibull berdasarkan persamaan

(2.7) adalah sebagai berikut

Jika persamaan di atas dioperasikan dengan logaritma natural maka akan

diperoleh

derivatif tersebut adalah nol maka akan diperoleh

Ã

Jika turunan parsial pada persamaan (3.19) di atas diselesaikan maka akan

diperoleh

=_… •

Dengan mensubstitusikan ke dalam persamaan (3.20) maka akan

Namun untuk memperoleh parameter dan digunakan metode

Newton-Raphson. Metode ini diaplikasikan untuk mencari nilai terlebih dahulu

dan kemudian digunakan untuk mencari nilai dari . Untuk itu akan dicari

derivatif parsial kedua dari ln ¿ yaitu sebagai berikut.

s

Rumus iterasi di atas dapat diubah menjadi

Åg. = Å+

Dengan pendekatan ini, metode Newton-Raphson hanya memerlukan