Associative memory model with temporal spike coding and
active dendrite
Masataka Watanabe
a,b,*, Yohei Takahashi
a, Kazuyuki Aihara
b,caDepartment of Quantum Engineering and Systems Science,Graduate School of Engineering,
The Uni6ersity of Tokyo7-3-1Hongo Bunkyo-ku Tokyo113,Japan
bCREST,Japan Science and Technology Corporation(JST),4-1-8Honmachi,Kawaguchi City,Saitama,Japan cDepartment of Mathematical Engineering and Information Physics,Graduate School of Engineering,
The Uni6ersity of Tokyo7-3-1Hongo Bunkyo-ku Tokyo113,Japan
Abstract
We propose a neuron model whose internal state is integrated on a two dimensional phase space composed of time and dendritic space. Here, the postsynaptic potential is given as a curved surface on the phase space. Using the proposed neuron model, we introduce a continuous-time associative memory model with spike propagation delay and multiple synaptic sites on the dendrite. We show by numerical simulation that the memory capacity is doubled due to the effects of temporal spike coding and active dendrite compared to the sparse coding associative memory model. © 2000 Elsevier Science Ireland Ltd. All rights reserved.
Keywords:Temporal coding; Active dendrite; Storage capacity; Associative memory
www.elsevier.com/locate/biosystems
1. Introduction
Today, there are two controversial hypotheses on the operation of cortical neurons. One is the traditional view, which considers the cortical neu-ron as an integrate-and-fire element Sherrington (1906), where the time constant of membrane potential is long enough compared to the average interval of synaptic inputs. According to this hy-pothesis, the neural information propagated along an axon is coded as the firing rate. Most neural
network models and physiological experiments are based on this assumption.
An alternative concept is the temporal spike coding, where the cortical neurons are assumed to operate as detectors for temporal coincidence of synaptic inputs Abeles (1982). Therefore, the time constant of membrane potential is assumed to be much shorter than the average interval of synaptic inputs. Here, the carrier of information is the temporal structure of spikes propagating along axons.
The latter concept has attracted special interest recently in the field of neuroscience due to experi-mental and theoretical results supporting this hy-* Tel.: +81-03-5841-6966; fax:+81-03-3818-3455.
E-mail address:[email protected] (M. Watan-abe).
pothesis (Vaadia et al. 1987; Softky and Koch 1993; Ko¨nig et al. 1996; Fujii et al. 1996; Watan-abe and Aihara 1997; WatanWatan-abe et al. 1998). Yet little is known on the dynamics of such neural networks composed of coincidence detector neurons.
Another interesting subject in relation with temporal spike coding is the active dendrite hy-pothesis Softky (1994). It was originally proposed to explain the highly irregular firing of cortical cells Softky and Koch (1993) leading to the as-sumption that neurons work as coincidence detectors.
In this paper, we introduce an associative mem-ory model which utilizes both temporal spike coding and active dendrite to increase its memory capacity. In the proposed model, we use a neuron model which integrates its postsynaptic potentials in a multi-dimensional phase space composed of time and dendritic space. Here, dendrites are as-sumed to be active and action potentials are gen-erated according to the local summation of postsynaptic potentials. Moreover, we decide the spike propagation delay and the synaptic site on the dendrite so that the postsynaptic potentials are localized in the time-dendritic phase space for each pattern. As a result, the signal to noise ratio is improved during retrieval leading to increased memory capacity.
2. Model
2.1. Network model
We introduce a neuron model which integrates its postsynaptic potential in a multi-dimensional phase space of time and dendritic space. For the sake of simplicity, we assume only one dimension for dendritic space, resulting in a two-dimensional phase space. A postsynaptic potential is given as a curved surface on the two-dimensional phase space (Fig. 1). We also assume that postsynaptic potential increases stepwise at the time of spike arrival and decays exponentially both in time and space.
Before giving equations and going into the de-tails of the model, we take up two assumptions
which we make to construct a simple model. The first is that neuronal firing is localized in time. We realize this by setting the variance of spike propa-gation delay small enough so that spikes sent from a temporally localized group of firing neu-rons do not spread out in time and do not overlap with spikes sent out by the next temporally local-ized neuronal firing resulting from the current. We call this group of spikes, a ‘spike group’. The second assumption is to fix the number of firing neurons resulting from a single spike group. This idea was introduced by Amari (1989) as ‘active threshold’assuming some kind of a fast negative feedback loop which keeps a moderate rate of activity in the network.
The summation of the postsynaptic potentials for neuron i in the k+1th spike group at time t
and dendritic space r is given as the following equation:
where, wij, dij and sij denote the synaptic weight,
spike propagation delay and the synaptic site from neuronjto neuroni, respectively. Moreover, t and D denote the time and spatial decay con-stant of the postsynaptic potential andNthe total number of neurons in the network. Finally,
xj(k,t) is the output of the jth neuron in the kth spike group given as,
If not choosed to fire in the kth spike group
xj(k,t)=0, (2)
If choosed to fire in thekth spike group
xj(k,t)=
!
0 tBtkf,j
1 t]tkf,j (3)
where tkf,j denotes the time of neuronal firing in
thekth spike group of the jth neuron.
From the integrated landscape of postsynaptic potentials in the phase space Eq. (1) we choose the peak point. We denote the coordinates of this maximum point as (tk+1,i
max
,rk+1,i
max
), with the value
Ik+1,i
max
. By assuming an active threshold Amari (1989), we choose the neurons which have theaN
highest peak values Ik+1,i
max to fire at time
tk+1,i
max .
Here, a is the network activity which determines the ratio of neurons to fire. One important feature of our network model is that, by putting t andD , it becomes equivalent to the original sparse coding model by Amari (1989).
2.2. Rules for synaptic site and spike propagation delay
In this subsection, we give the methods to determinewij,dijandsij. First, the synaptic weight
wij is given as the conventional autocorrelation
associative memory (Nakano 1972; Anderson 1972; Kohonen 1972; Hopfield 1982),
wij= % m
m=1
pimpjm, wii=0, (4)
to embed mrandom patterns pm, wherep i m is the
ith component of pm which takes binary values
either 0 or 1. Each pm have exactly aN
compo-nents which take 1 and (1−a)N components which take 0.
Next, spike propagation delay dij and synaptic
site sijis given as,
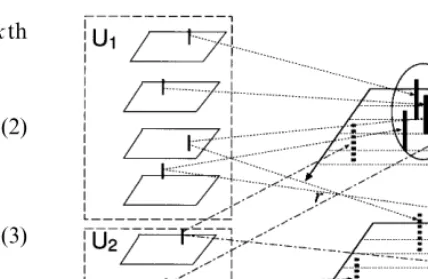
Fig. 2. The effect of pattern inherent spike propagation delay and synaptic site. U1denotes the group of firing neurons that
are included in the retrieved pattern, whereas U2 denotes the
group of firing neurons that are not. Left hand figures gives the neuronal firing in the previous spike group. Right upper and right lower phase space gives the distribution of spike arrival for neurons belonging to U1and U2, respectively.
where dmax, dmin and smax, smin give the ranges of the delay and the synaptic site, respectively. Moreover, mmax(i,j) and mmin(i,j) denote the maximum and minimum of pattern indexmwhere
pimpjm=1 is satisfied. By determining dij and sij as
in the above equations, patterns will likely to have its inherent delay and synaptic site. Consequently, spikes to neurons which should fire, namely, the neurons which compose the previous retrieving pattern, will likely to gather in a localized area in the two-dimensional phase space of the time-den-dritic space (Fig. 2). On the other hand, for the neurons which should not fire, incident spikes will have no correlations and will be dispersed in the phase space. As a result, the signal to noise ratio is improved, leading to increased memory capac-ity as seen in the next section.
3. Simulation results
First we look at the actual neuronal firing of our network model. Fig. 3 shows the retrieval of a memorized pattern. The network parameters are
N=80, a=0.1, dmax=21.0 dmin=11.0 smax=
Fig. 3. Network dynamics: correct retrieval of stored memory from a noisy initial state. We can recognize correct retrieval with synchronous firing.
to the fact that incident spikes form a group in the phase space and we chooseaNneurons to fire within this spike group. When the variance of spike propagation delay is small as in our simula-tion, the next spike group remain localized.
Fig. 4 shows the change of memory capacity with two neuronal parameters, namely, time de-cay constant tand spatial decay constantD. The storage capacity is defined as the upper limit of the number of embedded patterns where 90% of them are correctly retrieved within five steps.
As seen in the diagram, there is an optimal point where the storage capacity is maximized. As mentioned earlier, when both t and D approach to infinity, our model is equivalent to the sparse coding associative memory model Amari (1989).
Fig. 4. Change of memory storage capacity withtandD. There is an optimum parameter value where memory capacity is doubled
The plateau in the left front region corresponds to the parameter region of the sparse coding model. We can conclude that the storage capacity for the optimal neuronal parameter is twice as large as the conventional sparse coding associative mem-ory model.
4. Conclusion
We have introduced a neuron model where the postsynaptic potential is given as a curved surface in a two-dimensional phase space composed of time and dendritic space. Applying this neuron model to a continuous-time associative memory model with pattern specific spike propagation de-lay and synaptic site, we have shown that the storage capacity is doubled compared to the basic sparse coding model in a particular parameter region. This result gives an example of the advan-tage of temporal spike coding, where ‘time’ works as an additional degree of freedom to discriminate signal from noise.
References
Abeles, M., 1982. Role of the cortical neuron: integrator or coincidence detector? Israel J. Med. Sci. 18, 83 – 92.
Amari, S., 1989. Characteristics of sparsely encoded associa-tive memory. Neural Netw. 2, 451 – 457.
Anderson, J.A., 1972. A simple neural network generating interactive memory. Math. Biosci. 14, 197 – 220.
Fujii, H., Ito, H., Aihara, K., Ichinose, N., Tsukada, M., 1996. Dynamical cell assembly hypothesis — theoretical possibil-ity of spatio-temporal coding in the cortex. Neural Netw. 9, 1303 – 1350.
Hopfield, J.J., 1982. Neural networks and physical systems with emergent collective computational abilities. Proc. Natl. Acad. Sci. USA 79, 2445 – 2558.
Kohonen, T., 1972. Correlation matrix memories. IEEE Trans. Comput. C-21, 353 – 359.
Ko¨nig, P., Engel, A.K., Singer, W., 1996. Integrator or coinci-dence detector? The role of the cortical neuron revisited. TINS 19 (4), 30 – 137.
Nakano, K., 1972. Associatron — a model o associative memory. IEEE Trans. Syst. Man Cybern. 2, 381 – 388. Sherrington, C.S., 1906. Interactive Action of the Nervous
System. Yale University Press.
Softky, W.R., Koch, C., 1993. The highly irregular firing of cortical cells is inconsistent with temporal integration of random EPSPs. J. Neurosci. 13, 334 – 350.
Softky, W.R., 1994. Sub-millisecond coincidence detection in active dendritic trees. Neuroscience 58, 13 – 41.
Vaadia, E., Ahissar, E., Bergman, H., Lavner, Y., 1987. Correlated activity of neurons: a neural code for higher brain functions. In: Kruger, J. (Ed.), Neuronal Cooperativ-ity. Springer-Verlag.
Watanabe, M., Aihara, K., 1997. Chaos in neural networks composed of coincidence detector neurons. Neural Netw. 10 (8), 1353 – 1359.
Watanabe, M., Aihara, K., Kondo, S., 1998. A dynamical neural network with temporal coding and functional con-nectivity. Biol. Cybern. 78, 87 – 93.