Bahan kuliah Metoda Numerik Jurusan Teknik Sipil FT UGM Yogyakarta

(1)

M

E

_E

T

_T

O

_O

D

_D

A

_A

N

U

_U

M

_M

E

_E

R

_R

I

_I

K

_K

oleh

Ir. Djoko Luknanto, M.Sc., Ph.D. November 2001

Bahan kuliah Metoda Numerik Jurusan Teknik Sipil FT UGM

(2)

Metoda Numerik hal. ii

Ir. Djoko Luknanto, M.Sc., Ph.D. Jack la Motta

D:\My Documents\Publikasi\Metoda Numerik\Metoda Numerik.doc (2028 Kb)

PRAKATA

Buku berjudul “Metoda Numerik” ini merupakan bahan kuliah di Jurusan Teknik Sipil FT UGM. Buku ini tidak menjelaskan secara rinci teori-teori numerik secara lengkap, namun hanya membahas teori-teori numerik yang sering digunakan di lapangan. Pembaca yang ingin mengetahui secara lengkap Metoda Numerik diharapkan mencari dari acuan-acuan di luar buku ini.

Buku ini lebih merupakan petunjuk praktis bagi mahasiswa S1 maupun praktisi di lapangan. Dalam buku ini prinsip umum teori-teori numerik dijelaskan secara singkat, kemudian aplikasinya dijelaskan.

Semoga buku kecil ini berguna, kritik membangun sangatlah diharapkan.

Yogyakarta, November 2001 Dosen Jurusan Teknik Sipil FT UGM

Ir. Djoko Luknanto, M.Sc., Ph.D.

(3)

DAFTAR ISI

halaman

PRAKATA... ii

DAFTAR ISI... iii

DAFTAR GAMBAR...vi

1. Error: Asal & Rambatannya... 7

1.1. Pendahuluan ... 7

1.2. Bilangan Dalam Komputer ... 11

1.2.1. Underflow and Overflow ... 12

1.3. Definisi dan Asal ‘error’ ... 12

1.3.1. Angka signifikan (significant digits)... 13

1.3.2. Asal dari ‘error’ ... 13

1.4. Rambatan ‘Error’ ... 13

1.4.1. ‘Propagated Error’ pada Perkalian... 14

1.4.2. ‘Propagated Error’ pada Pembagian... 14

1.4.3. ‘Propagated Error’ pada Penjumlahan dan Pengurangan ... 14

2. Persamaan Non-Linier... 16

2.1. Metode Bagi Paruh (Bisection) ... 16

2.2. Metode Newton... 17

2.3. Metode Sekan... 19

2.4. Akar dari Persamaan Polinomial ... 20

3. Teori Interpolasi ... 22

3.1. Metoda Beda Terbagi Newton... 22

3.2. Interpolasi dengan tabel beda hingga ... 24

3.2.1. Beda Maju ... 24

3.2.2. Beda Mundur ... 26

3.3. Lagrange ... 26

(4)

DAFTAR ISI Buku kuliah

Metoda Numerik hal. iv

4. Integrasi Numeris... 28

4.1. Rumus trapesium dan Simpson... 28

4.1.1. Rumus trapesium terkoreksi... 30

4.1.2. Rumus Simpson ... 31

4.2. Rumus Newton–Cotes... 33

4.2.1. Rumus Newton-Cotes Tertutup ... 34

4.2.2. Rumus Newton–Cotes terbuka... 35

4.3. Kuadratur Gaussian... 36 4.3.1. Kuadratur Gauss-Legendre... 37 4.4. Polinomial Orthogonal ... 39 4.4.1. Kuadratur Gauss-Laquerre ... 40 4.4.2. Kuadratur Gauss-Chebysev... 42 4.4.3. Kuadratur Gauss-Hermite... 42

5. Sistem Persamaan Linier ... 43

5.1. Eliminasi Gauss ... 43

5.2. Eliminasi Gauss–Jordan... 45

5.3. Eliminasi Gauss–Jordan dengan ‘pivot’ maksimum... 46

5.3.1. Rekonstruksi pembentukan “scrambled inverse” ... 48

5.4. Metoda Iterasi ... 49

5.4.1. Metoda Jacobi... 49

5.4.2. Metoda Gauss-Seidel... 51

6. Matrik ... 52

6.1. Notasi dan Konsep-konsep Pendahuluan ... 52

6.2. Determinan dan invers ... 55

6.2.1. Menghitung determinan dengan eleminasi segitiga atas... 55

6.3. Matrik dan Vektor Eigen... 57

6.3.1. Metode ‘power’ untuk mendapatkan nilai & vektor eigen terbesar. ... 58

7. Persamaan Differensial Biasa... 61

7.1. Metoda Euler... 63

7.2. Metoda ‘Multi–Step’... 64

7.2.1. Metoda Trapesium ... 65

7.3. Metoda Runge-Kutta (RK) ... 66

7.3.1. Metoda RK derajat dua... 66

7.3.2. Metoda RK berderajat tiga ... 67

7.3.3. Metoda RK berderajat empat... 68

7.3.3.1. Metoda Pertama ... 68

7.3.3.2. Metoda Kedua... 68

7.3.3.3. Metoda Ketiga... 68

7.4. Metoda ‘Predictor-Corrector’ ... 69

(5)

DAFTAR ISI Buku kuliah

(6)

Metoda Numerik hal. vi

DAFTAR GAMBAR

halaman

Gambar 1 Teorema Nilai Antara ... 7

Gambar 2 Teorema Nilai Tengah ... 8

Gambar 3 Nilai Tengah Integral ... 9

Gambar 4 Interpretasi Deret Taylor secara geometris... 10

Gambar 5 Metoda Bagi Paruh untuk mencari akar ... 17

Gambar 6 Metoda Newton untuk mencari akar ... 18

Gambar 7 Metoda Sekan untuk mencari akar ... 19

Gambar 8 Konsep integrasi trapesium ... 28

Gambar 9 Konsep integrasi Simpson... 31

Gambar 10 Fungsi y = w(x) untuk metoda Simpson... 32

Gambar 11 Cara pertama pemindahan kolom dengan elemen pivot... 48

Gambar 12 Cara kedua pemindahan kolom dengan elemen pivot... 48

Gambar 13 Cara kedua pemindahan kolom dengan elemen pivot... 49

Gambar 14 Gaya-gaya yang bekerja pada struktur ... 60

(7)

Bab

1. ERROR: ASAL & RAMBATANNYA

1.1. Pendahuluan

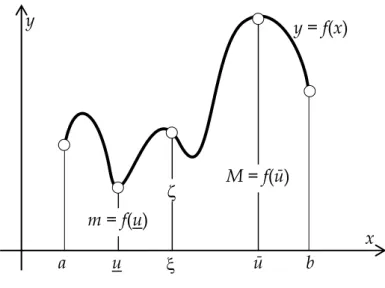
Teorema 1.1.: ‘Nilai Antara’ (lihat Gambar 1)

Jika f(x) suatu fungsi menerus pada x ∈ [a, b] dan

b x a x f Infimum m ≤ ≤ = ( ) serta b x a x f Supremum M ≤ ≤

= ( ), maka untuk setiap bilangan ζ pada interval tertutup [m, M]

paling tidak ada satu titik ξ∈ [a,b] sehingga f(ξ) = ζ. Khususnya ada dua titik u &

ū∈ [a, b] dimana m = f(u) dan M = f(ū)

Gambar 1 Teorema Nilai Antara y x a b u ξ ū y = f(x) M = f(ū) m = f(u) ζ

(8)

Error: Asal & Rambatannya Buku kuliah

Metoda Numerik hal. 8

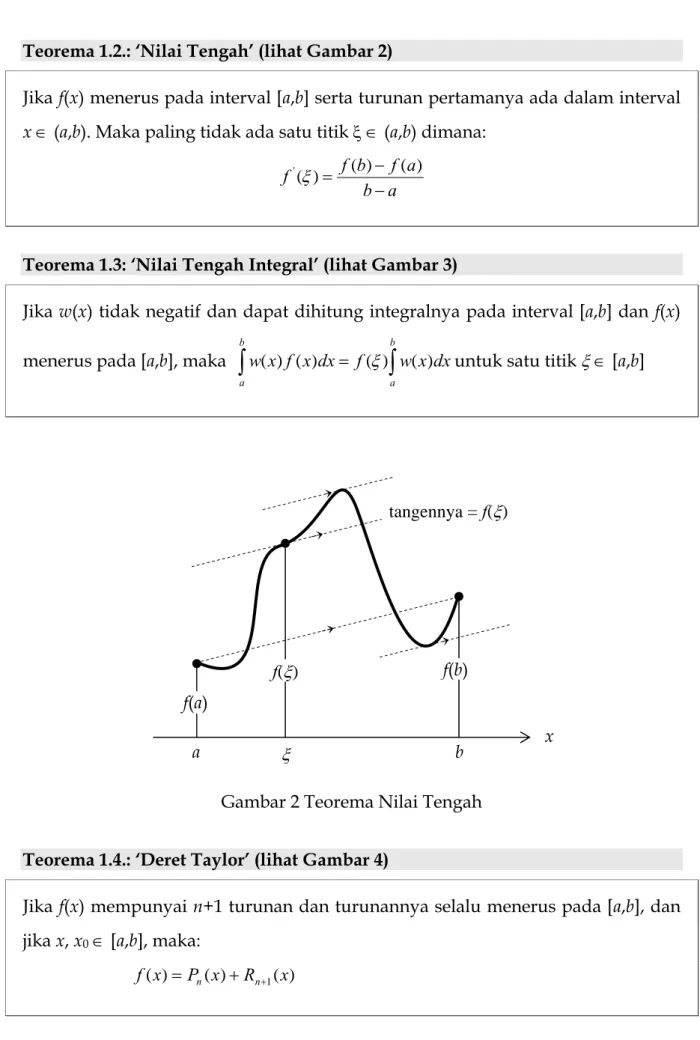
Teorema 1.2.: ‘Nilai Tengah’ (lihat Gambar 2)

Jika f(x) menerus pada interval [a,b] serta turunan pertamanya ada dalam interval

x∈ (a,b). Maka paling tidak ada satu titik ξ∈ (a,b) dimana:

a b a f b f f − − = ( ) ( ) ) ( ' ξ

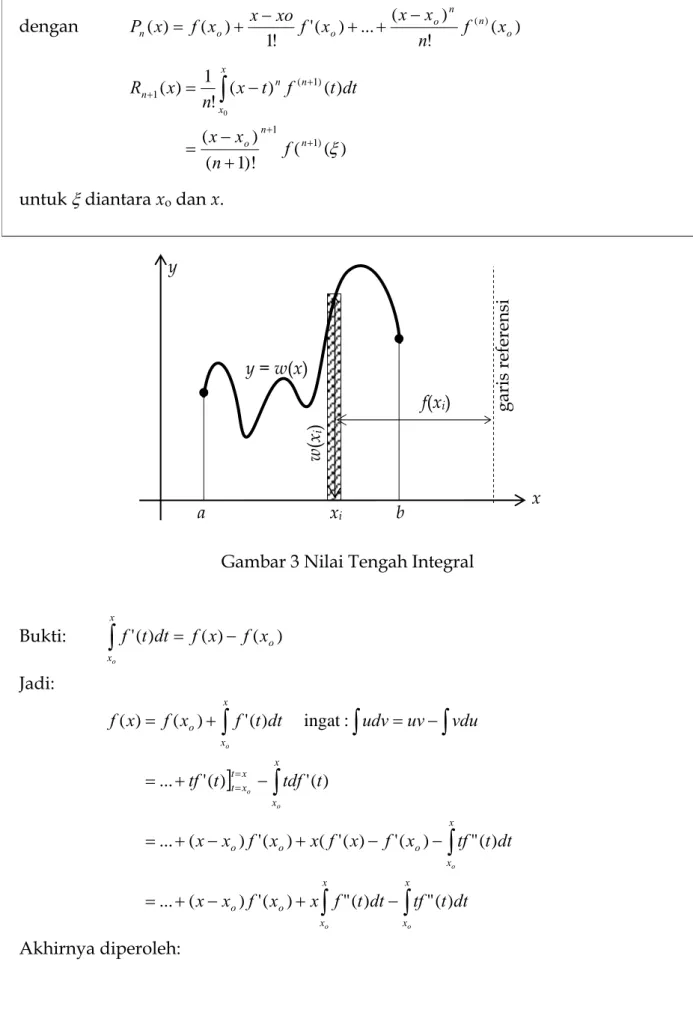
Teorema 1.3: ‘Nilai Tengah Integral’ (lihat Gambar 3)

Jika w(x) tidak negatif dan dapat dihitung integralnya pada interval [a,b] dan f(x)

menerus pada [a,b], maka

∫

b =

∫

a b a dx x w f dx x f x

w( ) ( ) (ξ) ( ) untuk satu titik ξ∈ [a,b]

Gambar 2 Teorema Nilai Tengah

Teorema 1.4.: ‘Deret Taylor’ (lihat Gambar 4)

Jika f(x) mempunyai n+1 turunan dan turunannya selalu menerus pada [a,b], dan

jika x, x0∈ [a,b], maka: ) ( ) ( ) (x P x R 1 x f = _n + _n₊ x f(a) f(b) a ξ b f(ξ) tangennya = f(ξ)

(9)

Error: Asal & Rambatannya Buku kuliah dengan ( ) ! ) ( ... ) ( ' ! 1 ) ( ) ( (n) _o n o o o n f x n x x x f xo x x f x P = + − + + − ) ( ( )! 1 ( ) ( ) ( ) ( ! 1 ) ( ) 1 1 ) 1 ( 1 0 ξ + + + + + − = − =

∫

n n o x x n n n f n x x dt t f t x n x R

untukξdiantara xo danx.

Gambar 3 Nilai Tengah Integral

Bukti:

∫

x = − x o o x f x f dt t f'( ) ( ) ( ) Jadi:

]

dt t tf dt t f x x f x x dt t tf x f x f x x f x x t tdf t tf vdu uv udv dt t f x f x f x x x x o o x x o o o x x x t x t x x o o o o o o o ) ( " ) ( " ) ( ' ) ( ... ) ( " ) ( ' ) ( ' ( ) ( ' ) ( ... ) ( ' ) ( ' ... : ingat ) ( ' ) ( ) (

∫

− + − + = − − + − + = − + = − = + = = = Akhirnya diperoleh: y x a b xi y = w(x) w ( xi ) f(x garis referensi i)

(10)

dst. ... ) ( ) ( " 2 1 ... dst. ... ) ( " ) ( ) ( ' ) ( ) ( ) ( 2 0 t x d t f dt t f t x x f x x x f x f x x x x o o o o − + = − + − + =

∫

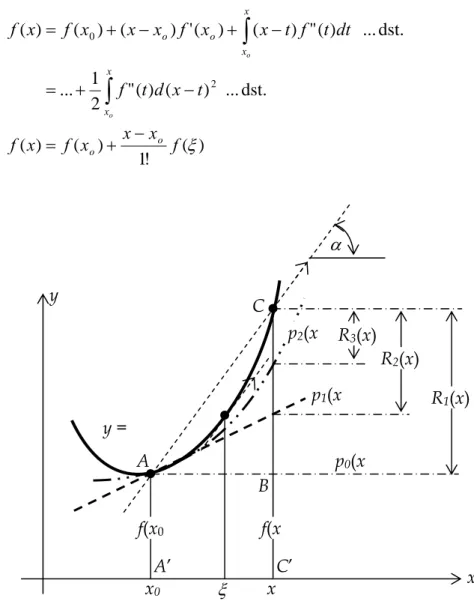
) ( ! 1 ) ( ) (x f x x x f ξ f o o − + =

Gambar 4 Interpretasi Deret Taylor secara geometris Secara geometris artinya:

{ { ) '( ) ( ) ( ) ( ' ' ' ' pemotongan kesalahan tan ' ' ' ' 0 1 0 ξ α f x x x R BC x p AA AB BC C A AA C A AA CC − = + = × + = + = 43 42 1

Jadi kesalahan pemotongan y = A x0 ξ x C α x y B R1(x) f(x0 f(x A’ C’ p0(x R2(x) p1(x p2(x R3(x)

(11)

Error: Asal & Rambatannya Buku kuliah 1 1 ) 1 ( 1 1 konstanta ) ( konstanta ) ( )! 1 ( ) ( ) ( + + + + + Δ × = − × = + − = n n o n n o n x x x f n x x x R ξ

Rn+1 (x) disebut sebagai kesalahan pemotongan order n+1 atau O(Δxn+1).

1.2. Bilangan Dalam Komputer

Komputer menyajikan bilangan dalam 2 mode yaitu (1) Integer, (2) Floating point.

Basis bilangan yang digunakan dalam komputer jarang sekali yang decimal (basis 10). Hampir semua komputer memakai basis 2 (binari) atau variannya seperti basis 8 (octal) dan basis 16 (hexadecimal).

Contoh:

a. Pada basis 2, semua bilangan terdiri dari 2 angka yaitu 0 dan 1.

Jadi (11011.01)2 = 1.24 + 1.23 + 0.22 + 1.21 + 1.20 + 0.2-1 + 1.2-2 = 27. 25

b. Pada basis 16, semua bilangan terdiri dari/dinyatakan dengan angka 0, 1, …, 9,

A,B, … ,F

Jadi (56C.F)16 = 5.1612+ 6.161 + 12.160 + 15.16-1 = 1338.9375

Jika basis bilangan suatu komputer adalah β, maka suatu bilangan non-zero x

disimpan didalam bentuk.

x = σ (.a1a2a3 … at)β . βe

dengan σ = -1 atau + 1, 0 ≤a1≤β-1, e = integer, dan

(

)

t_t t a a a a a a a β β β + + + = • _L 2₂ _L 1 1 3 2 1

dengan σ disebut tanda, e disebut eksponen Æ L ≤ e ≤ U, (•a1a2a3 … at) disebut

mantissa, dan • disebut radix.

Akurasi dari sajian ‘floating-point’ suatu komputer. Unit pembulatan, δ, suatu komputer adalah suatu bilangan positip terkecil yang mempunyai sifat bahwa

1 + δ > 1

Nilai nol, ε, suatu komputer adalah suatu bilangan positip terkecil dimana

1 + ε > 1

(12)

ε = 1.0 10 ε = ε/2.0

If (1.0 + ε .GT. 1.0) GOTO 10

δ = ε * 2.0

1.2.1. Underflow and Overflow

Jika suatu bilangan tidak mampu direpresentasikan oleh komputer karena e <

L atau e > U, maka akan terjadi under/overflow.

Jadi setiap bilangan harus berada dalam interval xL≤ |x| ≤xU

dengan xL = βL-1 dan xU = (1 – β-t)βL-1

Dalam FORTRAN:

♦ Jika suatu hasil hitungan, |x|≥xU, maka akan terjadi ‘overflow error’ dan

program akan berhenti.

♦ Jika suatu hasil hitungan, |x|≥xL, maka akan terjadi ‘underflow error’

biasanya x nilainya menjadi nol dan hitungan terus berlanjut.

1.3. Definisi dan Asal ‘error’

Dalam penyelesaian suatu masalah, dikehendaki jawaban yang sejati, yang

disimbolkan sebagai xT, tetapi biasanya jawaban pendekatanlah yang didapat (ini

disimbolkan sebagai xA). A T A x x x Error( )≡ −

Untuk banyak keperluan, bukan ‘error’ mutlak yang dikehendaki melainkan

‘error’ relatif dari xA yang dibutuhkan:

0 , ) ( Rel ≡ − _T ≠ T A T A x x x x x Contoh: x_T =e=2.7182818..., 2.7142857... 7 19 ₌ = A x

(13)

1.3.1. Angka signifikan (significant digits)

Nilai xA dikatakan mempunyai m angka signifikan terhadap xT, jika kesalahan

(xT-xA) mempunyai nilai ≤ 5 pada (m+1) angka dihitung ke kanan dari angka

non-zero didalam xT. Contoh: 1) 0.33333... 3 1 1 ⇑ = = T x , x_A =0.333, 4 3 2 1 3 0 0 0 . 0 ⇑ = − _A T x x

karena pada angka ke 4 kesalahannya < 5, maka xA dikatakan mempunyai 3

angka signifikan, sehingga x_A =0.333.

2) 213.496 23.494 0102.030425 ⇑ ⇑ = − = = _A _T _A T x x x x

3) 0.02138 0.02144 0.00006 3 2 1 1 ⇑ ⇑ = − = = _A _T _A T x x x x

1.3.2. Asal dari ‘error’

1. Simplifikasi dan asumsi yang digunakan untuk merubah peristiwa alam ke

dalam formula matematik.

2. Kesalahan/keteledoran : kesalahan aritmatik dan programming.

3. Ketidakpastian dalam data.

4. Kesalahan mesin.

5. Kesalahan matematis dalam kesalahan pemotongan

1.4. Rambatan ‘Error’

♦ Ditentukan semua operasi aritmatik digantikan dengan tanda ω. Jadi ω: + - ×

/ dan ŵ: + - × / → versi komputer

♦ Misalkan xA dan yA adalah bilangan yang akan digunakan dan kesalahannya

terhadap xT dan xT adalah

A

T x

x − =

(14)

♦ Jika dilakukan hitungan xAŵ yA, maka kesalahannya adalah

(

) (

)

4 4 4 3 4 4 4 2 1 4 4 4 3 4 4 4 2 1 II I ˆ ˆ _A _T _T _A _A _A _A _A _A A T T y x w y x y x y x y x w y x ω − = ω − ω + ω −

I = kesalahan karena rambatan (‘propagated error’) II = kesalahan karena ‘rounding’ ataupun ‘choping’

1.4.1. ‘Propagated Error’ pada Perkalian

εη ε η η ε χ − + = − − − = − T T T T T T A A T T y x y y x y x y x ( )( ) ) ( Rel ). ( Rel ) ( Rel ) ( Rel ) ( Rel A A A A T T T T T T A A T T A A y x y x y x y y x y x y x y x − + = − + = − ≡ χ εη ε η

Jika Rel(x_A), Rel(y_A) <<1, maka Rel(x_Ay_A)=Rel(x_A)+Rel(y_A)

1.4.2. ‘Propagated Error’ pada Pembagian

T T T T T T T T T T T T T T T T T T T T T A A T T A A x y x y y x x y x x y y x y x y x y x y x y x y x y x . . . ) ( ) ( 1 ) ( Rel η ε η η ε η ε − + − − = − − − = − − − = − ≡ ) ( Rel 1 ) ( Rel ) ( Rel ) ( Rel A A A A A y y x y x − − =

Jika Rel(y_A) <<1, maka Rel( ) Rel( _A) Rel( _A)

A

A _x _y

y

x ₌ ₋

Tampak bahwa pada perkalian dan pembagian ‘kesalahan relatif’ tidak membesar secara cepat.

1.4.3. ‘Propagated Error’ pada Penjumlahan dan Pengurangan

η ε± = − ± − = ± − ± ) ( ) ( ) ( ) (x_T y_T x_A y_A x_T x_A y_T y_A ) ( ) ( ) (x_A y_A Error x_A Error y_A Error ± = ±

(15)

Penjabaran ini tampak logis tetapi tidak baik karena tidak dinyatakan dalam ‘kesalahan relatif’ Contoh: , 3,1429 7 22 , 1416 . 3 , = = = = _A _T _A T x y y x π 6 10 35 . 7 × − − = − _A T x x 6 10 34 . 2 ) ( Rel x_A =− × − 5 10 29 . 4 × − − = − _A T y y 5 10 36 . 1 ) ( Rel y_A =− × − 5 10 55 . 3 ) 0013 . 0 ( 0012645 . 0 ) ( ) ( − × = − − − = − − − _T _A _A T y x y x 028 . 0 ) ( Rel x_A −y_A =−

Jadi meskipun kesalahan pada (x_A −y_A)adalah kecil, tetapi ‘kesalahan relatif’nya

(16)

Bab

2. PERSAMAAN NON-LINIER

Di dalam matematika aplikasi pencarian akar persamaan f(x)=0 sering

dijumpai. Biasanya jawaban analitis dari persamaan diatas tidak ada, sehingga harus dicari jawaban numeriknya yang biasa dilaksanakan dengan metode iterasi.

2.1. Metode Bagi Paruh (Bisection)

Jika terdapat suatu f(x) yang menerus ∈ [a,b] dan f(a)f(b) < 0, maka menurut

Teorema 1.1 paling tidak f(x) mempunyai satu akar f(x) mempunyai satu akar

∈ [a,b].

♦ Algoritma

Bisect(f, a, b, akar, ε)

1. Hitung c := (a+b)/2

2. Jika b – c≤ε , maka akar:= c, dan ‘ exit’

3. Jika {tanda f(b)•tanda f(c)} ≤_{0, maka}_a_:=_c_{, jika tidak}_b_:=_c

4. Kembali ke langkah nomor 1.

♦ Definisi

Suatu deret hasil suatu iterasi {xn|n≥0} dikatakan menuju ke titik  dengan

derajat p ≥_{1 , jika}

0

1 ≤ − ≥

−x_n₊ cα x_n p n

α

untuk beberapa nilai c>0. Jika p=1, deretnya disebut menuju ke titik  secara linier.

Pada kasus ini diperlukan nilai c<1; c disebut laju linier dari xn menuju .

Ada beberapa metode yang membutuhkan definisi yang agak berbeda dengan diatas yaitu 0 0 1 ≤ − ≥ −x ₊ cn x n n α α

(17)

Persamaan Non-Linier Buku kuliah

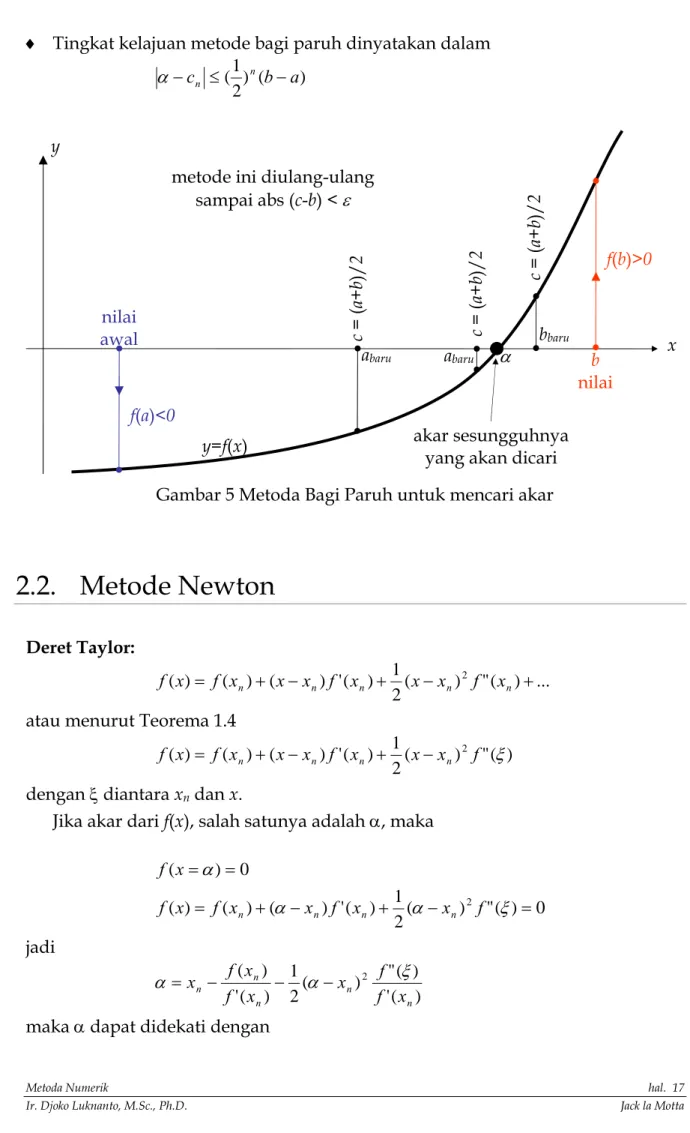
♦ Tingkat kelajuan metode bagi paruh dinyatakan dalam

) ( ) 2 1 ( b a c n n ≤ − − α

Gambar 5 Metoda Bagi Paruh untuk mencari akar

2.2. Metode Newton

Deret Taylor: ... ) ( " ) ( 2 1 ) ( ' ) ( ) ( ) (x = f x_n + x−x_n f x_n + x−x_n 2 f x_n + f

atau menurut Teorema 1.4

) ( " ) ( 2 1 ) ( ' ) ( ) ( ) (_x _f _x _x _x _f _x _x _x 2 _f ξ f = _n + − _n _n + − _n

dengan ξ diantara xn dan x.

Jika akar dari f(x), salah satunya adalah α, maka

0 ) ( " ) ( 2 1 ) ( ' ) ( ) ( ) ( 0 ) ( 2 = − + − + = = = ξ α α α f x x f x x f x f x f n n n n jadi ) ( ' ) ( " ) ( 2 1 ) ( ' ) ( 2 n n n n n x f f x x f x f x α ξ α = − − −

maka α dapat didekati dengan

y

x

y=f(x)

α

akar sesungguhnya yang akan dicari

nilai awal b nilai c = ( a + b )/ 2 f(a)<0 f(b)>0 abaru abaru bbaru

metode ini diulang-ulang

sampai abs (c-b) < ε c = ( a + b )/ 2 c = ( a + b )/ 2

(18)

0 ) ( ' ) ( 1 = − ≥ + n x f x f x x n n n n dengan ‘errornya’ 0 ) ( ) ( ' 2 ) ( " 2 1 =− − ≥ − ₊ x n x f f x _n n n α ξ α

Untuk nilai n→∞, ξ→α dan xn→α, jadi

2 2 1 ) ( konstanta ) ( ) ( ' 2 ) ( " n n n x x f f x − × = − − = − ₊ α α α α α

Sehingga metode Newton dikatakan mempunyai derajat kelajuan = 2

Gambar 6 Metoda Newton untuk mencari akar

♦ Algoritma

Newton (f, df, x0, ε, akar, itmax, ierr)

1. Keterangan : df adalah f’(x), itmax adalah iterasi maximum, ierr adalah ‘error

flag’ 2. noiter:=1

3. penyebut:=df(x0)

4. jika penyebut = 0 maka ierr:=2, dan ‘exit’

5. x1:= x0 - f(x0)/penyebut

6. jika |x1 – x0|≤ε, maka ierr:= 0, akar:= x1, dan ‘exit’

7. jika noiter = itmax maka ierr:= 1, dan ’exit’

8. noiter:= noiter +1, x0:=x1, dan ulangi langkah 3.

y x y=f(x) x0 x1 grs singgung α

(19)

2.3. Metode Sekan

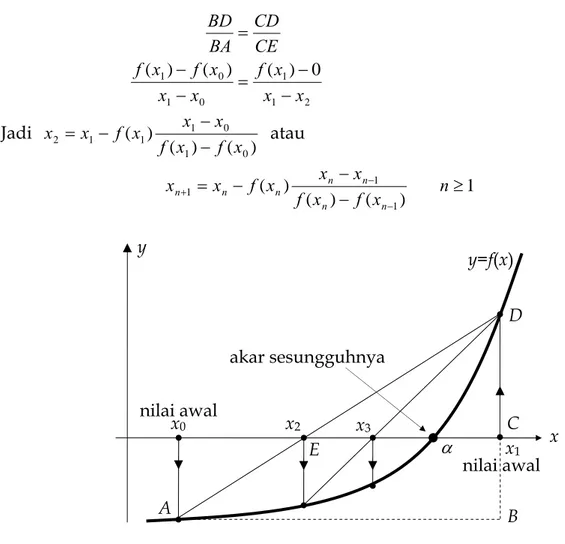
Dengan menggunakan sifat segitiga sebangun diperoleh

2 1 1 0 1 0 1) ( ) ( ) 0 ( x x x f x x x f x f CE CD BA BD − − = − − = Jadi ) ( ) ( ) ( 0 1 0 1 1 1 2 x f x f x x x f x x − − − = atau 1 ) ( ) ( ) ( 1 1 1 ₋ ≥ − − = − − + n x f x f x x x f x x n n n n n n n

Gambar 7 Metoda Sekan untuk mencari akar Metode sekan dapat dijabarkan dari metode Newton dimana

1 1) ( ) ( ) ( ' − − − − = n n n n n x x x f x f x f Derajat Konvergensi:

•

untuk metode Newton p = 2

•

untuk metode sekan p = ½(1+√5) = 1,618

•

untuk metode ‘bisection’ p = 1

y x y=f(x) x0 x1 α akar sesungguhnya nilai awal nilai awal x2 x3 B D E C A

(20)

2.4. Akar dari Persamaan Polinomial

p(x) = a0 + x(a1 + x(a2+…+x(an-1 + anx)…) (A)

atau

p(x) = a0 + a1x + a2x2+…+ anxn (B)

Pada Pers.(A) terdapat n perkalian & pertambahan, sedangkan dalam

Pers.(B) terdapat: (2n–1) perkalian & pertambahan. Oleh karena itu dalam

pemrograman komputer lebih disukai bentuk dalam Pers.(A), karena lebih efisien. Pers. (A) jika ditulis dalam FORTRAN menjadi

p = a(n)

do 10 i = n,1,-1 10 p = p*x + a(i–1)

Untuk menghitung akar dari persamaan p(x) = 0 akan digunakan Metoda

Newton. Untuk keperluan itu polinomial p(x) akan dimodifikasi sebagai berikut

Disyaratkan: bn= an

bk= ak + zbk+1 , k = n–1, n–2,… , 0

Dari syarat ini p(x) dapat ditulis sebagai

p(x) = b0 + (x– z)q(x)

dengan q(x) = b1 + b2x +…+ bnx n-1

sehingga p’(x) = (x– z)q’(x) + q(x) →p’(z) = q(z)

♦ Algoritma:

Polynew (a, n, x, ε, itmax, akar, b, ier)

1. Keterangan: a adalah vektor coef. dengan dimensi n, itmax adalah iterasi

maksimum, b adalah vektor coef. dari polinomial yang baru, ier adalah

indikator adanya error. 2. noiter: = 1

3. x: = x0 , bn:= c := an

4. Untuk k = n-1, …, 1, bk:= ak+ zbk+1, c := bk + zc

5. b0:= a0 + zb1

6. Jika c = 0, ier := 2, dan ‘exit

7. x1:= x0 – b0/c

8. Jika ⏐x1 – x0⏐≤ε , ier :=0 ,akar:= x1, dan ‘exit’

(21)

(22)

Bab

3. TEORI INTERPOLASI

Jika kita mempunyai satu set data:

(x0, y0) , (x1, y1), …, (xn, yn)

maka dalam bab ini akan di jelaskan bagaimana harus mencarti polinomial yang melalui, data di atas.

Jika polinomial ini ditulis sebagai:

p(x) = a0 + a1x +… + anxn

maka jika data diatas disubstitusikan akan didapat (n+1) persamaan dengan (n+1)

variabel tidak diketahuinya yaitu:

n n n n n n n y x a x a a y x a x a a = + + + = + + + L M M L 1 0 0 0 0 1 0

Persamaan diatas jika diselesaikan akan menghasilkan a0, …, an sehingga

polinomial p(x) dapat dicari .

3.1. Metoda Beda Terbagi Newton

Notasi yang digunakan:

[

]

[

] [

]

0 1 1 1 ... ... -x x ,x , x f ,x , x f , ... ,x ,x x f n n n n o − = Contoh Order 0: ƒ[x0] =ƒ[xn] Order 1:

[

]

[ ] [ ]

0 1 0 1 1 0, x x x f x f x x f − − = Order 2:

[

]

[

] [

]

0 2 1 0 2 1 2 1 0 , , , , x x x x f x x f x x x f − − = Order 3:

[

]

[

] [

]

0 2 1 0 3 2 1 3 2 1 0 , , , , , , x x x x f x x x f x x x x f − − =

(23)

Teori Interpolasi Buku kuliah

Rumus beda terbagi Newton:

pn(x) = ƒ[x0]+ (x3-x0)ƒ[x0,x1]+(x3-x0)(x-x1)ƒ[x0,x1]+…

+(x–x0)…(x–xn-1)ƒ[x0,x1,…,xn]

Contoh: Kita buat tabel beda terbagi berdasarkan polinomial

ƒ(x) = x3_{– 2}_x2_{+ 7}_x_{– 5} i xi f[xi] f[xi, xi+1] f2[ ] f3[ ] 0 0.0 -5.0 6 2 1 1 1.0 1.0 12 6 2 3.0 25.0 30 3 4.0 55.0 Keterangan:

( )

6 0 1 5 1 = − − − = A 12 1 3 1 25 = − − = B 30 3 4 25 55 ₌ − − = C 2 0 3− = − = B A D 6 1 4 12 30 = − − = E 1 0 4− = − = E D F Contoh hitungan pn(x=0.5) = ?

•

p1(x) = -5 + (x-0)6 = 6x – 5 ∴p1 (0.5) = -2

•

p2(x) = -5 + (x-0)6 + (x-0)(x–1)2 = 2x2 + 4x – 5 ∴p2 (0.5) = -2,5

•

p3(x) = -5 + (x-0)6 + (x-0)(x–1)2 +(x-0)(x-1)(x-3)1 = x3 – 2x2 + 7x – 5 ∴ p2 (0.5) = -15/8 = - 1.875

♦ Algoritma metoda beda terbagi Newton

Divdif (d, x , n)

1. Keterangan: d dan x adalah vektor f(xi) dan xi = 0,1,…,n. Pada saat ‘exit’ di

akan terisi oleh nilai f[x0,…,xi]

2. Kerjakan s/d langkah 4 untuk i = 1, 2 ,… ,n

3. Kerjakan sampai dengan langkah 4 untuk j = n, n-1, i

4. dj := (dj -dj-1) /(x-xj-1)

(24)

Interp(d, x, t, p)

1. Keterangan: Pada awalnya d dan x adalah vektor dari ƒ[x0,…,xi] dan xi, i = 0,

1 , …, n. Pada saat ‘exit’ p akan berisi pn(t).

2. p := dn

3. Kerjakan s/d langkah 4 untuk i = n-1 , n--2, …, 0

4. p := di + (t– xi)p

5. ‘ exit’

3.2. Interpolasi dengan tabel beda hingga

3.2.1. Beda Maju

Notasi: Δƒ(xi) = ƒ(xi+1) - ƒ(xi) dengan xi = x0 + ih, i = 0, 1, 2, 3, …

Untuk r≥ 0,

Δr+1_ƒ₍_z_{) =}_Δrƒ₍_z₊_h_{) -}_Δr_ƒ₍_z₎

Δr_ƒ₍_z_{) disebut ‘ beda maju order r ,‘}_Δ_{disebut ‘operator beda maju ‘}

Contoh: Δ0ƒ₍_x_{) =}ƒ₍_x₎

Δƒ(x) = Δ0ƒ₍_z₊_h_{) -}Δ0ƒ₍_z₎

= ƒ(x+h) - ƒ(x)

Δ2ƒ₍_x_{) =}Δƒ₍_x₊_h_{) -}Δƒ₍_x₎

Contoh hitungan : Kita gunakan polinomial x3_{– 2}_x2_{+ 7}_x_{– 5 dengan}_h_{= 1,0}

i xi f(xi) Δƒ Δ2ƒ Δ3ƒ Δ4ƒ 0 0.0 -5.0 6 2 6 0 1 1.0 1.0 8 8 6 2 2.0 9.0 16 14 3 3.0 25.0 30 4 4.0 55.0

Korelasi antara ‘beda maju’ dengan ‘ beda terbagi’

[

]

[ ] [ ]

h x f h x f h x f x x x f x f x x f , ( 0 ) ( 0) ( 0) 0 1 0 1 1 0 Δ = − + = − − =

(25)

[

]

₂0 2 0 2 0 1 0 1 1 2 1 2 2 1 0 2 ) ( ) ( ) ( ) ( ) ( , , h x f x x x x x f x f x x x f x f x x x f = Δ − − − − − − = Secara umum:

[

]

_n n n h n x f x x x f ! ) ( ,..., , 0 1 0 Δ =

Akan dijabarkan rumus interpolasi ‘beda maju’ dari rumus interpolasi ‘beda terbagi’ Newton. Didefinisikan

h x x− 0 =

α yang menunjukkan letak titik x

terhadap x0. Jadi misalnya α = 1.6, maka x terletak pada jarak 6/10 dari x1 ke arah

x2.

Diinginkan rumus untuk:

(x – x0) (x – x1) … (x – xk) dinyatakan dalam α x – xj = x0 + αh – (x0 + jh) = (α-j)h Jadi (x – x0) (x – x1) … (x – xk) = α(α -1)… (α -k)hk+1 sehingga n n n n h n f h n h f h h f h f x p ! ) 1 )...( 1 ( ... ! 2 ) 1 ( ) ( 0 2 0 2 2 0 0 Δ + − − + + Δ − + Δ + = α α α α α α

Jika didefinisikan koefisien binomial sbb:

! ) 1 )...( 1 ( k k k + − − = ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛α α α α , k>0 dan 1 0⎟⎟_⎠= ⎞ ⎜⎜ ⎝ ⎛α

maka didapat rumus interpolasi ‘beda maju’ sbb:

h x x x f j x p n j j n 0 0 0 dengan ) ( ) ( _⎟⎟Δ = − ⎠ ⎞ ⎜⎜ ⎝ ⎛ =

∑

= α α Contoh hitungan: p(x=1.5) = ? 5 . 1 0 . 1 0 . 1 5 . 1 0 = − = − = h x x α 1) p1(x) = ƒ(x0) + αΔƒ(x0) = -5 + 1.5 (6) = 4 2) p2(x) = ƒ(x0) + αΔƒ(x0) + α(α-1)∆2f(x0)/2! = -5 + 1.5 (6) + 1.5 (0.5)2/2! = 4.75

(26)

3.2.2. Beda Mundur

Notasi: ∇ƒ(z) = ƒ(z) - ƒ(z-h) ∇r+1_ƒ(_z₎₌_∇r_ƒ(_z₎_-_∇r_ƒ(_z_-_h₎_r_≥₁ Rumus interpolasinya 1 0 1 , dengan ) ( 1 ) ( 0 0 0 = ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛− − − = ∇ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ − − =

∑

= α α α h x x x f j j x p n j j n i xi f(xi) ∇ƒ ∇2ƒ ∇3ƒ ∇4ƒ -4 0.0 -5.0 6 2 6 0 -3 1.0 1.0 8 8 6 -2 2.0 9.0 16 14 -1 3.0 25.0 30 0 4.0 55.0 Contoh hitungan: p(x=3.5) = ? 5 . 0 0 . 1 0 . 4 5 . 3 0 − = − + = = h x x α 1) p1(x) = ƒ(x0) + (-α)∇ƒ(x0) = 55 + (-0.5) 30 = 40 2) p2(x) = p1(x) + (-α)(-α+1)∇2f(x0)/2! = 40 + (-0.5)(0.5)14/2! = 38.25 3) p3(x) = p2(x) + (-α)(-α+1) (-α+2)∇3f(x0)/3! = 38.25 + (-0.5)(0.5)(1.5)6/3! = 37.875

3.3. Lagrange

Polinomial Lagrange dibentuk dengan fomulasi berikut:

( )

( ) ( )

i n i i n x L x f x p

∑

= = 0

( )

_∑

≠ = = − − = n i j j i j j i i n x x x x x L 0 ,..., 1 , 0 Contoh:

( )

1 1 0 0 0 1 0 1 _f _x x x x x x f x x x x x p_i − − + − − =

( ) (

₍

₎₍

)(

)

_{) ( )}

₍

(

₎₍

)(

)

_{) ( )}

₍

(

₎

)(

₍

)

₎

( )

2 2 1 2 0 2 1 0 1 2 1 0 1 2 0 0 2 0 1 0 2 1 2 f x x x x x x x x x x f x x x x x x x x x f x x x x x x x x x p − − − − + − − − − + − − − − =

(27)

Contoh: hitung p2

( )

x yang melalui titik-titik

(

0,15

) ( ) (

;1,1; 3,25

)

( ) (

₍

)(

₎₍

)

₎

(

₍

)(

₎₍

)

₎

3 3 4 3 0 1 0 3 1 2 2 0 1 0 2 1 0 + − = − − − − = − − − − = x x x x x x x x x x x x x L

( ) (

₍

)(

₎₍

)

₎

(

₍

)(

₎₍

₎

)

2 3 3 1 0 1 3 0 2 2 1 0 1 2 0 1 − − = − − − − = − − − − = x x x x x x x x x x x x x L

( ) (

₍

₎₍

)(

)

₎

(

₍

)(

₎₍

₎

)

6 1 3 0 3 1 0 2 1 2 0 2 1 01 2 x x x x x x x x x x x x x L = − − − − − = − − − − = Jadi p2

( )

x =L0

( ) ( )

x × −5 +L1

( ) ( )

x × 1 +L2

( ) ( )

x × 25 =2x2 +4x−5

3.4. Beberapa fakta penting dari’beda terbagi’

1.

[

]

( )

! ,..., , ₁ 0 m f x x x f m m ξ = untuk ξ∈X

{

x0,x1,...,xn

}

dimana X

{

x0,...,xm

}

artinya interval terkecil dimana x0,x1,...,xm tercakup!

Contoh:

[ ]

( )

0 0 0 ! 0 f x f x f = ξ =

[

,

]

( ) ( )

'

( )

ξ 0 1 0 1 1 0 f x x x f x f x x f = − − = ξ∈

[

x0,x1

]

[

]

'

( )

ξ 2 1 , , 1 2 0 x x f x f = ξ∈X

{

x0,x1,x2

}

2. Jika f

( )

x adalah polynomial derajad m, maka

[

]

⎪ ⎩ ⎪ ⎨ ⎧ − > − = − < − − = 1 0 1 1 1 derajad polinomial , ,..., 0 m n m n a m n n m x x x f _n _m dengan

( )

1 0 1 1x ... a x a a x a x f m m m m + + + + = − −

3. Kesalahan dalam interpolasi

( )

( ) (

)(

₍

) (

₎

)

( )

_{( )}

x n n n f n x x x x x x x p x f 0 1 1 ξ ! 1 ... ₊ + − − − = − dengan ξ_x∈Η

{

x₀,....,x_n,x

}

4. f

[

x x x

] [

f x x x x x

]

dx d n n, , ,..., , , ,..., ₀ 0 =

(28)

Bab

4. INTEGRASI NUMERIS

4.1. Rumus trapesium dan Simpson

Pada bab ini akan dibicarakan cara menghitung integral secara numeris dari

∫

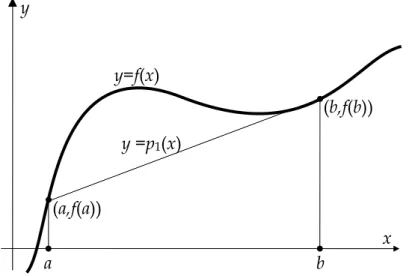
= b a f(x)dx I(f) dimana [a,b] berhingga

Gambar 8 Konsep integrasi trapesium

Rumus trapesium pada dasarnya adalah mendekati f(x) dengan garis lurus yang

melalui (a,f(a)) dan (b,f(b))

[

( ) ( )

]

2 ) ( 1 f a f b a b f I = − − y x y=f(x) b y =p1(x) a (b,f(b)) (a,f(a))

(29)

Integrasi Numeris Buku kuliah Error:

[

abx

]

f b x a x b f a b a x a f b a b x x f x p x f , , ) )( ( ) ( ) ( ) ( ) ( ) ( 1 − − = ⎭ ⎬ ⎫ ⎩ ⎨ ⎧ − − + − − − = −

ingat definisi ‘beda terbagi f[a,b,x].

Jadi ‘error’:

[

abx

]

dx f b x a x b f a f a b dx x f f E b a b a

∫

− − = + − − = , , ) )( ( )] ( ) ( )[ ( 2 1 ) ( ) ( 1

dengan harga tengah integral, didapat:

[

]

) ( " 12 ) ( ] , [ ) ( 6 1 ) ( " 2 1 ) )( ( , , ) ( 3 3 1 η η η ξ ξ f a b b a a b f b a dx b x a x b a f f E b a − − = ∈ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛₋ ₋ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ = ≤ ≤ − − =

∫

Jika interval [a,b] dibagi menjadi n pias sehingga untuk n≥1, h = (b-a)/n dan

xj = a + jh, j = 0,1,…,n, didapat:

[

]

∑

∑ ∫

∫

= − = ⎭ ⎬ ⎫ ⎩ ⎨ ⎧ − − = = = − n j j j j n j x x b a f h x f x f h f(x)dx f(x)dx I(f) j j 1 3 1 1 ) ( " 12 ) ( ) ( 2 1 η dengan xj-1≤_nj≤_xj.

Sehingga integralnya dapat didekati dengan

1 2 1 ... 2 1 ) (f =h_⎢⎣⎡ f₀ + f₁ + + f ₌₁ + f ⎤_⎥⎦ n≥ I_n _n _n

Kesalahan In(f) terhadap I(f) adalah

⎥ ⎦ ⎤ ⎢ ⎣ ⎡ − = − = − =

∑

= = n j j n j j n n f n n h f h f E f I f E 1 3 1 3 ) ( " 1 12 ) ( " 12 ) ( ) ( ) ( η η

(30)

Integrasi Numeris Buku kuliah

) ( " ) ( " 1 ) ( " 1 x f Max f n x f Min b x a n j j b x a≤ ≤ ≤

∑

₌ η ≤ ≤ ≤

karena f”(x) menerus pada a≤_x≤_b_{, maka}

η η η η ( " 12 ) ( ) ( " 12 ) ( ] , [ ) ( " 12 ) ( 2 3 2 3 f n a b f a b h b a f n h f E_n − − = − − = ∈ − =

Estimasi kesalahan asimtotis E~_n(f)

∫

∑

− = ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ − = ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ − = = ∞ → = ∞ → ∞ → b a n j j n n j j n n n dx x f h f Limit h f Limit h f E Limit ) ( " 12 1 ) ( " 12 1 ) ( " 12 1 ) ( 1 1 2 η η maka

{

'( ) '( )

}

12 ) ( ~ 2 a f b f h f E_n ≡− − Definisi:

Jika En(f) adalah kesalahan eksak, sedangkan E~_n(f)adalah estimasi darinya, maka

) ( ~

f

E_n disebut estimasi kesalahan asimtotis dari En(f) jika:

1 ) ( ) ( ~ = ∞ → _E _f f E Limit n n n atau ₍ ₎ 0 ) ( ~ ) ( = − ∞ → _E _f f E f E Limit n n n n

4.1.1. Rumus trapesium terkoreksi

Dengan menggunakanE~_n(f), rumus trapesium dapat ditingkatkan menjadi:

{

'( ) '( )

}

12 2 1 ... 2 1 ) ( ~ ) ( ) ( 2 1 1 0 f b f a h f f f f h f E f I f CT n n n n n − − ⎥⎦ ⎤ ⎢⎣ ⎡ ₊ ₊ ₊ ₊ = + = =

(31)

4.1.2. Rumus Simpson

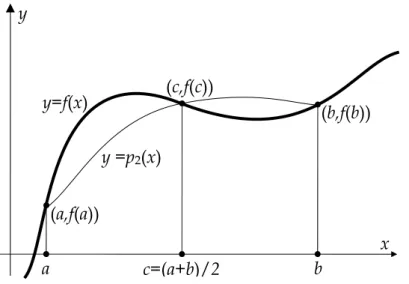
Gambar 9 Konsep integrasi Simpson

Dalam metode Simpson fungsi f(x) didekati dengan p2(x) yang melalui 3 titik

(a,f(a)), (c,f(c)) dan (b,f(b)) dimana c = (a+b)/2.

[

]

2 dengan ) ( ) ( 4 ) ( 3 ) ( ) )( ( ) )( ( ) ( ) )( ( ) )( ( ) ( ) )( ( ) )( ( ) ( 2 a b h b f c f a f h dx b f c b a b c x a x c f b c a c b x a x a f b a c a b x c x f I b a − = + + = ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ − − − − + − − − − + − − − − =

∫

Kesalahannya:

∫

− − − = − = b a dx x c b a f c x b x a x f I f I f E ] , , , [ ) )( )( ( ) ( ) ( ) ( 2 2

Harga tengah integral tidak dapat digunakan karena (x-a)(x-c)(x-b) berganti

tanda pada x = c. Didefinisikan: =

∫

x − − − a dt b t c t a t x w( ) ( )( )( )

Beberapa fakta mengenai w(x):

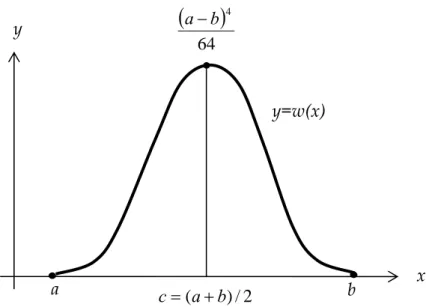
) )( )( ( ) ( ' untuk 0 ) ( , 64 ) ( ) ( , 0 ) ( ) ( 4 b x c x a x x w b x a x w b a c w b w a w − − − = < < > − = = = y x y=f(x) b y =p2(x) a (b,f(b)) (a,f(a)) c=(a+b)/2 (c,f(c))

(32)

Gambar 10 Fungsi y = w(x) untuk metoda Simpson

Jadi E2(f) dapat ditulis sebagai:

]

_∫

∫

− = = b a b a b a x c b a f dx d x w x c b a f x w dx x c b a f x w f E ] , , , [ ) ( ] , , , [ ) ( ] , , , [ ) ( ' ) ( 2 ] , [ ) ( 90 15 4 24 ) ( ] , [ ) ( ] , , , , [ ] , , , , [ ) ( ) ( ) 4 ( 5 5 ) 4 ( 2 b a f h h f b a dx x w c b a f dx x x c b a f x w f E b a b a ∈ − = ⎥⎦ ⎤ ⎢⎣ ⎡ − = ∈ − = − =

∫

η η η ξ ξ ξ

Jika interval [a,b] dibagi menjadi n pias, n≥_2, _h_{= (}_b_-_a_)/_n_, _xj=a+jh untuk

j = 1,2,3,…,n, sehingga

[

]

∑

∑ ∫

= − − = ⎭ ⎬ ⎫ ⎩ ⎨ ⎧ − + + = = = − 2 / 1 ) 4 ( 5 2 1 2 2 2 2 / 1 ) ( 90 4 3 genap ) ( ) ( 2 2 2 n j j j j j n j x x f h f f f h n dx x f f I j j η dengan x2j-2≤nj≤x2j Rumus Simpson: x y=w(x) 2 / ) (a b c= +

(

)

64 4 b a− y a b

(33)

[

n n n

]

n f f f f f f f f h f I = 0 +4 1 +2 2 +4 3 +2 4 +...+2 ₋2 +4 ₋1+ 3 ) ( Kesalahan estimasi: ) ( 180 ) ( ] , [ ) ( 180 ) ( ) ( 2 90 ) 2 / ( ) ( ) ( ) ( ) 4 ( 4 5 ) 4 ( 4 2 / 1 ) 4 ( 5 η η η η f n a b b a f a b h f n n h f I f I f E n j j n n − − = ∈ − − = − = − =

∑

=

Estimasi kesalahan asimtotis:

[

( ) ( )

]

180 ) ( ~ (3) (3) 4 a f b f h f E_n =− −

4.2. Rumus Newton–Cotes

Rumus trapesium dan Simpson sebetulnya merupakan dua buah rumus pertama dari rumus Newton-Cotes.

Untuk n≥_1,_h_{= (}_b_-_a_)/_n_,_xj=a+jh untuk j = 0,1,2,3,…,n. Didefinisikan In(f) dengan

mengganti f(x) dengan polinomial pn(x) pada titik-titik x0, x1,…, xn:

∫

= = b a n b a dx x p dx x f f I( ) ( ) _& ( )

Dengan interpolasi Lagrange untuk pn(x), maka

∫∑

∑

= = = = b a j n j n j n j j n j n f l x f x dx w x f x I ( ) ( ) ( ) ( ) ( ) 0 0 , , dengan w l x dx j n b a n j n j, =

∫

, ( ) =0,1,...,

Untuk nilai n = 1 dan 2 telah disajikan sebagai rumus trapesium dan Simpson.

Sekarang untuk n = 3, contoh untuk menghitung w0 adalah:

∫

₋− −₋ −₋ =b a dx x x x x x x x x x x x x w ) )( )( ( ) )( )( ( 3 0 2 0 1 0 3 2 1 0 Jika x = x0+μh, 0 ≤μ≤ 3, maka:

(34)

8 3 ) 3 )( 2 )( 1 ( 6 ) 3 ( ) 2 ( ) 1 ( 6 1 ) )( )( ( 6 1 3 0 3 0 3 3 2 1 3 0 3 0 h d h hd h h h h dx x x x x x x h w x x = − − − − = − − − − = − − − − =

∫

μ μ μ μ μ μ μ μ

Jika w1, w2, w3 dihitung dengan cara di atas, akhirnya akan didapat untuk n = 3

[

( ) 3 ( ) 3 ( ) ( )

]

8 3 ) ( ₀ ₁ ₂ ₃ 3 f x f x f x f x h f I = + + +

Kesalahan pada In(f) dinyatakan sebagai berikut:

a) Untuk n genap: ] , [ ) ( ) (f C h 3f( 2) a b E n n n n = ∈ + + _η _η dengan μ μ μ n dμ n C n n = ₊

∫

− − 0 2 ) )...( 1 ( )! 2 ( 1 b) Untuk n gasal: ] , [ ) ( ) (_f _C _h 2_f ( 1) _a _b E n n n n = ∈ + + _η _η dengan μ μ μ ndμ n C n n = ₊

∫

− − 0 2 ) )...( 1 ( )! 1 ( 1

4.2.1. Rumus Newton-Cotes Tertutup

n = 1, rumus trapesium

[

]

"( ) 12 ) ( ) ( 2 ) ( 3 ξ f h b f a f h dx x f b a

∫

= + − n = 2, rumus Simpson ) ( 90 ) ( ) 2 ( 4 ) ( 3 ) ( (4) 5 ξ f h b f b a f a f h dx x f b a

∫

− ⎥⎦ ⎤ ⎢⎣ ⎡ ₊ + ₊ = n = 3

[

]

( ) 80 3 ) ( ) ( 3 ) ( 3 ) ( 8 3 ) ( (4) 5 ξ f h b f h b f h a f a f h dx x f b a

∫

= + + + − + − n = 4, rumus Boole ) ( 945 8 ) ( 7 ) ( 32 ) 2 ( 12 ) ( 32 ) ( 7 45 2 ) ( (6) 7 ξ f h b f h b f b a f h a f a f h dx x f b a

∫

= _⎢⎣⎡ + + + + + − + _⎥⎦⎤−

(35)

Definisi: Integrasi numerik ~I(f) yang mendekatri I(f) disebut mempunyai

derajat ketepatan m jika: (a) I~(f)=I(f) untuk semua polinomial f(x) derajat

m

≤ , (b) ~I(f)≠ I(f) untuk beberapa polinomial f(x) derajat m+1

Contoh:

Pada rumus Newton-Cotes untuk n = 1, 3 dikatakan mempunyai derajat ketepatan

m = 1, 3. Sedangkan untuk n = 2, 4 mempunyai derajat ketepatan m = n + 1 = 3, 5.

Tampak bahwa rumus Newton–Cotes dengan n genap menghasilkan derajat

ketepatan ekstra dibandingkan dengan n gasal.

4.2.2. Rumus Newton–Cotes terbuka

Ada rumus Newton–Cotes yang tidak menggunakan salah satu atau kedua titik di ujung interval. Contoh yang paling sederhana adalah rumus titik tengah:

] , [ ) ( " 24 ) ( ) 2 ( ) ( ) ( 3 b a f a b b a f a b dx x f b a ∈ − + + − =

∫

η η Rumus kompositnya: (f) Ε (f) Ι f(x)dx _n _n b a + =

∫

)] f(x ) h[f(x (f) Ι_n = 1 +_L+ _n ] , [ ) 24 2 b a f"(η a) (b h (f) E_n = − η∈ dengan n a b h= ( − ) , x_j a j )h 2 1 ( − +

= sebagai titik tengah dari titik-titik

(

a+(j−1)h,a+ jh

)

untuk j=1,2,_K,n.

Rumus Newton–Cotes yang sedemikian ini disebut dengan rumus terbuka, sedangkan rumus yang terdahulu disebut tertutup.

2 = n :

∫

2 = + 0 ) ( " 3 ) ( 2 ) ( 3 1 x x f h x hf dx x f ξ 3 = n :

∫

3 = + + 0 ) ( " 4 3 )] ( ) ( [ 2 3 ) ( 3 2 1 x x f h x f x f h dx x f ξ 4 = n : ξ ( 45 14 )] ( 2 ) ( ) ( 2 [ 3 4 ) ( (4) 5 3 2 1 4 0 f h x f x f x f h dx x f x x + + − =

∫

) 5 = n :

(36)

) ( 144 95 )] ( 11 ) ( ) ( ) ( ) ( 11 [ 24 5 ) ( (4) 5 4 3 2 2 1 5 0 ξ f h x f x f x f x f x f h dx x f x x + + + + + =

∫

dimana n x x h= n − 0 , x

0 = batas bawah, xn = batas atas.

4.3. Kuadratur Gaussian

Pada metoda integrasi sebelumnya, rumus integrasinya berdasarkan

polinomial derajat rendah yang merupakan pendekatan f(x) dengan jumlah

pias semakin besar.

Kuadratur Gaussian, rumus integrasinya menggunakan polinomial yang derajatnya makin tinggi.

∑

∫

= ₌ = = n j jn jn n b a f I x f w dx x f x w f I 1 , , ( ) ( ) ) ( ) ( ) ( Sebagai ilustrasi:

∑

∫

₌ − = n j j j x f w dx x f 1 1 1 ) ( ) (

dengan w(x) ≡ 1 Faktor pemberat

{ }

wj dan titik nodal

{ }

xj dipilih sedemikian

sehingga kesalahan

∑

∫

₌ − − = n j j j n f f x dx w f x E 1 1 1 ) ( ) ( ) (

sama dengan nol untuk suatu polinomial f(x) dengan derajat setinggi mungkin.

) ( ) ( ) 1 ( ) (a₀ a₁x a x a₀E a₁E x a E x E m _n _n _m _n m n + +L+ = + +L+

Jadi E_n(f)=0 untuk setiap polinomial derajat ≤m, bila dan hanya bila

0 ) ( i =

n x

E i=0,1,_K,m.

♦ Kasus 1. n=1. Karena hanya 2 parameter, w1 dan x1 sehingga diperlukan 2

persamaan: 2 0 1 0 ) 1 ( 1 1 1 1 = → = − =

∫

− w w dx E_n 0 0 0 ) ( 1 1 1 1 1 = → = − =

∫

− x x w xdx x E_n sehingga

∫

− = 1 1 ) 0 ( 2 ) (x dx f f _&

♦ Kasus 2. n=2 . Ada 4 parameter w1, w2, x1, x2, sehingga dibutuhkan 4

(37)

Integrasi Numeris Buku kuliah 0 ) ( ) ( 1 1 2 2 1 1 + = − =

∫

− i i i i n x x dx w x w x E untuk i = 0,1,2,3 atau w₁+w₂ =2 w₁x₁+w₂x₂ =0 3 2 2 2 2 2 1 1x +w x = w w₁x₁3+w₂x₂3 =0 menghasilkan rumus: ) 3 3 1 ( ) 3 3 1 ( ) ( 1 1 f f dx x f = − +

∫

−

mempunyai derajat ketelitian 3. Bandingkan dengan rumus Simpson yang menggunakan tiga titik.

♦ Kasus 3. untuk n, Terdapat 2n parameter {w1} dan {x1} sehingga terdapat 2n

persamaan: ⎪⎩ ⎪ ⎨ ⎧ − = + − = = − = =

∑

= 0,2, ,2 2 1 2 1 2 , , 3 , 1 0 atau 1 2 , , 1 , 0 0 ) ( 1 _i i n n i x w n i x E n j i j j i n K K K

persamaan diatas merupakan sistem persamaan non-linier yang penyelesaiannya tidak selalu jelas. Oleh karena itu digunakan cara lain.

4.3.1. Kuadratur Gauss-Legendre

Untuk w(x)≡1, rumus Gauss pada interval [-1,1] adalah:

∫

∑

− = = 1 1 1 ) ( ) ( n j j j f x w dx x f

dengan titik xj adalah akar dari polinomial Legendre derajat n dalam interval

[-1,1]. Faktor pemberatnya adalah

n i x P x P n w i n i n i 1,2, , ) ( ) ( ) 1 ( 2 1 ' = K + − = + dan )! 2 ( ) ( ] )! 2 )[( 1 2 ( ) ! ( 2 ) ( ) 2 ( 2 4 1 2 n f n n n f E_n n n η + = +

Tabel 1 Gauss–Legendre titik dan pembobot

n x1 w1

2 ±0.5773502692 1.0

3 ±0.7745966692 0.5555555556

0.0 0.8888888889

(38)

n x1 w1 ±0.3399810436 0.6521451549 5 ±0.9061798459 0.2369268851 ±0.5384693101 0.4786286705 0.0 0.5688888889 6 ±0.9324695142 0.1712344924 ±0.6612093865 0.3607615730 ±0.2386191861 0.4679139346 7 ±0.9491079123 0.1294849662 ±0.7415311856 0.2797053915 ±0.4058451514 0.3818300505 0.0 0.4179591837 8 ±0.9602898565 0.1012285363 ±0.7966664774 0.2223810345 ±0.5255324099 0.3137066459 ±0.1834346425 0.3626837834 Contoh: ♦ n = 1: ) 3 3 1 5773502692 . 0 ( ) 3 3 1 5773502692 . 0 ( ) ( 1 1 4 4 8 4 4 7 6 4 4 8 4 4 7 6 − − − + =

∫

f x dx f f n = 3: ) 0 ( 8888888889 . 0 ) 7745966692 . 0 ( 5555555556 . 0 ) 7745966692 . 0 ( 5555555556 . 0 ) ( 1 1 f f f dx x f + − + =

∫

−

♦ Untuk integral pada interval umum [a,b], maka digunakan transformasi

sebagai berikut:

∑

∫

= − ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + + − − = ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ + + − − = n j j j b a x a b b a f w a b dx x a b b a f a b dt t f 1 1 1 2 ) ( 2 2 ) ( 2 ) ( ♦ 3 2 34 ) 1 ( 3 1 2 3₊ ₊ ₊ ₌

∫

x x x dx , dihitung dengan kuadratur Gaussian menghasilkan:

66666667 . 34 ) 3 3 1 2 ( ) 3 3 1 2 ( 2 3 3 1 ) 1 3 ( 3 1 0 . 1 2 3 3 1 ) 1 3 ( 3 1 0 . 1 2 1 3 ) ( 3 1 = − + + = ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ ⎟ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎜ ⎝ ⎛ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛− − + + × + ⎟ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎜ ⎝ ⎛ ₊ ₊ ₋ × − =

∫

f f f f dx x f