KONSTRUKSI ALGORITME PENANDAAN DIJITEL ELGAMAL BERBASIS GRUP KURVA ELIPTIK IS ES'M FIRMANESA

KONSTRUKSI ALGORITME PENANDAAN

DIJITEL ELGAMAL BERBASIS

GRUP

KURVA ELIPTIK

IS ES'M FIRMANESA

SEKOLAT3 PASCASARJANA

INSTITUT PERTANIAN BOGOR

BOGOR

2009

PERNYATAAN MENGENAI TESIS DAN

SUMBER INFORMASI

Dengan ini, saya menyatakan bahwa tesis Konstruksi Algoritme Penandaan Dijitel ElGamal Berbasis Grup K U N ~ Eliptik adalah karya saya dengan arahan dari komisi pembimbing dan belum diajukan dalam bentuk apa pun kepada perguruan tinggi mana pun. Sumber informasi yang berasal atau dikutip dari karya yang diterbitkan maupun tidak diterbitkan dari penulis lain telah disebutkan dalam teks d m dicantudcan ddam D a f k Pustaka di bagian akhir tesis ini.

Bogor, Pebruari 2009 Is Esti Firmanesa

ABSTRACT

IS EST1 FIRMANESA. The Construction of ElGamal Digital Signature Algorithm based of Elliptic Curve Group. Supervised by SUGI GURITMAN and NUR ALIATININGTYAS.

Business practice has changed with the introduction of computer-based technologies. The substitution of electronic transactions for their paper-based predecessors has reduced costs and improved efficiency. Trillions of dollars in funds and securities are transferred daily by telephone, wire services, and other electronic communication mechanisms. The high value or sheer volume of such transactions within an open environment exposes the financial community and its customers to potentially severe risks from accidental or deliberate alteration, substitution or destruction of data by adversaries. In an electronic-based environment, controls must be in place that provide the same degree of assurance and certainty as in a paper environment. The financial community is responding to these needs. One of the examples for this assurance is used the ElGamal digital signature algorithm.

The aim of this thesis is to construct a new digital signature which is analogue to the EIGarnal signature algorithm based on elliptic curve group. This constructed algorithm is called Elliptic Curve ElGamal Signature Algorithm (ECESA). Unlike the ordinary discrete logarithm problem and the integer factorization problem, no subexponential-time algorithm is known for the elliptic curve discrete logarithm problem. For this reason, the strength-per-key-bit is substantially greater in an algorithm that uses elliptic curves. This thesis describes ECESA and its related security, implementation, and interoperability issues based on the standard, ANSI X9.62-1998, public key cryptography for the financial services industry.

When implemented with proper controls, the techniques of the standard The Elliptic Curve Digital Signature Algorithm (ECDSA) provide data integrity, data origin authentication, and non-repudiation of the message origin and the message contents.

Keywords: cryptography, elliptic curve, digital signature, ElGamal signature, elliptic curve discrete logarithm problem.

RINGKASAN

IS EST1 FIRMANESA. Konstmksi Algoritme Penandaan Dijitel ElGamal Berbasis Grup KuNa Eliptik. Dibimbing oleh SUGI GURITMAN dan NUR ALIATININGTYAS

Dalam era globalisasi, teknologi memegang peranan yang sangat penting, contohnya teknologi informasi memudahkan seseorang dalam mendapatkan informasi yang dibutuhkannya. Perubahan transaksi secara elektronik dari konvensional (transaksi berdasarkan kertas) telah mengurangi biaya dan meningkatkan keefisiensian. Bertrilyun-trilyun dolar biaya dan keamanan ditransfer setiap hari melalui telepon, layanan kabel, dan mekanisme-mekanisme komunikasi elektronika lainnya. Beberapa transaksi yang besar telah membuka komunitas dan nasabahnya yang sangat berpotensial terhadap resiko perubahan, penggmtian, atau p e m s k data yang disengaja maupun tidak. Resiko ini dipersulit lagi dengan antar koneksi neiwork-neiwork dan jumlah lawan yang semakin besar.

Beberapa kontrol pengamanan konvensional yang menggunakan transaksi kertas adalah tidak ada dalam transaksi elektronik. Contoh beberapa kontrol konvensional yang aman adalah tanda tangan atau segel timbul untuk melindungi integritas dan mengindikasikan identitas pengirim yang asli. Pada bidang elektronik, kontrol-kontrol tersebut harus memberikan jaminan dan keyakinan seperti halnya dengan yang konvensional. Saat ini, komunitas-komunitas keuangan sedang merespon kebutuhan-kebutuhan seperti itu.

The Elliptic Curve Digital Signature Algorithm (ECDSA) adalah kurva eliptik yang analog dengan Digital Signature Algoriihm (DSA). Tidak seperti masalah logaritma-diskrit (MLD) dan masalah faktorisasi intejer (MFI) biasa, untuk ECDSA belum ada algoritme sub eksponensial yang diietahui untuk masalah logaritma diskret kurva eliptiWMLDKE (ANSI X9.52, 1998). Untuk alasan ini, the strength-per-key-bit pada dasarnya lebih besar dalam suatu algoritme yang menggunakan kurva-kurva eliptik. Hal-ha1 yang menjadi pertimbangan penggunaan ECC adalah ECC memberikan keefisiensian yang lebih besar daripada sistem faktorisasi intejer @I) atau sistem logaritma diskret (LD) dalam segi-segi komputasional, ukuran kunci maupun bandwidth-nya. Penghematan-penghematan ini berarti menunjukkan kecepatan yang lebih tinggi, pemakaian sumber daya yang lebih kecil, dan pengurangan ukuran kunci (J. Lopez dan R. Dahab).

-

Ada dua lapangan berhingga yang sering digunakan dalam kriptografi kurva eliptik, yaitu lapangan berhingga prima (&) dan lapangan karakteristik dua (F 2"').

Lapangan berhingga Z, lebih efekiif u& implem~ntasi sofhvae kriptografi kuma eliptik. Sedangkan lapangan berhingga

F

zm lebih efektif untuk hardware yang sistem kerjanya berdasarkan algoritme kriptografi kurva eliptik (ANSI

X9

62, 1998). Naxnun penulisan tesis ini hanya membahas tentang kurva eliptik

E(a, b) atas

z,

Kuwa eliptik E(a, b) atas Zp merupakan himpunan penyelesaian dari

sehingga memenuhi persamaan 4a3

+

27b2

*

0. Domain x dan y adalah F,. Salah satu penggunaan kurva eliptik sebagai algoritme kriptografi asimetrik adalah

untuk membuat penandaan dijitel (digital signature) yang melibatkan algoritme hash. Ketika diimplementasikan dengan kontrol-kontrol yang tepat, teknik ini rnemberikan integritas data, otentikasi data asli, serta non-repudiasi dari pesan asli dan isinya.

Berdasarkan sejarahnya, penggunaan penandaan dijitel berawal

dari

penggunaan teknik kriptograti yang digunakan untuk mengamankan infonnasi yang hendak ditransmisikan/di~~mpaikan kepada orang yang lain yang sudah digunakan sejak ratusan tahun yang lalu. Tujuan suatu tan& tangan dalam sebuah dokumen adalah

untuk

memastikan otentisitas dokumen tersebut. Penandaan dijitel sebenarnya adalah bukan tan& tangan seperti yang dikenal selama ini, penandaan ini men- cara yang berbeda untuk menandai suatu dokumen sehingga tidak hanya mengidentifikasi si pengirim, namun juga memastikan keutuhan dokumen tersebut tidak berubah selama proses lransmisi. Penandaan dijitel didasarkan pada isi pesan itu sendiri.

Proses pemberian tanda pada i n f o m i rabasia yang akan dikirim disebut penandaan (signing). Proses ini dilakukan untuk mengubah tan& menjadi dokumen dijitel, sehingga pada saat pengaksesan dokumen tersebut, terdapat verifikasi tanda yang diberikan. Ada tiga prosedur dalam skema penandaan dijitel, yaitu prosedur: pembangkitan kunci (key generation), pembuatan tanda (signature generation), dan verifikasi tanda (signature verification).

-

D& uraian-uraian di atas; &is

ini

ju&i melakukan penelitian tentang penggunaan ECC pada algoritme penandaan EIGamal, yaitu Algoritme Penandaan ElGamal Kurva Eliptik (ECESA), seperti halnya dengan penelitian sebelumnya, yaitu ECDSA yang telah menjadi standardisasi (ANSI X9.62, 1998). Penelitian tentang ECESA ini diharapkan memperoleh perbailcan dari algoritme pmmdaan ElGamal itu sendhi. Tesis ini menjelaskan ECESA dan menganalisa aspek keamanan, serta mengimplementasikan ECC.

Kata kunci: kriptografi, kurva eliptik, penandaan dijitel, penandaan ElGamal, masalah logaritma diskret kurva eliptik

Hak cipta dilindungi Undang-undang

1 IkImang n t e q p t p sebagMn a f m selumh A a y ~ tulrs in? lanpa

mencantumkan atau menyebut sumber.

a Pengutipan hrmya untuk kepentingan pendidikan, penelitian, penulisan Rmya ilmiah, penyusunan laporan, penulisan kritik,

atau tinjauan suatu masalah.

b Penguiipan tidak merugr'h kepeniingan yang wajar Institui Pertanian Bogor.

2 D i b a n g mengumumkan

dan

memperbanyak sebagian atau seluruh karya tulis dalam bentuk apapun tanpa izin Institut Pertanian Bogor.

KONSTRUKSI ALGORITME PENANDAAN

DIJITEL ELGAMAL BERBASIS

GRUP KURVA ELIPTIK

Tesis

sebagai salah satu syarat untuk memperoleh gelar Magister Sains pada

Departemen Matematika

SEKOLAH PASCASARTANA

INSTITUT PERTANIAN BOGOR

BOGOR

2009

Judul Tesis : Konstruksi Algoritme Penandaan Dijitel ElGamal Berbasis Grup Kuwa Eliptik

Nama : Is Esti Firmanesa NIM : G551060361

Disetujui Komisi Pembimbing

Diketahui

Ketua Program Studi kan Sekolah Pascasarjana Matematika Terapan

Dr. Ir. Endar H. Nugrahani,

PRAKATA

Puji syukur penulis panjatkan kepada Allah SWT atas segala karunia-Nya sehingga karya ilmiah ini berhasil diselesaikan. Terna yang dipilih dalam penelitian dilaksanakan sejak bulan Januari 2008 ini adalah kriptografi k u ~ a eliptik, dengan judul Konstruksi Algoritme Penandaan Dijitel ElGarnal Berbasis Grup Kuwa Eliptik

Terima kasih penulis ucapkan kepada Bapak Dr. Sugi Guritman dan Ibu Dra. Nur Aliatiningtyas, M.Si. selaku pembimbing, serta Ibu Dr. Ir Endar H.N., M.S. selaku pembimbing akademik dan Ibu Dr. Ir. Sri Nurdiati, M.Sc. yang telah memberikan banyak saran Di samping itu, penghargaan penulis sampaikan kepada para dosen yang telah memberikan ilmu dan pengetahuannya kepada penulis, serta para staf departemen Matematika yang telah membantu selama proses penyelesaian tesis ini. Ungkapan terima kasih juga disampaikan kepada ayahhunda tercinta atas kasih sayangnya dan suami (Aris Riyanto) / anak (Mas Farrell Zhafuafif) serta saudara-saudara tercinta atas segala doa, semangat, dan kasih sayangnya.

Semoga karya ilmiah ini bermanfaat

Bogor, Pebruari 2009 Is Esti Firmanesa

RIWAYAT HIDUP

Penulis dilahirkan di Bojonegoro, Jawa T i u r pada tanggal 23 Desember 1973 dari ayah

M.

Imam Soewito (Alm) dan ibu Endang Sri

Wahyuni

(Alm). Penulis merupakan putri ke-3 dari empat bersaudara.

Tahun 1992 penulis lulus dari SMA Negeri 1 Bojonegoro clan pada tahun yang sama lulus seleksi masuk Akademi Sandi Negara. Kemudian pada tahun 1996 penulis memperoleh bea siswa dari h b a g a Sandi Negara (penulis tercatat

sebagai Pegawai Negeri Sipil di Lembaga Sandi Negara sampai sekarang di bidang penelitian dan pengkajian kriptologi) untuk melaksanakan tugas belajar S1 ke program studi Matematika Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Indonesia Lulus pada tahun 2000. Tahun 2006 penulis memperoleh bea siswa kembali dari Lembaga Sandi Negara untuk melanjutkan studi ke jenjang S2 di program studi Matematika Terapan, Pascasajana di Institut

DAFTAR

IS1

Halaman DAFTAR GAMBAR ... ..., ,,...,

.

...

.

. . .

.

xi

..

DAFTAR TABEL ... ... ... . .. . . ...

.

. xll

...

DAFTAR LAMPIRAN

...

.

. .

.

.. .. ..

.

.

. . .

.. .. . . .. .

.

.. .. ..

..

,

. .

. . .

. . .

. . .

.

.

. . .

xlii 1.1 Latar Belakang . . . . ... 1 1.2 Perurnusan Masalah

. . . .. .

.. . . .. .. .. ..

.

. ..

.

.

. .. .. .. .. . .

.

.

. .

,

.

, , . . .

. .

.

. . .

. . . 4 1.3 Tujuan Penelitian

_.

_.

....

...

4 1.4 Manfaat Penelltian ... .. . .

.

.

. ... ..

.. .. .. .. . . .. . ... . .. .. . .

. . .

.

.

... 4 1.5 Batasan Masalah 4 I1 TINJAUAN PUSTAKA 2.1 Aritmatika Integer Modulo n .

..

... ... ...

.

. . . . . 5

2.2 Tes Probabilisrtic Primality ... 9

2.3 Struktur Aljabar 2.4 Logaritma Di 2.5 Fungsi Hash

_...

2.6 Penandaan Dijitel ... . .. .. .. ..

. . .. . . .. ..

..

.

... .. .. .. .. ..

. . .

,

.

, . . , . . . ,

.

,

.

, , , ... 16

3.1 Skema Penyandian Kunei Publik ... 22

3.2 Kriptografi Kuwa Eliptik ...

..

..

. . .. .. . .

..

..

.. .. .... .. ..

.. .

...

. . . . . .

. . .

23

3.3 Aritmatika Kuwa Eliptik

...

... 27

3.4 Parameter Domain Kuwa Eliptik 34 3.5 Tingkat Keamanan ECC

. ... .. ....

.. .. .. .. . ... ..

.

..

.. .. .. .

. .. ... . . . .

. . .

. . 34

3.6 Implementasi Algoritme ECC ... .. .. .. . ... .... .. ..

..

. ..

.

.. ... ... ... . . .

. . . . .

36

IV ALGORITME PENANDAAN ELGAMAL 4.1 Penyandian Kunei Publik ElGamal ... ... 38

4.2 Penyandian Kunci Publik ElGamal Digeneralisasi

...

42

4.3 Algoritme Enkripsi Kurva Eliptik ElGamal

...

43

4.4 Penandaan Dijitel dari Penyandian Kunci Publik Yang Dapat Dibalik ...

. ... .

... 45

4.5 Algoritme Penandaan ElGamal . .. .. ... ..

. . .. . . .

. .. .. . ....

.. .... ..

. . . .

46

4.6 Algoritme Penandaan Digeneralisasi 53 4.7 Implementasi Algoritme ElGamal . . .. ..

.

.

..

..

.. .. .. ..

.... .. .. .. .. ... ...

.. . .

55

V ECESA DAN ASPEK-ASPEK KEAMANAN ECC SEBAGAI PENGAMAN DATA PADA ECESA 5.1 Algoritme Penandaan ElGamal Kuwa Eliptik ... 59

5.2 Aspek-aspek Keamanan Kriptografi Kurva Eliptik Sebagai Pengaman

...

Data Pada ECESA 62

VI PENUTUP 6.1 Kesimpulan ... 78 ... 6.2 Saran 79 ... DAFTAR PUSTAKA 80

DAFTAR GAMBAR

Halaman

...

1 Fungsi penandaan SA dan h g s i verifikasi

V A

18

...

2 Skema penandaan dijitel dengan apendii 20

3 Enkripsi dengan teknik kunci publik

...

23

...

4 Penjumlahan dua titik P dan Q yang berbeda 25

...

5 Sifat asosiatif (P+Q)+R 26

...

6 Sifat asosiatif P+(Q+R) 26

...

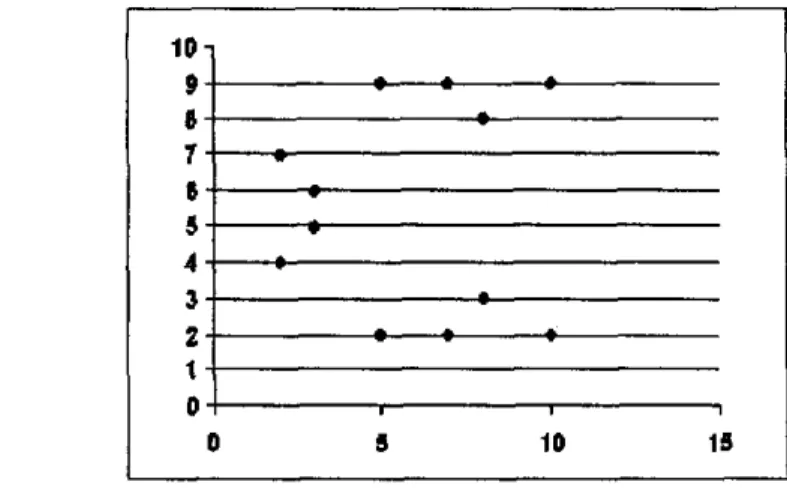
7 Scatterplot dari Grup Eliptik E1,(O, 1) 28

...

8 Operasi penjumlahan identitas 29

..

_...

9 Operasi doubling jlka yP = 0 31

...

DAFTAR TABEL

Halaman

Perbandingan waktu untuk memecahkan kunci

...

3

Order dari elemen-elemen pada

Zb

...

9

...

Subgrup siklik dari G 13

...

Tabel QRI1 33

...

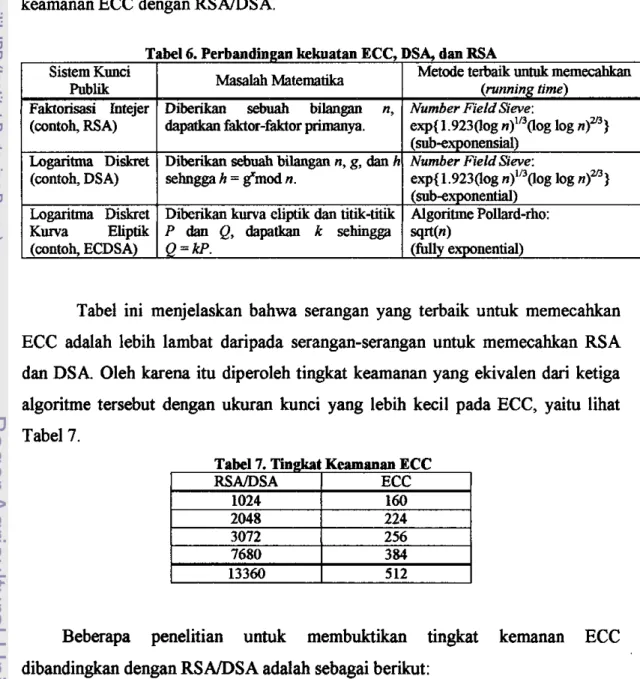
Tabel QRl dengan (x. y) 33 Perbandingan kekuatan ECC. DSA. dan RSA

...

35

Tingkat Keamanan ECC

...

35

.

...

Tingkat Keamanan ECC

dari

R Silverman 36 Tingkat Keamanan ECC dari Intelop

...

36

Elemen-elemen dari Fz5 yang bergenerator a ... 54

...

Hubungan antara grup

Zb

dan kurva eliptik E(Zp) 59

...

Notasi Penandaan ElGamal clan ECESA 59

...

Pengesetan Penandaan ElGamal dan ECESA 60 Pembangkitan Kunci Penandaan ElGamal clan ECESA

...

60

Pembangkitan Tanda dari Penandaan ElGamal clan ECESA

...

60

Pemverifikasian Tanda dari Penandaan ElGamal dan ECESA

...

60

DAFTAR LAMPIRAN

Halaman

1 Algoritma ECC

...

81

2 Program tes keprimaan dan pembangkitan kunci ElGamal

...

84 3 Program Aritmatika Kurva Eliptik

...

87

BAB I

PENDAHULUAN

1.1 Latar Belakang

Keamaaan informasi (information security) merupakan bagian yang sangat penting dari sebuah sistem dalam jaringan komputer terutama yang terhubung dengan internet. Suatu sistem yang mempermudah dan memanjakan pen- tidak akan berguna tanpa didukung oleh sistem keamanan yang tinggi. Oleh karena itu, informasi atau data rahasia yang akan dikirim hams disandikan agar tidak dapat dibaca oleh orang lain yang tidak berkepentingan. Untuk mengarnankan informasi rahasia tersebut diperlukan suatu teknik pengamanan, yaitu teknik k r i p t o d .

Kriptografi adalah studi teknik matematika yang berhubungan dengan aspek keamanan informasi seperti kerahasiaan, integritas data, otentikasi entitas, dan otentikasi data asli (Menezes, 1997). Algoritme kriptografi adalah suatu fungsi matematika yang digunakan untuk enkripsi (menyandi) dan dekripsi (membuka saudi) (Schneier, 1996). Algoritme kriptografi dibagi menjadi dua, yaitu simetrik dan asimetrik I kunci publii (Schneier 1996).

Konsep skema kriptografi asimetrik ditemukan oleh Whitfield D i e dan Martin Hellman. Kontribusi mereka terhadap kriptograS adalah notasi kunci yang digunakan adalah sepasang kunci enkripsi dan kunci dekripsi yang tidak mungkin

satu kunci diperoleh dari kunci lainnya. Skema ini disebut "kunci publik" karena kunci enkripsi dibuat publik. Orang lain dapat menggunakan kunci enkripsi untuk mengenkripsi pesan tetapi hanya orang tertentu yang mempunyai kunci dekripsi dapat mendekripsi pesan. Biasanya kunci enkripsi disebut kunci publii dan kunci dekripsi disebut kunci privat. Contoh dari algoritme asimetris adalah RSA, ElGamal, DSA (Digital Signature Algorithm), ECC (Elliptic Curve Cryptogcrply)

dan

lain-lain.

Skema kunci publii dibuat tahan terhadap serangan pilih-plainteks (chosen- plaintext attack), keamanannya terletak pa& sulitnya menebak kunci rahasia

dari

kunci publik dan sulitnya menebak teks terang dari teks sandi. Tetapi algoritme kunci publii rentan terhadap serangan pilii-siferteks (chosen-ciphertext attack).

Algoritme-algoritme yang di&an dalam skema enkripsi kunci publik yang berhubungan dengan masalah komputasi berbasis keamanan adalah Masalah Faktorisasi Intejer (MFI) yang aritmatikanya berbasis intejer modulo n, wntohnya RSA, Masalah Logaritma Diskret (MLD) yang aritmatikanya berbasis intejer grup siklik, wntohnya algoritme ElGamal clan DSA,

dan

Masalah Logaritma Diskret Kurva Eliptik (MLDKE) yang aritmatikanya berbasis struktur grup, contohnya

Elliptic Curve Digital Signature Algorithm (ECDSA).

Pada tahun 1985, ECC telah diperkenalkan pertama kali oleh Neal Koblik dan Victor Miller. ECC yang baru-baru ini diajukan, menarik perhatian bidang industri maupun akadernik sebagai alternatif dalam penggunaan sistem kunci publii RSAIDSA. Tingkat keamanannya bergantung pada Masalah Logaritma Diskret Kurva Eliptik (MLDKE).

Sampai saat ini belum ada algoritme sub-eksponensial yang diketahui untuk memecahkan pennasalahan logaritma diskret ECC. Serangan terbaik yang terkenal adalah algoritme Pohlig-Hellman dan algoritme Pollard Rho yang mempunyai fully-exponential running time dari

~ ( h )

dimana p adalah pembagi bilangan prima terbesar dari n. Untuk menahan serangan ini, parameter kurva eliptik hams dipilii dengan tepat, sehingga n dapat dibagi dengan suatu bilangan prima p yang cukup besar. Jadi f i s t e p adalah jumlah komputasi yang tidak

mungkin dilakukaa (misalkan, rP2'64. Di sisi lain, algoritme t e m p t untuk memecahkan MFI dan MLD yang diketahui adalah Number Field Sieve

(NFS)

mempuuyai sub-exponential running time qexp((cto(1) )(In n)IB(ln In nlm))

dengan c = 1.9229.

Dari uraian di atas, hal-ha1 yang menjadi pertimbangan dalam penggunaan ECC adalah ECC memberikan keefisiensian yang lebih besar daripada sistem

fhrisasi intejer (FI) atau sistem logaritma diskret (LD) dalam segi-segi komputasional, ukuran kunci maupun bandwidth-nya Penghematan-penghematan ini berarti menunjukkan kecepatan yang lebih ti@, pemakaian sumber daya yang lebih kecil, dan pengurangan

ukuran

kunci. Tabel 1 menunjukkau

perbandingan waktu uutuk memecahkan kunci antara ECC (basis keamanannya MLDKE), RSA (basis keam-ya adalah MFI), dan DSA (basis keamammya adalah MLD).

Sedwgkan Pemndaan Dijitel (Digital Signature)

adalah

kriptogmfi primitif (kriptograti yang memberikan keamman informasi) yang menjadi landasan di dalam otentikasi, otorisasi, dan non-tepdhsi. T u j u a ~ y a adalah memberikan

suatu alat yang digunakan oleh entitas

untuk

mengikat identitasnya menjadi satu bagian dari infonnasi. Proses pemberian tanda pada informasi rahasia yang

akan

Tabel 1. Perbandingan waktu untuk memecahkan kunci

Umur Proteksi

Sampai 20 1 0 Sampai 2030

Tabel ini memperlihatkan semakin besar panjang kunci, maka selisih lebar kunci yang digunakan semakin besar. Sebagai contoh

untuk

nilai keamanan 10" MIPS (Million Insfructions Per Second)

tahun,

ECC hanya membutuhkan 160 bit

sedan* RSAIDSA membutuhkan 1024 bit. Dengan kata lain RSA/DSA

membutuhkan 6,4 kali jumlah bit kunci ECC

untuk

nilai 10" MIPS tahun. MIPS

tahun

adalah satuan waktu yang menunjukkan kemampuan suatu algoritme

untuk

melakukan berjuta-juta instruksi per detik dalam satu

tahun.

Hal

ini

tentunya ECC dapat menjadi pilihan yang baik untuk membangun sistem kriptografi yang memilii tingkat keamanan yang tinggi (Nana Juhana, 2005).

Dari pertimbangan-pertimbangan tentang ECC di atas, tesis ini juga melakukan penelitian tentang penggunaan ECC pada algoritme Penandaan ElGamal (ECESA), seperti halnya dengan penelitian sebelumnya, yaitu ECDSA (Standmd, X9.62-1998, Public Key Cryptograpphy For The Financial Services

Zndusny). ECDSA mendefinisikan suatu teknik

untuk

membuat

dan

mengesahkan penandaan dijitel. Standard ini menjelaskan suatu metode

untuk

penandaan dijitel meng%unakan kurva eliptik yang analog dengan DSA. Namun penelitian ECESA ini

baru

penelitian awal

dan

belum diapliiikan ke

bentuk

program.

Algoritme Penandaan ElGarnal adalah algoritme yang aritmatikanya

berbasis intejer modulo n prima, Basis keanmmmya bergantung pada kesukaran

dari perhitungan Masalah Lopitma Diskret (MLD) dalam sebuah subgrup berorder prima atas Z i

.

Waktu Untuk Memecahkan Kunci

(MIPS

Tahun) l.OOE+ 12 1 .00E + 24 Jumlah Bit

ECC

160 224 1 024 2048

dikirim disebut penandaan (signing). Proses

ini

dilakukan untuk mengubah tanda menjadi dokumen dijitel. Dengan demikian, pada saat pengaksesan dokumen itu terdapat verifikasi tan& yang diberikan. Ada 3 prosedur dalam skema penandaan dijitel, yaitu prosedw pembangkitan kunci (key generation), pembuatan tan&

(signature generation), dan verifikasi tan& (signature verification).

1.2 Identifikasi Masalah

Penunusan pennasalahan dari latar belakang penelitian ini adalah.

-

Bagaimanakah mengonstruksi aritmafika ECC?

-

Ba@mad& mengonstruksi algoritme Penandaan ElGamal yang berbasis pada aritmatika ECC?

-

Bagaimanakah aspek-aspek keamanan ECC sebagai pengaman data pada algoritme Penandaan ElGamal Kurva Eliptik (ECESA)?

1 3 Tujnan Penelitian

Penelitian ini bertujuan untuk mengonstruksi aritmatika ECC, mengonstruksi algoritme Penandaan ElGamal yang berbasis aritmatika ECC, dan mengaualisa aspek-aspek keamanan ECC sebagai ~ pengaman data . . pada ECESA.

1.4 Manfaat Penelitian

Penggunaan aritmatika ECC pada algoritme Penandaan ElGamal akan memberikan suatu peningkatan kualitas pada aspek keamanan algoritme Penandaan ElGamal itu sendiri.

1.5 Batasan Masalah

Batasan

masalah

yaog

digunakan dalam tesis ini

adalah:

-

_{Persamaan kurva eliptik yang digunakan adalah}

₉

=

x'

+

m + b atas F,

dimanap adalah bilangan prima yang memenuhi 4 2

+

27b2 # 0, dimana x, y,

a, b E R atau didefinisikan sebagai:

G = {(XJJ) E ~ ~ / f l = 2 + m + b , 4 d + 2 7 b ~ # 0 ) .

-

Aspek kecepatan ECESA d i d i lebih cepat dari algoritme p d a a n

BAB

I1

TINJAUAN PUSTAKA

Untuk mencapai tujuan penulisan penelitian maka dalam subbab ini akan diberikan beberapa teori yang berupa definisi, teorema yang berkaitan dengan pembahasan, yaitu mengenai teori bilangan, tes keprimaan, struktur aljabar, logaritma diskret, fbngsi hash, dan penandaan dijitel.

2.1 Aritmatika Intejer Modulo n

Intejer adalah bilangan yang tidak mempunyai pecahan desimal, misalnya 2, 19, 0, -4, dan -29. Himpunan intejer {.

.

. , -2, -1, 0, 1, 2, . . . ) dinotasikan dengan Z. Semua bilangan yang dituliskan dalam definisi-definisi berikut adalah anBota himpunan intejer.

Definisi 1 (Menezes, 1997) Misalkan a, b E Z dan b # 0. Kita sebut b membagi

a, ditulis bla, jika ada intejer c sehingga a = bc. Dalam hal ini b disebut juga pembagilfaktor dari a atau a disebut kelipatan dari b. Jika a tidak membagi b dinotasikan dengan &b.

Contoh: 5

1

30 dan 7 142

Teorema 2 (Victor Shoup, 2005) Untuk setiap a, b, c G Z , diperoleh:

1. Jika alb dan blc maka

4.

2. Jika alb , maka aclbc .

3. Jika cJa dan clb, maka c)(& +eb), untuk setiap d, e E Z. 4. Jiia alb dan b +; 0, maka la1

<

Ibl .

5. Jika alb dan bla, maka la1 = Ibl.

Definisi 3 (Menezes, dkk, 1997) Floor dari x yang dinotasikan oleh adalah

L

intejer terbesar yang kurang dari atau sama dengan x.

Definisi 4 (Menezes, 1997) Algoritme Pembagian Intejer. Jika a dan b adalah bilangan bulat dengan b > 0, maka ada tepat satu q, r E Z sehingga a = qb

+

r, 0 5 r < b. Dalam ha1 ini, a disebut yang dibagi, b adalah pembagi, q

adalah hasil bagi, dan r adalah sisa pembagian. Selanjutnya sisa pembagian dinotasikan dengan a mod b dan hasil bagi dinotasikan a div b. Fakta bahwa misalkan a, b E Z , b ie 0 maka a div b = Lalbl d m a mod b = a - b Lalbi.

Definisi 5 (Menezes, 1997) Pembagi Bersama. Suatu intejer c dikatakan pembagi bersama dari a dan b jika cla dan clb .

Definisi 6 (Menezes, 1997) Pembagi Bersama Terbesar. Suatu intejer tak negatif

d disebut pembagi bersama terbesar (greatest common divisor/gcd) dari intejer a d m b, dinotasikan d = gcd(a,b) jika:

1 ) d adalah pembagi bersama a dan b; 2) jika 3c dengan cla dan clb , maka c I d.

Berikut ini adalah algoritme untuk menghitung pembagi bersama terbesar dari dua bilangan bulat.

Algoritme Euelid yang diperlnas (Menezes, 1997)

Input : dua bilangan bulat tidak negatif, a dan b dengan a 2 b

Output : d = gcd (a, b) dan intejer x dan y yang memenuhi mr

+

by = d

1. Jiiab=Omakatetapkand=a,x=l,y=O

2. Tetapkan nilai xz = 1, X I = 0, y~ = 0, yl = 1

3. Selama b > 0, dilakukan iterasi berikut: 3.1 Tentukan: q = Lalbl r = a - q b x = x z - q X 1 y=y2-@'I 3.2 Tentukan: a = b b = r xz = X l X1 = x

y2 = Y I

Yl = Y 4. Tetapkan d = a, x = x2, y = y2

Definisi 7 (Samuel, 2003) Prima. Suatu bilangan prima adalah intejer lebih besar dari pada 1 yang hanya dapat dibagi oleh 1 dan dirinya sendiri, dan tidak ada bilangan intejer lainnya. Suatu bilangan komposit adalah sebuah intejer yang lebih besar dari 1 yang bukan prima.

Definisi 8 (Menezes, 1997) Prima Relatif. Intejer a dan b diiatakan prima relatif atau disebut juga koprima jika gcd(a, b) = 1.

Contoh: Karena gcd(17,30) =1, maka 17 relatif prima dengan 30.

Definisi 9 (Menezes, 1997) Misalkan n intejer positif Himpunan intejer modulo

n dinotasikan Z, adalah himpunan intejer (0, 1, 2,

.

. . , n-1 ). Operasi penjumlahan, pengurangan, dan perkalian dinyatakan dalam modulo n.

Contoh: Zlo = (0, 1, 2,

...,

9). Di dalam ZIO, 6 + 7 = 3

4 x 8 = 2

3 - 9 = 3 + 1 = 4 .

Definisi 10 (Menezes, 1997) Kongruensi. Jika a dan b adalah intejer, a dikatakaa kongruen dengan b modulo n, ditulis a

=

b (mod

n)

jika nl(a - b). Selanjutnya n

dinamakan modulus kongruensi.

Contoh: 24

-

9 (mod 5) karena 24 - 9 = (3)(5) dan -1 1

=

17 (mod 7) karena -1 1

-

17 = (-4)(7):

Definisi 11 (Menezes, 1997) Invers Multiplikati~ Invers perkalian atau invers multiplikatif dari a modulo n adalah intejer x E Z,,, sehingga m

=

I(mod n). Jka terdapat bilangan x yang demikian, maka x unik dan a d i t a k a n invertibel yang dinotasikan 6'.

Definisi 12 (Menezes, 1997) Pembagian. Misalkan a,b E Z,,. Pembagian a oleh

b modulo n adalah perkalian a dengan b-' modulo n, yang terdefinisi jika b invertibel modulo n.

Detinisi 13 (Menezes, 1997) Grup multiplikatif dari Z adalah himpunan Z',= {a E Z,= gcd(a,n) = 1). Khususnya, untuk n prima, sebut saja p, maka Z; ={a1 l l a 5 n - 1 ) .

Contoh: Z;, = {I, 3, 7, 91, Z;, = (1, 2, 4, 7, 8, 11, 13, 141, dan Z; ={I, 2, 3, 4). Order dari Z', , yaitu

I

Z',

I

merupakan bilangan phi Euler (4n) menunjukkan jumlah intejer pada interval [I, n] yang relatif prima ke n), notasi 4 n ) =

I

Z',

I.

Order dari grup muliplikatif prima Z; adalah

1z;

I

=p-1.

Definisi 14 (Tilborg, 2005) Subgrup dari grup multiplikatif Z;adalah sebuah subset dari elemen-elemen Z; yang tertutup terhadap operasi multiplikasi.

Teorema 15 (Menezes, 1997) Teorema Fermat. Misalkan p adalah prima. Jika gcd(a, p ) =1, maka ap'

=

1 (modp). Khususnya, untuk sembarang intejer a, 8

-

a (mod p).

Teorema ini digunakan untuk tes keprimaan

Teorema 16 (Menezes, 1997) Teorema Euler. Misalkan n 2 2 adalah intejer. Jika a E Z', , maka '"'a

=

1 (mod n).

Kasus khusus teorema Euler adalah teorema Fermat, yaitu teorema Euler dengan bilangan prima.

Definisi 17 (Menezes, 1997) Misalkan a E Z', . Order dari a, dinotasikan ord(a) adalah intejer positif terkecil t sehingga a'= 1 (mod n).

Contoh: Misalkan n = 21, maka

Zf,

= (1, 2, 4, 5, 8, 0, 13, 16, 17, 19, 20). Order-

Tabel 2. Order dad elemen-elemen oada Z:.

Definisi 18 (Menezes, 1997) Misalkan a E Z i . Jika order dari a adalah fin), A,

a ~ z ; ,

1 1 1 2 1 4 1 5 1 8 ~ 1 0 ~ 1 1 ~ 1 3 ~ 1 6 ~ 1 7 ~ 1 9 ~ 2 0

maka a disebut generator atau elemen primitif dari Z', . Jika Z', mempunyai suatu generator, maka Z', disebut siklik.

Syarat-syarat generator dari Z', adalah:

a. Z', mempunyai sebuah generator jika n = 2, 4, pk, atau 2pk, dimana p adalah

prima ganjil dank

>

1. Khususnya, jikap adalah prima, maka Z; mempunyai suatu generator.

b. J i a a adalah generator dari Z', , maka Z', = {d mod n

1

0 5 i 5 &n>l ).

Contoh:

Z;, adalah bukan siklik karena tidak memiliki satu pun elemen yang mempunyai order 421) = 12 dan tidak memenuhi syarat generator a. Z;, adalah siklik dan mempunyai generator a = 2. Z;, adalah siklik dengan generator a = 2.

ordera

Definisi 19 (Menezes, 1997) Misalkan a E Z', , a adalah residu h d a t mod n, atau suatu h a d r a t mod n, jika ada suatu x E Z', sehingga

I?

-

a (mod n). Jika tidak ada x, maka a disebut bukan residu kuudrat mod n. Himpunan dari semua residu kuadrat mod n dinotasikan dengan

Q,,,

dan himpunan dari semua bukan residu kuadrat mod n dinotasikan dengan

g,,

1 6 3 6 2 6 6 2 3 6 6 2

2.2

TES

PROBABILISTIC PRIiWLITY

Intejer-intejer positif ganjil sembarang dites untuk memberikan informasi tentang keprimaan.

Definisi 20 (Menezes, 1997) Jika n adalah komposit, elemen-elemen pada W(n) disebut witness dari kekompositan n, dan elemen-elemen daii himpunan komplemen L(n) = Z. \ W(n) disebut liar.

Tes keprimaan ini menggunakan syarat-syarat dari W(n) berikut ini. Misalkan bahwa n adalah suatu intejer yang keprimaannya ditentukan. Sebuah intejer a E Z, yang dipilih secara random dan dicek jika a E W(n). Tes ini menghasilkan "komposit" jika a E W(n) dan "prima" jika a

e

W(n). Tentu saja

jika a E W(n), maka n disebut gaga1 tes keprimaan berbasis a, dalam kasus ini n

adalah komposit. Jika a W(n), maka n disebut 1010s tes keprimaan berbasis a, dalam kasus ini tidak ada kesimpulan tentang keprimaan dari n.

Definisi 21 (Menezes, 1997) Sebuab intejer n dipercaya prima berbasis pada tes keprimaan yang mungkin disebut probable prima.

Salah satu tes keprimaan ini adalab tes Miller-Rabin yang akan dibahas dalam tesis ini.

TES

MILLER-RABIN

Tes probabilistic primality yang paling banyak digunakan dalam praktek adalah tes Miller-Rabin yang juga dikenal sebagai tes pseudoprima kuat (strong pseudoprime). Tes ini didasarkan pada definisi-definisi sebagai berikut:

Definisi 22 (Menezes, 1997) Misalkan n adalah prima ganjil dan misalkan n-1

= 2% dimana r ganjil. Misalkan a adalah suatu intejer sehingga gcd(a, n) = 1,

maka d r 1 (mod n) atau aZJr

=

-1 (mod n) untuk beberapa j, 0 5 j 5 s-1.

Definisi 23 (Menezes, 1997) Misalkan n adalah sebuah intejer komposit ganjil dan misalkan n-1 = 2% dimana r ganjil. Misalkan a adalah suatu intejer dalam

interval [1, n-11.

(i) Jika d# 1 (mod n) dan jika a''' f -1 (mod n) untuk j, 0 5 j 5 s-I, maka a disebut suatu strong witness (untuk kekompositan) untuk n.

(ii) Sebaliknya, yaitu jika d

=

1 (mod n) dan jika aZJr

=

-1 (mod n) untuk beberapa j, 0 5 j

i

s-1, maka n disebut suatu strongpseudoprime berbasis

Contoh: (strong pseudoprime)

Misalkan intejer komposit n = 91 (= 7 x 13). Karena 91 - 1 = 90 = 2 x 45, s = 1 dan r = 45. Karena 9'= 945

=

1 (mod 91), 91 adalah suatu strongpseudoprime berbasis 9. Himpunan dari semua strong liar untuk 91 adalah:

{ I , 9, 10, 12, 16, 17, 22, 29, 38, 53, 62, 69, 74, 75, 79, 81, 82, 90)

Catatan bahwa jumlah strong liar untuk 91 adalah 18 =

4

(91) / 4, dimana

4

adalah fbngsi Euler phi (menunjukkan jumlah intejer pada interval [I, n] yang

relatif prima ken). ¤

Algoritme tes Miller-Rabin dapat dilihat pada Algoritms 4 di Bab IV.

2.3 STRUKTUR ALJABAR 2.3.1. Gmp

Berikut ini dijelaskan mengenai suatu struktur aljabar yang disebut dengan grup. Grup merupakan suatu himpunan tak kosong yang dilengkapi dengan operasi biner dan memenuhi beberapa sifat, seperti yang dijelaskan berikut ini.

Definisi 24 (Fraleigh, 1994) Diberikan sebarang himpunan tidak kosong G dan operasi biner "*" pada G, maka G disebut grup terhadap operasi biner

"*"

dan ditulis (G,

*

) jika dipenuhi:

a) Operasi biner "

*

" pada G bersifat asosiatif,

b) Terdapat dengan tunggal elemen identitas yaitu e E G sedemikian hingga

u n t u k s e t i a p a ~ G berlaku e

*

a = a * e = a

c) Untuk setiap a E G, terdapat elemen inversnya, yaitu sedemikian a-I E G

hingga berlaku a

*

6' = 6'

*

a = e.

Suatu grup ( G , * ) disebut Abelian j i b operasi binernya bersifat komutatif Selanjutnya, grup (G, * ) dapat dituliskan dengan G apabila operasi binernya diketahui sebagai operasi perkalian.

Definisi 25 (Nur Aliatiningtyas) Misalkan G grup dan a G G, dan n bilangan bulat positif, maka: 1. a"= a a

...

a, (sebanyak n kali)

1 -1

2. a n = d a

...

a-',dan 3. a0 = e .

Definisi 26 (Fraleigh, 1994) Jika G mempunyai banyak elemen yang berhingga, maka G disebut gmp berhingga Wnite group) dan banyaknya elemen G disebut order G, ditulis [GI atau o(G).

Definisi 27 (Fraleigh, 1994) Diberikan grup G dan subset tak kosong H

c

G

.

Subset H disebut mbgrup G jika H grup di bawah operasi biner yang sama pada G, maka H membentuk grup, ditulis H (1 G.

Teorema 28 (Mu Aliatiningtyas) Misalkan G grup, H c_ G, H # 0

.

H subgrup dari G jika dan hanya jika berlaku Vx, y E H,

v-'

E H.

Teorema 29 (Nur Aliatiningtyas) Misalkan G grup, C koleksi subgrup dari G, maka irisan subgrup-subgrup dari G di C merupakan subgrup dari G.

Teorema 30 (Nur Aliatiningtyas) Misalkan G grup, H subgrup dari G, maka berlaku

1. HH =

H,

2. IE' = {h-' I h G H) = H.

Misalkan G grup, a E G, maka menurut Teorema 29 irisan semua subgroup yang memuat a akan merupakan subgroup terkecil dari seluruh subgroup yang memuat

a. Akan diberikan teorema yang menyatakan bahwa subgroup yang demikian merupakan himpunan {

...,

a-', am', ao=e, a, 2, ...). Secara umum dinotasikan dengan (6: n E

Z).

Jiia G grup aditif maka dinotasikan (nu

I

n G Z),

Teorema 31 (Nur Aliatiningtyas) Misalkan G grup dan a E G , maka

H =

(8:

ie Z ) mempakan subgrup dari G dan merupakan subgrup terkecil dari G

yang memuat a.

Definisi 32 (Nur Aliatiningtyas) Subgrup H dalam Teorema 3 1 disebut subgrup

Definisi 33 (Raleigh, 1994) Misalkan a s G dan G = (a), maka G disebut grup

siklik yang dihasilkan oleh a dan a disebut generator untuk G.

Definisi 34 (Menezes, 1997) Misalkan

G

adalah grup dan a E

G.

Order dxi a atau o(a) didefinisikan sebagai intejer positif terkecil t sehingga

d

= e. Jika suatu t tidak ada, maka order dari a didefinisikan tak berhingga.

Teorema 35 (Fraleigh, 1994) Sifat-sifat dasar order unsur dari grup.

1. Jika o(a) = n, maka ada tepat n kuasa dari a (power of a) yang masing-masing

berbeda, yaitu a' = e,a, a',

.

..,aw' .

2. Jika o(a) tak hingga, maka semua kuasa dari a berbeda. Artinya, jika r dan s

yaitu dua bilangan bulat yang berbeda, maka a' + a s .

3. Misalkan a yaitu unsur dari grup G dan o(a) = n, maka at = e jika dan hanya

jika t yaitu kelipatan dari n (t kelipatan n artinya ada bilangan bulat q sehingga t = nq).

4. Misalkan G adalah grup dan misalkan a E G berorder hingga t, maka o((a)) =o(a) = t .

Misalkan a E G, G = (a), dan o(a) = n. Berdasarkan Teorema 35, jika o(G) = n

maka dapat ditunjukkan bahwa G= (a) = {a0 = e, a,

2, d ,

..., Z').

Contoh: Misalkan grup multiplikatif Z;,= (1, 2, ..., 18) yang berorder 18. Grup tersebut adalah siklik dan generator a = 2. Subgrup-subgrup dari ZY9 dan generatomya diperlihatkan dalam Tabel 3.

Tabel 3. Subgn~p siklik dari G Subgrup (11 (1, 18) {I, 7, 111 {I, 7, 8, 11, 12, 18) {1,4,5,6,7,9,11,16,17) {I, 2. 3, ..., 18) Generator 1 18 7, 11 8, 12 4,5,6,9,16,17 2,3, 10, 13, 14, 15 Order 1 2 3 6 9 18

2.3.2 Lapangan (Field)

Berikut ini diperkenalkan suatu struktur aljabar yang lain, yaitu lapangan. Serta diberikan beberapa definisi yang berhubungan dengan lapangan.

Definisi 36 (Hankerson, 2003) Suatu lapangan adalah himpunan F tak kosong yang dilengkapi dengan dua operasi biner yaitu operasi penjumlahan

"+"

dan operasi multiplikasi

"."

yang memenuhi

1) (F,+) merupakan grup abelian dengan unsur identitas (penjumlahan) 0;

2) (F, -) merupakan grup abelian dengan unsur identitas (multiplikasi) 1; 3) Untuk setiap a, b, c E F berlaku sifat distributif, yaitu:

(a+b).c = a.c

+

b.c.

Definisi 37 Ojraleigh, 1994) Diberikan lapangan F. Subset tak kosong S F disebut sub-lapangan (subfield) jika S merupakan lapangan terhadap operasi biner yang sama pada F.

Definisi 38 (ANSI X9.62, 1998) Lapangan Berhingga (Finite Field F,).

Jiia q = p adalah suatu bilangan prima ganjil, maka elemen-elemen dari lapangan berhingga Fp direpresentaskan dengan intejer 0, 1,2,

.

.

.

, p-I.

1. Elemen identitas multiplikatif adalah intejer 1. 2. Elemen no1 adalah intejer 0.

3. Penjumlahan dari elemen-elemen lapangan adalah penjumlahan intejer modulop, yaitu jika a, b ~ F p , maka a

+

b = (a

+

b) modp.

4. Multiplikasi dari elemen-elemen lapangan adalah multiplikasi intejer modulop, yaitu jika a, b ~ F p , maka a.b = (a.b) modp.

2.4 LOGARITMA DISKRET

Keamanan dari beberapa teknik kriptografi tergantung pada kekuatan dari masalah logaritma diskret, contohnya penyandian ElGamal, algoritme Penandaan ElGamal, dan lain-lain.

Definisi 39 (Menezes, 1997) Logarima Diskret. Misalkan G adalah suatu grup

siklik berorder n. Misalkan a adalah generatorlakar primitif dari G, dan misalkan

a

E G. Logaritma diskret dari

a

untuk basis a; yang dinotasikan sebagai log$

adalah intejer unik x, 0 5 x 5 n-1 sehingga =

6.

Definisi 40 (Menezes, 1997) Masalah Logaritma Diskref (MLD) adalah sebagai berikut: diberikan suatu primap, sebuah generator a dari Z

',

dan elemen

a

E Z',

.

dapatkan intejer x, 0 I x < p 2 , sehingga

6

=

a(modp).

Definisi 41 (Hankerson, 2003) M d a h Logariha Diskret Kurva Elipfik

(MLDKE) adalah diberikan suatu kurva eliptik E atas finite field F,, sebuah titik PEE(F,) yang berorder n dan sebuah titik QE(P), dapatkan bilangan bulat

l ~ [ O , n - I ] sehingga Q = IP. Bilangan bulat 1 disebut logaritma diskret dari Q

berbasis P, dinotasikan dengan 1 =log, Q . (Catatan: (P) adalah grup yang dibangkitkan oleh P atau (P) = (0, P, P+P, P+P+P,. .

.

})

2.5 FUNGSIHASH

Salah satu primitif kriptografi modern adalah hngsi hash kriptografi, sering kali disebut fungsi hash satu-arah. Berikut diberikan definisi sederhana hngsi hash.

Definisi 42 (Menezes, 1997) Fungsi hash adalah fungsi yang secara komputasi efisien memetakan string bit dengan panjang sembarang ke string bit dengan panjang tetap yang disebut nilai hash (hash value).

Definisi 43 (Tilborg, 2005) One W q Hashfirnction (OWHF) adalah suatu fimgsi

h yang memenuhi kondisi-kondisi sebagai berikut:

a) input x dengan panjang sembarang dan hasil h(x) mempunyai panjang n bit y a w tetap,

b) fkngsi hash menjadi satu arah (one way) jika diberikan suatu y dalam h, ini adalah komputasional yang tak layak untuk memperoleh x sehingga h(x)-y dan jika diberikan x dan h(x) maka secara perhitungan talc layak untuk memperoleh suatu pesan x

*

x' sehingga h(x) = h(xl).

Definisi 44 (Menezes, 1997) Fungsi hash adalah hngsi h yang mempunyai sifat- sifat sebagai berikut:

a) Kompresi (compression): h memetakan input x dengan sembarang panjang bit yang berhingga, ke output h(x) dengan panjang bit tetap n;

b) Kemudahan komputasi (ease of computation): diketahui h dan suatu input x, h(x) adalah mudah dihitung.

c) Ketahanan preimej ereimage resistance): jika diketahui sembarang nilai hash y, maka secara perhitungan tak-layak mencari x sehingga h(x) = y. Istilah lain untuk ketahanan preimej adalah satu-arah (one-way).

d) Ketahanan preimej kedua (2nd-preimage resistance): jika diketahui x; maka secara perhitungan tak layak mencari x'

+

x sehingga h(x') = h(x). Istilah lain untuk ketahanan preimej kedua adalah ketahanan tumbukan lemah (weak collision resistance).

e) Ketahanan tumbukan (collision resistance): secara perhitungan tak layak mencari dua input berbeda x, x' sehingga h(x) = h(x').

Istilah lain untuk ketahanan tumbukan adalah ketahanan tumbukan kuat (strong coNision resistance).

Definisi 45 (ANSI X9.62, 1998) Cryptographic Hash Function. Suatu fUngsi matematika yang memetakan nilai-nilai domain berukuran besar (large domain) ke nilai-nilai yang berukuran lebih kecil (smaller range). Fungsi tersebut mempunyai sifat-sifat sebagai berikut:

a) Secara komputasional yang tidak mungkin untuk memperoleh sembarang input yang dipetakan ke sembarang output yang ditentukan sebelumnya; b) Secara komputasional yang tidak mungkin untuk memperoleh sembarang

dua input yang berbeda yang dipetakan ke sembarang output yang sama.

2.6 PENANDAAN DIJITEL (DIGITAL SIGNATURE)

Terkait dengan kegunaan penandaan dijitel secara praktis, berikut diberikan definisi dasar dengan pengertian yang lebih luas untuk skema penandaan dijitel. 1. Penandaan Dijitel adalah suatu rangkaian data yang menghubungkan pesan

2. Algoritme Pembuatan Tanda Dijtel (atau algoritme pembuatan tanda)

adalah suatu metode untuk membuat tanda dijitel.

3. Algoritme Pemeriksaan Tanda Dijitel (atau algoritme pemeriksaan tanda)

adalah suatu metode untuk memeriksa apakah tanda dijitel asli atau tidak (yaitu benar-benar dibuat oleh entitas tertentu).

4 . Skema/mekanisme Tanda Dijitel yang terdiri dari algoritme pembuatan

tanda dan algoritme pemeriksaan tanda yang berkaitan.

5 . Boses4rosedur Penandaan Tanda Dijitel yang terdiri dari Algoritme

Pembuatan tanda dijitel yang berhubungan dengan metode untuk memformat data menjadi pesan-pesan yang dapat ditandai.

6 . Boses/prosedur Pemeriksmn Tanda Dijitel yang terdiri dari Algoritme

Pemeriksaan tanda dijitel yang berhubungan dengan metode untuk memperoleh kembali data dari pesan.

Penandm Dijiiel adalah suatu kriptografi yang berdasarkan otentikasi, integritas data, dan non-repudiasi. Penandaan Dijitel memiliki kunci yang terdiri atas kunci publik (public key) dan kunci rahasia (private key). Kriptografi kunci publik tersebut dapat mudah diserang dengan peniruan kunci publik, tetapi pemakai bertanggung jawab untuk menjaga kunci rahasia dengan aman. Dari tanda yang diterima, hams memiliki kunci publik yang dibangkitkan oleh pengirim. kunci publik ini yang merupakan informasi pengirim yang terdapat pada penerima yang hams sesuai dengan tanda yang dihasilkan oleh pengirim.

Tujuannya adalah memberikan suatu cara bagi pengguna untuk mencantumkan identitasnya dalam suatu informasi. Proses dari penandaan (signing) memerlukan pentransformasian beberapa pesan rahasia yang dibawa oleh pengguna ke dalam suatu tanda pengenal yang disebut tanda tangan. Berikut diberikan dekripsi umum dari penandaan dijitel.

ht

adalah himpunan pesan yang anggotanya akan diberi tanda.

S adalah himpunan yang anggotanya disebut tanda, dan tanda biasanya berupa bitstring dengan panjang tetap.

VA adalah suatu transformasi dari himpunan

Ax

S ke himpunan (T (benar), F

(salah)). VA disebut transformasi verifikasi untuk semua tanda milik A;

diketahui oleh publik, dan transformasi ini digunakan oleh entitas lainnya untuk memeriksa kebenaran tanda dibuat oleh A.

Definisi 46 (Menezes, 1997) Transformasi SA dan VA mernberikan suatu skema penandaan dijitel untuk A.

Contoh: (skema penandaan dijitel) M=(ml, mz, m3} dan S={ sl, s2, s3}. Gambar 1

adalah suatu fungsi penandaan SA dari himpunan A Man fungsi verifikasi VA.

::

x:

(ml,sl) (ml m3 ~3 (ml,s3) SA (mz,sl) True (m2,s~) (m~fi,) (m3~1) (m~,sz) (m3,sd VA Gambar 1. Fungsi penandaan SA dm fungsi veriliiasi V,

Prosedue penandaan (signing)

Penanda A membuat sebuah tanda untuk pesan m E A dengan melakukan

langkah-langkah sebagai berikut: 1. Menghitung s = S A ( ~ ) .

2. Mengirim pasangan (m, s), s disebut tanda untuk pesan m. Prosedur Verifrkasi

Untuk memeriksa bahwa suatu tanda

s

pada pesan m adalah benar dibuat oleh A,

maka B (pemeriksa) melakukan langkah-langkah sebagai berikut: 1. Mendapatkan hngsi verifikasi VA

dari

A.

2. Menghitung u = V~(m,s).

3. Menerima tanda yang dibuat oleh A jika u = True dan ditolak jika u = False.

1 . Mendapatkan fungsi verifikasi VA dari A. 2. Menghitung u = V A ( ~ , S ) .

3. Menerima tanda yang dibuat oleh A jika u = True dan ditolak jika u =False.

Dua sifat yang hams dipenuhi untuk transformasi penandaan dan verifikasi: (a) s adalah tanda yang sah dari A jika dan hanya jika V~(rn, s) = T.

@) Secara perhitungan tak layak untuk entitas selain A untuk mendapatkan

s E S , sembarang m E A, sehingga V~(rn, s) = T.

Pada implementasinya, suatu sistem pembuatan tanda selalu memerlukan hngsi hash. Fungsi hash digunakan sebagai integritas data pada

penggabungannya dengan skema penandaan dijitel. Klasifikasi dari skema penandaan dijitel adalah:

1 . Skema Penandaan Dijitel dengan Apendiks

2. Skema Penandaan Dijitel dengan Pemulihan Kembali Pesan.

Namun skema yang akan dibahas dalam tesis ini adalah skema pertama karena skema ini berhubungan dengan algoritme penandaan ElGamal.

Definisi 47 (Menezes, 1997) Skema penandaan dijtel dengan upend*, yaitu

skema yang memerlukan pesan asli sebagai input untuk algoritme verifikasi.

Prosedur skema tersebut diberikan dalam algoritme-algoritme herikut ini:

1) Algoritme Pembangkitan Kunci

Setiap entitas membuat kunci pribadi digunakan untuk menandai pesan dan terkait dengan kunci publik yang digunakan oleh entitas lainnya untuk memeriksa tanda.

a. Setiap entitas A memilih kunci rahasia yang mendefinisikan suatu himpunan transformasi SA = {Sas / k E R). Masing-masing SA+ adalah

pemetaan 1 - 1 dari &, ke S dan disebut i r a n f o n n a s i p e e .

b. SA mendefinisikan suatu pemetaan terkait VA dari &, x S ke {T,

FJ

T , jikaS,, (15) = s',

sedemikian sehingga

LU, (iZ,s')

=

c. Untuk semua 2 E A h , s* E S, disini 2 = h(m) untuk semua m E A. VA disebut iransformusi v e n j ? h i dan dikonstruksi sedemikian sehingga ia bisa dihitung tanpa mengetahui kunci rahasia penanda.

d. Kunci publik A adalah VA, kunci rahasia A adalah himpunan SA.

Algoritme Pembangkitan dan Verifikasi Tanda

Entitas A membuat tanda s E

S

untuk pesan m E X , yang kemudian diverifikasi

oleh siapapun entitas B.

2) Algoritme Pembangkitan Tanda Entitas A hams melakukan ha1 berikut ini: a. Memilih suatu unsur k E R.

b. Menghitung iii = h(m) dan s* = S~k(iii ).

c. Tanda milik A untuk m adalah s*. Keduanya disiapkan untuk entitas

siapapun yang ingin memeriksanya.

3) Algoritme Veriiikasi Tanda. Entitas B h a s melakukan ha1 berikut ini: a. Mencari kunci publik otentik VA milik A.

b. Menghitung iii = h(m) dan u = VA(% ; s*).

c. Tanda diterima jika dan hanya jika u = T.

a Proses penandaan

_ _ _ _ _ _ - - -

Sifat-sifat yang diperlukan oleh transformasi penandaan dan verifikasi adalah: 1) untuk setiap k E R, seharusnya efisien untuk menghitung SA+; 2) untuk menghitung VA sehmsnya efisien; dan

3) untuk siapapun entitas selain A, sehmsnya secara perhitungan tak layak mendapatkan m E ht dan s* E S sehingga VA(% ,s*) = T, dimana

% = h(m).

Catatan (penggunaan fungsi-fungsi hash):

Paling banyak skema penandaan dijitel dengan apendiks diaplikasikan pada pesan dengan panjang sembarang. Fungsi hash h pada algoritme pembangkitan dan verifikasi tanda dipilih tahan terhadap tumbukan (Definisi 45).

BAB

111

KRIPTOGRAFI KURVA ELIPTIK

(Elliptic Curve CryptographyIECC)

3.1 Skema Penyandian Kunci Publik

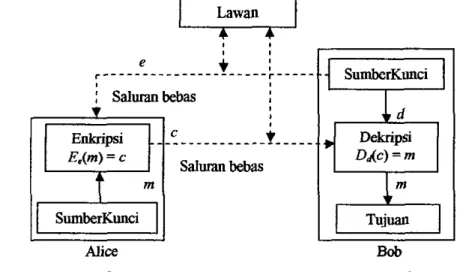
Misalkan { E : e e X } adalah himpunan dari transformasi penyandianlenkripsi, dan misalkan {Dd: de%} adalah himpunan dari transformasi pengupasan sandiidekripsi dimana X ad& mang kunci. Misalkan beberapa pasangan transformasi enkripsildekripsi (E,, Dd) dan misalkan setiap pasangan mempunyai syarat bahwa dengan mengetahui E, adalah secara komputasional tidak mungkidayak jika diberikan sebuah siferteks acak c 6

e,

untuk

memperoleh m E JU sehingga E,(m)=c. Syarat ini menyatakan bahwa jika

diberikan e maka hal ini tidak mungkin untuk menentukan kunci dekripsi d-nya. (Tentunya e dan d menjelaskan fungsi-fungsi enkripsi dan dekripsi) E, diperlihatkan sebagai suatu fungsi hapdoor one-way (adalah fungsi one-way f:

X+Y dengan syarat tambahan yang diberikan beberapa informasi ekstra (disebut

informasi frupdoor), ini menjadi tidak mungkin untuk mendapatkan suatu x E X

sehinggaflx) 7, jika diberikan beberapa y E ImV)) dengan d menjadi informasi

t r u p h r untuk menghitung fungsi invers dan karena itu memenuhi dekripsi. Di bawah asumsi ini, misalkan komunikasi dua kelompok antara Alice dan Bob diilustrasikan dalam Gambar 3. Bob memilih pasangan kunci (e,

4.

Bob mengirimkan kunci enkripsi e (disebut kunci publik) ke Alice melalui beberapa saluran tetapi kunci delcripsi (kunci pribadi) d tetap dijaga kerahasiaan dan keamanannya. Alice kemudian mengirimkan sebuah pesan m ke Bob dengan mengaplikasikan transformasi enkripsi yang ditentukan oleh kunci publik Bob untuk mendapatkan c=E,(m). Bob mendekripsi siferteks c dengan mengaplikasikan transfonnasi invers Dd secara unik yang ditentukan oleh d.

Karena kunci enkripsi e tidak perlu dijaga kerahasiaannya, kunci ini dibuat umum. Beberapa entitas dapat mengirimkan berita yang disandi setelah itu ke Bob

Penyandian kunci publik mengasumsikan bahwa pengetahuan tentang kunci publik e tidak memberikan komputasi untuk kunci pribadi d. Dengan kata lain, penyandian ini mengasumsikan keberadaan fungsi-fungsi trapdoor one-way.

I/

SnmberKnnci

I

I

Alice

Gambar 3. Enkripsi dengan tekoik kunci pnblik

Berikut ini akan dibahas tentang salah satu contoh skema penyandian kunci publik, yaitu ECC.

3.2 Kriptografi Kurva Eliptik (ECC)

ECC dapat digunakan untuk beberapa keperluan seperti skema enkripsi (contohnya ElGamal ECC), tanda tangan digital (contohnya ECDSA) dan protokol pertukaran kunci (contohnya Diffie-Hielman ECC). Dalam penulisan tesis ini, dibahas tentang algoritme penandaan dijitel ElGamal berbasis ECC dan hal-hal yang diperlukan atau berkaitan dengan algoritme tersebut. Kemudian dibuat program yang merupakan implementasi dari ECC.

Definisi 48 (Koblitz, 1994) Definisi Kurva Eliptik

1. Misalkan K adalah lapangan dengan karakteristik it 2 , 3 . Misalkan 2 + m

+

b,

(a, b E K ) dengan

4d

+

27b2 # 0, merupakan polinomial pangkat tiga yang

tidak mempunyai akar perkalian (multiple root). Kurva eliptik K adalah himpunan titik (x, y) dengan x, y E K yang memenuhi persamaan

,?=i'+mc+b

...

(1) disertai dengan sebuah elemen tunggal, yaitu

0

(titik infinity).

Lapangan K dapat berupa lapangan R (lapangan bilangan real), lapangan Q

(lapangan bilangan rasional), lapangan C (lapangan bilangan kompleks) atau

K dapat berupa lapangan berhingga F, dengan q = pr, p adalah suatu bilangan

prima dan F, memiliki q elemen.

2. Jika K adalah lapangan yang memiliki karakteristik 2, maka kurva eliptik pada K adalah himpunan titik (x, y) yang memenuhi persamaan:

y + c y = ? + m + b atau $ + x y = . ? + d + b

...

(2) ditambah dengan O sebagai titik infniv.

3. Jika K adalah lapangan yang berkarakteristik 3, maka kurva eliptik pHda K adalah himpunan titik (x, y) yang memenuhi persamaan:

$ = ? + d + b x + c

...

(3) ditambah dengan O sebagai titik inzniq.

Setiap k ~ eliptik akan berbentuk simetris terhadap sumbu x atau garis ~ a @.

Karena untuk setiap nilai XGR, terdapat sepasang nilai y e R yang memenuhi

persamaan (I), yaitu y,,, =

4 2

+a+ b

.

Kurva eliptik juga dapat dipandang sebagai suatu himpunan yang terdiri dari titik-titik (x, y) yang memenuhi persamaan (1). Himpunan tersebut dinotasikan dengan E(a, b). Untuk setiap nilai a dan b yang berbeda, dihasilkan himpunan E(a, b) yang berbeda pula.

3.2.1 Order Grup

Kurva eliptik pada lapangan berhingga Z, dengan q = pr dan p adalah suatu

bilangan prima, dinotasikan dengan E(Zq) dan juga memenuhi persyaratan

4d

+

27b2 t 0. Titik-titik pada E(&) membentuk suatu grup modulo q.

Jumlah maksimun titik yang terdapat pada suatu kurva eliptik (Z,) dengan q = pr adalah 29 + 1, yaitu 29 pasangan (x, y), dimana x, y E

Z,

yang

memenuhi persamaan kuwa eliptik ditambah dengan sebuah elemen identitas, yaitu C). Jumlah titik pada E(Z,) dinotasikan dengan #E(&), disebut order dari E

3.2.2 Penentuan Titik pada K u w a Eliptik

Penentuan titik pada kurva eliptik E(Zp) dengan persamaan

9

= x3 + a x + b, secara sederhana dapat dijelaskan sebagai berikut:

Untuk setiap x dengan 0 5 x i p , hitung nilai

.?

+

ax + b. Setiap hasil yang didapat diperiksa apakah hasil tersebut mempunyai akar kuadrat modulo p. Jika tidak, maka tidak ada titik dengan nilai x pada E(Zp). Demikian juga untuk sebaliknya, jika ada, maka akan ada dua nilai y yang memenuhi persamaan tersebut (kecuali nilai y tunggal, yaitu 0). Titik (x, y) tersebut merupakan titik pada kunra-kwa eliptik

E(G)

dengan persamaan$ =

2

+

ax

+

b.

Order dari suatu titik P G E adalah bilangan bulat positif terkecil k,

sehingga

kP

= B dan titik P disebut titik hingga Gnitepoint). Jika tidak ada intejer

positif yang memenuhinya, maka order titik tersebut dikatakan tidak berhingga (infinite).

3.2.3 Struktur Grup Kurva Eliptik secara Geometri

Akan dibuktikan bahwa k u ~ a eliptik merupakan suatu grup, yaitu sebagai berikut:

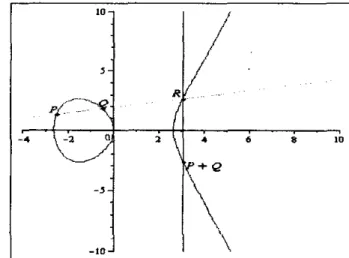
a. Misal diberikan P = (-2.5,-1.369)~ E(R'), Q=(-0.5,1.837)~ E(R') ,

dan P

+

+Q , maka P

+

Q =R merupakan garis yang memotong kurva eliptik tepat di satu titik, sebut -R. Titik -R diiefleksikan dengan sumbu x ke titik R seperti terlihat pada Gambar 4. Dari sini jelas P+Q=R tertutup terhadap

penjumlahan dalam E(F).

I I

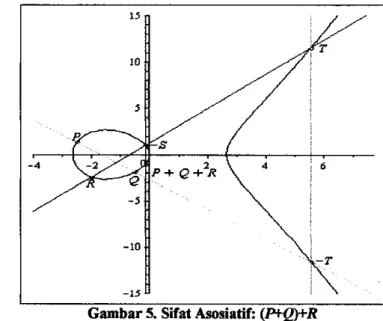
b. Kedua, akan dibuktikan (P+Q)+R=P+(Q+R) memenuhi sifat asosiatif. Misal diberikan titik P=(-2.5, -1.369) E E(R2), Q=(-0.5, 1.837) E E(R'), dan

R = (-2,-&) E E ( R ' ) . Dengan demikian akan dilakukan sebanyak dua tahap. Tahap pertama menyelesaikan operasi sisi sebelah kiri yaitu kerjakan (P+Q). Seperti terlihat pada Gambar 5, (P+Q)=T.

I -- I

Gambar 5. S i Asosiatik (P+e)tR

Kemudian tambahkan titik R yang diperoleh dengan titik T dengan menghubungkan kedua titik tersebut akan diperoleh perpotongan dengan k ~eliptik tepat di satu titik, sebut ~ a -S. Titik -S direfleksikan dengan sumbu x diperoleh titik S yang merupakan hasil terakhir dari penjumlahan.

J Gambar 6. Sifat Asosiatik Pl(QtK)

Demikian pula dengan tahap kedua yaitu menyelesaikan operasi sisi sebelah kanan. Yang dilakukan sama seperti pada tahap pertama, bedanya yang dilakukan pertama kali adalah Q+R. Hasil tahapan ini dapat dilihat pada

Gambar 6.

c. Ketiga akan dibuktikan mempunyai identitas. Misal penambahan titik P i - 2 , -6) E E(R 2 , dan -P merupakan garis vertikal yang tidak memotong kurva eliptik dititik ketiga, maka titik P dan -P tidak dapat ditambahkan seperti penambahan titik P dan Q yang berbeda. Hal ini menyebabkan kurva eliptik meliputi point at infinity dengan definisi P+(-P)=U.

Sebagai hasil dari persamaan ini P+U=P berada dalam grup dan U disebut identitas penjumlahan.

d. Dari pembuktian ketiga dari grup di atas secara otomatis sudah terbukti kuma eliptik ini mempunyai invers dari titik P yaitu -P. Dari keempat bukti di atas dapat disimpulkan bahwa E ( R ~ ) memenuhi grup kurva eliptik. Apakah

memenuhi grup komutatif! Dari pembuktian pertama jelas E(R') terbukti

memenuhi grup komutatif Jadi dapat dibuktikan bahwa kurva eliptik memenuhi sifat-sifat grup.

3.3 Aritmatika Kurva Eliptik

Mekanisme kriptograti yang didasarkan pada kuma eliptik tergantung pada aritmatika yang melibatkan titik-titik pada kuma. Kurva eliptik didefinisikan pada operasi-operasi lapangan. Operasi-operasi kurva yang efisien juga sangat penting untuk hasilnya.

Ada dua lapangan berhingga yang sering digunakan dalam kriptografi kuwa eliptik, yaitu lapangan berhingga prima

(Z,)

dan lapangan karakteristik 2 (F 2"').

Lapangan berhingga Zp lebih efektif untuk implementasi soflware kriptografi kurva eliptik. Sedangkan lapangan berhingga F zrn lebih efektif untuk hardware yang sistem kerjanya berdasarkan algoritme kriptograii kurva eliptik.