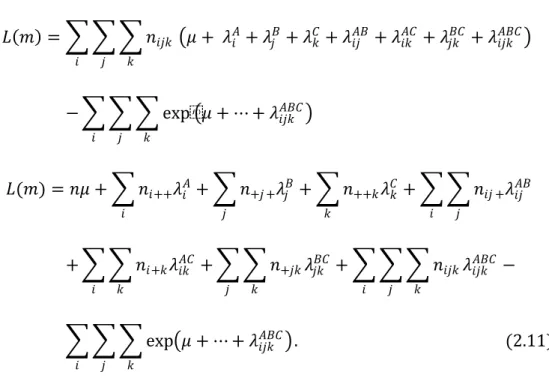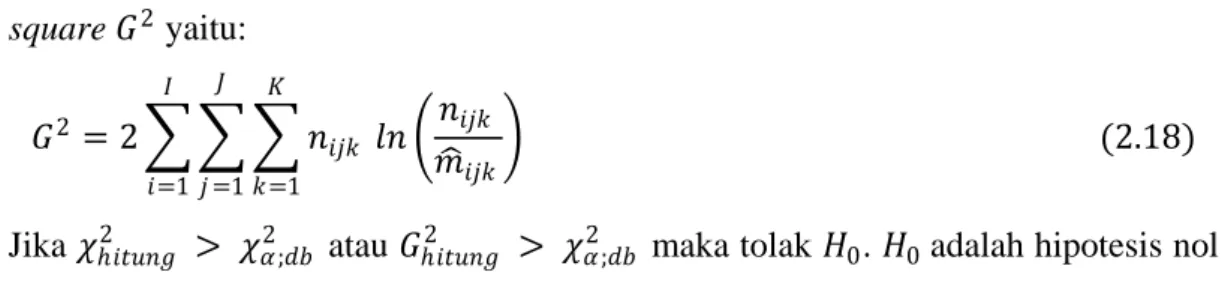BAB 2
LANDASAN TEORI
2.1 Kawasan Metropolitan Mebidang
Kawasan Mebidang (Medan, Binjai dan Deli Serdang) saat ini menjadi pusat pertumbuhan ekonomi di wilayah Propinsi Sumatera Utara dan juga sebagai pintu gerbang keluar masuknya barang sebagai pusat pertumbuhan ekonomi, penyediaan fasilitas pendidikan tentunya lebih baik dibanding di daerah luar kawasan metropolitan. Secara resmi kawasan Mebidang telah ditetapkan oleh Gubenur Propinsi Sumatera Utara sebagai Mebidang Metropolitan Area (MMA) pada tahun 1985. Wilayah Mebidang terdiri dari 40 kecamatan yang meliputi 21 kecamatan di Kota Medan, 5 kecamatan di Kota Binjai dan 14 kecamatan (dari 33 kecamatan) di Kabupaten Deli Serdang.
Tabel 2.1 Wilayah Administrasi Mebidang
Kabupaten/Kota Kecamatan
Medan Medan Tuntungan, Medan Selayang, Medan Johor, Medan Amplas, Medan Denai, Medan Tembung, Medan Kota, Medan Area, Medan Baru, Medan Polonia, Medan Maimun, Medan Sunggal, Medan Helvetia, Medan Petisah, Medan Barat, Medan Timur, Medan Perjuangan, Medan Deli, Medan Labuhan, Medan Marelan, dan Medan Belawan.
Binjai Binjai Selatan,Binjai Kota, Binjai Timur, Binjai Utara, dan Binjai Barat
Deli Serdang Hamparan Perak, Labuhan Deli, Sunggal, Percut Sei Tuan, Batang Kuis, Tanjung Morawa, Lubuk Pakam, Pagar Merbau, Beringin, Pantai Labu, Patumbak, Deli Tua, Namo Rambe, dan Pancur Batu
Menggunakan definisi Mebidang, daerah asal bersekolah dikelompokkan menjadi dua yaitu dalam daerah dan luar daerah. Dalam daerah merupakan asal daerah mahasiswa bersekolah SMA atau sederajat yang berada pada kawasan Mebidang. Luar Daerah merupakan asal daerah mahasiswa bersekolah SMA atau sederajat yang berada pada kawasan di luar Mebidang. Konsep Mebidang penulis gunakan sebagai perbandingan potensi mahasiswa yang bersekolah SMA atau sederajat. Mebidang dipilih sebagai dasar pengelompokkan karena kawasan metropolitan memberikan gambaran kemajuan kota di dalam kawasan tersebut di berbagai bidang.
2.2 Skala Pengukuran
Kesesuaian antara macam data dengan metode analisis statistiknya didasarkan pada skala pengukuran datanya. Ada empat macam skala pengukuran yaitu:
1. Skala nominal
Angka yang berfungsi hanya untuk membedakan, merupakan identitas/lambang/simbol, urutan tidak berlaku, operasi matematika juga tidak berlaku, misalnya jenis kelamin.
2. Skala ordinal
Angka yang berfungsi sebagai nominal dan juga menunjukkan urutan, misalnya tingkat kualitas.
3. Skala interval
Angka yang selain berfungsi sebagai nominal dan ordinal juga menunjukkan jarak yang sama, titik nol letaknya sembarang dan dipergunakan untuk rating misalnya kenaikan suhu.
4. Skala rasio
Angka yang berfungsi sebagai nominal, ordinal dan interval. Skala rasio memiliki titik nol yang tidak sembarang misalnya tinggi badan.
Skala pengukuran variabel, menggambarkan pemahaman terhadap data yang dimiliki. Skala pengukuran variabel dibagi menjadi katagorik (nominal,ordinal) dan numerik (rasio,interval)
2.3 Klasifikasi Data
Data merupakan kumpulan angka atau huruf hasil dari penelitian terhadap sifat/karakteristik yang diteliti. Menurut Sudjana (2005) data menurut sumbernya terbagi dua jenis yaitu:
a. Data intern adalah data yang diambil/diperoleh dari dalam suatu badan usaha atau dirinya sendiri, misalnya data hasil penjualan pegawai perusahaan A.
b. Data ekstern adalah data yang diperoleh di luar suatu badan atau dirinya sendiri, misalnya data hasil penjualan perusahaan A digunakan perusahaan B maka perusahaan B menggunakan data ekstern. Data ekstern dibagi menjadi dua yaitu ekstern primer (data primer) dan data ekstern sekunder (data sekunder). Jika data itu diperoleh/dikumpulkan dan diolah oleh badan yang sama atau dirinya sendiri maka disebut data primer misalnya data hasil wawancara. Jika data yang diperoleh dari badan atau instansi lain disebut data sekunder misalnya data BPS.
Menurut Sudjana (2005) berdasarkan bentuk/jenis data dibagi menjadi dua jenis yaitu:
a. Data yang berbentuk bilangan disebut data kuantitatif atau numerik. Menurut nilainya, dikenal dua golongan data kuantitatif ialah:
1. Data dengan variabel diskrit (data diskrit) merupakan data hasil menghitung dan mebilang misalnya Kabupaten B sudah membangun 85 gedung sekolah.
2. Data dengan variabel kontinu (data kontinu) merupakan data hasil pengukuran misalnya tinggi badan seseorang 155 cm.
b. Data yang berbentuk bukan bilangan disebut data kualitatif atau data katagorik, misalnya katagori mahasiswa berprestasi dan tidak berprestasi. Data katagorik merupakan data dimana variabel-variabelnya dapat dikelompokkan menjadi beberapa kelompok atau katagori seperti jenis kelamin, agama yang dianut atau ras kulit dari responden. Menurut Bayo lawal (2003) data
katagorik muncul setiap kali variabel diukur pada skala yang hanya mengklasifikasikan responden ke dalam sejumlah kelompok. Dengan demikian, data katagorik dari hasil suatu pengamatan mengandung variabel-variabel yang berkatagorik. Dalam analisis statistik seringkali data numerik dirubah ke dalam data katagorik dengan cara dilakukan pengelompokan/pengklasifikasian.
2.4 Variabel (Peubah)
Isi data pada umumnya bervariasi sehingga muncul istilah variabel. Oleh karena itu, variabel merupakan karakteristik yang nilai datanya bervariasi dari satu pengukuran ke pengukuran berikutnya. Menurut Saefuddin, dkk (2009) variabel (peubah) menurut sifatnya dibedakan menjadi dua jenis yaitu:
1. Variabel (peubah) kuantitatif adalah peubah yang sifatnya kontinu dan hasil pengukuran merupakan nilai pendekatan yang tergantung kepada ketelitian alat ukur yang digunakan. Nilai sebenarnya dari peubah tersebut sulit dinyatakan oleh nilai tunggal tertentu tetapi dalam bentuk selang nilai. Misalnya tinggi badan seseorang 160 cm.
2. Variabel (peubah) kualitatif adalah peubah yang nilai-nilainya ditetapkan menurut katagori tertentu dinamakan variabel (peubah) katagorik. Variabel (peubah) katagorik sifatnya terputus atau diskrit. Atribut pengamatan dalam hal ini dikelaskan kedalam katagori-katagori tertentu yang tidak saling tumpang tindih. Misalnya jenis kelamin yaitu perempuan dan laki-laki.
Variabel kuantitatif dikenal sebagai variabel numerik sedangkan variabel kualitatif dikenal sebagai variabel katagorik. Variabel katagorik pada umumnya berisi variabel yang berskala nominal dan ordinal. Menurut Bayo lawal (2003) ada dua jenis variabel katagorik yaitu variabel nominal dan ordinal. Variabel nominal adalah sekumpulan katagori yang saling lepas dan tidak memiliki urutan. Variabel ordinal adalah sekumpulan kategori yang memiliki urutan. Variabel numerik berisi variabel yang berskala interval dan rasio.
2.5 Distribusi Poisson
Menurut Saefuddin, dkk (2009) apabilla rataan banyaknya sukses dalam selang pengamatan tersebut diketahui sebesar 𝜇𝜇, maka distribusi poisson yang menyatakan peluang diperolehnya sukses sebanyak 𝑥𝑥 pada selang tertentu adalah:
𝑝𝑝(𝑥𝑥; 𝜇𝜇) =𝑒𝑒−𝜇𝜇𝑥𝑥!𝜇𝜇𝑥𝑥, 𝑥𝑥 = 0,1,2, … , ∞; 𝑒𝑒 = 2,71828 (2.1)
Keterangan:
𝜇𝜇 = rataan banyaknya sukses 𝑥𝑥 = banyaknya kejadian sukses 𝑒𝑒 = eksponensial
Menurut Sudjana (2005) distribusi Poisson sering digunakan untuk menetukan peluang sebuah peristiwa yang dalam area kesempatan tertentu diharapkan terjadinya sangat jarang. Distribusi Poisson dapat dianggap sebagai pendekatan terhadap distribusi Binomial. Jika dalam hal distribusi binom, jumlah observasi 𝑛𝑛 cukup besar sedangkan peluang terjadinya peristiwa 𝐴𝐴 adalah 𝑝𝑝 sangat dekat kepada nol sedemikian sehingga 𝜆𝜆 = 𝑛𝑛. 𝑝𝑝 tetap, maka distribusi Binomial sangat baik didekati oleh distribusi Poisson. Pendekatan ini sering dilakukan jika 𝑛𝑛 ≥ 50 sedangkan 𝑛𝑛. 𝑝𝑝 < 5 atau 𝑝𝑝 < 0,1
2.6 Model Pengambilan Sampel
Menurut Stephen E. Fienberg (2007) dalam membentuk suatu tabel kontingensi harus berdasarkan cara pengambilan sampel untuk tiap sel yang terkandung. Sebagai asumsi distribusi frekuensi pengamatan dalam tiap sel tabel kontingensi maka digunakan suatu model pengambilan sampel. Ada tiga jenis model pengambilan sampel yang sering digunakan pada data klasifikasi silang yaitu:
1. Poisson: Kumpulan observasi mengikuti proses poisson, tiap sel pada klasifikasi silang diamati pada suatu interval waktu tertentu. Pengamatan sampel yang dilakukan untuk setiap sel dalam tabel ini tanpa diketahui lebih dulu banyaknya jumlah observasi yang akan diambil.
2. Multinomial: Jumlah sampel sebanyak 𝑛𝑛 telah ditentukan, kemudian setiap individu sampelnya diklasifikasikan ke dalam sel tabel kontingensi yang bersesuaian.
3. Product Multinomial: Setiap katagori pada variabel baris mengikuti pengambilan sampel multinomial dengan ukuran sampel 𝑥𝑥𝑖𝑖+ dan klasifikasi setiap anggota pada sampel menurut katagori variabel kolom (peran baris dan kolom bertukar tempat).
Pada penulisan skripsi ini data yang ada diperoleh melalui pengambilan sampel dengan model multinomial.
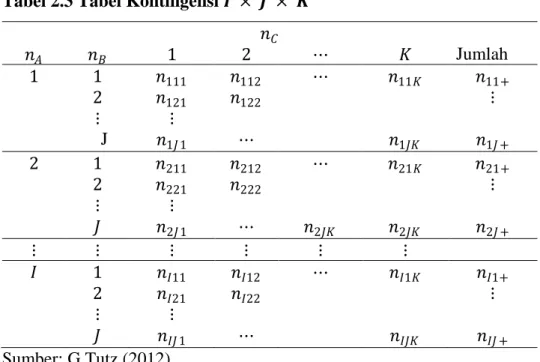
2.7 Tabel Kontingensi
Menurut Razia Azen dan Cindy M. Walker (2011) ketika subyek atau objek diklasifikasikan secara simultan oleh dua atau lebih atribut, hasil pada klasifikasi silang dapat disusun dengan baik sebagai tabel hitung yang disebut tabel kontingensi. Tabel kontingensi digunakan untuk melihat hubungan antara dua atau lebih variabel katagorik. Penggunaan tabel kontingensi yang akan dibahas pada penelitian ini penulis kelompokkan menjadi dua yaitu tabel kontingensi dua dimensi dan tabel kontingensi tiga dimensi.
1. Tabel Kontingensi Dua Dimensi
Menurut G. Tutz (2012), nilai sel 𝑛𝑛𝑖𝑖𝑖𝑖 adalah nilai observasi dengan sel(𝑖𝑖, 𝑖𝑖) dengan 𝑛𝑛𝐴𝐴 = 𝑖𝑖, 𝑛𝑛𝐵𝐵 = 𝑖𝑖. Tabel kontingensi dua dimensi merupakan klasifikasi antar variabel 1 misal variabel observasi A yaitu 𝑛𝑛𝐴𝐴 sebagai baris dengan tingkat 𝑖𝑖 = 1,2, ⋯ , 𝐼𝐼 dan variabel 2 misal variabel observasi B yaitu
𝑛𝑛𝐵𝐵 sebagai kolom dengan tingkat 𝑖𝑖 = 1,2, ⋯ , 𝐽𝐽. Penyajian dalam daftar baris
dan kolom tersebut biasa dikenal dengan tabel kontingensi dua dimensi. Jika data disajikan dalam bentuk tabel frekuensi menurut variabel katagorik 𝐴𝐴 dan 𝐵𝐵 yang mempunyai dua baris dan dua kolom disebut tabel kontingensi 2 × 2. Data yang disusun dalam tabel katagorik 𝐼𝐼 × 𝐽𝐽 sebagai berikut:
Tabel 2.2 Tabel Kontingensi 𝑰𝑰 × 𝑱𝑱
𝑛𝑛𝐵𝐵 1 2 ⋯ 𝐽𝐽 𝑛𝑛𝐴𝐴 1 𝑛𝑛11 𝑛𝑛12 ⋯ 𝑛𝑛1𝐽𝐽 𝑛𝑛1+ 2 𝑛𝑛21 ⋱ ⋮ ⋮ ⋮ ⋮ ⋱ ⋮ 𝐼𝐼 𝑛𝑛𝐼𝐼1 ⋯ 𝑛𝑛𝐼𝐼𝐽𝐽 𝑛𝑛𝐼𝐼+ 𝑛𝑛+1 ⋯ 𝑛𝑛+𝐽𝐽 Sumber: G. Tutz (2012) Keterangan: 𝑛𝑛+𝑖𝑖 = ∑𝐽𝐽𝑖𝑖 =1𝑛𝑛𝑖𝑖𝑖𝑖 ,𝑛𝑛+𝑖𝑖 = ∑𝐼𝐼𝑖𝑖=1𝑛𝑛𝑖𝑖𝑖𝑖
𝑛𝑛+𝑖𝑖 = jumlah marginal pada variabel baris
𝑛𝑛+𝑖𝑖 = jumlah marginal pada variabel kolom
Subskrip “+” menyatakan penjumlahan pada indeks tersebut.
2. Tabel Kontingensi Tiga Dimensi
Menurut G Tutz (2012), nilai sel 𝑛𝑛𝑖𝑖𝑖𝑖𝑖𝑖 adalah nilai observasi dengan sel (𝑖𝑖, 𝑖𝑖, 𝑖𝑖) dengan 𝑛𝑛𝐴𝐴 = 𝑖𝑖, 𝑛𝑛𝐵𝐵 = 𝑖𝑖, 𝑛𝑛𝐶𝐶 = 𝑖𝑖. Tabel kontingensi tiga dimensi
merupakan klasifikasi antar variabel 1 misal variabel observasi A yaitu 𝑛𝑛𝐴𝐴 sebagai baris dengan tingkat 𝑖𝑖 = 1,2, ⋯ , 𝐼𝐼 dan variabel 2 misal variabel
observasi B yaitu 𝑛𝑛𝐵𝐵 sebagai kolom dengan tingkat 𝑖𝑖 = 1,2, ⋯ , 𝐽𝐽 dan variabel 3 misal variabel observasi C yaitu 𝑛𝑛𝐶𝐶 sebagai layer dengan tingkat 𝑖𝑖 = 1,2, ⋯ , 𝐾𝐾 maka data tersebut dapat disusun dalam tabel kontingensi I × J × K sebagai berikut:
Tabel 2.3 Tabel Kontingensi 𝑰𝑰 × 𝑱𝑱 × 𝑲𝑲 𝑛𝑛𝐶𝐶 𝑛𝑛𝐴𝐴 𝑛𝑛𝐵𝐵 1 2 ⋯ 𝐾𝐾 Jumlah 1 1 𝑛𝑛111 𝑛𝑛112 ⋯ 𝑛𝑛11𝐾𝐾 𝑛𝑛11+ 2 𝑛𝑛121 𝑛𝑛122 ⋮ ⋮ ⋮ J 𝑛𝑛1𝐽𝐽1 ⋯ 𝑛𝑛1𝐽𝐽𝐾𝐾 𝑛𝑛1𝐽𝐽+ 2 1 𝑛𝑛211 𝑛𝑛212 ⋯ 𝑛𝑛21𝐾𝐾 𝑛𝑛21+ 2 𝑛𝑛221 𝑛𝑛222 ⋮ ⋮ ⋮ 𝐽𝐽 𝑛𝑛2𝐽𝐽1 ⋯ 𝑛𝑛2𝐽𝐽𝐾𝐾 𝑛𝑛2𝐽𝐽𝐾𝐾 𝑛𝑛2𝐽𝐽+ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ 𝐼𝐼 1 𝑛𝑛𝐼𝐼11 𝑛𝑛𝐼𝐼12 ⋯ 𝑛𝑛𝐼𝐼1𝐾𝐾 𝑛𝑛𝐼𝐼1+ 2 𝑛𝑛𝐼𝐼21 𝑛𝑛𝐼𝐼22 ⋮ ⋮ ⋮ 𝐽𝐽 𝑛𝑛𝐼𝐼𝐽𝐽1 ⋯ 𝑛𝑛𝐼𝐼𝐽𝐽𝐾𝐾 𝑛𝑛𝐼𝐼𝐽𝐽+ Sumber: G Tutz (2012) di mana 𝑛𝑛𝑖𝑖++= � � 𝑛𝑛𝑖𝑖𝑖𝑖𝑖𝑖 𝐾𝐾 𝑖𝑖=1 𝐽𝐽 𝑖𝑖 =1 𝑛𝑛+𝑖𝑖 + = � � 𝑛𝑛𝑖𝑖𝑖𝑖𝑖𝑖 𝐾𝐾 𝑖𝑖=1 𝐼𝐼 𝑖𝑖=1 𝑛𝑛++𝑖𝑖 = � � 𝑛𝑛𝑖𝑖𝑖𝑖𝑖𝑖 𝐽𝐽 𝑖𝑖 =1 𝐼𝐼 𝑖𝑖=1 Keterangan:
𝑛𝑛𝑖𝑖++= jumlah marginal pada variabel baris
𝑛𝑛+𝑖𝑖 + = jumlah marginal pada variabel kolom
𝑛𝑛++𝑖𝑖 = jumlah marginal pada variabel layer
2.8 Model Loglinier
Menurut Razia Azen dan Cindy M. Walker (2011) model loglinier digunakan untuk memodelkan jumlah sel pada tabel kontingensi. Tujuan yang ingin dicapai pada model loglinier adalah mengestimasi parameter yang menjelaskan hubungan antar variabel kategori. Tidak adanya perbedaan antara variabel penjelas dengan variabel respon, sehingga model loglinier hanya dapat menggambarkan struktur interaksi antar variabelnya. Analisis log linier merupakan perluasan dari tabel kontingensi dua dimensi di mana hubungan bersyarat di antara dua atau lebih variabel kategori diskrit dianalisis dengan mengambil logaritma natural dari frekuensi sel pada tabel kontingensi. Model loglinier yang akan dibahas adalah model loglinier dua dimensi dan model loglinier tiga dimensi.
1. Model Loglinier Pada Tabel Kontingensi Dua Dimensi a. Model Loglinier Independen
Andaikan probabilitas sel pada tabel kontingensi dua dimensi adalah 𝜋𝜋𝑖𝑖𝑖𝑖 dengan jumlah observasi 𝑛𝑛 dan nilai harapan 𝑚𝑚𝑖𝑖𝑖𝑖 = 𝑛𝑛. 𝜋𝜋𝑖𝑖𝑖𝑖. Berdasarkan sifat independen maka 𝑚𝑚𝑖𝑖𝑖𝑖 = 𝑛𝑛. 𝜋𝜋𝑖𝑖+. 𝜋𝜋+𝑖𝑖 dimana 𝜋𝜋𝑖𝑖+ adalah probabilitas dari variabel baris 𝐴𝐴 dan 𝜋𝜋+𝑖𝑖 adalah probabilitas dari variabel kolom 𝐵𝐵. Ketika praktek, 𝜋𝜋𝑖𝑖𝑖𝑖 tidak diketahui yang diamati adalah 𝑛𝑛𝑖𝑖𝑖𝑖, sehingga probabilitas harus ditaksir untuk mencari frekuensi harapan. Besarnya probabilitas dapat dihitung dengan 𝜋𝜋�𝑖𝑖+ = 𝑛𝑛𝑖𝑖+
𝑛𝑛 , 𝜋𝜋�+𝑖𝑖 = 𝑛𝑛+𝑖𝑖
𝑛𝑛 , sehingga
estimasi nilai harapannya sebagai berikut:
𝑚𝑚�𝑖𝑖𝑖𝑖 = 𝑛𝑛. 𝜋𝜋�𝑖𝑖+. 𝜋𝜋�+𝑖𝑖 =(𝑛𝑛𝑖𝑖+)(𝑛𝑛𝑛𝑛 +𝑖𝑖) (2.2)
Keterangan :
𝑚𝑚�𝑖𝑖𝑖𝑖𝑖𝑖 = nilai harapan
𝑛𝑛𝑖𝑖+ =∑𝐽𝐽𝑖𝑖 =1𝑛𝑛𝑖𝑖𝑖𝑖 = jumlah marginal pada variabel baris ke 𝑖𝑖
𝑛𝑛+𝑖𝑖 = ∑𝐼𝐼𝑖𝑖=1𝑛𝑛𝑖𝑖𝑖𝑖 = jumlah marginal pada variabel kolom ke 𝑖𝑖
Setelah terbentuk tabel kontingensi dua dimensi, model loglinier akan menggambarkan pola hubungan antar variabel katagorik. Model independen logliniernya berdasarkan peluang yaitu:
𝑙𝑙𝑖𝑖𝑖𝑖 = 𝜇𝜇 + 𝜆𝜆𝑖𝑖𝐴𝐴+ 𝜆𝜆𝑖𝑖𝐵𝐵 (2.3)
Keterangan:
𝑖𝑖 = 1,2, ⋯ , 𝐼𝐼 dan 𝑖𝑖 = 1,2, ⋯ , 𝐽𝐽
𝑙𝑙𝑖𝑖𝑖𝑖 = ln 𝑚𝑚�𝑖𝑖𝑖𝑖 = logaritma natural dari frekuensi harapan sel ke 𝑖𝑖𝑖𝑖
𝜇𝜇 = parameter rataan umum
𝜆𝜆𝑖𝑖𝐴𝐴 = parameter pengaruh utama variabel pertama (𝐴𝐴) pada katagori ke 𝑖𝑖
𝜆𝜆𝑖𝑖𝐵𝐵 = parameter pengaruh utama variabel kedua (𝐵𝐵) pada katagori ke 𝑖𝑖
b. Model Loglinier Lengkap
Frekuensi harapan pada model loglinier lengkap sama dengan nilai observasinya 𝑚𝑚�𝑖𝑖𝑖𝑖 = 𝑛𝑛𝑖𝑖𝑖𝑖. Model umum disebut juga model saturated. Model lengkap pada dua dimensi sebagai berikut:
𝑙𝑙𝑖𝑖𝑖𝑖 = 𝜇𝜇 + 𝜆𝜆𝑖𝑖𝐴𝐴+ 𝜆𝜆𝑖𝑖𝐵𝐵 + 𝜆𝜆𝑖𝑖𝑖𝑖𝐴𝐴𝐵𝐵 (2.4)
Keterangan:
𝑖𝑖 = 1,2, ⋯ , 𝐼𝐼 dan 𝑖𝑖 = 1,2, ⋯ , 𝐽𝐽
𝑙𝑙𝑖𝑖𝑖𝑖 = ln 𝑚𝑚�𝑖𝑖𝑖𝑖 = logaritma natural dari frekuensi harapan sel ke 𝑖𝑖𝑖𝑖
𝜇𝜇 = parameter rataan umum
𝜆𝜆𝑖𝑖𝐴𝐴 = parameter pengaruh utama variabel pertama (𝐴𝐴) pada katagori ke 𝑖𝑖
𝜆𝜆𝑖𝑖𝐵𝐵 = parameter pengaruh utama variabel kedua (𝐵𝐵) pada katagori ke 𝑖𝑖
𝜆𝜆𝑖𝑖𝑖𝑖𝐴𝐴𝐵𝐵 = parameter pengaruh interaksi variabel pertama (𝐴𝐴) katagori ke 𝑖𝑖
dengan variabel kedua (𝐵𝐵) katagori ke 𝑖𝑖
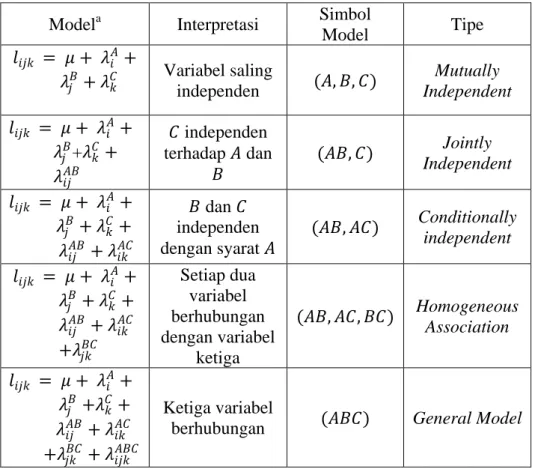
2. Model Loglinier Pada Tabel Kontingensi Tiga Dimensi
Model loglinier tiga dimensi merupakan pengembangan model loglinier dua dimensi. Semakin banyak dimensi pada tabel kontingensi maka semakin
banyak model loglinier yang dianalisis. Pada tabel tiga dimensi, model-model loglinier tersebut sebagai berikut:
Tabel 2.4 Model-model Loglinier Tiga Dimensi
Modela Interpretasi Simbol
Model Tipe
𝑙𝑙𝑖𝑖𝑖𝑖𝑖𝑖 = 𝜇𝜇 + 𝜆𝜆𝑖𝑖𝐴𝐴+
𝜆𝜆𝑖𝑖𝐵𝐵+ 𝜆𝜆𝑖𝑖𝐶𝐶 Variabel saling independen (𝐴𝐴, 𝐵𝐵, 𝐶𝐶) Independent Mutually
𝑙𝑙𝑖𝑖𝑖𝑖𝑖𝑖 = 𝜇𝜇 + 𝜆𝜆𝑖𝑖𝐴𝐴+ 𝜆𝜆𝑖𝑖𝐵𝐵+𝜆𝜆𝑖𝑖𝐶𝐶+ 𝜆𝜆𝑖𝑖𝑖𝑖𝐴𝐴𝐵𝐵 𝐶𝐶 independen terhadap 𝐴𝐴 dan 𝐵𝐵 (𝐴𝐴𝐵𝐵, 𝐶𝐶) Jointly Independent 𝑙𝑙𝑖𝑖𝑖𝑖𝑖𝑖 = 𝜇𝜇 + 𝜆𝜆𝑖𝑖𝐴𝐴+ 𝜆𝜆𝑖𝑖𝐵𝐵+ 𝜆𝜆𝑖𝑖𝐶𝐶+ 𝜆𝜆𝑖𝑖𝑖𝑖𝐴𝐴𝐵𝐵 + 𝜆𝜆𝑖𝑖𝑖𝑖𝐴𝐴𝐶𝐶 𝐵𝐵 dan 𝐶𝐶 independen dengan syarat 𝐴𝐴 (𝐴𝐴𝐵𝐵, 𝐴𝐴𝐶𝐶) Conditionally independent 𝑙𝑙𝑖𝑖𝑖𝑖𝑖𝑖 = 𝜇𝜇 + 𝜆𝜆𝑖𝑖𝐴𝐴+ 𝜆𝜆𝑖𝑖𝐵𝐵 + 𝜆𝜆𝑖𝑖𝐶𝐶+ 𝜆𝜆𝑖𝑖𝑖𝑖𝐴𝐴𝐵𝐵 + 𝜆𝜆 𝑖𝑖𝑖𝑖 𝐴𝐴𝐶𝐶 +𝜆𝜆𝑖𝑖𝑖𝑖𝐵𝐵𝐶𝐶 Setiap dua variabel berhubungan dengan variabel ketiga (𝐴𝐴𝐵𝐵, 𝐴𝐴𝐶𝐶, 𝐵𝐵𝐶𝐶) Homogeneous Association 𝑙𝑙𝑖𝑖𝑖𝑖𝑖𝑖 = 𝜇𝜇 + 𝜆𝜆𝑖𝑖𝐴𝐴+ 𝜆𝜆𝑖𝑖𝐵𝐵 +𝜆𝜆𝑖𝑖𝐶𝐶+ 𝜆𝜆𝑖𝑖𝑖𝑖𝐴𝐴𝐵𝐵 + 𝜆𝜆𝑖𝑖𝑖𝑖𝐴𝐴𝐶𝐶 +𝜆𝜆𝑖𝑖𝑖𝑖𝐵𝐵𝐶𝐶 + 𝜆𝜆 𝑖𝑖𝑖𝑖𝑖𝑖 𝐴𝐴𝐵𝐵𝐶𝐶 Ketiga variabel
berhubungan (𝐴𝐴𝐵𝐵𝐶𝐶) General Model a
Formula untuk model yang tidak tertulis memiliki kemiripan, misalnya untuk (XZ, Y), 𝑙𝑙𝑖𝑖𝑖𝑖𝑖𝑖 = 𝜇𝜇 + 𝜆𝜆𝑖𝑖𝐴𝐴+ 𝜆𝜆𝑖𝑖𝐵𝐵 +𝜆𝜆𝑖𝑖𝐶𝐶+ 𝜆𝜆𝑖𝑖𝑖𝑖𝐴𝐴𝐶𝐶. Sumber: Agresti (2002)
Pada tabel 2.4 model umum loglinier tiga dimensi yaitu:
𝑙𝑙𝑖𝑖𝑖𝑖𝑖𝑖 = 𝜇𝜇 + 𝜆𝜆𝑖𝑖𝐴𝐴 + 𝜆𝜆𝑖𝑖𝐵𝐵 +𝜆𝜆𝑖𝑖𝐶𝐶+ 𝜆𝜆𝑖𝑖𝑖𝑖𝐴𝐴𝐵𝐵 + 𝜆𝜆𝑖𝑖𝑖𝑖𝐴𝐴𝐶𝐶 + 𝜆𝜆𝑖𝑖𝑖𝑖𝐵𝐵𝐶𝐶 + 𝜆𝜆𝑖𝑖𝑖𝑖𝑖𝑖𝐴𝐴𝐵𝐵𝐶𝐶 (2.5)
Keterangan:
𝑖𝑖 = 1,2, ⋯ , 𝐼𝐼 ; 𝑖𝑖 = 1,2, ⋯ , 𝐽𝐽 dan 𝑖𝑖 = 1,2, ⋯ , 𝐾𝐾
𝑙𝑙𝑖𝑖𝑖𝑖𝑖𝑖 = ln 𝑚𝑚�𝑖𝑖𝑖𝑖𝑖𝑖 = logaritma natural dari frekuensi harapan sel ke 𝑖𝑖𝑖𝑖𝑖𝑖
𝜇𝜇 = parameter rataan umum
𝜆𝜆𝑖𝑖𝐴𝐴 = parameter pengaruh utama variabel pertama (𝐴𝐴) pada katagori ke 𝑖𝑖
𝜆𝜆𝑖𝑖𝐵𝐵 = parameter pengaruh utama variabel kedua (𝐵𝐵) pada katagori ke 𝑖𝑖
𝜆𝜆𝑖𝑖𝑖𝑖𝐴𝐴𝐵𝐵 = parameter pengaruh interaksi variabel pertama (𝐴𝐴) katagori ke 𝑖𝑖
dengan variabel kedua (𝐵𝐵) katagori ke 𝑖𝑖
𝜆𝜆𝑖𝑖𝑖𝑖𝐴𝐴𝐶𝐶 = parameter pengaruh interaksi variabel pertama (𝐴𝐴) katagori ke 𝑖𝑖
dengan variabel ketiga (𝐶𝐶) katagori ke 𝑖𝑖
𝜆𝜆𝑖𝑖𝑖𝑖𝐵𝐵𝐶𝐶 = parameter pengaruh interaksi variabel kedua (𝐵𝐵) katagori ke 𝑖𝑖 dengan
variabel ketiga (𝐶𝐶) katagori ke 𝑖𝑖
𝜆𝜆𝑖𝑖𝑖𝑖𝑖𝑖𝐴𝐴𝐵𝐵𝐶𝐶 = parameter pengaruh interaksi variabel pertama (𝐴𝐴) katagori ke- 𝑖𝑖
variabel kedua (𝐵𝐵) katagori ke- 𝑖𝑖 dengan variabel ketiga (𝐶𝐶) katagori ke 𝑖𝑖
2.9 Kendala Parameter
Menurut Agresti (2002) perbedaan software menggunakan perbedaaan kendala. Menurut Bayo lawal (2003) penggunaan software menggunakan PROC GENMOD pada SPSS sehingga identifikasi kendala yaitu untuk hanya parameter pada katagori terakhir dari setiap variabel dan hubungan interaksinya yang diatur bernilai nol. Ini disebut means model atau 𝜇𝜇-model. Identifikasi kendala penting dilakukan agar tidak overparameterized. Menurut A. W. Vogelesang (1996) Metode yang lain untuk membatasi jumlah parameter pada model adalah ANOVA-model, yang mana jumlah parameter pada setiap pengaruh adalah nol. Pada ANOVA-model, rata-rata umum merupakan intercept sedangkan pada 𝜇𝜇-model rata-rata umum ditambah parameter pada setiap tingkat terakhir variabel merupakan intercept, ini artinya bahwa pengurangan tingkat terakhir pada setiap tingkat variabel. Pada penelitian ini menggunakan kendala 𝜇𝜇-model.
Misalkan untuk model dua dimensi pada persamaan (2.4) maka estimasi adalah 𝜇𝜇̂ = ln�𝑛𝑛𝐼𝐼𝐽𝐽� = 𝑙𝑙𝐼𝐼𝐽𝐽
𝜆𝜆̂𝑖𝑖𝐴𝐴 = 𝑙𝑙𝑖𝑖𝐽𝐽 − 𝑙𝑙𝐼𝐼𝐽𝐽
𝜆𝜆̂𝑖𝑖𝐵𝐵 = 𝑙𝑙𝐼𝐼𝑖𝑖 − 𝑙𝑙𝐼𝐼𝐽𝐽
𝜆𝜆̂𝑖𝑖𝑖𝑖𝐴𝐴𝐵𝐵 = 𝑙𝑙𝑖𝑖𝑖𝑖 − 𝑙𝑙𝑖𝑖𝐽𝐽 − 𝑙𝑙𝐼𝐼𝑖𝑖 + 𝑙𝑙𝐼𝐼𝐽𝐽
𝜆𝜆̂𝐼𝐼𝐴𝐴 = 𝜆𝜆̂𝐽𝐽𝐵𝐵 = 0,0 dan 𝜆𝜆̂𝑖𝑖𝐽𝐽𝐴𝐴𝐵𝐵 = 𝜆𝜆̂𝐼𝐼𝑖𝑖𝐴𝐴𝐵𝐵 = 𝜆𝜆̂𝐼𝐼𝐽𝐽𝐴𝐴𝐵𝐵 = 0,0
Dimana
𝑙𝑙𝑖𝑖𝑖𝑖 = ln 𝑛𝑛𝐼𝐼𝐽𝐽; 𝑙𝑙𝑖𝑖𝐽𝐽 = ln 𝑛𝑛𝑖𝑖𝐽𝐽
Menggunakan cara yang sama untuk 𝑙𝑙𝐼𝐼𝑖𝑖, 𝑙𝑙𝐼𝐼𝑖𝑖, 𝑙𝑙𝑖𝑖𝑖𝑖.
Jika diketahui nilai harapan, model dapat ditaksir estimasinya dengan yaitu dengan substitusi 𝑙𝑙𝑖𝑖𝑖𝑖 = ln 𝑚𝑚�𝑖𝑖𝑖𝑖 dimana 𝑖𝑖 = 1,2, ⋯ , 𝐼𝐼 ; 𝑖𝑖 = 1,2, ⋯ , 𝐽𝐽.
Model tiga dimensi pada persamaan (2.5) maka estimasi adalah 𝜇𝜇̂ = ln�𝑛𝑛𝐼𝐼𝐽𝐽𝐾𝐾� = 𝑙𝑙𝐼𝐼𝐽𝐽𝐾𝐾 𝜆𝜆̂𝑖𝑖𝐴𝐴 = 𝑙𝑙𝑖𝑖𝐽𝐽𝐾𝐾 − 𝑙𝑙𝐼𝐼𝐽𝐽𝐾𝐾 𝜆𝜆̂𝑖𝑖𝐵𝐵 = 𝑙𝑙 𝐼𝐼𝑖𝑖𝐾𝐾 − 𝑙𝑙𝐼𝐼𝐽𝐽𝐾𝐾 𝜆𝜆̂𝑖𝑖𝑖𝑖𝐴𝐴𝐵𝐵 = 𝑙𝑙 𝑖𝑖𝑖𝑖 +− 𝑙𝑙𝑖𝑖𝐽𝐽 +− 𝑙𝑙𝐼𝐼𝑖𝑖 ++ 𝑙𝑙𝐼𝐼𝐽𝐽+ 𝜆𝜆̂𝑖𝑖𝑖𝑖𝐴𝐴𝐶𝐶 = 𝑙𝑙 𝑖𝑖+𝑖𝑖 − 𝑙𝑙𝑖𝑖+𝐾𝐾 − 𝑙𝑙𝐼𝐼+𝑖𝑖 + 𝑙𝑙𝐼𝐼+𝐽𝐽 𝜆𝜆̂𝑖𝑖𝑖𝑖𝑖𝑖𝐴𝐴𝐵𝐵𝐶𝐶 = 𝑙𝑙𝑖𝑖𝑖𝑖𝑖𝑖 − 𝑙𝑙𝑖𝑖𝑖𝑖𝐾𝐾 − 𝑙𝑙𝐼𝐼𝐽𝐽𝑖𝑖 + 𝑙𝑙𝐼𝐼𝐽𝐽𝐾𝐾
Estimasi yang serupa untuk parameter 𝜆𝜆̂𝑖𝑖𝐶𝐶 dan 𝜆𝜆̂𝑖𝑖𝑖𝑖𝐵𝐵𝐶𝐶. Dengan kendala 𝜆𝜆̂𝐼𝐼𝐴𝐴 = 𝜆𝜆̂𝐽𝐽𝐵𝐵 = 𝜆𝜆̂𝐾𝐾𝐶𝐶 = 0,0 𝜆𝜆̂𝑖𝑖𝐽𝐽𝐴𝐴𝐵𝐵 = 𝜆𝜆̂𝐼𝐼𝑖𝑖𝐴𝐴𝐵𝐵 = 𝜆𝜆̂𝑖𝑖𝐾𝐾𝐵𝐵𝐶𝐶 = 𝜆𝜆̂𝐽𝐽𝑖𝑖𝐵𝐵𝐶𝐶 = 𝜆𝜆̂𝑖𝑖𝐾𝐾𝐴𝐴𝐶𝐶 = 𝜆𝜆̂𝐼𝐼𝑖𝑖𝐴𝐴𝐶𝐶 = 0,0 𝜆𝜆̂𝑖𝑖𝑖𝑖𝐾𝐾𝐴𝐴𝐵𝐵𝐶𝐶 = 𝜆𝜆̂𝑖𝑖𝐽𝐽𝑖𝑖𝐴𝐴𝐵𝐵𝐶𝐶 = 𝜆𝜆̂𝐼𝐼𝑖𝑖𝑖𝑖𝐴𝐴𝐵𝐵𝐶𝐶 = 0,0 dimana 𝑙𝑙𝑖𝑖𝑖𝑖𝑖𝑖 = ln 𝑛𝑛𝑖𝑖𝐽𝐽𝑖𝑖 ; 𝑙𝑙𝑖𝑖𝑖𝑖𝐾𝐾 = ln 𝑛𝑛𝑖𝑖𝑖𝑖𝐾𝐾 𝑙𝑙𝑖𝑖𝑖𝑖 + = ∑𝐾𝐾𝑖𝑖=1ln 𝑛𝑛𝑖𝑖𝑖𝑖𝑖𝑖; 𝑙𝑙𝐼𝐼𝑖𝑖 + = ∑𝐾𝐾𝑖𝑖=1ln 𝑛𝑛𝐼𝐼𝑖𝑖𝑖𝑖 ; 𝑙𝑙𝐼𝐼𝐽𝐽+ = ∑𝐾𝐾𝑖𝑖=1ln 𝑛𝑛𝐼𝐼𝐽𝐽𝑖𝑖
Menggunakan cara yang sama untuk 𝑙𝑙𝑖𝑖𝑖𝑖𝐾𝐾, 𝑙𝑙𝐼𝐼𝐽𝐽𝐾𝐾, 𝑙𝑙𝐼𝐼𝐽𝐽+, 𝑙𝑙𝑖𝑖𝐽𝐽 +, 𝑙𝑙𝑖𝑖+𝑖𝑖, 𝑙𝑙𝑖𝑖+𝐾𝐾 dimana 𝑖𝑖 = 1,2, ⋯ , 𝐼𝐼 ; 𝑖𝑖 = 1,2, ⋯ , 𝐽𝐽.
2.10 Prinsip Hirarki
Menurut Bayo lawal (2003) model loglinier menggunakan prinsip hierarki yaitu jika order pengaruh yang lebih tinggi ada dalam model maka order terendah juga ada dalam model. Menurut Razia Azen dan Cindy M.Walker (2011) pada tiga
variabel, jika ada interaksi dua arah yang masuk ke dalam model maka pengaruh utama pada variabel juga masuk ke dalam model. Misal mengikuti model loglinier secara hirarki jika ada mengandung dua interaksi yaitu satu untuk 𝐴𝐴 dan 𝐵𝐵 dan satu untuk 𝐴𝐴 dan 𝐶𝐶, maka juga mengandung pengaruh utama semua tiga variabel:
𝑙𝑙𝑖𝑖𝑖𝑖𝑖𝑖 = 𝜇𝜇 + 𝜆𝜆𝑖𝑖𝐴𝐴+ 𝜆𝜆𝑖𝑖𝐵𝐵+ 𝜆𝜆𝑖𝑖𝐶𝐶+ 𝜆𝜆𝑖𝑖𝑖𝑖𝐴𝐴𝐵𝐵 + 𝜆𝜆𝑖𝑖𝑖𝑖𝐴𝐴𝐶𝐶 (2.6)
Jika ada salah satu dari pengaruh utama yang tidak masuk ke dalam model maka model tidak hirarki.
2.11 Statistik Cukup Minimal dan Fungsi Likelihood
Setelah diperoleh model loglinier yang terbaik, maka selanjutnya melakukan estimasi parameter dari model loglinier tersebut. Estimasi suatu parameter dalam model loglinier berarti menaksir nilai harapan tiap sel pada tabel kontingensi. Misalkan terpilih model (𝐴𝐴𝐶𝐶, 𝐵𝐵𝐶𝐶), maka untuk mendapatkan estimasi parameter 𝜇𝜇, 𝜆𝜆𝑖𝑖𝐴𝐴, 𝜆𝜆𝑖𝑖𝐵𝐵, 𝜆𝜆𝐶𝐶𝑖𝑖, 𝜆𝜆𝑖𝑖𝑖𝑖𝐴𝐴𝐵𝐵, 𝜆𝜆𝑖𝑖𝑖𝑖𝐴𝐴𝐶𝐶 adalah dengan estimasi nilai 𝑚𝑚𝑖𝑖𝑖𝑖𝑖𝑖. Metode penaksiran yang
digunakan adalah metode maksimum likelihood adalah prosedur untuk menemukan nilai estimasi dari satu atau lebih parameter yang memaksimumkan fungsi likelihood. Sebelum mendapatkan estimasi nilai harapan dari model loglinier dengan metode maksimum likelihood, terlebih dahulu dicari statistik cukup dari model loglinier.
Menurut Agresti (2002), sebelum menentukan kecocokan model loglinier, hal pertama yang harus diperoleh adalah statistik cukup minimal. Statistik cukup adalah tabel marginal yang melambangkan model. Menurut Bayo lawal (2003), statistik cukup minimal adalah susunan penjumlahan yang berhubungan dengan pengaruh pada model loglinier. Peluang gabungan poisson pada {𝑛𝑛𝑖𝑖𝑖𝑖𝑖𝑖} adalah � � �𝑒𝑒 −𝑚𝑚𝑖𝑖𝑖𝑖𝑖𝑖𝑚𝑚 𝑖𝑖𝑖𝑖𝑖𝑖 𝑛𝑛𝑖𝑖𝑖𝑖𝑖𝑖 𝑛𝑛𝑖𝑖𝑖𝑖𝑖𝑖! 𝑖𝑖 𝑖𝑖 𝑖𝑖 (2.7)
𝐿𝐿(𝑚𝑚) = � � � 𝑛𝑛𝑖𝑖𝑖𝑖𝑖𝑖 𝑖𝑖 ln(𝑚𝑚𝑖𝑖𝑖𝑖𝑖𝑖) 𝑖𝑖 𝑖𝑖 − � � � 𝑚𝑚𝑖𝑖𝑖𝑖𝑖𝑖 𝑖𝑖 𝑖𝑖 𝑖𝑖 (2.8)
Model umum loglinier tiga dimensi (𝐴𝐴𝐵𝐵𝐶𝐶) pada tabel 2.3, yaitu:
𝑙𝑙𝑖𝑖𝑖𝑖𝑖𝑖 = 𝜇𝜇 + 𝜆𝜆𝑖𝑖𝐴𝐴+ 𝜆𝜆𝑖𝑖𝐵𝐵+ 𝜆𝜆𝑖𝑖𝐶𝐶+ 𝜆𝜆𝑖𝑖𝑖𝑖𝐴𝐴𝐵𝐵 + 𝜆𝜆𝑖𝑖𝑖𝑖𝐴𝐴𝐶𝐶 + 𝜆𝜆𝑖𝑖𝑖𝑖𝐵𝐵𝐶𝐶 + 𝜆𝜆𝑖𝑖𝑖𝑖𝑖𝑖𝐴𝐴𝐵𝐵𝐶𝐶 (2.9)
Diketahui 𝑙𝑙𝑖𝑖𝑖𝑖𝑖𝑖 = ln 𝑚𝑚𝑖𝑖𝑖𝑖𝑖𝑖 pada persamaan (2.9), jika persamaan tersebut dirubah menjadi bentuk logaritma maka diperoleh
𝑚𝑚𝑖𝑖𝑖𝑖𝑖𝑖 = exp�𝜇𝜇 + 𝜆𝜆𝑖𝑖𝐴𝐴+ 𝜆𝜆𝑖𝑖𝐵𝐵 + 𝜆𝜆𝑖𝑖𝐶𝐶+ 𝜆𝜆𝑖𝑖𝑖𝑖𝐴𝐴𝐵𝐵 + 𝜆𝜆𝑖𝑖𝑖𝑖𝐴𝐴𝐶𝐶+ 𝜆𝜆𝑖𝑖𝑖𝑖𝐵𝐵𝐶𝐶 + 𝜆𝜆𝑖𝑖𝑖𝑖𝑖𝑖𝐴𝐴𝐵𝐵𝐶𝐶� (2.10)
Persamaan (2.10) disubstitusi ke persamaan log likelihood, yaitu: 𝐿𝐿(𝑚𝑚) = � � � 𝑛𝑛𝑖𝑖𝑖𝑖𝑖𝑖 𝑖𝑖 �𝜇𝜇 + 𝜆𝜆𝑖𝑖𝐴𝐴+ 𝜆𝜆 𝑖𝑖𝐵𝐵 + 𝜆𝜆𝑖𝑖𝐶𝐶+ 𝜆𝜆𝑖𝑖𝑖𝑖𝐴𝐴𝐵𝐵 + 𝜆𝜆𝑖𝑖𝑖𝑖𝐴𝐴𝐶𝐶 + 𝜆𝜆𝑖𝑖𝑖𝑖𝐵𝐵𝐶𝐶 + 𝜆𝜆𝑖𝑖𝑖𝑖𝑖𝑖𝐴𝐴𝐵𝐵𝐶𝐶� 𝑖𝑖 𝑖𝑖 − � � � exp�𝜇𝜇 + ⋯ + 𝜆𝜆𝑖𝑖𝑖𝑖𝑖𝑖𝐴𝐴𝐵𝐵𝐶𝐶� 𝑖𝑖 𝑖𝑖 𝑖𝑖 𝐿𝐿(𝑚𝑚) = 𝑛𝑛𝜇𝜇 + � 𝑛𝑛𝑖𝑖++𝜆𝜆𝑖𝑖𝐴𝐴 𝑖𝑖 + � 𝑛𝑛+𝑖𝑖 +𝜆𝜆𝑖𝑖𝐵𝐵 + � 𝑛𝑛++𝑖𝑖𝜆𝜆𝑖𝑖𝐶𝐶 𝑖𝑖 𝑖𝑖 + � � 𝑛𝑛𝑖𝑖𝑖𝑖 +𝜆𝜆𝑖𝑖𝑖𝑖𝐴𝐴𝐵𝐵 𝑖𝑖 𝑖𝑖 + � � 𝑛𝑛𝑖𝑖+𝑖𝑖𝜆𝜆𝑖𝑖𝑖𝑖𝐴𝐴𝐶𝐶+ 𝑖𝑖 𝑖𝑖 � � 𝑛𝑛+𝑖𝑖𝑖𝑖𝜆𝜆𝑖𝑖𝑖𝑖𝐵𝐵𝐶𝐶+ � � � 𝑛𝑛𝑖𝑖𝑖𝑖𝑖𝑖𝜆𝜆𝑖𝑖𝑖𝑖𝑖𝑖𝐴𝐴𝐵𝐵𝐶𝐶 − 𝑖𝑖 𝑖𝑖 𝑖𝑖 𝑖𝑖 𝑖𝑖 � � � exp�𝜇𝜇 + ⋯ + 𝜆𝜆𝑖𝑖𝑖𝑖𝑖𝑖𝐴𝐴𝐵𝐵𝐶𝐶�. (2.11) 𝑖𝑖 𝑖𝑖 𝑖𝑖
Notasi 𝜆𝜆 merupakan parameter-parameter dalam model yang menjelaskan respon dari masing-masing variabel. Pada persamaan (2.11), {𝑛𝑛𝑖𝑖++}, {𝑛𝑛+𝑖𝑖 +} dan {𝑛𝑛++𝑖𝑖} merupakan koefisien dari masing-masing parameter dan jika {𝑛𝑛𝑖𝑖++}, {𝑛𝑛+𝑖𝑖 +}
dan {𝑛𝑛++𝑖𝑖} berdiri sendiri tanpa diikuti oleh parameter-parameter maka {𝑛𝑛𝑖𝑖++},
{𝑛𝑛+𝑖𝑖 +} dan {𝑛𝑛++𝑖𝑖} adalah statistik cukup. Beberapa statistik cukup sesuai model
sebagai berikut:
Model Statistik Cukup Minimal (𝐴𝐴, 𝐵𝐵, 𝐶𝐶) {𝑛𝑛𝑖𝑖++}, {𝑛𝑛+𝑖𝑖 +}, {𝑛𝑛++𝑖𝑖} (𝐴𝐴𝐵𝐵, 𝐶𝐶) {𝑛𝑛𝑖𝑖𝑖𝑖 +}, {𝑛𝑛++𝑖𝑖} (𝐴𝐴𝐵𝐵, 𝐵𝐵𝐶𝐶) {𝑛𝑛𝑖𝑖𝑖𝑖 +}. {𝑛𝑛+𝑖𝑖𝑖𝑖} (𝐴𝐴𝐵𝐵, 𝐴𝐴𝐶𝐶, 𝐵𝐵𝐶𝐶) {𝑛𝑛𝑖𝑖𝑖𝑖 +}, {𝑛𝑛𝑖𝑖+𝑖𝑖}, {𝑛𝑛+𝑖𝑖𝑖𝑖} Sumber: Agresti (2002)
Menurut Agresti (2002), nilai harapan pada suatu model merupakan penyelesaian menggunakan persamaan likelihood. Derivatif persamaan likelihood terhadap parameter-parameternya masing-masing disama dengankan nol sehingga diperoleh statistik cukup sama dengan nilai harapan. Misalkan untuk model (𝐴𝐴𝐶𝐶, 𝐵𝐵𝐶𝐶). Log likehood persamaan (2.10) dengan 𝜆𝜆𝑖𝑖𝑖𝑖𝐴𝐴𝐵𝐵 = 𝜆𝜆
𝑖𝑖𝑖𝑖𝑖𝑖
𝐴𝐴𝐵𝐵𝐶𝐶 = 0. Derivatif
persamaan log likelihood 1. Derifatif L(m) terhadap 𝜇𝜇 ∂L(m) ∂𝜇𝜇 = 𝑛𝑛 − � � � 𝑒𝑒𝑥𝑥𝑝𝑝�𝜇𝜇 + 𝜆𝜆𝑖𝑖𝐴𝐴 + 𝜆𝜆𝑖𝑖𝐵𝐵 + 𝜆𝜆𝐶𝐶𝑖𝑖+ 𝜆𝜆𝑖𝑖𝑖𝑖𝐴𝐴𝐶𝐶 + 𝜆𝜆𝑖𝑖𝑖𝑖𝐵𝐵𝐶𝐶� 𝑖𝑖 𝑖𝑖 𝑖𝑖 Karena ln�𝑚𝑚𝑖𝑖𝑖𝑖𝑖𝑖� = 𝜇𝜇 + 𝜆𝜆𝑖𝑖𝐴𝐴 + 𝜆𝜆𝑖𝑖𝐵𝐵 + 𝜆𝜆𝐶𝐶𝑖𝑖+ 𝜆𝜆𝑖𝑖𝑖𝑖𝐴𝐴𝐶𝐶+ 𝜆𝜆𝑖𝑖𝑖𝑖𝐵𝐵𝐶𝐶 exp�𝜇𝜇 + 𝜆𝜆𝑖𝑖𝐴𝐴 + 𝜆𝜆𝑖𝑖𝐵𝐵 + 𝜆𝜆𝐶𝐶𝑖𝑖+ 𝜆𝜆𝑖𝑖𝑖𝑖𝐴𝐴𝐶𝐶+ 𝜆𝜆𝑖𝑖𝑖𝑖𝐵𝐵𝐶𝐶� = 𝑚𝑚𝑖𝑖𝑖𝑖𝑖𝑖 diperoleh ∂L(m) ∂𝜇𝜇 = 𝑛𝑛 − � � � 𝑚𝑚𝑖𝑖 𝑖𝑖 𝑖𝑖 𝑖𝑖𝑖𝑖𝑖𝑖 0 = 𝑛𝑛 − � � � 𝑚𝑚𝑖𝑖𝑖𝑖𝑖𝑖 𝑖𝑖 𝑖𝑖 𝑖𝑖 𝑛𝑛 = � � � 𝑚𝑚𝑖𝑖𝑖𝑖𝑖𝑖 𝑖𝑖 𝑖𝑖 𝑖𝑖 𝑛𝑛 = 𝑚𝑚�+++ (2.12) 2. Derifatif L(m)terhadap 𝜆𝜆𝑖𝑖𝐴𝐴 ∂L(m) ∂𝜆𝜆𝑖𝑖𝐴𝐴 = 𝑛𝑛𝑖𝑖++− � � 𝑒𝑒𝑥𝑥𝑝𝑝�𝜇𝜇 + 𝜆𝜆𝑖𝑖𝐴𝐴 + 𝜆𝜆𝑖𝑖𝐵𝐵 + 𝜆𝜆𝐶𝐶𝑖𝑖 + 𝜆𝜆𝑖𝑖𝑖𝑖𝐴𝐴𝐶𝐶+ 𝜆𝜆𝑖𝑖𝑖𝑖𝐵𝐵𝐶𝐶� 𝑖𝑖 𝑖𝑖 Karena ln�𝑚𝑚𝑖𝑖𝑖𝑖𝑖𝑖� = 𝜇𝜇 + 𝜆𝜆𝑖𝑖𝐴𝐴 + 𝜆𝜆𝑖𝑖𝐵𝐵 + 𝜆𝜆𝐶𝐶𝑖𝑖+ 𝜆𝜆𝑖𝑖𝑖𝑖𝐴𝐴𝐶𝐶+ 𝜆𝜆𝑖𝑖𝑖𝑖𝐵𝐵𝐶𝐶
diperoleh ∂L(m) ∂𝜆𝜆𝑖𝑖𝐴𝐴 = 𝑛𝑛𝑖𝑖++− � � 𝑚𝑚𝑖𝑖𝑖𝑖𝑖𝑖 𝑖𝑖 𝑖𝑖 0 = 𝑛𝑛𝑖𝑖++− � � 𝑚𝑚𝑖𝑖𝑖𝑖𝑖𝑖 𝑖𝑖 𝑖𝑖 𝑛𝑛𝑖𝑖++= � � 𝑚𝑚𝑖𝑖𝑖𝑖𝑖𝑖 𝑖𝑖 𝑖𝑖 𝑛𝑛𝑖𝑖++= 𝑚𝑚�𝑖𝑖++ semua 𝑖𝑖 (2.13)
Menggunakan cara yang sama untuk 𝜆𝜆𝑖𝑖𝐵𝐵. 3. Derifatif L(m)terhadap 𝜆𝜆𝑖𝑖𝑖𝑖𝐴𝐴𝐶𝐶 ∂L(m) ∂𝜆𝜆𝑖𝑖𝑖𝑖𝐴𝐴𝐶𝐶 = 𝑛𝑛𝑖𝑖+𝑖𝑖 − � 𝑒𝑒𝑥𝑥𝑝𝑝�𝜇𝜇 + 𝜆𝜆𝑖𝑖𝐴𝐴 + 𝜆𝜆𝑖𝑖𝐵𝐵 + 𝜆𝜆𝐶𝐶𝑖𝑖+ 𝜆𝜆𝑖𝑖𝑖𝑖𝐴𝐴𝐶𝐶+ 𝜆𝜆𝑖𝑖𝑖𝑖𝐵𝐵𝐶𝐶� 𝑖𝑖 Karena ln�𝑚𝑚𝑖𝑖𝑖𝑖𝑖𝑖� = 𝜇𝜇 + 𝜆𝜆𝑖𝑖𝐴𝐴 + 𝜆𝜆𝑖𝑖𝐵𝐵 + 𝜆𝜆𝐶𝐶𝑖𝑖+ 𝜆𝜆𝑖𝑖𝑖𝑖𝐴𝐴𝐶𝐶+ 𝜆𝜆𝑖𝑖𝑖𝑖𝐵𝐵𝐶𝐶 exp�𝜇𝜇 + 𝜆𝜆𝑖𝑖𝐴𝐴 + 𝜆𝜆 𝑖𝑖𝐵𝐵 + 𝜆𝜆𝐶𝐶𝑖𝑖+ 𝜆𝜆𝑖𝑖𝑖𝑖𝐴𝐴𝐶𝐶+ 𝜆𝜆𝑖𝑖𝑖𝑖𝐵𝐵𝐶𝐶� = 𝑚𝑚𝑖𝑖𝑖𝑖𝑖𝑖 diperoleh ∂L(m) ∂𝜆𝜆𝑖𝑖𝑖𝑖𝐴𝐴𝐶𝐶 = 𝑛𝑛𝑖𝑖+𝑖𝑖 − � 𝑚𝑚𝑖𝑖𝑖𝑖𝑖𝑖 𝑖𝑖 0 = 𝑛𝑛𝑖𝑖+𝑖𝑖 − � 𝑚𝑚𝑖𝑖𝑖𝑖𝑖𝑖 𝑖𝑖 𝑛𝑛𝑖𝑖+𝑖𝑖 = � 𝑚𝑚𝑖𝑖𝑖𝑖𝑖𝑖 𝑖𝑖 𝑛𝑛𝑖𝑖+𝑖𝑖 = 𝑚𝑚�𝑖𝑖+𝑖𝑖 semua 𝑖𝑖 dan 𝑖𝑖 (2.14)
Menggunakan cara yang sama untuk 𝜆𝜆𝑖𝑖𝑖𝑖𝐵𝐵𝐶𝐶.
Berdasarkan model (𝐴𝐴𝐶𝐶, 𝐵𝐵𝐶𝐶) tersebut, terlihat nilai harapan mempunyai kesamaan dengan total marginal observasi data 𝐴𝐴𝐶𝐶 dan 𝐵𝐵𝐶𝐶.
Menyelesaikan persamaan likelihood pada model (𝐴𝐴𝐶𝐶, 𝐵𝐵𝐶𝐶) berdasarkan bentuk peluangnya yaitu:
𝜋𝜋𝑖𝑖𝑖𝑖𝑖𝑖 = 𝜋𝜋𝑖𝑖+𝑖𝑖𝜋𝜋 𝜋𝜋+𝑖𝑖𝑖𝑖
++𝑖𝑖 untuk semua 𝑖𝑖, 𝑖𝑖 dan 𝑖𝑖 (2.15)
Bukti:
Diketahui 𝜋𝜋(𝐴𝐴𝐵𝐵) = 𝜋𝜋(𝐵𝐵)𝜋𝜋(𝐴𝐴|𝐵𝐵) Jika 𝐴𝐴 dan 𝐵𝐵 bebas bersyarat 𝐶𝐶 berlaku, 𝜋𝜋(𝐴𝐴𝐵𝐵𝐶𝐶) = 𝜋𝜋(𝐶𝐶)𝜋𝜋(𝐴𝐴𝐵𝐵|𝐶𝐶)
= 𝜋𝜋(𝐶𝐶)𝜋𝜋(𝐴𝐴|𝐶𝐶)𝜋𝜋(𝐵𝐵|𝐶𝐶) = 𝜋𝜋(𝐶𝐶)𝜋𝜋(𝐴𝐴𝐶𝐶)𝜋𝜋(𝐶𝐶) 𝜋𝜋(𝐵𝐵𝐶𝐶)𝜋𝜋(𝐶𝐶)
=𝜋𝜋(𝐴𝐴𝐶𝐶)𝜋𝜋(𝐵𝐵𝐶𝐶)𝜋𝜋(𝐶𝐶)
Dengan mengaitkan pada tabel kontingensi 𝐼𝐼 × 𝐽𝐽 × 𝐾𝐾 diperoleh: 𝜋𝜋𝑖𝑖𝑖𝑖𝑖𝑖 =𝜋𝜋𝑖𝑖+𝑖𝑖𝜋𝜋 𝜋𝜋+𝑖𝑖𝑖𝑖
++𝑖𝑖 untuk semua 𝑖𝑖, 𝑖𝑖 dan 𝑖𝑖
Nilai harapan multinomial pada 𝑛𝑛 observasi yaitu 𝑚𝑚𝑖𝑖𝑖𝑖𝑖𝑖 = 𝑛𝑛. 𝜋𝜋𝑖𝑖𝑖𝑖𝑖𝑖 atau 𝜋𝜋𝑖𝑖𝑖𝑖𝑖𝑖 =
𝑚𝑚𝑖𝑖𝑖𝑖𝑖𝑖
𝑛𝑛 dimana �𝑚𝑚𝑖𝑖𝑖𝑖𝑖𝑖 =
𝑚𝑚𝑖𝑖+𝑖𝑖𝑚𝑚+𝑖𝑖𝑖𝑖
𝑚𝑚++𝑖𝑖 �. Persamaan likelihood pada (2.12) , (2.13) , dan
(2.14) menspesifikasi bahwa estimasi maksimum likelihood yaitu 𝑚𝑚�𝑖𝑖+𝑖𝑖 = 𝑛𝑛𝑖𝑖+𝑖𝑖 ,
𝑚𝑚�+𝑖𝑖𝑖𝑖 = 𝑛𝑛+𝑖𝑖𝑖𝑖 dan 𝑚𝑚�++𝑖𝑖 = 𝑛𝑛++𝑖𝑖. Oleh karena estimasi maksimum likelihood pada
persamaan parameter adalah persamaan yang sama pada estimasi maksimum likelihood pada parameter tersebut,
𝑚𝑚�𝑖𝑖𝑖𝑖𝑖𝑖 =𝑚𝑚�𝑖𝑖+𝑖𝑖𝑚𝑚� 𝑚𝑚�+𝑖𝑖𝑖𝑖 ++𝑖𝑖 = 𝑛𝑛𝑖𝑖+𝑖𝑖. 𝑛𝑛+𝑖𝑖𝑖𝑖 𝑛𝑛++𝑖𝑖 (2.16) Keterangan : 𝑚𝑚�𝑖𝑖𝑖𝑖𝑖𝑖 = frekuensi harapan
𝑛𝑛𝑖𝑖+𝑖𝑖 =∑𝐽𝐽𝑖𝑖 =1𝑛𝑛𝑖𝑖𝑖𝑖𝑖𝑖 = jumlah marginal pada variabel baris ke 𝑖𝑖 dan layer ke 𝑖𝑖
𝑛𝑛+𝑖𝑖𝑖𝑖 = ∑𝐼𝐼𝑖𝑖=1𝑛𝑛𝑖𝑖𝑖𝑖𝑖𝑖 = jumlah marginal pada variabel kolom ke 𝑖𝑖 dan layer ke 𝑖𝑖
𝑛𝑛++𝑖𝑖 = ∑𝐾𝐾𝑖𝑖=1𝑛𝑛𝑖𝑖𝑖𝑖𝑖𝑖 = jumlah marginal pada variabel layer ke 𝑖𝑖
Nilai estimasi harapan disesuaikan dengan model masing-masing.
2.13 Uji Kebaikan Khi Kuadrat (Chi Squared Goodness of Fit Tests)
Menurut Saefuddin, dkk (2013) distribusi khi kuadrat digunakan sebagai uji kebaikan pengepasan (goodness of fit test). Statistik uji ini bertujuan menghitung jumlah kuadrat selisih antara nilai harapan dengan nilai observasi. Menurut S. Michael agar pengujian hipotesis dengan chi-kuadrat dapat digunakan dengan baik, maka hendaknya memenuhi asumsi sebagai berikut:
1. Random sampling tidak diperlukan, asalkan sampel tidak bias. Namun, yang terbaik cara untuk memastikan sampel tidak bias adalah pilihan acak.
2. Pengamatan bersifat independen. Asumsi penting untuk chi square adalah pengamatan yang independen.
3. Mutually exclusive baris dan kolom pada variabel katagorik yang termasuk dalam pengamatan.
4. Uji chi square tidak dapat dilakukan ketika katagori tumpang tindih atau tidak termasuk pada pengamatan.
5. Nilai harapan yang besar. Uji chi square untuk perkiraan yang terbaik ketika nilai harapan cukup besar dengan syarat tidak ada nilai harapan yang kurang dari 1 dan tidak lebih dari 20% dari nilai yang diharapkan kurang dari 5. Jika ditemukan data demikian maka dilakukan penggabungan katagori.
Pada pengujian chi square dengan banyak katagori, bila terdapat lebih dari satu nilai harapan kurang dari 5 maka nilai-nilai harapan tersebut dapat digabungkan dengan konsekuensi jumlah kategori akan berkurang dan informasi yang diperoleh juga berkurang.
Jika nilai observasi 𝑛𝑛𝑖𝑖𝑖𝑖𝑖𝑖 dan nilai harapan 𝑚𝑚�𝑖𝑖𝑖𝑖𝑖𝑖 , statistik uji pearson chi square 𝜒𝜒2 untuk tabel kontingensi tiga dimensi yaitu:
𝜒𝜒2 = � � �(𝑛𝑛𝑖𝑖𝑖𝑖𝑖𝑖 − 𝑚𝑚�𝑖𝑖𝑖𝑖𝑖𝑖)2 𝑚𝑚�𝑖𝑖𝑖𝑖𝑖𝑖 𝐾𝐾 𝑖𝑖=1 𝐽𝐽 𝑖𝑖 =1 𝐼𝐼 𝑖𝑖=1 (2.17)
Statistika alternatif untuk menguji kebaikan pengepasan adalah uji likelihood ratio square 𝐺𝐺2 yaitu: 𝐺𝐺2 = 2 � � � 𝑛𝑛 𝑖𝑖𝑖𝑖𝑖𝑖 𝑙𝑙𝑛𝑛 �𝑚𝑚�𝑛𝑛𝑖𝑖𝑖𝑖𝑖𝑖 𝑖𝑖𝑖𝑖𝑖𝑖� 𝐾𝐾 𝑖𝑖=1 𝐽𝐽 𝑖𝑖 =1 𝐼𝐼 𝑖𝑖=1 (2.18)
Jika 𝜒𝜒ℎ𝑖𝑖𝑖𝑖𝑖𝑖𝑛𝑛𝑖𝑖2 > 𝜒𝜒𝛼𝛼;𝑑𝑑𝑑𝑑2 atau 𝐺𝐺ℎ𝑖𝑖𝑖𝑖𝑖𝑖𝑛𝑛𝑖𝑖2 > 𝜒𝜒𝛼𝛼;𝑑𝑑𝑑𝑑2 maka tolak 𝐻𝐻0. 𝐻𝐻0 adalah hipotesis nol model yang ingin diuji. Taraf signifikansi (𝛼𝛼 ) yang digunakan 𝛼𝛼 = 0,05.
Nilai harapan dan derajat bebas disesuaikan dengan model yang diuji. Derajat bebas adalah banyaknya sel dalam tabel kontingensi dikurangi banyaknya parameter yang ditaksir dalam model.
Tabel 2.6 Derajat Kebebasan
Model Derajat Kebebasan (𝐴𝐴, 𝐵𝐵, 𝐶𝐶) 𝐼𝐼𝐽𝐽𝐾𝐾 − 𝐼𝐼 − 𝐽𝐽 − 𝐾𝐾 + 2 (𝐴𝐴𝐵𝐵, 𝐶𝐶) (𝐾𝐾 − 1)(𝐼𝐼𝐽𝐽 − 1) (𝐴𝐴𝐶𝐶, 𝐵𝐵) (𝐽𝐽 − 1)(𝐼𝐼𝐾𝐾 − 1) (𝐵𝐵𝐶𝐶, 𝐴𝐴) (𝐼𝐼 − 1)(𝐽𝐽𝐾𝐾 − 1) (𝐴𝐴𝐵𝐵, 𝐵𝐵𝐶𝐶) 𝐽𝐽(𝐼𝐼 − 1)(𝐾𝐾 − 1) (𝐴𝐴𝐶𝐶, 𝐵𝐵𝐶𝐶) 𝐾𝐾(𝐼𝐼 − 1)(𝐽𝐽 − 1) (𝐴𝐴𝐵𝐵, 𝐴𝐴𝐶𝐶) 𝐼𝐼(𝐽𝐽 − 1)(𝐾𝐾 − 1) (𝐴𝐴𝐵𝐵, 𝐴𝐴𝐶𝐶, 𝐵𝐵𝐶𝐶) (𝐼𝐼 − 1)(𝐽𝐽 − 1)(𝐾𝐾 − 1) (𝐴𝐴𝐵𝐵𝐶𝐶) 0 Sumber: Agresti (2002)
Menurut Agresti (2002), nilai 𝜒𝜒2 atau 𝐺𝐺2 yang besar menunjukkan kesesuian yang rendah antara frekuensi pengamatan dengan frekuensi harapan atau model diuji kurang sesuai, dan sebaliknya. Menurut Saefuddin, dkk (2009) nilai 𝜒𝜒2 atau 𝐺𝐺2 yang kecil menunjukkan kesesuaian yang tinggi antara nilai observasi dengan
nilai harapan, dan semakin besar nilai 𝜒𝜒2 atau 𝐺𝐺2 menunjukkan ketaksesuaian antara nilai observasi dengan nilai pengamatan yang berarti tertolaknya 𝐻𝐻0.
2.14 Uji Independensi
Uji independensi adalah uji untuk melihat ada tidaknya hubungan antar dua atau lebih variabel katagorik suatu hasil observasi. Pada tabel tiga dimensi dengan peluang gabungan �𝜋𝜋𝑖𝑖𝑖𝑖𝑖𝑖� pada tiga variabel respon, hipotesis nol statistik independen adalah
𝐻𝐻0: 𝜋𝜋𝑖𝑖𝑖𝑖𝑖𝑖 = 𝜋𝜋𝑖𝑖++𝜋𝜋+𝑖𝑖 +𝜋𝜋++𝑖𝑖 untuk semua 𝑖𝑖, 𝑖𝑖 dan 𝑖𝑖 ( tidak ada hubungan antara
ketiga variabel)
Statistik uji independensi yang digunakan adalah uji pearson chi square 𝜒𝜒2 dan statistik alternatif yaitu uji likelihood ratio square 𝐺𝐺2.
Menurut Kazmier (2005) independensi mengimplikasikan bahwa pengetahuan terhadap katagori yang menjadi dasar penggolongan observasi dalam hal satu variabel tidak ada dampaknya pada probabilitas masuknya variabel yang lain ke dalam salah satu dari beberapa katagori. Ketika tiga variabel terlibat, frekuensi yang diamati dimasukkan ke dalam tabel klasifikasi tiga arah yaitu tabel kontingensi tiga dimensi 𝐼𝐼 × 𝐽𝐽 × 𝐾𝐾 , di mana 𝐼𝐼 mengindikasi jumlah baris, 𝐽𝐽 mengindikasi jumlah kolom, dan 𝐾𝐾 mengindikasi jumlah layer.
Jika hipotesis nol tentang independensi ditolak untuk data-data tersebut, hal ini mengindikasikan bahwa dua variabel tersebut saling terikat atau dependen dan hal ini berarti terdapat hubungan antar keduanya. Berdasarkan hipotesis tentang independensi dari ketiga variabel, nilai yang diharapkan yang terkait dengan setiap sel dalam tabel kontingensi harus proporsional dengan nilai total yang diamati termasuk dalam kolom, baris dan layer yang memuat sel tersebut, yang terkait dengan ukuran sampel total. Andaikan 𝑛𝑛𝑖𝑖++ adalah nilai total marginal baris, 𝑛𝑛+𝑖𝑖 + adalah nilai total marginal kolom, 𝑛𝑛++𝑖𝑖 adalah nilai total marginal layer, rumus nilai yang diharapkan adalah:
Uji independensi memiliki nilai yang sama dengan estimasi nilai harapan pada model loglinier mutually independent. Derajat kebebasan uji independen juga sama dengan model loglinier mutually independent 𝐼𝐼𝐽𝐽𝐾𝐾 − 𝐼𝐼 − 𝐽𝐽 − 𝐾𝐾 + 2.
2.15 Uji Asosiasi Parsial
Uji asosiasi parsial bertujuan untuk menguji hubungan ketergantungan antara dua variabel dalam setiap level variabel (conditional association). Hubungan ketergantungan beberapa variabel yang merupakan parsial dari suatu model lengkap. Misalkan ingin menguji parameter 𝜆𝜆𝑖𝑖𝑖𝑖𝐴𝐴𝐵𝐵 = 0 yang artinya menguji model hipotesisnya adalah sebagai berikut:
H0 : variabel satu dan variabel dua independen dalam setiap level variabel tiga
(𝜆𝜆𝑖𝑖𝑖𝑖𝐴𝐴𝐵𝐵 = 0)
H1 : 𝐻𝐻���� (𝜆𝜆0 𝑖𝑖𝑖𝑖𝐴𝐴𝐵𝐵 ≠ 0)
Parameter – parameter dalam model loglinier akan diuji signifikansinya dengan selisih statistik uji likelihood ratio square (deviance). Pengujian ini memerlukan selisih statistik uji likelihood ratio square (deviance) sebagai berikut:
a. Statisik likelihood ratio square berdasarkan model sederhana dinyatakan dengan simbol 𝐺𝐺2(𝑚𝑚1), dengan derajat bebas 𝑑𝑑𝑑𝑑1.
b. Statistik likelihood ratio berdasarkan model lengkap dinyatakan dengan simbol 𝐺𝐺2(𝑚𝑚0), dengan derajat bebas 𝑑𝑑𝑑𝑑0.
c. Selisih statistik likelihood ratio (deviance): 𝐺𝐺2[(𝑚𝑚1)|(𝑚𝑚0)] = 𝐺𝐺2(𝑚𝑚1) − 𝐺𝐺2(𝑚𝑚
0), dengan derajat bebas 𝑑𝑑𝑑𝑑 = 𝑑𝑑𝑑𝑑1 − 𝑑𝑑𝑑𝑑0.
d. Jika 𝐺𝐺2(𝑚𝑚1|𝑚𝑚0) ≥ 𝜒𝜒(𝑑𝑑𝑑𝑑 ,𝛼𝛼)2 maka model 𝑚𝑚1 ditolak. Kemudian analisis untuk model – model sederhana yang lain terhadap model lengkapnya. Model yang diterima adalah model terbaik.
Menurut Agresti (2002) interpretasi parameter model loglinier menggunakan efek order tertinggi. Interpretasi model yang menggunakan efek dua faktor di gambarkan dengan conditional odds ratio. Odds ratio pada tabel parsial sebagai conditional odds ratio. Misalkan untuk setiap tingkat 𝑖𝑖 pada variabel 𝑍𝑍, conditional association antara 𝑋𝑋 dan 𝑌𝑌 menggunakan (𝐼𝐼 − 1)(𝐽𝐽 − 1) odds ratio, seperti
𝜃𝜃𝑖𝑖𝑖𝑖 (𝑖𝑖)= 𝜋𝜋𝜋𝜋𝑖𝑖𝑖𝑖𝑖𝑖𝜋𝜋𝑖𝑖+1,𝑖𝑖 +1,𝑖𝑖
𝑖𝑖,𝑖𝑖 +1,𝑖𝑖𝜋𝜋𝑖𝑖+1,𝑖𝑖 ,𝑖𝑖 , 1 ≤ 𝑖𝑖 ≤ 𝐼𝐼 − 1, 1 ≤ 𝑖𝑖 ≤ 𝐽𝐽 − 1. (2.20)
dengan cara yang sama, (𝐼𝐼 − 1)(𝐾𝐾 − 1) odds ratio {𝜃𝜃𝑖𝑖(𝑖𝑖 )𝑖𝑖} yang menggambarkan conditional association 𝑋𝑋𝑍𝑍 dan (𝐽𝐽 − 1)(𝐾𝐾 − 1) odds ratio {𝜃𝜃(𝑖𝑖)𝑖𝑖𝑖𝑖} yang menggambarkan conditional association 𝑌𝑌𝑍𝑍. Model loglinier biasa menggunakan kendala pada conditional odds ratio, misalkan conditional association antara 𝑋𝑋 dan 𝑌𝑌 maka {𝜃𝜃𝑖𝑖𝑖𝑖 (𝑖𝑖)= 1, 𝑖𝑖 = 1, … , 𝐼𝐼 − 1, 𝑖𝑖 = 1, … , 𝐽𝐽 − 1, 𝑖𝑖 = 1, … , 𝐾𝐾}.
Parameter dua faktor secara langsung berhubungan terhadap conditional odds ratio, yaitu ln 𝜃𝜃𝑖𝑖𝑖𝑖 (𝑖𝑖)= 𝑙𝑙𝑛𝑛𝑚𝑚𝑚𝑚𝑖𝑖𝑖𝑖𝑖𝑖𝑚𝑚𝑖𝑖+1,𝑖𝑖 +1,𝑖𝑖 𝑖𝑖+1,𝑖𝑖𝑖𝑖𝑚𝑚1,𝑖𝑖 +1,𝑖𝑖 = 𝜆𝜆𝑖𝑖𝑖𝑖 𝑋𝑋𝑌𝑌 + 𝜆𝜆 𝑖𝑖+1,𝑖𝑖 +1𝑋𝑋𝑌𝑌 − 𝜆𝜆𝑖𝑖,𝑖𝑖 +1𝑋𝑋𝑌𝑌 − 𝜆𝜆𝑖𝑖+1,𝑖𝑖𝑋𝑋𝑌𝑌 𝜃𝜃𝑖𝑖𝑖𝑖 (𝑖𝑖) = exp�𝜆𝜆𝑖𝑖𝑖𝑖𝑋𝑋𝑌𝑌 + 𝜆𝜆𝑖𝑖+1,𝑖𝑖 +1𝑋𝑋𝑌𝑌 − 𝜆𝜆𝑖𝑖,𝑖𝑖 +1𝑋𝑋𝑌𝑌 − 𝜆𝜆𝑖𝑖+1,𝑖𝑖𝑋𝑋𝑌𝑌 � (2.21)
Karena disisi kanan sama untuk semua 𝑖𝑖 adalah sama, dengan tidak adanya faktor ketiga sehingga ekivalen
𝜃𝜃𝑖𝑖𝑖𝑖 (1)= 𝜃𝜃𝑖𝑖𝑖𝑖 (2) = ⋯ = 𝜃𝜃𝑖𝑖𝑖𝑖 (𝐾𝐾) untuk semua 𝑖𝑖 dan 𝑖𝑖.
Model loglinier menggunakan kendala sehingga jika tabel kontingensi 2 × 2 maka conditional odds ratio 𝑋𝑋𝑌𝑌 adalah exp(𝜆𝜆11𝑋𝑋𝑌𝑌) karena 𝜆𝜆22𝑋𝑋𝑌𝑌 = 𝜆𝜆12𝑋𝑋𝑌𝑌 = 𝜆𝜆21𝑋𝑋𝑌𝑌 = 0.
Jika 𝑋𝑋 dan 𝑌𝑌 independen pada setiap tabel parsial, maka 𝑋𝑋 dan 𝑌𝑌 dikatakan conditionally independent, dengan syarat 𝑍𝑍. Semua conditional odds ratio antara 𝑋𝑋 dan 𝑌𝑌 bernilai 1. Conditionally independent 𝑋𝑋 dan 𝑌𝑌, syarat 𝑍𝑍, tidak berarti marginal independence 𝑋𝑋 dan 𝑌𝑌. Hal tersebut berarti ketika odds ratio antara 𝑋𝑋 dan 𝑌𝑌 bernilai 1 untuk setiap tingkatan dari 𝑍𝑍, marginal odds ratio mungkin berbeda dari 1.
ln 𝜃𝜃𝑖𝑖𝑖𝑖 (𝑖𝑖)= ln𝑚𝑚𝑚𝑚𝑖𝑖𝑖𝑖𝑖𝑖𝑚𝑚𝑖𝑖+1,𝑖𝑖 +1,𝑖𝑖 𝑖𝑖+1,𝑖𝑖𝑖𝑖𝑚𝑚1,𝑖𝑖 +1,𝑖𝑖
ln 𝜃𝜃𝑖𝑖𝑖𝑖 (𝑖𝑖)= ln 𝑚𝑚𝑖𝑖𝑖𝑖𝑖𝑖 + ln 𝑚𝑚𝑖𝑖+1,𝑖𝑖 +1,𝑖𝑖 − ln 𝑚𝑚𝑖𝑖+1,𝑖𝑖𝑖𝑖 − ln 𝑚𝑚1,𝑖𝑖 +1,𝑖𝑖 = 0
𝜃𝜃𝑖𝑖𝑖𝑖 (𝑖𝑖) = exp(0) = 1 (2.22)
Bernilai satu juga untuk hubungan conditionally independent lainnya. Menurut Razia Azen dan Cindy M. Walker (2011) misal 𝑋𝑋 dan 𝑌𝑌 dikatakan conditionally independent, dengan syarat 𝑍𝑍, marginal dan partial odds ratio pada 𝑋𝑋 dan 𝑍𝑍 akan sama dengan marginal dan partial odds ratio pada 𝑍𝑍 dan 𝑌𝑌.