SIFAT ASIMTOTIK NORMALITAS DAN KETAKBIASAN PENDUGA KEMUNGKINAN MAKSIMUM PARAMETER DISTRIBUSI GENERALIZED GAMMA

(1)

J. Sains MIPA, Edisi Khusus Tahun 2008, Vol. 14, No. 1, Hal.: 41 - 46 ISSN 1978-1873

SIFAT ASIMTOTIK NORMALITAS DAN KETAKBIASAN PENDUGA

KEMUNGKINAN MAKSIMUM PARAMETER DISTRIBUSI GENERALIZED GAMMA

Dian Kurniasari, Dona Rani Maninja, Warsono

Jurusan Matematika, FMIPA Universitas Lampung Jl. S. Brojonegoro No.1 Bandar Lampung 35145, Indonesia

Diterima 28 Agustus 2007, perbaikan 10 Desember 2007, disetujui untuk diterbitkan 27 Desember 2007

ABSTRACT

This paper introduces a generalized gamma distribution. The generalized gamma distribution is generalization of a gamma distribution which is commonly used for analyzing any survival data. Main objectives are to discuss how a maximum likelihood method estimates parameters of the generalized gamma, an asymptotic normality property of maximum likelihood estimates, and an unbiased property of maximum likelihood estimates. The results show that parameter estimation using maximum likelihood method can be solved by Newton-Raphson iterations, maximum likelihood estimates have asymptotic normality property, and the intensity of the bias of maximum likelihood estimates of the parameters is smaller as the sample size increases.

Keywords: generalized gamma distribution, maximum likelihood method, asymptotic normality property

1. PENDAHULUAN

Distribusi gamma merupakan salah satu distribusi yang paling sering digunakan dalam pemodelan data kelangsungan hidup (survival data). Distribusi gamma merupakan salah satu dari keluarga distribusi peluang kontinu dengan dua parameter. Akan tetapi distribusi ini tidak selalu mengepas data dengan baik untuk semua jenis data kelangsungan hidup. Salah satu cara untuk mengatasi hal ini adalah dengan mengembangkan distribusi gamma menjadi distribusi yang lebih umum lagi. Agar dalam pemodelan dapat berlaku umum untuk setiap keadaan data, maka distribusi gamma digeneralisasikan dengan tiga parameter yang disebut juga distribusi generalized gamma (GG).

Suatu peubah acak X dikatakan mempunyai distribusi peluang generalized gamma dengan parameter , dan jika

dan hanya jika fungsi kepekatan peluang dari X adalah (Persamaan 1)1)

0 , , ; 0 ; 1 ) ( x x e x x f (1)

Parameter dan dikenal sebagai parameter bentuk dan parameter dikenal sebagai parameter skala. Fungsi distribusi kumulatif dari distribusi generalized gamma seperti terdapat pada Persamaan (2) adalah:

1 1 )! 1 ( ) 3 ( ) 2 )( 1 ( ) 2 ( ) 1 ( ) 1 ( 1 ) ( x x x x e x F (2)

Dalam inferensia statistika, metode kemungkinan maksimum (maximum likelihood estimation method) merupakan salah satu metode yang sangat populer untuk menduga parameter dari suatu distribusi2, 3)_{. Namun, metode kemungkinan}

maksimum didasarkan pada teori sampel yang berukuran besar. Sehingga metode ini sering kali bekerja kurang baik untuk data dengan ukuran sampel kecil atau bahkan untuk data dengan ukuran sampel sedang. Oleh karena itu ruang lingkup yang dibahas dalam tulisan ini adalah seputar karakteristik dugaan parameter yang dihasilkan dari metode kemungkinan maksimum. Secara spesifik tujuan dari penelitian ini adalah untuk mengkaji sifat asimtotik normalitas dan ketakbiasan penduga parameter distribusi GG.

2. METODE PENELITIAN

Metode yang digunakan dalam penelitian ini mengikuti langkah-langkah sebagai berikut:

(2)

Dian Kurniasari dkk... Sifat Asimtotik Normalitas dan Ketakbiasan Penduga

b. Menurunkan fungsi kemungkinan distribusi generaliized gamma dengan fungsi ln.

c. Mencari turunan pertama dari ln fungsi kemungkinan terhadap parameter , , dan yang hendak di duga dan menyamaknnya dengan nol.

2. Memeriksa sifat asimtotik normalitas dari penduga kemungkinan maksimum distribusi distribusi generaliized gamma.

3. Memverifikasi kinerja metode kemungkinan maksimum dalam menduga parameter distribusi generalized gamma, melalui studi simulasi Monte Carlo4_{. Skenario simulasi Monte Carlo yang dilakukan adalah dengan mengambil}

kombinasi nilai parameter =1, ß={ 0.2; 1} dan ={0.3; 0.4} dan ukuran sampel sebanyak n = 10, n = 30, dan n = 100 yang masing-masing diulang sebanyak 100 kali.

3. HASIL DAN PEMBAHASAN

3.1. Pendugaan Parameter Generalized Gamma Dengan Metode Kemungkinan Maksimum

Pendugaan parameter dengan metode kemungkinan maksimum diawali dengan membangun fungsi kemungkinan (likelihood function) sebagai berikut (Persamaan 3):

n i i X f L 1 , , ; , , n i i x f L 1 , , ; , ,

i i x e x n i 1 1 n n x e x e x e x x x 2 1 2 1 1 1 1 1 1 1 n i i x e n i i x n 1 1 1 1 1

(3)

dan diperoleh (Persamaan 4):

n i i x e n i i x n L 1 1 1 1 1 ln , , ln (4)

Melalui penyelesaian aljabar biasa akan diperoleh Persamaan 5: n i i x x n n n L i n i ₁ 1 ln 1 ln ln ln , , ln 1 (5)

Selanjutnya penduga kemungkinan maksimum dapat diperoleh dengan mencari turunan pertama dari logaritma natural fungsi kemungkinan terhadap , dan dan menyamakan dengan, seperti dijelaskan sebagai berikut:

Turunan pertama dari logaritma natural fungsi kemungkinan terhadap (Persamaan 6):

0 , , ln L 0 ln ) ( ) ( ' ln 1 n i i x n n (6)

(3)

J. Sains MIPA, Edisi Khusus Tahun 2008, Vol. 14, No. 1 Karena ) ( ) ( ' ) ( ln ) ( d d

Dalam hal ini

(

)

merupakan fungsi psi (Digamma)6,7)

Sehingga Persamaan (6) menjadi Persamaan (7): 0 ln ) ( ln 1 n i i x n n

(7) Turunan pertama dari logaritma natural fungsi kemungkinan terhadap (Persamaan 8):

0 , , ln L 0 1 ln ln 1 1 n i i n i i x x n n 0 ln ln 1 ln ln 1 1 1 n i i i n i i n i i x x x x n n ₍₈₎

Karena solusi persamaan di atas tidak dapat dinyatakan secara analitik, maka diperlukan pendekatan metode numerik. Dalam tulisan ini untuk menyelesaikan persamaan tersebut menggunakan metode iterasi Newton-Raphson, yaitu5)

(Persamaan 9): k k k k g g ' 1 (9) di mana k = 1, 2,

Langkah-langkah dari metode Newton-Raphson adalah sebagai berikut:

1. Menentukan nilai awal _k untuk parameter

2. Menentukan persamaan fungsi g _k dan turunan pertamanya g' _k , yaitu:

0 ln ln , 1 1 1 n i i i n i i n i i x x x n x n g g

(10) n i i i n i i n i i i n i i x x x n x x x n n g 1 2 1 2 1 2 1 2 ln ln '

(11)

3. Memasukkan persamaan fungsi _g _k dan turunan pertamanya g' _k ke dalam rumus Newton-Raphson

hingga

k

k 1 dengan > 0, sehingga diperoleh nilai penduga parameter .

4. Selanjutnya nilai penduga _k ₁ yang telah diperoleh dari langkah (3), digunakan untuk mendapatkan nilai

penduga _k ₁.

3.2. Sifat Asimtotik Normalitas Penduga Kemungkinan Maksimum Dari Distribusi Generalized Gamma

Dalam mengkaji sifat asimtotik normalitas penduga kemungkinan maksimum dari distribusi generalized gamma, dapat didukung oleh beberapa teori sebagai berikut:

3.2.1. Hukum bilangan besar(Law of Large Numbers)

Suatu distribusi dari sampel

x

₁

,

x

₂

,

x

_n i.i.d., dimana E(X1) terhinga, dst. Dan ₍ ₎

1 X

E , maka rata-rata sampel

adalah: ₍ ₎ 1 1 _E _X n x x

x_n n d konvergen dalam peluang menuju x1, jika 0 maka

0

1 Ex x

(4)

3.2.2. Teorema limit pusat

Suatu distribusi dari sampel

x

₁

,

x

₂

,

x

_n i.i.d., dimana E(X1) terhingga, dst. Dan E(X₁) dan ) var( 2 _X _maka: 2 1 N0, Ex x

n n d konvergen dalam distribusi menuju distribusi normal dengan rata-rata 0 dan ragam 2.

Atau dalam interval [a,b]dapat juga dinyatakan dengan:

dx e b a Ex x n P b a x d n 2 2 2 1 2 1 ] , [

dengan kata lain, peubah acak n xn Ex₁ akan menjadi suatu peubah acak dari distribusi normal ketika n yang

diberikan besar.

Untuk mengkaji sifat asimtotik normalitas, maka akan dibuktikan teorema di bawah ini: Teorema:

Sifat asimtotik normalitas dari penduga kemungkinan maksimum dapat dinyatakan sebagai berikut:

, , 0, 1( , , )

3 I

N n

n

n _MLE _MLE _MLE (12)

Bukti:

Penduga kemungkinan maksimum merupakan maksimum dari n

i i n f x n L 1 ) , , | ( ln 1 ) , , ( , dimana 0 ) , , ( ' n L

Berdasarkan teorema nilai tengah 6_{, maka:}

0 0 0 1 1 1 1 1 1 0 0 0 0 0 0 _''₍ _, _, ₎ _;₍ _, _, ₎ _, _, _, _, _, , , , , ) , , ( ) , , ( n L f f ₍₁₃₎

Dengan menggunakan aljabar biasa maka diperoleh:

) , , ( ' ) , , ( ' ' , , , , ₀ ₀ ₀ L_n ₁ ₁ ₁ L_n ₀ ₀ ₀

(14) Pada kedua ruas persamaan (14) dikalikan dengan

n

diperoleh hasil:

) , , ( '' ) , , ( ' , , , , 1 1 1 0 0 0 0 0 0 n n L L n n

(15) Menurut lemma sebelumnya, maka persamaan (15) dapat dinyatakan sebagai berikut:

n i i n l x n n L n 1 0 0 0 '( | , , ) 0 1 ) , , ( '

)) , , | ( ' ( var , ( ) , , | ( ' ) , , | ( ' _, _,_, ₁ ₀ ₀ ₀ 1 0 0 0 1 , , 1 0 0 0 0 0 0 l x N o l x E x l n n i i n

Konvergen dalam peluang berdasarkan teorema limit pusat.

Selanjutnya, berdasarkan hukum bilangan besar(Law of large numbers), maka: n i i n l x E l x n L 1 0 0 0 1 , , ''( | , , ) ) , , | ( ' ' 1 ) , , ( ' ' 0 0 0

(16) karena 0 0 0 0 0 0 , , 1 , 0 , , , , I N n d , mengakibatkan _, _, _, _, ₀ 0 0 0 sehingga 0 0 0, , , ,

dan juga karena

0 0 0 0 0 0 1 1

1, , , , , , , , dimana , , 0, 0, 0 maka mengakibatkan

0 0 0 1 1 1, , , , .

Dan berdasarkan teorema sebelumnya, maka:Ln''( 1, 1, 1) E 0, 0,0l''x1| 0, 0, 0 I( 0, 0, 0) sehingga dari Persamaan (16) dan jika

2 0 0 0 2 0 0 0 0 0 0 1 , , ('( | , , )) ('( | , , )) ( '( | , , )) var 0 , 0 , 0 0 , 0 , 0 0 0 0 l x E l x E l x

(5)

J. Sains MIPA, Edisi Khusus Tahun 2008, Vol. 14, No. 1 ) , , ( 0 ) , , ( 0 0 0 I 0 0 0 I , maka: 2 0 0 0 0 0 0 1 , , 1 1 1 0 0 0 0 0 0 , , , , ' var , 0 , , ' ' , , ' , , , , 0 0 0 I x l N Ln Ln n n d

atau dapat dinyatakan dengan

) , , ( 1 , 0 , , , , 0 0 0 0 0 0 I N n d

Jadi berdasarkan teorema diatas, maka sifat asimtotik normalitas penduga kemungkinan maksimum dari distribusi

generalized gamma dapat dinyatakan dengan:

) , , ( , 0 , , n n N3 I 1

n MLE MLE MLE

3.3. Sifat Ketakbiasan Penduga Kemungkinan Maksimum dari Distribusi Generalized Gamma

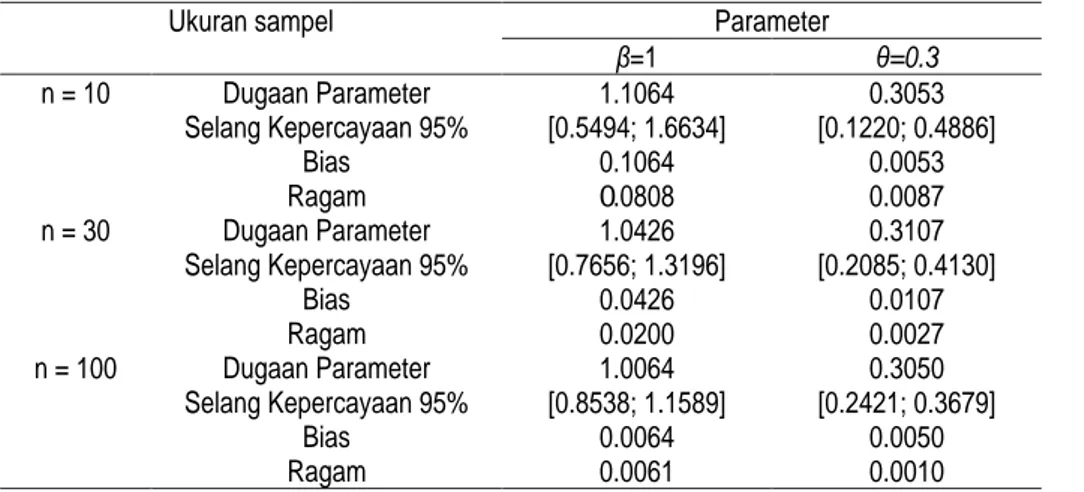
Seperti terlihat pada Tabel 1, studi simulasi menunjukkan bahwa untuk nilai toleransi = 01, = 1, = 1, dan = 0.3, semakin besar ukuran sampel maka bias dan ragam dugaan yang dihasilkan semakin kecil. Selain itu, selang kepercayaan 95% menunjukkan semakin besar ukuran sampel yang diambil berakibat semakin pendek dugaan selang yang dihasilkan. Oleh karena itu, dapat dikatakan bahwa semakin besar ukuran sampel dugaan kemungkinan maksimum akan memberikan dugaan yang lebih tepat dan akurat.

Tabel 1. Nilai dugaan , selang kepercayaan 95%, bias dan ragam penduga parameter distribusi generalized gamma

untuk nilai parameter = 1, = 1 dan = 0.3 serta ukuran sampel n = {10; 30; 100) dan nilai toleransi = 0.1.

Ukuran sampel Parameter

=1 =0.3 n = 10 Dugaan Parameter

1.1064 0.3053 Selang Kepercayaan 95% [0.5494; 1.6634] [0.1220; 0.4886] Bias 0.1064 0.0053 Ragam 0.0808 0.0087 n = 30 Dugaan Parameter

1.0426 0.3107 Selang Kepercayaan 95% [0.7656; 1.3196] [0.2085; 0.4130] Bias 0.0426 0.0107 Ragam 0.0200 0.0027 n = 100 Dugaan Parameter 1.0064 0.3050 Selang Kepercayaan 95% [0.8538; 1.1589] [0.2421; 0.3679] Bias 0.0064 0.0050 Ragam 0.0061 0.0010

Berdasarkan output yang diperoleh pada Tabel 1, nilai dugaan parameter { , , } mempunyai nilai yang semakin mendekati parameter yang sebenarnya, jika nilai toleransi dan ukuran sampel yang dipilih semakin besar.

Untuk setiap nilai { , , }, secara keseluruhan mempunyai bias dan ragam yang cukup kecil. Bias dan ragam ini akan

semakin kecil jika ukuran sampelnya semakin besar. Selang kepercayaan bagi dugaan parameter yang diperoleh,

cenderung pendek artinya tingkat kepercayaan yang tinggi (95%), dugaan selang yang diperoleh memiliki keakuratan

yang tinggi dan dengan tingkat keyakinan yang tinggi. Sedangkan selang kepercayaan bagi dugaan parameter akan

semakin pendek jika nilai toleransi dan ukuran sampel yang dipilih semakin besar.

4. KESIMPULAN

Berdasarkan hasil yang diperoleh, maka dapat diambil beberapa kesimpulan sebagai berikut:

Pendugaan parameter distribusi generalized gamma dengan menggunakan metode kemungkinan maksimum mempunyai bentuk logaritma natural fungsi kemungkinan yaitu:

n i i x x n n n L i n i ₁ 1 ln 1 ln ln ln , , ln 1

(6)

Logaritma natural fungsi kemungkinan tersebut tidak dapat dinyatakan secara analitik/eksplisit, sehingga untuk memperoleh nilai penduga parameter distribusi generalized gamma digunakan metode iterasi Newton-Raphson. Penduga parameter distribusi generalized gamma dengan menggunakan metode kemungkinan maksimum mempunyai sifat asimtotik normalitas dan ketakbiasan, dimana sifat asimtotik normalitas dapat dinyatakan dengan:

) , , ( , 0 , , n n N3 I 1

n MLE MLE MLE

Untuk karakteristik ketakbiasan dugaan yang diperoleh untuk setiap nilai { , , }, secara keseluruhan mempunyai bias yang cukup kecil. Bias akan semakin kecil jika ukuran sampelnya semakin besar. dan sangat bergantung terhadap rata-rata dari dugaan parameter.

DAFTAR PUSTAKA

1. DiCiccio, T.J. 1987. Approximate Inference for The Generalized Gamma Distribution. Technometrics 29(1): 33-40. 2. Hogg, R.V. and Craig, A.T. 1995. Introduction to Mathematical Statistics. Fifth Edition. Prentice-hall Inc., New

jersey.

3. Hogg, R.V. and Tanis, E.A. 1997. Probability and Statistical Inference. Sixth Edition. Prentice-hall Inc., New jersey. 4. Ross, Sheldon M. 1997. Simulation. Second Edition. Academic Press, California.

5. Munir, R. 2003. Metode Numerik. Informatika, Bandung.

6. Abramowitz, Milton and Stegun, Irene A. 1972. Handbook of Mathematical Functions with Formulas, Graphs, and

mathematical Tables. U.S.Government, Washington.