PENGOPTIMUMAN PADA FUNGSI PRODUKSI CROPPES

PENGOPTIMUMAN PADA FUNGSI PRODUKSI CROPPES

NURJANAH

G54104008

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM

INSTITUT PERTANIAN BOGOR

ABSTRACT

NURJANAH. Optimization in Croppes production function. Supervised by RETNO BUDIARTI and DONNY CITRA LESMANA.

Every company has a purpose to change input production into output. The relation between various combinations of input productions to obtain output are compiled in production function. In economics, there are some production functions that have constant return to scale. They were differentiated according to their value of elasticity of substitution. There are infinite, zero, one (known as Cobb-Douglass production function) or positive constant (known as CES production function) elasticity.

In this manuscript, we discuss CROPPES production function (constant ratio of pairwise partial elasticities of substitution) which is the general form of CES production function (constant elasticities of substitution). We also discuss the optimal solution of input production based on optimization profit in perfect competition market.

ABSTRAK

NURJANAH. Pengoptimuman Pada Fungsi Produksi Croppes. Dibimbing oleh RETNO BUDIARTI dan DONNY CITRA LESMANA.

Setiap perusahaan mempunyai tujuan untuk mengubah input produksi menjadi output. Hubungan antara berbagai kombinasi input produksi untuk memperoleh output disusun dalam fungsi produksi. Dalam ilmu ekonomi, ada beberapa fungsi produksi yang mempunyai return to scale yang konstan. Fungsi produksi ini dibedakan menurut nilai elastisitas substitusinya. Ada yang bernilai tak hingga, nol, satu (dikenal dengan fungsi produksi Cobb-Douglas) ataupun bernilai konstan positif (dikenal dengan fungsi produksi CES ).

Pada karya tulis ini dibahas fungsi produksi CROPPES (constant ratio of pairwise partial

elasticities of substitution) yang merupakan bentuk umum dari fungsi produksi CES (constant elasticities of substitution). Di samping itu, dibahas pula solusi input produksi optimal yang didasarkan

PENGOPTIMUMAN PADA FUNGSI PRODUKSI CROPPES

Skripsi

Sebagai salah satu syarat untuk memperoleh gelar Sarjana Sains

pada Fakultas Matematika dan Ilmu Pengetahuan Alam

Institut Pertanian Bogor

Oleh:

NURJANAH

G54104008

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM

INSTITUT PERTANIAN BOGOR

BOGOR

2008

Judul : Pengoptimuman Pada Fungsi Produksi CROPPES

Nama : Nurjanah

NRP :

G54104008

Menyetujui:

Pembimbing I,

Pembimbing II,

Ir. Retno Budiarti, MS

Donny Citra Lesmana, M.Fin.Math

NIP. 131 842 409

NIP. 132 311 927

Mengetahui:

Dekan Fakultas Matematika dan Ilmu Pengetahuan Alam

Institut Pertanian Bogor

Dr. Drh. Hasim, DEA

NIP. 131 578 806

KATA PENGANTAR

Puji dan syukur penulis panjatkan kepada Allah S.W.T atas segala rahmat dan karunia-Nya, penulis dapat menyelesaikan tugas akhir yang berjudul Pengoptimuman pada Fungsi Produksi

Croppes. Shalawat serta salam senantiasa tercurah kepada Rasulullah SAW beserta keluarga, sahabat

dan umatnya hingga akhir zaman.

Tugas akhir ini penulis persembahkan untuk keluarga yang selalu mendukung, menasehati dan mendoakan penulis dengan dukungan yang luar biasa. Tak lupa penulis mengucapkan terimakasih kepada pihak-pihak yang telah memberikan dorongan terhadap penulis dalam menyelesaikan tugas akhir ini, yaitu:

1. Kedua dosen pembimbing penulis, Ir. Retno Budiarti, MS dan Donny Citra Lesmana, M.Fin.Math atas bantuan dan bimbingannya sehingga penulis mampu menyelesaikan tugas akhir ini.

2. Bapak Dr. Tony Bakhtiar, M.Sc. yang telah menjadi dosen penguji penulis saat sidang.

3. Untuk kedua orang tuaku (ayah dan Ibu), terima kasih atas segala cinta dan kasih sayangnya. Kalian adalah panutan dalam hidupku.

4. Untuk segenap keluargaku di rumah mamang Amung, mamang Udih, encing Acum, serta ketiga kakakku Nana, Eni dan Ela yang telah memberikan kasih sayang, nasehat, dukungan, serta doanya selama ini.

5. Sahabat-sahabat penulis di Depok, Rahma, April, Igars, Indah serta Mega yang berada di Padang terima kasih atas semangat dan doanya. Terima kasih atas kebersamaan kita selama ini. Semoga persahabatan kita tiada akhir.

6. Teman seperjuanganku di IPB Ratih STK 41 (makasih ya atas ilmu yang telah diberikan serta semangat dan doanya).

7. Buat teman-temanku di Mahadewi crew, Jeany, Ramah, Deka, serta adik-adik kelasku Ganis, Sihol, Nova, Neneh, Apri dan Puput, makasih ya atas doa, support dan semua pengalaman bersama kalian, dengan kalian penulis belajar banyak hal.

8. Mahar (makasih atas semua bantuannya, maaf karena sering merepotkan. Semangat yach!!), Maryam (makasih buat nasehat dan bantuannya selama ini), Sifa (makasih karena telah menjadi teman sekamarku yang banyak memberikan saran dan nasehat), Ika (makasih yach karena sering menjadi tempat curhatku, dukungan dan juga bantuannya).

9. Teman-teman matematika angkatan 41, Mukti, Nene’, Eli, Liam,Tities, Fitrie, Penny, Sita, Ro’fah, Eci, Roma, Enny, Eva, Endit, Uwie, Iyank, Dian, Dee-dee , Liay, Ayu, Armi, Nyit-nyit, Darwisah, Enyon, Rizul, Tia , Rite, Ria, Kurenz, Yeni, Kokom, Fred, Adji, Racil, Dika, Iboy, Udin, Great, Chubby, Mahnur, Jali, Yaya, Idris, Mora, Mazid, Mimin, Triyadi, Cumi, Amin, Deni, Yos Hendra, Hendri. Terima kasih atas semua tawa canda, susah senang yang telah dilewati bersama. Kebersamaan kita selama kuliah akan selalu menjadi kenangan terindah dalam hidupku. 10. Seluruh dosen matematika IPB, penulis mampu menyelesaikan tugas akhir ini atas segala ilmu

yang telah diberikan, dan kepada pegawai dan TU matematika IPB, bu Susi, bu Ade, mas Deni, bu Marisi, mas Yono, dan lain-lain, atas bantuan yang telah diberikan kepada penulis.

11. Juga untuk semua pihak yang membantu penulis, yang tidak bisa penulis sebutkan satu persatu, makasih banyak untuk semuanya.

Penulis menyadari bahwa tugas akhir ini masih jauh dari kesempurnaan. Semoga tugas akhir ini dapat bermanfaat bagi penulis khususnya dan bagi pihak lain umumnya yang membutuhkan.

RIWAYAT HIDUP

Penulis dilahirkan di Jakarta, 9 April 1986 dari pasangan Sayadi (Alm) dan Marhumah (Alm) sebagai anak keempat dari empat bersaudara.

Pada tahun 1998 penulis menyelesaikan pendidikan sekolah dasar di MI Nasyatul Khair Depok. Kemudian penulis melanjutkan pendidikannya ke Sekolah Lanjut Tingkat Pertama di MTs Nasyatul Khair Depok. Pada tahun 2001 penulis memasuki pendidikan Sekolah Menengah Atas di SMAN 98 Jakarta. Setelah lulus SMU pada tahun 2004, penulis melanjutkan kuliah di Institut Pertanian Bogor melalui jalur Ujian Seleksi Masuk Institut Pertanian Bogor (USMI) di Departemen Matematika, Fakultas Matematika dan Ilmu Pengetahuan Alam IPB.

Selama mengikuti kegiatan perkuliahan, penulis aktif pada beberapa kegiatan kemahasiswaan, yaitu penulis pernah menjadi anggota himpro Gugus Mahasiswa Matematika IPB periode 2005-2006 sebagai anggota divisi keputrian. Penulis juga aktif sebagai panitia pada beberapa acara-acara antara lain Try Out Gumatika tahun 2006, Matematika Ria tahun 2006, Ramadhan in Action serta mengikuti Pelatihan Penyegaran Materi tahun 2007.

DAFTAR ISI

Halaman

DAFTAR GAMBAR ... viii

DAFTAR TABEL ... ix DAFTAR LAMPIRAN ... x I PENDAHULUAN 1.1 Latar Belakang ... 1 1.2 Tujuan ... 1 1.3 Sistematika Penulisan ... 1 II LANDASAN TEORI ... 1 III PEMBAHASAN 3.1 Fungsi Produksi ... 6

3.2 Fungsi Produksi CES ... 6

3.3 Fungsi Produksi CROPPES ... 7

3.4 Elastisitas Parsial Substitusi ... 10

3.5 Pengoptimuman Input Produksi ... 13

IV STUDI KASUS ... 15

V KESIMPULAN ... 19

DAFTAR PUSTAKA ... 20

LAMPIRAN ... 21

DAFTAR GAMBAR

Halaman Gambar 1 Isokuan ... 6 Gambar 2 Ilustrasi kurva produksi total dan produk marjinal ... 10 Gambar 3 Nilai output produksi bila input x2 dan input x3 dianggap konstan ... 16

DAFTAR TABEL

Halaman

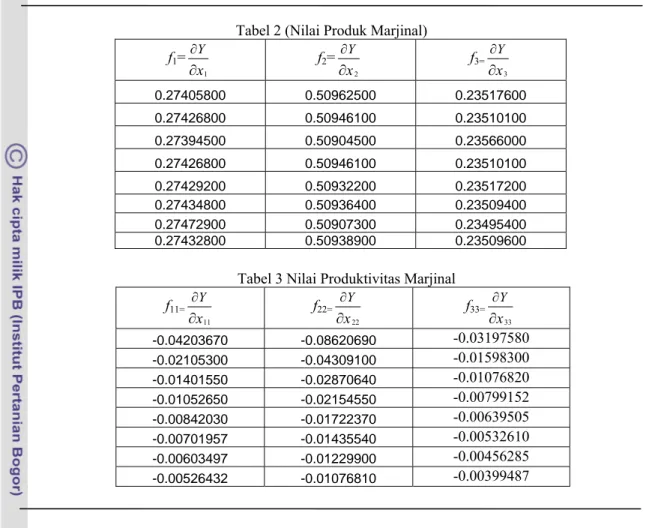
Tabel 1 Data input produksi ... 16

Tabel 2 Nilai produk marjinal ... 17

Tabel 3 Nilai produktivitas marjinal ... 17

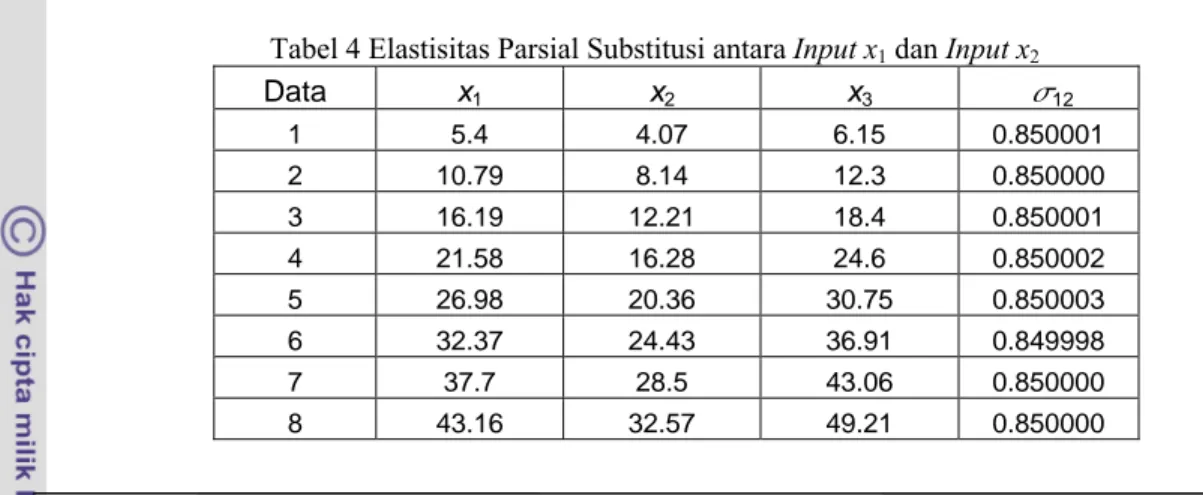
Tabel 4 Elastisitas parsial substitusi ... 18

DAFTAR LAMPIRAN

Halaman

Bukti Teorema 1 ... 22

Penurunan elastisitas substitusi pada fungsi produksi CES ... 23

Menentukan solusi input produksi pada kasus 1 dan kasus 2 ... 25

Menentukan ouput produksi, produk marjinal dan produktivitas marjinal ... 30

I. PENDAHULUAN

1.1 Latar Belakang

Setiap perusahaan menyadari bahwa total biaya produksi sangat berkaitan dengan output-nya. Jika perusahaan meningkatkan kapasitas produksi, maka perusahaan tersebut tentunya membutuhkan input yang lebih banyak dan biaya produksi yang digunakan juga akan semakin tinggi. Oleh karena itu, perusahaan dituntut membuat keputusan dan perencanaan yang tepat dalam masalah produksi. Dalam ilmu ekonomi, ada dua waktu perencanaan yang biasa diambil perusahaan mengenai masalah produksi, yaitu (1) jangka pendek, yang merupakan jangka waktu ketika hanya ada satu input produksi yang berubah. Satu-satunya cara memproduksi output adalah dengan menyesuaikan input produksi variabel terhadap produksinya sampai tingkat

output yang diinginkan bisa tercapai. (2) Jangka

panjang, yaitu jangka waktu ketika semua input produksi dapat diubah sehingga ada berbagai cara yang efisien secara teknik untuk memproduksi output yang diinginkan.

Dalam menentukan pilihannya, perusahaan akan berusaha untuk menghindari inefisien secara teknis. Akan tetapi efisien secara teknis tidaklah cukup. Untuk menjadi efisien secara ekonomis, perusahaan harus menentukan input optimal dan metode produksi yang meminimumkan biaya agar keuntungan maksimum bisa tercapai. Salah satu caranya adalah dengan prinsip substitusi. Dalam prinsip substitusi, perusahaan akan menggunakan lebih banyak input produksi yang relatif lebih murah dan menggunakan lebih sedikit input produksi yang relatif lebih mahal. Dua konsep mendasar mengenai prinsip substitusi adalah konsep

return to scale dan konsep elastisitas substitusi.

Return to scale mengukur respon output saat input produksi berubah sedangkan konsep

elastisitas substitusi mengukur seberapa mudah menukarkan suatu input dengan input lainnya dalam proses produksi.

Dalam ilmu ekonomi, ada beberapa fungsi produksi yang memiliki return to scale yang konstan. Tiap tipenya dibedakan menurut elastisitas substitusi, ada yang bernilai tak hingga, nol ataupun satu. Pada karya ilmiah ini, kita akan membahas fungsi produksi yang memiliki nilai elastisitas konstan positif atau sering disebut dengan fungsi produksi

CROPPES (constant ratio of pairwise partial elasticities of substitution).

1.2 Tujuan Penulisan

Tujuan dari penulisan karya ilmiah ini adalah:

1. mempelajari sifat-sifat dari fungsi produksi

croppes

2. mempelajari elastisitas parsial substitusi dalam fungsi produksi croppes

3. menentukan input produksi yang optimal. 1.3 Sistematika Penulisan

Pada Bab Pertama dijelaskan latar belakang dan tujuan dari penulisan karya ilmiah ini. Bab Dua berisi landasan teori yang menjadi konsep dasar dalam penyusunan pembahasan. Pada Bab Tiga diberikan pembahasan tentang fungsi produksi croppes. Bab Empat berisi tentang studi kasus. Bab Lima merupakan kesimpulan. Kemudian Bab Enam berisikan daftar pustaka yang digunakan dalam penulisan karya ilmiah ini.

II. LANDASAN TEORI Pada Bab ini akan diberikan teori yang

menjadi landasan pengerjaan karya ilmiah ini. Berikut ini adalah definisi-definisi mengenai istilah ekonomi yang digunakan.

Definisi 1 (Faktor Produksi)

Faktor produksi adalah variabel-variabel input yang digunakan dalam proses produksi untuk menghasilkan output.

(Rahardja & Manurung, 1999) Definisi 2 (Input Produksi Tetap)

Input produksi tetap adalah input produksi yang

jumlah penggunaannya tidak tergantung pada jumlah produksi.

Definisi 3 (Input Produksi Variabel)

Input produksi variabel adalah input produksi

yang tergantung pada tingkat produksinya. Semakin besar tingkat produksi, maka akan semakin banyak pula input produksi variabel yang digunakan.

(Rahardja & Manurung, 1999) Definisi 4 (Fungsi Produksi)

Fungsi produksi untuk suatu barang tertentu,

Y=f(K,L,…) dengan K menyatakan input kapital

dan L menyatakan input tenaga kerja sedangkan tanda titik-titik pada fungsi di atas menunjukkan kemungkinan digunakannya

input produksi yang lain, memperlihatkan

jumlah output maksimum yang dapat diperoleh dengan menggunakan berbagai alternatif kombinasi input produksi.

(Nicholson, 1999)

Definisi 5 (Produk Marjinal)

Misalkan didefinisikan fungsi produksi

Y=f(K,L) dengan K menyatakan input kapital

dan L menyatakan input tenaga kerja. Produk marjinal dari suatu input adalah output tambahan yang dapat diperoleh dengan menambah input yang bersangkutan 1 unit, sedangkan input-input lain dianggap konstan. Secara matematis dinotasikan sebagai berikut: produk marjinal kapital

K Y _K PM f L ∂ = = ∂

produk marjinal tenaga kerja

L Y _L PM f L ∂ = = ∂

.

(Nicholson, 1999) Definisi 6 (Diminishing Return / Produktivitas

yang semakin menurun)

Misalkan didefinisikan fungsi produksi

Y=f(K,L), Produktivitas marjinal dari satu unit input tenaga kerja tidak selalu sama besarnya.

Ketika input tenaga kerja yang digunakan masih sedikit, biasanya produktivitas marjinal yang dihasilkannya sangat tinggi. Tetapi semakin banyak input tenaga kerja tersebut digunakan, dan input modal dibiarkan konstan maka produktivitas marjinal tenaga kerja tersebut akan semakin berkurang. Secara matematis dinotasikan sebagai berikut:

2 2 0 K KK PM Y _f K _K ∂ _{= = <} ∂ _∂∂ 2 2 0 . L LL PM Y _f L _L ∂ = = < ∂ ∂_∂ (Nicholson, 2002) Definisi 7 (Isokuan)

Isokuan yaitu sebuah kurva yang menunjukkan berbagai kombinasi input produksi yang akan menghasilkan output dalam jumlah yang sama.

(Nicholson, 2002)

Definisi 8 (Rate of Technical Substitution/ RTS)

Misalkan didefinisikan fungsi produksi

Y=f(K,L). Rate of technical substitution atau

tingkat substitusi teknis yaitu banyaknya pengurangan salah satu input ketika satu unit

input lainnya ditambahkan untuk output tetap.

Secara matematis dinotasikan sebagai berikut

( L terhadap K ) . L K dK RTS dL PM PM = − = Bukti:

didefinisikan fungsi produksi dengan dua input adalah sebagai berikut

(

)

(

)

(

)

, K L Y f K L f f dY dK dL K L dY PM dK PM dL = ∂ ∂ ⎛ ⎞ ⎛ ⎞ =_{⎜ ⎟} +_{⎜ ⎟} ∂ ∂ ⎝ ⎠ ⎝ ⎠ = +

di sepanjang isokuan dY=0 sehingga

(

)

(

)

(

)

(

)

0 . K L L K L LK K PM dK PM dL PM dL PM dK dK PM dL PM RTS + = = − − _{= =}

Persamaan di atas menyatakan bahwa di sepanjang isokuan hasil yang diperoleh karena adanya peningkatan input L persis sama dengan pengorbanan output produksi karena

dikuranginya input K.

(Nicholson, 1999) Definisi 9 (Return to Scale)

Return to scale yaitu suatu keadaan ketika output meningkat sebagai respon adanya

kenaikan yang proporsional dari seluruh input. Jika diketahui fungsi produksi Y=f(K,L) dan semua input dikalikan dengan suatu bilangan konstan positif m, maka return to scale-nya bisa diklasifikasikan menjadi

Efek dalam output Return to scale f(mK,mL)= mf(K,L) konstan f(mK,mL)> mf(K,L) berkurang f(mK,mL)< mf(K,L) meningkat (Nicholson, 2002) Definisi 10 (Elastisitas)

Elastisitas yaitu ukuran persentase perubahan suatu variabel yang disebabkan oleh satu persen perubahan variabel lainnya.

(Nicholson, 2002) Definisi 11 (Elastisitas Harga dari

Permintaan)

Elastisitas harga dari permintaan mengukur berapa persen permintaan terhadap suatu barang berubah bila harganya berubah sebesar satu persen. Secara matematis dinotasikan sebagai berikut

( )

( )

% % P Q Q Q P Q P P Q P P E ∂ ∂ ∂ = = = ∂ ∂ ∂ .

Nilai elastisitas harga dari permintaan adalah: 1. inelastis (Ep<1), yaitu bila perubahan

permintaan (dalam persentase) lebih kecil dari pada perubahan harga

2. elastis (Ep>1), yaitu bila perubahan harga suatu barang menyebabkan perubahan permintaan yang lebih besar

3. elastis unitari (Ep=1), yaitu bila kenaikan harga menyebabkan penurunan permintaan dengan proporsi yang sama

4. inelastis sempurna (Ep=0), yaitu bila terjadi perubahan harga baik turun maupun naik, orang akan tetap membeli jumlah yang dibutuhkan

5. elastis sempurna (Ep=¶), yaitu bila terjadi perubahan harga sedikit saja memyebabkan perubahan permintaan dari tak terhingga menjadi nol.

(Rahardja & Manurung, 1999) Definisi 12 (Elastisitas Substitusi/s)

Untuk fungsi produksi Y=f(K,L), elastisitas substitusi mengukur perubahan proporsional yang terjadi dalam ratio K/L relatif terhadap perubahan proporsional yang terjadi dalam RTS di sepanjang sebuah isoquan. Secara matematis dinotasikan sebagai berikut

( )

(

)

(

)

(

)

( )

K = d L RTS K dRTS _L σ .

Nilai s berada pada interval 0 dan ∞. Semakin besar s, maka semakin besar pula kemampuan substitusi kedua input. Kasus khusus di mana s=0 terjadi bila kedua input harus digunakan dengan proporsi yang tetap sebagai pelengkap dari masing-masing input. Kasus khusus lainnya dengan s=∞ adalah bila kedua input merupakan substitusi sempurna.

(Nicholson, 1999) Definisi 13 (Barang Komplemen)

Komplemen yaitu sifat dua barang yang jika harga satu barang meningkat, maka kuantitas barang lain yang diminta akan turun.

(Nicholson, 2002) Definisi 14 (Keuntungan)

Keuntungan adalah nilai penerimaan total dikurangi biaya total yang dikeluarkan perusahaan. Keuntungan nol disebut juga keuntungan normal yaitu tingkat keuntungan yang memberikan tingkat pengembalian yang sama (penerimaan total sama dengan biaya total), sedangkan keuntungan ekonomis adalah tingkat keuntungan yang memberikan tingkat pengembalian yang positif (penerimaan total lebih besar daripada biaya total).

(Rahardja & Manurung, 1999) Definisi 15 (Pasar Persaingan Sempurna) Dalam pasar persaingan sempurna, jumlah perusahaan sangat banyak dan kemampuan setiap perusahaan dianggap sedemikian kecilnya sehingga tidak mampu mempengaruhi pasar. Berikut ini adalah beberapa karakteristik agar sebuah pasar dapat dikatakan persaingan sempurna:

1. semua perusahaan memproduksi barang yang homogen

2. produsen dan konsumen memiliki informasi yang sempurna

3. output sebuah perusahaan relatif kecil bila dibandingkan dengan output pasar

4. perusahaan menerima harga yang ditentukan oleh pasar

5. semua perusahaan bebas untuk keluar masuk pasar.

(Rahardja & Manurung, 1999) Definisi 16 (Monomial)

Monomial adalah variabel bebas maupun perkalian dari variabel bebas yang mempunyai pangkat berupa intejer positif.

Contoh: 2_{, xy}2_{atau .}2_y3_z

x x

(www.wikipedia.com) Definisi 17 (Fungsi Polinomial Homogen) Fungsi polinomial homogen adalah fungsi polinom yang terbentuk dari penjumlahan monomial, dengan derajat total dari masing-masing monomial tersebut adalah sama. Contoh:

1. fungsi monomial berderajat 10 2

5 3

( , , )

f x y z =x y z

2. fungsi polinomial homogen berderajat 5

2 2

5 3 3

( , , ) 2 9

f x y z =x + x y + y z

3. bukan fungsi polinomial homogen _{f x y z( , , )} 4 ₂ 3_y2 _9y 3

x x z

= + + .

(www.wikipedia.com) Definisi 18 (Fungsi Homogen Berderajat k) Misalkan f adalah fungsi polinomial homogen dari n variabel yang terdefinisi dalam domain D. Bila (x1,x2,….,xn)œD dan t>0, maka

(tx1,tx2,….,txn) juga terletak dalam D. Fungsi f dikatakan homogen berderajat k pada D jika

f(tx1,tx2,….,txn)= tk f(x1,x2,….,xn) untuk t>0 dengan k∈R.

(Saeter & Hammond, 2006) Definisi 19 (Kofaktor)

Misalkan A adalah matriks berukuran nxn, elemen-elemen dari matriks A dilambangkan aij dengan i, j=1,2,....,n. Misalkan pula Mij adalah submatriks A berukuran (n-1)x(n-1) yang diperoleh dengan menghapus baris ke-i dan kolom ke-j dari matriks A. Determinan dari Mij disebut minor dari aij. Kofaktor dari aij dalam matriks A dinotasikan dengan Aij didefinisikan sebagai perkalian dari (-1)i+j _{dengan M}

ij.

(Zhang, 2005) Definisi 20 (Fungsi Produksi Neoklasik) Fungsi produksi Y=f(K,L), dengan K menyatakan input kapital dan L menyatakan

input tenaga kerja disebut neoklasik jika

memenuhi kondisi berikut:

1. f(K,L) adalah fungsi taknegatif jika K dan L taknegatif

2. f(0,0)=0

3. fK dan fL adalah fungsi taknegatif

4. ada turunan parsial kedua dari fungsi f

terhadap K dan L

5. fungsi tersebut homogen berderajat satu

6. f(λK,λL)=λf(K,L) untuk semua λ yang taknegatif

7. fungsi produksi tersebut adalah fungsi

strictly quasiconcave.

(Zhang, 2005) Beberapa definisi tentang kekonveksan dan kekonkafan fungsi yang terdiferensiabel.

Definisi 21 (Kedefinitan dari Fungsi yang Terdiferensiabel)

Misalkan fungsi Y=f(x1,x2,….,xn) adalah fungsi kontinu dan terdiferensiabel dua kali pada suatu domain D. Turunan orde kedua dari fungsi f dilambangkan dengan 2

n

d Y= H = Δ yang didefinisikan sebagai berikut:

11 12 1 21 22 2 2 1 2 n n n n n nn f f f f f f d Y H f f f = = Δ =

.

Dengan: 1 1 1 2 2 2 11 12 2 , ,..., _nn n n f =_∂∂_{x x}f f =_∂∂_{x x}f f =_∂∂_{x x}f

,

11 1= f Δ

,

11 12 2 21 22 f f f f = Δ

,

11 12 1 21 22 2 1 2 n n n n n nn f f f f f f H f f f = = Δ

.

2 n

d Y= H = Δ dikenal dengan istilah Hessian

determinant. H merupakan matriks simetrik

berukuran nxn, misalkan Δ_k adalah minor utama ke-k dari matriks H untuk 1 k n≤ ≤ maka

1. H adalah definit positif jika dan hanya jika 0

k>

Δ untuk k=1,2,..n

2. H adalah definit negatif jika dan hanya jika

( )

−1kΔk>0 untuk k=1,2,..n

3. jika Δ1>0, 0,..., 0Δ2> Δn−1> dan Δn=0

maka H adalah semidefinit positif

4. jika

( )

−1kΔk>0 untuk k=1,2,..n-1 dan 0

n=

Δ maka H adalah semidefinit negatif. (Peressini, 1988)

Definisi 21 (Fungsi Konveks dan Konkaf) Misalkan fungsi Y=f(x1,x2,….,xn) adalah fungsi kontinu dan terdiferensiabel dua kali pada suatu domain D. Turunan orde kedua dari fungsi f dilambangkan dengan 2

n

d Y= H = Δ

,

maka: 1. fungsi Y disebut fungsi konkaf jika dan

hanya jika 2

n

d Y= H = Δ adalah semidefinit negatif

2. fungsi Y disebut fungsi strictly konkaf jika

2

n

d Y= H = Δ adalah definit negatif

3. fungsi Y disebut fungsi konveks jika dan hanya jika 2

n

d Y= H = Δ adalah semidefinit positif

4. fungsi Y disebut fungsi strictly konveks jika

2

n

d Y= H = Δ adalah definit positif. (Chiang & Wainwright, 2005) Definisi 22 (Fungsi strictly quasiconcave) Misalkan Y=f(x1,x2,….,xn) adalah fungsi kontinu dan terdiferensiabel dua kali pada suatu domain

D. Domain D hanya terdefinisi untuk nilai

x1,x2,x3….,xn >0. Kuasi kekonkafan dapat dicek dengan menggunakan prinsip minor utama yang disusun dalam bordered determinant sebagai berikut: 1 1 11 1 1 0 _n n n n n nn f f f f f F F f f f = =

.

Dengan: 1 2 2 1 11 1 1 ,..., ,..., ,..., _{n nn} n n n f =_∂∂_xf f =_∂∂_xf f =_∂∂_{x x}f f =_∂∂_{x x}f

,

1 1 1 11 0 f F f f =

,

1 2 2 1 11 12 2 21 22 0 f f F f f f f f f =

,

1 1 11 1 1 0 _n n n n n nn f f f f f F F f f f = =

.

Fungsi Y=f(x1,x2,….,xn) disebut fungsi strictly

quasiconcave jika: 1 2 1 2 0, 0, 0, jika ganjil 0, 0, 0, jika genap. n n F n F n F F F F F F < > = < < > = > …… ……

(Chiang & Wainwright, 2005)

Definisi 23 (Metode Pengali Lagrange) Misalkan didefinisikan sebuah masalah Maksimumkan (minimumkan) f(x,y) Terhadap kendala g(x,y)=c.

Langkah-langkah untuk menemukan solusi yang optimal bagi masalah di atas adalah sebagai berikut:

1. tuliskan fungsi Lagrange-nya

( )

( )

(

( )

)

£ ,x y = f x y, −λ g x y, −c

dengan λ adalah pengali Lagrange-nya 2. turunkan £ terhadap x, y dan λ, lalu turunan

parsial yang didapatkan bernilai sama dengan nol

3. langkah (2), menghasilkan tiga persamaan sebagai berikut

(

)

( , ) ( , ) ( , ) 0 ( , ) ( , ) ( , ) 0 ( , ) 0 £ £ £ x x x y y y x y f x y g x y x y f x y g x y g x y c λ λ λ = − = = − = = − − =

4. selesaikan tiga persamaan ini untuk mencari nilai x, y dan λ.

Langkah (3) sering disebut kondisi orde pertama untuk masalah (1).

(Saeter & Hammond, 2006)

Teorema 1 (Teorema Euler)

Misalkan f adalah fungsi yang terturunkan dari n variabel dalam domain terbuka D, didefinisikan

X=(x1,x2,….,xn) dan t>0 sehingga tX œ D. Fungsi f adalah fungsi homogen berderajat k dalam D jika dan hanya jika persamaan berikut berlaku untuk semua x dalam D

( )

( )

1 n i i i x f X kf X = = ∑

.

Dengan: f(X)=f(x1,x2,….,xn)

( )

( )

i i f X f X x =∂ ∂ i =1,2,...n.

(Saeter & Hammond, 2006) Bukti: Lihat Lampiran 1.

Teorema 2 (Teorema Young)

Andaikan f(x1,x2,….,xn) adalah fungsi kontinu dan terdiferensiabel pada suatu daerah D sehingga f D: _f →R, n

f

D ⊆_R . Misalkan f12

dan f21 yang kontinu di D adalah turunan

parsial orde dua dari fungsi f terhadap x1 dan

x2, maka kedua turunan parsial itu adalah sama.

i j j i f f x x x x ⎛ ⎞ ⎛ ⎞ ∂ _⎜ ∂ _{⎟ =} ∂ ∂ ⎜ ⎟ ⎜ ⎟ ⎜ ⎟ ∂ _⎝∂ _⎠ ∂ _⎝∂ _⎠ i, j=1,2,...n.

(Saeter & Hammond, 2006)

III. PEMBAHASAN 3.1 Fungsi produksi

Hubungan antara input dan output dapat ditransformasikan oleh sebuah fungsi produksi. Secara matematis, fungsi produksi dapat dituliskan sebagai berikut:

(

, , ,....

)

Y= f K L M

dengan:

Y = output yang dihasilkan selama 1 periode waktu

K = input kapital

L = input tenaga kerja

M = input material.

Tanda titik-titik pada fungsi di atas menunjukkan kemungkinan digunakannya

input produksi yang lain. Untuk menunjukkan berbagai kombinasi input yang digunakan dalam memproduksi tingkat output tertentu, kita menggunakan konsep isokuan.

Isokuan adalah kurva yang menggambarkan berbagai kombinasi input produksi secara efisien yang menghasilkan tingkat produksi yang sama. Misalkan dalam berproduksi perusahaan hanya menggunakan dua input produksi saja, yaitu input modal dan input tenaga kerja maka fungsi produksi menjadi

Y=f(K,L) dengan K menyatakan input modal dan L menyatakan input tenaga kerja. Isokuan untuk fungsi produksi seperti ini dapat digambarkan sebagai berikut

Gambar 1 Isokuan

Slope kurva ini menunjukkan suatu tingkat ketika sebuah input dapat dipertukarkan dengan

input lainnya dengan output dianggap konstan. Slope yang negatif ini disebut sebagai tingkat marjinal substitusi teknik. Jika kuantitas tenaga kerja yang digunakan perusahaan meningkat, perusahaan seharusnya dapat mengurangi input modal dan masih tetap menghasilkan output konstan. Jika tenaga kerja sebelumnya diasumsikan memiliki produktivitas marjinal positif, perusahaan seharusnya dapat menggunakan input modal yang lebih sedikit saat lebih banyak tenaga kerja yang digunakan. Untuk tingkat output yang tetap, jika kenaikan jumlah tenaga kerja pada akhirnya mengharuskan perusahaan untuk menggunakan lebih banyak modal, hal ini menandakan bahwa produktivitas marjinal tenaga kerja adalah negatif. Semua isokuan memiliki slope negatif yang menunjukkan bahwa terdapat pertukaran antara input modal dan input tenaga kerja.

Hal lain yang penting dari fungsi produksi adalah seberapa mudah suatu input dapat digantikan oleh input lainnya. Kita telah mengasumsikan bahwa tingkat output tertentu dapat diproduksi dengan berbagai variasi input yang berbeda. Perusahaan dapat melakukan substitusi tenaga kerja terhadap modal dengan mempertahankan output tetap konstan. Secara umum, kasus substitusi input diukur dengan konsep elastisitas substitusi. Elastisitas substitusi dilambangkan dengan s dan nilainya biasanya berbeda di sepanjang isoquan untuk

return to scale yang berbeda. Jika return to

scale diasumsikan konstan, maka nilai elastisitas substitusinya akan sama di sepanjang semua isokuan (Nicholson, 1999).

3.2 Fungsi produksi CES

Fungsi produksi yang mempunyai elastisitas substitusi konstan positif sering disebut dengan fungsi produksi CES (constant elasticities of

substitution). Fungsi produksi yang termasuk ke dalam constant elasticities of substitution mempunyai dua karakteristik utama, yaitu:

a. fungsi tersebut adalah fungsi homogen berderajat satu, dan

b. mempunyai elastisitas substitusi yang konstan.

Bentuk umum fungsi produksi CES adalah:

1 1 n i i i Y _{γ δ}x ρ ρ − − = = ⎛_⎜∑ ⎞_⎟ ⎝ ⎠

.

Dengan:

g=parameter efisiensi yang menunjukkan indikator dari tingkat teknologi

di=parameter distribusi yang berhubungan dengan proporsi penggunaan input produksi terhadap output dengan

1 1 n i i δ = = ∑

.

xi=input produksi ke-i r=parameter substitusi.

Misalkan perusahaan hanya menggunakan input modal dan input tenaga kerja saja dalam berproduksi, maka fungsi produksinya dapat didefinisikan sebagai berikut:

(

,

)

(

(

1

)

)

1

Y= f K L =γ δL−ρ+ −δ K−ρ −ρ

.

Dengan:

Y=ouput produksi

K=input modal

L=input tenaga kerja g=parameter efisiensi d=parameter distribusi r=parameter substitusi.

Asumsikan g >0, 0§ d §1 dan r >-1, nilai r ≠0 karena mengakibatkan nilai output produksi menjadi tidak terdefinisi.

Fungsi produksi CES mempunyai return to

scale yang konstan karena

(

)

(

( )

(

)(

)

)

( )

(

( )

(

)( )

)

(

)

1 1 1 , 1 1 , . F mK mL mL mK m L K mF K L ρ ρ ρ ρ ρ ρ ρ ρ γ δ δ γ δ δ − − − − − − − − = + − = + − =

Untuk semua m>0, maka persamaan di atas juga menunjukkan bahwa fungsi produksi CES adalah homogen berderajat satu. Fungsi produksi CES mempunyai nilai elastisitas substitusi sebagai berikut

1 1 σ ρ = + . (3.2.1) Bukti: Lihat Lampiran 2.

Karena r >-1 maka nilai elastisitas yang didapat pastilah konstan positif.

3.3 Fungsi produksi CROPPES

Fungsi produksi croppes (constant ratio of

pairwise partial elasticities of substitution) merupakan bentuk umum dari fungsi produksi

CES (constant elasticities of substitution). Secara umum, fungsi produksi croppes didefinisikan sebagai berikut

1 n _e e i i i i Y− γ β x− = = ∑

.

(3.3.1) Dengan: Y = output produksi

xi = input produksi ke-i g=parameter efisiensi

e dan ei = parameter substitusi bi=parameter distribusi dengan

1 1 n i i β = = ∑

.

Fungsi produksi croppes memiliki sifat dasar neoklasik. Sifat dasar tersebut di antaranya adalah:

a. memiliki produk marjinal yang positif b. fungsi produksi croppes merupakan fungsi

homogen secara linear dan berderajat satu c. memiliki produktivitas yang semakin

berkurang.

Karakteristik fungsi produksi croppes: a. Memiliki produk marjinal yang positif.

Sebagaimana diketahui, produk marjinal adalah turunan pertama dari fungsi produksi. Produk marjinal (MPi)= i Y x ∂ ∂ sehingga

(

)

( ) 1 1 1 1 1 1 1 1 1 1 1 1 1 1 . e e n _{e e} i i i i i i i i i n _e i i i i i _ei i _i e n _{e e} i i i i i ei _i i e i i ei i Y x e x x e e x e x e x e x e Y e x γ β γ β γβ γ β γβ _{γ β} γβ − − ⎛ ⎞ −⎜ ⎟_{⎝ ⎠} − − − = ⎛ ⎞ −⎜ ⎟_{⎝ ⎠} − + = − − − + ₌ + + ⎛ ⎞ ∂ ₌− ₋ ⎜ ⎟ ∂ _{⎝ ⎠} ⎛ ⎞ = ⎜ ⎟ ⎝ ⎠ ⎛ ⎞ = _{⎜ ⎟} ⎝ ⎠ = ∑ ∑ ∑

(3.3.2)

Diasumsikan tanda ei dan e sama serta γ >0 dan bi >0, sehingga berlaku ( )1 1 0 e i i i ei i e MP Y e x γβ + + = > .

Terbukti produk marjinal adalah positif. Ini artinya jika perusahaan meningkatkan penggunaan input produksi maka output yang dihasilkan juga akan mengalami peningkatan. Diasumsikan perusahaan adalah penerima harga dalam pasar persaingan sempurna. Suatu perusahaan akan berhenti menambah input produksi pada saat tambahan biaya yang harus dibayar adalah sama dengan tambahan pendapatan yang diterima. Tambahan biaya dalam hal ini adalah harga input produksi sedangkan tambahan pendapatan adalah produk marjinal dikalikan harga jual output. Jika harga

input produksi dinotasikan dengan Pi

sedangkan harga jual output dinotasikan dengan

PY, maka alokasi input produksi dianggap efisien bila:

Pi=(MPi)(PY) (3.3.3) dengan:

Pi= harga dari input produksi ke-i

PY= harga dari output Y dengan demikian: ( ) (1 e e 1) i i i i e _{i Y} P Y x P e γ β + − + ⎛ ⎞ = ⎜_⎝ ⎟_⎠

.

b. Fungsi produksi croppes merupakan fungsi homogen secara linear dan berderajat satu. Jika perusahaan meningkatkan semua input produksinya sebesar m kali, dengan m>0 maka Persamaan (3.3.1) menjadi

( )

(

)

(

)

(

)

( )

1 1 11 1 1 1 1 1 1 ... ... . e e e e n _ei i i i e_i e_i e_i e_i n n e_i e_i e_i n n ei n ei e _{i i} i Y mx m x m x m x x x m γ β γβ γβ γβ γβ γ β − − − − ⎛ ⎞ ⎜ ⎟ ⎝ ⎠ − = ⎛ ⎞ ⎜ ⎟ − − − − _{⎝ ⎠} ⎛ ⎞ ⎜ ⎟ − − − _{⎝ ⎠} ⎛ ⎞ ⎜ ⎟ ⎝ ⎠ − = ⎛ ⎞ = ⎜ ⎟ ⎝ ⎠ = + + = + + ⎛ ⎞ = _{⎜ ⎟} ⎝ ⎠ ∑ ∑ (3.3.4) Dari Persamaan (3.3.4) dapat dilihat bahwa apabila nilai ei≠e maka fungsi produksi

croppes tidak menunjukkan homogen secara

linear dan berderajat satu. Oleh karena itu, untuk pembahasan selanjutnya kita asumsikan bahwa nilai ei=e untuk memenuhi sifat kehomogenan

linear. Bila diasumsikan nilai e_i=e maka

Persamaan (3.3.4) menjadi sebagai berikut:

( )

(

)

(

)

(

)

1 1 11 1 1 1 1 1 1 ... ... . e e e e n _e i i i e e e e n n e e e n n n _e i i i Y mx m x m x m x x m x γ β γβ γβ γβ γβ γ β − − − − ⎛ ⎞ ⎜ ⎟ ⎝ ⎠ − = ⎛ ⎞ ⎜ ⎟ − − − − _{⎝ ⎠} ⎛ ⎞ ⎜ ⎟ − − − _{⎝ ⎠} ⎛ ⎞ ⎜ ⎟ ⎝ ⎠ − = ⎛ ⎞ = ⎜ ⎟ ⎝ ⎠ = + + = + + ⎛ ⎞ = ⎜ ⎟ ⎝ ⎠ ∑ ∑ (3.3.5) Dari Persamaan (3.3.5) dapat dilihat bahwa fungsi produksi croppes adalah homogen secara linear dan berderajat satu. Asumsi homogen secara linear ini akan sama dengan asumsi ekonomi mengenai return to scale yang konstan. Karena bersifat homogen secara linear, berarti kenaikan semua input sebesar m kali akan selalu menaikkan output sebesar m kali pula. Akibatnya, fungsi produksi croppes seperti halnya fungsi produksi homogen lainnya yang menunjukkan constant return to scale memenuhi syarat penerapan Teorema Euler. Teorema Euler menyatakan bahwa nilai sebuah fungsi yang homogen secara linear selalu dapat dinyatakan sebagai penjumlahan dari hasil kali salah satu variabel bebas dengan turunan parsial orde pertama terhadap variabel tersebut. Secara ekonomi, sifat ini berarti bahwa pada kondisi

constant return to scale, keuntungan ekonomi yang murni akan nol. Situasi ini merupakan gambaran keseimbangan jangka panjang pada pasar persaingan sempurna. Keuntungan ekonomi yang sebesar nol dalam keseimbangan jangka panjang itu merupakan hasil kekuatan persaingan melalui keluar dan masuknya perusahaan.

c. Memiliki produktivitas yang semakin berkurang atau 2₂ 0 i Y x ∂ _< ∂

.

( )1 1 e i i ei i i e Y Y x e x γβ + + ∂ ₌ ∂

(

)

1 1 1 ( ) 1 e n e e i i i i i i i i i e Y x x x e γβ γ β −⎛ ⎞_{⎜ ⎟}− ⎝ ⎠ − + − = ⎛ ⎞ ∂ ₌ ⎜ ⎟ ∂ _⎝ ∑ _⎠

.

Turunkan persamaan di atas terhadap xi sehingga didapatkan ( )

₍

₎

( )

(

)

( ) ( ) 2 1 1 1 2 1 2 2 1 2 ( ) ( ) 2 1 ( ) 1 1 1 1 1 1 e i i ei e i ei i i i i i n _{e e} i i i i i i i i e e i i i i i i i e e e Y x Y x e e x x e x e e e e x Y e e e γβ γβ γ β γ β γ β γβ − − − + + − + ⎛ ⎞ ⎜ ⎟ ⎝ ⎠ − + − = − + + − + ∂ _{= +} ∂ ⎛ ⎞ ⎜⎛_{− −} ⎞⎛ ⎞ ₋ ⎟ ⎜ ⎟ ⎜⎜_⎝ ⎟_⎠⎝ ⎟ ⎠ ⎜ ⎟ ⎝ ⎠ ⎛ ⎞ ⎛ ⎞ = −_⎜ + _⎟+ +_{⎜ ⎟} ⎝ ⎠ ⎝ ⎠ ∑

(

)

(

)

1 1 1 2 1 2 2 2 1 1 ( ) 1 1 ( ) 1 1 ( ) 1 1 1 1 e n n e_i e_i e_i i i i i i i i e e i i i i i i i n ei e ei i i i i x x x e e e x Y e e e x Y x γ β γ β γ β γβ γ β −⎛ ⎞⎜ ⎟_{⎝ ⎠}− − − + − − = = − + + − − + + − = ⎛ ⎞ ⎛ ⎞ ⎜ ⎟ ⎜ ⎟ ⎝ ⎠ ⎝ ⎠ ⎛ ⎞ ⎛ ⎞ = −_⎜ + _⎟+ +_{⎜ ⎟} ⎝ ⎠ ⎝ ⎠ ⎛ ⎞ ⎜ ⎟ ⎝ ⎠ ∑ ∑ ∑

(

)

(

)

(

)

2 1 1 2 1 2 1 2 ( ) ₁ ( ) 1 ( ) 1 1 1 1 1 1 e e _{i i i} i n _e i i i i i i ei _i i e i i i i i ei _ei n _ei i _{i i i} i e i i i i ei _ei i i i i e x e Y e x e e e x e e Y e e e x _{x x} e e Y e x _{x x} γ β γβ γ β γ β γ β γ β γ β γ β γ β − − + − + ₌ + + − = + + − ⎛ _{⎛ ⎞ ⎛ ⎞} ⎞ ⎜ ⎟ = − + + +_{⎜ ⎟ ⎜ ⎟} ⎜ ⎝ ⎠ ⎝ ⎠ ⎟ ⎝ ⎠ ⎛ ⎛ ⎞⎞ ⎜ ⎜ ⎟⎟ ⎛ ⎞ ⎜ ⎜ ⎟⎟ = _{⎜ ⎜ ⎜}+ − +_{⎟ ⎟⎟} ⎛ ⎞⎝ ⎠ ⎜ ⎜_⎜ ⎜ ⎟ ⎟_⎟⎟ ⎜ _{⎝ ⎝ ⎠ ⎠}⎟ ⎝ ⎠ = ∑ ∑

(

)

1 1 . i i i n ei i e e e e = ⎛ ⎛ ⎞⎞ ⎜ ⎜ ⎟⎟ ⎛ ⎞ ⎜ ⎜ _{⎜ + ⎟− +} ⎟⎟ ⎜ ⎜ _{⎛ ⎞⎝ ⎠} ⎟⎟ ⎜ ⎜_⎜ ⎜ ⎟ ⎟_⎟⎟ ⎜ _{⎝ ⎝ ⎠ ⎠}⎟ ⎝ ∑ ⎠ (3.3.6) Misalkan: 2 1 1 , e ei i i i n e_i e_i i i i i Y x e e x x θ γ β ψ γ β + + − = = Φ = ⎛ ⎞ = _{⎜ ⎟} ⎝ ∑ ⎠

maka Persamaan (3.3.6) menjadi

(

)

2 2 i i i i 1 . i e Y e e e x γβ θ ψ ⎡ ⎧⎛ ⎞ ⎫⎤ ∂ _{= Φ}⎪ ⎛ ₊ ⎞_{− +} ⎪ ⎢ ⎨⎜ ⎟⎜ ⎟ ⎬⎥ ⎝ ⎠ ∂ ⎢⎣ ⎪⎩⎝ ⎠ ⎪⎭⎥⎦

Diasumsikan nilai ei dan e pada persamaan di atas adalah sama sehingga akan mengakibatkan

fungsi q, f, y akan bernilai positif. Karena fungsi produksi croppes memiliki return to

scale yang konstan saat ei=e untuk semua i

dengan e> maka Persamaan (3.3.6) dapat 0

dituliskan sebagai berikut

(

) (

)

2 2 1 2 ( ) 1 1 1 . e i i e _e n _e i i i i i i Y Y e e x x _{x x} γβ γβ γ β + + − = ⎛ ⎛ ⎞⎞ ⎜ ⎜ ⎟⎟ ∂ ₌ ⎜ ⎜ _{+ − +} ⎟⎟ ⎜ ⎜ ⎛ ⎞ ⎟⎟ ∂ _{⎜ ⎜ ⎟⎟} ⎜ ⎟ ⎜ ⎟ ⎜ _{⎝ ⎝ ⎠ ⎠}⎟ ⎝ ∑ ⎠ (3.3.7) Sederhanakan Persamaan (3.3.7) sehingga menjadi

( )( ) ( ) ( )( )

( )( ) ( )

( )(

)

( )(

)

( )

( )(

)

2 2 2 2 2 2 2 1 ( ) 1 1 1 ( ) ( ) 1 1 1 ( ) ( ) 1 1 1 1 1 1 1 e i i i e _e n _e i i i i i i e e i i i e n e e e i i i i i i e e i i e e e e i i i e e i _xi Y Y e e x x _{x x} Y Y e e x _{x x} x Y Y e x x Y x Y e Y γβ γβ γβ γ β γβ γβ γβ γ β γβ γβ γβ γβ + + − = + + + ₋ + = + + + − + + ⎛ ⎞ ⎜ ⎟ ∂ _{= ⎜ + − + ⎟} ⎜ _{⎛ ⎞} ⎟ ∂ _{⎜ ⎟} ⎜ ⎟ ⎜ _{⎝ ⎠} ⎟ ⎝ ⎠ = + − + ⎛ ⎞ ⎜ ⎟ ⎝ ⎠ ⎛ ⎞ = + ⎜_⎜ − ⎟_⎟ ⎝ ⎠ = + ∑ ∑ ⎛ ⎞ ⎜ ⎟ ⎝ ⎠

( )

( )(

)

2 2 1 1 e i e _xi i i i e i i _xi i i Y x x x Y x Y e x x Y Y γβ + ⎛ ⎞ ⎜ − ⎟ ⎜ ⎟ ⎝ ⎠ ∂ ⎛ _∂ ⎞ ⎜ ⎟ = + _⎜ − _⎟ ⎜ ⎟ ⎝ ⎠ ⎛ ⎞ ⎜ ⎟ ⎝ ⎠ ⎛ ⎞ ⎜ ⎟ ⎝ ⎠

( )(

1

)

_{2 2} . e _i i i _xi i i Y _x x Y e x x Y γβ ⎛⎛_⎜∂ ⎞_⎟ ⎞ ⎜_⎝ ∂ _⎠ ⎟ = + ⎜ − ⎟ ⎜ ⎟ ⎜ ⎟ ⎝ ⎠ ⎛ ⎞ ⎜ ⎟ ⎝ ⎠

(3.3.8) Persamaan (3.3.8) akan bernilai negatif jika

0 i i Y _{x Y} x ⎛∂ ⎞ _{− <} ⎜_∂ ⎟

⎝ ⎠

.

Karena fungsi produksi croppes bersifat constant return to scale maka Teorema Euler berlaku, sehingga

0 i i i i Y x Y x f Y x ⎛∂ ⎞_{− → − <} ⎜_∂ ⎟ ⎝ ⎠ 1 karena i n i i f_x Y = ⎛ ₌ ⎞ ⎜ ⎟ ⎝

∑

⎠ terbukti bahwa 22 0. i Y x ∂ < ∂

Nilai produktivitas marjinal yang negatif pada fungsi produksi croppes ini menunjukkan terjadinya diminishing return to scale yang artinya ketika input variabel yang digunakan

jumlahnya masih sedikit maka produk marjinal yang dihasilkan sangat tinggi. Tetapi semakin banyak input variabel tersebut digunakan, sementara input lain dibiarkan konstan maka

produk marjinal tersebut akan semakin berkurang.

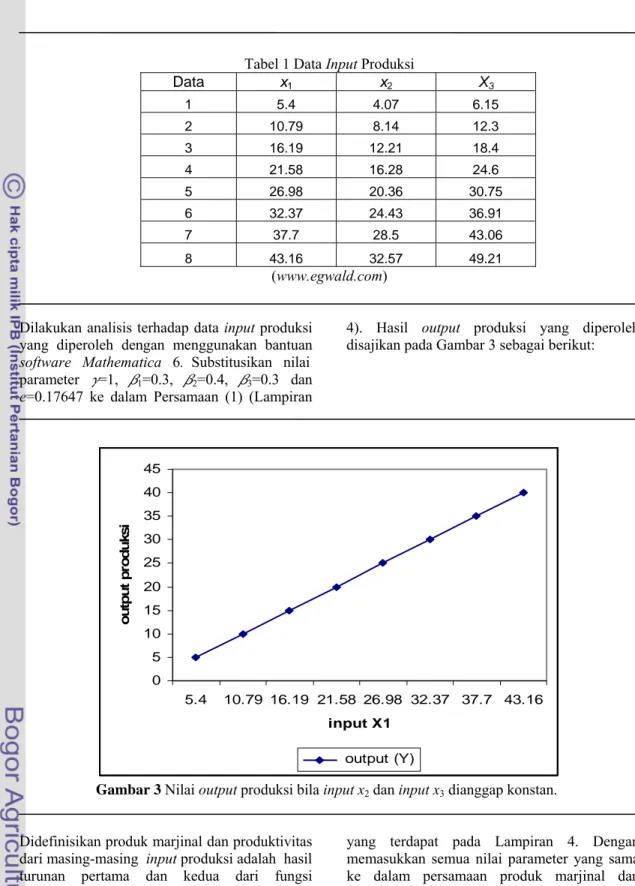
Gambar 2 Kurva Produksi Total dan Produk Marjinal

Keterangan: TP=total product MP=marginal product.

Dari Kurva di atas, dapat dibagi menjadi tiga tahap produksi sebagai berikut:

1. Tahap 1, yaitu dari titik asal sampai titik A. Pada tahap ini, penambahan input produksi akan meningkatkan produk total. Namun bila perusahaan berhenti berproduksi pada tahap ini, perusahaan akan kehilangan kesempatan untuk mendapatkan keuntungan yang lebih besar lagi karena perusahaan sebenarnya masih dapat meningkatkan

output produksinya hingga mencapai hasil yang lebih optimal.

2. Tahap 2, yaitu daerah antara titik A dan titik B. Pada tahap ini, karena berlakunya the law

of diminishing return, maka produk marjinal mengalami penurunan. Namun nilainya masih positif. Penambahan input produksi akan tetap menambah produk total sampai mencapai nilai maksimum.

3. Tahap 3, yaitu saat MP (marginal product) bernilai nol yaitu di titik B. Pada tahap ini perusahaan tidak mungkin melanjutkan produksi, karena penambahan input produksi

justru menurunkan produksi total. Perusahaan akan mengalami kerugian.

3.4 Elastisitas parsial substitusi

Dalam pembahasan fungsi produksi

croppes, ada hal penting lainnya yang perlu diketahui yaitu seberapa mudah menukarkan suatu input dengan input lainnya dalam proses produksi. Alat yang biasa digunakan untuk mengukur respon ini adalah elastisitas substitusi. Bentuk umum fungsi produksi

croppes dengan asumsi e_i=e untuk semua i

dengan e> dapat didefinisikan sebagai berikut 0

(

)

1 1 . 3.4.1 n _{e e} i i i Y γ βx ⎛ ⎞ −⎜ ⎟_{⎝ ⎠} − = =⎛_⎜ ∑ ⎞_⎟ ⎝ ⎠

Misalkan dalam berproduksi perusahaan diasumsikan hanya menggunakan dua input produksi saja, yaitu input xr dan input xs sehingga fungsi produksinya menjadi Y=f(xr,xs) maka menurut definisi elastisitas substitusi diperoleh

s r r s rs s r r s f x d f x x f d x f σ ⎛ ⎞ ⎜ ⎟ ⎝ ⎠ = ⎛ ⎞ ⎜ ⎟ ⎝ ⎠ . Dengan _r r f f x ∂ ₌ ∂ dan s s f f x ∂ ₌ ∂ . (3.4.2) Turunan r s f d f ⎛ ⎞ ⎜ ⎟

⎝ ⎠ dapat dicari sebagai berikut

(

)

. 3.4.3 r r s s r r s s r s f f f f f d dx dx f x x ⎛ ⎞ ⎛ ⎞ ∂_{⎜ ⎟} ∂_{⎜ ⎟} ⎛ ⎞ _{⎝ ⎠ ⎝ ⎠} = + ⎜ ⎟ ∂ ∂ ⎝ ⎠

Dari definisi RTS (xr terhadap xs) diperoleh terhadap ( ) RTS_{x x} r s s r s r f dx f dx = = −

(

)

. sehingga 3.4.4 s r s r f dx = −⎜ ⎟⎛_f ⎞dx ⎝ ⎠

Substitusikan Persamaan (3.4.4) ke Persamaan (3.4.3) sehingga

(

)

. 3.4.5 r r s s s r s s s r r s r r s s s r s r s r f f f f f f d _{f f} dx dx x x f f f f dx _{f f} f x x ⎛ ⎞ ⎛ ⎞ ∂⎜ ⎟_{⎛ ⎞} ∂⎜ ⎟ ⎛ ⎞_{= ⎝ ⎠ −}⎛ ⎞ _{+ ⎝ ⎠} ⎜ ⎟ ⎜ ⎟ _⎜ ⎜ ⎟ _⎟ ∂ ⎝ ⎠ ∂ ⎝ ⎠ ⎝ ⎠ ⎛ _∂⎛ ⎞ _∂⎛ ⎞⎞ ⎜ ⎜ ⎟ ⎜ ⎟⎟ ⎜ ⎝ ⎠ ⎝ ⎠ ⎟ = _⎜ − _⎟ ∂ ∂ ⎜ ⎟ ⎜ ⎟ ⎝ ⎠

Turunan dari rasio antara xs dan xr dinotasikan

dengan s r x d x ⎛ ⎞ ⎜ ⎟

⎝ ⎠, dan nilainya adalah sebagai berikut

(

)

2 . 3.4.6 r s s r s r r x dx x dx x d x x − ⎛ ⎞ = ⎜ ⎟ ⎝ ⎠

Substitusikan Persamaan (3.4.4) ke Persamaan (3.4.6) sehingga

( )

(

)

(

)

2 2 2 . 3.4.7 r r r s s r r s r s s r s r s r r s s r x dx x dx x d x f dx x x _f dx _{f f} x x f x x x − ⎛ ⎞₌ ⎜ ⎟ ⎝ ⎠ ⎛ ⎛ ⎞⎞ = ⎜_⎜ + ⎜ ⎟⎟_⎟ ⎝ ⎠ ⎝ ⎠ = + Selanjutnya akan dicari rasio s r

s r f x d d f x ⎛ ⎞ ⎛ ⎞ ⎜ ⎟ ⎜ ⎟ ⎝ ⎠ ⎝ ⎠

.

Dengan menggunakan Persamaan (3.4.5) dan (3.4.7) diperoleh

( )

(

)

(

)

( )

2 2 . r r s s r r s s r r r r r s s s s r s r s r r r s s r r s s r s s r dx x f x f x d _f x f f f d f _dx f f f f f x x f x f x f f f f f f x x x x ⎛ ⎞ ₊ ⎜ ⎟ ⎝ _{⎠ =} ⎛ ⎞ ⎛ ⎛ ⎞ ⎛ ⎞⎞ ∂ ∂ ⎜ ⎟ ⎜ ⎜ ⎟ ⎜ ⎟⎟ ⎝ ⎠ ⎜ ⎝ ⎠₋ ⎝ ⎠ ⎟ ⎜ _{∂ ∂} ⎟ ⎜ ⎟ ⎜ ⎟ ⎝ ⎠ + = ⎛ _∂⎛ ⎞ _∂⎛ ⎞⎞ ⎜ ⎜ ⎟ ⎜ ⎟⎟ ⎜ ⎝ ⎠₋ ⎝ ⎠ ⎟ ⎜ _{∂ ∂} ⎟ ⎜ ⎟ ⎜ ⎟ ⎝ ⎠

(

)

3.4.8

Substitusikan Persamaan (3.4.8) ke Persamaan (3.4.2) untuk mencari elastisitas substitusi

(

)

( )

(

)

2 . s r s r r s rs s r r s r r r s s s r r r s s r s s r r r r s s r r s s s r s r s s r f x d f x x f d x f f f x f x f x f f x f f f f x x f f x f x f f f f f x x f f x x x σ ⎛ ⎞ ⎜ ⎟ ⎝ ⎠ = ⎛ ⎞ ⎜ ⎟ ⎝ ⎠ ⎛ ⎞ ⎜ ⎟ + _{⎝ ⎠} = ⎛ ⎛ ⎞ ⎛ ⎞⎞ ∂ ∂ ⎜ ⎜ ⎟ ⎜ ⎟⎟ ⎜ ⎝ ⎠₋ ⎝ ⎠ ⎟ ⎜ _{∂ ∂} ⎟ ⎜ ⎟ ⎜ ⎟ ⎝ ⎠ + = ⎛ ⎛ ⎞ ⎛ ⎞⎞ ∂ ∂ ⎜ ⎜ ⎟ ⎜ ⎟⎟ ⎜ ⎝ ⎠₋ ⎝ ⎠ ⎟ ⎜ _{∂ ∂} ⎟ ⎜ ⎟ ⎜ ⎟ ⎝ ⎠

(

)

3.4.9

Nilai r s s f f x ⎛ ⎞ ∂⎜_⎝ ⎟_⎠ ∂ dan r s r f f x ⎛ ⎞ ∂⎜_⎝ ⎟_⎠ ∂ diberikan oleh

(

)

(

)

2 2 . 3.4.10 3.4.11 r s rs s r ss s _s r s rr s r sr r _s f f f f f f x f f f f f f x f f ⎛ ⎞ ∂⎜_⎝ ⎟ ₋ ⎠ = ∂ ⎛ ⎞ ∂⎜_⎝ ⎟ ₋ ⎠ = ∂

Berdasarkan Teorema Young maka berlaku

rs sr

f =f sehingga dengan menyubstitusikan Persamaan (3.4.10) dan Persamaan (3.4.11) ke Persamaan (3.4.9) maka akan diperoleh

(

)

(

)

(

)

(

)

(

)

(

)

(

)

2 2 2 r r r s s rs rs s r ss rr s r sr s r s r s s s r r r s s s rr s r sr r rs s r ss r s s s _s r s r r s s r rs s r ss s rr s r r s f f _x f _x f f f f f f f f f x x f f f f x f x f f f f f f f f f f x x f f f f f x f x f f f f f f f f f f x x f f f σ = + ⎛ ⎛ ₋ ⎞ ⎛ ₋ ⎞⎞ ⎜ ⎜ ⎟− ⎜ ⎟⎟ ⎜ ⎜_⎝ ⎟_⎠ ⎜_⎝ ⎟_⎠⎟ ⎝ ⎠ + = ⎛ ⎛ ₋ ⎞⎞ ⎜ − − ⎜ ⎟⎟ ⎜ ⎜_⎝ ⎟_⎠⎟ ⎝ ⎠ + = − − −

(

)

( )

( )

(

)

(

)

(

)

2 2 2 = . 3.4.12 r s r r s s r s rs ss rr r s r s rs r r s s r s f f f _x f _x f f f f f f f x x F f x f x F x x + = − − + Didefinisikan:

( )

2

( )

2 2 _{r s rs r ss s rr} F = f f f − f f − f f 0 _{s r} s ss rs r sr rr f f F f f f f f f = = bordered determinant

Frs = fr fs adalah kofaktor dari frs pada F.

Nilai elastisitas substitusi pada persamaan (3.4.12) selalu bernilai positif. Karena Fungsi produksi croppes bersifat neoklasik, maka input produksi (dalam hal ini input xs dan input xr) dan produk marjinal ( fsdanfr) selalu bernilai

non-negatif. Oleh karena itu, untuk menunjukkan bahwa nilai elastisitas substitusi adalah positif, maka kita tinggal membuktikan bahwa

( )

2

( )

2

(

)

2f f f_{r s rs}− f_r f_ss− f_s f_rr>0 . 3.4.13

Untuk membuktikan Persamaan (3.4.13), cukup dibuktikan bahwa frs> 0, frr dan <0fss . Nilai

rs

f dapat dicari dengan menurunkan fungsi produksi terhadap variabel xr dan xs. Berdasarkan Teorema Young berlaku frs=fsr

sehingga

(

)

( )

(

)

1 1 1 . e rs sr r _e s r e s r r r f f e f f e x Y x Y x γβ γβ + = = + = + ⎛_⎜ ⎞_⎟ ⎝ ⎠

Karena xr dan fs bernilai non negatif, serta

diasumsikan semua parameter bernilai positif, terbukti bahwa frs=fsr >0 .

Produktivitas marjinal (f_rr dan f_ss) selalu bernilai negatif, dan nilainya dapat dicari sebagai berikut:

(

)

( )

₍

₎

( )

(

)

(

)

(

)

(

)

( )

₍

₎

( )

(

)

(

)

2 2 2 1 1 2 1 ₁ 2 1 1 1 1 1 1 1 e e e e r r rr r r e e r r r r r r e r r r r r e e e e s s ss s s e e s s s s s s s f e Y f x e Y x f Y e x f x Y e x x x f e Y f e Y f Y e x Y Y x x x Y x Y Y x x x γβ γβ γβ γβ γβ γβ − + + − + − + + − + = + − + ⎛ ⎞ ⎜ ⎟ = + _⎜ − _⎟ ⎜ ⎟ ⎝ ⎠ ⎡ ₋ ⎤ = + ⎢ ⎥ ⎢ ⎥ ⎣ ⎦ = + − + ⎛ ⎞ ⎜ ⎟ = + _⎜ − _⎟ ⎜ ⎟ ⎝ ⎠ = ⎛ ⎞ ⎛ ⎞ ⎜ ⎟ ⎜ ⎟ ⎝ ⎠ ⎝ ⎠ ⎛ ⎞ ⎜ ⎟ ⎝ ⎠ ⎛ ⎞ ⎛ ⎞ ⎜ ⎟ ⎜ ⎟ ⎝ ⎠ ⎝ ⎠

(

1

)

₂ . e s s s s f x Y e Y x x ⎡ ₋ ⎤ ⎢ ⎥ + ⎢ ⎥ ⎣ ⎦ ⎛ ⎞ ⎜ ⎟ ⎝ ⎠

Untuk menunjukkan frr dan fss bernilai

negatif, maka cukup dibuktikan bahwa f x_{r r}−Y

dan f xs s−Y kurang dari nol. Karena fungsi

produksi mempunyai return to scale yang konstan, maka Teorema Euler berlaku sehingga berlaku f x_{r r}− <Y 0dan f x_{s s}− <Y 0

(

karena f x_{r r}+ f x_{s s}=Y

)

Persamaan (3.4.12) dapat diperluas untuk penggunaan sejumlah n input produksi menjadi

1 i n i i rs rs r s f x _F x x F σ =

∑

=

.

(3.4.14) Dengan: 1 1 11 1 1 0 _n n n n nn f f f f f F f f f = … … … = bordered determinant

Frs=kofaktor dari frs pada F.

Persamaan (3.4.14) digunakan untuk mencari nilai elastisitas parsial substitusi antara input x_r

dengan input xs, sedangkan banyaknya input

produksi yang lain (x_i dengan i≠r dan i≠s) dipertahankan tetap konstan.

3.5 Pengoptimuman input produksi

Pada pembahasan ini, kita akan mencari solusi input produksi yang didasarkan pada pemaksimuman keuntungan. Diasumsikan perusahaan berproduksi pada pasar persaingan sempurna. Bentuk umum fungsi produksi

croppes dengan asumsi ei=e untuk semua i

dengan e>0 adalah sebagai berikut

(

)

1 1 . 3.5.1 n _e e i i i Y γ βx − − = =⎛⎜ ∑ ⎞⎟ ⎝ ⎠

Sedangkan PY adalah harga output yang didefinisikan sebagai berikut

PY=g Y

( )

.

(

3.5.2

)

Misalkan P=(P1,P2,P3,….,Pn) adalah vektor harga dari input produksi. Pi dengan i=1,2,3,....n diasumsikan positif. Sementara itu, didefinisikan pula x=(x1,x2,….,xn) sebagai vektor

input produksi yang meminimumkan biaya.

Karena permintaan input produksi perusahaan dipengaruhi oleh harganya, maka persamaan untuk input produksi dapat dituliskan sebagai berikut

( )

i 1,2,... i

x = f _P i= n

dengan:

Pi= harga input produksi ke-i

xi = banyaknya input produksi ke-i.

Penerimaan total (Revenue) sama dengan jumlah

output (Y) dikalikan dengan harga jual output (PY). Secara matematis dinotasikan sebagai berikut

( )

( )

(

)

( )

. (3.5.3) Y i i R P Y g Y Y g f x f x = = =

Total biaya produksi perusahaan (cost) adalah jumlah dari semua perkalian input produksi dengan harganya. Secara matematis dinotasikan sebagai berikut 1 . (3.5.4) n i i i C _Px = =∑

Keuntungan adalah nilai penerimaan total perusahaan dikurangi biaya total yang dikeluarkan perusahaan. Jika keuntungan dinotasikan dengan π maka

( )

(

)

( )

1 1 .

penerimaan total - biaya produksi

(3.5.5) n Y i i i n i i i i i P Y P x g f x f x P x π = = = − = − = ∑ ∑

Dalam karya tulis ini, ada dua kasus yang akan diamati. Kasus pertama ketika input kapital (dalam tulisan ini berarti tanah) telah ditetapkan dalam persediaan sementara input lain bersifat elastis sempurna. Pada kasus kedua input tanah dan input tenaga kerja telah ditetapkan, sedangkan input lain tersedia dalam industri pada saat harganya mengalami kenaikan.

Kasus 1

Asumsi yang digunakan:

i. Input tanah bernilai tetap dinotasikan dengan xa=ao.

ii. Input produksi lain bersifat elastis sempurna.

Penerimaan total sama dengan jumlah output (Y) dikalikan dengan harga jual (PY).

( )

(

)

( )

(

)

. 3.5.6 Y i i R P Y g f x f x = =

Sementara itu, fungsi biaya produksinya adalah

1 1 n i i i C − P x = = ∑ dengan i≠a. (3.5.7)