Peramalan Beban Jangka Pendek untuk Hari-hari Libur Menggunakan Fuzzy Linear Regression (FLR) yang dioptimisasi dengan Artificial Immune System

(1)

Menggunakan Fuzzy Linear Regression (FLR) yang dioptimisasi

dengan Artificial Immune System (AIS)

( Studi Kasus di Kalimantan Selatan - Tengah )

Oleh:

Dessy Rika Astuti

2205 100 055

Dosen Pembimbing :

Prof. Dr. Ir. Imam Robandi, MT

Oleh:

Dessy Rika Astuti

2205 100 055

Dosen Pembimbing :

(2)

LATAR BELAKANG

KalSel-Teng Permintaan beban yang meningkat Penyediaan listrik oleh PLN Ketidakmampuan pembangkit Pemadaman

Solusi :

Peramalan beban jangka pendek

Fluktuasi beban pada hari libur

(3)

• Peramalan beban jangka pendek (short-term load

forecasting) yang meramalkan beban dalam

jangka waktu perjam hingga perminggu.

• Peramalan beban jangka menengah

(medium-term load forecasting) yang meramalkan beban

dalam jangka waktu mingguan hingga 1 tahun.

• Peramalan beban jangka panjang (long-term load

forecasting) yang meramalkan beban tahunan

atau lebih dari satu tahun kedepan.

• Peramalan beban jangka pendek (short-term load

forecasting) yang meramalkan beban dalam

jangka waktu perjam hingga perminggu.

• Peramalan beban jangka menengah

(medium-term load forecasting) yang meramalkan beban

dalam jangka waktu mingguan hingga 1 tahun.

• Peramalan beban jangka panjang (long-term load

forecasting) yang meramalkan beban tahunan

(4)

LATAR BELAKANG

Peramalan yang telah dilakukan [8]:

• Fuzzy Linear Regression (FLR)

Rata-rata error beban puncak = 4.545 %

Peramalan yang dilakukan :

• Fuzzy Linear Regression

(FLR) dengan Metode

Optimisasi Artificial Immune System (AIS) via Clonal

Selection Algorithm (CSA)

Rata-rata error beban puncak = 3.89 %

Peramalan yang telah dilakukan [8]:

• Fuzzy Linear Regression (FLR)

Rata-rata error beban puncak = 4.545 %

Peramalan yang dilakukan :

• Fuzzy Linear Regression

(FLR) dengan Metode

Optimisasi Artificial Immune System (AIS) via Clonal

Selection Algorithm (CSA)

(5)

Parameter Fuzzy

Penelitian sebelumnya,

parameter fuzzy ditentukan

dengan Metode Simplek [8]

Penelitian sebelumnya,

parameter fuzzy ditentukan

dengan Metode Simplek [8]

Penentuan parameter

dengan Metode Optimisasi

Penentuan parameter

dengan Metode Optimisasi

Fuzzy Linear Regression

(FLR)

Fuzzy Linear Regression

(FLR)

Artificial Immune System (AIS) merupakan algoritma optimisasi yang digunakan

untuk mengoptimisasi parameter fuzzy dan tidak terjebak dalam lokal optimum.

Penentuan parameter

dengan Metode Optimisasi

Penentuan parameter

dengan Metode Optimisasi

[8] Agus Dharma, Mauridhi Hery P, Imam Robandi, “Peramalan Beban Jangka Pendek untuk Hari-hari Libur Menggunakan Metode Fuzzy Linear Regression (Studi Kasus di Pulau Bali)”, Seminar Teknik Elektro Universitas Negeri Surabaya, 2006.

(6)

TUJUAN

Tujuan Penelitian :

Menyelesaikan permasalahan peramalan beban jangka pendek pada

hari-hari libur di Kalimantan Selatan-Tengah dengan menggunakan metode

FLR-AIS, dan membandingkan peramalan FLR (metode simplek) dengan FLR-AIS.

Tujuan Penelitian :

Menyelesaikan permasalahan peramalan beban jangka pendek pada

hari-hari libur di Kalimantan Selatan-Tengah dengan menggunakan metode

FLR-AIS, dan membandingkan peramalan FLR (metode simplek) dengan FLR-AIS.

Tujuan Peramalan Beban:

Mempersiapkan unit-unit pembangkit yang akan beroperasi.

Tujuan Peramalan Beban:

(7)

Di Sisi Demand :

Terpenuhinya penyesuaian antara permintaan dan pembangkitan energi.

Di Sisi Demand :

Terpenuhinya penyesuaian antara permintaan dan pembangkitan energi.

Di Sisi Sistem Tenaga :

1. Ketepatan pengaturan jadwal pengiriman daya.

2. Perencanaan pemeliharaan unit-unit pembangkit dan evaluasi

keandalan sistem.

Di Sisi Sistem Tenaga :

1. Ketepatan pengaturan jadwal pengiriman daya.

2. Perencanaan pemeliharaan unit-unit pembangkit dan evaluasi

(8)

BATAS MASALAH

1. Data yang diambil adalah data dari PT. PLN (Persero), Area

Pengatur dan Penyalur Beban (AP2B) Kalimantan

Selatan-Tengah, yaitu data beban harian tiap satu jam dari hari H-4

sampai hari H selama tahun 2005 sampai dengan 2009.

2. Data diolah dengan menggunakan metode Fuzzy Linear

Regression

(FLR)

dengan menggunakan Artificial Immune

System (AIS) via Clonal Selection Algorithm (CSA) untuk

optimisasi parameternya.

3. Data diprediksi berdasarkan hari libur nasional kemudian

dievaluasi terhadap realisasi data beban.

4. Hasil peramalan diolah menggunakan program MATLAB.

1. Data yang diambil adalah data dari PT. PLN (Persero), Area

Pengatur dan Penyalur Beban (AP2B) Kalimantan

Selatan-Tengah, yaitu data beban harian tiap satu jam dari hari H-4

sampai hari H selama tahun 2005 sampai dengan 2009.

2. Data diolah dengan menggunakan metode Fuzzy Linear

Regression

(FLR)

dengan menggunakan Artificial Immune

System (AIS) via Clonal Selection Algorithm (CSA) untuk

optimisasi parameternya.

3. Data diprediksi berdasarkan hari libur nasional kemudian

dievaluasi terhadap realisasi data beban.

(9)

FLR-AIS

Fuzzy linear Regression

(FLR)

Fuzzy linear Regression

(FLR)

FLR-AIS

Peramalan beban

Artificial Immune System

(AIS)

Artificial Immune System

(AIS)

FLR-AIS

Optimisasi

Parameter Fuzzy

(10)

KAJIAN TEORI

FLR-AIS

Start Input Data Beban Puncak

Bentuk Bilangan –bilangan Fuzzy Segitiga :

X_i: (x_i, _i) dan Y_i: (y_i, e_i)

Dapatkan Nilai Optimum dari :

A0: (a0,0) dan A1: (a1,1) Dengan Metode AIS (CSA)

Yi = A0  (A1  Xi)

A

Bentuk Bilangan –bilangan Fuzzy Segitiga : X_i: (x_i, _i) dan Y_i: (y_i, e_i) M m m m m x_i 4 4 3 2 1    4 ) ( ) ( ) ( ) (1 2 2 2 3 2 4 2 i M m i M m i M m i M m i x x x x          2 5 dan e ( 5 y) M m y_i _i m_M _i Peramalan Beban Error Stop A

(11)

FUZZY LINEAR REGRESSION (FLR)

REGRESI LINEAR

FUZZY (FLR)

3.5

4

4.5 Series 1

.

_0.8

1 Series 1

.

0

0.5

1

1.5

2

2.5

3

3.5 x1

x2

x3

x4

x5

Series 1

.

_.

.

0

0.2

0.4

0.6

0.8 x1 x2 x3 x4 x5

Series 1

.

(12)

FUZZY LINEAR REGRESSION (FLR)

• Gambar Keanggotaan dari Koefisien Fuzzy :

KAJIAN TEORI

~ A  1.0 0 pi a ~ i A ci ci 1 ~ ebaliknya

|

1 ( )

0

i i i i i i i A i i s

p a

p c x p c

a

c









   









• Gambar Keanggotaan dari Koefisien Fuzzy :

~ A  1.0 0 pi a ~ i A ci ci 1 ~ ebaliknya

|

1 ( )

0

i i i i i i i A i i s

p a

p c x p c

a

c









   









Y = A

₀

+ A

₁

x

(13)

FUZZY LINEAR REGRESSION (FLR)



Fungsi objektif :



_{ }

_ _





m j n i

c

i

x

ij

O

1 1

min



 n i1pixij



 n i 1cixij



 n i1cixij

Fungsi output fuzzy

Batasan-batasan :













n i n i i ij ij i j

p

x

h

c

x

y

1

(

1 )

1















n

i

n

i

ij

i

j

p

x

h

c

x

y

1 (

1 )

1

(14)

FUZZY LINEAR REGRESSION (FLR)

Konsep Peramalan Beban dengan FLR :

 Bentuk Bilangan – bilangan Fuzzy Segitiga :

X

_i

: (x

_i

,

_i

) dan Y

_i

: (y

_i

, e

_i

)

 Nilai optimal :

A

₀

: (a

₀

, 

₀

) dan A

₁

: (a

₁

, 

₁

)

Dengan Metode Pemrograman Linier :

Y

_i

=

= ( a

₀

+ a

₁

x

_i

, max (

₀

, |a

₁

|

_i

, 

₁

|x

_i

|) )

KAJIAN TEORI

Konsep Peramalan Beban dengan FLR :

 Bentuk Bilangan – bilangan Fuzzy Segitiga :

X

_i

: (x

_i

,

_i

) dan Y

_i

: (y

_i

, e

_i

)

 Nilai optimal :

A

₀

: (a

₀

, 

₀

) dan A

₁

: (a

₁

, 

₁

)

Dengan Metode Pemrograman Linier :

Y

_i

=

(15)

FUZZY LINEAR REGRESSION (FLR)

• Prediksi maksimum beban puncak pada hari

libur :

P

*

Max

= Y

4 x P

WD

Max

• Error dari peramalan :

• Prediksi maksimum beban puncak pada hari

libur :

P

*

Max

= Y

4 x P

WD

Max

(16)

Keterangan :

• X

_i

: (x

_i

,

_i

)

= Anggota rata-rata dan simpangan baku dari

beban puncak harian untuk 4 hari sebelum hari

libur.

• Y

_i

: (y

_i

, e

_i

)

= Informasi saat hari libur, menyatakan rata-rata

dan simpangan baku dari beban puncak saat

hari libur.

• m1,m2,m3,m4

= beban puncak harian untuk 4 hari

sebelum hari libur

• M

= beban paling besar diantara 4 nilai-nilai dari beban

puncak harian

• m5 = beban puncak dari hari libur

• P

WD

Max

= beban maksimum dari empat hari sebelum

hari hari libur.

• P*

_Max

= ramalan beban maksimum hari libur.

• Jika X

₄

menjadi masukan data fuzzy untuk beban maksimum dari

4 hari sebelum hari libur , maka Y

₄

= nilai perkiraan.

Keterangan :

• X

_i

: (x

_i

,

_i

)

= Anggota rata-rata dan simpangan baku dari

beban puncak harian untuk 4 hari sebelum hari

libur.

• Y

_i

: (y

_i

, e

_i

)

= Informasi saat hari libur, menyatakan rata-rata

dan simpangan baku dari beban puncak saat

hari libur.

• m1,m2,m3,m4

= beban puncak harian untuk 4 hari

sebelum hari libur

• M

= beban paling besar diantara 4 nilai-nilai dari beban

puncak harian

• m5 = beban puncak dari hari libur

• P

WD

Max

= beban maksimum dari empat hari sebelum

hari hari libur.

• P*

_Max

= ramalan beban maksimum hari libur.

• Jika X

₄

menjadi masukan data fuzzy untuk beban maksimum dari

(17)

ARTIFICIAL IMMUNE SYSTEM (AIS)

Clonal Selection :

Clonal selection adalah proses

yang digunakan oleh sistem

kekebalan

untuk

memilih

antibodi

yang

dapat

mengenali antigen.

Antigen Seleksi Berkembangbiak (Cloning) Pembedaan respon Plasma Cells Memory Cells M M Populasi Antibody

Clonal Selection :

Clonal selection adalah proses

yang digunakan oleh sistem

kekebalan

untuk

memilih

antibodi

yang

dapat

mengenali antigen.

Antigen Seleksi Berkembangbiak (Cloning) Pembedaan respon Plasma Cells Memory Cells M M Populasi Antibody

(18)

1. Pengkodean Input Antigen

Berupa 4 parameter fuzzy :

a

₀

, 

₀

,

a

₁

, 

₁

2. Inisialisasi Populasi Antibodi

Pengkodean : real - number encoding

Ukuran populasi antibodi : 40

Immune=Rb + (Ra - Rb)* rand (Num_Ab,Cell)

3. Perhitungan Affinity

Evaluasi bagus atau jeleknya antibodi sesuai affinity.

KAJIAN TEORI

ARTIFICIAL IMMUNE SYSTEM (AIS)

1. Pengkodean Input Antigen

Berupa 4 parameter fuzzy :

a

₀

, 

₀

,

a

₁

, 

₁

2. Inisialisasi Populasi Antibodi

Pengkodean : real - number encoding

Ukuran populasi antibodi : 40

Immune=Rb + (Ra - Rb)* rand (Num_Ab,Cell)

3. Perhitungan Affinity

Evaluasi bagus atau jeleknya antibodi sesuai affinity.

|

( )

( ) |

(%)

100%

( )

Forecast Actual Actual

p

t

P

t

Error

x

P

t





(19)

4. Kloning

• Diambil 12 % (p

_c

= 0.12) antibodi terbaik (sekitar 5 antibodi).

• Dikloning 8x tiap kandidat.

ARTIFICIAL IMMUNE SYSTEM (AIS)

0.7022 4.9063 8.6436 3.9986

.

1.7325 4.0960 9.0055 4.5018

4.8452 0.8142 7.9604 18.4807

0.8499 5.8127 12.3911 14.8026

0.5881 6.4059 18.9210 1.7870

0.7022 4.9063 8.6436 3.9986

.

1.7325 4.0960 9.0055 4.5018

4.8452 0.8142 7.9604 18.4807

0.8499 5.8127 12.3911 14.8026

0.5881 6.4059 18.9210 1.7870

8x

(20)

5. Hypermutasi

Affinity bagus=peluang mutasi kecil, dan sebaliknya.

6. Seleksi Ulang

Populasi antibodi setelah proses hypermutasi akan diurutkan

kembali berdasarkan nilai affinity.

ARTIFICIAL IMMUNE SYSTEM (AIS)

KAJIAN TEORI

5. Hypermutasi

Affinity bagus=peluang mutasi kecil, dan sebaliknya.

6. Seleksi Ulang

Populasi antibodi setelah proses hypermutasi akan diurutkan

kembali berdasarkan nilai affinity.

(21)

Input Data Beban Puncak

Bentuk Bilangan –bilangan Fuzzy Segitiga :

X_i: (x_i, _i) dan Y_i: (y_i, e_i) M m m m m x_i 4 4 3 2 1    4 ) ( ) ( ) ( ) (1 2 2 2 3 2 4 2 i M m i M m i M m i M m i x x x x          2 5 dan e ( 5 y) M m y m_M _i i i   A Max Iterasi Kloning Hypermutasi Populasi antibodi solusi terbaik

Beban Puncak Hari Libur Diestimasi Oleh :

P* Max= Y4 x PWDMax Tidak Ya 2 5 dan e ( 5 y) M m y m_M _i i i  

Dapatkan Nilai Optimum dari :

A0: (a0,0) dan A1: (a1,1)

Dengan Metode pemrograman Linear :

Y_i = A0 (A1 Xi)

Inisialisasi awal dari populasi antibodi

A

Seleksi Ulang

Beban Puncak Hari Libur Diestimasi Oleh :

P* Max= Y4 x PWDMax Error Stop

Flowchart FLR-AIS

 

(22)

HASIL DAN PEMBAHASAN

• Optimisasi dilakukan untuk mencari nilai

optimum dari 4 parameter fuzzy, yaitu parameter

a

₀

,

₀

dan a

_1,



₁

• Simulasi :

1. 3 tahun sebelumnya

2. 2 tahun sebelumnya

• Pengambilan data :

1. Data Training

2. Data Testing

• Optimisasi dilakukan untuk mencari nilai

optimum dari 4 parameter fuzzy, yaitu parameter

a

₀

,

₀

dan a

_1,



₁

• Simulasi :

1. 3 tahun sebelumnya

2. 2 tahun sebelumnya

• Pengambilan data :

1. Data Training

2. Data Testing

(23)

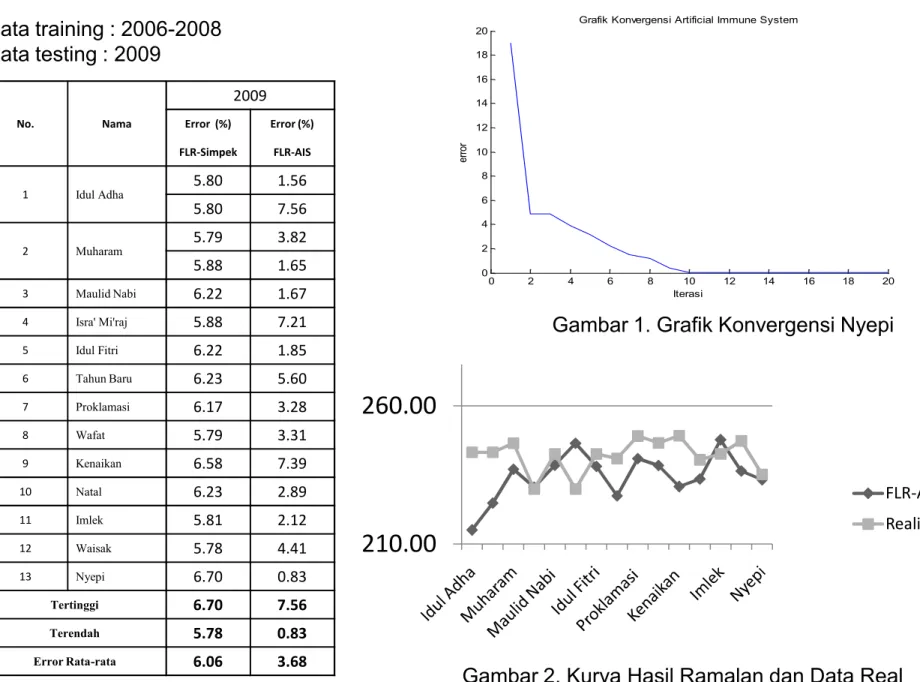
No. Nama 2009 Error (%) Error (%) FLR-Simpek FLR-AIS 1 Idul Adha 5.80 1.56 5.80 7.56 2 Muharam 5.79 3.82 5.88 1.65 3 Maulid Nabi 6.22 1.67 0 2 4 6 8 10 12 14 16 18 20 0 2 4 6 8 10 12 14 16 18 20

Grafik Konvergensi Artificial Immune System

Iterasi er ro r Data training : 2006-2008 Data testing : 2009

Gambar 1. Grafik Konvergensi Nyepi

4 Isra' Mi'raj _5.88 _7.21 5 Idul Fitri 6.22 1.85 6 Tahun Baru 6.23 5.60 7 Proklamasi 6.17 3.28 8 Wafat 5.79 3.31 9 Kenaikan 6.58 7.39 10 Natal 6.23 2.89 11 Imlek _5.81 _2.12 12 Waisak 5.78 4.41 13 Nyepi 6.70 0.83 Tertinggi 6.70 7.56 Terendah 5.78 0.83 Error Rata-rata 6.06 3.68

210.00

260.00

FLR-AIS (MW) Realisasi (MW)

Tabel 1. Perbandingan error

Gambar 1. Grafik Konvergensi Nyepi

(24)

HASIL DAN PEMBAHASAN

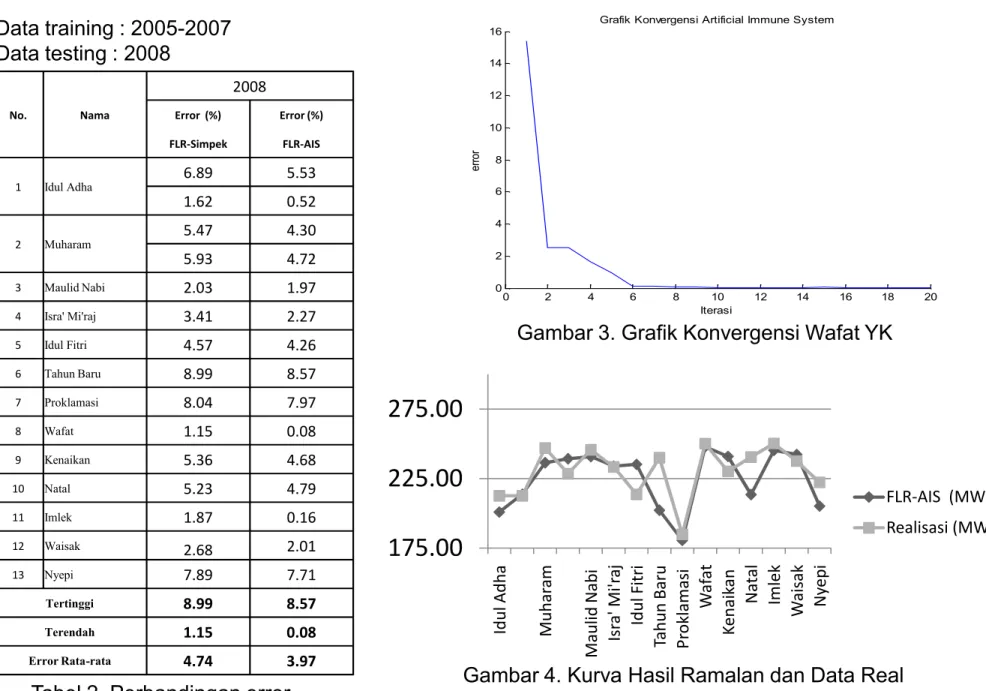
No. Nama 2008 Error (%) Error (%) FLR-Simpek FLR-AIS 1 Idul Adha 6.89 5.53 1.62 0.52 2 Muharam 5.47 4.30 5.93 4.72 3 Maulid Nabi 2.03 1.97 Isra' Mi'raj _3.41 _2.27 0 2 4 6 8 10 12 14 16 18 20 0 2 4 6 8 10 12 14 16

Iterasi er ro r Data training : 2005-2007 Data testing : 2008 4 Isra' Mi'raj _3.41 _2.27 5 Idul Fitri _4.57 _4.26 6 Tahun Baru 8.99 8.57 7 Proklamasi 8.04 7.97 8 Wafat _1.15 _0.08 9 Kenaikan 5.36 4.68 10 Natal 5.23 4.79 11 Imlek _1.87 _0.16 12 Waisak _2.68 _2.01 13 Nyepi 7.89 7.71 Tertinggi 8.99 8.57 Terendah _1.15 _0.08 Error Rata-rata 4.74 3.97 0 2 4 6 8 10 12 14 16 18 20 0 2 4 6 8 10 12 14 16

Iterasi er ro r

175.00

225.00

275.00

Idul Adha Muhar am Maulid Nabi Isr a' Mi'r aj Idul Fitri Tahun Baru Pr oklamasi W af at K enaik an Natal Imlek W aisak _Nyepi FLR-AIS (MW) Realisasi (MW)

Gambar 3. Grafik Konvergensi Wafat YK

(25)

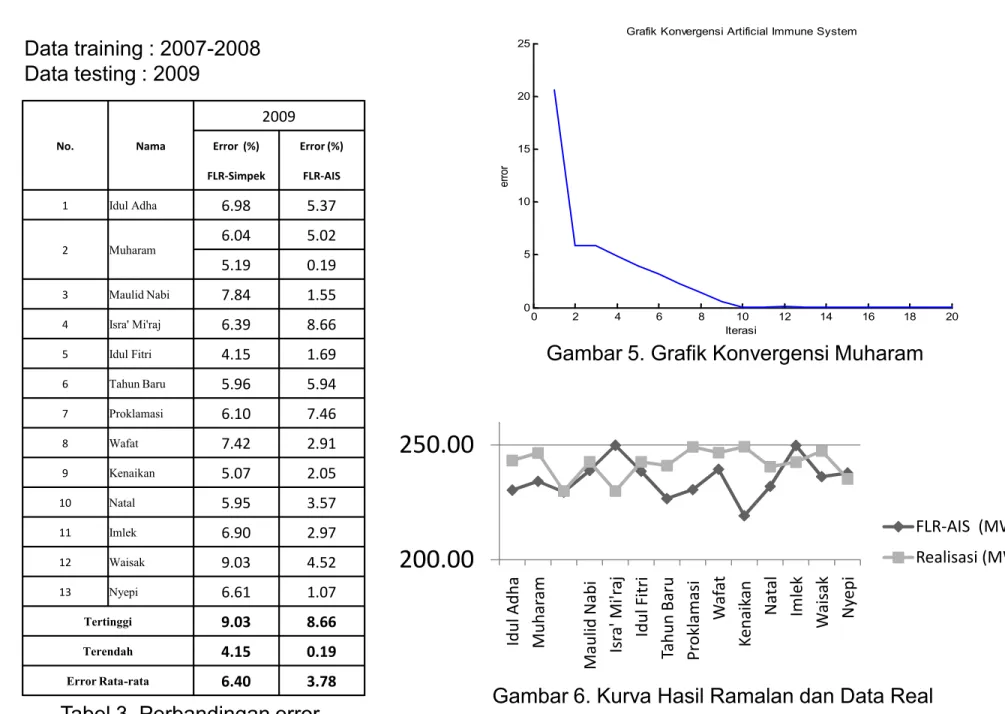
No. Nama 2009 Error (%) Error (%) FLR-Simpek FLR-AIS 1 Idul Adha _6.98 _5.37 2 Muharam 6.04 5.02 5.19 0.19 3 Maulid Nabi _7.84 _1.55 4 Isra' Mi'raj 6.39 8.66 0 2 4 6 8 10 12 14 16 18 20 0 5 10 15 20 25 Iterasi e rr o r Data training : 2007-2008 Data testing : 2009 4 Isra' Mi'raj 6.39 8.66 5 Idul Fitri 4.15 1.69 6 Tahun Baru _5.96 _5.94 7 Proklamasi _6.10 _7.46 8 Wafat 7.42 2.91 9 Kenaikan 5.07 2.05 10 Natal _5.95 _3.57 11 Imlek 6.90 2.97 12 Waisak 9.03 4.52 13 Nyepi _6.61 _1.07 Tertinggi 9.03 8.66 Terendah 4.15 0.19 Error Rata-rata 6.40 3.78 0 2 4 6 8 10 12 14 16 18 20 0 5 10 15 20 25 Iterasi e rr o r

200.00

250.00

Gambar 5. Grafik Konvergensi Muharam

(26)

HASIL DAN PEMBAHASAN

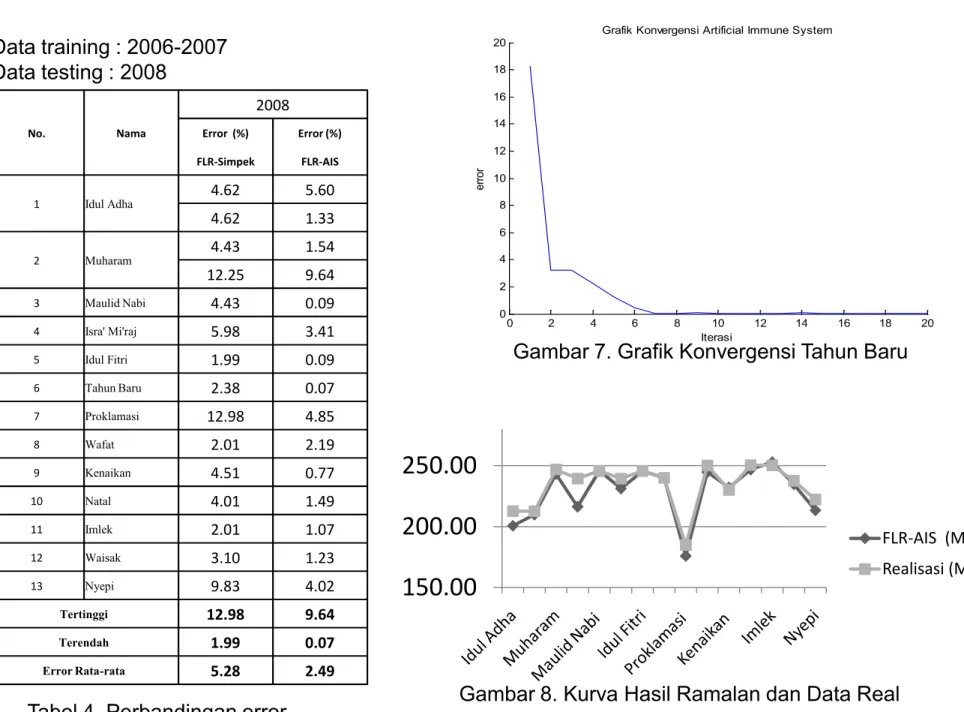
No. Nama 2008 Error (%) Error (%) FLR-Simpek FLR-AIS 1 Idul Adha 4.62 5.60 4.62 1.33 2 Muharam 4.43 1.54 12.25 9.64 3 Maulid Nabi _4.43 _0.09 4 Isra' Mi'raj 5.98 3.41 0 2 4 6 8 10 12 14 16 18 20 0 2 4 6 8 10 12 14 16 18 20

Iterasi e rr o r Data training : 2006-2007 Data testing : 2008 4 Isra' Mi'raj 5.98 3.41 5 Idul Fitri 1.99 0.09 6 Tahun Baru _2.38 _0.07 7 Proklamasi 12.98 4.85 8 Wafat 2.01 2.19 9 Kenaikan _4.51 _0.77 10 Natal _4.01 _1.49 11 Imlek 2.01 1.07 12 Waisak 3.10 1.23 13 Nyepi _9.83 _4.02 Tertinggi 12.98 9.64 Terendah 1.99 0.07 Error Rata-rata _5.28 _2.49 0 2 4 6 8 10 12 14 16 18 20 0 2 4 6 8 10 12 14 16 18 20

Iterasi e rr o r

150.00

200.00

250.00

FLR-AIS (MW) Realisasi (MW)

Gambar 8. Kurva Hasil Ramalan dan Data Real Gambar 7. Grafik Konvergensi Tahun Baru

(27)

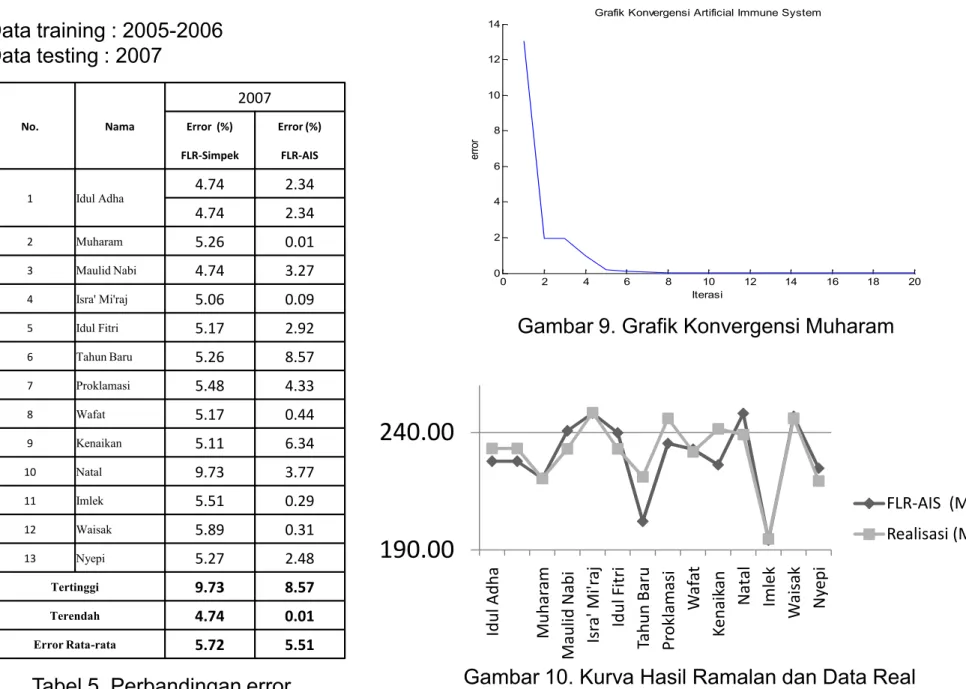
No. Nama 2007 Error (%) Error (%) FLR-Simpek FLR-AIS 1 Idul Adha 4.74 2.34 4.74 2.34 2 Muharam 5.26 0.01 3 Maulid Nabi 4.74 3.27 4 Isra' Mi'raj _5.06 _0.09 0 2 4 6 8 10 12 14 16 18 20 0 2 4 6 8 10 12 14 Iterasi er ro r Data training : 2005-2006 Data testing : 2007

Gambar 9. Grafik Konvergensi Muharam 5.06 0.09 5 Idul Fitri _5.17 _2.92 6 Tahun Baru 5.26 8.57 7 Proklamasi 5.48 4.33 8 Wafat 5.17 0.44 9 Kenaikan _5.11 _6.34 10 Natal _9.73 _3.77 11 Imlek 5.51 0.29 12 Waisak 5.89 0.31 13 Nyepi 5.27 2.48 Tertinggi 9.73 8.57 Terendah _4.74 _0.01 Error Rata-rata 5.72 5.51

190.00

240.00

Gambar 9. Grafik Konvergensi Muharam

(28)

HASIL DAN PEMBAHASAN

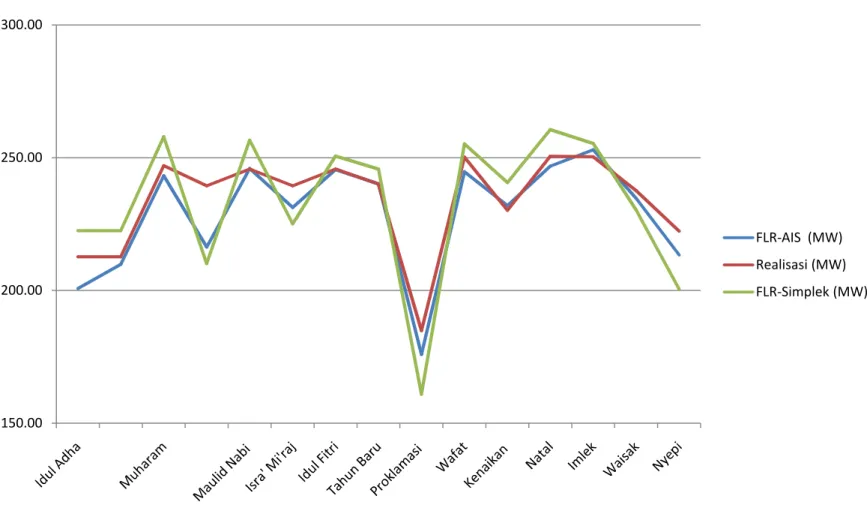
300.00

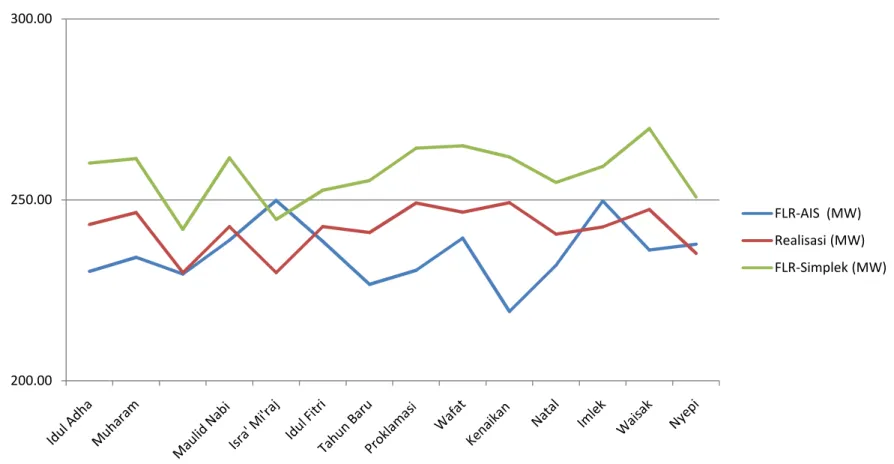
Grafik Perbandingan FLR-AIS, FLR-Simplek dan Realisasi Beban

Periode 2006-2009.

200.00 250.00 FLR-AIS (MW) Realisasi (MW) FLR-Simplek (MW)

(29)

Grafik Perbandingan FLR-AIS, FLR-Simplek dan Realisasi Beban

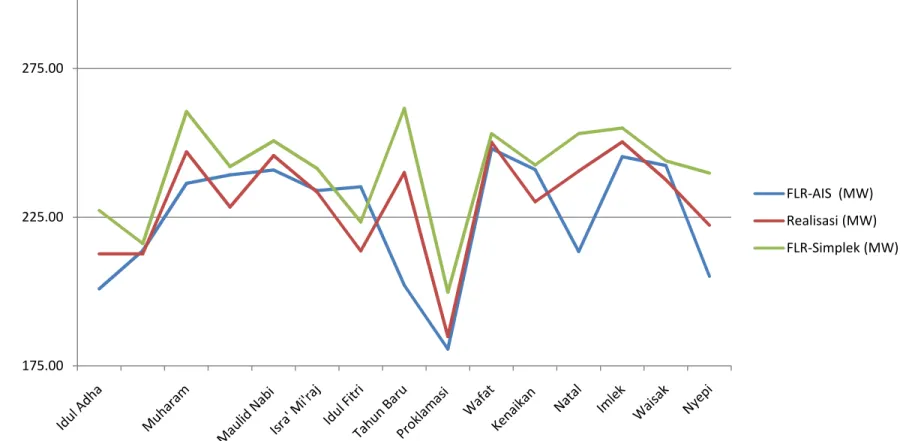
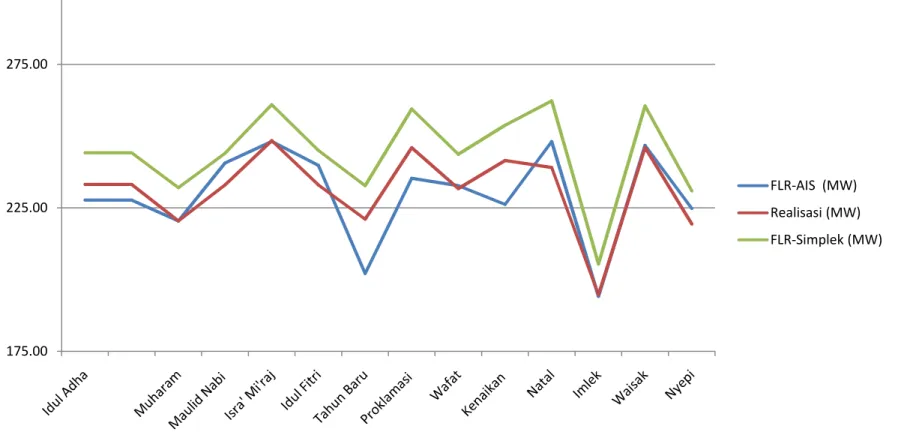
Periode 2005-2008.

275.00 175.00 225.00 FLR-AIS (MW) Realisasi (MW) FLR-Simplek (MW)

(30)

HASIL DAN PEMBAHASAN

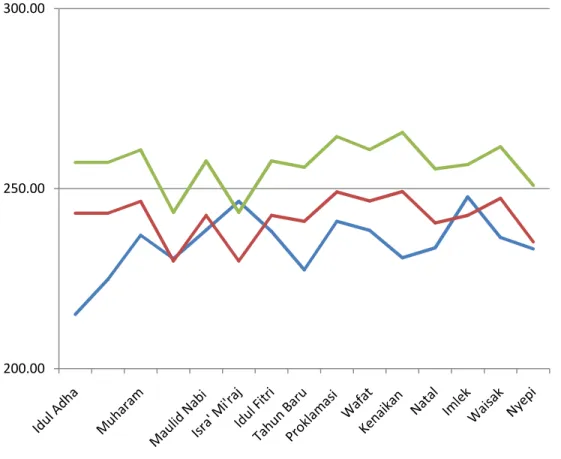
Grafik Perbandingan FLR-AIS, FLR-Simplek dan Realisasi Beban

Periode 2007-2009.

(31)

Grafik Perbandingan FLR-AIS, FLR-Simplek dan Realisasi Beban

Periode 2006-2008.

250.00 300.00 150.00 200.00 FLR-AIS (MW) Realisasi (MW) FLR-Simplek (MW)

(32)

HASIL DAN PEMBAHASAN

Grafik Perbandingan FLR-AIS, FLR-Simplek dan Realisasi Beban

Periode 2005-2007.

(33)

 AIS cocok digunakan sebagai metode optimisasi peramalan

beban karena menghasilkan error minimum.

 Kelebihan metode AIS dalam optimisasi adalah proses

pencariannya yang secara global pada proses training-nya.

 Peramalan dengan metode simplek, diperoleh rata-rata

error sebesar 5.64% (Sistem KalSel-Teng).

 Peramalan dengan metode FLR-AIS (CSA), diperoleh

rata-rata error sebesar 3.89% (Sistem KalSel-Teng).

KESIMPULAN

 AIS cocok digunakan sebagai metode optimisasi peramalan

beban karena menghasilkan error minimum.

 Kelebihan metode AIS dalam optimisasi adalah proses

pencariannya yang secara global pada proses training-nya.

 Peramalan dengan metode simplek, diperoleh rata-rata

error sebesar 5.64% (Sistem KalSel-Teng).

 Peramalan dengan metode FLR-AIS (CSA), diperoleh

rata-rata error sebesar 3.89% (Sistem KalSel-Teng).

SARAN



Dapat dikembangkan dengan metode lain, seperti FLR-PSO atau

SVR-AIS.

(34)

DAFTAR

PUSTAKA

[1] H. Tanaka, S. Uejima, and K. Asai,”Linear regression analysis with fuzzy model,” IEEE Trans. Syst. Man Cybern., vol.12, pp.1291-1294, Dec, 1982.

[2] H. Tanaka and J. Watada,”Possibilistic linear systems and their application to linear regression model,” Fuzzy Sets and Syst., vol.27, pp.275-289, 1988.

[3] J. Nazarko and W. Zalewski,” The fuzzy regression approach to peak load estimation in power distribution systems,” IEEE Trans. Power Syst., vol. 14, pp.809-814, Aug, 1999.

[4] _____,”An application of the fuzzy regression analysis to the electrical load estimation,” in Proc. 8th Mediterranean Electrotechnical Conf. MELECON’96—Industrial Application in Power System , Computer Science and telecommunications, Bari, Italy, May 1996, pp.1563-1566.

[5] Kyung-Bin Song et al, “Short-term load forecasting for the holidays Using Fuzzy Linear Regression Method,” IEEE Trans. Power Syst., vol. 20, pp.96-101, Feb, 2005.

[6] Timothy J Ross, “Fuzzy Logic with Engineering Appications”, McGraw-Hill, Singapore, 1997

[7] D. H. Hong et al.,”Fuzzy linear regression analysis for fuzzy input-output data using shape preserving operations,” Fuzzy Sets and Syst., vol.122, pp.513-526, Sept. 2001.

[8] Agus Dharma, Mauridhi Hery P, Imam Robandi,.“Peramalan Beban Jangka Pendek Untuk Hari-hari Libur Menggunakan Metode Fuzzy Linear Regression (Study Kasus di Pulau Bali)”, Seminar Teknik Elektro Universitas Negeri Surabaya, 2006. [9] De Castro, L. N. and Von Zuben, F. J, “Artificial Immune System: Part I – Basic Theory and Applications”, Technical Report

– RT DCA 01/99. 1999.

[10] Tonegawa, S. (1983), “Somatic Generation of Antibody Diversity”, Nature, 302, pp. 575-581.

[11] Tonegawa, S. (1985), “The Molecules of the Immune System”, Scientific American, 253(4), pp. 104-113.

[12] Janeway Jr, C. A. & P. Travers (1997), “Immunobiology The Immune System in Health and Disease”, Artes Médicas (in Portuguese), 2nd Ed.

[13] Perelson, A. S. & Weisbuch, G. (1997), “Immunology for Physicists”, Rev. of Modern Physics, 69(4), pp. 1219-1267.

[14] De Castro, L. N. and Von Zuben, F. J, “Learning and Optimization Using the Clonal Selection Principle’, IEEE Transaction on Evolutionary Computation, Vol.6, No. 3, pp. 239-251, 2002.