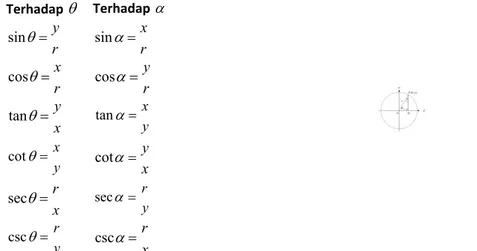Mat Persamaan Trigonometri (Modul)

(1)

1

_{Persamaan Trigonometri}

LC~2017/2018~XI IPA~Matematika Peminatan~Bab 1 LC~2017/2018~XI IPA~Matematika Peminatan~Bab 1

SMA Kolese Loyola SMA Kolese Loyola

Persamaan

Trigonometri

Matematika Peminatan XI IPA Matematika Peminatan XI IPA

Monica Sendi Afa

2017/2018 2017/2018 Nama: Nama: Kelas/No: Kelas/No:

(2)

A. Identitas Trigonometri

Perbandingan trigonometri untuk titik P ( x,y) pada lingkaran yang berpusat di O dengan jari-jari r adalah sebagai berikut.

Terhadap Terhadap r y



 sin r x



 sin r x



 cos r y



 cos x y



 tan y x   tan y x   cot x y



 cot x r



 sec y r   sec y r   csc x r



 csc

Gambar 1 Perbandingan Trigonometri

Dari rumus-rumus di atas, dapat diperoleh hal-hal berikut. I. Rumus-rumus Pasangan Sudut Komplemen

Jumlah sudut







90









90





 , maka r

x



  cos

sin atau sin



90



cos r

y



  sin

cos atau cos



90



sin

y x

    cot

tan atau tan



90



cot x

y



  tan

(3)

18

Persamaan Trigonometri

Latihan 1.B.3

Tentukan himpunan penyelesaian dari 1. cos xsin74 untuk 0x360. 2. sec csc58 untuk 0 360. 3. sin xsin37 untuk 0x360. 4. tan xtan55 untuk 0x360. 5. sin cos untuk 0 360. 6. sin



x60



cos2x untuk 0x360. 7. 6 csc sec x  untuk 0 x2 . 8. 3 2 1 sin x untuk 0x360. 9. 5 4 cos x untuk 0x360. 10.tan x 3 untuk 0x360. 11.4cos x30 untuk 0 x2 . 12.tan x30 untuk 0 x2 .

13.4sin2 7cos 7 untuk 0 360. 14.sin



 30



cos2 untuk 0 360.

15.6sin cos 3cos 4sin 2 untuk 0 360. 16.6sin x8cosx5 untuk 0x360.

17.10sin x24cosx13untuk . 18.14sin x



48cosx



25 2 untuk . 19.8sin x15cosx70 untuk . 20.12sin x





15cosx



10 3 untuk .







360 0 x     ₃₆₀ 0 x







360 0 x







360 0 x 3

Persamaan Trigonometri

y r     csc

sec atausec



90



csc x r



  sec csc atau csc



90



sec II. Rumus Hubungan Perbandingan

   cos sin tan



dan    sin cos cot



.

III. Rumus Hubungan Pythagoras 1

r y



sin atau y r sin r

x



cos atau x



r cos

Berdasarkan Teorema Pythagoras: 2 2 2

r y x





, maka



 

2



2 2 sin cos r r r    



2 2



2 2 sin cos r r







 

Jadi,cos2 _sin2 _1 

 .

IV. Rumus Hubungan Pythagoras 2 1

sin cos2 _ 2 _



 (kedua ruas dibagi dengan 2 cos )    2 2 2 cos 1 cos sin 1   2 2 cos 1 cos sin 1                  

   

2 2 sec tan 1    

Jadi,1tan2 sec2 .

V. Rumus Hubungan Pythagoras 3 1

sin cos2 _ 2 _



 (kedua ruas dibagi dengan 2 sin )    2 2 2 sin 1 1 sin cos _ _ 

(4)

2 2 sin 1 1 sin cos                  

 

2

 

2 csc 1 cot     Jadi, 2 2 csc 1 cot   .

VI. Rumus Hubungan Kebalikan

1 csc sin     y r r y    sin csc 1 atau   sin 1 csc



1 sec cos









x r r x 

  cos sec 1 atau

  cos 1 sec



1 cot tan     y x x y 

  tan cot 1 atau

 

tan 1 cot



Identitas trigonometri diatas digunakan untuk:

(i) Membuktikan identitas trigonometri yang lain, (ii) Menyelesaikan persamaan trigonometri. Perbandingan trigonometri sudut-sudut istimewa

Sudut istimewa



0 30



45



60



90



sin 0 2 1 2 2 1 3 2 1 1 cos 1 3 2 1 2 2 1 2 1 0 tan 0 3 3 1 1 3 tidak terdefinisi

Jadi, himpunan penyelesaiannya adalah



97,337



. Cara b: Diketahui 2 5 cos 4 sin

3 x



x



. Karena 3sin x4cos x5cos



x37



, maka diperoleh





2 5 37 cos 5 x   sehingga





2 1 37 cos x   .

Dengan demikian, untuk





2 1 37 cos x   , diperoleh



37



cos60 cos x maka  x3760k 360 sehingga x97k 360, atau  x3760k 360 sehingga x23k 360. Untuk k 0,       97 0 360 97 1 x          ₂₃ ₀ ₃₆₀ ₂₃ 2 x (tidak memenuhi0x360) Untuk k 1,       ₉₇ ₁ ₃₆₀ ₄₅₇ 3 x (tidak memenuhi 0x360)         ₂₃ ₁ ₃₆₀ ₃₃₇ 4 x

Jadi, himpunan penyelesaiannya adalah



97,337



. Latihan 1.B.4 (Boleh menggunakan kalkulator)

Tentukan himpunan penyelesaian dari 1. 5sin x12cosx4

(5)

16

Persamaan Trigonometri

Jawab

Diketahui asin xbcos x3sin x4cos x, maka didapat a3 dan b4 sehingga

_

2

_

2

_

32

_

42

_

9

_

16

_

25

_

5 b a r . a. Menurut Teorema 1, 3 4 tan



a b  sehingga          53 3 4 tan1  .

Karenaasin xbcos xr sin



x



, maka 3sin x4cos x5sin



x53



. b. Menurut Teorema 2, 4 3 tan



b a  sehingga          37 4 3 tan1  .

Karena asin xbcos xr cos



x 



, maka



 



 ₄_cos ₅_cos ₃₇ sin 3 x x x c. Cara a: Diketahui 2 5 cos 4 sin

3 x



x



. Karena 3sin x4cos x5sin



x53



, maka diperoleh





2 5 53 sin 5 x   sehingga





2 1 53 sin x   . Dengan demikian, untuk





2 1 53

sin x   , diperoleh sin x





53







sin30



maka  _x₅₃₃₀_k₃₆₀ sehingga x23k 360, atau  _x₅₃

_

₁₈₀₃₀

_

_k₃₆₀₁₅₀_k₃₆₀ sehingga     ₉₇ _k ₃₆₀ x . Untuk k 0,          23 0 360 23 1 x (tidak memenuhi0x360)       97 0 360 97 2 x Untuk k 1,         23 1 360 337 3 x       97 1360 457 4 x (tidak memenuhi 0x360) 5

Persamaan Trigonometri

Contoh 1.A.1 Buktikan bahwa 4 4 2 sin 2 1 sin cos    . Jawab

   

₂ 2 ₂ 2 4 4 sin cos sin cos       





         2 2 2 2 2 2 2 2 2 sin 2 1 sin sin 1 sin cos 1 sin cos sin cos                4 2 4 sin 2 1 sin cos     ∎ Latihan 1.A.1

Buktikan setiap identitas berikut.

1.



 



      cos sin 2 csc 90 sin sec 90 cos





_





_

(6)

Contoh 1.A.2

Jika

3 1

sin A



dan A pada kuadran kedua, tentukan cos Atanpa menggunakan kalkulator.

Jawab Cara I:

Berdasarkan gambar di atas, nilai sisi samping adalah 9



1



8



2 2. Karena nilai kosinus bernilai negatif pada kuadran kedua maka

2 3 2 3 2 2 cos A  Cara II:

Dengan menggunakan identitas trigonometri cos2 _sin2 _1 A A , maka 9 8 9 1 1 sin 1

cos2 A





2A







sehingga 2

3 2 9 8

cos A  . Karena A di kuadran 2, maka 2

3 2 cos A





.

(*) identitas jumlah sudut yang digunakan adalah





sin cos cos sin

sin x  x  x yang akan dipelajari di bab selanjutnya. Dengan demikian persamaan trigonometri asin xbcos xc dapat ditulis sebagai r sin



x



c dan diperoleh persamaan trigonometri





r c x







sin yang dapat diselesaikan dengan rumus persamaan dasar trigonometri yang telah dibahas sebelumnya. Catatan: Mengingat

a b





tan , maka sudut  dapat diperoleh dengan















 a b 1 tan  . Latihan 1.B.3

Buktikan Teorema 2 berikut:

Jika diberikan persamaan trigonometri asin xbcos xc dengan a ,,bc adalah bilangan real, maka asin xbcos xr cos



x 



, r



a2



b2, dan

b a





tan .

Hint: 1. bayangkan suatu titik dengan koordinat



a,b



pada bidang XY . 2. identitas selisih sudut yang digunakan adalah







cos cos sin sin

cos x  x  x yang akan dipelajari di bab selanjutnya.

Contoh 1.B.2

a. Nyatakan 3sin x4cos x dalam bentuk r sin



x





. b. Nyatakan 3sin x4cos x dalam bentuk r cos



x







. c. Tentukan himpunan penyelesaian dari

2 5 cos 4 sin 3 x



x



.

(7)

14

Persamaan Trigonometri

Teorema 1

Jika diberikan persamaan trigonometri asin xbcos xc dengan a ,,bc adalah bilangan real, maka persamaan tersebut dapat diselesaikan

dengan menggunakan 2 2

b a

r





, asin xbcos xr sin



x



, dan a b



 tan . Bukti

Bentuk asin xbcos x dapat ditulis ulang dalam bentuk yang lebih sederhana dengan menggunakan identitas jumlah dan selisih sudut (yang akan dipelajari di bab selanjutnya). Langkahnya adalah dengan mengubah a ke dalam bentuk yang memuat sin dan b ke dalam bentuk yang memuat cos . Selanjutnya dapat digunakan identitas penjumlahan. Hal ini dapat dilakukan dengan membayangkan suatu titik pada bidang XY dengan koordinat

 

a,b . Jika  adalah sudut yang menghubungkan titik

 

a,b dengan titik asal O

 

0,0 dan sumbu X , maka

2 2 cos b a a





 , 2 2 sin b a b





 , dan a b



 tan .

Selanjutnya, (dengan menggunakan identitas jumlah sudut) dapat dituliskan bahwa



















x b a b x b a a b a x b x

asin cos sin cos

2 2 2 2 2 2



x x



b

a2

_

2 cos

_

sin

_

sin

_

cos



 



sin cos cos sin



2 2

_

_

_

_



a b x x













a2 b2 sinx _(*)







 r sin x dengan 2 2 b a r   . 7

Persamaan Trigonometri

Latihan 1.A.2 Buktikan bahwa

1. cos 



1tan



cos sin 2. 4 2 4 2 cos cos sin sin    Latihan 1.A.3 Sederhanakan 1.     sin cos cos sin _ 2.   2 2 sin 1 tan 1  

Buktikan setiap identitas trigonometri berikut. 3. A A A A tan 1 cos cot sin 2   4. x x x 2 sec 2 sin 1 1 sin 1 1 _    5. B A B A B A ₂ ₂ 2 2 2 2 cos cos sin sin tan tan     B A 2 2 sec tan 2   6. 4 x 2 x



2 x



sin 1 cos sin 1







7.





    cos 1 cos 1 csc cot  2 _

8.



cos sin



2



cos sin



22

9. sec Atan



90 A



cscA 10. A A A A sin cos 1 cos 1 sin

_





(8)

B. Persamaan Trigonometri

Untuk menyelesaikan persamaan trigonometri sin x



sin , cos xcos , dan tan xtan untuk 0





x



360



, yang perlu diperhatikan adalah sebagai berikut.

(i) Tanda untuk fungsisin x, cos , dan x tan x pada tiap kuadran.

Gambar 2 Tanda Kuaradan

Kuadran I II III IV sin + + - -cos + - - + tan + - +

-(ii) Relasi kuadran

Kuadran II (90





x



180



)



180 



sin sin  



180 



cos cos  



180 



tan tan   Kuadran III (180





x



270



)



180 



sin sin  



180 



cos cos  



180 



tan tan   Kuadran IV (270





x



360



)



360 



sin sin  



360 



cos cos  



360 



tan tan  

Gambar 3 Relasi Kuadran

Latihan 1.B.2

Tentukan semua sudut yang memenuhi persamaan: 1. 3tan 5sin untuk 0 360.

2. 5cos2__3cos__2_0_untuk __ _ _

360

0  .

3. 2tan2__sec__1_0

(9)

12

Persamaan Trigonometri

Contoh 1.B.2

Tentukan himpunan penyelesaian persamaan tan x0,8391 untuk







₃₆₀ 0 x . (Hint: tan400,8391) Jawab

Periode untuk fungsi ytan x adalah180



atau  sehingga untuk

 tan

tan x



, maka x 





k



180



atau x





k



 .

Dengan demikian, untuk tan x0,8391, diperoleh tan x



tan40



maka











₄₀ _k₁₈₀ x . Untuk k



0, x140018040. Untuk k



1, x2401180220.

Untuk k



2, x1402180400 tidak memenuhi 0





x



360



) Jadi, himpunan penyelesaiannya adalah



40, 220



.

Rumus Persamaan Dasar Trigonometri

 sin

sin x





x 





k



360



atau



180



k 360 untuk k 0,1,2,



. 

cos

cos x  x k 360 atau  k 360 untuk k 0,1,2,.

 tan

tan x  x k 180atau x k  untuk k 0,1,2,.

Strategi Penyelesaian Persamaan Trigonometri 1. Membuat ruas kanan sama dengan nol

2. Memfaktorkan ruas kiri dengan mengeluarkan faktor yang sama 3. Menggunakan aturan hasil kali nol faktor-faktor

4. Menyelesaikan persamaan trigonometri dasar yang diperoleh 5. Menentukan semua solusi dalam selang interval yang diberikan

9

Persamaan Trigonometri

(iii) Dua segitiga istimewa

Gambar 4 Dua Segitiga Istimewa

Menyelesaikan persamaan trigonometri berarti menentukan sudut x yang memenuhi persamaan tersebut.

Contoh 1.B.1

Tentukan himpunan penyelesaian dari

2 1

sin x untuk 0





x



360



. Jawab

Cara I:

Nilai x yang dimaksud dapat dijawab dengan menggunakan grafik fungsi trigonometri.

Berikut ini gambar grafik fungsi y sin x dan 2 1



(10)

Kedua kurva berpotongan di titik       _ 2 1 , 30 A dan       _ 2 1 , 150 B .

Jadi, nilai x yang memenuhi persamaan

2 1

sin x adalah x



30



dan





150

x atau himpunan penyelesaiannya adalah



30,150



. Cara II:

Periode ysin x adalah360 atau



2 .





 sin180 sin



  



sin k 360

sehingga untuksin x



sin maka x 





k



360



atau



180



k 360

untuk k 0,1,2,



. Dalam satuan radian,

Jika sin x



sin maka x





k



2 atau



 



k 2 untuk k 0,1,2,



. Dengan demikian, untuk

2 1

sin x , diperolehsin x



sin30



maka

 x



30





k



360



, atau  x

_

18030

_

k 360150k 360 Untuk k



0,       30 0 360 30 1 x       150 0 360 150 2 x Untukk



1,















30 1360 390 3 x (tidak memenuhi 0





x



360



)       ₁₅₀ ₁ ₃₆₀ ₅₁₀ 4 x (tidak memenuhi 0





x



360



) Jadi, himpunan penyelesaiannya adalah



30,150



.

Latihan 1.B.1

Tentukan himpunan penyelesaian persamaan 2 2 1 cos x untuk







₃₆₀ 0 x .