i
RUANG VEKTOR EUCLIDES KABUR
Skripsi
Diajukan untuk Memenuhi Salah Satu Syarat Memperoleh Gelar Sarjana Matematika
Oleh:
Yulius Nuky Canny Widargo NIM: 173114049
PROGRAM STUDI MATEMATIKA JURUSAN MATEMATIKA FAKULTAS SAINS DAN TEKNOLOGI
UNIVERSITAS SANATA DHARMA YOGYAKARTA
2021
SKruPSI
RT}ANS
YEKT{}R
EUCLItrES KABUROleh"
Yulius }.{uky Cann3, Widarga }r{IM: 1731 14049
ii
ririftrFsI
ffi[gerff ffi ffixjffiffi,ffi,Hf,Affi[$ffi
ffifp*rs{mp@m * dm d*t*l*x *[eh:
h{$,Fd; $?#$ *4#4S
I t lul,ri :*? [
["it*tjm -ta*sa;t
"f".elalt
*{;:ru-r"tae*r*srkam r$i d*pa*r []a*xx*t*m $]*r:6ari*
.,.t. ,, :i I i,I :
1:1.,i' :{1";r1;..' ::r-
PERNYATAAN KEASLIAN KARYA
Saya menyatakan dengan sesungguhnya bahwa skripsi yang saya tulis ini tidak memuat karya atau bagian karya orang lain, kecuali yang telah disebutkan dalam kutipan atau daftar pustaka, sebagaiman a layahayakarya ilmiah.
Yogyakarta,Z0 Mei 2021 Penulis,
Yulius ir{uky Canny Widargo
iv
.
LEMBARPERNYATAAN PERSETUJUANPUBLIKASI KARYA ILMIAH UNTUK KEPENTINGAN AKADEMIS
Yang bertanda tangan di bawah ini, saya mahasiswa Universitas Sanata Dharma:
Nama
: Yulius Nuky Canny V/idargoNIM
:173114049Demi pengembangan ilmu pengetahuan, saya memberikan kepada Perpustakaan Universitas Sanata Dharma kuryailmiah saya yang berjudul:
RUANG VEI(IOR EUCLIDES KABUR
beserta perangkat yang diperlukan (bila ada). Dengan demikian saya inemberikan
keppda Perpustakaan Universitas Sanata Dharma
hak
untuk 'menyimpan, mengalihkan rlalam bentuk media lain, mengolahnya dalam bentuk pangkalan rlata, mendiskibusikan secara teraatas, dan mernpublikasikannya di'Internet atau"n'riia lain ,rnfuk kepentingan akademis tanpa perlu r-eminta izin dari saya maupun memberikan royalti kepada saya selama tetap mencantumkan nama saya sebagai penulis.
Demikian pernyataan ini saya buat dengan sebenarnya.
Dibuat di Yogyakarta Pada tangg al: 20 Mei 2021
Yang menyataken
Yulius h{uky Canny Widargo
v
vi
ABSTRAK
Ruang vektor merupakan suatu struktur aljabar pada himpunan yang dilengkapi dengan dua operasi, yaitu operasi penjumlahan dan operasi perkalian dengan skalar. Suatu himpunan yang dilengkapi dengan dua operasi tersebut dinamakan ruang vektor apabila memenuhi beberapa aksioma. Kemudian, bilangan kabur adalah himpunan kabur dalam semesta real yang memenuhi beberapa sifat tertentu. Semua himpunan kabur dalam semesta real yang dinyatakan dengan fungsi keanggotaan segitiga merupakan bilangan kabur.
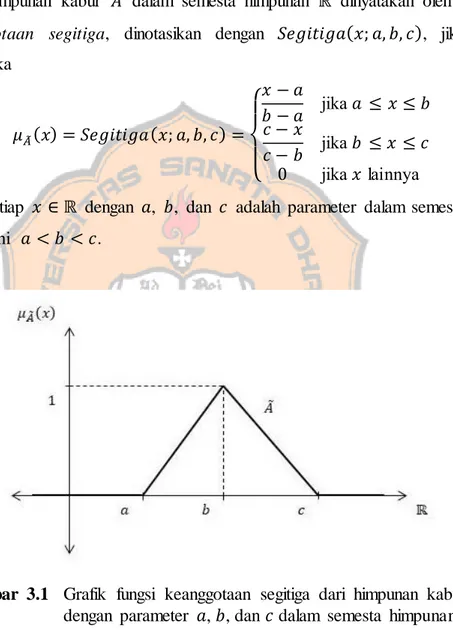
Himpunan adalah himpunan bilangan-bilangan kabur yang dinyatakan dengan fungsi keanggotaan segitiga dengan suatu parameter .
Himpunan merupakan ruang vektor. Himpunan dapat dimodifikasi menjadi suatu himpunan baru dengan menyubstitusi setiap komponen vektor di dengan bilangan kabur di . Himpunan tersebut dinamakan himpunan Euclides kabur. Himpunan Euclides kabur yang dilengkapi dengan operasi penjumlahan dan operasi perkalian dengan skalar, yang didefinisikan secara khusus, memenuhi semua aksioma ruang vektor. Dengan demikian, himpunan Euclides kabur merupakan ruang vektor sehingga semua sifat ruang vektor berlaku pada ruang vektor Euclides kabur. Akibatnya, dapat diselidiki pula konsep-konsep terkait dari ruang vektor pada ruang vektor Euclides kabur seperti konsep basis, perkalian-dalam, transformasi linear, dan sebagainya. Selain itu, himpunan dapat pula dimodifikasi dengan cara lain, seperti menyubstitusi komponen vektornya dengan bilangan kabur yang menggunakan fungsi keanggotaan yang berbeda (bukan fungsi keanggotaan segitiga).
Kata kunci: Ruang vektor, himpunan Euclides kabur, bilangan kabur.
vii
ABSTRACT
Vector space is an algebra structure on a set with two operations, addition and scalar multiplication. A nonempty set on which those operations are defined is called vector space if it satisfies some particular axioms. Meanwhile, fuzzy number is fuzzy set that is defined on the set of real numbers and satisfies some certain properties. Every fuzzy set that is defined on the set of real numbers is fuzzy number if it uses the triangular membership function. The set of fuzzy numbers that use the triangular membership functions with parameter is notated by .
The set is a vector space. However, it can be modified through substitution of every vector component in it by fuzzy number in . The set is then called fuzzy Euclidean set. Specific addition and scalar multiplication are defined on the set afterward. It turns out to satisfy all vector space axioms. Thus, fuzzy Euclidean set is a vector space and also satisfies every vector space property. As a result, any concepts within the scope of vector space can also be investigated on fuzzy Euclidean vector space, such as: basis, inner-product, linear transformation, and so on. Furthermore, the set can also be modified on many different ways. As an example, every vector component can be substituted with fuzzy number that uses membership function aside from triangular membership function.
Keywords: Vector space, fuzzy Euclidean set, fuzzy number.
viii
KATA PENGANTAR
“RUANG VEKTOR EUCLIDES KABUR” adalah karya ilmiah (skripsi) yang penulis susun sebagai salah satu syarat untuk memperoleh gelar sarjana di Universitas Sanata Dharma. Di dalamnya, penulis meneliti dan memaparkan struktur aljabar suatu himpunan yang memuat unsur-unsur bilangan kabur.
Struktur aljabar yang dimaksud adalah struktur ruang vektor. Dengan kata lain, skripsi ini membahas salah satu contoh ruang vektor dari himpunan yang dilengkapi dengan operasi-operasi yang tidak biasa.
Dalam proses pengerjaan skripsi ini, penulis kerap kali menemui kesulitan.
Terlebih, skripsi ini penulis kerjakan dalam masa pandemi Covid-19 sehingga penulis harus mengerjakan skripsi ini dalam kondisi yang tidak biasa. Untungnya, penulis telah dibantu dan didukung oleh banyak pihak. Oleh karena itu, penulis hendak mengucapkan terima kasih yang sebesar-besarnya kepada:
1. Tuhan Yesus Kristus sang Penyelenggara Kehidupan dan Juru Selamat.
2. Prof. Dr. Frans Susilo, SJ, selaku dosen pembimbing skripsi yang dengan sabar dan penuh integritas membimbing penulis untuk menyelesaikan skripsi ini dengan baik.
3. Ibu Maria Vianney Any Herawati, S.Si., M.Si. dan Bapak Dr. rer. nat. Herry Pribawanto Suryawan, selaku dosen penguji skripsi atas masukan-
masukannya terhadap skripsi ini.
4. Bapak Sudi Mungkasi, Ph.D., selaku Dekan Fakultas Sains dan Teknologi.
5. Bapak Hartono, Ph.D., selaku Kaprodi Matematika sekaligus dosen pembimbing akademik yang setia membimbing proses akademis penulis.
6. Bapak/Ibu dosen/karyawan yang telah mengajar, mendidik, membantu, dan mendampingi penulis selama proses belajar di Universitas Sanata Dharma.
7. Bapak dan Ibu di rumah atas segala kasih dan cintanya, yang selalu sabar mendukung dan mendoakan penulis.
8. Seluruh anggota keluarga yang selalu mendukung dan mendoakan penulis.
9. Yoseph Wastu Winayaka, selaku sahabat dalam perjalanan dan berdiskusi.
10. Teman-teman dan semua orang yang telah membantu, mendukung, dan mendoakan penulis, yang tidak dapat penulis sebutkan satu persatu.
Penulis menyadari bahwa masih banyak kekurangan dari penulis dan dari
skripsi yang telah penulis kerjakan
ini.
Maka, dengan senang hati penulis menerima dan mengharapkan kritik serta masukan yang dapat membuat pribadi penulis ataupun skripsi ini menjadi lebih baik lagi. Selain itu, penulis berharapskripsi
ini
dapat bermanfaat bagi para pembaca, baik sebagai media belajar, maupun sebagai referensi penelitian berikutnya.Yogyakarta,ZO Mei 2A21 Penulis,
Yulius ].{uky Canny Widargo
ix
x
DAFTAR ISI
HALAMAN JUDUL ... i
HALAMAN PERSETUJUAN PEMBIMBING ... ii
HALAMAN PENGESAHAN ... iii
PERNYATAAN KEASLIAN KARYA ... iv
LEMBAR PERNYATAAN PERSETUJUAN PUBLIKASI ... v
ABSTRAK ... vi
ABSTRACT ... vii
KATA PENGANTAR ... viii
DAFTAR ISI ... x
DAFTAR GAMBAR ... xii
BAB I PENDAHULUAN ... 1
A. Latar Belakang ... 1
B. Rumusan Masalah ... 3
C. Batasan Masalah ... 3
D. Tujuan Penulisan ... 3
E. Manfaat Penulisan ... 3
F. Metode Penelitian ... 3
G. Sistematika Penulisan ... 4
BAB II RUANG VEKTOR DAN SISTEM BILANGAN REAL ... 6
A. Ruang Vektor ... 6
B. Ruang Vektor dan ... 9
C. Sistem Bilangan Real ... 20
BAB III HIMPUNAN KABUR ... 41
A. Himpunan Kabur ... 41
B. Bilangan Kabur ... 59
BAB IV RUANG VEKTOR EUCLIDES KABUR ... 95
A. Himpunan Euclides Kabur ... 95
B. Operasi Penjumlahan dan Perkalian Dengan Skalar pada Himpunan Euclides Kabur ... 99
xi
C. Ruang Vektor Euclides Kabur ... 103
BAB V KESIMPULAN DAN SARAN ... 115
A. Kesimpulan ... 115
B. Saran ... 115
DAFTAR PUSTAKA ... 116
xii
DAFTAR GAMBAR
Gambar 2.1 ... 6
Gambar 2.2 ... 30
Gambar 2.3 ... 40
Gambar 3.1 ... 46
Gambar 3.2 ... 57
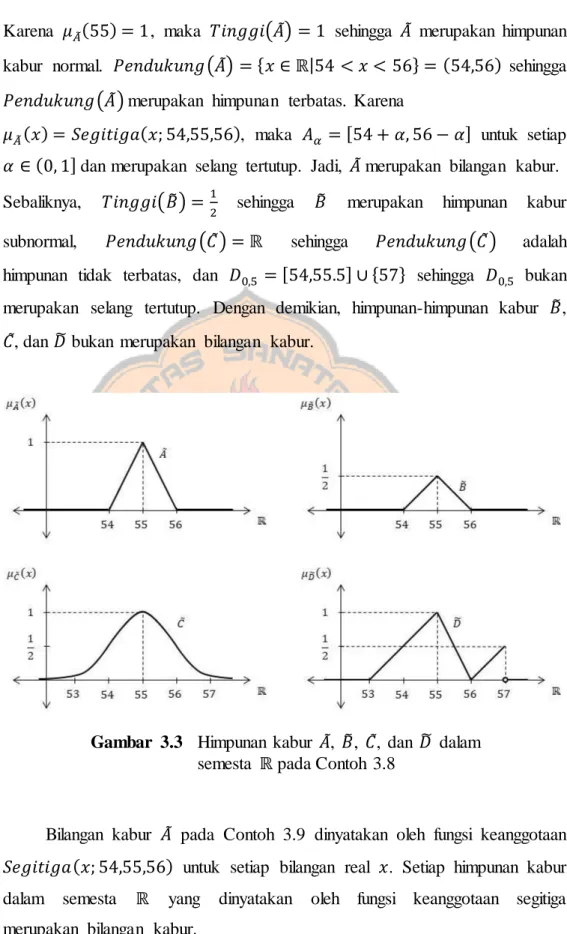
Gambar 3.3 ... 61
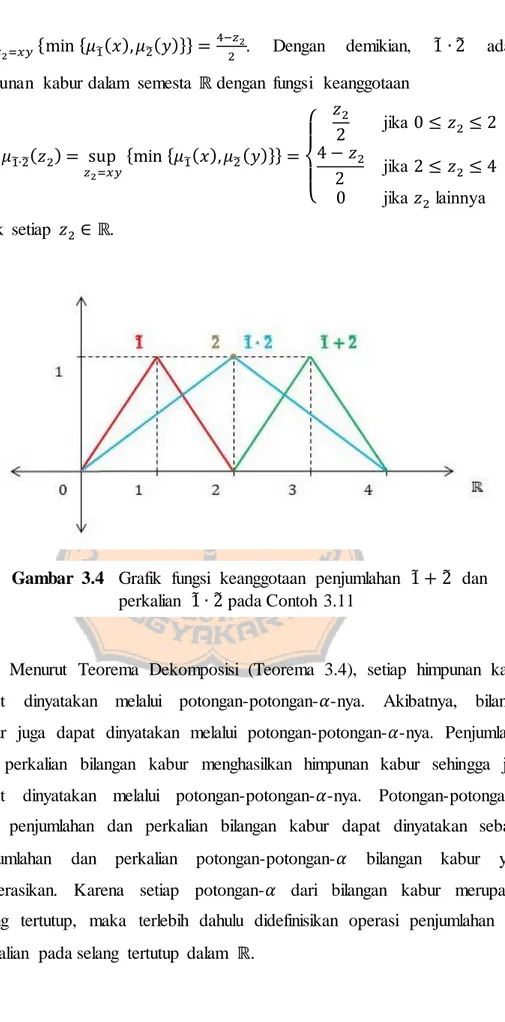
Gambar 3.4 ... 66
Gambar 4.1 ... 96
Gambar 4.2 ... 97
BAB I
PENDAHULUAN
A. Latar Belakang
Ruang vektor merupakan konsep yang diperoleh dari perluasan ilmu geometri, khususnya vektor di bidang dan di ruang. Definisi ruang vektor pertama kali dikemukakan oleh Peano pada tahun 1888 ketika ia mendefinisikan ruang vektor atas lapangan bilangan real, yaitu sebagai suatu himpunan vektor dengan kombinasi aturan-aturan terhadap vektor dan skalar.
Pada masa kini, kita memperoleh definisi ruang vektor secara lebih umum, yaitu sebagai berikut:
Misalkan himpunan tak kosong serta didefinisikan dua operasi pada himpunan tersebut, penjumlahan ( ) dan perkalian dengan skalar ( ).
Himpunan disebut ruang vektor jika untuk setiap ̅ ̅ ̅ dan untuk setiap skalar berlaku:
1. ̅ ̅ ̅ ̅.
2. ̅ ( ̅ ̅) ( ̅ ̅) ̅ .
3. Terdapat ̅ sedemikian sehingga untuk setiap ̅ berlaku ̅ ̅ ̅ ̅ ̅.
4. Untuk setiap ̅ terdapat ̅ sedemikian sehingga ̅ ̅ ̅ ̅ ̅.
5. ( ̅ ̅) ̅ ̅.
6. ( ) ̅ ̅ ̅.
7. ( ̅) ( ) ̅.
8. ̅ ̅.
Dari definisi ruang vektor tersebut, telah diperoleh bahwa bukan hanya ruang berdimensi dari bilangan real ( ) saja yang dapat membentuk ruang vektor, melainkan juga himpunan-himpunan lain seperti himpunan matriks dan himpunan fungsi.
Kemudian, teori kabur merupakan ilmu yang relatif baru dalam dunia matematika. Teori kabur diperkenalkan pertama kali pada tahun 1965 oleh Lotfi Aliasker Zadeh. Teori kabur merupakan ilmu yang mempelajari tentang kekaburan semantik pada istilah-istilah yang digunakan dalam kehidupan sehari-hari serta berusaha menangkap dan memberi arti dari istilah tersebut.
Dalam teori kabur, pertama-tama diperkenalkan konsep tentang himpunan kabur yang merupakan perluasan dari himpunan tegas. Apabila himpunan tegas yang dikenal selama ini menyatakan secara pasti keanggotaan dari setiap elemen himpunan semesta, lain halnya dengan himpunan kabur yang menyatakan keanggotaan setiap elemen himpunan semesta melalui derajat keanggotaan. Derajat keanggotaan suatu elemen dalam himpunan kabur merupakan nilai dari fungsi keanggotaan yang dikaitkan dengan himpunan kabur tersebut. Himpunan tegas hanya memiliki dua nilai fungsi keanggotaan, yaitu anggota atau bukan anggota, sedangkan himpunan kabur bisa memiliki tak hingga banyak nilai fungsi keanggotaan.
Teori kabur terus mengalami perkembangan hingga memunculkan konsep bilangan kabur. Konsep bilangan kabur tidak sama dengan konsep bilangan yang sudah dikenal secara umum seperti bilangan asli, bilangan bulat, atau bilangan real. Pada dasarnya, bilangan kabur merupakan suatu himpunan kabur. Bilangan kabur didefinisikan sebagai berikut:
Bilangan kabur adalah himpunan kabur dalam semesta himpunan semua bilangan real yang memenuhi tiga sifat berikut:
1. Normal.
2. Mempunyai pendukung yang terbatas.
3. Semua potongan- -nya adalah selang tertutup dalam .
Berdasarkan fakta-fakta pengetahuan tersebut, hendak dibangun suatu himpunan yang beranggotakan vektor-vektor seperti pada , namun memiliki komponen berupa bilangan-bilangan kabur. Himpunan tersebut kemudian dinamakan himpunan Euclides kabur. Didefinisikan pula operasi penjumlahan dan perkalian dengan skalar pada himpunan tersebut. Menarik
untuk diselidiki apakah himpunan dengan operasi penjumlahan dan perkalian dengan skalar tersebut membentuk ruang vektor atau tidak.
B. Rumusan Masalah
Permasalahan yang akan dibahas di dalam skripsi adalah:
1. Bagaimana membentuk himpunan Euclides kabur?
2. Bagaimana mendefinisikan operasi penjumlahan dan operasi perkalian dengan skalar pada himpunan Euclides kabur?
3. Apakah himpunan Euclides kabur yang dilengkapi dengan operasi penjumlahan dan perkalian dengan skalar membentuk suatu ruang vektor?
C. Batasan Masalah
Bilangan kabur yang digunakan dalam skripsi ini adalah bilangan kabur segitiga. Operasi perkalian dengan skalar yang digunakan adalah perkalian dengan skalar bilangan real.
D. Tujuan Penulisan
Tujuan penulisan skripsi ini adalah untuk mengetahui keterbentukan ruang vektor pada himpunan Euclides kabur dengan operasi penjumlahan dan perkalian dengan skalar.
E. Manfaat Penulisan
Manfaat yang diperoleh dari skripsi ini adalah mengetahui apakah himpunan Euclides kabur dengan operasi penjumlahan dan perkalian dengan skalar membentuk ruang vektor atau tidak.
F. Metode Penelitian
Metode penelitian yang digunakan untuk menulis skripsi ini adalah metode studi pustaka, yaitu dengan membaca literatur-literatur yang berkaitan
dengan konsep ruang vektor dan teori kabur serta literatur lain yang mendukung.
G. Sistematika Penulisan
Sistematika penulisan skripsi ini adalah sebagai berikut:
BAB I PENDAHULUAN A. Latar Belakang B. Rumusan Masalah C. Batasan Masalah D. Tujuan Penulisan E. Manfaat Penulisan F. Metode Penelitian G. Sistematika Penulisan
BAB II RUANG VEKTOR DAN SISTEM BILANGAN REAL A. Ruang Vektor
B. Ruang Vektor dan C. Sistem Bilangan Real
BAB III HIMPUNAN KABUR A. Himpunan Kabur
B. Bilangan Kabur
BAB IV RUANG VEKTOR EUCLIDES KABUR A. Himpunan Euclides Kabur
B. Operasi Penjumlahan dan Perkalian Dengan Skalar pada Himpunan Euclides Kabur
C. Ruang Vektor Euclides Kabur
BAB V KESIMPULAN DAN SARAN A. Kesimpulan
B. Saran
DAFTAR PUSTAKA
BAB II
RUANG VEKTOR DAN SISTEM BILANGAN REAL
A. Ruang Vektor
Secara sederhana, bilangan real adalah bilangan yang dapat dituliskan dalam bentuk desimal. Himpunan semua bilangan real biasa dinotasikan dengan lambang . Representasi geometris dari adalah berupa garis, yang dinamakan garis bilangan real, dengan setiap titik pada garis tersebut mewakili bilangan real tertentu. Bilangan real yang lebih besar diwakili oleh titik yang terletak di sebelah kanan titik bilangan real lain yang lebih kecil.
Bilangan real yang diwakili oleh titik yang terletak di sebelah kanan titik yang mewakili bilangan real disebut bilangan real positif. Sebaliknya, bilangan real yang diwakili oleh titik yang terletak di sebelah kiri titik yang mewakili bilangan real disebut bilangan real negatif. Beberapa contoh bilangan real adalah sebagai berikut:
merupakan bilangan real positif.
merupakan bilangan real negatif.
merupakan bilangan real positif.
√ merupakan bilangan real negatif.
Sebuah bilangan real dapat dijumlahkan dan dikalikan dengan bilangan real lainnya. Penjumlahan dilambangkan dengan tanda , sementara perkalian dilambangkan dengan tanda . Penjumlahan dan perkalian dua bilangan real dan berturut-turut ditulis dengan dan . Terdapat beberapa sifat aljabar yang berkaitan dengan penjumlahan dan perkalian
Gambar 2.1 Garis bilangan real
tersebut. Sebelum memaparkannya, terlebih dahulu diberikan beberapa definisi berikut.
Definisi 2.1.1
Diberikan dua himpunan tak kosong dan . Darab Cartesius dari himpunan dan , dinotasikan dengan , adalah himpunan semua pasangan terurut ( ) dengan dan , yaitu
*( )| +.
Contoh 2.1
Jika * + dan { √ }, maka
{( √ ) ( ) ( √ ) ( ) ( √ ) ( )} dan {( √ ) ( √ ) ( √ ) ( ) ( ) ( )}.
Definisi 2.1.2
Diberikan himpunan dan . Fungsi dari ke adalah himpunan dari pasangan terurut di dalam sedemikian sehingga untuk setiap terdapat dengan tunggal dengan ( ) , dinotasikan dengan
.
Dengan kata lain, jika ( ) dan ( ) , maka . Jika ( ) , maka biasanya ditulis ( ) atau .
Contoh 2.2
Jika himpunan dan seperti pada Contoh 2.1, maka {( √ ) ( √ ) ( √ )}
adalah fungsi dari ke dengan ( ) √ untuk setiap , sedangkan
{( √ ) ( ) ( √ ) ( )} dan {( √ ) ( )}
bukanlah fungsi dari ke karena ( ) tidak tunggal dan ( ) tidak terdefinisi.
Definisi 2.1.3
Diberikan himpunan tak kosong . Operasi biner pada adalah fungsi dari ke .
Definisi 2.1.3 menunjukkan bahwa:
i. Untuk setiap pasangan ( ) , ( ) terdefinisi secara tunggal (dari Definisi 2.1.2).
ii. Untuk setiap pasangan ( ) , ( ) adalah anggota dari (sifat tertutup).
Penamaan operasi biner diberikan karena anggota dari domain fungsinya merupakan pasangan terurut. Secara umum, operasi biner adalah fungsi dari darab Cartesius dua himpunan yang tidak harus sama. Untuk selanjutnya, operasi biner disebut operasi saja.
Salah satu contoh operasi adalah penjumlahan pada himpunan semua bilangan asli . Sebaliknya, pembagian bukan merupakan operasi pada . Penjumlahan dan perkalian juga merupakan operasi pada , yaitu
dan ,
atau biasa ditulis dan dengan ( ) dan . Dengan demikian, berlaku sifat tertutup pada kedua operasi tersebut, yakni untuk setiap berlaku dan . Selain itu, kedua operasi tersebut juga memenuhi sifat-sifat yang disebut sifat aljabar pada .
Sifat Aljabar pada
i. untuk setiap . (sifat komutatif penjumlahan) ii. ( ) ( ) untuk setiap .
(sifat asosiatif penjumlahan)
iii. Terdapat sedemikian sehingga dan untuk
setiap . (eksistensi elemen netral
terhadap penjumlahan) iv. Untuk setiap terdapat sedemikian sehingga
( ) dan ( ) . (eksistensi elemen negatif) v. untuk setiap . (sifat komutatif perkalian) vi. ( ) ( ) untuk setiap .
(sifat asosiatif perkalian) vii. Terdapat dengan sedemikian sehingga dan
untuk setiap . (eksistensi elemen netral terhadap perkalian)
viii. Untuk setiap dengan terdapat sedemikian sehingga dan . (eksistensi elemen kebalikan) ix. ( ) ( ) ( ) dan ( ) ( ) ( )
untuk setiap . (sifat distributif perkalian terhadap penjumlahan)
B. Ruang Vektor dan
Dengan memperluas gagasan himpunan yang direpresentasikan oleh garis menjadi himpunan-himpunan yang direpresentasikan oleh bidang, ruang, dan seterusnya, didefinisikan himpunan berikut.
Definisi 2.2.1
Rangkap bilangan real terurut adalah barisan dari bilangan real ( ) dengan merupakan bilangan bulat positif. Himpunan semua rangkap bilangan real terurut disebut ruang dan dilambangkan dengan
.
Anggota dari disebut titik atau vektor yang biasa ditulis mengguna- kan huruf kecil dengan garis di atasnya.
Definisi 2.2.2
Vektor ̅ di adalah rangkap bilangan real terurut ( ), ditulis
̅ ( ) atau ̅ [ ],
dengan , , ..., disebut komponen dari vektor ̅.
Untuk setiap * +, disebut sebagai komponen ke- dari vektor ̅. Jika seluruh komponennya adalah , maka vektor ̅ ( ) disebut vektor nol dan ditulis ̅.
Definisi 2.2.3
Vektor ̅ ( ) dan ̅ ( ) di dikatakan sama, ditulis ̅ ̅, jika dan hanya jika untuk setiap * +.
Anggota-anggota dapat saling dijumlahkan dan dapat dikalikan dengan skalar bilangan real. Penjumlahan dan perkalian skalar pada didefinisikan sebagai berikut.
Definisi 2.2.4
Diberikan vektor ̅ ( ) dan ̅ ( ) di serta bilangan real . Didefinisikan penjumlahan dan perkalian skalar vektor berturut-turut sebagai berikut:
i. ̅ ̅ ( ).
ii. ̅ ( ).
Contoh 2.3
Jika ̅ ̅ dengan ̅ ( ) dan ̅ ( ), maka ̅ ̅ (( ) ( ) ) ( ) dan
̅ ( ( ) ) ( ) sehingga ̅ ̅ ̅.
Berdasarkan definisi-definisi tersebut, diperoleh teorema sebagai berikut.
Teorema 2.1
Jika ̅ ̅ ̅ dan , maka:
i. ̅ ̅ ̅ ̅. (sifat komutatif penjumlahan) ii. ̅ ( ̅ ̅) ( ̅ ̅) ̅ . (sifat asosiatif penjumlahan) iii. ̅ ̅ ̅ ̅ ̅. (eksistensi elemen nol)
iv. Terdapat ̅ sedemikian sehingga ̅ ( ̅) ( ̅) ̅ ̅.
(eksistensi elemen invers penjumlahan untuk setiap elemen dalam ) v. ( ̅ ̅) ̅ ̅. (sifat distributif)
vi. ( ) ̅ ̅ ̅.
vii. ( ̅) ( ) ̅.
viii. ̅ ̅.
Bukti:
Ambil sebarang ̅ ̅ ̅ dan dengan ̅ ( ), ̅ ( ), dan ̅ ( ).
i. ̅ ̅ ( ) (Definisi 2.2.4 butir (i)) ( ) (sifat komutatif penjumlahan
pada )
̅ ̅. (Definisi 2.2.4 butir (i)) Jadi, terbukti ̅ ̅ ̅ ̅.
ii. ̅ ( ̅ ̅) ( ( ) ( )
( )) (Definisi 2.2.4 butir (i)) (( ) ( ) ( )
) (sifat asosiatif penjumlahan
pada )
( ̅ ̅) ̅ . (Definisi 2.2.4 butir (i)) Jadi, terbukti ̅ ( ̅ ̅) ( ̅ ̅) ̅.
iii. ̅ ̅ ( ) (Definisi 2.2.4 butir (i))
( ) (sifat eksistensi elemen netral terhadap penjumlahan pada ) ̅.
Menurut Teorema 2.1 butir (i), ̅ ̅ ̅ ̅.
Jadi, terbukti ̅ ̅ ̅ ̅ ̅.
iv. Dipilih ̅ dengan ̅ ( ) ̅
(( ) ( ) ( ) ) (Definisi 2.2.4 butir (ii)) ( ).
Karena untuk setiap * + berlaku (Definisi 2.2.2), maka sehingga ̅ . Dengan demikian,
̅ ( ̅) ( ( ) ( ) ( )) (Definisi 2.2.4 butir (i))
( ) (sifat eksistensi elemen negatif pada ) ̅.
Menurut Teorema 2.1 butir (i), ̅ ( ̅) ( ̅) ̅. Jadi, terbukti terdapat ̅ sedemikian sehingga ̅ ( ̅) ( ̅) ̅ ̅.
v. ( ̅ ̅) ( ( ) ( ) ( ))
(Definisi 2.2.4 butir (i) dan (ii)) (( ) ( ) ( ) ( ) ( )
( )) (sifat distributif perkalian terhadap penjumlahan pada )
( ) ( ) (Definisi 2.2.4 butir (i)) ̅ ̅. (Definisi 2.2.4 butir (ii)) Jadi, terbukti ( ̅ ̅) ̅ ̅.
vi. ( ) ̅ (( ) ( ) ( ) ) (Definisi 2.2.4 butir (ii)) (( ) ( ) ( ) ( ) ( )
( )) (sifat distributif perkalian terhadap penjumlahan pada )
( ) ( ) (Definisi 2.2.4 butir (i)) ̅ ̅. (Definisi 2.2.4 butir (ii)) Jadi, terbukti ( ) ̅ ̅ ̅.
vii. ( ̅) ( ( ) ( ) ( ))
(Definisi 2.2.4 butir (ii)) (( ) ( ) ( ) )
(sifat asosiatif perkalian pada ) ( ) ̅. (Definisi 2.2.4 butir (ii))
Jadi, terbukti ( ̅) ( ) ̅.
viii. ̅ ( ) (Definisi 2.2.4 butir (ii))
( ) (sifat eksistensi elemen netral terhadap perkalian pada ) ̅.
Jadi, terbukti ̅ ̅.
Sifat-sifat pada tersebut merupakan perampatan sifat-sifat yang dimiliki oleh . Gagasan melengkapi sebuah himpunan dengan dua operasi sehingga memenuhi sifat-sifat tertentu seperti pada dapat diperluas untuk sebarang himpunan yang dilengkapi dengan dua operasi, yaitu penjumlahan dan perkalian dengan skalar. Kedua operasi tersebut hanyalah penamaan saja, dapat didefinisikan berbeda dengan operasi pada . Namun, jika himpunan dengan kedua operasi tersebut memenuhi sifat-sifat seperti pada , maka sifat-sifat lainnya (turunannya) dapat dipelajari pula seperti pada (atau
pada ). Himpunan dengan operasi penjumlahan dan perkalian skalar tersebut dinamakan ruang vektor.
Definisi 2.2.5
Diberikan himpunan tak kosong dan dua operasi yang terdefinisi pada , yaitu penjumlahan dan perkalian skalar. Penjumlahan adalah aturan yang mengaitkan setiap ̅ dan ̅ anggota dengan ̅ ̅ . Perkalian skalar adalah aturan yang mengaitkan setiap bilangan real dan setiap ̅ dengan ̅ . Himpunan dengan kedua operasi tersebut dinamakan ruang vektor jika dan hanya jika untuk setiap ̅ ̅ ̅ dan , semua aksioma berikut terpenuhi.
1. ̅ ̅ ̅ ̅.
2. ̅ ( ̅ ̅ ) ( ̅ ̅) ̅ .
3. Terdapat ̅ sedemikian sehingga ̅ ̅ ̅ ̅ ̅ untuk setiap ̅ .
4. Terdapat ̅ sedemikian sehingga ̅ ( ̅) ( ̅) ̅ ̅.
5. ( ̅ ̅) ̅ ̅.
6. ( ) ̅ ̅ ̅.
7. ( ̅) ( ) ̅.
8. ̅ ̅.
Anggota dari ruang vektor disebut vektor. Vektor ̅ pada aksioma 3 disebut vektor nol, sementara vektor ̅ pada aksioma 4 disebut negatif dari vektor ̅.
Contoh 2.4
i. Teorema 2.1 menunjukkan bahwa himpunan dengan operasi penjumlahan dan perkalian skalar pada Definisi 2.2.4 merupakan ruang vektor.
ii. Diberikan himpunan , yaitu himpunan semua fungsi dari ke di mana ̅ adalah fungsi dengan nilai fungsi ̅( ) untuk setiap . Didefinisikan operasi penjumlahan dan perkalian skalar pada sebagai berikut:
Jika ̅ ̅ dan , maka ̅ ̅ adalah fungsi dari ke dengan nilai fungsi ( ̅ ̅)( ) ̅( ) ̅( ) dan ̅ adalah fungsi dari ke dengan nilai fungsi ( ̅)( ) ̅( ) untuk setiap .
Penjumlahan dan perkalian skalar pada bersifat tertutup dan tunggal. Karena ̅( ) ̅( ) , maka ̅( ) ̅( ) dan ̅( ) , dan masing-masing nilainya tunggal. Dengan demikian, untuk setiap ̅ ̅ dan , ̅ ̅ dan ̅ adalah fungsi dari ke sehingga ̅ ̅ dan ̅ . Selanjutnya, jika diambil sebarang ̅ ̅ ̅ dan , maka
( ̅ ̅)( ) ̅( ) ̅( ) ̅( ) ̅( ) ( ̅ ̅)( ) sehingga ̅ ̅ ̅ ̅,
. ̅ ( ̅ ̅)/ ( ) ̅( ) ( ̅ ̅)( ) ̅( ) . ̅( ) ̅( )/
. ̅( ) ̅( )/ ̅( ) ( ̅ ̅)( ) ̅( ) .( ̅ ̅) ̅/ ( ) sehingga ̅ ( ̅ ̅) ( ̅ ̅) ̅,
. ( ̅ ̅)/ ( ) ( ̅ ̅)( ) . ̅( ) ̅( )/
. ̅( )/ ( ̅( )) ( ̅)( ) ( ̅)( ) ( ̅ ̅)( )
sehingga ( ̅ ̅) ̅ ̅,
.( ) ̅/ ( ) ( ) ̅( )
. ̅( )/ . ̅( )/
( ̅)( ) ( ̅)( ) ( ̅ ̅)( ) sehingga ( ) ̅ ̅ ̅,
. ( ̅)/ ( ) ( ̅)( ) . ̅( )/
( ) ̅( ) .( ) ̅/ ( ) sehingga ( ̅) ( ) ̅, dan
( ̅)( ) ̅( ) ̅( ) sehingga ̅ ̅.
Artinya, aksioma 1, 2, 5, 6, 7, dan 8 terpenuhi.
Dipilih ̅ dengan nilai fungsi ̅( ) untuk setiap . Untuk setiap ̅ berlaku
( ̅ ̅)( ) ̅( ) ̅( ) ̅( ) ̅( )
yang berarti ̅ ̅ ̅. Menurut aksioma 1, ̅ ̅ ̅ ̅ sehingga aksioma 3 terpenuhi.
Dipilih ̅ dengan nilai fungsi ( ̅)( ) . ̅( )/ untuk setiap . Diperoleh
. ̅ ( ̅)/ ( ) ̅( ) ( ̅)( ) ̅( ) ( . ̅( )/)
̅( )
sehingga ̅ ( ̅) ̅. Menurut aksioma 1, ̅ ( ̅) ( ̅) ̅ sehingga aksioma 4 terpenuhi. Karena seluruh aksioma pada Definisi 2.2.5 terpenuhi, himpunan dengan operasi penjumlahan dan perkalian skalarnya merupakan ruang vektor.
Dari Definisi 2.2.5, dapat diturunkan beberapa sifat yang berlaku untuk sebarang ruang vektor. Sifat-sifat tersebut terangkum dalam teorema berikut.
Teorema 2.2
Diberikan ruang vektor . Jika ̅ dan , maka:
i. ̅ ̅.
ii. ̅ ̅.
iii. ( ) ̅ ̅.
iv. ( ̅) ̅.
v. ̅ ̅ jika dan hanya jika atau ̅ ̅.
Bukti:
Ambil sebarang ̅ dan .
i. Karena ̅ dan , maka ̅ (Definisi 2.2.5).
̅ ̅ ( ) ̅ (Definisi 2.2.5 aksioma 6)
̅. (sifat eksistensi elemen netral terhadap penjumlahan pada ) (1) Karena ̅ , maka terdapat ̅ (Definisi 2.2.5 aksioma 4) sehingga dengan menjumlahkannya di kedua ruas pada persamaan (1), diperoleh:
( ̅ ̅) ( ̅) ̅ ( ̅)
̅ ( ̅ ( ̅)) ̅ ( ̅) (Definisi 2.2.5 aksioma 2)
̅ ̅ ̅ (Definisi 2.2.5 aksioma 4)
̅ ̅. (Definisi 2.2.5 aksioma 3)
Jadi, terbukti ̅ ̅.
ii. Karena ̅ dan , maka ̅ (Definisi 2.2.5).
̅ ̅ ( ̅ ̅) (Definisi 2.2.5 aksioma 5)
̅. (Definisi 2.2.5 aksioma 3) (2) Karena ̅ , maka terdapat ̅ (Definisi 2.2.5 aksioma 4) sehingga dengan menjumlahkannya di kedua ruas pada persamaan (2), diperoleh:
( ̅ ̅) ( ̅) ̅ ( ̅)
̅ ( ̅ ( ̅)) ̅ ( ̅) (Definisi 2.2.5 aksioma 2)
̅ ̅ ̅ (Definisi 2.2.5 aksioma 4)
̅ ̅. (Definisi 2.2.5 aksioma 3)
Jadi, terbukti ̅ ̅.
iii. Karena ̅ dan , maka ( ) ̅ (Definisi 2.2.5). Untuk menunjukkan ( ) ̅ ̅, terlebih dahulu diperlihatkan bahwa vektor ( ) ̅ merupakan negatif dari vektor ̅ di , yakni
̅ ( ) ̅ ̅.
̅ ( ) ̅ ̅ ( ) ̅ (Definisi 2.2.5 aksioma 8) ( ( )) ̅ (Definisi 2.2.5 aksioma 6)
̅ (sifat eksistensi elemen negatif pada ) ̅. (Teorema 2.2 butir (i))
Karena ̅ ( ) ̅ ̅ dan berdasarkan Definisi 2.2.5 aksioma 4, terdapat ̅ sedemikian sehingga ̅ ( ̅) ̅, maka diperoleh:
̅ ( ) ̅ ̅ ( ̅)
( ̅) ( ̅ ( ) ̅) ( ̅) ( ̅ ( ̅)) (( ̅) ̅) ( ) ̅ (( ̅) ̅) ( ̅)
(Definisi 2.2.5 aksioma 2) ̅ ( ) ̅ ̅ ( ̅) (Definisi 2.2.5 aksioma 4)
( ) ̅ ̅. (Definisi 2.2.5 aksioma 3)
Jadi, terbukti ( ) ̅ ̅.
iv. Menurut Definisi 2.2.5 aksioma 4, terdapat ̅ sedemikian sehingga ̅ ( ̅) ̅. Karena ̅ , maka terdapat ( ̅)
sedemikian sehingga ( ̅) ( ( ̅)) ̅ (Definisi 2.2.5 aksioma 4). Dengan demikian, berlaku
( ̅) ̅ ( ( ̅)) (Definisi 2.2.5 aksioma 3) ( ̅ ( ̅)) ( ( ̅))
̅ .( ̅) ( ( ̅))/ (Definisi 2.2.5 aksioma 2) ̅ ̅
̅. (Definisi 2.2.5 aksioma 3)
Jadi, terbukti ( ̅) ̅.
v. ( ) Diketahui ̅ ̅. Terdapat tiga kejadian yang mungkin. Yang pertama adalah apabila dan ̅ ̅ sehingga pembuktian tidak perlu dipaparkan lebih lanjut. Dua kemungkinan lainnya adalah:
Jika , maka dengan memilih diperoleh ̅ ̅ atau ̅ ̅ (Definisi 2.2.5 aksioma 8). Dengan demikian, jika , maka ̅ ̅.
̅ ̅
Andaikan . Menurut sifat eksistensi elemen kebalikan (sifat aljabar pada butir (viii)), terdapat yang berakibat:
̅ ̅ ( ̅) ̅
. / ̅ ̅ (Definisi 2.2.5 aksioma 7)
̅ ̅ (sifat eksistensi elemen kebalikan pada )
̅ ̅ (Definisi 2.2.5 aksioma 8) ̅ ̅. (Teorema 2.2 butir (ii))
Terjadi kontradiksi, yaitu ̅ ̅ dan ̅ ̅. Dengan demikian, ingkaran dari pengandaian adalah pernyataan yang benar, yakni .
Kasus kedua dan ketiga menunjukkan bahwa jika ̅ ̅, maka tidak mungkin dan ̅ ̅ secara bersamaan. Dari ketiga kasus tersebut diperoleh bahwa ̅ ̅ mengakibatkan dan atau ̅ ̅. Dengan demikian, jika ̅ ̅, maka atau ̅ ̅.
( ) Diketahui atau ̅ ̅. Jika , maka ̅ ̅ ̅ (Teorema 2.2 butir (i)), dan jika ̅ ̅, maka ̅ ̅ ̅ (Teorema 2.2 butir (ii)), sehingga dapat disimpulkan bahwa jika atau ̅ ̅ maka ̅ ̅.
Jadi, terbukti ̅ ̅ jika dan hanya jika atau ̅ ̅.
Terdapat berbagai konsep dan sifat lainnya yang dapat diperoleh dari mempelajari sebuah ruang vektor. Sifat-sifat dari ruang vektor juga dipenuhi oleh sebarang himpunan yang merupakan ruang vektor dengan operasi penjumlahan dan perkalian dengan skalarnya.
C. Sistem Bilangan Real
Pemaparan pada subbab sebelumnya mengklasifikasikan bilangan real positif dan negatif berdasarkan posisi titik yang mewakili sebuah bilangan real terhadap titik yang mewakili bilangan real dalam garis bilangan real.
Secara matematis, bilangan-bilangan real positif (dan negatif) dapat diklasifikasikan melalui definisi himpunan bagian dari yang memenuhi karakteristik tertentu.
Definisi 2.3.1
Himpunan bilangan real positif adalah himpunan bagian tak kosong dari yang memenuhi aksioma-aksioma berikut.
1. Jika , maka . 2. Jika , maka .
3. Jika , maka tepat satu pernyataan berikut terpenuhi:
, , .
Definisi 2.3.1 aksioma 3 disebut sifat trikotomi karena membagi menjadi tiga himpunan bagian yang saling asing, yaitu himpunan , * +, dan * | +. Himpunan * | + dinamakan himpunan bilangan real negatif. Dengan demikian, * + .
Dalam , terdapat sifat urutan yang berkenaan dengan kriteria sebuah bilangan real lebih besar atau lebih kecil dari bilangan real lainnya. Pada pemaparan subbab sebelumnya, sebuah bilangan real dikatakan lebih besar atau lebih kecil dari bilangan real lainnya berdasarkan posisi titik-titik yang mewakili bilangan-bilangan real tersebut dalam garis bilangan real.
Pemahaman tersebut hanyalah pemahaman secara intuitif yang dibantu oleh ilustrasi geometris saja. Secara matematis, sifat urutan pada dapat didefinisikan menggunakan bantuan himpunan .
Pada Definisi 2.3.1, operasi penjumlahan, perkalian, serta elemen netral dan negatif terhadap penjumlahan muncul dalam karakteristik . Operasi- operasi dan elemen-elemen tersebut telah diperkenalkan dan dipaparkan sebelumnya dalam sifat aljabar pada . Urutan antara dua bilangan real dapat diketahui apabila mengoperasikan kedua bilangan real tersebut sehingga sifat urutan pada berkaitan dengan sifat aljabarnya. Sifat-sifat lainnya juga dapat diturunkan menggunakan bantuan sifat aljabar. Oleh karena itu, untuk kesederhanaan penulisan, penjumlahan dua bilangan real dan – selanjutnya ditulis yang didefinisikan sebagai
( ).
Selain itu, perkalian dua bilangan real dan selanjutnya ditulis yang didefinisikan sebagai
. Secara khusus, didefinisikan sebagai
dengan . Sifat urutan antara dua bilangan real didefinisikan sebagai berikut.
Definisi 2.3.2
Diberikan dua bilangan real dan .
i. Bilangan real dikatakan lebih besar dari atau lebih kecil dari , ditulis atau , jika dan hanya jika .
ii. Bilangan real dikatakan lebih besar dari atau sama dengan , atau lebih kecil dari atau sama dengan , ditulis atau , jika dan hanya jika * +.
Notasi menunjukkan bahwa adalah bilangan real positif sebab , dan menunjukkan bahwa adalah bilangan real negatif sebab sehingga ( ) . Notasi dan berturut-turut menunjukkan bahwa merupakan bilangan real tak negatif dan merupakan bilangan real tak positif.
Teorema 2.3
Jika , maka . Bukti:
Karena , maka (Definisi 2.3.2 butir (i)) sehingga berlaku atau * +. Artinya, * + sehingga (Definisi 2.3.2 butir (ii)). Jadi, terbukti jika , maka .
Jika dan , maka urutan tersebut biasa dinotasikan dengan . Demikian pula, , , dan didefinisikan serupa.
Contoh 2.5
Bilangan-bilangan real dan adalah anggota-anggota dari , sehingga keduanya merupakan bilangan real positif. Bilangan real adalah anggota dari sebab ( ) , sehingga bilangan real tersebut merupakan bilangan real negatif. Karena dan
( ) , maka lebih besar dari dan lebih besar dari , ditulis dan , atau .
Teorema 2.4
Dua bilangan real jika dan hanya jika dan . Bukti:
( ) Jika , maka
dan (sifat eksistensi elemen negatif pada ). Karena dan , maka * + dan * + sehingga dan (Definisi 2.3.2 butir (ii)). Jadi, jika , maka dan .
( ) Jika dan , maka * + dan * + (Definisi 2.3.2 butir (ii)). Karena * +, maka atau * +. Andaikan . Menurut sifat trikotomi, ( ) . Padahal
( ) ( )( ) (Teorema 2.2 butir (iii))
(( ) ) (( )( )) (sifat distributif perkalian terhadap penjumlahan pada )
( ) ( ( )) (Teorema 2.2 butir (iii)) ( ) (Teorema 2.2 butir (iv))
. (sifat komutatif penjumlahan pada ) Dengan demikian, ( ) . Karena himpunan dan * + saling asing, dan , maka * +. Terjadi kontradiksi, yaitu * + dan * + sehingga pernyataan yang benar adalah ingkaran dari pengandaian, yakni . Dengan demikian, * + sehingga diperoleh:
( )
(( ) ) (sifat asosiatif penjumlahan pada ) (sifat eksistensi elemen negatif pada )
. (sifat eksistensi elemen netral terhadap penjumlahan pada )
Jadi, jika dan , maka .
Jadi, terbukti bahwa jika dan hanya jika dan .
Dari sifat urutan tersebut, dapat diturunkan beberapa sifat yang terangkum dalam teorema berikut.
Teorema 2.5
Diberikan bilangan-bilangan real , , , dan . Sifat Transitif
i. Jika dan , maka . Sifat Trikotomi
ii. Tepat satu pernyataan berikut terpenuhi:
, , .
Sifat Monoton
iii. Jika , maka .
iv. Jika dan , maka . v. Jika dan , maka . Sifat Antimonoton
vi. Jika dan , maka . Bukti:
Ambil sebarang .
i. Karena dan , maka dan (Definisi 2.3.2 butir (i)).
( ) (sifat eksistensi elemen netral terhadap penjumlahan pada ) (( ) ) (sifat asosiatif penjumlahan pada ) ( ) (sifat komutatif penjumlahan pada )
.(( ) ) / (sifat eksistensi elemen negatif pada )
(( ) ( )) (sifat asosiatif penjumlahan pada ) ( ) ( ). (sifat asosiatif penjumlahan pada ) Menurut Definisi 2.3.1 aksioma 1, karena dan , maka ( ) ( ) sehingga (Definisi 2.3.2 butir (i)). Jadi, terbukti jika dan , maka .
ii. Karena , maka menurut sifat trikotomi Definisi 2.3.1 aksioma 3, tepat satu pernyataan berikut terpenuhi:
, , ( ) .
Untuk , berlaku (Definisi 2.3.2 butir (i)). Untuk , dengan menjumlahkan pada kedua ruas diperoleh:
( ) (( ) )
(sifat asosiatif penjumlahan pada ) (sifat eksistensi elemen
negatif pada )
. (sifat eksistensi elemen netral terhadap penjumlahan pada ) Untuk ( ) , berlaku
( ) ( )( ) (Teorema 2.2 butir (iii))
(( ) ) (( )( )) (sifat distributif perkalian terhadap penjumlahan pada ) ( ) ( ( )) (Teorema 2.2 butir (iii))
( ) (Teorema 2.2 butir (iv)
. (sifat komutatif penjumlahan pada ) Diperoleh ( ) atau (Definisi 2.3.2 butir (i)).
Jadi, terbukti bahwa tepat satu pernyataan berikut terpenuhi:
, , .
iii. Karena , maka (Definisi 2.3.2 butir (i)).
( ) ( ) ( ) (( )( ))
(Teorema 2.2 butir (iii)) ( ) .(( ) ) (( ) )/
(sifat distributif perkalian terhadap penjumlahan pada )
( ) (( ) ) (Teorema 2.2 butir (iii)) ( ) (( ) ) (sifat komutatif
penjumlahan pada ) . (( ) )/ (sifat asosiatif
penjumlahan pada ) (( ) ) (sifat asosiatif
penjumlahan pada ) ( ) (sifat eksistensi elemen
negatif pada )
. (sifat eksistensi elemen netral terhadap penjumlahan pada ) Dengan demikian, diperoleh ( ) ( ) sehingga (Definisi 2.3.2 butir (i)). Jadi, terbukti jika , maka .
iv. Karena dan , maka dan (Definisi 2.3.2 butir (i)).
( ) ( ) ( ) (( )( ))
(Teorema 2.2 butir (iii)) ( ) .(( ) ) (( ) )/
(sifat distributif perkalian terhadap penjumlahan pada ) ( ) (( ) ) (Teorema 2.2 butir (iii))
. (( ) )/ (sifat asosiatif penjumlahan pada ) (( ) ) (sifat asosiatif
penjumlahan pada ) .(( ) ) / (sifat komutatif
penjumlahan pada ) (( ) ( )) (sifat asosiatif
penjumlahan pada ) ( ) ( ). (sifat asosiatif
penjumlahan pada ) Menurut Definisi 2.3.1 aksioma 1, karena dan , maka ( ) ( ) ( ) ( ) sehingga
(Definisi 2.3.2 butir (i)). Jadi, terbukti jika dan , maka .
v. Karena dan , maka dan (Definisi 2.3.2 butir (i)).
( ) ( ) ( ) (( )( )) (Teorema 2.2 butir (iii)) ( ) .(( ) ) / (sifat asosiatif perkalian
pada )
( ) .( ( )) / (sifat komutatif perkalian pada )
( ) . (( ) )/ (sifat asosiatif perkalian pada )
( ) ( ( )) (Teorema 2.2 butir (iii)) ( ). (sifat distributif perkalian
terhadap penjumlahan pada )
Menurut Definisi 2.3.1 aksioma 2, karena dan , maka ( ) ( ) ( ) sehingga (Definisi 2.3.2 butir (i)). Jadi, terbukti jika dan , maka .
vi. Karena dan , maka dan (Definisi 2.3.2 butir (i)).
( ) ( ) .( ( )) / ( ) (Teorema 2.2 butir (iv)) .(( )( )) / (( )( ))
(Teorema 2.2 butir (iii)) .(( )( )) / (( )( ))
(sifat komutatif perkalian pada ) .( )(( ) )/ .(( ) ) /
(sifat asosiatif perkalian pada ) (( )( )) (( ) ) (Teorema 2.2 butir (iii)) ( )(( ) ) (sifat distributif perkalian terhadap
penjumlahan pada )
( )( ). (sifat komutatif penjumlahan pada ) Menurut Definisi 2.3.1 aksioma 2, karena dan , maka ( ) ( ) ( )( ) sehingga (Definisi 2.3.2 butir (i)). Jadi, terbukti jika dan , maka .
Selalu terdapat bilangan real yang terletak di antara dua bilangan real berbeda dan . Artinya, jika , maka terdapat sedemikian sehingga . Hal tersebut ditunjukkan dalam teorema berikut.
Teorema 2.6
Diberikan dua bilangan real dan . Jika , maka .
Bukti:
Ambil sebarang dengan . Karena , maka dengan menjumlahkan pada kedua ruas diperoleh:
(Teorema 2.5 butir (iii)) ( ) ( ) (Definisi 2.2.5 aksioma 8) ( ) (Definisi 2.2.5 aksioma 6)
( ) ( ) (Teorema 2.5 butir (v))
. / (Definisi 2.2.5 aksioma 7)
(sifat eksistensi elemen kebalikan pada )
. (Definisi 2.2.5 aksioma 8)
Demikian pula, dengan menjumlahkan pada kedua ruas diperoleh:
(Teorema 2.5 butir (iii)) ( ) ( ) (Definisi 2.2.5 aksioma 8) ( ) (Definisi 2.2.5 aksioma 6)
( ) ( ) (Teorema 2.5 butir (v))
. / (Definisi 2.2.5 aksioma 7)
(sifat eksistensi elemen kebalikan pada )
. (Definisi 2.2.5 aksioma 8)
Karena dan , maka . Jadi, terbukti jika ,
maka .
Jika , maka bilangan real yang terletak di antara keduanya ada tak hingga banyak. Selain , dapat ditemukan pula bilangan real lain antara dan , antara dan b, dan seterusnya. Bilangan-bilangan real tersebut dapat dikumpulkan ke dalam sebuah himpunan, yakni himpunan bilangan real
yang terletak di antara bilangan real dan . Himpunan tersebut dinamakan selang.
Definisi 2.3.3
Diberikan dua bilangan real dan dengan .
i. Selang terbuka yang ditentukan oleh dan , dinotasikan dengan ( ), adalah himpunan yang didefinisikan sebagai
( ) * | +.
ii. Selang tertutup yang ditentukan oleh dan , dinotasikan dengan , -, adalah himpunan yang didefinisikan sebagai
, - * | +.
Titik dan disebut titik ujung selang. Kedua titik ujung selang tidak termuat dalam himpunan pada selang terbuka, sedangkan pada selang tertutup, kedua titik ujung selang termuat dalam himpunan. Jika hanya salah satu titik ujung selang yang termuat dalam himpunan, maka himpunan tersebut dinamakan selang setengah terbuka (atau setengah tertutup).
Himpunan tersebut dinotasikan dengan , ) atau ( - tergantung pada titik ujung selang yang menjadi anggota himpunan. Jika , maka selang terbukanya adalah himpunan kosong dan selang tertutupnya adalah himpunan berelemen tunggal, yaitu ( ) dan , - * +.
Contoh 2.6
Himpunan ( ), , -, dan , ) berturut-turut adalah selang terbuka yang ditentukan oleh dan , selang tertutup yang ditentukan oleh dan , serta selang setengah terbuka yang ditentukan oleh dan dengan
( ) * | +,
, - * | +, dan , ) * | +.
Himpunan yang beranggotakan semua bilangan real yang lebih besar (atau lebih kecil) dari bilangan real tertentu dinamakan selang tak berhingga.
Definisi 2.3.4
Diberikan dua bilangan real dan .
i. Selang terbuka tak berhingga adalah himpunan yang didefinisikan dengan notasi
( ) * | + dan ( ) * | +.
ii. Selang tertutup tak berhingga adalah himpunan yang didefinisikan dengan notasi
, ) * | + dan ( - * | +.
Masing-masing selang tak berhingga pada Definisi 2.3.4 hanya memiliki satu titik ujung selang. Tanda dan adalah lambang yang menunjukkan ketakberhinggaan. Keduanya bukanlah anggota dari . Oleh karena itu, keduanya tidak pernah termuat dalam himpunan. Himpunan juga dapat dipandang sebagai selang, yaitu ( ) .
Gambar 2.2 Ilustrasi dari (a) selang terbuka, (b) selang tertutup, dan
(c) selang setengah terbuka (setengah tertutup) yang ditentukan oleh 𝑎 dan 𝑏
Gabungan kedua himpunan tersebut adalah ( - ( ) ( ) atau * + , yang tak lain adalah .
Sifat urutan dalam yang ditunjukkan dengan notasi (lebih kecil dari atau sama dengan) membentuk suatu hubungan antara dua elemen dalam yang disebut relasi. Secara umum, relasi pada himpunan didefinisikan sebagai berikut.
Definisi 2.3.5
Diberikan himpunan dan . Relasi dari ke adalah himpunan pasangan terurut ( ) di mana berelasi dengan , yaitu
*( )| erela i den an +.
Elemen berelasi dengan dinotasikan dengan lambang .
Seperti pada operasi, karena relasi didefinisikan pada dua himpunan dan , maka relasi tersebut dinamakan relasi biner. Relasi dari himpunan ke himpunan merupakan himpunan bagian dari darab Cartesius . Demikian pula sebaliknya, setiap himpunan bagian dari darab Cartesius dapat dipandang sebagai relasi dari himpunan ke himpunan . Jika merupakan relasi dari himpunan ke himpunan , maka disebut relasi pada himpunan .
Contoh 2.8
Jika himpunan * + dan relasi pada adalah rela i “kuadrat dari”, maka *( )+ dengan .
Beberapa relasi pada himpunan yang memenuhi sifat tertentu menjadikan relasi tersebut sebuah relasi khusus. Beberapa relasi khusus didefinisikan sebagai berikut.
Definisi 2.3.6
Diberikan relasi pada himpunan .
i. Relasi dikatakan bersifat refleksif jika dan hanya jika untuk setiap anggota .
ii. Relasi dikatakan bersifat simetrik jika dan hanya jika untuk setiap dan anggota berlaku: jika , maka .
iii. Relasi dikatakan bersifat antisimetrik jika dan hanya jika untuk setiap dan anggota berlaku: jika dan , maka . iv. Relasi dikatakan bersifat transitif jika dan hanya jika untuk setiap ,
, dan anggota berlaku: jika dan , maka .
Terdapat relasi khusus yang memenuhi beberapa sifat sekaligus pada Definisi 2.3.6. Salah satunya adalah relasi urutan parsial.
Definisi 2.3.7
Diberikan relasi pada himpunan . Relasi disebut relasi urutan parsial jika dan hanya jika relasi bersifat refleksif, antisimetrik, dan transitif. Himpunan yang dilengkapi dengan relasi urutan parsial disebut himpunan terurut parsial, seringkali ditulis ( ).
Rela i “le ih kecil dari atau ama den an” merupakan uatu rela i pada himpunan yang dinotasikan dengan lambang . Lebih spesifik, relasi pada merupakan relasi urutan parsial sehingga adalah himpunan terurut parsial.
Teorema 2.7
Himpunan yang dilengkapi dengan relasi adalah himpunan terurut parsial.
Bukti:
Ambil sebarang . Karena (sifat eksistensi elemen negatif pada ), maka sehingga (Teorema 2.4). Dengan
demikian, untuk setiap berlaku sehingga relasi pada bersifat refleksif (Definisi 2.3.6 butir (i)). Ambil sebarang dengan dan . Karena dan , maka (Teorema 2.4).
Dengan demikian, untuk setiap dengan dan berlaku sehingga relasi pada bersifat antisimetrik (Definisi 2.3.6 butir (iii)). Ambil sebarang dengan dan . Jika , karena , maka . Jika , karena , maka . Jika
, maka (Teorema 2.4). Jika , , dan , karena dan , maka dan sehingga (Teorema 2.5 butir (i)). Karena , maka (Teorema 2.3). Dengan demikian, untuk setiap dengan dan berlaku sehingga relasi pada bersifat transitif (Definisi 2.3.6 butir (iv)). Karena relasi pada bersifat refleksif, antisimetrik, dan transitif, maka relasi pada merupakan relasi urutan parsial (Definisi 2.3.7). Jadi, terbukti bahwa himpunan yang dilengkapi dengan relasi adalah himpunan terurut parsial (Definisi 2.3.7).
Relasi urutan parsial pada suatu himpunan memunculkan konsep batas atas dan batas bawah.
Definisi 2.3.8
Diberikan himpunan yang dilengkapi dengan relasi urutan parsial dan .
i. Elemen disebut batas atas dari jika dan hanya jika untuk setiap berlaku . Himpunan yang memiliki batas atas disebut himpunan yang terbatas ke atas.
ii. Elemen disebut batas bawah dari jika dan hanya jika untuk setiap berlaku . Himpunan yang memiliki batas bawah disebut himpunan yang terbatas ke bawah.
iii. Himpunan dikatakan terbatas jika dan hanya jika himpunan tersebut terbatas ke atas dan terbatas ke bawah.
Dalam himpunan yang terbatas ke atas (ke bawah), dapat dipilih batas atas (batas bawah) yang dikatakan terkecil (terbesar).
Definisi 2.3.9
Diberikan himpunan yang dilengkapi dengan relasi urutan parsial dan .
i. Elemen disebut batas atas terkecil (supremum) dari , ditulis , jika dan hanya jika:
adalah batas atas dari , dan
untuk setiap yang merupakan batas atas dari berlaku . ii. Elemen disebut batas bawah terbesar (infimum) dari , ditulis
, jika dan hanya jika:
adalah batas bawah dari , dan
untuk setiap yang merupakan batas bawah dari berlaku .
Contoh 2.9
i. Diberikan himpunan semua bilangan bulat positif dan himpunan * + . Pada didefinisikan relasi sebagai berikut:
jika dan hanya jika merupakan faktor dari untuk setiap , yaitu terdapat sedemikian sehingga . Maka merupakan relasi urutan parsial pada Karena
, maka
, , dan
sehingga adalah batas atas dari . Batas-batas atas dari lainnya adalah , , , dan seterusnya sehingga himpunan batas atas dari
adalah * | +. Karena batas atas dari dan untuk setiap * | + berlaku , maka . Demikian pula karena
, , dan , maka
, , dan
sehingga adalah batas bawah dari . Faktor-faktor dari hanyalah dan , dan faktor-faktor dari hanyalah dan . Artinya, tidak ada dengan sedemikian sehingga merupakan faktor dari dan sekaligus. Dengan demikian, adalah satu-satunya faktor yang sama dari semua anggota . Oleh karena itu, adalah satu-satunya batas bawah dari . Jadi, .
ii. Diberikan himpunan yang dilengkapi dengan relasi urutan parsial dan ( ) . Karena untuk setiap berlaku , maka untuk setiap berlaku sehingga adalah batas bawah dari . Karena untuk setiap yang merupakan batas bawah dari berlaku dan adalah batas bawah dari , maka . Di sisi lain, tidak terbatas ke atas sehingga tidak memiliki supremum.
Supremum dan infimum dari himpunan juga dapat ditentukan melalui elemen terbesar dan terkecil dari himpunan tersebut. Oleh karena itu, terlebih dahulu didefinisikan elemen terbesar dan terkecil pada himpunan bagian dari himpunan terurut parsial.
Definisi 2.3.10
Diberikan himpunan yang dilengkapi dengan relasi urutan parsial dan .
i. Elemen disebut elemen terbesar (maksimum) dari , ditulis , jika dan hanya jika untuk setiap .
ii. Elemen disebut elemen terkecil (minimum) dari , ditulis , jika dan hanya jika untuk setiap .
Contoh 2.10
Diberikan himpunan seperti pada Contoh 2.9 butir (i). Karena , , dan ,
maka . Di sisi lain, karena relasi , , dan tidak terpenuhi, maka tidak memiliki elemen minimum.
Tidak semua himpunan memiliki elemen maksimum dan minimum seperti pada Contoh 2.10. Oleh karena itu, sifat-sifat mengenai maksimum (minimum) berlaku pada himpunan yang diasumsikan memiliki maksimum (minimum).
Teorema 2.8
Diberikan himpunan yang dilengkapi dengan relasi urutan parsial dan .
i. Jika , maka . ii. Jika , maka . Bukti:
i. Ambil sebarang . Karena , maka (Definisi 2.3.10 butir (i)). Dengan demikian, untuk setiap sehingga adalah batas atas dari (Definisi 2.3.8 butir (i)). Ambil sebarang yang merupakan batas atas dari . Karena , maka , dan karena adalah batas atas dari , maka (Definisi 2.3.8 butir (i)). Dengan demikian, untuk setiap yang merupakan batas atas dari berlaku . Karena adalah batas atas dari dan untuk setiap yang merupakan batas atas dari berlaku , maka (Definisi 2.3.9 butir (i)). Jadi, terbukti jika , maka .
ii. Ambil sebarang . Karena , maka (Definisi 2.3.10 butir (ii)). Dengan demikian, untuk setiap sehingga adalah batas bawah dari (Definisi 2.3.8 butir (ii)). Ambil
sebarang yang merupakan batas bawah dari . Karena , maka , dan karena adalah batas bawah dari , maka (Definisi 2.3.8 butir (ii)). Dengan demikian, untuk setiap yang merupakan batas bawah dari berlaku . Karena adalah batas bawah dari dan untuk setiap yang merupakan batas bawah dari berlaku , maka (Definisi 2.3.9 butir (ii)). Jadi, terbukti jika , maka .
Dapat ditunjukkan bahwa maksimum dan minimum dari himpunan adalah tunggal.
Teorema 2.9
Diberikan himpunan yang dilengkapi dengan relasi urutan parsial dan .
i. Elemen maksimum dari adalah tunggal.
ii. Elemen minimum dari adalah tunggal.
Bukti:
i. Andaikan elemen maksimum dari tidak tunggal. Artinya, terdapat dengan sedemikian sehingga dan . Karena dan adalah elemen maksimum dari , maka untuk setiap berlaku dan (Definisi 2.3.10 butir (i)). Karena dan untuk setiap berlaku , maka . Demikian pula karena dan untuk setiap berlaku , maka . Karena relasi merupakan relasi urutan parsial, maka relasi bersifat antisimetrik (Definisi 2.3.7) dan karena dan , maka (Definisi 2.3.6 butir (iii)). Terjadi kontradiksi, yaitu dan sehingga pernyataan yang benar adalah ingkaran dari pengandaian. Jadi, terbukti bahwa elemen maksimum dari adalah tunggal.
ii. Andaikan elemen minimum dari tidak tunggal. Artinya, terdapat dengan sedemikian sehingga dan . Karena dan adalah elemen minimum dari , maka untuk setiap berlaku dan (Definisi 2.3.10 butir (ii)). Karena dan untuk setiap berlaku , maka . Demikian pula karena dan untuk setiap berlaku , maka . Karena relasi merupakan relasi urutan parsial, maka relasi bersifat antisimetrik (Definisi 2.3.7) dan karena dan , maka (Definisi 2.3.6 butir (iii)). Terjadi kontradiksi, yaitu dan sehingga pernyataan yang benar adalah ingkaran dari pengandaian. Jadi, terbukti bahwa elemen minimum dari adalah tunggal.
Supremum dari himpunan yang terbatas ke atas dapat dinyatakan sebagai minimum dari himpunan batas-batas atas dari himpunan tersebut.
Demikian pula infimum dari himpunan yang terbatas ke bawah dapat dinyatakan sebagai maksimum dari himpunan batas-batas bawah dari himpunan tersebut. Dengan kata lain, supremum dan infimum himpunan selalu tunggal sebab maksimum dan minimum himpunan juga tunggal.
Teorema 2.10
Diberikan himpunan dengan relasi urutan parsial dan . Misalkan
* | adalah ata ata dari + dan * | adalah ata a ah dari +.
i. Elemen jika dan hanya jika . ii. Elemen jika dan hanya jika . Bukti:
i. Elemen jika dan hanya jika batas atas dari dan untuk setiap batas atas dari (Definisi 2.3.9 butir (i)). Dengan kata lain, jika dan hanya jika dan untuk setiap
sehingga (Definisi 2.3.10 butir (ii)). Jadi, terbukti jika dan hanya jika .
ii. Elemen jika dan hanya jika batas bawah dari dan untuk setiap batas bawah dari (Definisi 2.3.9 butir (ii)).
Dengan kata lain, jika dan hanya jika dan untuk setiap sehingga (Definisi 2.3.10 butir (i)).
Jadi, terbukti jika dan hanya jika .
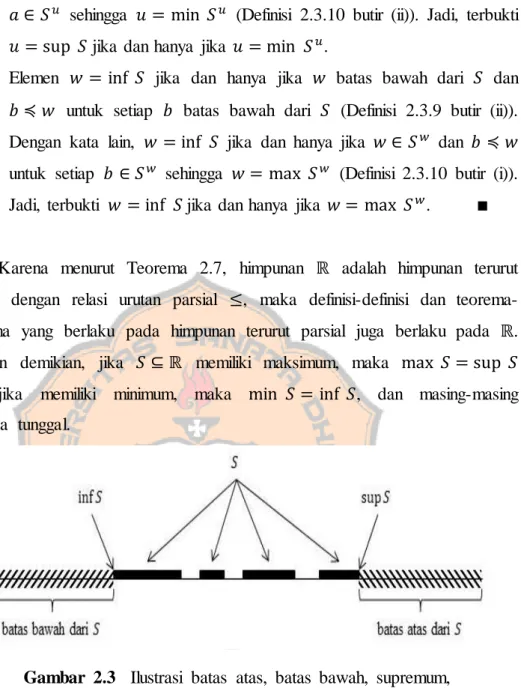
Karena menurut Teorema 2.7, himpunan adalah himpunan terurut parsial dengan relasi urutan parsial , maka definisi-definisi dan teorema- teorema yang berlaku pada himpunan terurut parsial juga berlaku pada . Dengan demikian, jika memiliki maksimum, maka dan jika memiliki minimum, maka , dan masing-masing nilainya tunggal.
Gambar 2.3 Ilustrasi batas atas, batas bawah, supremum, dan infimum dari 𝑆