METODE KETIDAKPASTIAN DAN KESAMARAN
DALAM SISTEM PAKAR
Putu Manik Prihatini
Staf Pengajar Jurusan Teknik Elektro, Politeknik Negeri Bali E-mail : [email protected]
Abstrak
Kecerdasan buatan dikembangkan untuk membuat agar mesin (komputer) dapat melakukan pekerjaan seperti dan sebaik manusia. Sistem Pakar merupakan bagian dari kecerdasan buatan yang mengandung pengetahuan dan pengalaman yang dimasukkan oleh satu atau banyak pakar ke dalam satu area pengetahuan tertentu. Pengetahuan dan pengalaman yang ada dalam dunia nyata yang akan direpresentasikan kedalam sistem pakar penuh dengan unsur ketidakpastian dan kesamaran. Beberapa metode yang sering digunakan untuk menangani masalah ketidakpastian dan kesamaran adalah dengan menggunakan teknik probabilitas, faktor kepastian dan logika fuzzy. Teorema Bayes merupakan bagian dari teknik probabilitas yang menekankan pada konsep probabilitas hipotesis dan evidence, sedangkan teknik probabilitas dengan teori Dempster-Shaffer menekankan pada konsep beliefe dan plausability. Pada metode dengan faktor kepastian menekankan pada nilai kepercayaan yang diberikan oleh seorang pengguna dan pakar. Pada metode dengan logika fuzzy menekankan pada derajat keanggotaan dari suatu evidence pada suatu himpunan fuzzy sehingga mampu menangani masalah kesamaran. Untuk memberikan solusi yang lebih baik, metode-metode yang ada bisa dikombinasikan antara yang satu dengan yang lainnya.
Kata Kunci: Sistem Pakar, Teknik Probabilitas, Faktor Kepastian, Logika Fuzzy Abstract
Artificial Intelligence is developed to make the machine (computer) can act as well as human. Expert systems as a part of Artificial Intelligence have knowledge and experience that inputted by one or more expert in a certain knowledge domain. Knowledge and experience in the real world that represented to expert systems have many uncertainty and vagueness. Some methods is used to solve this problem are probability technique, certainty factor and fuzzy logic. Bayes Theorem is a part of probability technique that point to hypothesis and evidence concept, while probability technique by Dempster-Shaffer is pointing to belief and plausibility concept. Certainty factor method points to value of believe that give by user and expert. Fuzzy logic method points to membership degree of an evidence in the fuzzy set so that can solve vagueness problem. To give the better solution, the methods can combine one to each other. Key words : Expert Systems, Probability Technique, Certainty Factor, Fuzzy Logic
1. Pendahuluan
Manusia diciptakan dengan kecerdasan yang luar biasa. Sejak dilahirkan hingga tumbuh dewasa, kecerdasannya akan berkembang dengan sangat pesat, baik kecerdasan kognitif, kecerdasan emosional, maupun kecerdasan spiritualnya. Sampai saat ini, belum ada satu mesin pun yang bisa menyamai kecerdasan manusia secara keseluruhan.
Selama bertahun-tahun para filsuf berusaha mempelajari kecerdasan manusia. Dari pemikiran para filsuf tersebut, lahirlah Artificial Intelligence atau kecerdasar buatan sebagai cabang ilmu yang berusaha memahami kecerdasan manusia. Kecerdasan buatan merupakan salah satu bagian dari ilmu komputer yang membuat agar mesin (komputer) dapat melakukan pekerjaan seperti dan sebaik yang dilakukan manusia. Kecerdasan buatan memungkinkan komputer untuk menirukan cara berpikir manusia sehingga informasi baru dapat diserap dan digunakan sebagai acuan di masa mendatang. Kecerdasan atau kepandaian tersebut didapat berdasarkan pengetahuan dan pengalaman. Untuk itu agar perangkat lunak yang dikembangkan mempunyai kecerdasan, maka perangkat lunak tersebut harus diberi pengetahuan dan kemampuan untuk menalar dari pengetahuan sebelumnya dan pengetahuan yang baru sehingga mampu memberikan solusi atau kesimpulan spesifik layaknya seorang pakar.
Sistem Pakar adalah salah satu bagian dari kecerdasan buatan yang mengandung pengetahuan dan pengalaman yang dimasukkan oleh satu atau banyak pakar ke dalam satu area pengetahuan tertentu sehingga setiap orang dapat menggunakannya untuk memecahkan berbagai masalah yang bersifat spesifik. Dengan sistem pakar, orang awam pun dapat menyelesaikan masalahnya atau sekedar mencari suatu informasi berkualitas yang sebenarnya hanya dapat diperoleh dengan bantuan para ahli di bidangnya.
Seorang pakar adalah orang yang mempunyai keahlian dalam bidang tertentu, yaitu pakar yang mempunyai knowledge atau kemampuan khusus yang tidak dimiliki oleh orang lain.
Dalam penyusunannya, sistem pakar mengkombinasikan kaidah-kaidah penarikan kesimpulan (inference rule) dengan basis pengetahuan tertentu yang diberikan satu atau lebih pakar dalam bidang tertentu. Kombinasi dari kedua hal tersebut disimpan dalam komputer, yang selanjutnya digunakan dalam proses pengambilan keputusan untuk penyelesaian masalah tertentu.
Permasalahannya adalah pengetahuan-pengetahuan yang ada dalam dunia nyata yang akan direpresentasikan kedalam sistem pakar penuh dengan unsur ketidakpastian dan kesamaran, sementara komputer tidak memiliki kemampuan untuk memproses sesuatu yang tidak pasti dan bersifat samar mengingat komputer pada dasarnya diciptakan sebagai alat hitung.
Melalui penelitian ini, pembahasan akan dilakukan terhadap beberapa teori yang umum digunakan untuk mengatasi permasalahan ketidakpastian dan kesamaran dalam sistem pakar sehingga dapat digunakan sebagai referensi dalam pengembangan sistem pakar yang mengandung ketidakpastian dan kesamaran pengetahuan.
2. Pembahasan 2.1. Ketidakpastian
Jika sistem kecerdasan buatan yang dikembangkan memiliki pengetahuan yang lengkap tentang permasalahan yang akan ditanganinya, maka sistem tersebut dapat dengan mudah memberikan solusi dengan menggunakan pendekatan logika. Akan tetapi, sistem hampir tidak pernah dapat mengakses seluruh fakta yang ada dalam lingkungan permasalahan yang akan ditanganinya, sehingga sistem harus bekerja dalam ketidakpastian dan kesamaran. Untuk itu, sistem harus menggunakan teknik-teknik khusus yang dapat menangani ketidakpastian dan kesamaran dalam menyelesaikan permasalahan yang ditanganinya.
Untuk mengawali pembahasan ini, diberikan sebuah kasus mengenai diagnosa media. Potongan pengetahuan berikut yang direpresentasikan dalam aturan produksi menggambarkan gejala-gejala dari suatu penyakit [1].
Rule 1:
IF Has_fever (Patient) AND Has_rash (Patient) AND
Has_high_body_ache(Patient) THEN Bears-Typhoid (Patient)
Berdasarkan aturan diatas, terlihat bahwa jika seorang pasien mengalami ketiga gejala yang disebutkan dalam aturan, maka sistem akan mendiagnosa pasien tersebut menderita tifus (typhoid). Aturan ini akan diterapkan pada seluruh pasien yang mengalami ketiga gejala tersebut. Jika sistem ini diterapkan dalam kasus nyata, apakah gejala-gejala yang disebutkan telah mewakili seluruh gejala dari penyakit tifus? Bagaimana jika ada penyakit lain yang memiliki gejala yang sama dengan ketiga gejala tersebut? Bagaimana jika derajat gejala yang dialami seorang pasien dengan pasien yang lainnya berbeda? Pertanyaan-pertanyaan ini tidak dapat ditangani oleh aturan tersebut karena jawaban dari pasien sebagai pengguna tidak hanya “ya” atau “tidak”, sehingga muncul ketidakpastian dan kesamaran pengetahuan dalam permasalahan ini.
Ada tiga teknik yang dapat digunakan untuk menangani ketidakpastian dan kesamaran pengetahuan, yaitu:
a. Teknik Probabilitas, yang dikembangkan dengan memanfaatkan teorema Bayes yang menyajikan hubungan sebab akibat yang terjadi diantara evidence-evidence yang ada. Pendekatan alternatif lainnya yang dapat digunakan adalah teori Dempster-Shafer.
b. Faktor Kepastian, merupakan teknik penalaran tertua, yang digunakan pada sistem MYCIN. Teknik ini bersifat semi probabilitas, karena tidak sepenuhnya menggunakan notasi probabilitas.
c. Logika Fuzzy, merupakan teknik baru yang diperkenalkan oleh Zadeh. Setiap variabel dalam teknik ini memiliki rentang nilai tertentu, yang akan digunakan untuk menghitung nilai fungsi keanggotaannya.
2.2. Teknik Probabilitas 2.2.1. Teorema Bayes
Thomas Bayes menemukan pendekatan penalaran statistik yang jauh lebih maju dibandingkan dengan pola pikir matematis tradisional pada saat itu. Fokus matematika pada saat itu adalah pada tingkah laku sampel dari populasi yang diketahui. Akan tetapi, Bayes mengemukakan ide untuk menentukan properti dari populasi berdasarkan sampel tersebut. Dalam “An Essay Towards the Solving a Problem in the Doctrines of Chance”, dia menyajikan tentang “Proposition 9”, yang akhirnya dikenal dengan “Teorema Bayes”. Selanjutnya, teorema ini menjadi dasar dalam pengambilan keputusan modern.
Teorema Bayes diperoleh dari aturan produksi konjungsi dengan notasi sebagai berikut [5]:
Atau dapat juga ditulis sebagai berikut:
2.2.2. Teori Dempster-Shaffer
Secara umum teori Dempster-Shafer dapat ditulis dalam suatu interval [5]: [Belief, Plausability]
Belief (Bel) adalah ukuran kekuatan evidence dalam mendukung suatu himpunan proposisi. Jika bernilai 0 maka mengindikasikan bahwa tidak ada evidence, dan jika bernilai 1 maka menunjukkan adanya kepastian. Plausability (Pl) dinotasikan sebagai :
Pl(s) = 1 – Bel(¬s)
Plausability juga bernilai antara 0 dan 1. Jika kita yakin terhadap ¬s, maka dapat dikatakan bahwa Bel(¬s) = 1 dan Pl(s) = 0. Pada teori ini dikenal juga adanya frame of discernment yang dinotasikan dengan q, merupakan semesta pembicaraan dari sekumpulan hipotesis. Tidak semua evidence secara langsung mendukung tiap-tiap elemen. Untuk itu diperlukan adanya probabilitas fungsi densitas (m). Nilai m tidak hanya mendefinisikan elemen-elemen saja, namun juga semua subset-nya, sehingga jika q berisi n elemen, maka m mendefinisikan 2n elemen. Jumlah semua m dalam subset q sama dengan 1. Andaikan tidak ada informasi apapun untuk memilih keempat hipotesis tersebut, maka m{q} = 1,0. Andaikan diketahui X adalah subset dari q, dengan m1 sebagai fungsi densitasnya, dan Y juga merupakan subset dari q dengan m2 sebagai fungsi densitasnya, maka dapat dibentuk fungsi kombinasi m1 dan m2 sebagai m3, yaitu :
2.3. Faktor Kepastian
P(Y | X) = P(X | Y) . P(Y) P(X)
P(Y | X, e) = P(X | Y, e) . P(Y |e) P(X | e)
Faktor kepastian (Certainty Factor-CF) diperkenalkan oleh Shortliffe Buchanan dalam pembuatan MYCIN. Faktor kepastian merupakan nilai parameter klinis yang diberikan MYCIN untuk menunjukkan besarnya kepercayaan [3].
Ada dua macam faktor kepastian yang dapat digunakan, yaitu faktor kepastian yang diisikan oleh pakar bersama aturan dan faktor kepastian yang diberikan oleh pengguna. Faktor kepastian yang diisikan oleh pakar menggambarkan kepercayaan pakar terhadap hubungan antara antecedent dan consequent pada aturan kaidah produksi. Faktor kepastian dari pengguna menunjukkan besarnya kepercayaan terhadap keberadaan masing-masing elemen dalam antecedent.
Faktor kepastian didefinisikan sebagai berikut [3]. CF(H,E) = MB(H,E) – MD(H,E)
dimana:
CF(H,E) faktor kepastian dari hipotesis H yang dipengaruhi oleh premis (evidence) E. MB(H,E) ukuran kepercayaan terhadap hipotesis H yang dipengaruhi oleh premis (evidence)
E
MD(H,E) ukuran ketidakpercayaan terhadap hipotesis H yang dipengaruhi oleh premis (evidence) E.
Pengguna akan memberikan faktor kepastian terhadap setiap premis yang ada dalam aturan. Untuk menentukan faktor kepastian dari suatu aturan yang didalamnya terdapat beberapa premis dengan faktor kepastiannya masing-masing, maka perlu dilakukan perhitungan CF paralel.
CF paralel merupakan CF yang diperoleh dari beberapa premis pada sebuah aturan. Besarnya CF paralel dipengaruhi oleh CF pengguna untuk masing-masing premis dan operator dari premis. Rumus untuk masing-masing operator diberikan sebagai berikut[3].
CF(x and y) = Min(CF(x), CF(y)) CF(y or y) = Max(CF(x), CF(y)) CF(not x) = - CF(x)
Suatu aturan akan memiliki nilai faktor kepastian dari seorang pakar, sementara aturan tersebut juga memiliki faktor kepastian yang diperoleh dari premis-premis yang ada didalamnya (CF paralel), sehingga perlu dilakukan perhitungan nilai faktor kepastian untuk suatu aturan berdasarkan CF paralel dan CF yang diberikan oleh pengguna, yang disebut dengan CF sekuensial.
CF sekuensial diperoleh dari hasil perhitungan CF paralel dari semua premis dalam satu aturan dengan CF aturan yang diberikan oleh pakar. Rumus untuk menghitung CF sekuensial adalah sebagai berikut [3].
CF(x,y) = CF(x) * CF(y) dimana: CF(x,y) CF sekuensial CF(x) CF paralel CF(y) CF pakar
Suatu hipotesis pada kenyataannya bisa dihasilkan dari beberapa aturan yang berbeda, dimana setiap aturan memiliki faktor kepastian masing-masing, sehingga perlu dilakukan perhitungan CF gabungan dari seluruh aturan yang ada untuk suatu hipotesis.
CF gabungan merupakan CF akhir dari sebuah calon kesimpulan. CF ini dipengaruhi oleh semua CF sekuensial dari aturan yang menghasilkan kesimpulan tersebut. Rumus untuk melakukan perhitungan CF gabungan adalah sebagai berikut [3].
Jika CF(x) > 0 dan CF(y) > 0, maka: CF(x,y) = CF(x) + CF(y) – (CF(x)*CF(y))
Jika salah satu, CF(x) atau CF(y) < 0, maka:
Jika CF(x) < 0 dan CF(y) < 0, maka: CF(x,y) = CF(x) + (CF(y) * (1+ CF(x)))
2.4. Logika Fuzzy
Logika fuzzy pertama kali diperkenalkan oleh Prof. Lotfi A. Zadeh pada tahun 1965. Dasar logika fuzzy adalah teori himpunan fuzzy. Pada teori himpunan fuzzy, peranan derajat keanggotaan/nilai keanggotaan sebagai penentu keberadaan elemen dalam suatu himpunan sangatlah penting [4].
Logika fuzzy digunakan sebagai suatu cara untuk memetakan permasalahan dari input menuju ke output yang diharapkan. Pada himpunan fuzzy, nilai keanggotaan terletak pada rentang 0 sampai 1. Himpunan fuzzy merupakan suatu grup yang mewakili suatu kondisi atau keadaan tertentu dalam suatu variabel fuzzy. Variabel fuzzy merupakan variabel yang hendak dibahas dalam suatu sistem fuzzy, misalnya umur, temperature, dan lain-lain.
Fungsi keanggotaan (membership function) adalah suatu kurva yang menunjukkan pemetaan titik-titik input data ke dalam nilai keanggotaannya yang memiliki interval antara 0 sampai 1. Ada beberapa fungsi keanggotaan yang dapat digunakan dalam logika fuzzy, tetapi fungsi yang paling sering digunakan dalam pembangunan system pakar adalah representasi kurva trapesium.
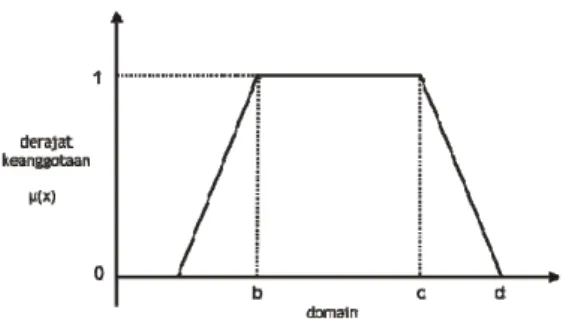
Kurva trapezium memiliki bentuk dasar seperti kurva segitiga, tetapi memiliki beberapa titik yang mempunyai nilai keanggotaan 1 seperti yang terlihat pada gambar 1.
Gambar 1 Representasi Kurva Trapesium Fungsi keanggotaannya adalah:
µ(x) =
0; x ≤ a atau x ≥ d (x–a)/(b–a); a ≤ x ≤ b
1; b ≤ x ≤ c
(d–x)/(d–c) x ≥ d
Suatu himpunan fuzzy dapat dikombinasikan dengan himpunan fuzzy lainnya dengan menggunakan operator. Ada tiga operator dasar yang diciptakan oleh Zadeh, yaitu:
a. Operator AND
Hasil operasi dengan operator AND diperoleh dengan mengambil nilai keanggotaan terkecil antar elemen pada himpunan-himpunan yang bersangkutan
µA B = min(µA(x), µB(y)) CF(x,y) =
CF(x) + CF(y)
b. Operator OR
Hasil operasi dengan operator OR diperoleh dengan mengambil nilai keanggotaan terbesar antar elemen pada himpunan-himpunan yang bersangkutan
µA B = max(µA(x), µB(y)) c. Operator NOT
Hasil operasi dengan operator NOT diperoleh dengan mengurangkan nilai keanggotaan elemen pada himpunan yang bersangkutan dengan 1
µA’ = 1 - µA(x)
Tiap-tiap aturan pada basis pengetahuan fuzzy akan berhubungan dengan suatu relasi fuzzy. Bentuk umum dari aturan yang digunakan dalam fungsi implikasi adalah:
IF x is A THEN y is B
dengan x dan y adalah skalar, sedangkan A dan B adalah himpunan fuzzy. Secara umum, ada dua fungsi implikasi yang dapat digunakan, yaitu:
a. Min (minimum), akan memotong output himpunan fuzzy b. Dot (product), akan menskala output himpunan fuzzy
Metode penalaran fuzzy ada tiga, yaitu metode Tsukamoto, metode Mamdani dan metode Sugeno.
Pada metode Tsukamoto, setiap konsekuen pada aturan yang berbentuk IF-THEN harus direpresentasikan dengan suatu himpunan fuzzy dengan fungsi keanggotaan monoton. Sebagai hasilnya, output hasil inferensi dari tiap-tiap aturan diberikan secara tegas berdasarkan α-predikat. Hasil akhirnya diperoleh dengan menggunakan rata-rata terbobot.
Metode Mamdani sering dikenal dengan metode Max-Min, diperkenalkan oleh Ebrahim Mamdani pada tahun 1975. Untuk mendapatkan output diperlukan empat tahapan, yaitu pembentukan himpunan fuzzy, aplikasi fungsi implikasi, komposisi dan defuzzifikasi.
Metode Sugeno memiliki penalaran yang hampir sama dengan penalaran Mamdani, tetapi output yang dihasilkan tidak berupa himpunan fuzzy, melainkan berupa konstanta atau persamaan linear. Metode ini diperkenalkan oleh Takagi-Sugeno Kang pada tahun 1985, terdiri dari dua jenis, yaitu metode Fuzzy Sugeno Orde-Nol dan metode Fuzzy Sugeno Orde-Satu.
3. Kombinasi CF dan Logika Fuzzy
Dalam kasus nyata, seringkali permasalahan yang dihadapi tidak bisa diselesaikan hanya dengan menggunakan satu metode saja, melainkan solusi bisa diperoleh dengan menggabungkan beberapa metode, misalnya metode faktor kepastian (CF) dan logika fuzzy.
Ada beberapa model bentuk aturan IF-THEN yang mungkin bisa dijadikan pertimbangan dalam permasalahan yang akan diselesaikan dengan metode kombinasi CF dan logika fuzzy, yaitu:
a. Bentuk Aturan 1
Pada bentuk aturan yang pertama, seluruh premis dalam antecedent dan consequent berupa himpunan fuzzy, tetapi consequent memiliki nilai berupa faktor kepastian.
IF (a is A) and (b is B) THEN c is C, CF
Pada bentuk ini, nilai kepastian dari aturan tersebut akan diperoleh dengan menggunakan aturan perhitungan metode faktor kepastian. CF paralel diperoleh dengan mengambil nilai minimum dari derajat keanggotaan a is A dan b is B sebagai berikut.
CF(x) = min(µA[a], µB[b])
b. Bentuk Aturan 2
Pada bentuk aturan yang kedua, premis-premis dalam antecedent merupakan gabungan antara himpunan fuzzy dan faktor kepastian, sedangkan consequent tidak berupa himpunan fuzzy.
IF (a is A) and B THEN C, CF
Pada bentuk ini, nilai kepastian dari aturan tersebut akan diperoleh dengan menggunakan aturan perhitungan metode CF. CF paralel diperoleh dengan mengambil nilai minimum dari derajat keanggotaan a is A dan faktor kepastian dari premis B sebagai berikut.
CF(x) = min(µA[a], CF(b))
Sedangkan, CF sekuensial dihitung sesuai dengan rumus pada metode faktor kepastian.
c. Bentuk Aturan 3
Pada bentuk aturan yang ketiga, premis-premis dalam antecedent dan consequent bukan merupakan himpunan fuzzy, tetapi CF pada consequent berupa himpunan fuzzy.
IF A and B THEN C, CF(y) is CF
Pada bentuk ini, nilai kepastian dari aturan tersebut akan diperoleh dengan menggunakan aturan perhitungan metode CF. CF paralel diperoleh dengan mengambil nilai minimum dari faktor kepastian premis A dan premis B sebagai berikut.
CF(x) = min(CF(a), CF(b))
CF sekuensial dihitung sesuai dengan rumus pada metode faktor kepastian, dimana nilai CF(y) diperoleh dengan menentukan derajat keanggotaan dari CF(y) dalam himpunan fuzzy CF.
d. Bentuk Aturan 4
Pada bentuk aturan yang keempat, premis-premis dalam antecedent dan consequent merupakan himpunan fuzzy, dan CF pada consequent juga berupa himpunan fuzzy.
IF a is A and b is B THEN c is C, CF(y) is CF
Pada bentuk ini, nilai kepastian dari aturan tersebut akan diperoleh dengan menggunakan aturan perhitungan metode CF. CF paralel diperoleh dengan mengambil nilai minimum dari derajat keanggotaan a is A dan b is B sebagai berikut.
CF(x) = min( A[a], B[b])
CF sekuensial dihitung sesuai dengan rumus pada metode faktor kepastian, dimana nilai CF(y) diperoleh dengan menentukan derajat keanggotaan dari CF(y) dalam himpunan fuzzy CF.
4. Contoh Kasus 4.1. Teorema Bayes
Asumsikan bahwa ruang hipotesis dan ruang evidence untuk masalah diagnosa medis seperti pada gambar 2 berikut[1].
Aturan yang diberikan menyajikan tentang hubungan sebab akibat diantara ruang evidence dan ruang hipotesis dengan beberapa probabilitas kondisi.
Rule 1: IF symptoms are F(P(F/T) = 0.9), HBA (P(HBA/T) = 0.6)
THEN the Patient hopefully bears T Rule 2: IF symptoms are
F(P(F/GM) = 0.8), R(P(R/GM) = 0.7), HBA (P(HBA/GM) = 0.8)
THEN the Patient hopefully bears GM Rule 3: IF symptoms are
F(P(F/CP) = 0.9), R(P(R/CP) = 0.9), HBA (P(HBA/CP) = 0.6)
THEN the Patient hopefully bears CP
Tentukan probabilitas penyakit yang diderita oleh seorang pasien, jika penyakit yang diderita ditentukan dari probabilitas tertinggi!
Solusi:
Langkah 1 :
Menghitung probabilitas seorang pasien menderita penyakit T P(T|F,HBA) = P(T) * P(F|T) * P(HBA|T)
= 0.2 * 0.9 * 0.6 = 0.108
Langkah 2 :
Menghitung probabilitas seorang pasien menderita penyakit GM P(GM|F,R,HBA) = P(GM) * P(F|GM) *
P(R|GM) * P(HBA|GM) = 0.3 * 0.8 * 0.7 * 0.8 = 0.1344
Langkah 3 :
Menghitung probabilitas seorang pasien menderita penyakit CP P(CP|F,R,HBA) = P(CP) * P(F|CP) *
P(R|CP) * P(HBA|CP) = 0.5 * 0.9 * 0.9 * 0.6 = 0.243
Dari langkah 1 sampai 3 dengan menghitung probabilitas penyakit T, GM dan CP terhadap gejala F, R dan GM diperoleh probabilitas tertinggi 0.243 yaitu penyakit CP (Chicken Pox), sehingga sistem akan memberikan informasi kepada pasien (pengguna) bahwa pasien menderita penyakit Chicken Pox dengan probabilitas 0.243.
4.2. Teori Dempster-Shaffer
Untuk contoh kasus dengan teori Dempster-Shaffer, akan digunakan asumsi untuk ruang hipotesis dan ruang evidence seperti pada gambar 2. Ada tiga penyakit yang mungkin diderita oleh seorang pasien berdasarkan gejala F, yaitu penyakit T, GM dan CP.
Asumsikan diketahui nilai kepercayaan F sebagai gejala dari penyakit T, GM dan CP adalah:
m1{T,GM,CP} = 0.7
Kemudian, muncul gejala baru yaitu High Body Ache (HBA) yang merupakan gejala dari penyakit F (Flu), T dan GM, dengan nilai kepercayaan yaitu:
m2{F,GM,CP} = 0.8
m2{θ} = 1 – 0.8 = 0.2
Maka, tentukanlah penyakit apa yang diderita si pasien berdasarkan gejala F dan HBA tersebut!
Solusi:
Munculnya gejala HBA mengharuskan untuk menghitung densitas baru (m3) untuk beberapa kombinasi m1 dan m2.
Langkah 1 :
Membuat tabel aturan kombinasi untuk m3
{F,GM,CP} (0.8) (0.2 ) {T,GM,CP } (0.7) {GM,CP} (0.56) {T,GM,CP} (0.1 4) (0.3) {F,GM,CP} (0.24) (0.0 6) Langkah 2 :
Menghitung nilai untuk m3
m3{GM,CP } = 0.56/(1–0) = 0.56/1 = 0.56 m3{F,GM,CP}= 0.24/(1-0) = 0.24/1 = 0.24 m3{T,GM,CP}= 0.14/(1-0) = 0.14/1 = 0.14 m3{θ} = 0.06/(1-0) = 0.06/1 = 0.06
Dari hasil perhitungan diatas, terlihat bahwa, pada mulanya dengan hanya adanya gejala F, m{T,GM,CP) bernilai 0.7; namun setelah adanya gejala baru yaitu HBA, maka nilai m{T,GM,CP} menjadi 0.14. Demikian juga halnya dengan hanya adanya gejala HBA, m{F,GM,CP} bernilai 0.8; namun setelah ada gejala yaitu F, maka nilai {F,GM,CP} menjadi 0.24. Dengan adanya dua gejala yaitu F dan HBA, nilai densitas yang paling kuat adalah m{GM,CP} yaitu sebesar 0.56, sehingga sistem akan memberikan informasi kepada pasien (pengguna) bahwa pasien menderita penyakit GM dan CP dengan nilai densitas 0.56.
4.3. Faktor Kepastian
Untuk contoh kasus dengan faktor kepastian, akan digunakan asumsi untuk ruang hipotesis dan ruang evidence seperti pada gambar 2, tetapi dengan aturan sebagai berikut. Rule 1:
IF symptoms are F, CF: 0.9 and HBA, CF: 0.6 THEN
the Patient hopefully bears T, CF: 0.8 Rule 2:
IF the Patient bears T and R, CF: 0.7 THEN
the Patient hopefully bears CP, CF:0.6 Rule 3:
IF the Patient bears T and R, CF: 0.9 THEN
Tentukan nilai kemungkinan seorang pasien menderita penyakit CP!
Solusi:
Langkah 1 :
Menghitung CF Paralel dan CF Sekuensial Rule 1 CF Paralel = Min(CF(F), CF(HBA))
= Min(0.9; 0.6)
= 0.6
CF Sekuensial = CF Paralel * CF Pakar = 0.6 * 0.8
= 0.48
CF Sekuensial ini menunjukkan besarnya derajat kepercayaan terhadap kesimpulan seorang pasien menderita penyakit T.
Langkah 2 :
Menghitung CF Paralel dan CF Sekuensial Rule 2 CF Paralel = Min(CF(T), CF(R))
= Min(0.48; 0.7)
= 0.336
CF Sekuensial = CF Paralel * CF Pakar = 0.336 * 0.6
= 0.2016
CF Sekuensial ini menunjukkan besarnya derajat kepercayaan terhadap kesimpulan seorang pasien menderita penyakit CP.
Langkah 3 :
Menghitung CF Paralel dan CF Sekuensial Rule 3 CF Paralel = Min(CF(T), CF(R))
= Min(0.48; 0.9)
= 0.432
CF Sekuensial = CF Paralel * CF Pakar = 0.432 * 0.8
= 0.3456
CF Sekuensial ini menunjukkan besarnya derajat kepercayaan terhadap kesimpulan seorang pasien menderita penyakit CP.
Langkah 4 :
Berdasarkan aturan yang ada, ada dua aturan yang menghasilkan kesimpulan bahwa seorang pasien menderita penyakit CP, sehingga harus dicari nilai CF Gabungan dari kedua aturan tersebut.
Karena CF(Rule 1) > 0 dan CF(Rule 2) > 0, maka: CF(x,y) = CF(x) + CF(y) – (CF(x)*CF(y))
= 0.2016 + 0.3456 – (0.2016*0.3456) = 0.2016 + 0.3456 – 0.069673 = 0.2016 + 0.275927
= 0.477527 0.48
Berdasarkan nilai CF Gabungan yang diperoleh pada langkah 4 maka sistem akan memberikan informasi kepada pasien (user) bahwa pasien menderita penyakit Chicken Pox dengan derajat kepercayaan sebesar 0.48 atau 48%.
4.4. Logika Fuzzy
Untuk contoh kasus dengan logika fuzzy, akan digunakan asumsi untuk ruang hipotesis dan ruang evidence seperti pada gambar 2, tetapi dengan aturan sebagai berikut.
Rule 1:
IF symptoms are F is high and R is high
and HBA is high THEN
the Patient hopefully bears CP is high Rule 2:
IF symptoms are F is high and R is very high and HBA is high THEN
the Patient hopefully bears CP is very high
Tentukan nilai kemungkinan seorang pasien menderita penyakit CP jika pasien memberikan nilai untuk gejala yang dirasakannya sebagai berikut:
Gejala F : 60 Gejala R : 70
Gejala HBA : 55
Solusi:
Langkah 1 :
Pemodelan Variabel dan Himpunan Fuzzy
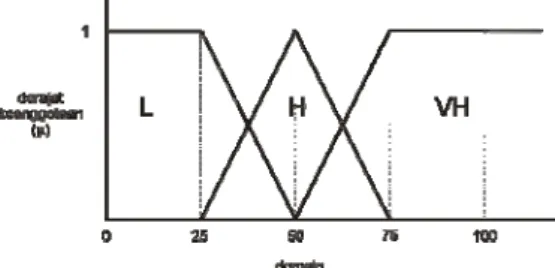
Asumsikan metode penalaran yang digunakan adalah metode Mamdani. Ada empat variabel fuzzy yang akan dimodelkan yaitu gejala F, gejala R, gejala HBA dan penyakit CP, dengan tiga himpunan fuzzy, yaitu:
Low (L) : 0 - 50
High (H) : 25 - 75 Very High (VH) : 50 - 100
Representasi kurva dari variabel fuzzy tersebut dapat dilihat pada gambar 3 berikut.
Gambar 3. Representasi Kurva Himpunan Fuzzy Fungsi keanggotaannya adalah:
µ(L) = 1; (50–x)/25; 25 x < 25 ≤ x ≤ 50 µ(H) = (x–25)/50; 25 1; 50 ≤ x ≤ 50 (75–x)/25; 50 ≤ x ≤ 75 µ(VH) = (x–50)/25; 50 ≤ x ≤ 75 1; x ≥ 75
Langkah 2 :
Perhitungan nilai fungsi keanggotaan untuk gejala F pada himpunan High dan Very High µFH[60] = (75–x) / 25 = (75–60)/25 = 15/25 = 0.6 µFVH[60] = (x–50) / 25 = (60–50)/25 = 10/25 = 0.4
Perhitungan nilai fungsi keanggotaan untuk gejala R pada himpunan High dan Very High µRH[70] = (75–x) / 25 = (75–70)/25 = 5/25 = 0.2 µRVH[70] = (x–50) / 25 = (70–50)/25 = 20/25 = 0.8
Perhitungan nilai fungsi keanggotaan untuk gejala HBA pada himpunan High dan Very High µHBAH[55] = (75–x) / 25 = (75–55)/25 = 20/25 = 0.8 µHBAVH[55] = (x–50) / 25 = (55–50)/25 = 5/25 = 0.2 Langkah 3 :
Perhitungan fungsi implikasi untuk setiap aturan dengan fungsi MIN α-predikat1 = min(µFH[60], µRH[70], µHBAH[55]
= min(0.6; 0.2; 0.8) = 0.2
α-predikat2 = min(µFH[60], µRVH[70], µHBAH[55] = min(0.6; 0.8; 0.8)
= 0.6 Langkah 4 :
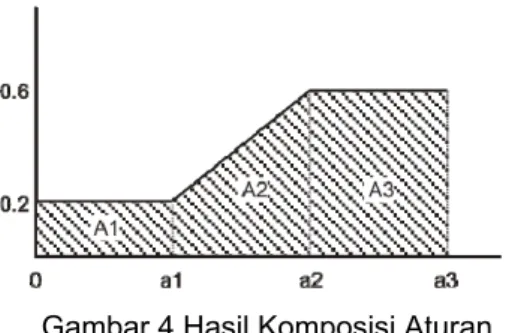
Berdasarkan hasil perhitungan fungsi implikasi dari tiap aturan, maka dilakukan komposisi aturan dengan metode MAX sehingga hasilnya seperti pada gambar 4.
Gambar 4 Hasil Komposisi Aturan
Pada gambar terlihat bahwa daerah hasil terbagi menjadi tiga yaitu A1, A2, dan A3. Selanjutnya, titik a1 dan a2 dicari dengan cara berikut.
(a1–25)/50 = 0.2 a1 = 35 (a2–25)/50 = 0.6 a2 = 55
Dengan demikian, fungsi keanggotaan untuk hasil komposisi ini adalah:
µ(z) = 0.2 (z–25)/50; 35 z < 35 ≤ z ≤ 55 0.6 z > 55 Langkah 5 :
Metode penegasan yang digunakan adalah metode centroid.
35 35 M1= ∫ (0.2)z dz = 0.1z2 = 122.5 0 0 55 M2= ∫ (z-25)/50 z dz 35 55 = ∫ (0.02z2-0.5z) dz 35 55 = 0.0067z3-0.25z2 = 377.45 35 55 55 M3= ∫ (0.6)z dz = 0.3z2 = 780 75 75
Kemudian, luas setiap daerah dihitung. A1 = 35*0.2 = 7
A2 = (0.2+0.6)*(55-35)/2 = 8 A3 = (75-55)*0.6 = 12
Selanjutnya, titik pusat dapat diperoleh dari: 122.5 + 377.45 + 780
z = = 47.4
7 + 8 + 12
Berdasarkan nilai titik pusat yang diperoleh pada langkah 5 maka sistem akan memberikan informasi kepada pasien (pengguna) bahwa pasien menderita penyakit Chicken Pox dengan derajat kepercayaan sebesar 47.4%.
5. Kesimpulan
Permasalahan yang dihadapi dalam kehidupan sehari-hari seringkali melibatkan pengetahuan yang tidak lengkap, sehingga untuk memperoleh solusi bagi permasalahan tersebut tidak dapat dilakukan dengan menggunakan aturan yang bersifat pasti. Kecerdasan buatan sebagai ilmu dasar bagi pengembangan sistem cerdas diharapkan dapat memberikan solusi tentang cara menangani masalah ketidakpastian dan kesamaran yang terjadi dalam kehidupan sehari-hari.
Beberapa metode yang sering digunakan untuk menangani masalah ini adalah dengan menggunakan teknik probabilitas, faktor kepastian dan logika fuzzy. Teorema Bayes dan Teori Dempster-Shafer merupakan bagian dari teknik probabilitas yang mampu menangani masalah ketidakpastian yang terjadi dalam kehidupan sehari-hari, dengan menekankan pada konsep probabilitas hipotesis dan evidence pada teorema Bayes, dan konsep beliefe dan plausability
pada teori Dempster-Shafer. Pada metode dengan faktor kepastian menekankan pada nilai kepercayaan yang diberikan oleh seorang pengguna terhadap evidence-evidence yang ada dan nilai kepercayaan yang diberikan oleh seorang pakar terhadap aturan-aturan yang ada. Pada metode dengan logika fuzzy menekankan pada derajat keanggotaan dari suatu evidence pada suatu himpunan fuzzy sehingga mampu menangani masalah kesamaran.
Mengingat semakin kompleksnya permasalahan yang terjadi di dalam kehidupan sehari-hari, maka penggunaan satu metode saja dianggap kurang mampu memberikan solusi yang diharapkan sehingga metode-metode yang ada bisa dikombinasikan antara yang satu dengan yang lainnya sehingga diharapkan mampu menyelesaikan masalah dengan lebih baik.
6. Daftar Pustaka
[1] Amit Konar. Artificial Intelligence and Soft Computing Behavioral and Cognitive Modelling of the Human Brain. Washington DC: CRC Press. 2000.
[2] Joseph Giarratano, Gary Riley. Expert Systems Principles and Programming Third Edition. PWS Publishing Company. 1998.
[3] Kusrini. Aplikasi Sistem Pakar. Yogyakarta: ANDI Offset. 2008.
[4] Sri Kusumadewi. Aplikasi Logika Fuzzy untuk Pendukung Keputusan. Yogyakarta: Graha Ilmu. 2010.
[5] Sri Kusumadewi. Artificial Intelligence (Teknik dan Aplikasinya). Yogyakarta: Graha Ilmu. 2003.
[6] Stuart Russell, Peter Norvig. Artificial Intelligence A Modern Approach. New Jersey: Prentice Hall. 2003.