BAB II LANDASAN TEORI

BAB II

LANDASAN TEORI

2.1. Citra Digital

Citra adalah suatu representasi(gambaran), kemiripan, atau imitasi dari suatu objek. Citra sebagai keluaran suatu sistem perekaman data dapat bersifat optik berupa foto, bersifat analog berupa sinyal-sinyal video seperti gambar pada monitor televisi atau bersifat digital yang dapat langsung disimpan pada suatu media penyimpan[11].

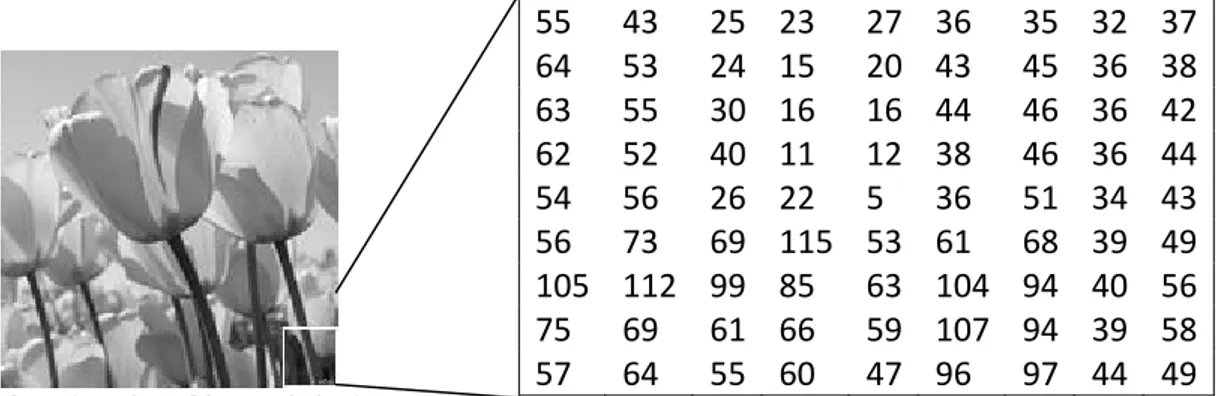
Citra digital adalah citra yang dapat diolah oleh komputer. Seperti pada Gambar 2.1, sebuah citra grayscale ukuran 150 x 150 pixel(elemen terkecil dari sebuah citra) diambil sebagian berukuran 9 x 9 pixel. Maka monitor akan menampilkan sebuah kotak kecil. Namun, yang disimpan dalam memori komputer hanyalah angka-angka yang menunjukkan besar intensitas pada masing-masing pixel tersebut [3].

Gambar 2.1 Citra Digital

Sebuah citra digital adalah kumpulan pixel-pixel yang disusun dalam larik dua dimensi. Jumlah pixel dalam ukuran lebar dan tinggi dari sebuah citra digital disebut dengan dimensi pixel dari sebuah citra. Jumlah pixel per unit panjang dari sebuah citra 55 43 25 23 27 36 35 32 37 64 53 24 15 20 43 45 36 38 63 55 30 16 16 44 46 36 42 62 52 40 11 12 38 46 36 44 54 56 26 22 5 36 51 34 43 56 73 69 115 53 61 68 39 49 105 112 99 85 63 104 94 40 56 75 69 61 66 59 107 94 39 58 57 64 55 60 47 96 97 44 49

dikenal sebagai resolusi citra, biasanya dalam satuan pixel per inchi(ppi). Sebuah citra dengan resolusi tinggi terdiri atas banyak pixel kecil daripada citra dengan resolusi rendah. Citra digital ukuran 1 inchi x 1 inchi dengan resolusi 72ppi memiliki total pixel 72 x 72 atau 5184 pixel. Citra digital dengan ukuran yang sama dan resolusinya 300ppi memiliki total pixel 90000 pixel [9].

2.1.1. Jenis-Jenis Citra Digital

Citra Biner, adalah citra digital yang hanya memilik dua kemungkinan nilai pixel yaitu hitam dan putih. Citra biner juga disebut sebagai citra B&W (Black and White) atau citra monokrom. Hanya dibutuhkan 1 bit untuk mewakili nilai setiap pixel dari citra biner.

Citra Grayscale merupakan citra digital yang hanya memiliki satu nilai kanal pada setiap pixelnya, dengan kata lain nilai bagian Red = Green = Blue. Nilai tersebut digunakan untuk menunjukkan tingkat intensitas. Warna yang dimiliki adalah warna dari hitam, keabuan, dan putih. Tingkatan keabuan di sini merupakan warna abu dengan berbagai tingkatan dari hitam hingga mendekati putih.

Citra Warna(24 bit) adalah citra yang setiap pixel dari citra warna 24 bit diwakili dengan 24 bit sehingga total 16.777.216 variasi warna. Variasi ini sudah lebih dari cukup untuk memvisualisasikan seluruh warna yang dapat dilihat penglihatan manusia. Setiap informasi warna disimpan ke dalam 1 byte data. 8 bit pertama menyimpan nilai biru, kemudian diikuti dengan nilai hijau pada 8 bit kedua dan 8 bit terakhir merupakan nilai warna merah [4].

2.1.2. Warna

Isi dari sebuah citra digital adalah pixel atau kotak warna. Manusia dapat melihat radiasi elektromagnetik dengan panjang gelombang 400 sampai 700 nanometers(nm) sebagai warna. Hewan juga bisa melihat sisi yang berbeda dari spectrum elektromagnetik dan dapat melihat warna yang berbeda dari apa yang tidak dapat dilihat oleh manusia.

Pengalaman warna secara natural adalah proses kombinasi dari mata dan otak. Mata bertindak sebagai penerima cahaya dan otak menginterpretasikan data dari mata sebagai informasi visual dan menerjemahkan data tersebut sebagai warna.

Penglihatan manusia didasarkan atas tiga penerima, satu untuk merah, yang lain untuk hijau, sisanya untuknya biru. Ada banyak representasi warna dari banyak perbedaan lingkup warna, atau model yang biasanya memiliki tiga atau empat channel.

2.1.2.1. RGB

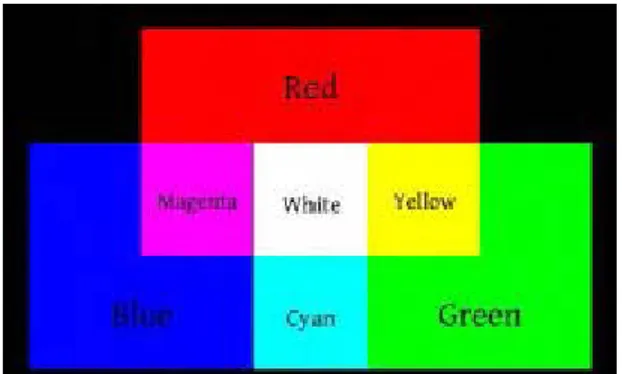
Salah satu dari model warna yang paling banyak digunakan adalah RGB. Dalam model warna ini, ada tiga kanal: merah, hijau, dan biru. Setiap warna dalam model ini dibuat menggunakan kombinasi dari ketiga kanal ini.

Setiap pixel dalam model warna RGB di definisikan sebagai (r,g,b) di mana r,g, dan b adalah nilai dari masing channel. Nilai yang mungkin untuk masing-masing kanal dimulai dari 0 (tidak ada cahaya) samapai dengan 255. Perpaduan warna setiap kanal menghasilkan warna yang berbeda-beda seperti pada gambar 2.2

Gambar 2.2 Kombinasi warna 3 kanal

2.1.2.2. CYMK

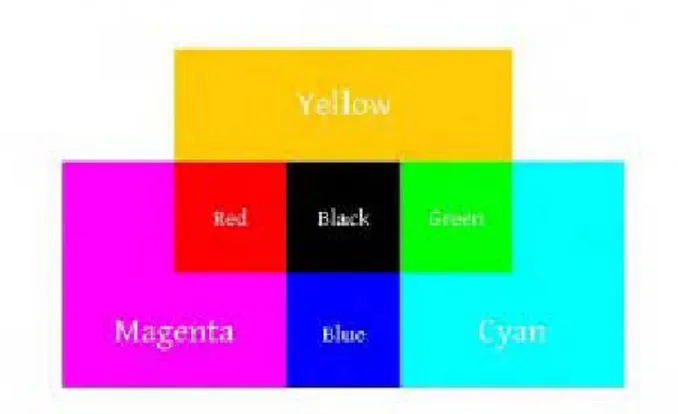
Model warna ini biasanya digunakan untuk percetakan. CYMK pada dasarnya terdiri atas empat kanal: cyan, magenta, yellow dan key. Warna-warna dalam model ini

dibentuk menggunakan substrak pencampuran warna, yang menunjukkan bagaimana

pigment warna bekerja.

Mulai dari kertas putih, pewarna tinta substrak cahaya dari kertas mengandung warna yang berbeda. Hanya tiga kanal yang dibutuhkan untuk merepresentasikan semua warna(cyan,magenta, dan yellow), tetapi untuk alasan praktikal, hitam juga ditambahkan ke dalam model warna. Dengan mengganti nilai dari tiap kanal, semua perbedaan warna yang dihasilkan dari model warna ini ditunjukkan dalam gambar 2.3

Gambar 2.3 Kombinasi warna dari tiap kanal CYMK

2.1.2.3. HSV

HSV singkatan dari Hue, Saturation dan Value. Dalam model warna ini, Hue merepresentasikan warna utama, dan saturation serta value merepresentasikan bayangan spesifik dari Hue. Penggunaan utama dari model warna ini untuk membuat interaksi yang lebih baik dengan manusia karena manusia biasanya me-recognize perbedaan warna dan kemudian memilih bayangan spesifik untuk HSV.

2.1.2.4. YUV

YUV merupakan model warna yang mengkomposisikan kanal luma(Y) yang merupakan kecerahan citra dan dua kanal chrominance (U dan V) yang mendeskripsikan warna spesifik dari citra[7].

2.1.3.Format Citra Digital

2.1.3.1. Joint Photographic Experts Group(JPEG)

JPG, atau JPEG(Joint Photographic Experts Group), adalah format file yang paling popular di dalam digital fotografi. JPEG mendukung kedalaman warna 24 bit (3 saluran warna masing-masing 8 bit). Hampir setiap kamera digital mampu menyimpancitra menggunakan format ini dan secara luas didukung dalam berbagai program penampil citra.

JPEG menghasilkan file dengan ukuran kecil menggunakan kompresi lossy. Setiap kali menyimpan gambar dalam format ini, kualitas terdegradasi oleh kompresi

lossy. Kompresi lossy menghilangkan detail gambar sehingga dapat direpresentasikan

dengan kurangnya informasi.

JPEG juga menggunakan analisis matematis yang komples untuk menghapus bit yang paling terlihat pada gambar sehingga mata manusia tidak dapat membedakannya. Format ini juga mendukung fitur yang disebut progresif JPEG.

Fitur ini memungkinkan untuk menyimpan gambar sehingga informasi yang diperintahkan dengan cara tertentu dari berbagai resolusi gambar yang disajikan kepada pengguna sampai kepada gambar yang lengkap diterima. Hal ini sangat berguna untuk gambar besar yang sedang ditransfer ke komputer melalui koneksi yang lambat.

2.1.3.2. Graphics Interchange Fomat (GIF)

Merupakan format citra digital yang dapat menyimpan kedalaman warna hanya 8 bit (256 warna). GIF dapat menangani transparansi dalam bentuk yang sangat dasar. Keuntungan utama penggunaan GIF adalah GIF dapat digunakan untuk menyimpan animasi. GIF juga format citra digital yang tua dan sangat cocok dengan versi web terdahulu dan beberapa perangkat lunak lainnya.

2.1.3.3. Portable Network Graphics (PNG)

Format citra digital ini secara publik tersedia dan pengembangan dari format citra digital GIF. PNG dapat menangani kedalaman warna sampai dengan 48 bit (3 kanal warna dengan tiap kanal 16 bit).

Format ini memiliki dukungan yang lebih baik untuk transparansi daripada Format citra digital GIF. Secara keseluruhan PNG format yang lebih baik daripada GIF karena menawarkan kompresi yang lebih baik selain itu dapat menyimpan lebih banyak warna [7].

2.2. Noise

Sumber noise pada citra digital bisa terjadi sejak pengambilan dan atau transmisi citra. Kinerja dari sensor citra dipengaruhi oleh banyak faktor seperti kondisi lingkungan selama pengambilan citra dan oleh kualitas sensitivas elemen itu sendiri. Sebagai contoh, dalam pengambilan citra dengan kamera CCD, level pencahayaan dan suhu sensor adalah faktor utama yang mempengaruhi tingkat noise pada citra yang dihasilkan [10].

2.2.1. Periodic Noise

Noise periodik merupakan noise yang sifatnya periodik(bukan acak). Citra yang

terkorupsi oleh noise periodik secara visual tampak terdapat garis-garis pada citra. Garis-garis tersebut tersebar secara merata dengan periode tertentu. Pada Gambar 2.4 terlihat banyak terkorupsi oleh noise periodik .

2.3. Pengolahan Citra

Ada dua prinsip daerah aplikasi pengolahan citra digital: peningkatan informasi pictorial untuk interpretasi manusia dan pengolahan citra digital untuk penyimpanan, transmisi dan representasi bagi peralatan persepsi. Tujuan utama dari pengolahan citra digital adalah memperbolehkan manusia untuk mendapatkan kualitas tinggi atau karakteristik deskriptif dari citra asli [15].

2.3.1. Pengolahan Citra dalam Domain Frekuensi

2.3.1.1. Transformasi Fourier Diskrit 2-D dan Domain Frekuensi

f(x,y) untuk x=0,1,2,…M-1 dan y=0,1,2,…N-1 menyatakan citra M x N. Discrete

Fourier Transformation(DFT) 2-D dari f dinyatakan oleh F(u,v) yang diberikan oleh

formula 2.1:

𝐹𝐹(𝑢𝑢, 𝑣𝑣) = ∑𝑀𝑀−1_𝑥𝑥=0 ∑𝑁𝑁−1_𝑦𝑦=0𝑓𝑓(𝑥𝑥, 𝑦𝑦)𝑒𝑒−𝑗𝑗2𝜋𝜋(𝑢𝑢𝑥𝑥𝑀𝑀+𝑣𝑣𝑦𝑦𝑁𝑁) ... 2.1 [10]

untuk u=0,1,2,..,M-1 dan v=0,1,2,..N-1. Domain frekuensi adalah rentang sistem koordinat oleh F(u,v) dengan u dan v sebagai variable frekuensi. Ini merupakan analogi domain spasial di mana rentang sistem koordinat oleh f(x,y) dengan x dan y sebagai variabel spasial. Region persegi panjang M x N didefinisikan oleh u=0,1,2,…M-1 dan v= 0,1,2,…N-1 sering disebut sebagai rentang frekuensi yang memiliki ukuran yang sama dengan citra input.

Invers dari transformasi Fourier diberikan oleh formula 2:

𝑓𝑓(𝑥𝑥, 𝑦𝑦) =_{𝑀𝑀𝑁𝑁}1 ∑_𝑥𝑥=0𝑀𝑀−1∑𝑁𝑁−1_𝑦𝑦=0𝐹𝐹(𝑢𝑢, 𝑣𝑣)𝑒𝑒−𝑗𝑗2𝜋𝜋�𝑢𝑢𝑥𝑥𝑀𝑀+𝑣𝑣𝑦𝑦𝑁𝑁� ... (2.2)[10]

untuk x=0,1,2,…,M-1 dan y=0,1,2,…,N-1. Jadi dengan F(u,v) bisa mendapatkan f(x,y) kembali dengan merata-rata invers DFT. Nilai F(u,v) dalam formula ini kadang disebut sebagai Fourier coefficients dari ekspansi.

F(u,v) : nilai intensitas spectrum fourier pada titik (u,v) f(x,y) : nilai intensitas citra noise pada titik(x,y) e : natural number(2.718281828459045….) M,N : M lebar citra, N tinggi citra

j : bilangan imajiner(konstanta fourier)

Nilai transformasi pada origin domain frekuensi [F(0,0)] disebut dengan komponen dc transformasi Fourier. Jika f(x,y) adalah real, transformasinya secara umum kompleks. Metode prinsip analisis secara visual sebuah transformasi adalah untuk menghitung spektrum dan menampilkannya sebagai citra. Jika R(u,v) dan I(u,v) merepresentasikan real dan komponen imaginary F(u,v), spektrum Fourier didefinisikan sebagai:

𝐹𝐹(𝑢𝑢, 𝑣𝑣) = �𝑅𝑅2_{(𝑢𝑢, 𝑣𝑣) + 𝐼𝐼}2_{(𝑢𝑢, 𝑣𝑣) ...(2.3)[6]}

2.3.1.2. DFT Terpusat

Perhitungan DFT 2-D sekarang mentransformasikan titik-titik ke dalam interval persegi panjang seperti ditunjukkan pada gambar 2.3. Persegi panjang dengan garis putus-putus adalah pengulangan periodik. Daerah dengan garis utuh menunjukkan nilai F(u,v) yang sekarang meliputi empat back-to-back perempatan periode yang bertemu pada titik yang ditunjukkan pada gambar 2.3(a). Analisis visual spektrum hanya dengan memindahkan nilai origin transformasi ke pusat dari persegi panjang frekuensi.

Nilai spektrum di (M/2, N/2) dalam gambar 2.3(b) adalah sama dengan nilai di (0, 0) dalam gambar 2.3(a) dan nilai di (0, 0) dalam gambar 2.3(b) sama dengan nilai di (-M/2, -N/2) dalam gambar 2.3(a). Dengan cara yang sama, nilai di (M-1, N-1) dalam gambar 2.3(b) adalah sama dengan nilai di (M/2-1, N/2-1) dalam gambar 2.5(a). Proses ini dinamakan dengan proses shifting. [10]

Gambar 2.5 Spektrum Fourier 2D, (a) kiri, (b) kanan [10]

Berdasarkan penjelasan di atas dapat diambil kesimpulan untuk mendapatkan DFT terpusat dapat dihitung dengan menggunakan formula 2.4:

𝐹𝐹(𝑢𝑢′_{, 𝑣𝑣}′_{) ≡ 𝐹𝐹 �𝑢𝑢 −}𝑀𝑀 2, 𝑣𝑣 − 𝑁𝑁 2� ... (2.4)[11 ]

cara lain untuk menghitung DFT terpusat adalah dengan mengasumsikan bahwa DFT F(u,v) dari f(x,y) telah diperoleh dengan menggunakan formula DFT, kemudian menukarkan kuadran pertama dari F(u,v) dengan kuadran ketiga dan menukarkan kuadran kedua dengan kuadran keempat seperti yang ditunjukkan pada gambar 2.4. Cara ini lebih efektif dari pada menggunakan formula sebelumnya karena menghemat proses komputasi yang dilakukan.

Gambar 2.6 Proses pemusatan DFT dapat dilakukan dengan menukarkan kuadran 1 dengan 3, dan 2 dengan 4 [11]

2.3.1.3. Fast Fourier Transform (FFT)

Banyaknya perkalian dan penjumlahan bilangan kompleks untuk menghitung Diskrit Fourier Transform adalah 𝑂𝑂(𝑁𝑁2). Dengan mengadopsi pendekatan algoritma

divide-and-conquer proses penghitungan bilangan kompleks menjadi 𝑂𝑂( 𝑁𝑁 𝑙𝑙𝑙𝑙𝑙𝑙₂ 𝑁𝑁).

Algoritma ini dikenal sebagai Fast Fourier Transform (FFT) [2]. Berdasarkan hal inilah untuk mendapatkan transformasi Fourier dan inversnya, penulis menggunakan FFT untuk mendapatkan hasil transformasi dan invers Fourier.

Untuk menghitung DFT satu dimensi digunakan formula 2.5,

𝐹𝐹(𝑢𝑢) =_𝑁𝑁1∑𝑁𝑁−1𝑥𝑥=0𝑓𝑓(𝑥𝑥)𝐾𝐾𝑁𝑁𝑢𝑢𝑥𝑥 ... (2.5)[2]

Dimana

𝐾𝐾𝑁𝑁 = exp[ −𝑗𝑗𝑁𝑁2𝜋𝜋]

Asumsikan bahwa N adalah nilai pangkat dari bilangan 2 maka untuk mendapatkan

Fast Fourier Transformation satu dimensi diperoleh dengan formula 2.6,

𝐹𝐹(𝑢𝑢) =_𝑁𝑁1∑𝑁𝑁−1 𝑓𝑓(𝑥𝑥)𝑒𝑒−𝑗𝑗 𝑢𝑢 2 𝜋𝜋 𝑥𝑥 /𝑁𝑁

𝑥𝑥=0 ... (2.6)[2] sedangkan untuk menghitung invers Fast Fourier Transformation diperoleh dengan formula 7,

𝑓𝑓(𝑥𝑥) = ∑𝑁𝑁−1 𝐹𝐹(𝑢𝑢)𝑒𝑒−𝑗𝑗 𝑢𝑢 2 𝜋𝜋 𝑥𝑥 /𝑁𝑁

𝑢𝑢=0 ... (2.7)[2] Untuk menghitung FFT2D dapat dilakukan dengan menghitung nilai kompleks FFT 1D dari tiap baris citra digital kemudian dilanjutkan dengan menghitung nilai kompleks FFT 1D dari tiap kolom citra digital. Begitu juga untuk menghitung nilai invers dari Fast Fourier Transform 2D.

2.3.2. Konsep Filter dalam Domain Frekuensi

Dasar untuk filter linier dalam domain spasial dan frekuensi adalah teori konvolusi, yang dapat dituliskan dengan:

𝑓𝑓(𝑥𝑥, 𝑦𝑦) ∗ ℎ(ℎ, 𝑦𝑦) ⟺ 𝐻𝐻(𝑢𝑢, 𝑣𝑣)𝐹𝐹(𝑢𝑢, 𝑣𝑣) dan sebaliknya:

𝑓𝑓(𝑥𝑥, 𝑦𝑦)ℎ(ℎ, 𝑦𝑦) ⟺ 𝐻𝐻(𝑢𝑢, 𝑣𝑣) ∗ 𝐺𝐺(𝑢𝑢, 𝑣𝑣)

Simbol * menunjukkan konvolusi dari dua fungsi dan pernyataan di sisi panah dobel mengatur pasangan transformasi Fourier. Sebagai contoh, formula yang pertama adalah konvolusi dua fungsi spasial yang bisa didapatkan dengan menghitung invers transformasi Fourier dari perkalian dua fungsi transformasi Fourier. Sebaliknya transformasi Fourier dari konvolusi dua fungsi spasial memberikan hasil transformasi dua fungsi [10].

Pemfilteran dalam domain spasial berisi konvolusi citra f(x,y) mask filter h(x,y). Seperti halnya teori konvolusi, juga bisa mendapatkan hasil yang sama dalam domain frekuensi dengan perkalian antara F(u,v) dengan H(u,v), transformasi Fourier

filter. Biasanya H(u,v) disebut sebagai filter transfer function[10].

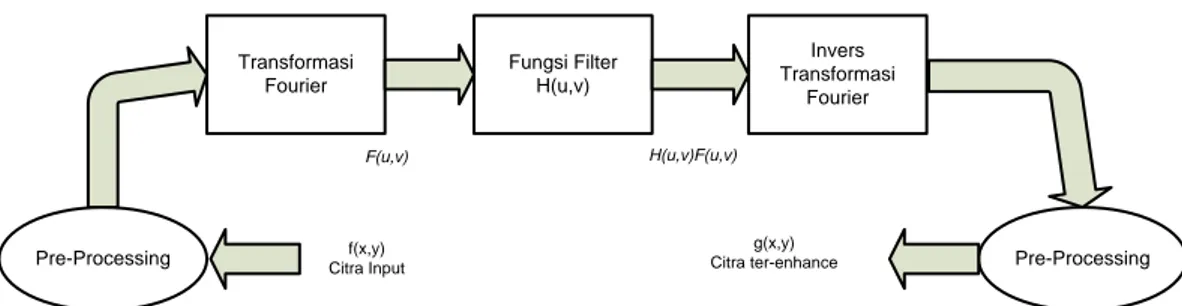
Keuntungan melakukan pemfilteran di dalam domain frekuensi adalah proses konvolusi dapat diterapkan dalam bentuk perkalian langsung. Untuk melakukan pemfilteran dalam domain frekuensi harus mengikuti diagram pada gambar 2.7:

Pre-Processing Transformasi Fourier Fungsi Filter H(u,v) Invers Transformasi Fourier Pre-Processing F(u,v) H(u,v)F(u,v) f(x,y) Citra Input g(x,y) Citra ter-enhance

Penjelasan gambar 2.7:

1. Input citra digital berupa citra *.jpg dengan ukuran lebar = ukuran tinggi serta lebar dan tinggi merupakan nilai dari 2𝑛𝑛.

2. Lakukan proses transformasi fourier dari citra input dengan menggunakan FFT 2D untuk mendapatkan F(u,v) yang merupakan nilai kompleks dari transformasi fourier.

3. Hitung filter mask H(u,v) dengan ukuran lebar dan tinggi sama dengan ukuran citra input. Filter mask yang dibahas di dalam skripsi ini adalah Band Reject Filter dan Optimum Notch Filter.

4. Kalikan F(u,v) dengan H(u,v) untuk mendapatkan G(u,v) yang merupakan hasil perkalian antara transformasi dengan filter mask.

5. Lakukan proses invers transformasi fourier dari G(u,v) menggunakan invers FFT2D sehingga diperolehlah citra hasil g(x,y).

2.3.3. Selective Filter

Noise periodik dapat dianalisis dan difilter dengan sangat efektif menggunakan teknik domain frekuensi. Ide dasar noise periodik dimunculkan sebagai konsentrasi ledakan energi dalam transformasi Fourier, pada lokasi yang bersesuaian dengan frekuensi dari interferensi periodik. Pendekatannya adalah menggunakan selective filter untuk mengisolasi noise [10].

Selective Filteradalah filter yang bekerja dengan cara melakukan seleksi pada

area citra digital yang akan dilakukan proses filter. Dalam skripsi ini, selective filter yang akan uji adalah Band Reject Filter dan Optimum Notch Filter. Berdasarkan tingkatkan kelembutan dari sebuah filter, Filter dapat dibedakan menjadi tiga kategori yaitu:

1. Ideal, merupakan tipe filter yang sangat tajam. Artinya penerapannya sangat tajam di dalam proses filter.

2. Butterworth, merupakan filter antara dimana untuk nilai yang tinggi, Butterworth Filter mendekati bentuk dari ideal filter. Sementara untuk nilai yang rendah, Butterworth lebih lembut mendekati bentuk dari Gaussian filter

3. Gaussian, merupakan filter yang sangat lembut di dalam proses penerapan filternya.

Masing-masing dari selective filter memiliki kriteria dari kategori filter tersebut. Sehingga di dalam implementasinya, Band Reject Filter dan Optimum Notch

Filter diterapkan dan ujicoba untuk masing-masing ideal, butterworth, dan gaussian.

2.3.3.1. Band Reject Filter (BRF)

Band Reject Filter adalah filter yang memproses pada band frekuensi tertentu atau

region kecil dari persegi panjang frekuensi. Formula untuk Ideal Bandreject Filter

𝐻𝐻(𝑢𝑢, 𝑣𝑣) = � 0 𝑗𝑗𝑗𝑗𝑗𝑗𝑗𝑗 𝐷𝐷0− 𝑊𝑊2 ≤ 𝐷𝐷 ≤ 𝐷𝐷0+ 𝑊𝑊

2

1 𝑙𝑙𝑗𝑗𝑗𝑗𝑛𝑛𝑛𝑛𝑦𝑦𝑗𝑗 ...(2.8)[10] Formula untuk Butterworth Bandreject Filter

𝐻𝐻(𝑢𝑢, 𝑣𝑣) = 1 1+� 𝐷𝐷𝑊𝑊

𝐷𝐷2−𝐷𝐷02�

2𝑛𝑛 ...(2.9)[10]

Formula untuk Gaussian Bandreject Filter

𝐻𝐻(𝑢𝑢, 𝑣𝑣) = 1 − 𝑒𝑒−�𝐷𝐷2−𝐷𝐷02𝐷𝐷𝑊𝑊 � 2

Gambar 2.8Perspective plot dari (a)Ideal, (b)Butterworth, dan (c)Gaussian Band Reject Filter [11]

Keterangan formula 2.8, 2.9 dan 2.10:

H(u,v) : merupakan nilai intensitas filter mask pada pixel (u,v) D0 : radius filter

D atau D(u,v): merupakan jarak antara titik (u,v) dalam domain frekuensi W : lebar pita (band)

M, N : menyatakan lebar dan tinggi citra n : orde (khusus untuk Butterworth)

Filter ini nantinya akan menghasilkan filter mask H(u,v) yang sebelumnya telah disinggung pada Gambar 2.5. Nilai dari tiap-tiap elemen pada filter mask yang dihasilkan tidak dipengaruhi oleh intensitas citra digital asli melainkan dipengaruhi oleh dimensi sebuah citra digital itu sendiri.

Sebagai contoh, sebuah citra input dengan ukuran dimensi citra 3 x 3. Maka untuk filter mask dari Band Reject Filter akan menghasilkan filter mask dengan ukuran yang sama yaitu 3 x 3. Banyaknya elemen dari filtermask diketahui dengan mengalikan jumlah lebar dan tinggi citra input. Pada contoh ini akan menghasilkan 9 elemen filter mask.

Dengan D0=80 dan W=10 maka sebelum melakukan pemfilteran terlebih dahulu menghitung nilai array jarak dari D.

Perhitungan array jarak dari D 𝐷𝐷(0,0) = �02_{+ 0}2 _{= 0} 𝐷𝐷(0,1) = �02_{+ 1}2 _{= 1}

𝐷𝐷(0,2) = �02_{+ 2}2 _{= 2} 𝐷𝐷(1,0) = �12_{+ 0}2 _{= 1} 𝐷𝐷(1,1) = �12_{+ 1}2 _{= 1.414214} 𝐷𝐷(1,2) = �12_{+ 2}2 _{= 2.236068} 𝐷𝐷(2,0) = �22_{+ 0}2 _{= 2} 𝐷𝐷(2,1) = �22_{+ 1}2 _{= 2.236068} 𝐷𝐷(2,2) = �22_{+ 2}2 _{= 2.828427}

maka diperolehlah array dari jarak D hasil perhitungan :

0 1 2

1 1.41 2.24 2 2.24 2.83

Perhitungan filter mask untuk ideal Band Reject Filter 1. Hitung nilai untuk a1= 𝐷𝐷0 −𝑊𝑊

2 a1= 80 −10

2 = 75

2. Hitung nilai untuk a2= 𝐷𝐷0 +𝑊𝑊 2 a2= 80 +10

2 = 85

3. Hitung nilai intensitas untuk tiap elemen pixel filter mask H(0,0)  D(0,0)= 0

75 ≤ 𝐷𝐷(0,0) ≤ 85 (salah) maka H(0,0)= 1 H(0,1)  D(0,1)= 1

75 ≤ 𝐷𝐷(0,1) ≤ 85 (salah) maka H(0,1)= 1 H(0,2)  D(0,2)= 2

75 ≤ 𝐷𝐷(0,2) ≤ 85 (salah) maka H(0,2)= 1 H(1,0)  D(1,0)= 1 75 ≤ 𝐷𝐷(1,0) ≤ 85 (salah) maka H(1,0)= 1 H(1,1)  D(1,1)= 1.41 75 ≤ 𝐷𝐷(1,1) ≤ 85 (salah) maka H(1,1)= 1 H(1,2)  D(1,2)= 2.23 75 ≤ 𝐷𝐷(1,2) ≤ 85 (salah) maka H(1,2)= 1 H(2,0)  D(2,0)= 2 75 ≤ 𝐷𝐷(2,0) ≤ 85 (salah) maka H(2,0)= 1 H(2,1)  D(2,1)= 2.23 75 ≤ 𝐷𝐷(2,1) ≤ 85 (salah) maka H(2,1)= 1 H(2,2)  D(2,2)= 2.28 75 ≤ 𝐷𝐷(2,2) ≤ 85 (salah) maka H(2,2)= 1

maka diperolehlah mask filter dari ideal band reject filter sebagai berikut: 1 1 1

1 1 1 1 1 1

Perhitungan filter mask untuk Butterworth Band Reject Filter dengan n=1

𝐻𝐻(0,0) = 1 1 + �_{𝐷𝐷(0,0)}𝐷𝐷(0,0)∗𝑊𝑊2_−𝐷𝐷02� 2 = 1 1 + �₀₋₆₄₀₀0 �2 = 1 𝐻𝐻(0,1) = 1 1 + �_{𝐷𝐷(0,1)}𝐷𝐷(0,1)∗𝑊𝑊2_−𝐷𝐷02� 2 = 1 1 + �₁₋₆₄₀₀10 �2 = 0.999 𝐻𝐻(0,2) = 1 1 + �_{𝐷𝐷(0,2)}𝐷𝐷(0,2)∗𝑊𝑊_{2−𝐷𝐷02}�2 = 1 1 + �₄₋₆₄₀₀20 �2 = 0.999

𝐻𝐻(1,0) = 1 1 + �_{𝐷𝐷(1,0)}𝐷𝐷(1,0)∗𝑊𝑊2_−𝐷𝐷02� 2 = 1 1 + �₁₋₆₄₀₀10 �2 = 0.999 𝐻𝐻(1,1) = 1 1 + �_{𝐷𝐷(1,1)}𝐷𝐷(1,1)∗𝑊𝑊_{2−𝐷𝐷02}�2 = 1 1 + �₂₋₆₄₀₀14.14 �2 = 0.999 𝐻𝐻(1,2) = 1 1 + �_{𝐷𝐷(1,2)}𝐷𝐷(1,2)∗𝑊𝑊2_−𝐷𝐷02� 2 = 1 1 + �₅₋₆₄₀₀22.36 �2 = 0.999 𝐻𝐻(2,0) = 1 1 + �_{𝐷𝐷(2,0)}𝐷𝐷(2,0)∗𝑊𝑊2_−𝐷𝐷02� 2 = 1 1 + �₄₋₆₄₀₀20 �2 = 0.999 𝐻𝐻(2,1) = 1 1 + �_{𝐷𝐷(2,1)}𝐷𝐷(2,1)∗𝑊𝑊2_−𝐷𝐷02� 2 = 1 1 + �₅₋₆₄₀₀22.36 �2 = 0.999 𝐻𝐻(2,2) = 1 1 + �_{𝐷𝐷(2,2)}𝐷𝐷(2,2)∗𝑊𝑊2_−𝐷𝐷02� 2 = 1 1 + �₈₋₆₄₀₀28.28 �2 = 0.999

maka diperolehlah mask filter butterworth Band Reject Filter sebagai berikut: 1 0.99 0.99

0.99 0.99 0.99 0.99 0.99 0.99

Perhitungan filter mask untuk Gaussian Band Reject Filter 𝐻𝐻(0,0) = 1 − 𝑒𝑒−�(𝐷𝐷2(0,0)−𝐷𝐷02𝐷𝐷(0,0)𝑊𝑊 � 2 = 1 − 𝑒𝑒−�0−64000 ∗0 � 2 = 0 𝐻𝐻(0,1) = 1 − 𝑒𝑒−�(𝐷𝐷2(0,1)−𝐷𝐷02𝐷𝐷(0,1)𝑊𝑊 � 2 = 1 − 𝑒𝑒−�1−64001 ∗10 � 2 = 1 𝐻𝐻(0,2) = 1 − 𝑒𝑒−�(𝐷𝐷2(0,2)−𝐷𝐷02𝐷𝐷(0,2)𝑊𝑊 � 2 = 1 − 𝑒𝑒−�4−64002 ∗10 � 2 = 1 𝐻𝐻(1,0) = 1 − 𝑒𝑒−�(𝐷𝐷2(1,0)−𝐷𝐷02𝐷𝐷(1,0)𝑊𝑊 � 2 = 1 − 𝑒𝑒−�1−64001 ∗10 � 2 = 1 𝐻𝐻(1,1) = 1 − 𝑒𝑒−�(𝐷𝐷2(1,1)−𝐷𝐷02𝐷𝐷(1,1)𝑊𝑊 � 2 = 1 − 𝑒𝑒−�1.41 ∗102−6400� 2 = 1

𝐻𝐻(1,2) = 1 − 𝑒𝑒−�(𝐷𝐷2(1,2)−𝐷𝐷02𝐷𝐷(1,2)𝑊𝑊 � 2 = 1 − 𝑒𝑒−�2.23 ∗105−6400� 2 = 1 𝐻𝐻(2,0) = 1 − 𝑒𝑒−�(𝐷𝐷2(2,0)−𝐷𝐷02𝐷𝐷(2,0)𝑊𝑊 � 2 = 1 − 𝑒𝑒−�4−64002 ∗10 � 2 = 1 𝐻𝐻(2,1) = 1 − 𝑒𝑒−�(𝐷𝐷2(2,1)−𝐷𝐷02𝐷𝐷(2,1)𝑊𝑊 � 2 = 1 − 𝑒𝑒−�2.23 ∗105−6400� 2 = 1 𝐻𝐻(2,2) = 1 − 𝑒𝑒−�(𝐷𝐷2(2,2)−𝐷𝐷02𝐷𝐷(2,2)𝑊𝑊 � 2 = 1 − 𝑒𝑒−�2.82 ∗108−6400� 2 = 1

maka diperolehlah mask filter GaussianBand Reject Filter sebagai berikut: 0 1 1

1 1 1 1 1 1

2.3.3.2. Optimum Notch Filter (ONF)

Optimum Notch Filter sama halnya dengan Notch Reject Filter menolakfrekuensi dalam tetangga yang didefinisikan terhadap pusat frekuensi. Filter notch reject dibuat sebagai hasil filter highpass yang pusatnya telah ditranslasikan ke pusat notch. Format umum Notch Reject Filter bisa dilihat pada formula 2.11:

𝐻𝐻𝑁𝑁𝑅𝑅(𝑢𝑢, 𝑣𝑣) = 𝐻𝐻𝑗𝑗(𝑢𝑢, 𝑣𝑣)𝐻𝐻−𝑗𝑗(𝑢𝑢, 𝑣𝑣) ...(2.11)[6]

Di mana Hk(u,v) dan H-k(u,v) adalah filter highpass yang pusatnya pada lokasi(uk, vk).

Q adalah jumlah pasangan notch dalam filter. Komputasi jarak untuk setiap filter dilakukan dengan formula 2.12 dan formula 2.13:

Dk(u,v) =[(u –M/2 – uk)2 + v – N/2 - vk)2]1/2 ... (2.12)[6]

dan

Gambar 2.9. perspective plot dari (a) Ideal, (b) Butterworth, dan (c) Gaussian Notch Filters [6]

Formula Ideal Notch Reject Filter diperoleh dengan:

𝐻𝐻𝑁𝑁𝑅𝑅(𝑢𝑢, 𝑣𝑣) = �0 𝐷𝐷_{1 𝑙𝑙𝑗𝑗𝑗𝑗𝑛𝑛𝑛𝑛𝑦𝑦𝑗𝑗} 𝑗𝑗(𝑢𝑢, 𝑣𝑣) ≤ 𝐷𝐷0 𝑗𝑗𝑎𝑎𝑗𝑗𝑢𝑢 𝐷𝐷−𝑗𝑗(𝑢𝑢, 𝑣𝑣) ≤ 𝐷𝐷0 ...(2.14)[6]

Formula Butterworth Notch Reject Filterdiperoleh dengan: 𝐻𝐻𝑁𝑁𝑅𝑅(𝑢𝑢, 𝑣𝑣) = �_{1+ [𝐷𝐷𝑙𝑙𝑗𝑗/𝐷𝐷}1_{𝑗𝑗(𝑢𝑢,𝑣𝑣)]}2𝑛𝑛� �

1

1+ [𝐷𝐷𝑙𝑙𝑗𝑗/𝐷𝐷−𝑗𝑗(𝑢𝑢,𝑣𝑣)]2𝑛𝑛� ...(2.15)[6]

Formula Gaussian Notch Reject Filter diperoleh dengan: 𝐻𝐻𝑁𝑁𝑅𝑅(𝑢𝑢, 𝑣𝑣) = �1 − 𝑒𝑒−

𝐷𝐷𝑗𝑗(𝑢𝑢,𝑣𝑣)2

2 𝐷𝐷02 � �1 − 𝑒𝑒−𝐷𝐷−𝑗𝑗(𝑢𝑢,𝑣𝑣)22 𝐷𝐷02 � ...(2.16)[6]

2.4. Penilaian Kualitas Citra

Hasil evaluasi mengenai kegunaan sejumlah langkah kualitas objektif untuk gambar menggunakan perhitungan numerik dapat digunakan untuk menspesifikasikan besarnya degradasi dalam gambar yang direkonstruksi. Kombinasi dari perhitungan numerik dan grafis terbukti lebih berguna dalam menilai kualitas gambar [1].

Model Human Visual System (HVS) yang digunakan untuk pengukuran kualitas didasarkan pada pengolahan yang lebih rendah urutan dalam system visual yaitu pemodelan fungsi optik, retina, dan korteks striate. Setiap manusia memiliki kemampuan visual yang berbeda-beda dan pandangan yang berbeda terhadap suatu

objek gambar. Hal ini yang menjadi kelemahan dari penilaian kualitas gambar menggunakan HVS. Untuk itulah penulis menggunakan perhitungan numerik MSE dan PSNR sebagai parameter penilai kualitas citra hasil pemfilteran [14].

2.4.1. Mean Square Error(MSE) dan Peak Signal to Noise Ratio(PSNR)

MSE adalah rata-rata kuadrat nilai kesalahan antara citra asli dengan citra hasil pengolahan yang secara matematis dapat dirumuskan pada formula 2.17:

𝑀𝑀𝑀𝑀𝑀𝑀 =_{𝑀𝑀𝑁𝑁}1 ∑ ∑𝑁𝑁−1|(𝑓𝑓(𝑥𝑥, 𝑦𝑦) − 𝑙𝑙(𝑥𝑥, 𝑦𝑦))2_| 𝑦𝑦=0

𝑀𝑀−1

𝑥𝑥=0 ...(2.17)[12] Keterangan:

F(x,y): intensitas citra asli

g(x,y): intensitas citra hasil filter

Semakin kecil nilai MSE,maka semakin bagus kualitas citra hasil filter.

PSNR merupakan nilai perbandingan antara harga maksimum warna pada citra hasil filtering dengan kuantitas gangguan(noise) yang dinyatakan dalam satuan decibel(dB), noise yang dimaksud adalah akar rata-rata kuadrat nilai kesalahan (√𝑀𝑀𝑀𝑀𝑀𝑀). Secara matematis, nilai PSNR dapat dirumuskan pada formula 2.18:

𝑃𝑃𝑀𝑀𝑁𝑁𝑅𝑅 = 20 . log 10 (_{√𝑀𝑀𝑀𝑀𝑀𝑀}255 ) ...(2.18) [13]