Bab 5 Diagram Pohon (Tree diagram)

(1)

Suryadi Siregar Metode Penelitian

KK Astronomi ITB Page 46

Bab 5 Diagram Pohon (Tree diagram)

Diagram pohon adalah cara memvisualisasikan suatu organisasi dari berbacam kemungkinan yang dihasilkan. Untuk tiap tiap kejadian digambarkan dalam satu garis dan ditulis probabilitas yang terjadi. Kemudian pada tiap kemungkinan berikutnya digambarkan lagi garis dan

probabilitas yang terjadi berikutnya

Berikut adalah contoh Tree-Diagramsederhana dari sebuah dadu, yang memberikan kemungkinan 6 sisi yang berbeda.

Ingat tiap outcome (bilangan 1 sampai 6) diragakan dalam satu garis bernilai 1 apabila

kemungkinan itu terjadi. Kita akan lihat bagaimana menghitung probabiltasnya dengan bantuan diagram.

Tree-Diagram tidak bermanfaat untuk kejadian yang bebas (independent), karena probabilitasnya tinggal dikalikan saja. Ingat

( ) ( )

( )

P A dan B =P A ×P B

Tree-Diagram baru berguna untuk menganalisis kejadian yang tidak bebas (dependent)

5.1 Cara Menggambar Tree-diagram

5.2 Estimasi akan terjadi hujan

Pada hari tertentu terjadi hujan, probabilitas terjadinya hujan besok hari adalah 1/3. Jika tidak turun hujan pada hari tertentu, probabilitas hujan hari berikutnya adalah 1/6. Pobabilitas akan

(2)

Suryadi Siregar Metode Penelitian

hujan besok hari adalah 1/5. Pertanyaannya , berapakah probabilitas hujan setelah besok hari ( a day after tomorrow). Gambarkan Tree-diagramnya?

Jawab

Menggambar level -1 Tree-Diagram

Sebelum ditentukan kejadian setelah besok ( a day after tomorrow), mula-mula kita hitung apa yang akan terjadi besok. Diketahui ada 1/5 probabilitas akan hujan besok. Disini informasinya digambarkan dalam Tree-diagram

Menggambar level -2 Tree-Diagram

Dikatakan juga bahwa jika terjadi hujan, hari berikutnya probabilitasnya adalah 1/3. Dengan kata lain jika tidak hujan dalam satu hari hanya ada probabilitas 1/6 akan hujan pada hari berikutnya. Gunakan informasi ini untuk melengkapi diagram.

(3)

Suryadi Siregar Metode Penelitian

Hitung probabilitas

Kita ditanya probabilitas akan terjadi hujan lusa ( a day after tomorrow). Pada

Tree-Diagramdiatas dapat dilihat bahwa ada 2 situasi lusa akan hujan. Ditandai dengan warna merah dibawah

Untuk memperoleh probabilitas pada situasi pertama (bahwa besok dan lusa hujan) kita mempunya probabilitas sepanjang garis merah

(

)

1 1 1

5 3 15

P besok dan lusa hujan = × =

Untuk memperoleh probabilitas pada situasi kedua (besok tidak hujan, tetapi lusa hujan) kita mempunyai probabilitas sepanjang garis merah kedua

(

)

4 1 4 2

5 6 30 15

P besok tidak hujan dan lusa hujan = × = =

Oleh sebab itu probabilitas akan hujan lusa adalah jumlah probabilitas sepanjang kedua garis merah, yakni

1 2 1 5+15=5

(4)

Suryadi Siregar Metode Penelitian

Example 2: Menggambar Tree diagram

5.3 Estimasi permainan Coin

Permainan undi coin. Jika muncul ekor anda dapat poin 2 dan selesai. Jika yang muncul kepala dapat 1 poin, dan dapat lanjutkan, ditambah satu poin. Anda dapat melempar 3 kali setiap satu putaran. Berapakah probabilitas setelah 3 kali putaran. Gambarkan Tree-Diagram untuk kemungkinan yang berbeda

Jawab

Menulis kejadian dan simbolnya

Masing-masing koin mempunyai dua kemungkinan, sebut kepala (H) dan ekot (T), masing-masing outcome mempunyai probabilitas ½. Kita ditanya jumlah poin, sehingga menunjukkan berapa banyak poin tiap outcome

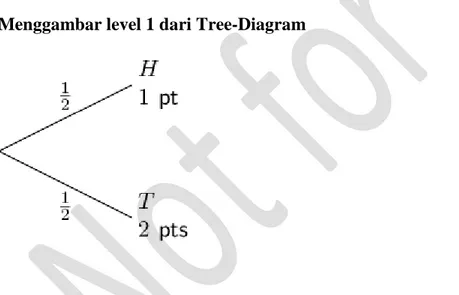
Menggambar level 1 dari Tree-Diagram

Diagram ini menunjukkan kemungkinan yang dihasilkan setelah 1 kali lemparan koin. Ingat kita dapat 3 kali lemparan, sehingga diagram belum lengkap. Jika koin muncul kepala, kita lempar sekali lagi. Jika koin muncul ekor berhenti.

(5)

Suryadi Siregar Metode Penelitian

Dalam diagram ini anda lihat, kita menambah 1 poin untuk setiap lemparan. Setelah tiga lemparan koin permainan selesai.

Tentukan hasil yang relevan dan hitung probabilitas

Kita mendapatkan tepat 3 poin selama permainan. Untuk menentukan hasilnya kita hanya lihat ujung pohonnya. Kita akhiri tepat 3 lemparan, ketika undian selesai.

(

)

(

)

1 1 1 : dengan probabilitas= 2 2 4 1 1 1 1 : : dengan probabilitas= 2 2 2 8 H T H H H × = × × =

Catatan, kita menentukan probabilitas yang dihasilkan dengan mengalikan semua probabilitas sepanjang lintasan dari awal sampai puncak pohon. Selanjutnya jumlahkan probabilitas untuk mendapatkan hasil akhir setelah 3 lemparan=1 1 3

4+ =8 8

5.4 Estimasi Uji Coba Obat

Uji coba obat “Talwar”. Uji-coba dilakukan terhadap 50 orang sakit. Setengah (25 orang) diberi Talwar, sisanya Permen.Talwar memberikan kemungkinan 60% kesembuhan, mereka yang menggunakan Permen masih punya peluang sembuh 10%. Gambarkan Tree-Diagramdan hitung probabilitas Talwar untuk penyembuhan

(6)

Suryadi Siregar Metode Penelitian

Ringkasan permasalahan

Ada dua ketidak pastian dalam soal ini. Tiap orang menerima obat (p=1/2) yang menggunakan Permen (p=1/2). Mereka yang menggunakan obat peluang sembuhnya 3/5. Sedangkan yang menggunakan Permen peluangnya 1/10 atau mereka tetap sakit peluang 2/5 dengan menggunkan Talwar dan 9/10 yang menggunakan Permen

Menggambar Tree- diagram

Pada level 1 kita lihat Tree-Diagrammereka yang menggunakan Talwar dan Permen. Level-2 Tree-Diagramyang memeperlihatkan kesembuhan atau tidak, bergantung pada pilihan

menggunakan Talwar atau Permen.

Menghitung probabilitas yang dihasilkan

Kita hitung probabilitas sepanjang lintasan Tree-diagram, mereka yang sembuh menggunkan Talwar. 1 3 3 2 5 10 1 1 1 2 10 20 × = × =

(7)

Suryadi Siregar Metode Penelitian

( )

3 1 7 10 20 20

p T = + =

5.5 Estimasi Lempar Dadu

You roll a die twice and add up the dots to get a score. Draw a Tree-Diagramto represent this experiment. What is the probability that your score is a multiple of 5?

Permainan undi dadu. Gambarkan Tree-Diagram dan hitung berapakah probabilitas keluarnya balak- 5 (5 bulatan titik) jika dadu dilempar dua kali?

Jawab 1:

Untuk menghemat ruang, probabilitas tidak ditunjukkan pada cabang dari Tree-diagram, namun tiap cabang punya probabilitas 1/6. Kelipatan balak-5 digarisbawahi. Karena probabilitas

masing-masing keluaran besarnya 1/6×1/6 =1/36 dan karena ada 7 keluaran dikalikan dengan 5, diperoleh probabilitas balak-5 adalah 7/36

Problem 2:

Berapakah probabilitas paling sedikit balak-5 dari 6 sisi dadu bila dilempar 4 kali. Petunjuk tidak perlu menunjukkan seluruh kemungkinan dari masing-masing lemparan dari dadu. Kita tertarik apakah yang keluar balak-5 atau bukan

(8)

Suryadi Siregar Metode Penelitian

Keluaran balak-5 paling sedikit dalam 5 lemparan diberi tanda pada tree-diagram. Jumlahkan semua probabilitas pada cabang yang diberikan menghasilkan

1 5 1 5 5 1 5 5 5 1 671 6 6 6 6 6 6 6 6 6 6 1296   ₊ _×  ₊ _{× ×}  ₊ _{× × ×} ₌                 Problem 3:

Undian sebuah koin dengan 4 lemparan

1. Berapakah prbabilitas untuk mendapatkan tepat 3 kali kepala?

2. Berapakah probabiltas untuk mendapatkan paling sedikit 3 kali kepala? Jawab 3:

Ada 24=16 kemungkinanuntuk 4 kali lemparana. Ada 4 keluaran yang tepat 3 kepala, nyatakan dengan

{

H H H T: : :

} {

, H H T H: : :

} {

, H T H H: : :

} {

, T H H H: : :

}

1. Oleh sebab itu probabiliats keluar kepala 3 kali adalah 4/16=1/4

2. Untuk memperoleh paling sedikit 3 kepala atau tepat 4 kepala . Kita sudah lihat ada 4 cara untuk memperoleh 3 kepala. Ada 1 cara memperoleh tepat 4 kepala sebut keluarannya

{

H H H H: : :

}

akibatnya ada 5 cara memperoleh 3 kepala dan probabiltasnya adalah 5/16 Problem 4:

(9)

Suryadi Siregar Metode Penelitian

Anda mengundi 4 koin berbeda pada satu waktu

1. Berapakah probabilitas mendapatlan tepat 3 kepala

2. Berapakah probabilitas mendapatlan paling sedikit 3 kepala

Jawab 4:

1. Secara matematika problem ini tepat sama dengan problem sebelumnya, karena itu tidak penting bila kita undi 4 koin berbeda pada waktu yang sama atau koin yang sama diundi 4 kali. Jawabannya sama tetap 1/4