MATEMATIKA DISKRIT
UNTUK
ILMU KOMPUTER DAN SAINS
(Discreate Mathematical For Computer & Sains)Lecture Module Version
Materi diringkas dari : Rinaldi Munir (Dosen ITB)
Dosen Pengampu:
Maxrizal, S.Pd.Si., M.Sc.
JURUSAN SISTEM INFORMASI
STMIK ATMA LUHUR PANGKALPINANG
DAFTAR ISI
Daftar Isi ... 2
Pertemuan 1. Pengantar Matematika Diskrit... 3
Pertemuan 2. Logika ... 5
Pertemuan 3. Himpunan ... 13
Pertemuan 4. Fungsi ... 24
Pertemuan 5. Induksi Matematika ... 36
Pertemuan 6. Teori Bilangan ... 41
Pertemuan 9. Aplikasi Teori Bilangan ... 52
Pertemuan 10. Kombinatorika (Permutasi) ... 63
Pertemuan 11. Kombinatorika (Kombinasi)... 70
Pertemuan 12. Pengantar Teori Graf ... 75
Pertemuan 13. Graf Khusus ... 87
Pertemuan 1
Pengantar Matematika Diskrit
A. Matematika Diskrit
Matematika diskrit adalah cabang matematika yang mengkaji objek-objek diskrit. Suatu benda dikatakan diskrit jika:
1. Terdiri dari sejumlah berhingga elemen yang berbeda, atau 2. Elemen-elemennya tidak bersambungan (unconnected).
Contoh:
Himpunan bilangan bulat (integer)
B. Peran Matematika Diskrit
Pada prinsipnya, komputer digital bekerja secara diskrit. Informasi yang disimpan dan dimanipulasi oleh komputer adalah dalam bentuk diskrit sehingga matematika diskrit merupakan ilmu dasar dalam pendidikan informatika atau ilmu komputer.
Matematika diskrit memberikan landasan matematis untuk kuliah-kuliah lain di informatika seperti algoritma, struktur data, basis data, otomata dan teori bahasa formal, jaringan komputer, keamanan komputer, sistem operasi, teknik kompilasi, dsb. Karena sangat penting dan krusial, matematika diskrit sering dikatakan matematika-nya orang informatika.
Beberapa materi yang akan dibahas dalam matematika diskrit, yaitu: 1. Logika (logic)
2. Teori Himpunan (set)
3. Relasi dan Fungsi (relation and function) 4. Induksi Matematik (mathematical induction) 5. Teori Bilangan Bulat (integers)
8. Kompleksitas Algoritma (algorithm complexity)
C. Contoh Permasalah Matematika Diskrit
Contoh-contoh persoalan di dalam matematika diskrit, yaitu:
1. Berapa banyak kemungkinan jumlah password yang dapat dibuat dari 8 karakter? 2. Bagaimana nomor ISBN sebuah buku divalidasi?
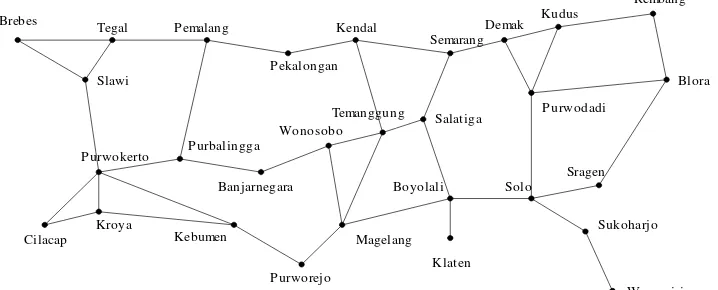
3. Berapa banyak string biner yang panjangnya 8 bit yang mempunyai bit 1 sejumlah ganjil? 4. Bagaimana menentukan lintasan terpendek dari satu kota a ke kota b?
5. Buktikan bahwa perangko senilai n (n 8) rupiah dapat menggunakan hanya perangko 3 rupiah dan 5 rupiah saja
6. Diberikan dua buah algoritma untuk menyelesaian sebuah persoalan, algoritma mana yang terbaik?
7. Bagaimana rangkaian logika untuk membuat peraga digital yang disusun oleh 7 buah batang (bar)?
8. Dapatkah kita melalui semua jalan di sebuah kompleks perubahan tepat hanya sekali dan kembali lagi ke tempat semula?
Pertemuan ke 2
Logika
A. Proposisi
Logika merupakan dasar dari semua penalaran (reasoning). Penalaran didasarkan pada hubungan antara pernyataan (statements). Pernyataan atau kalimat deklaratif yang bernilai benar (true) atau salah (false), tetapi tidak keduanya disebut proposisi.
Contoh:
1. “12 10 “merupakan proposisi bernilai salah.
2. “Sekarang tahun 2015 dan 9 1 “merupakan proposisi bernilai salah.
3. “Jangan memakai HP saat kelas sedang berlangsung” bukan merupakan proposisi. 4. “y 2 5 “ bukan merupakan proposisi.
Suatu proposisi dilambangkan dengan huruf kecil yaitu p q r, , , .
B. Menggabungkan 2 Proposisi atau Lebih
Jika diberikan proposisi p dan q maka berlaku: 1. Ingkaran : tidak p
Ingkaran dari p dinotasikan p 2. Konjungsi (conjunction): p dan q
Dinotasikan : pq,
3. Disjungsi (disjunction): p atau q Dinotasikan : pq
4. Implikasi : Jika p maka q
Dinotasikan : pq
5. Biimplikasi : p jika dan hanya jika q
Perhatikan bahwa p dan q disebut proposisi atomic. Sedangkan kombinasi p dengan q
menghasilkan proposisi majemuk (compound proposition).
C. Tabel Kebenaran
Berikut ini disajikan tabel kebenaran:
p q p pq pq pq pq
B B S B B B B
B S S S B S S
S B B S B B S
S S B S S B B
Contoh:
Tentukan tabel kebenaran dari ekspresi logika
pq
p ! Jawab:p q p pq
pq
pB B S B B
B S S S S
S B B B B
S S B B B
D. Tautologi dan Kontradiksi
Suatu proposisi majemuk disebut tautologi jika semua kasusnya bernilai benar (B). Sedangkan proposisi majemuk disebut kontradiksi untuk semua kasus bernilai salah (S). Jika tidak berlaku keduanya makan proposisi itu disebut kontingensi (campuran B dan S).
Contoh:
(Silakan cek tabel kebenaran)
1.
p
pq
merupakan tautologi.E. Ekuivalensi logis
Kedua ekspresi logika disebut ekuivalensi logis jika memiliki nilai kebenaran yang sama pada tiap baris tabel kebenaran.Selanjutnya, ekuivalensi logis disimbolkan dengan “”.
Contoh:
1. p q q p,
2. p q q p.
F. Hukum-Hukum Logika
Beberapa hukum-hukum logika, yaitu:
No. Nama Hukum Logika Ekuivalensi Logis 1 Hukum Negasi Ganda p p
2 Hukum Komutatif
p q q p
p q q p
p q q p
3 Hukum Asosiatif
p q
r p
q r
p q
r p
q r
4 Hukum Distributif
p q r p q pr
p q r p q pr
5 Hukum Idempoten
p p p
p p p
6 Hukum Identitas
p S p
p B B
p S S
p B p
p p S
8 Hukum DeMorgan
p q
p q
p q
p q
9 Hukum Kontrapositif p q q p 10 Hukum Implikasi p q p q
11 HukumBiimplikasi p q
pq
q p
12 Hukum Absorsi
p pq p
p pq p
Contoh:
Buktikan sifat ekuivalensi logis dengan menggunakan hukum logika pada ekspresi
p q
p q
p.Jawab:
p q
p q
p
q q
(Hukum Distributif)p B
(Hukum Negasi)
p
≡ p (Hukum Identitas) Jadi, terbukti
p q
p q
p.G. Sifat Implikasi
Sifat Implikasi secara umum disajikan dalam tabel berikut: Implikasi pq Konvers qp Invers p q Kontraposisi q p
Contoh:
Tentukan konvers, invers, dan kontraposisi dari “Jika Amir mempunyai mobil maka ia orang kaya”
Konvers : Jika Amir orang kaya maka ia mempunyai mobil.
Invers : Jika Amir tidak mempunyai mobil maka ia bukan orang kaya. Kontraposisi : Jika Amir bukan orang kaya maka ia tidak mempunyai mobil.
Selanjutnya perbandingan nilai kebenaran keempat sifat di atas akan ditunjukkan pada tabel kebenaran berikut ini.
H. Penarikan Kesimpulan Dengan Aturan Inferensi
Selain menggunakan hukum-hukum logika, dalam penarikan kesimpulan, kita membutuhkan beberapa konsep tambahan, yaitu:
e. Simplikatif
Diberikan beberapa premis berikut ini:
1:
Apakah penarikan kesimpulan dari premis-premis di atas valid? Jawab:
Langkah ke- Ekspresi Alasan 1 pq Premis 1 2 qr Premis 2 3 r Premis 3
4 pr Langkah 1,2; Silogisme hipotetikal 5 p Langkah 3,4; Modus tollens
Perhatikan bahwa pada langkah 5 telah menunjukkan kesimpulan yang diketahui. Dengan demikian, argumen yang diselidiki valid.
Contoh:
Diberikan beberapa premis berikut ini:
1:
2:
P Anda tidak pintar membuat program atau mengelola anti virus. :
C Anda pintar membuat program atau mengelola anti virus. Apakah penarikan kesimpulan dari premis-premis di atas valid? Jawab:
Sebelumya untuk memudahkan penalaran, premis-premis dan kesimpulan di atas kita ubah ke dalam simbol, sehingga diperoleh:
1:
P pq.
2:
P p r. :
C qr.
Berikut langkah pembuktian:
Langkah ke- Ekspresi Alasan 1 pq Premis 1 2 p r Premis 2
3 q p Langkah 1; Hukum Komutatif
4 q p Langkah 3; Hukum Implikasi 5 pr Langkah 2; Hukum Implikasi
6 q r Langkah 4,5; Silogisme Hipotetikal 7 qr Langkah 6; Hukum Implikasi
Perhatikan bahwa langkah 7 menunjukkan kesimpulan yang diberikan. Jadi, penarikan kesimpulan dari argumen di atas valid.
I. Latihan Mandiri
1. Manakah yang merupakan proposisi? Jika merupakan proposisi maka tentukanlah nilai kebenarannya.
a. Siapa namamu? b. Hari ini hari Rabu. c. x y 0
d. 15 adalah bilangan negatif.
2. Buatlah tabel kebenaran dari ekspresi logika
pq
q
p .3. Diberikan ekspresi logika
p q
p q
. Tentukan apakah termasuk tautologi, kontradiksi atau kontingensi?4. Tentukan invers, konvers dan kontraposisi dari “Jika hari hujan maka kuliah matematika diskrit diliburkan”
5. Tunjukkan validitas dari kesimpulan dengan aturan inferensi. Jika Zeta rajin bekerja maka ia mendapat reputasi kerja yang baik.
Bila Zeta memiliki reputasi yang baik maka karirnya akan meningkat dengan cepat. Karir Zeta mandek.
Pertemuan 3
Himpunan
A. Pengertian Himpuan
Himpunan (sets) adalah kumpulan objek-objek yang didefinisikan dengan jelas.
Contoh:
a. Kumpulan mahasiswa jurusan Teknik Informatika STIMIK Atma Luhur.
b. Kumpulan mahasiswa jurusan Manajemen Informatika yang berumur di atas 19 tahun.
Dalam matematika, tidak semua pengelompokkan benda atau manusia disebut dengan himpunan.
Contoh:
a. Kumpulan mahasiswa jurusan TI yang ganteng. b. Kumpulan masakan Bangka yang enak.
Perhatikan bahwa kedua contoh diatas melibatkan sisi kualitas sehingga menimbulkan sifat ambiguitas. Kita tidak bisa mendefinisikan dengan jelas, kriteria-kriteria ganteng ataupun kriteria suatu makanan dikatakan enak. Pada intinya, setiap kelompok yang tidak dapat didefinisikan dengan jelas bukanlah suatu himpunan.
B. Notasi Himpunan
Himpunan biasanya dinyatakan dengan huruf kapital seperti A B C, , , dan diikuti oleh tanda kurung kurawal
. Anggota atau elemen dari himpunan berupa huruf, biasanya dinyatakan dalam huruf kecil.Contoh:
b. B
x x3,x
c. C
a b c d, , ,
Berdasarkan contoh di atas, 1 adalah anggota dari himpunan A dinotasikan 1A dan d adalah anggota himpunan C , dinyatakan sebagai dC. Selanjutnya, a bukan anggota dari himpunanA dinotasikan aA. Banyaknya anggota himpunan A ada 3 dan dinotasikan
3n A atau A 3 .
Selanjutnya cara penyajian pada contoh a) dan c) disebut bentuk pendaftaran (tabular-form) dan cara penyajian pada contoh c) disebut bentuk perincian (set-builder form).
Contoh:
1. Misalkan A
1,3,5,
2. B
Andi Canas Toni, ,
Bentuk diatas bisa diubah menjadi bentuk perincian (set-builder form). 1. A
x x adalah bilangan ganjil
2. B
x x adalah pelajar pemenang lomba
Perhatikan bahwa pada bentuk pendaftaran (tabular-form), semua elemen/anggota himpunan dituliskan dalam kurung kurawal. Sedangkan pada bentuk perincian (set-builder form), elemen himpunan hanya diwakili dengan sifat/ketentuan yang sesuai.
C. Jenis-Jenis Himpunan
a. Himpunan kosong (null sets)
Himpunan kosong adalah himpunan yang tidak memiliki anggota. Notasi untuk himpunan kosong adalah
atau .Contoh:
2.
2
4
B x x dan xganjil
Jelas bahwa A , karena tidak ada manusia normal yang berkaki empat. Sedangkan B , karena tidak ada angka ganjil yang memenuhi persamaan itu. Nilai x yang mungkin hanyalah
2 atau 2 .
b. Himpunan semesta (universal sets)
Himpunan yang memuat semua anggota yang sedang dibicarakan disebut himpunan semesta.
Contoh:
1. Misalkan A
1,3,5,
atau himpunan bilangan ganjil dan B
2, 4, 6,
atau himpunan bilangan genap. Paling tidak kita bisa memilih himpunan bilangan asli
sebagai himpunan semesta yaitu S .2. Misalkan diberikan beberapa himpunan berikut ini.
A x x adalah mahasiswaTI STMIK
C x x adalah mahasiswa MI STMIK
Maka dapat dipilih himpunan semesta yaitu S
x x adalah mahasiswa STIMIK
.c. Himpunan bagian (subsets)
Himpunan A dikatakan himpunan bagian dari himpunan B jika setiap anggota A merupakan
anggota B, yang dinotasikan dengan AB.
Jika paling sedikit ada satu anggota dari A bukan merupakan anggota B maka A bukan
himpunan bagian dari B, dinotasikan AB.
Contoh:
Perhatikan bahwa AB dibaca A subset B atau bisa juga dinyatakan sebagai B super set
dari A .
Jika himpunan A memiliki n anggota maka banyak himpunan bagian dari A adalah 2n. Misalkan A
a b c, ,
maka himpunan bagiannya adalah
,
1 ,
2 ,
3 ,
1, 2 ,
1, 3 ,
2,3 dan
1, 2,3
.d. Keluarga himpunan (family of sets)
Himpunan A dinamakan keluarga himpunan jika semua elemennya berupa himpunan.
Contoh :
1. A
1 , 1, 2
2. B
x x bilangan genap
,
a b c, ,
,
Selanjutnya C
0, 1 ,
a b,
bukan merupakan contoh keluarga himpunan karena ada satu anggota yang bukan merupakan himpunan yaitu 0 .e. Himpunan kuasa (power sets)
Himpunan kuasa
2A adalah keluarga himpunan dari semua himpunan bagian dari himpunanA.
Contoh:
1. Diberikan A
1, 2 , maka banyak himpunan bagian dari A adalah 22 4 yaitu
, 1 , 2 , 1, 2
.
Jadi 2A
, 1 , 2 , 1, 2
.2. Diberikan B
a , maka banyak himpunan bagian dari B adalah 212 yaitu
, a
Jadi 2B
,
a
.f. Himpunan terhingga (finite) dan tak terhingga (infinite)
Himpunan terhingga adalah himpunan yang banyak anggotanya berhingga.
Contoh:
1. Himpunan
2. Himpunan dengan n anggota.
3. M
x x adalah mahasiswa TI STIMIK
4. P
y y adalah banyak UKM yang ada di STMIK
Himpunan tak terhingga adalah himpunan yang berkorespondensi satu-satu dengan bilangan asli, yaitu himpunan yang banyak anggotanya tak terhingga.
Contoh:
1. Himpunan bilangan asli. 2. Himpunan bilangan bulat.
g. Himpunan terhitung (countable) dan tak terhitung (uncountable)
Himpunan terhitung adalah himpunan terhingga (finite) atau tak terhingga (infinite). Contoh:
1. A
a b c, ,
2. Himpunan bilangan ganjil.
Himpunan tak terhitung adalah himpunan yang tidak terhitung jumlahnya.
h. Himpunan saling lepas (disjoint sets)
Himpunan A dan B dikatakan saling lepas jika himpunan A dan B tidak memiliki elemen
yang sama.
Contoh:
Misalkan himpunan A
1, 2,3
dan B
a b, maka himpunan A dan B dikatakan salinglepas.
D. Kesamaan Himpunan
Himpunan A dikatakan sama dengan himpunan B jika setiap elemen dari A merupakan
elemen dari B dan sebaliknya.
Contoh:
1. A
1, 2,3
dan B
3, 2,1
maka AB.2. C
1, 2, 2, 2,1
dan D
2,1, 2
maka CD.3. E
5, 6 ,
2
11 30
F x x x maka EF .
Perhatikan bahwa jika ada elemen yang sama cukup dihitung sekali dan pada himpunan urutan elemen tidak dipermasalahkan.
Berdasarkan sifat himpunan bagian, himpunan A dikatakan sama dengan himpunan B jika
berlaku AB dan BA .
E. Representasi Himpunan
a. Diagram Venn
Pada diagram Venn, daerah persegi untuk menggambarkan himpunan semesta dan daerah lingkaran untuk menggambarkan himpunan di dalamnya.
Contoh:
1. Misalkan S
a b c d e, , , ,
, A
a b, dan B
c d, .2. Diberikan diagram Venn sebagai berikut.
Dari diagram diperoleh S
a b c d e, , , ,
, AS dan B
c d, . Perhatikan bahwa berlaku BA .Pada contoh 1, himpunan A dan B tidak dapat diperbandingkan (not comparable) sedangkan pada contoh 2, himpunan A dan B dapat diperbandingkan (comparable).
b. Diagram garis
Contoh:
1. Misalkan A
1, 2,3
, B
3 dan C
1, 2 .Jelas bahwa BA , CA dan BC .
2. Perhatikan diagram garis berikut ini!
Jelas bahwa B A E , B A F, C A E, C A F, BCdan EF.
F. Operasi Pada Himpuan
Jika kita memiliki dua himpunan atau lebih, kita bisa mengoperasikan himpunan-himpunan tersebut.
Beberapa operasi yang dikenakan pada himpunan: a. Irisan
A B x xA dan xB
b. Gabungan
c. Penjumlahan
, ,
A B x xA xB x A B
d. Selisih
A B x xA dan xB
e. Komplemen
c
A x xA dan xS
Contoh:
1. Diketahui S
1, 2, ,10
, A
2,3 dan B
2, 4, 6,8,10
maka diperoleh a. A B
2b. A B
2,3, 4, 6,8,10
c. A B
3, 4, 6,8,10
d. A B
3e. B A
4, 6,8,10
f. Ac
1, 4,5, 6, 7,8,9,10
g. Bc
1,3,5, 7,9
2. Perhatikan diagram Venn berikut ini!
Berdasarkan diagram diperoleh S
a b c d e f g h, , , , , , ,
a. A
a b f h, , ,
c. C
d e f g h, , , ,
d. A B e. A C
f h,G. Sifat-Sifat Operasi Himpunan
Beberapa sifat yang berlaku pada operasi himpunan: a. Sifat komutatif
A B B A dan A B B A.
b. Sifat Asosiatif
AB
C A
BC
dan
AB
C A
BC
. c. Sifat Distributif
A BC AB BC dan A
BC
AB
BC
. d. Sifat IdentitasA , A S A,A A dan A S S. e. Sifat Idempoten
A A A dan A A A.
f. Sifat De Morgan
c c cAB A B dan
c c cAB A B .
H. Latihan Soal
1. Manakah yang merupakan himpunan bagian dari
bilangan kelipatan 3,
A x x x
a. M
0,3, 6,9
b. N
x x bilangan kelipatan 6, x
c. O
99,103,106
2. Diberikan S
x x7,xbil cacah.
7, .
A x x xbil prima .
2 4,
B x x x
Tentukanlah: a. AB b. AB c. A B d. A B e. c c
A B
f.
AB
cg.
AB
c h. Diagram Venn i. Diagram Garis3. Perhatikan diagram Venn di bawah ini!
Tentukan himpunan dari a. Laut
b. Sungai c. Danau
e. Laut Sungai f. Sungai Danau
g. Laut Danau Sungai
4. Berikut ini daftar olahraga favorit beberapa mahasiswa kelas Agribisnis A.
Yuda menyukai sepak bola dan futsal. Siska menyukai bulutangkis. Amri tidak menyukai sepak bola, dan menyukai futsal. Bambang menyukai semua jenis olahraga. Aqida tidak menyukai semua jenis olahraga yang ada.
Pertemuan 4
Fungsi
A. Pengertian Fungsi
Diberikan dua buah himpunan tak kosong yaitu himpunan A dan B. Elemen pada himpunanA dapat dihubungkan dengan elemen pada himpunan B , hubungan atau aturan ini dinamakan
relasi.
Relasi yang mengaitkan setiap elemen A dengan tepat satu elemen B disebut dengan fungsi.
Fungsi dari himpunan A ke B ditulis f A: B, dimana A disebut sebagai daerah asal atau domain
Df dan B disebut sebagai daerah kawan atau kodomain. Selanjutnya aAdisebut sebagai pra-bayangan (pre-image) dari b dan f a
B disebut sebagai bayangan(image) dari a. Himpunan Rf
b B b f a a
, A
disebut sebagai daerah hasil ataurange.
Berikut ini ilustrasi dari suatu fungsi.
fungsi
bukan fungsi, sebab ada elemen A yang mempunyai 2 kawan
A yang tidak mempunyai kawan
Untuk lebih mudahnya memahami definisi fungsi pahami 2 aturan berikut ini:
1) Setiap elemen himpunan A harus habis terkait dengan elemen himpunan B. 2) Tidak boleh membentuk cabang seperti ini.
Contoh:
Diberikan himpunan A
x, y, z,
dan himpunan B
1, 2, . didefinisikan suatu fungsi:
f AB sebagai berikut: x1, y2, z1 atau f x
1,f y
2, f z
1 .Dari contoh diatas dapat dikatakan bahwa image darix adalah 1 atau x adalah pre-image dari 1 dan Rf
1, 2 .B. Cara menyajikan fungsi
Fungsi dapat dispesifikasikan dalam berbagai bentuk, diantaranya: 1. Himpunan pasangan terurut.
Contoh: Penulisan pada relasi. R
1,a , 2,a , 3,b
. 2. Formula pengisian nilai (assignment).Contoh: f(x) = 2x + 10, f(x) = x2, dan f(x) = 1/x.
3. Kata-kata
Contoh: “f adalah fungsi yang memetakan jumlah bit 1 di dalam suatu string biner”.
4. Kode program (source code) Contoh: Fungsi menghitung |x| function abs(x:integer):integer; begin
abs:=x; end;
Contoh:
Diberikan relasi
f = {(1, u), (2, v), (3, w)} dari A = {1, 2, 3} ke B = {u, v, w}. Apakah f merupakan fungsi? Jawab:
Relasi f adalah fungsi dari A ke B. Karena f(1) = u, f(2) = v, dan f(3) = w. Daerah asal dari f
adalah A dan daerah hasil adalah B. Range atau daerah hasil dari f adalah {u, v, w}, yang dalam hal ini sama dengan himpunan B.
Contoh:
Diberikan relasi
f = {(1, u), (2, u), (3, v)} dari A = {1, 2, 3} ke B = {u, v, w}. Apakah f merupakan fungsi? Jawab:
Relasi f adalah fungsi dari A ke B, meskipun u merupakan bayangan dari dua elemen A. Daerah asal fungsi adalah A, daerah hasilnya adalah B, dan range fungsi adalah {u, v}.
Contoh:
Diberikan relasi
f = {(1, u), (2, v), (3, w)} dari A = {1, 2, 3, 4} ke B = {u, v, w}. Apakah f merupakan fungsi? Jawab:
Relasi f bukan fungsi, karena tidak semua elemen A dipetakan ke B.
Contoh:
Diberikan relasi
f = {(1, u), (1, v), (2, v), (3, w)} dari A = {1, 2, 3} ke B = {u, v, w}. Apakah f merupakan fungsi? Jawab:
a 1
A B
2
3
4
5 b
c
d
C. Jenis-Jenis Fungsi
Ada 3 macam jenis fungsi yaitu: 1. Fungsi Injektif
Fungsi f dikatakan satu-ke-satu (one-to-one) atau injektif (injective) jika tidak ada dua elemen himpunan A yang memiliki bayangan sama.
Contoh:
Diberikan relasi
f = {(1, w), (2, u), (3, v)}
dari A = {1, 2, 3} ke B = {u, v, w, x}. Apakah merupakan fungsi injektif? Jawab:
Relasi f adalah fungsi satu-ke-satu.
Contoh:
Diberikan relasi
f = {(1, u), (2, u), (3, v)} dari A = {1, 2, 3} ke B = {u, v, w}. Apakah merupakan fungsi injektif? Jawab:
Relasi f bukan fungsi satu-ke-satu, karena f(1) = f(2) = u.
Contoh:
Misalkan f : Z Z. Tentukan apakah f(x) = x2 + 1 merupakan fungsi satu-ke-satu?
a 1
A B
2 3 b
c d
f(x) = x2 + 1 bukan fungsi satu-ke-satu, karena untuk dua x yang bernilai mutlak sama tetapi
tandanya berbeda nilai fungsinya sama, misalnya f(2) = f(-2) = 5 padahal –2 2. 2. Fungsi Surjektif
Fungsi f dikatakan dipetakan pada (onto) atau surjektif (surjective) jika setiap elemen himpunan
B merupakan bayangan dari satu atau lebih elemen himpunan A.
Dengan kata lain seluruh elemen B merupakan jelajah atau range dari f. Fungsi f disebut fungsi pada himpunan B.
Contoh:
Diberikan relasi
f = {(1, u), (2, u), (3, v)} dari A = {1, 2, 3} ke B = {u, v, w} . Apakah merupakan fungsi pada? Jawab:
Relasi f bukan fungsi pada karena w tidak termasuk jelajah atau range dari f.
Contoh:
Diberikan relasi
f = {(1, w), (2, u), (3, v)} dari A = {1, 2, 3} ke B = {u, v, w}. Apakah merupakan fungsi pada?
Relasi f merupakan fungsi pada karena semua anggota B merupakan jelajah dari f.
Contoh:
Misalkan f : Z Z. Tentukan apakah f(x) = x2 + 1 merupakan fungsi pada?
Jawab:
a
Fungsi f dikatakan berkoresponden satu-ke-satu atau bijeksi (bijection) jika ia fungsi satu-ke-satu dan juga fungsi pada.
Contoh:
Diberikan relasi
f = {(1, u), (2, w), (3, v)} dari A = {1, 2, 3} ke B = {u, v, w}. Apakah merupakan fungsi bijektif? Jawab:
Relasi f adalah fungsi yang berkoresponden satu-ke-satu, karena f adalah fungsi satu-ke-satu
Jika f adalah fungsi berkoresponden satu-ke-satu dari A ke B, maka kita dapat menemukan balikan (invers) dari f.
Balikan fungsi dilambangkan dengan f –1. Misalkan a adalah anggota himpunan A dan b adalah anggota himpunan B, maka f -1(b) = a jika f(a) = b.
Fungsi yang berkoresponden satu-ke-satu sering dinamakan juga fungsi yang invertible (dapat dibalikkan), karena kita dapat mendefinisikan fungsi balikannya. Sebuah fungsi dikatakan not invertible (tidak dapat dibalikkan) jika ia bukan fungsi yang berkoresponden satu-ke-satu, karena fungsi balikannya tidak ada.
Contoh:
Diberikan relasi
f = {(1, u), (2, w), (3, v)} dari A = {1, 2, 3} ke B = {u, v, w}. Apakah fungsi ini invertible? Jawab:
Relasi f adalah fungsi yang berkoresponden satu-ke-satu. Balikan fungsi f adalah
f -1= {(u, 1), (w, 2), (v, 3)}
Jadi, f adalah fungsi invertible.
Contoh:
Tentukan balikan fungsi f(x) = x – 1.
Jawab:
Fungsi f(x) = x – 1 adalah fungsi yang berkoresponden satu-ke-satu, jadi balikan fungsi tersebut
ada. Misalkan f(x) = y, sehingga y = x – 1, maka x = y + 1. Jadi, balikan fungsi balikannya adalah
f-1(y) = y +1.
E. Komposisi Dua Fungsi.
Misalkan g adalah fungsi dari himpunan A ke himpunan B, dan f adalah fungsi dari himpunan B
ke himpunan C. Komposisi f dan g, dinotasikan dengan f g, adalah fungsi dari A ke C yang didefinisikan oleh
Contoh:
Diberikan fungsi
g = {(1, u), (2, u), (3, v)} yang memetakan A = {1, 2, 3} ke B = {u, v, w}, dan fungsi
f = {(u, y), (v, x), (w, z)}
yang memetakan B = {u, v, w} ke C = {x, y, z}. Tentukan fungsi komposisi dari A ke C.
Jawab:
Fungsi komposisi dari A ke C adalah
fg = {(1, y), (2, y), (3, x) }
Contoh:
Diberikan fungsi f(x) = x – 1 dan g(x) = x2 + 1. Tentukan fg dan gf .
Jawab:
a. (fg)(x) = f(g(x)) = f(x2 + 1) = x2 + 1 – 1 = x2.
b. (g f)(x) = g(f(x)) = g(x – 1) = (x –1)2 + 1 = x2 - 2x + 2.
F. Beberapa Fungsi Khusus
1. Fungsi Floor dan Ceiling
Misalkan x adalah bilangan riil, berarti x berada di antara dua bilangan bulat. Fungsi floor dari x:
x menyatakan nilai bilangan bulat terbesar yang lebih kecil atau sama dengan x
Fungsi ceiling dari x:
x menyatakan bilangan bulat terkecil yang lebih besar atau sama dengan x
Dengan kata lain, fungsi floor membulatkan x ke bawah, sedangkan fungsi ceiling membulatkan x
ke atas.
Contoh:
Beberapa contoh nilai fungsi floor dan ceiling:
0.5 = 0 0.5 = 1 4.8 = 4 4.8 = 5 – 0.5 = – 1 – 0.5 = 0
–3.5 = – 4 –3.5 = – 3
Contoh:
Di dalam komputer, data dikodekan dalam untaian byte, satu byte terdiri atas 8 bit. Jika panjang data 125 bit, maka jumlah byte yang diperlukan untuk merepresentasikan data adalah 125/8 = 16 byte. Perhatikanlah bahwa 16 8 = 128 bit, sehingga untuk byte yang terakhir perlu ditambahkan 3 bit ekstra agar satu byte tetap 8 bit (bit ekstra yang ditambahkan untuk menggenapi 8 bit disebut padding bits).
2. Fungsi modulo
Misalkan a adalah sembarang bilangan bulat dan m adalah bilangan bulat positif.
a mod m memberikan sisa pembagian bilangan bulat bila a dibagi dengan m a mod m = r sedemikian sehingga a = mq + r, dengan 0 r < m.
Contoh:
Beberapa contoh fungsi modulo 25 mod 7 = 4 15 mod 5 = 0 3612 mod 45 = 12 0 mod 5 = 5
–25 mod 7 = 3 (sebab –25 = 7 (–4) + 3 )
3. Fungsi Faktorial
1 , 0
!
1 2 . ( 1) , 0
n n
n n n
1 , 0
Untuk kasus perpangkatan negatif,
1
Fungsi f dikatakan fungsi rekursif jika definisi fungsinya mengacu pada dirinya sendiri.
Contoh: Fungsi rekursif disusun oleh dua bagian:
a. Basis
Bagian yang berisi nilai awal yang tidak mengacu pada dirinya sendiri. Bagian ini juga sekaligus menghentikan definisi rekursif.
b. Rekurens
Bagian ini mendefinisikan argumen fungsi dalam terminologi dirinya sendiri. Setiap kali fungsi mengacu pada dirinya sendiri, argumen dari fungsi harus lebih dekat ke nilai awal (basis).
Contoh definisi rekursif dari faktorial: a. basis:
n! = 1 , jika n = 0 b. rekurens:
Contoh:
Hitunglah nilai 5!. Jawab:
5! dihitung dengan langkah berikut:
(1) 5! = 5 4! (rekurens)
Di bawah ini adalah contoh-contoh fungsi rekursif lainnya:
G. Latihan
1. Diberikan relasi
f = {(1, u), (2, u), (3, v), (3,w)} dari A = {1, 2, 3, 4} ke B = {u, v, w, x} . Apakah merupakan fungsi? 2. Diberikan relasi
f = {(1, u), (2, u), (3, u), (4, u)}
dari A = {1, 2, 3, 4} ke B = {u, v, w, x} . Apakah merupakan fungsi bijektif? 3. Diberikan f x
2x1 ,
2g x x dan h x
4 . Tentukan: a.
f g
xb.
g f
x c.
f h
x d.
g h
x e.
f g
2 4. Tentukan nilai dari:a. 3.1 = ... b. 5.6 = ... c. 1.26 = ... d. - 4.8 = ... e. – 100.1 = ...
5. Hitunglah nilai fungsi Fibonacci untuk n5 dan n6
0 , 0
( ) 1 , 1
( 1) ( 2) , 1
n
f n n
f n f n n
Pertemuan 5
Induksi Matematika
A. Pengertian Induksi Matematika
Metode pembuktian untuk pernyataan perihal bilangan bulat adalah induksi matematik.
Contoh :
Diketahui p(n): “Jumlah bilangan bulat positif dari 1 sampai n adalah
1
2 n n”. Buktikan p(n)
benar!
Contoh:
1. Setiap bilangan bulat positif n (n 2) dapat dinyatakan sebagai perkalian dari (satu atau lebih) bilangan prima.
2. Untuk semua n 1, n3 + 2n adalah kelipatan 3.
3. Untuk membayar biaya pos sebesar n sen dolar (n 8) selalu dapat digunakan hanya perangko 3 sen dan 5 sen dolar.
4. Di dalam sebuah pesta, setiap tamu berjabat tangan dengan tamu lainnya hanya sekali. Jika ada n orang tamu maka jumlah jabat tangan yang terjadi adalah n(n +1)/2.
5. Banyaknya himpunan bagian yang dapat dibentuk dari sebuah himpunan yang beranggotakan n elemen adalah 2n
Induksi matematik merupakan teknik pembuktian yang baku di dalam matematika. Melalui induksi matematik kita dapat mengurangi langkah-langkah pembuktian bahwa semua bilangan bulat termasuk ke dalam suatu himpunan kebenaran dengan hanya sejumlah langkah terbatas.
Prinsip dasar induksi matematika yaitu:
a. Misalkan p(n) adalah pernyataan yang memuat bilangan bulat positif.
b. Kita ingin membuktikan bahwa p(n) benar untuk semua bilangan bulat positif n. c. Untuk membuktikan pernyataan ini, kita hanya perlu menunjukkan bahwa:
1. p(1) benar, dan
2. jika p(n) benar, maka p(n + 1) juga benar, untuk setiap n 1,
Perhatikan bahwa langkah 1 dinamakan basis induksi, sedangkan langkah 2 dinamakan langkah induksi. Langkah induksi berisi asumsi (andaian) yang menyatakan bahwa p(n) benar. Asumsi tersebut dinamakan hipotesisinduksi. Bila kita sudah menunjukkan kedua langkah tersebut benar maka kita sudah membuktikan bahwa p(n) benar untuk semua bilangan bulat positif n.
Contoh:
Gunakan induksi matematik untuk membuktikan bahwa jumlah n buah bilangan ganjil positif pertama adalah n2.
Jawab:
a. Basis induksi:
Untuk n = 1, jumlah satu buah bilangan ganjil positif pertama adalah 12 = 1. Ini benar
karena jumlah satu buah bilangan ganjil positif pertama adalah 1.
b. Langkah induksi:
Andaikan p(n) benar, yaitu pernyataan
1 + 3 + 5 + … + (2n – 1) = n2
adalah benar (hipotesis induksi)
[catatlah bahwa bilangan ganjil positif ke-n adalah (2n – 1)].
Kita harus memperlihatkan bahwa p(n +1) juga benar, yaitu 1 + 3 + 5 + … + (2n – 1) + (2n + 1) = (n + 1)2
juga benar. Hal ini dapat kita tunjukkan sebagai berikut:
1 + 3 + 5 + … + (2n – 1) + (2n + 1) = [1 + 3 + 5 + … + (2n – 1)] + (2n + 1) = n2 + (2n + 1)
= n2 + 2n + 1
Karena langkah basis dan langkah induksi keduanya telah diperlihatkan benar, maka jumlah n buah bilangan ganjil positif pertama adalah n2 .
Contoh:
Buktikan jumlah n bilangan bulat positif yang pertama adalah 1
1
2n n yaitu;
Andaikan p(n) benar, yaitu pernyataan
adalah benar (hipotesis induksi)
Kita harus memperlihatkan bahwa p(n +1) juga benar, yaitu
1
1 2 3 1 1 2
2
n n n n
juga benar. Hal ini dapat kita tunjukkan sebagai berikut:
Karena langkah basis dan langkah induksi keduanya telah diperlihatkan benar, maka jumlah n bilangan bulat positif yang pertama adalah 1
1
2n n .
Untuk semua bilangan bulat tidak-negatif n, buktikan dengan induksi matematik bahwa 20 + 21 +
22 + … + 2n= 2n+1 - 1
Jawab:
a. Basis induksi.
Untuk n = 0 (bilangan bulat tidak negatif pertama), kita peroleh: 20 = 20+1 – 1.
Ini jelas benar, sebab 20 = 1 = 20+1 – 1
= 21 – 1
= 2 – 1 = 1
b. Langkah induksi.
Andaikan bahwa p(n) benar, yaitu 20 + 21 + 22 + … + 2n = 2n+1 - 1
adalah benar (hipotesis induksi). Kita harus menunjukkan bahwa p(n +1) juga benar, yaitu
20 + 21 + 22 + … + 2n + 2n+1 = 2(n+1) + 1 - 1
juga benar. Ini kita tunjukkan sebagai berikut:
20 + 21 + 22 + … + 2n + 2n+1 = (20 + 21 + 22 + … + 2n) + 2n+1
= (2n+1 – 1) + 2n+1 (hipotesis induksi)
= (2n+1 + 2n+1) – 1
= (2 . 2n+1) – 1
= 2n+2 - 1
= 2(n+1) + 1 – 1
Karena langkah 1 dan 2 keduanya telah diperlihatkan benar, maka untuk semua bilangan bulat tidak-negatif n, terbukti bahwa 20 + 21 + 22 + … + 2n = 2n+1 – 1
Contoh:
Buktikan pernyataan “Untuk membayar biaya pos sebesar n sen (n 8) selalu dapat digunakan hanya perangko 3 sen dan perangko 5 sen” benar.
Jawab:
a. Basis induksi.
b. Langkah induksi.
Andaikan p(n) benar, yaitu untuk membayar biaya pos sebesar n (n 8) sen dapat digunakan perangko 3 sen dan 5 sen (hipotesis induksi). Kita harus menunjukkan bahwa
p(n +1) juga benar, yaitu untuk membayar biaya pos sebesar n + 1 sen juga dapat menggunakan perangko 3 sen dan perangko 5 sen. Ada dua kemungkinan yang perlu diperiksa:
a. Kemungkinan pertama, misalkan kita membayar biaya pos senilai n sen dengan sedikitnya satu perangko 5 sen. Dengan mengganti satu buah perangko 5 sen dengan dua buah perangko 3 sen, akan diperoleh susunan perangko senilai n + 1 sen.
b. Kemungkinan kedua, jika tidak ada perangko 5 sen yang digunakan, biaya pos senilai n sen menggunakan perangko 3 sen semuanya. Karena n 8, setidaknya harus digunakan tiga buah perangko 3 sen. Dengan mengganti tiga buah perangko 3 sen dengan 2 buah perangko 5 sen, akan dihasilkan nilai perangko n + 1 sen.
C. Latihan
1. Buktikan proposisi berikut:
2 2 2
1 2
1
:1 2
6
n n n
p n n
2. Buktikan proposisi berikut:
:1 4 7
3 2
3 1
2 n n
p n n
3. Buktikan proposisi berikut:
Pertemuan 6
Teori Bilangan
A. Bilangan Bulat
Misalkan a dan b bilangan bulat, a 0.
a habis membagi b (a divides b) jika terdapat bilangan bulat c sedemikian sehingga b = ac. Notasi: a | b jika b = ac, c Z dan a 0.
Contoh:
4 | 12 karena 124 = 3 (bilangan bulat) atau 12 = 4 3. Tetapi 4 | 13 karena 134 = 3.25 (bukan bilangan bulat).
B. Teorema Euclidan
Misalkan m dan n bilangan bulat, n > 0. Jika m dibagi dengan n maka terdapat bilangan bulat unik q (quotient) dan r (remainder), sedemikian sehingga berlaku
m = nq + r
dengan 0 r < n.
Contoh:
a. 1987:97 = 20, sisa 47. Jadi dapat dinyatakan 1987 = 97 20 + 47 b. –22/3 = –8, sisa 2. Jadi dapat dinyatakan –22 = 3(–8) + 2
Perhatikan bahwa –22 = 3(–7) – 1 salah, karena r = –1 (syarat 0 r < n) .
C. Faktor Persekutuan Terbesar (FPB)
Misalkan a dan b bilangan bulat tidak nol. Faktor persekutuan terbesar (FPB – greatest common
divisor atau gcd) dari a dan b adalah bilangan bulat terbesar d sedemikian hingga d | a dan d | b. Dalam hal ini kita nyatakan bahwa PBB(a, b) = d.
Contoh:
Faktor pembagi 45: 1, 3, 5, 9, 15, 45; Faktor pembagi 36: 1, 2, 3, 4, 9, 12, 18, 36; Faktor pembagi bersama 45 dan 36: 1, 3, 9 Jadi, FPB(45, 36) = 9.
(Teorema 2)
Misalkan m dan n bilangan bulat, dengan syarat n > 0 sedemikian sehingga
m = nq + r , 0 r < n
maka FPB(m, n) = FPB(n, r)
Contoh:
Diberikan m = 60, n = 18,
60 = 18 3 + 12 maka PBB(60, 18) = PBB(18, 12) = 6
D. Algoritma Euclidean
Algoritma Euclidean digunakan untuk mencari FPB dari dua buah bilangan bulat. Penemu algoritma Euclides, seorang matematikawan Yunani yang menuliskan algoritmanya tersebut dalam buku, Element.
Misalkan m dan n adalah bilangan bulat tak negatif dengan m n. Misalkan r0 = m dan r1 = n. Lakukan secara berturut-turut pembagian untuk memperoleh
r0 = r1q1 + r2 0 r2r1,
r1 = r2q2 + r3 0 r3r2,
rn–1 = rnqn + 0 Menurut Teorema 2,
PBB(m, n) = PBB(r0, r1) = PBB(r1, r2) = … = PBB(rn– 2, rn– 1) = PBB(rn– 1, rn) = PBB(rn, 0) = rn Jadi, PBB dari m dan n adalah sisa terakhir yang tidak nol dari runtunan pembagian tersebut. Diberikan dua buah bilangan bulat tak-negatif m dan n (m n). Algoritma Euclidean berikut mencari pembagi bersama terbesar dari m dan n.
Secara umum, Algoritma Euclidean yaitu: 1. Jika n = 0 maka m adalah PBB(m, n);
stop.
tetapi jika n 0, lanjutkan ke langkah 2.
2. Bagilah m dengan n dan misalkan r adalah sisanya.
3. Ganti nilai m dengan nilai n dan nilai n dengan nilai r, lalu ulang kembali ke langkah 1.
Contoh:
Diberikan m = 80, n = 12 dan dipenuhi syarat mn.
80 6. 12 8
12 1. 8 4
8 2. 4 0
Sisa pembagian terakhir sebelum 0 adalah 4, maka PBB(80, 12) = 4.
E. Kombinasi Linear
FPB (a,b) dapat dinyatakan sebagai kombinasi linear (linear combination) a dan b dengan dengan koefisien-koefisennya.
Contoh:
FPB(80, 12) = 4 , dapat dinyatakan sebagai 4 = (-1) 80 + 7 12.
(Teorema 3)
Contoh:
Nyatakan FPB(21, 45) sebagai kombinasi lanjar dari 21 dan 45. Jawab:
45 = 2 (21) + 3 21 = 7 (3) + 0
Sisa pembagian terakhir sebelum 0 adalah 3, maka FPB(45, 21) = 3. Substitusi dengan persamaan–persamaan di atas menghasilkan:
3 = 45 – 2 (21)
yang merupakan kombinasi linear dari 45 dan 21.
Contoh:
Nyatakan FPB(312, 70) sebagai kombinasi lanjar 312 dan 70. Jawab:
Terapkan algoritma Euclidean untuk memperoleh PBB(312, 70): 312 = 4 70 + 32 (1)
70 = 2 32 + 6 (2) 32 = 5 6 + 2 (3) 6 = 3 2 + 0 (4)
Sisa pembagian terakhir sebelum 0 adalah 2, maka PBB(312, 70) = 2 Susun pembagian nomor (3) dan (2) masing-masing menjadi
2 = 32 – 5 6 (5) 6 = 70 – 2 32 (6) Suubsitusikan (6) ke dalam (5) menjadi
2 = 32 – 5(70 – 232) = 132 – 570 + 1032 = 11 32 – 5 70 (7) Susun pembagian nomor (1) menjadi
32 = 312 – 4 70 (8) Subsitusikan (8) ke dalam (7) menjadi
2 = 11 32 – 5 70 = 11 (312 – 4 70) – 5 70 = 11 . 312 – 49 70 Jadi, PBB(312, 70) = 2 = 11 312 – 49 70
Dua buah bilangan bulat a dan b dikatakan relatif prima jika PBB(a, b) = 1.
Contoh:
20 dan 3 relatif prima sebab PBB(20, 3) = 1.
Jika a dan b relatif prima, maka terdapat bilangan bulat m dan n sedemikian sehingga
ma + nb = 1 Contoh:
Bilangan 20 dan 3 adalah relatif prima karena PBB(20, 3) =1, atau dapat ditulis 2 . 20 + (–13) . 3 = 1 (m = 2, n = –13)
Tetapi 20 dan 5 tidak relatif prima karena PBB(20, 5) = 5 1 sehingga 20 dan 5 tidak dapat dinyatakan dalam m . 20 + n . 5 = 1.
G. Aritmatika Modulo
Misalkan a dan m bilangan bulat (m > 0). Operasi a mod m (dibaca “a modulo m”) memberikan
sisa jika a dibagi dengan m.
Notasi a mod m = r sedemikian sehingga
a = mq + r, dengan 0 r < m.
m disebut modulus atau modulo, dan hasil aritmetika modulo m terletak di dalam himpunan {0, 1, 2, …, m – 1}.
Contoh:
Beberapa hasil operasi dengan operator modulo: a. 23 mod 5 = 3 (23 = 5 4 + 3) b. 27 mod 3 = 0 (27 = 3 9 + 0)
H. Kongruen
Misalnya 38 mod 5 = 3 dan 13 mod 5 = 3, maka dikatakan 38 13 (mod 5) . (dibaca: 38 kongruen dengan 13 dalam modulo 5).
Contoh:
a. 17 2 (mod 3) karena 3 habis membagi 17 – 2 = 15.
b. –7 15 (mod 11) karena 11 habis membagi –7 – 15 = –22
c. –7 / 15 (mod 3) karena 3 tidak habis membagi –7 – 15 = –22.
ab (mod m) dalam bentuk “sama dengan” dapat dituliskan sebagai a = b + km (k adalah bilangan bulat)
Contoh:
a. 17 2 (mod 3) 17 = 2 + 5 3 b. –7 15 (mod 11) –7 = 15 + (–2)11
a mod m = r dapat juga ditulis sebagai ar (mod m)
Contoh:
a. 23 mod 5 = 3 23 3 (mod 5) b. 27 mod 3 = 0 27 0 (mod 3)
(Teorema 4)
Misalkan m adalah bilangan bulat positif.
a. Jika ab (mod m) dan c adalah sembarang bilangan bulat maka (i) (a + c) (b + c) (mod m)
(ii) acbc (mod m)
(iii) apbp (mod m) , p bilangan bulat tak-negatif b. Jika ab (mod m) dan cd (mod m), maka
(i) (a + c) (b + d) (mod m) (ii) acbd (mod m)
Contoh:
17 + 5 = 2 + 5 (mod 3) 22 = 7 (mod 3) 17 . 5 = 5 2 (mod 3) 85 = 10 (mod 3) 17 + 10 = 2 + 4 (mod 3) 27 = 6 (mod 3) 17 . 10 = 2 4 (mod 3) 170 = 8 (mod 3)
Teorema 4 tidak memasukkan operasi pembagian pada aritmetika modulo karena jika kedua ruas dibagi dengan bilangan bulat, maka kekongruenan tidak selalu dipenuhi.
Contoh:
a. 10 4 (mod 3) dapat dibagi dengan 2 , karena 10/2 = 5 dan 4/2 = 2, dan 5 2 (mod 3) b. 14 8 (mod 6) tidak dapat dibagi dengan 2, karena 14/2 = 7 dan 8/2 = 4, tetapi
7 / 4 (mod 6).
I. Kekongruenan Linear
Kekongruenan linear berbentuk:
axb (mod m)
dengan m > 0, a dan b sembarang bilangan bulat, dan x adalah peubah bilangan bulat.
Solusi dari ax = b + km berbentuk x b km a
.
(Cobakan untuk k = 0, 1, 2, … dan k = –1, –2, … yang menghasilkan x sebagai bilangan bulat)
Contoh:
Tentukan solusi dari 4x 3 (mod 9) . Jawab:
Solusi untuk 4x 3 (mod 9) adalah 3 9 4
k x .
k = 0 x = (3 + 0 9)/4 = 3/4 (bukan solusi)
k = 1 x = (3 + 1 9)/4 = 3
k = 2 x = (3 + 2 9)/4 = 21/4 (bukan solusi)
k = 3, k = 4 tidak menghasilkan solusi
…
k = –1 x = (3 – 1 9)/4 = –6/4 (bukan solusi)
k = –2 x = (3 – 2 9)/4 = –15/4 (bukan solusi)
k = –3 x = (3 – 3 9)/4 = –6 …
k = –6 x = (3 – 6 9)/4 = –15
…
Nilai-nilai xyang memenuhi: 3, 12, … dan –6, –15, …
J. Chinese Remainder Problem
Pada abad pertama, seorang matematikawan China yang bernama Sun Tse mengajukan pertanyaan sebagai berikut:
“Tentukan sebuah bilangan bulat yang bila dibagi dengan 5 menyisakan 3, bila dibagi 7 menyisakan 5, dan bila dibagi 11 menyisakan 7.”
Misakan bilangan bulat tersebut = x. Formulasikan kedalam sistem kongruen linear: x 3 (mod 5)
x 5 (mod 7)
x 7 (mod 11)
Teorema 5. (Chinese Remainder Theorem)
Misalkan m1, m2, …, mn adalah bilangan bulat positif sedemikian sehingga FPB(mi, mj) = 1 untuk i j. Maka sistem kongruen lanjar
xak (mod mk)
mempunyai sebuah solusi unik dalam modulo m = m1m2 … mn.
Contoh:
Tentukan solusi dari pertanyaan Sun Tse di atas. Jawab:
x 3 (mod 5) x = 3 + 5k1 (i)
3 + 5k1 5 (mod 7) k1 6 (mod 7), atau k1 = 6 + 7k2 (ii) Subsitusikan (ii) ke dalam (i):
x = 3 + 5k1 = 3 + 5(6 + 7k2) = 33 + 35k2 (iii) Subsitusikan (iii) ke dalam kongruen ketiga menjadi:
33 + 35k2 7 (mod 11) k2 9 (mod 11) atau k2 = 9 + 11k3. Subsitusikan k2 ini ke dalam (iii) menghasilkan:
x = 33 + 35(9 + 11k3) = 348 + 385k3 atau x 348 (mod 385). Ini adalah solusinya.
348 adalah bilangan bulat positif terkecil yang merupakan solusi sistem kekongruenan di atas. Perhatikan bahwa 348 mod 5 = 3, 348 mod 7 = 5, dan 348 mod 11 = 7. Catatlah bahwa 385 = 5 7 11.
Solusi unik ini mudah dibuktikan sebagai berikut. Solusi tersebut dalam modulo:
m = m1m2m3 = 5 7 11 = 5 77 = 11 35. Karena
77 . 3 1 (mod 5), 55 6 1 (mod 7), 35 6 1 (mod 11),
maka solusi unik dari sistem kongruen tersebut adalah x 3 77 3 + 5 55 6 + 7 35 6 (mod 385)
3813 (mod 385) 348 (mod 385)
K. Bilangan Prima
Bilangan bulat positif p (p > 1) disebut bilangan prima jika pembaginya hanya 1 dan p. Karena bilangan prima harus lebih besar dari 1, maka barisan bilangan prima dimulai dari 2, yaitu 2, 3, 5, 7, 11, 13, ….Seluruh bilangan prima adalah bilangan ganjil, kecuali 2 yang merupakan bilangan genap. Bilangan selain prima disebut bilangan komposit (composite). Misalnya 20 adalah bilangan komposit karena 20 dapat dibagi oleh 2, 4, 5, dan 10, selain 1 dan 20 sendiri.
Setiap bilangan bulat positif yang lebih besar atau sama dengan 2 dapat dinyatakan sebagai perkalian satu atau lebih bilangan prima.
Contoh:
a. 9 = 3 3
b. 100 = 2 2 5 5 c. 13 = 13 (atau 1 13)
Algoritma uji bilangan prima:
a. Bagi n dengan sejumlah bilangan prima, mulai dari 2, 3, … , bilangan prima n. b. Jika n habis dibagi dengan salah satu dari bilangan prima tersebut, maka n adalah
bilangan komposit,
c. Tetapi jika n tidak habis dibagi oleh semua bilangan prima tersebut, maka n adalah bilangan prima.
Contoh:
Tes apakah (i) 171 dan (ii) 199 merupakan bilangan prima atau komposit. Jawab:
a. 171 = 13.077. Bilangan prima yang 171 adalah 2, 3, 5, 7, 11, 13. Karena 171 habis dibagi 3, maka 171 adalah bilangan komposit. b. 199 = 14.107. Bilangan prima yang 199 adalah 2, 3, 5, 7, 11, 13.
Karena 199 tidak habis dibagi 2, 3, 5, 7, 11, dan 13, maka 199 adalah bilangan prima.
Teorema 7 (Teorema Fermat).
Jika p adalah bilangan prima dan a adalah bilangan bulat yang tidak habis dibagi dengan p, yaitu PBB(a, p) = 1, maka
ap–1 1 (mod p)
Contoh:
Ambil a = 2 karena PBB(17, 2) = 1 dan PBB(21, 2) = 1.
a. 217–1 = 65536 1 (mod 17), karena 17 habis membagi 65536 – 1 = 65535. Jadi, 17 prima.
b. 221–1 =1048576 \ 1 (mod 21), karena 21 tidak habis membagi 1048576 – 1 = 1048575. Jadi, 21 bukan prima.
Kelemahan Teorema Fermat: terdapat bilangan komposit n sedemikian sehingga 2n–1 1 (mod
n). Bilangan bulat seperti itu disebut bilangan prima semu (pseudoprimes).
Contoh:
341 adalah komposit (karena 341 = 11 31) sekaligus bilangan prima semu, karena menurut teorema Fermat,
2340 1 (mod 341)
Untunglah bilangan prima semu relatif jarang terdapat.
Untuk bilangan bulat yang lebih kecil dari 1010 terdapat 455.052.512 bilangan prima, tapi hanya
14.884 buah yang merupakan bilangan prima semu terhadap basis 2.
L. Latihan
1. Nyatakan FPB(315, 80) sebagai kombinasi lanjar 315 dan 80. 2. Tentukan solusi dari 5x 2 (mod 8) .
3. Tentukan solusi dari sistem kongruen linear: x 2 (mod 5)
x 5 (mod 8)
x 8 (mod 10)
Pertemuan 9
Aplikasi Teori Bilangan
A. Penerapan Teori Bilangan
Beberapa penerapan teori bilangan yaitu;
a. ISBN (International Book Serial Number)
b. Fungsi hash c. Kriptografi
d. Pembangkit bilangan acak-semu
B. ISBN
Kode ISBN terdiri dari 10 karakter, biasanya dikelompokkan dengan spasi atau garis, misalnya 0–3015–4561–9.
ISBN terdiri atas empat bagian kode:
a. kode yang mengidentifikasikan bahasa, b. kode penerbit,
c. kode unik untuk buku tersebut,
d. karakter uji (angka atau huruf X (=10)).
Karakter uji dipilih sedemikian sehingga
0 : kode kelompok negara berbahasa Inggris, 3015 : kode penerbit
4561 : kode unik buku yang diterbitkan 8 : karakter uji.
Karakter uji ini didapatkan sebagai berikut:
1 0 + 2 3 + 3 0 + 4 1 + 5 5 + 6 4 +7 5 + 8 6 + 9 1 = 151 Jadi, karakter ujinya adalah 151 mod 11 = 8.
Perhatikan bahwa untuk kode ISBN ini,
10 9
1 1
i i
i i
ix ix
+ 10x10 = 151 + 10 8 = 231.dan 231 mod 11 = 0 atau 231 0 (mod 11).
C. Fungsi Hash
Tujuan fungsi hash adalah pengalamatan (pengalokasian) di memori. Bentuknya
h(k) = k mod m m : jumlah lokasi memori yang tersedia
k : kunci (integer)
h(k) :lokasi memori untuk record dengan kunci k
Contoh:
Diambil m = 11 mempunyai sel-sel memori yang diberi indeks 0 sampai 10. Akan disimpan data
record yang masing-masing mempunyai kunci 15, 558, 32, 132, 102, dan 5.
h(15) = 15 mod 11 = 4
h(558) = 558 mod 11 = 8
h(32) = 32 mod 11 = 10
h(132) = 132 mod 11 = 0
h(102) = 102 mod 11 = 3
h(5) = 5 mod 11 = 5
132 102 15 5 558 32
Beberapa istilah pada fungsi hash yaitu;
a. Kolisi (collision) terjadi jika fungsi hash menghasilkan nilai h yang sama untuk k yang berbeda.
b. Jika terjadi kolisi, cek elemen berikutnya yang kosong.
c. Fungsi hash juga digunakan untuk me-locate elemen yang dicari.
D. Kriptografi
Kriptografi (cryptography) berasal dari Bahasa Yunani yang artinya “secret writing”. Ilmu
kriptografi adalah ilmu dan seni untuk menjaga keamanan pesan.
Berikut diberikan beberapa istilah pada ilmu kriptografi yaitu: a. Pesan
Data atau informasi yang dapat dibaca dan dimengerti maknanya. Nama lain: plainteks (plaintext). Pesan dapat berupa: teks, gambar, audio, video. Pesan ada yang dikirim atau disimpan di dalam media penyimpanan.
b. Cipherteks (ciphertext)
Pesan yang telah disandikan sehingga tidak memiliki makna lagi. Tujuannya agar pesan tidak dapat dimengerti maknanya oleh pihak lain. Cipherteks harus dapat diubah kembali ke plainteks semula
Contoh:
Plainteks: culik anak itu jam 11 siang Cipherteks: t^$gfUi89rewoFpfdWqL:p[uTcxZ
c. Enkripsi (encryption): proses menyandikan plainteks menjadi ciphertek. d. Dekripsi (decryption): Proses mengembalikan cipherteks menjadi plainteksnya.