3. Analisis Spektral
3.1 Analisis Fourier
Hampir semua sinyal Geofisika dapat dinyatakan sebagai suatu dekomposisi sinyal ke dalam fungsi sinus dan cosinus dengan frekuensi yang berbeda-beda (juga disebut sebagai sifat harmonik). Hal ini dikenal dengan istilah analisis Fourier. Kita mengenal konsep ini, pertama kali di dalam kuliah kalkulus atau fisika di mana fungsi sinus dan kosinus dinyatakan sebagai deret Fourier yang digunakan untuk menyatakan fungsi waktu periodik. (Pada 1822, matematikawan Perancis Joseph Fourier adalah orang pertama yang mencoba untuk membuktikan konvergensi deret ini). Ada kondisi umum yang dimiliki oleh suatu sinyal yaitu:
1. tidak dapat multivalued pada suatu waktu,
2. tidak dapat memiliki jumlah tak terbatas diskontinuitas, atau maksimum atau minimum
3. Sinyal harus terbatasi dalam jangka periodanya.
Frekuensi dari fungsi trigonometri merupakan komponen spektral dari deret Fourier. Frekuensi-frekuensi ini yang ditentukan oleh periodisitas, T dari fungsi dan sama dengan n/T, n = 1, 2, ... Oleh karena itu, spektrum frekuensi terdiri dari garis spektrum diskrit. Bila sinyal tidak periodik, maka spektrumnya tidaklah diskrit dan Deret Fourier harus digeneralisasi ke dalam Intergral Fourier atau Transformasi Fourier. Selama integral dari nilai absolut sinyal adalah konvergen, maka sinyal kontinu s(t) dapat dinyatakan sebagai Integral Fourier.
(3.1.1)
dimana
(3.1.2)
Persamaan 3.1.2 mendefinisikan Transformasi Fourier dari s(t); persamaan 3.1.1 merupakan Invers Transformasi Fourier yang dapat mengembalikan s(t) dari S(f). Kedua persamaan ini merupakan persamaan kunci di dalam Analisis spektral dan keduanya sangat terkait erat sehingga dikenal dengan istilah pasangan Transformasi Fourier.
Sudah menjadi kebiasaan untuk menggunakan simbol huruf kecil untuk fungsi domain ruang atau waktu dan simbol huruf besar untuk fungsi domain frekuensi. Jadi S(f) dan s(t) merupakan representasi sinyal dalam domain frekuensi dan waktu. Di dalam bahasa tranfromasi umum, suku-suku di dalam integral diluar S(f) dan s(t) di kenal dengan istilah
kernel dari transformasi. Di dalam pasangan Transformasi Fourier, kernel hanya sedikit berbeda, tanda eksponensial pada Transformasi Fourier adalah (–) dan invers Transformasi Fourier adalah (+). Untuk mempersingkat penulisan pasangan transformasi Fourier, biasanya ditulis S(f) = [s(t)] and s(t) = -1[S(f)]. Notasi lainya yang juga biasa
digunakan adalah tanda panah dua arah yaitu s(t) S(f).
Angka 2π muncul di dalam kernel transformasi dapat dimasukkan dalam frekuensi f untuk menyatakan Pasangan Transformasi Fourier dalam domain frekuensi sudut, dω (radians/s) dan ditulis sebagai berikut :
(3.1.3)
dan
(3.1.4)
Kita sepertinya telah membuat lompatan jauh dari tinjauan digitalisasi s(t) hingga sekarang mengungkapkannya dalam pasangan transformasi Fourier. Selanjutnya, jelas dari persamaan-persamaan tadi bahwa pasangan transformasi merupakan fungsi kompleks
dengan masuknya i = (-1)1/2 dalam kernel tranformasi. Mari kita sederhanakan hal ini
hanya dengan mengingat beberapa hal dari matematika dasar. Pertama, kernel transfromasi, misalnya, exp(i2πf) adalah bentuk umum dari persamaan Euler,
(3.1.5a)
sehingga
(3.1.5b)
Dari hubungan Euler ini, kita dapat melihat bahwa pasangan Transformasi Fourier memiliki suku-suku seperti deret Fourier. Dan oleh karena kita tahu bahwa integral merupakan ekspresi terbatas dari penjumlahan yang kontinu, maka kita juga menyadari bahwa Transfromasi Fourier merupakan gambaran dari penjumlahan kontinu tak terhingga fungsi sinus dan kosinus. Bahkan, Transfromasi Fourier dapat diekpresikan menggunakan transfromasi sinus dan kosinus secara terpisah. Jadi, Analisis Fourier yang digambarkan oleh Transformasi Fourier merupakan dekomposisi sederhana dari suatu sinyal ke dalam komposit komponen frekuensi (sinus dan kosinus).
Dengan menggunakan hubungan Euler, transformasi Fourier (persamaan 3.1.2) dapat ditulis kembali ke dalam komponen transfromasi sinus dan kosinus sebagai:
(3.1.6)
Dari persamaan ini, kita dapat menggambarkan Transformasi Fourier dari suatu fungsi real, s(t) dengan melakukan :
1. Menghitung bagian real dari Transformasi Fourier, pada frekuensi f = f0, kita
mengalikan s (t) dengan cos(2πf0t) dan mengintegrasikan (mencari luas di bawah
kurva yang dihasilkan).
2. Menghitung bagian imajiner dari Transformasi Fourier, pada frekuensi f = f0, kita
mengalikan s (t) dengan sin(2πf0t) dan mengintegrasikan (mencari luas di bawah
kurva yang dihasilkan).
3. Transformasi Fourier pada f = 0 adalah hanya integral (luas daerah di bawah kurva) s(t).
Selain dari garis spektrum diskrit (frekuensi) yang muncul dalam sebuah deret Fourier, transformasi Fourier memiliki spektrum kontinu (seperti yang terlihat dalam Gambar 2.5) untuk mewakili proses nonperiodik. Transformasi sinyal ke dalam komponen frekuensi secara kontinu sudah tidak asing lagi bagi kita, di alam ketika cahaya putih melewati prisma kaca menghasilkan spektrum warna (Gambar 3.1a). Ketika hal ini terjadi disertai dengan turunnya hujan, ini disebut sebut sebagai pelangi. Jadi pelangi merupakan fenomena alam yang menggambarkan Fourier Transform (Gambar 3.1b) meskipun kita tidak pernah mendengar orang menyebut pelangi sebagai Transformasi Fourier.
Gambar 3.1b. Nature's Fourier transform during a New Mexico thunderstorm
3.2 Notasi Komplek
Sifat kompleks dari ekpresi transformasi Fourier menuntut kita untuk mengingat kembali dasar notasi kompleks dan beberapa definisi. Representasi s(t) dalam domain frekuensi menghasilkan S(f), yaitu suatu fungsi kompleks yang disebut spektrum kompleks atau densitas spektral kompleks dari s(t). Oleh karena itu, secara umum, dapat diungkapkan oleh bagian real dan imajiner dalam bentuk persegi panjang sebagai
(3.2.1)
Atau, dalam bentuk spektrum amplitudo, A(f) dan spektrum fasa, (f) dalam koordinat polar dinyatakan sebagai :
(3.2.2)
dimana,
(3.2.3)
(3.2.4)
Adalah spektrum fasa (phase spectrum) dari s(t).
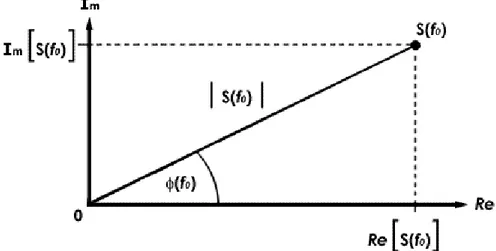
Karena fungsi arctan merupakan fungsi multivalued dan diskontinu, maka spektrum fasa biasanya dinyatakan dalam batas -180 derajat hingga + 180 derajat (-π and +π radians. Kadangkala spketrum amplitudo merupakan hasil kuadrat dari densitas energi spektrum. Gambar 3.2 secara geometri mendefinisikan hubungan antara bentuk kuantitas kompleks S(f) pada frekuensi, f0.
Gambar 3.2. Definitions of amplitude and phase spectra.
3.3 Sifat simetri fungsi Kompleks
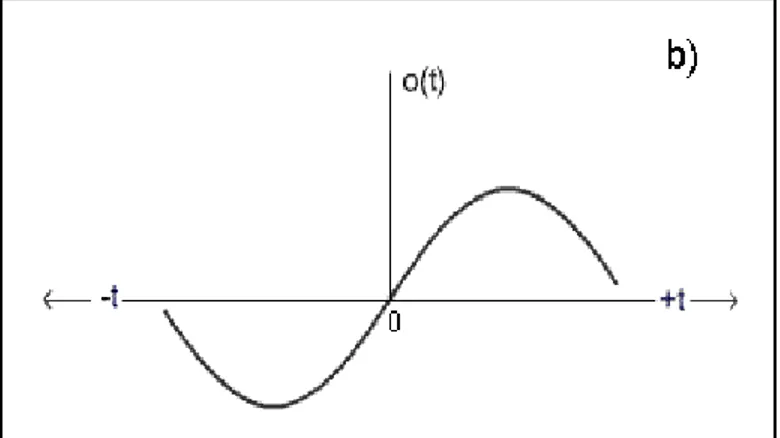
Sifat simetri yang melekat pada pasangan transformasi Fourier kompleks sangat berguna dalam aplikasi praktis. Simetri mengacu pada bagian genap dan ganjil fungsi s(t) atau S(f) dalam waktu atau domain frekuensi. Fungsi, e (t) memiliki simetri genap jika fungsi ini simetris terhadap sumbu nol, yaitu, e(-t) = e(t); fungsi memiliki simetri ganjil jika cerminan dari sumbu nol berlawanan tanda (antisymmetric) dimana o(-t) =-o(t). simetri genap dan ganjil diilustrasikan pada Gambar 3.3a dan b.
Gambar 3.3a. Symmetry properties of an even function,
Gambar 3.3b. Symmetry properties of an odd function, o(t).
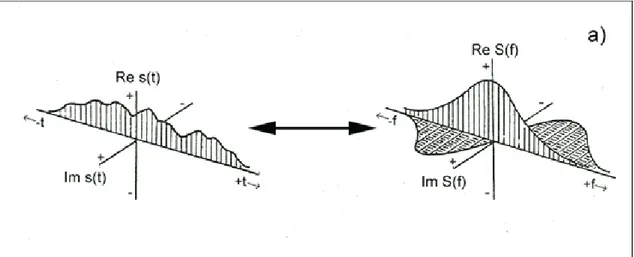
Fungsi sembarang, s(t) selalu dapat dipisahkan menjadi bagian genap dan ganjil. Komponen-komponen ini, secara umum, kompleks, kombinasi simetri untuk pasangan transformasi Fourier seperti yang dijelaskan oleh Bracewell (1965). Kita tidak perlu mempertimbangkan semuanya karena segala sesuatu yang kita hadapi dalam aplikasi geofisika adalah fungsi riil dalam domain waktu (atau ruang). Sinyal tersebut berubah menjadi fungsi yang mempunyai bagian riil, atau genap dan bagian imajiner, atau ganjil di dalam domain frekuensi. Gambar 3.4a memperlihatkan hubungan ini dengan menggunakan teknik visualisasi seperti yang disajikan oleh Bracewell (1995), yang memungkinkan kedua bagian real dan imajiner dari fungsi yang akan diplot pada satu grafik dalam kedua domain.
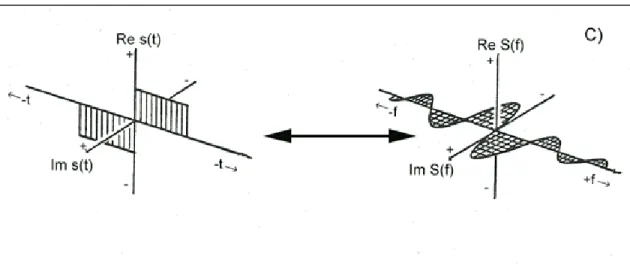
Suatu fungsi yang memiliki bagian riil adalah genap dan bagian imajiner adalah ganjil disebut sebagai fungsi Hermitian terlepas dari apakah dalam domain waktu atau domain frekuensi. Misalnya fungsi dalam domain frekuensi yang memiliki spektrum amplitudo yang genap dan spektrum fase yang ganjil. Karena fungsi riil dalam domain waktu (atau ruang) menghasilkan fungsi Hermitian dalam domain frekuensi, sinyal geofisika riil, s(t) yang genap memiliki transformasi Fourier yang riil dan genap (Gambar 3.4b). Dan, sinyal, s(t) yang riil dan ganjil memiliki transform Fourier yang imajiner dan ganjil (Gambar 3.4c). Pengetahuan simetri kompleks ini sangat berguna dalam aplikasi praktis dari analisis spektral.
Gambar 3.4a. Symmetry properties of Fourier transform pairs when a real signal, s(t) is
arbitrary, neither even nor odd. The Fourier transforms are: Hermitian. Double-ended arrows indicate Fourier transform pairs.
Gambar 3.4b. Symmetry properties of Fourier transform pairs when a real signal, s(t) is
is an even function. The Fourier transforms are: real, even. Double-ended arrows indicate Fourier transform pairs.
Gambar 3.4c. Symmetry properties of Fourier transform pairs when a real signal, s(t) is
is an odd function. The Fourier transforms are: imaginary, odd; respectively. Double-ended arrows indicate Fourier transform pairs.
3.4. Contoh-contoh Transformasi Fourier
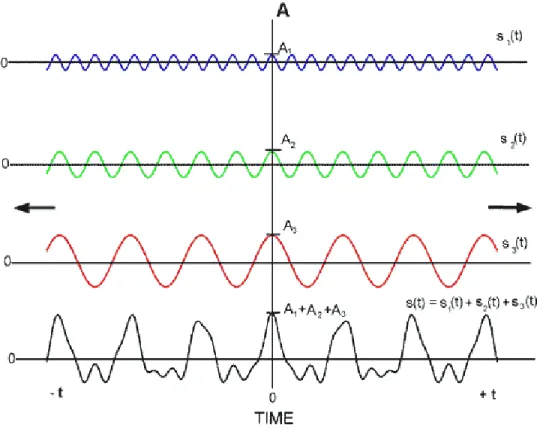
Pada bagian ini, mari kita lihat kembali apa yang dihasilkan bila representasi domain frekuensi dari sinyal s(t) diperoleh dari transfromasi Fourier (3.1.2 atau 3.1.4). Gambar 3.5 berisi suatu sinyal kompsit dalam domain waktu yang terbentuk dari tiga fungsi cosinus. Asumsikan bahwa fungsi cosinus ini terdefinisi dari waktu – tak-hingga sampai + tak-hingga, Transfromasi Fourier dari sinyal komposit ini menghasilkan tampilan sinyal seperti pada gambar 3.6
Gambar 3.5. Three cosine waves with amplitudes A1, A2, and A3 combine to form a
composite signal with amplitude A1 + A2 + A3.
Gambar 3.6. Fourier transform of three-cosine composite signal in Gambar 3.5 yields
three pairs of real, even delta functions with corresponding amplitudes A1/2, A2/2, and A3/2.
Karena sinyal asli adalah riil dan genap (fungsi cosinus jelas merupakan fungsi genap), Transformasi Fouriernya harus riil dan genap pula. Tiga osilasi cosinus dijumlahkan untuk menghasilkan s(t), jadi hanya tiga garis spektral yang terdapat pada hasil transformasi Fourier, S(f). Fungsi spike (paku) ini dapat direpresentasikan oleh fungsi delta Dirac yang merupakan fungsi frekuensi, bukan waktu seperti yang kita definisikan pada bab 2.3. Misalnya Tranformasi Fourier dari A1cos(2πf1t) adalah
(3.4.1)
Ini mengungkapkan aspek menarik dari Transformasi Fourier bahwa kita menghindari pembicaraan tentang sebelumnya, yaitu bahwa ada nilai-nilai (garis spektrum) di kedua frekuensi positif dan negatif. Dalam hal ini mereka muncul di mana fungsi delta non-nol, yaitu, di mana argumennya adalah nol, pada f = + f1 dan f =-f1.
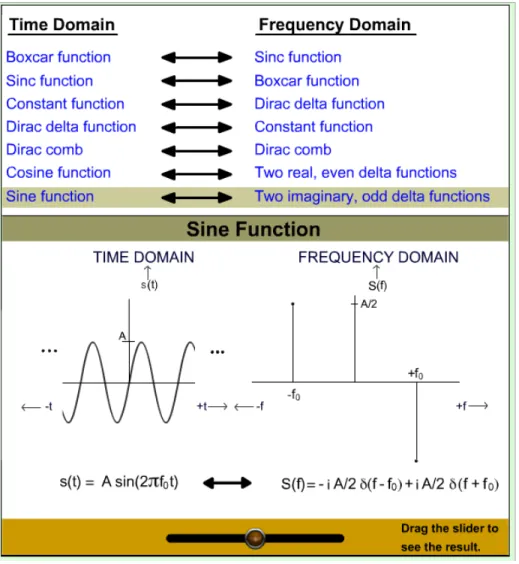
Konsep frekuensi negatif tidak dipahami secara luas, meskipun penanganan yang tepat dari konsep ini sangat penting untuk aplikasi praktis dari pengolahan digital dalam domain frekuensi. Oleh karena itu, kita terdorong untuk meyakinkan Anda tentang keabsahan baik positif dan negatif frekuensi sehingga Anda akan menghargai ketika bekerja dengannya. Ini akan kita lakukan dalam Lampiran B. Pertama mari kita lihat seprti apa Fourier transformasi dari beberapa fungsi yang kita temui sejauh ini. Pasangan Transformasi Fourier yang terlihat pada Gambar 3.7 adalah sama pentingnya.
Gambar 3.7 Equations and graphs of several important, famous Fourier transform pairs.
Select a pair and guess what will happen in the frequency domain before you move the drag button to vary the spacing in the time domain function.