DURASI PADA MASALAH KEBANGKRUTAN PENJUDI
Aditya Candra Laksmana, Respatiwulan, dan Ririn Setiyowati Program Studi Matematika
Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Sebelas Maret
Abstrak. Masalah kebangkrutan penjudi merupakan kejadian seorang penjudi
meng-alami kebangkrutan sampai kehilangan seluruh modal yang dimiliki. Pada permainan judi, perubahan modal yang terjadi merupakan suatu kejadianrandom yang diamati berdasarkan waktu. Probabilitas penjudi memperoleh atau kehilangan seluruh modal disebut probabilitas absorpsi, dan nilai harapan dari banyaknya permainan sampai penjudi menang total atau bangkrut disebut ekspektasi durasi. Probabilitas absorpsi dan ekspektasi durasi diperoleh dari penurunan persamaandifference yang menyata-kan hubungan kenaimenyata-kan dan penurunan modal penjudi. Tujuan penelitian ini adalah menentukan probabilitas absorpsi dan ekpektasi durasi pada masalah kebangkrutan penjudi dan diterapkan pada contoh kasus. Dari penerapan kasus, dengan probabilitas menang 0.49 dan probabilitas kalah 0.51 untuk modal awal 50, diperoleh bahwa
pen-judi mengalami kebangkrutan pada permainan ke-1904 dengan probabilitas absorpsi bangkrut sebesar 0.880825.
Kata kunci: kebangkrutan penjudi, probabilitas absorpsi, ekspektasi durasi
1. PENDAHULUAN
Menurut Kartini [4], perjudian adalah kegiatan mempertaruhkan sesuatu
yang dianggap bernilai pada permainan atau kejadian yang belum pasti
hasil-nya. Kejadian seorang penjudi yang mengalami kehilangan semua modal sampai
habis disebut sebagai kejadian kebangkrutan penjudi. Perjudian terus berlanjut
sampai semua modal yang dimiliki penjudi habis atau mendapat seluruhnya dari
yang dipertaruhkan, sehingga salah satu dari penjudi bangkrut (Feller [3]).
Per-ubahan modal yang terjadi pada setiap permainan judi bisa saja bertambah atau
berkurang sampai permainan berhenti. Perubahan modal dapat dipandang
seba-gai suatu kejadian random yang diamati berdasarkan waktu. Kejadian tersebut
merupakan kejadian khusus dari proses stokastik. Masalah kebangkrutan penjudi
merupakan rantai Markov waktu diskrit pada proses random walk. Hal tersebut
dikarenakan kondisi permainan yang berikutnya dipengaruhi oleh permainan saat
ini (Allen [1]).
El-Shehawey [2] mengembangkan masalah kebangkrutan penjudi pada
ran-tai Markov berhingga dengan probabilitas menang atau kalah bergantung pada
jumlah modal yang dimiliki penjudi saat ini. Katriel [5] mengembangkan
modal lawan memiliki distribusi probabilitas. Pada masalah kebangkrutan
pen-judi, probabilitas seorang penjudi memperoleh atau kehilangan seluruh modal
yang dipertaruhkan disebut sebagai probabilitas absorpsi. Nilai harapan dari
ba-nyaknya permainan sampai penjudi memperoleh atau kehilangan seluruh modal
yang dipertaruhkan disebut sebagai ekspektasi durasi. Pada penelitian ini,
di-lakukan penentuan serta penerapan probabilitas absorpsi dan ekspektasi durasi
pada masalah kebangkrutan penjudi.
2. RANTAI MARKOV WAKTU DISKRIT
Menurut Allen [1], proses stokastik adalah kumpulan variabel random{Xn(s) :
n ∈ T, s ∈ S}, dengan T adalah himpunan indeks dan S adalah ruang sampel
dari variabel random. Rantai Markov waktu diskrit adalah proses stokastik
de-ngan kejadian berikutnya hanya bergantung pada kejadian saat ini dede-ngan ruang
sampel berhingga {0,1,2, ..., N} dan waktu diskritT ={0,1,2, ...}. Berikut dua
definisi tentang rantai Markov waktu diskrit menurut Allen[1].
Definisi 2.1. Proses stokastik waktu diskrit{Xn}dikatakan rantai Markov waktu
diskrit jika
Prob {Xn=in|X0 =i0, ..., Xn−1 =in−1} = Prob {Xn=in|Xn−1 =in−1}
Definisi 2.2. Probabilitas transisi satu langkah, pji(n), didefinisikan dengan
pji(n) =P rob{Xn+1 =j|Xn =i}
probabilitas bahwa proses berada di state j pada waktu n+1 diberikan oleh proses
di state i pada waktu n, dengan i, j = 1,2, ... .
Probabilitas transisi berpengaruh terhadap perpindahanstate yang
menya-takan perubahan modal dari modal semula. Perubahan modal sampai dengan
permainan berhenti dapat dinyatakan sebagai rantai Markov yang diamati
ber-dasarkan waktu, serta bergantung pada probabilitas transisi (Ross [6]).
3. PERSAMAAN DIFFERENCE PADA KEBANGKRUTAN PENJUDI
Pada masalah kebangkrutan penjudi, persamaandifferencedigunakan untuk
menentukan probabilitas absorpsi dan ekspektasi durasi. Probabilitas absorpsi
dibagi menjadi 2 yaitu ak yang menyatakan probabilitas absorpsi ketika
meng-alami kebangkrutan danbkyang menyatakan probabilitas absorpsi ketika menang
difference dari probabilitas kebangkrutanak, untuk k merupakan modal penjudi
dengan kϵ[0, N]. Jika penjudi menang, maka modal menjadi k+1 dan
probabi-litas kebangkrutan adalah ak+1. Jika penjudi kalah, maka modal menjadi k-1
dan probabilitas kebangkrutan adalahak−1. Hubungan antaraak+1,ak, danak−1
diberikan dalam bentuk persamaan difference berikut
ak=pak+1+qak−1, 1≤k ≤N −1 (3.1)
dengan p dan q masing-masing adalah probabilitas penjudi menang dan kalah.
Kondisi batas untuk ak adalaha0 = 1 danaN = 0.
Seperti pada probabilitas absorpsi, persamaan difference untuk ekspektasi
durasi yang dinotasikan denganτkdapat diturunkan. Jika penjudi menang, maka
modal menjadik+1 dengan ekspektasi durasi adalah 1+τk+1. Jika penjudi kalah,
maka modal menjadi k-1 dengan ekspektasi durasi adalah 1+τk−1. Persamaan
difference untuk τk adalah
τk =p(1 +τk+1) +q(1 +τk−1), 1≤k ≤N −1, (3.2)
dengan kondisi batas yang diberikan adalah τ0=0=τN. Penyelesaian dari
per-samaan (3.1) dan (3.2) diperoleh dengan memberikan nilai ak = λk ̸= 0 dan
τk =λk ̸= 0. Solusi untuk menyelesaikan persamaan difference dari probabilitas
absorpsi dan ekspektasi durasi dibagi menjadi 2 kasus, yaitu ketika p ̸= q dan
p=q = 1/2.
4. HASIL DAN PEMBAHASAN
4.1. Persamaan Difference. Penentuan probabilitas absorpsi dan ekspektasi durasi diperoleh dengan menurunkan persamaan difference (3.1) dan (3.2).
Per-samaandifference (3.1) untuk probabilitas absorpsi merupakan persamaan linear
orde dua, homogen serta memiliki koefisien konstan. Untuk persamaandifference
dari ekspektasi durasi telah diberikan pada persamaan (3.2). Mengingat bahwa
p+q=1, persamaan (3.2) dapat diubah ke dalam bentuk
pτk+1−τk+qτk−1 =−1, (4.1)
yang merupakan persamaan linear orde dua, nonhomogen, dan memiliki
berdasarkan persamaan difference homogen dari persamaan tersebut. Berikut
diberikan persamaandifference homogen untuk ekspektasi durasi adalah
pτk+1−τk+qτk−1 = 0. (4.2)
4.2. Nilai Persamaan Karakteristik. Persamaan (3.1) dan (4.2) berturut-turut merupakan persamaan difference homogen dari probabilitas absorpsi dan
ekspektasi durasi. Persamaan difference homogen tersebut diselesaikan dengan
menentukan persamaan karakteristik yang diperoleh dari mensubstitusi nilaiak =
λk ̸= 0 dan τ
k = λk ̸= 0. Berikut adalah persamaan karakteristik untuk
menye-lesaikan nilai ak dan τk
pλk+1−λk+qλk−1 = 0, (4.3)
dengan nilaiλ merupakan nilai persamaan karakteristik. Bentuk sederhana
per-samaan (4.3) yaitu dengan mengambil nilai k = 1, dan diperoleh persamaan
karakteristik sederhana untuk probabilitas absorpsi serta ekspektasi durasi
ada-lah
pλ2−λ+q = 0. (4.4)
Penentuan nilai persamaan karakteristik dari persamaandifferencehomogen untuk
probabilitas absorpsi dan ekspektasi durasi diperoleh dengan mencari nilaiλ1 dan
λ2 yang diterapkan pada kasus p ̸= q dan p =q = 1/2. Pada kasus p ̸=q, nilai
persamaan karakteristik (4.4), dengan mengingatp+q = 1 diperoleh nilai untuk
λ1 adalah
λ1 =
1 + (p−q) 2p =
(p+q) + (p−q)
2p =
2p
2p = 1,
sedangkan nilai untuk λ2 adalah
λ2 =
1−(p−q) 2p =
(p+q)−(p−q)
2p =
q p.
Pada kasus nilaip=q = 1/2, nilai persamaan karakteristik (4.4) yaitu nilai λ1,2
diperoleh
λ1,2 =
1±(p−q) 2p =
1±(1/2−1/2) 2(1/2) =
4.3. Probabilitas Absorpsi. Persamaandifference untuk probabilitas absorpsi diberikan pada persamaan (3.1) dan diselesaikan pada dua kasus yaitu ketika
p ̸= q dan p = q = 1/2. Ketika p ̸= q, diperoleh nilai persamaan karakteristik
(4.4) adalah λ1 = 1 dan λ2 = pq. Solusi umum untuk persamaan difference ak
adalahak =c1+c2(qp)k, denganc1 dan c2 adalah suatu konstanta yang diperoleh
dari menerapkan kondisi batas a0 = 1 = c1 +c2 dan aN = 0 = c1 +c2(qp)N.
Diperoleh nilai c1 = −(
q p)
N
1−(
q p)
N dan c2 = 1−(1q p)
N, selanjutnya disubstitusi ke solusi
umum ak dan diperoleh solusi khusus untuk ak dan bk adalah
ak=
(pq)N −(q p)
k
(qp)N −1 (4.5)
bk=
(qp)k−1
(pq)N −1, (4.6)
denganak+bk = 1.
Ketika p = q = 1/2, diperoleh nilai persamaan karakteristik (4.4) adalah
λ1 =λ2 = 1. Solusi umum untuk persamaan difference ak adalahak =c1+c2k,
denganc1 danc2 adalah suatu konstanta yang diperoleh dari menerapkan kondisi
batas a0 = 1 = c1 dan aN = 0 = c1 +c2N. Diperoleh nilai c1 = 1 dan c2 = −N1,
selanjutnya disubstitusi ke solusi umumak dan diperoleh solusi khusus untukak
dan bk adalah
ak =
N−k
N (4.7)
bk =
k
N. (4.8)
4.4. Ekspektasi Durasi. Persamaan difference untuk ekspektasi durasi dibe-rikan pada persamaan (4.1) dan diselesaikan untuk dua kasus. Untuk p ̸= q,
solusi umum persamaan difference homogen adalah τk = c1 +c2(qp)k.
Selanjut-nya, diberikan nilai τk = ck dengan c merupakan suatu konstanta, untuk
men-cari solusi umum dari persamaan nonhomogen (4.1). Nilai konstanta c dicari
dengan substitusi τk = ck ke persamaan (4.1), dan diperoleh c = q1
−p. Solusi umum nonhomogen untuk persamaan difference adalah τk = c1+c2(qp)k+ q−kp.
Selanjutnya, dengan menerapkan kondisi batas diperoleh τ0 = 0 = c1 +c2 dan
τN = 0 = c1+c2(qp)N+qN−p. Nilai dari konstantac1danc2 adalahc1 = (q−p)(1−N−(q p)N)
untukτk, dengan substitusi nilaic1 danc2 ke solusi umum nonhomogen diperoleh
τk =
1
q−p[k−N(
1−(qp)k
1−(qp)N)]. (4.9)
Ketika nilai p = q = 1/2, solusi umum persamaan difference homogen
adalahτk =c1+c2k.Untuk mencari solusi umum pada persamaan nonhomogen
(4.1), diberikan nilaiτk =ck2, dengancmerupakan suatu konstanta dan diperoleh
c= −1. Selanjutnya, nilai c= −1 disubstitusi ke τk =ck2 dan diperoleh solusi
umum persamaandifference nonhomogen adalahτk =c1+c2k−k2.Solusi khusus
dari persamaandifference τk (4.1) diselesaikan dengan menerapkan kondisi batas
τ0 = c1 = 0 dan τN = c1 +c2(N)−(N)2 = 0, sehingga diperoleh nilai untuk
c1 = 0 dan c2 = N. Selanjutnya, dari substitusi nilai c1 dan c2 ke solusi umum
nonhomogen diperoleh solusi khusus persamaan difference nonhomogen adalah
τk =k(N −k). (4.10)
4.5. Penerapan Kasus. Pada penerapan ini diberikan parameter yang menga-cu pada Allen [1] yaitu modal total N = 100, modal awal yang dimiliki penjudi
k = 50, probabilitas menang p = 0.49 dan probabilitas kalah q = 0.51, untuk
menentukan nilai probabilitas absorpsi serta ekspektasi durasi. Pada permainan
judi ini diasumsikam bahwa pemain hanya 2 orang dengan probabilitas absorpsi
dan ekspektasi durasi ditinjau dari salah satu pemain. Nilai probabilitas absorpsi
terdiri atas probabilitas bangkrutakdan probabilitas menang totalbksampai
per-mainan berhenti. Diketahui probabilitas menangp= 0.49 dan probabilitas kalah
q = 0.51, karena p ̸=q sehingga probabilitas absorpsi ditentukan dengan
persa-maan (4.5) dan (4.6). Nilai probabilitas absorpsi untuk probabilitas bangkrutak
adalah
a50 = (0.51
0.49)
100−(0.51 0.49)
50
(0.51
0.49)100−1 = 0.880825.
Dari hasil yang diperoleh, diketahui bahwa probabilitas seorang penjudi
meng-alami kebangkrutan pada akhir permainan adalah 0.880825. Setelah diperoleh
nilai probablitas absorpsi penjudi mengalami kebangkrutan, selanjutnya
adalah
b50 = (0.51
0.49)100−1 (0.51
0.49)50−1 = 0.119175.
Diketahui bahwa probabilitas seorang penjudi mengalami menang total pada
akhir permainan adalah 0.119175. Dari nilai probabilitas absorpsi yang telah
diperoleh, dapat disimpulkan bahwa probabilitas penjudi mengalami
kebangkrut-an lebih besar daripada probabilitas penjudi mengalami menkebangkrut-ang total pada akhir
permainan. Oleh karena itu, pada kasus ini diketahui bahwa penjudi mengalami
kebangkrutan pada akhir permainan.
Setelah diperoleh probabilitas absorpsi, selanjutnya ditentukan nilai
harap-an dari bharap-anyaknya permainharap-an judi sampai berhenti (ekspektasi durasi). Nilai
ekspektasi durasi ditentukan dengan menerapkan persamaan (4.9) dan diperoleh
τ50 =
1
0.51−0.49[50−100(
1−(0.51 0.49)
50
1−(0.51 0.49)100
)] = 1904.
Untuk mengamati perubahan banyaknya modal setiap permainan serta
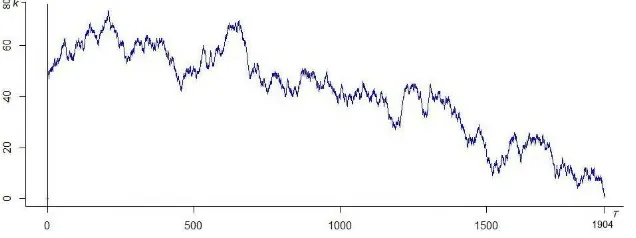
[image:7.595.141.459.463.582.2]ekspek-tasi durasi permainan telah diberikan pada Gambar 1.
Gambar 1. Perubahan modal setiap permainan dan ekspektasi durasi
Berdasarkan Gambar 1, menunjukkan perubahan modal untuk setiap
per-mainan, dengan setiap kali menang atau kalah mengakibatkan modal yang
fluktuasi naik atau turun. Ketika penjudi menang, modal yang dimiliki
ber-tambah sebesar 1. Demikian pula ketika penjudi kalah, modal yang dimiliki
berkurang sebesar 1. Ketika modal mencapai titik 0 menyatakan seorang
pen-judi mengalami suatu kebangkrutan. Hal ini dikarenakan modal yang dimiliki
penjudi telah habis, sehingga permainan berhenti. Perubahan modal yang
Pada penerapan kasus ini, penjudi mengalami kebangkrutan pada permainan
ke-1904 dengan modal awal yang dimiliki sebesar k = 50 dan probabilitas absorpsi
bangkrut sebesar a50= 0.880825.
5. KESIMPULAN
Berdasarkan pembahasan yang dilakukan dapat diambil dua kesimpulan.
(1) Probabilitas absorpsi kebangkrutan (ak) dan menang total (bk) untukp̸=
q dinyatakan dengan ak =
(qp)N
−(pq)k (qp)N
−1 dan bk = (qp)k
−1 (qp)N
−1, sedangkan untuk
p = q = 1/2 dinyatakan dengan ak = NN−k dan bk = Nk. Selanjutnya,
ekspektasi durasi untukp̸=qdinyatakan denganτk = q−1p[k−N(
1−(qp)k 1−(qp)N)], sedangkan untuk p=q= 1/2 dinyatakan denganτk =k(N −k).
(2) Dari penerapan kasus yang mengacu pada Allen [1], diketahui modal total
N = 100, modal awal penjudi k = 50, probabilitas menang p = 0.49,
dan probabilitas kalah q = 0.51. Probabilitas absorpsi untuk bangkrut
adalah a50 = 0.880825 dan menang total adalah b50 = 0.119175, serta
ekspektasi durasi τ50 = 1904. Pada kasus ini, permainan judi berhenti
pada permainan ke-1904, dan pemain judi mengalami kebangkrutan dari
modal awal yang dimiliki adalah 50 menjadi 0.
DAFTAR PUSTAKA
1. Allen, L.J.S.,An Introduction to Stochastic Processes with Applications to Biology, Prentice Hall, Upper Saddle River, N.J., 2003.
2. El-Shehawey, M.A., On the Gamblers Ruin Problem for a Finite Markov Chain, Statistics and Probability Letters79(2009), 1590–1595.
3. Feller, W., An Introduction to Probability Theory and Its Applications, third ed., vol. 1, Wiley, New York, 1968.
4. Kartini, K.,Patologi Sosial, Rajagrafindo Press, Jakarta, 2003.
5. Katriel, G., Gambler’s Ruin- A General Formula, Probability Letters 83 (2013), no. 10,
2205–2210.