smk11 FisikaTeknik Endarko

Informasi Dokumen

Penulis:

Endarko
Melania Suweni
Muntini Lea Prasetio
Heny Faisal

Pengajar:

Darminto

Sekolah: Direktorat Pembinaan Sekolah Menengah Kejuruan

Mata Pelajaran: Fisika

Topik: Fisika Jilid 2 Untuk SMK Teknologi

Tipe: buku ajar

Tahun: 2008

Kota: Jakarta

Ringkasan Dokumen

I. BAB 1: BESARAN DAN SATUAN

Bab ini membahas tentang konsep dasar fisika yang meliputi pengertian besaran, satuan, dan alat ukur. Besaran fisika adalah segala sesuatu yang dapat diukur, sementara satuan adalah ukuran yang digunakan untuk menyatakan besaran tersebut. Alat ukur berfungsi untuk mendapatkan nilai numerik dari besaran yang diukur. Pemahaman tentang besaran dan satuan sangat penting dalam fisika karena menjadi dasar bagi pengukuran yang lebih kompleks.

1.1. Besaran dan Satuan

Dalam sub-bab ini, dijelaskan berbagai jenis besaran fisika, seperti besaran pokok dan turunan. Besaran pokok meliputi panjang, massa, waktu, dan lainnya, sedangkan besaran turunan adalah hasil dari kombinasi besaran pokok. Pemilihan satuan yang tepat untuk setiap besaran juga dibahas, termasuk sistem SI yang digunakan secara internasional.

1.2. Standar Satuan Besaran

Standar satuan adalah acuan yang digunakan untuk mengukur besaran. Sub-bab ini menguraikan berbagai standar yang digunakan dalam pengukuran fisika, seperti meter untuk panjang dan kilogram untuk massa. Penjelasan tentang bagaimana standar ini ditetapkan dan pentingnya konsistensi dalam pengukuran juga diulas.

1.3. Macam Alat Ukur

Berbagai alat ukur yang digunakan dalam fisika diperkenalkan dalam sub-bab ini. Alat ukur seperti penggaris, neraca, dan stopwatch dijelaskan fungsinya serta cara penggunaannya. Pentingnya kalibrasi alat ukur untuk memastikan akurasi hasil pengukuran juga ditekankan.

1.4. Konversi Satuan

Konversi satuan adalah proses mengubah satuan dari satu bentuk ke bentuk lainnya. Sub-bab ini memberikan contoh-contoh konversi yang umum terjadi, seperti dari kilometer ke meter atau dari Celsius ke Kelvin. Pemahaman tentang konversi satuan sangat penting untuk aplikasi fisika di dunia nyata.

1.5. Dimensi

Dimensi dari suatu besaran fisika menjelaskan hubungan antar besaran tersebut. Sub-bab ini membahas tentang analisis dimensi dan bagaimana dimensi dapat digunakan untuk memeriksa konsistensi persamaan fisika. Ini membantu siswa memahami pentingnya dimensi dalam pengukuran dan perhitungan.

1.6. Angka Penting

Angka penting adalah angka yang menunjukkan ketelitian dalam pengukuran. Sub-bab ini menjelaskan bagaimana menentukan angka penting dalam hasil pengukuran dan aturan-aturan yang harus diikuti. Hal ini sangat penting dalam laporan eksperimen untuk menunjukkan tingkat akurasi.

1.7. Notasi Ilmiah (Bentuk Baku)

Notasi ilmiah digunakan untuk menyederhanakan penulisan angka yang sangat besar atau sangat kecil. Sub-bab ini mengajarkan cara menulis angka dalam bentuk baku dan pentingnya notasi ilmiah dalam komunikasi ilmiah.

1.8. Pengukuran

Pengukuran adalah proses menentukan nilai dari suatu besaran. Sub-bab ini membahas metode pengukuran yang tepat dan pentingnya ketelitian serta akurasi dalam pengukuran. Berbagai teknik pengukuran yang digunakan dalam eksperimen fisika juga dijelaskan.

1.9. Vektor

Vektor adalah besaran yang memiliki arah dan besar. Sub-bab ini menjelaskan konsep dasar vektor, termasuk cara menjumlahkan dan mengurangkan vektor. Pemahaman tentang vektor sangat penting dalam fisika, terutama dalam studi gerakan.

1.10. Rangkuman

Rangkuman dari semua konsep yang telah dibahas dalam bab ini, menekankan pentingnya pemahaman besaran dan satuan dalam fisika.

1.11. Tugas Mandiri

Tugas mandiri yang diberikan untuk menguji pemahaman siswa tentang konsep-konsep yang telah diajarkan dalam bab ini.

1.12. Soal Uji Kompetensi

Soal-soal yang dirancang untuk menguji kompetensi siswa dalam memahami materi yang telah diajarkan dalam bab ini.

II. BAB 2: MENERAPKAN HUKUM GERAK DAN GAYA

Bab ini membahas hukum-hukum dasar gerak dan gaya, termasuk hukum Newton yang menjadi dasar mekanika klasik. Pemahaman tentang gerak dan gaya penting untuk menganalisis berbagai fenomena fisika yang terjadi di sekitar kita.

2.1. Gerak dan Gaya

Sub-bab ini memperkenalkan konsep gerak dan gaya, serta hubungan antara keduanya. Penjelasan tentang jenis-jenis gerak, seperti gerak lurus dan gerak melingkar, juga disertakan.

2.2. Gerak Lurus Beraturan (GLB)

GLB adalah gerakan dengan kecepatan tetap. Sub-bab ini membahas karakteristik GLB dan bagaimana menganalisis gerakan ini menggunakan grafik dan persamaan.

2.3. Gerak Lurus Berubah Beraturan (GLBB)

GLBB adalah gerakan dengan percepatan tetap. Sub-bab ini menjelaskan bagaimana menghitung jarak, kecepatan, dan waktu dalam GLBB.

2.4. Hukum-Hukum Newton tentang Gerak

Hukum Newton terdiri dari tiga hukum dasar yang menjelaskan hubungan antara gaya dan gerak. Sub-bab ini membahas masing-masing hukum dan aplikasinya dalam kehidupan sehari-hari.

2.5. Gerak Benda yang Dihubungkan dengan Katrol

Sub-bab ini menjelaskan konsep katrol dan bagaimana benda yang terhubung dengan katrol dapat mempengaruhi gaya dan gerakan.

2.6. Benda Bergerak pada Bidang Miring

Penjelasan tentang gerakan benda pada bidang miring, termasuk gaya-gaya yang bekerja dan analisis gerakan.

2.7. Gaya Gesek

Sub-bab ini membahas tentang gaya gesek, jenis-jenisnya, dan bagaimana gaya gesek mempengaruhi gerakan benda.

2.8. Gerak Melengkung

Gerak melengkung adalah gerakan yang mengikuti lintasan melengkung. Sub-bab ini menjelaskan konsep dan analisis gerak melengkung.

2.9. Kegiatan

Kegiatan praktis yang dirancang untuk membantu siswa memahami konsep gerak dan gaya melalui eksperimen.

2.10. Rangkuman

Rangkuman dari semua konsep yang telah dibahas dalam bab ini, menekankan pentingnya pemahaman hukum gerak dan gaya.

2.11. Soal Uji Kompetensi

III. BAB 3: HUKUM KEKEKALAN ENERGI MEKANIK

Bab ini membahas hukum kekekalan energi mekanik, yang menyatakan bahwa energi total dalam sistem tertutup tetap konstan. Pemahaman tentang energi sangat penting dalam fisika dan aplikasinya.

3.1. Energi Kinetik dan Energi Potensial

Sub-bab ini menjelaskan dua jenis energi utama dalam fisika: energi kinetik (energi gerak) dan energi potensial (energi yang tersimpan).

3.2. Hukum Kekekalan Energi

Hukum kekekalan energi menyatakan bahwa energi tidak dapat diciptakan atau dimusnahkan, hanya dapat diubah dari satu bentuk ke bentuk lainnya. Sub-bab ini membahas aplikasinya dalam berbagai situasi.

3.3. Energi Mekanik dalam Sistem Terisolasi

Energi mekanik total dalam sistem terisolasi adalah jumlah energi kinetik dan energi potensial. Sub-bab ini membahas bagaimana energi ini tetap konstan dalam sistem tertutup.

3.4. Contoh Penerapan Hukum Kekekalan Energi

Sub-bab ini memberikan contoh konkret tentang penerapan hukum kekekalan energi dalam kehidupan sehari-hari, seperti dalam sistem pegas dan gerakan bola.

3.5. Hukum Kekekalan Momentum Sudut

Momentum sudut juga merupakan besaran yang dilestarikan dalam sistem tertutup. Sub-bab ini membahas konsep dan aplikasinya dalam fisika.

3.6. Kesetimbangan Benda

Kesetimbangan benda terjadi ketika semua gaya yang bekerja pada benda saling menetralkan. Sub-bab ini menjelaskan kondisi kesetimbangan dan aplikasinya.

3.7. Rangkuman

Rangkuman dari semua konsep yang telah dibahas dalam bab ini, menekankan pentingnya pemahaman hukum kekekalan energi.

3.8. Soal Kompetensi

IV. BAB 4: USAHA DAN ENERGI

Bab ini membahas konsep usaha dan energi dalam fisika, termasuk bagaimana usaha dilakukan dan bagaimana energi diubah dari satu bentuk ke bentuk lainnya.

4.1. Pengertian Usaha

Usaha adalah produk dari gaya yang bekerja pada suatu benda dan jarak yang ditempuh benda tersebut. Sub-bab ini menjelaskan konsep dasar usaha dan satuannya.

4.2. Daya

Daya adalah laju usaha yang dilakukan. Sub-bab ini membahas hubungan antara usaha dan daya serta contoh perhitungan daya.

4.3. Konsep Energi

Energi adalah kemampuan untuk melakukan usaha. Sub-bab ini menjelaskan berbagai bentuk energi, termasuk energi kinetik, energi potensial, dan energi mekanik.

4.4. Energi Mekanik

Energi mekanik adalah jumlah energi kinetik dan energi potensial dalam suatu sistem. Sub-bab ini membahas konsep dan aplikasinya.

4.5. Kerja oleh Gaya Konservatif dan oleh Gaya Non-Konservatif

Gaya konservatif adalah gaya yang kerjanya tidak tergantung pada jalur yang dilalui, sedangkan gaya non-konservatif bergantung pada jalur. Sub-bab ini membahas perbedaan antara keduanya.

4.6. Kegiatan

Kegiatan praktis yang dirancang untuk membantu siswa memahami konsep usaha dan energi melalui eksperimen.

4.7. Rangkuman

Rangkuman dari semua konsep yang telah dibahas dalam bab ini, menekankan pentingnya pemahaman usaha dan energi.

4.8. Soal Uji Kompetensi

V. BAB 5: MOMENTUM DAN IMPULS

Bab ini membahas konsep momentum dan impuls, serta hukum kekekalan momentum yang berlaku dalam sistem tertutup.

5.1. Pengertian Momentum dan Impuls

Momentum adalah produk massa dan kecepatan suatu benda. Impuls adalah perubahan momentum. Sub-bab ini menjelaskan hubungan antara keduanya.

5.2. Impuls sebagai Perubahan Momentum

Sub-bab ini membahas bagaimana impuls yang diterima oleh suatu benda dapat mengubah momentumnya.

5.3. Hukum Kekekalan Momentum

Hukum kekekalan momentum menyatakan bahwa total momentum dalam sistem tertutup tetap konstan. Sub-bab ini membahas aplikasinya dalam berbagai situasi.

5.4. Tumbukan

Tumbukan adalah interaksi antara dua benda yang bertabrakan. Sub-bab ini membahas jenis-jenis tumbukan dan analisis momentum dalam tumbukan.

5.5. Kegiatan

Kegiatan praktis yang dirancang untuk membantu siswa memahami konsep momentum dan impuls melalui eksperimen.

5.6. Rangkuman

Rangkuman dari semua konsep yang telah dibahas dalam bab ini, menekankan pentingnya pemahaman momentum dan impuls.

VI. BAB 6: SIFAT MEKANIK BAHAN

Bab ini membahas sifat mekanik bahan, termasuk elastisitas, kekuatan, dan deformasi.

6.1. Sifat Mekanik Bahan

Sifat mekanik bahan adalah karakteristik yang menggambarkan respons bahan terhadap gaya. Sub-bab ini menjelaskan berbagai sifat mekanik, seperti elastisitas dan kekuatan.

6.2. Rangkuman

Rangkuman dari semua konsep yang telah dibahas dalam bab ini, menekankan pentingnya pemahaman sifat mekanik bahan.

6.3. Soal Uji Kompetensi

VII. BAB 7: SUHU DAN KALOR

Bab ini membahas konsep suhu dan kalor, serta hukum-hukum yang mengatur perpindahan kalor.

7.1. Pengukuran Temperatur

Suhu adalah ukuran panas atau dinginnya suatu benda. Sub-bab ini menjelaskan berbagai cara pengukuran suhu dan alat yang digunakan.

7.2. Temperatur Gas Ideal, Termometer Celsius, dan Termometer Fahrenheit

Sub-bab ini membahas hubungan antara berbagai skala suhu dan prinsip pengukuran suhu pada gas ideal.

7.3. Asas Black dan Kalorimetri

Asas Black menjelaskan hubungan antara kalor yang dilepas dan diserap oleh zat. Sub-bab ini juga membahas alat ukur kalor jenis zat.

7.4. Hantaran Kalor

Hantaran kalor adalah proses perpindahan kalor dari satu tempat ke tempat lain. Sub-bab ini membahas tiga cara hantaran kalor: konduksi, konveksi, dan radiasi.

7.5. Kegiatan

Kegiatan praktis yang dirancang untuk membantu siswa memahami konsep suhu dan kalor melalui eksperimen.

7.6. Rangkuman

Rangkuman dari semua konsep yang telah dibahas dalam bab ini, menekankan pentingnya pemahaman suhu dan kalor.

7.7. Soal Uji Kompetensi

VIII. BAB 8: DINAMIKA FLUIDA

Bab ini membahas tentang fluida, tekanan, dan hukum-hukum yang mengatur aliran fluida.

8.1. Cek Kemampuan Pra Syarat

Sebelum mempelajari materi ini, siswa diminta untuk menyelesaikan beberapa soal yang berkaitan dengan fluida.

8.2. Tekanan

Tekanan adalah gaya per satuan luas yang bekerja pada suatu permukaan. Sub-bab ini menjelaskan pengertian dan satuan tekanan.

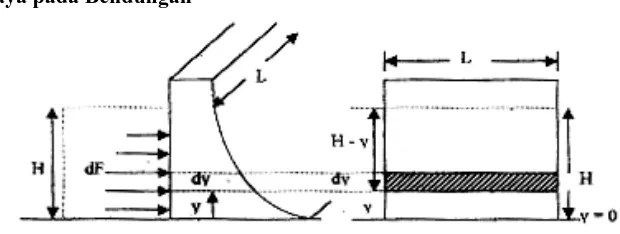
8.3. Hukum Pokok Hidrostatika

Hukum pokok hidrostatika menjelaskan hubungan antara tekanan, kedalaman, dan massa jenis fluida.

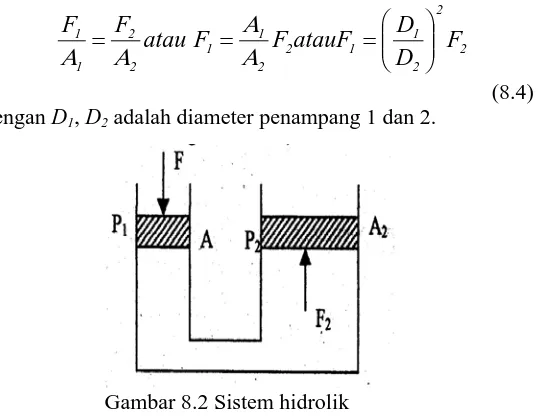
8.4. Hukum Pascal

Hukum Pascal menyatakan bahwa tekanan yang diberikan pada fluida dalam ruang tertutup akan diteruskan ke segala arah dengan sama rata.

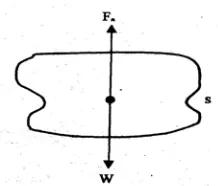
8.5. Hukum Archimedes

Hukum Archimedes menjelaskan gaya apung yang dialami oleh benda yang dicelupkan ke dalam fluida.

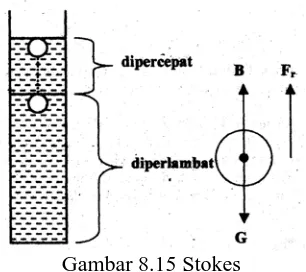
8.6. Tegangan Permukaan dan Viskositas Zat Cair

Tegangan permukaan adalah fenomena yang terjadi pada permukaan zat cair, sedangkan viskositas adalah ukuran kekentalan fluida.

8.7. Aliran Fluida

Sub-bab ini membahas konsep aliran fluida, termasuk aliran laminer dan turbulen.

8.8. Persamaan Kontinuitas

Persamaan kontinuitas menjelaskan hubungan antara kecepatan dan luas penampang dalam aliran fluida yang tidak kompresibel.

8.9. Persamaan Bernoulli

Persamaan Bernoulli menghubungkan tekanan, kecepatan, dan ketinggian dalam aliran fluida.

8.10. Pemakaian Persamaan Bernoulli

Sub-bab ini memberikan contoh penerapan persamaan Bernoulli dalam kehidupan sehari-hari.

8.11. Kegiatan

Kegiatan praktis yang dirancang untuk membantu siswa memahami konsep dinamika fluida melalui eksperimen.

8.12. Rangkuman

Rangkuman dari semua konsep yang telah dibahas dalam bab ini, menekankan pentingnya pemahaman dinamika fluida.

8.13. Soal Uji Kompetensi

Referensi Dokumen

Fisika Untuk Sains dan Teknik ( Tippler, Paul A )

FISIKA, Jilid 1 Edisi 5 ( Douglas C Giancoli )

Fisika Untuk SMA Kelas IX,X, dan XI- ( Marthen Kanginan )

Physics for Scientists and Engineers ( Raymond Serway, et. al )

Diktat Fisika Dasar I ( Dosesn-Dosen Fisika FMIPA ITS )