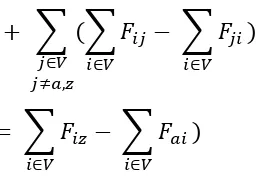BAB 8
MODEL-MODEL JARINGAN DAN JARINGAN-JARINGAN PETRI
8.1 MODEL-MODEL JARINGAN
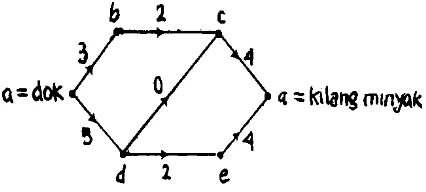
Perhatikan graf terarah pada Gambar 1 yang mewakili sebuah jaringan pipa minyak. Minyak dilepaskan di dok dan dipompa sepanjang jaringan menuju kilang minyak . verteks-verteks dan mewakili stasiun pompa lanjutan. Rusuk-rusuk terarah mewakili bagian-bagian pipa dari sistem dan menunjukkan arah minyak dapat mengalir. Label-label pada rusuk menunjukkan kapasitas bagian pipa. Masalahnya adalah mencari sebuah jalan untuk memaksimalkan aliran dari dok menujukilang minyak danmenghitung nilai aliran maksimum tersebut.gambar 1 menyediakan sebuah contoh jaringan transpor(transpor network).
Gambar 8.1.1. Sebuah jaringan transfor Definisi 8.1.1
Sebuah jaringan transpor (atau cukup jaringan) adalah graf terarah berbobot sederhana yang memenuhi
a. Verteks bertanda, yang merupakan sumber, tidak mempunyai rusuk yang masuk b. Verteks bertanda, yang merupakan tujuan , tidak mempunnyai rusuk yang keluar.
Contoh 8.1.2
Graf pada Gambar 8.1.1. Merupakan sebuah jaringan transpor. Sumbernya adalah verteks dan tujuannya adalah verteks . kapasitas rusuk , adalah 3 dan kapasitas dari rusuk
adalah 2. □
Dalam bab ini , jika merupakan sebuah jaringan, kita akan menyatakan sumbernya dengan dan tujuannya dengan .
Aliran ( flow) dalam sebuah jaringan menempatkan sebuah aliran dalam setiap rusuk terarah yang tidak melampaui kapasitas rusuk itu. Selain itu diasumsikan bahwa aliran ke dalam verteks , yang bukan merupakan sumber ataupun tujuan, sama dengan aliran keluardari . definisi berikut membuat gagasan ini tepat.
Definisi 8.1.3
Misalkan sebuah jaringan transpor. Misalkan menyatakan kapasitas rusuk terarah sebuah aliran di menempatkan bilangan tak negatif pada setiap rusuk terarah
Sehingga:
a.
b. Untuk setiap verteks , yang bukan merupakan sumber atau pun tujuan.
∑ ∑ (8.1.1)
[Dalam penjumlahan sepert (8.1.1), asalkan tidak dispesifikasikan, penjumlahan itu dilakukan untuk semua verteks . Juga, jika bukan merupakan rusuk, kita tetapkan
.]
Kita sebut aliran dalam rusuk untuk sembarang verteks , kita sebut ∑
aliran ke dalam j dan kita sebut
∑
Sifat yang dinyatakan dalam persamaan (8.1.1) disebut konservasi aliran (conservation of flow). Dalam contoh pemompaan minyak pada Gambar 8.1.1, konservasi aliran berarti minyak tidak digunakan atau dipasok pada stasiun pemompaan dan
Contoh 8.1.4 Penandaan
mendefinisikan sebuah aliran untuk jaringan pada gambar 8.1.1. Sebagai contoh, aliran ke dalam verteks .
sama dengan aliran keluar dari verteks
□
Pada gambar 8.1.2 kita telah menggambar ulang jaringan dari Gambar 8.1.1 untuk menunjukkan aliran pada Contoh 8.1.4. Sebuah rusuk dibeli jika kapasitas adalah dan aliran di adalah Notasi ini akan digunakan dalam bab ini.
Perhatikan dalam Contoh 8.1.4, aliran keluar dari sumber .
sama dengan aliran ke dalam tujuan .
Gambar 8.1.2. Aliran dalam sebuah jaringan . rusuk - rusuk dilabeli untuk mengindikasikan kapasitas dan aliran .
Teorema 8.1.5
Jika diketahui sebuah aliran dalam sebuah jaringan , aliran keluar dari sumber sama dengan aliran ke dalam tujuan , yakni
∑ ∑
Pembuktian. Misalkan adalah himpunan verteks . Kita mempunyai
∑ (∑
dengan merupakan himpunan rusuk. Kini
∑ ∑
∑
∑
∑
karena untuk semua , dan (Definisi 8.1.3b) ∑ ∑ jika .
Dengan keterangan dari teorema 5, kita dapat menyatakan definisi berikut
Definisi 8.1.6
Misalkan F adalah sebuah aliran dalam sebuah jaringan . Nilai
∑ ∑
disebut nilai aliran Contoh 8.1.7.
Nilai aliran dan jaringan pada gambar 8.1.7 adalah 5.
Masalah untuk jaringan transpor dapat dinyatakan sebagai berikut: Carilah sebuah aliran maksimal di , yakni diantara semua aliran yang mungkin di , carilah sebuah aliran sehingga nilai adalah nilai maksimum. Pada bagian selanjutnya kita akan memberikan sebuah algoritma yang memecahkan masalah ini dengan efisien. Kita akan mengakhiri bagian ini dengan memberikan contoh-contoh tambahan.
Contoh 8.1.8 Sebuah Jaringan Pemompaan
Gambar 8. 1 .3 Sebuah jaringan pemompaan. Air untuk kota dan dikirim dari sumur w1, w2, dan w3. Kapasitas – kapasitasnya ditunjukkan pada rusuk – rusuk.
Verteks – verteks dan mewakili stasiun pemompaan lanjutan.Buatlah model sistem ini sebagai sebuah jaringan transpor.
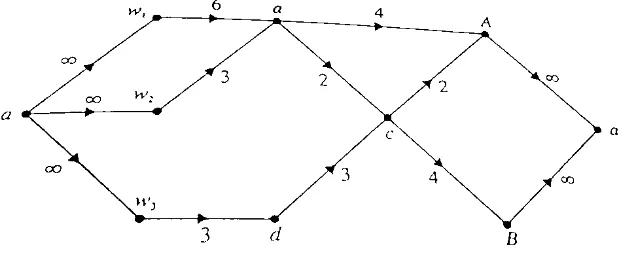
Untuk memperoleh sumber dan tujuan yang ditandai, kita dapat memperoleh sebuah jaringan transpor ekuivalen dengan menyatukan bersama sumber – sumber tersebut ke dalam sumber raya (supersource) dan menyatukan bersama tujuan – tujuan menjadi sebuah tujuan raya (supersink) (lihat gambar 8.1.4). Pada Gambar 8.1.4, mewakili sebuah kapasitas tak terbatas.
Gambar 8.1.4 jaringan pada gambar 8.1.3 dengan sebuah sumber dan tujuan yang ditandai.
Contoh 8.1.9 Sebuah Jaringan Lalu Lintas
Ada kemungkinan untuk pergidari kota A ke kota B secara langsung atau dengan melalui kota B. Selama periode 6:00 hingga 7:00 malam, waktu perjalanan rata – rata adalah
A ke B (15 menit)
B ke C (30 menit)
Kapasitas maksimum dari rute – rute tersebut adalah
A ke B (3000 kendaraan)
B ke C (2000 kendaraan)
A ke C (4000 kendaraan)
Gambarkanlah aliran lalu – lintas dari A ke C selama periode 6:00 hingga 7:00 malam sebagai sebuah jaringan.
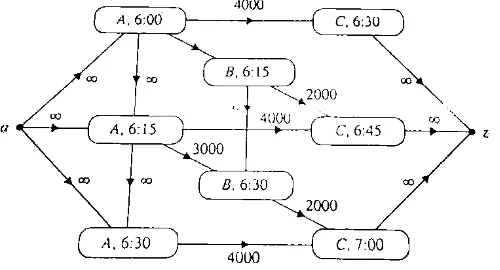
Sebuah verteks akan mewakili sebuah kota pada saat tertentu (lihat Gambar 8.1.5). Sebuah rusuk menghubungkan , t1 ke ,t2 jika kita dapat meninggalkan kota pada t1 sampai di kota pada t2. Kapasitas sebuah rusuk merupakan kapasitas dari rute. Rusuk – rusuk dari kapasitas tak terbatas menghubungkan ,t1 ke ,t2 dan ,t1 ke B,t2 untuk menyatakan bahwa sembarang jumlah mobil dapat menunggu di kota atau kota . Akhirnya, kita memperkenalkan sebuah sumber raya dan tujuan raya.
Gambar 8.1.5 Sebuah jaringan yang mewakili aliran lalu lintas dari kota ke kota selama periode 6:00 hingga 7:00 malam.
Varian dari aliran jaringan telah digunakan dalam rancangan jaringan komputer yang efisien (lihat [Jones; Kleinrock]). Dalam pemodelan sebuah jaringan komputer, sebuah verteks merupakan pesan atau pusat pengatur, sebuah rusuk mewakili kanal yang di sini data dapat ditransmisikan di antara verteks – verteks, sebuah aliran merupakan jumlah bit rata – rata per detik yang ditransmisikan pada sebuah kanal, dan kapasitas sebuah rusuk merupakan kapasitaskanal yang bersesuaian.
8.2 ALGORITMA ALIRAN MAKSIMAL
nilai maksimum yang sama. Pada subbab ini kita memberikan sebuah algoritma untuk mencari sebuah aliran maksimal. Gagasan dasarnya adalah sederhana mulai dengan suatu aliran awal dan menaikkan secara iteratif nilai dari aliran sampai tidak ada peningkatan lagi. Aliran yang dihasilkan selanjutnya akan merupakan sebuah aliran maksimal.
Kita dapat mengambil aliran awal sebagai salah satu aliran pada mana aliran di masing – masing rusuk adalah nol. Untuk menaikkan nilai aliran yang diketahui, kita harus mencarisebuah lintasan dari ssumber ke tujuan dan menaikkan aliran sepanjang lintasan ini.
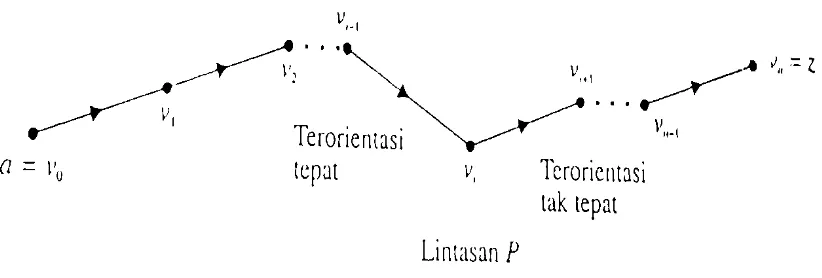
Pada saat ini sangat membantu untuk memperkenalkan beberapa terminologi. Sepanjang subbab ini, menyatakan sebuah jaringan dengan sumber , tujuan , dan kapasitas . Sementara itu, perhatikan rusuk – rusuk dari sebagai tak terarah dan misalkan
merupakan sebuah lintasan dari ke dalam graf tak terarah ini. (Semua lintasan dalam bagian ini dengan referensi pada graf tak berarah dasar). Jika sebuah rusuk di diarahkan dari ke , kita katakan bahwa terorientasi secara tepat atau properly oriented (dengan mengacu pada ); jika sebaliknya, kita katakan terorientasi tak tepat atau improperly oriented (dengan mengacu pada P) (lihat Gambar 8.2.1).
Jika kita dapat mencari sebuah lintasan dari sumber ke tujuan dengan setiap rusuk di terorientasi dengan tepat dan aliran dalam setiap rusuk kurang dari kapasitas rusuk, maka mungkin untuk menaikkan nilai aliran.
Contoh 8.2.1
Perhatikan lintasan dari ke dalam Gambar 8.2.2. Semua rusuk dalam terorientasi dengan tepat. Nilai aliran dalam jaringan ini dapat dinaikkan dengan 1, seperti yang ditunjukkan dalam Gambar 8.2.3.
Gambar 8.2.2 Sebuah lintasan dari rusuk-rusuk yang teriorentasi dengan tepat.
Gambar 8.2.3 Setelah penaikan aliran pada Gambar 8.2.2 dengan 1. □
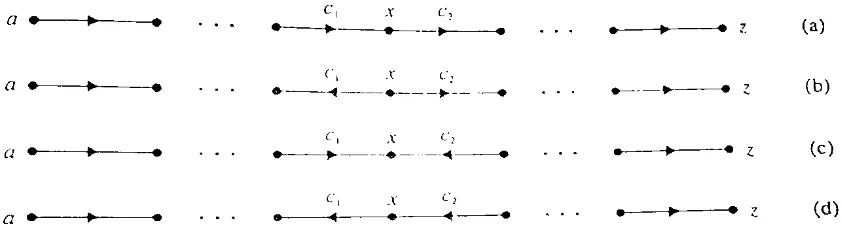
Mungkin juga untuk menaikkan aliran dalam lintasan-lintasan tertentu dari sumber ke tujuan tempat kita mempunyai rusuk-rusuk yang terorientasi dengan tepat dan tak tepat. Misalkan sebuah lintasan dari ke dan misalkan sebuah verteks di yang bukan ataupun (lihat Gambar 8.2.4).
dengan sehingga aliran ke dalam akan tetap sama dengan aliran keluar dari . Kasus (c) serupa dengan kasus (b), kecuali kita menaikkan aliran di dengan dan menurunkan aliran di dengan . Pada kasus (d), kita menurunkan aliran di kedua rusuk dengan . Dalam setiap kasus, perlakuan rusuk yang dihasilkan memberikan sebuah aliran. Tentu saja, untuk menjalankan pengubahan ini, kita harus mempunyai aliran kurang dari kapasitas dalam sebuah rusuk yang terorientasi dengan tepat dan sebuah aliran tak nol dalam sebuah rusuk yang terorientasi tak tepat.
Contoh 8.2.2
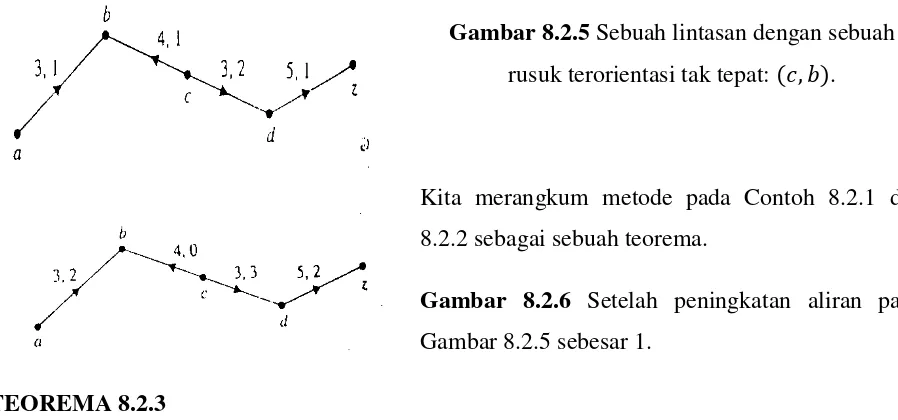
Perhatikan lintasan dari ke pada Gambar 8.2.5. Rusuk-rusuk dan terorientasi dengan tepat dan rusuk terorientasi tak tepat. Kita menurunkan aliran sebesar 1 dalam rusuk terorientasi tak tepat dan meningkatkan aliran sebesar 1 dalam rusuk-rusuk terorientasi dengan tepat dan (lihat Gambar 8.2.6). nilai aliran baru adalah 1 lebih dari aliran yang asli.
Gambar 8.2.5 Sebuah lintasan dengan sebuah rusuk terorientasi tak tepat: .
Kita merangkum metode pada Contoh 8.2.1 dan 8.2.2 sebagai sebuah teorema.
Gambar 8.2.6 Setelah peningkatan aliran pada Gambar 8.2.5 sebesar 1.
TEOREMA 8.2.3
Misalkan sebuah lintasan dari ke dalam sebuah jaringan G yang memenuhi:
(a) Untuk setiap rusuk terorientasi dengan tepat di (b) Untuk setiap rusuk terorientasi tak tepat di ,
Misalkan
dengan terdiri dari bilangan-bilangan , untuk rusuk-rusuk terorientasi dengan tepat
di , dan , untuk rusuk-rusuk terorientasi tak tepat di . Definisikan
{
Maka * merupakan sebuah aliran yang nilainya lebih besar dari nilai .
Pembuktian. (lihat Gambar 8.2.2, 8.2.3, 8.2.5, dan 8.2.6.) Argumen bahwa * merupakan sebuah aliran diberikan tepat sebelum Contoh 8.2.2. Oleh karena rusuk di dinaikkan sebesar , nilai * lebih besar dari nilai .
Dalam bagian selanjutnya kita akan menunjukkan jika tidak terdapat lintasan yang memenuhi kondisi pada Teorema 8.2.3, aliran tersebut maksimal. Jadi, adalah mungkin untuk membentuk sebuah algoritma yang berdasarkan pada Teorema 8.2.3. intinya adalah
1. Mulailah denagn sebuah aliran (yakni, aliran yang aliran dalam setiap rusuknya 0).
2. Carilah sebuah aliran yang memenuhi kondisi dari Teorema 8.2.3. Jika tidak ada lintasan yang seperti itu, berhentilah; aliran tersebuty maksimal.
3. Naikkan aliran sepanjang lintasan dengan , didefinisikan seperti dalam Teorema 8.2.3, dan kembalilah ke baris 2.
Dalam algoritma formal, kita mencari sebuah lintasan yang memenuhi kondisi Teorema 8.2.3 sementara secar bersamaan tetap menjajaki kuantitas
ALGORITMA 8.2.4 Mencari Sebuah Aliran Maksimal dalam Sebah Jaringan
Algoritma ini mencari sebuah aliran maksimal dalam sebuah jaringan. Kapasitas setiap rusuk adalah sebuah bilangan bulat tak negatif.
Keluaran: sebuiha aliran maksimal
52.end
end aliran_maks
Sebuah pembuktian bahwa Algoritma 8.2.4 berakhir diberikan sebagai latihan (Latihan 19). Jika kapasitas-kapasitas diperbolehkan sebagai bilangan rasional tak negatif, algoritma tersebut juga berakhir, akan tetapi, jika kapasitas real tak negatif diperbolehkan dan kita mengizinkan rusuk-rusuk pada baris 20 untuk diuji dalam sembarang urutan, algoritma tersebut tidak akan berakhir (lihat [Ford, halaman 21-22]).
Algoritma 8.2.4 seringkali diacu sebagai prosedur pelabelan (labelling procedure). Kita akan mengilustrasikan algoritma tersebut dengan dua contoh.
Contoh 8.2.5
Dalam pembahasan ini, jika verteks memenuhi dan kita menunjukkan label pada graf sebagai Pada baris 1 dan 2, kita mengawali aliran pada 0 dalam setiap rusuk (lihat Gambar 8.2.7). Selanjutnya, pada baris 5-9 kita menetapkan semua label sebagai . Kemudian, pada baris 10 dan 11 kita melabeli verteks sebagai . Pada baris 12 kita menetapkan . Selanjutnya kita masukkan loop while (baris 13).
Gambar 8.2.7 Setelah pelabelan pertama. Varteks dilabeli ( ) Oleh karena itu z tidak dilabeli dan Utidak kosong, kita beralih ke baris 17, disinni kita memilih verteks a di U dan mwmindahkannya dari Upada baris 18. Pada saat ini, U . Kita menetapkan
pada pada baris 19. Pada baris 20 kita menguji rusuk-rusuk dan karena baik maupun tidak terlabeli. Untuk rusuk kita mempunyai
Pada baris 23 dan 24, kita melabeli verteks sebagai karena
dan
Pada baris 25, kita menambahkan pada . Demikian juga, kita melabeli verteks sebagai dan menambahkan d pada . Pada saat ini,
Selanjutnya kita kembali pada puncak loop while (baris 13). Karena tidak berlabel dan tidak kosong, kita bergerak ke baris 17, di sini kita memilih sebuah verteks di .andaikan kita memilih b. Kita memindahkan dari pada baris 18. Kita menetapkan sebagai pada baris 19. Pada baris 20 kita menguji rusuk Pada baris 23 dan 24 kita melabeli verteks sebagai karena
dan
Pada baris 25 kita tambahkan pada Pada saait ini,
Selanjutnya kita kembali ada puncak loop while (baris 13). Karena tidak berlabel dan tidak kosong, kita bergerak ke baris 17, di sini kita memilih sebuah verteks di Andaikan kita memilih Kita memindahkan dari ke baris 18. Kita menetapkan sebagai pada baris 19. Pada baris 20 kita menguji rusuk Pada baris 23 dan 24 kita melabeli verteks
sebagai Pada baris 25, kita menambahkan pada Pada saat ini
Kemudian kita kembali pada puncak loop while (baris 13). Karena sudah diberi label kita meloncat pada baris 35. Pada baris 35-42, dengan mengikuti pendahulu dari , menemukan lintasan
dari ke . Pada baris 42 kita menetapkan sebagai 2. Karena setiap rusuk di terorientasi dengan tepat, pada baris 48 kita menaikkan aliran dalam setiap rusuk dengan untuk memperoleh Gambar 8.2.8.
Gambar 8.2.8 Setelah peningkatan aliran pada lintasan dengan 2 dari pelabelan kedua.
Selanjtnya kita kembali pada puncak loop while (baris 3). Kemudian pada baris 5-9 kta menetapkan semua label null. Kemudian pada baris 10 dan 11 kita memberi label verteks sebagai (lihat Gambar 8.2.8). pada baris 12 kita tetapkan Kita masuki loop while (baris 13).
Karena tidak berlabel dan tidak kosong, kita bergerak ke baris 17, yang di sini kita memilih sebuah verteks di Andaikan kita memilih . Kita memindahkan dari pada baris 18. Pada baris 23 dan 24 kita melabeli verteks b sebagai dan kita labeli sebagai Kita menambahkan dan pada sehingga
Selanjutnya kita kembali pada puncak loop while (baris 13). Karena tidak berlabel dan tidak kosong, kita bergerak ke baris 17, dimana kita memilih sebuh verteks . Andaikan kita memilih . Kita memindahkan dari pada baris 18. Pada baris 20 kita menguji rusuk Karena , kita tidak melabeli verteks pada saat ini. Sekarang
Kemudian kita kembali ke puncak loop while (baris 13). Karena tidak dilabeli, kita langsung ke baris 35. Pada baris 42 kita mendapatkan bahwa
Oleh karena setiap rusuk di terorientasi dengan tepat, pada baris 48 kita meningkatkan aliran dalam setiap rusuk di dengan untuk memperoleh Gambar 8.2.9.
Anda harus mengecek bahwa iterasi algoritma berikutnya menghasilkan pelabelan yang ditunjukkan pada Gambar 8.2.9. Peningkatan aliran dengan menghasilkan Gambar 8.2.10.
Selanjutnya kita kembali pada puncak loop while (baris 3). Kemudian pada baris 5-9 kita menetapkan semua label sebagai null. Kemudian pada baris 10 dan 11 kita melabeli verteks sebagai (lihat Gambar 8.2.8). pada baris 12 kita menetapkan Kita msuki loop while (baris 13).
Gambar 8.2.9 Setelah peningkatan aliran pada lintasan dengan 2 dan pelabelan ketiga.
Karena tidak berlabel dan tidak kosong, kita bergerak ke baris 17, yang disini kita memilih verteks di . Andaikan kita memilih . Kita memindahkan dari ke pada baris 18. Pada baris 23 dan 24 kita melabeli verteks sebagai dan kita labeli sebagai Kitambahkan dan pada sehingga
memilih . Kita memindahkan dari pada baris 18. Pada baris 20 kita menguji rusuk Karena , tidak melabeli verteks pada saat ini. Sekarang
Kemudian kita kembali ke puncak loop while (baris 13). Karena tidak berlabel dan tidak kosong, kita bergerak ke baris 17, yang disini kita memilih sebuah verteks di . Andaikan kita memilih . Kita memindahkan dari pada baris 18. Pada baris 20 kita menguji rusuk dan karena , kita melabeli verteks maupun verteks . Sekarang
Kita kembali ke puncak loop while (baris 13). Oleh karena tidak dilabeli, kita bergerak ke baris 15. Oleh karena kosong, algoritma berakhir. Aliran pada Gambar 8.2.10 maksimal.
Contoh kita terakhir menujukkan bagaimana memodifikasi Algoritma 8.2.4 untuk membentuk sebuah aliran maksimal dari sebuah aliran yang diberikan.
Gambar 8.2.10 Setelah peningkatan aliran pada lintasan dengan 2 dan seterusnya dan
pelabelan akhir. Aliran tersebut masksimal. □
Contoh 8.2.6
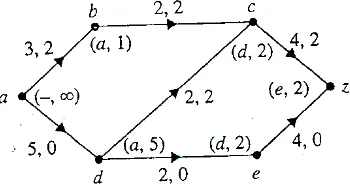
Gantilah aliran nol ada baris 1 dan 2 dari Algoritma 8.2.4 dengan aliran pada Gambar 8.2.11 kemudian carilah sebuah aliran maksimal.
Gambar 8.2.11 Setelah pelabelan.
Oleh karena tidak dilabeli dan tidak kosong, kita bergerak ke baris 17, dimana kita memilih verteks di dan memindahkannya dari pada baris 18. Pada baris 23 dan 24, kita melabeli verteks sebagai dan kita melabeli verteks sebagai Kita menambahkan dan pada sehingga
Selanjutnya kita kembali pada puncak loop while (baris 13).oleh karena tidak dilabeli dan tidak kosong, kita bergerak ke baris 17, dimana kita memilih sebuah verteks di . Andaikan kita memilih . Kita memindahkan dari pada baris 18. Pada baris 20 kita menguji rusuk-rusuk dan Oleh karena , kita dapat melabeli verteks . Pada baris 30 dan 31, verteks dilabeli karena
Kemudian kita kembali pada puncak loop while (baris 13). Kita segera melabeli (lihat Gambar 8.2.11) dan pada baris 42 kita mencari lintasan
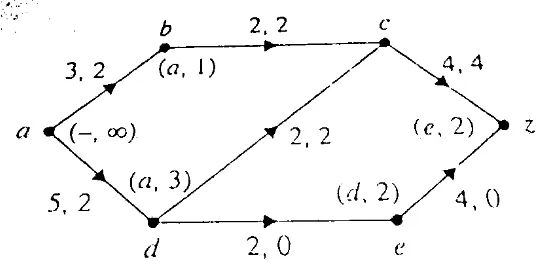
Gambar 8.2.12 Setelah peningkatan aliran pada lintasan dengan 1. Perhatikan bahwa rusuk terorientasi dengan tidak tepat sehingga alirannya berkurang 1.
Gambar 8.2.13 Setelah peningkatan aliran pada lintasan dengan 1. Aliran tersebut maksimal.
8.3 TEOREMA POTONG MIN, ALIRAN MAKS
Kita akan menunjukkan bahwa pada akhir Algoritma 8.2.4, aliran dalam jaringan adalah maksimal. Kita akan mendefinisikan dan membahas pemotongan dalam jaringan-jaringan.
Misalkan sebuah jaringan dan perhatikan aliran pada akhir algoritma 8.2.4. Beberapa verteks dilabeli dan beberapa tidak. Misalkan ̅ menyatakan himpunan verteks berlabel (tidak berlabel). (Ingat ̅ menyatakan komplemen dari ). Maka sumber berada di P dan tujuan berada di ̅. Himpunan dari rusuk-rusuk , dengan dan ̅, disebut pemotongan (cut) dan jumlah kapasitas rusuk-rusuk di S disebut kapasitas pemotongan (capacity of the cut). Kita akan melihat pemotongan ini mempunyai kapasitas minimum dan, karena sebuah pemotongan minimal berhubungan dengan sebuah aliran maksimal (Teorema 8.3.9), aliran maksimal. Kita mulai dengan definisi formal pemotongan. merupakan sebuah jaringan dengan sumber dan tujuan Kapasitas rusuk adalah .
Definisi 8.3.1
Contoh 8.3.2
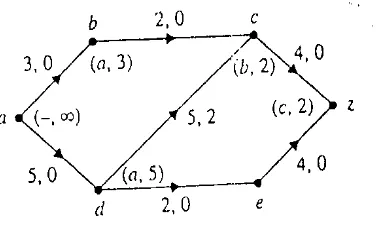
Perhatikan jaringan G pada Gambar 8.3.1. Jika kita misalkan , maka ̅ dan ̅ adalah sebuah pemotongan di G. Seperti ditunjukkan, kadang-kadang kita mengindikasikan sebuah pemotongan dengan menggambar garis putus-putus untuk membagi verteks-verteks.
Gambar 8.3.1 Sebuah pemotongan dalam sebuah jaringan. Garis putus-putus membagi verteks-verteks menjadi himpunan dan ̅ yang menghasilkan pemotongan ̅ .
Contoh 8.3.3
Gambar 8.2.10 menunjukkan pelabelan pada akhir Algoritma 8.2.4 untuk sebuah jaringan tertentu. Jika kita misalkan ̅ menyatakan himpunan verteks berlabel (tak berlabel), kita dapatkan pemotongan yang ditunjukkan pada Gambar 8.3.2. Selanjutnya kita definisikan kapasitas sebuah pemotongan.
Definisi 8.3.4
Teorema berikut menunjukkan kapasitas sembarang pemotongan selalulebih dari atau sama dengan nilai alirannya.
Pemotongan minimal (minimal cut) adalah pemotongan yang mempunyai kapasitas minimum.
Teorema 8.3.9 Teorema Potong Min, Aliran Maks
Misalkan sebuah aliran di dan misalkan ̅ sebuah pemotongan di . Jika kesamaan berlaku dalam (8.3.1), maka aliran maksimal dan pemotongan minimal. Lagipula, kesamaan berlaku dalam (8.3.1) jika dan hanya jika
(a) untuk ̅ (b) untuk ̅
Pembuktian. Pernyataan pertama berlaku dengan sendirinya.
Pembuktian Teorema 8.3.7 menunjukkan bahwa kesamaan berlaku dengan tepat apabila ∑ ∑ dan ∑ ∑ ∑ ∑
Sehingga pernyataan juga benar. Contoh 8.3.10
Pada Gambar 8.3.2, nilai aliran dan kapasitas pemotongan keduanya adalah 6; oleh karena itu
alirannya maksimal dan pemotongan minimal. □
Kita dapat menggunakan Teorema 8.3.9 untuk menunjukkan bahwa Algoritma 8.3.4 menghasilkan sebuah aliran maksimal.
TEOREMA 8.3.11
Pada akhirnya, Algoritma 8.2.4 menghasilkan sebuah aliran maksimal. Lagi pula, jika
(demikian juga ̅ merupakan himpunan verteks berlabel (demikian juga, tak berlabel) pada akhir Algoritma 8.2.4, pemotongan ̅ minimal.
Pembuktian. Misalkan ̅ adalah himpunan verteks berlabel (tak berlabel) dari pada akhir Algoritma 8.2.4. Perhatikan sebuah rusuk (i,j) dengan ̅. Oleh karena dilabeli, kita