THESIS – SM 142501
GRACEFUL LABELING IN DOUBLE DRAGON GRAPH AND
PENDANT DRAGON GRAPH
RESTU RIA WANTIKA NRP 1213 201 030
SUPERVISOR
Dr. Darmaji, S.Si., M.T. MAGISTER’S DEGREE
MATHEMATICS DEPARTEMENT
FACULTY OF MATHEMATICS AND NATURAL SCIENCES SEPULUH NOPEMBER INSTITUTE OF TECHNOLOGY SURABAYA
PELABELAN
GRACEFUL
PADA GRAF DRAGON GANDA
DAN GRAF DRAGON PENDANT
Nama Mahasiswa : Restu Ria Wantika
NRP : 1213201030
Jurusan : Matematika FMIPA-ITS
Pembimbing : Dr. Darmaji, S.Si., M.T. ABSTRAK
Pelabelan graf adalah suatu pemetaan (fungsi) yang memasangkan unsur-unsur graf (simpul atau sisi) dengan bilangan (biasanya bilangan bulat positif). Jika domain fungsi adalah simpul, maka pelabelan disebut pelabelan simpul (vertex labeling). Jika domainnya adalah sisi, maka disebut pelabelan sisi (edge labeling), dan jika domainnya simpul dan sisi, maka disebut pelabelan total (total labeling). Pelabelan graceful pada graf G adalah fungsi injektif f dari V (G) ke {0, 1, 2,…,q}, dengan q adalah ukuran graf G
sedemikian hingga jika sisi uv dilabeli dengan | ( ) ( )| maka label sisinya akan berbeda untuk semua sisi di G. Graf yang memenuhi pelabelan
graceful disebut graf graceful. Dalam penelitian ini dikaji pelabelan graceful
pada graf dragon yang dimodifikasi dengan menambahkan graf lingkaran pada bagian simpul akhir ekor graf dragon. Graf hasil modifikasi disebut graf dragon ganda dan dinotasikan 2 ( ) dengan . Modifikasi kedua dilakukan dengan menambahkan pendant pada setiap simpul kepala yang tidak terhubung pada graf lintasan. Hasil modifikasi yang demikian
disebut dengan graf dragon pendant dan dinotasikan ( ) dengan
, dan . Hasil penelitian menunjukkan bahwa graf dragon ganda 2 ( ) dengan dan adalah graf graceful dan graf dragon pendant ( ) dengan , dan adalah graf graceful
GRACEFUL LABELING IN DOUBLE DRAGON GRAPH
AND PENDANT DRAGON GRAPH
Name : Restu Ria Wantika
NRP : 1213201030
Department : Mathematics FMIPA-ITS Supervisor : Dr. Darmaji, S.Si., M.T.
ABSTRACT
Labeling in a graph is a mapping (function) which maps the element of graph (vertex or edge) with a number (usually a positive integer). If the domain of function is vertex, the labeling called vertex labeling. Meanwhile, if the domain of function is edge, then it is called edges labeling. And if the domain are both vertex and edge, then it is called as total labeling. Graceful Labeling in a graph G is injective function f from V (G) to {0, 1, 2,…,q}, with q is size of graph G such that if edge of uv labeled by| ( ) ( )|then edges label will be different for all edges in G. A graph which satisfied graceful labeling is called graceful graph. In this research, we examined the graceful labeling on a dragon graph which was modified by adding circle graph at the end of dragon graphs tail vertex. Graph which was result of modification is called double dragon graph denoted by 2 ( ) with . Second modification was conducted by adding pendant in every head vertex that is not connected in path graph. That result is called pendant dragon graph and denoted by ( ) with , and . The result showed that double dragon graph with was graceful graph and pendant dragon graph with , and was graceful graph.
KATA PENGANTAR
Puji syukur penulis panjatkan kepada Tuhan Yang Maha Esa yang telah melimpahkan rahmat dan berkat-Nya sehingga penulis dapat menyelesaikan Tesis yang berjudul “PELABELAN GRACEFUL PADA GRAF DRAGON GANDA
DAN GRAF DRAGON PENDANT” ini terselesaikan dengan baik. Tesis ini merupakan sebagian persyaratan kelulusan dalam memperoleh gelar Magister di Program Studi Magister Matematika, Fakultas MIPA, Institut Teknologi Sepuluh Nopember.
Penyusunan Tesis ini tidak lepas dari bimbingan, bantuan, dan dukungan moral maupun spiritual dari banyak pihak. Oleh sebab itu, penulis mengucapkan terima kasih yang sebesar-besarnya kepada:
1. Bapak, Ibu, Adek beserta keluarga tercinta yang selalu memberikan dukungan, doa, dan motivasi agar penulis dapat menyelesaikan Tesis ini. 2. Dr. Darmaji, S.Si., M.T. selaku dosen pembimbing tesis yang telah
memberikan motivasi, arahan, masukkan, dam bimbingan selama penulis menyelesaikan Tesis ini.
3. Prof. Dr. Erna Apriliani, M.Si, selaku Ketua Jurusan Matematika Institut Teknologi Sepuluh Nopember.
4. Dr. Chairul Imron, MI.Komp dan Endah Rokhmati MP, S.Si.,M.T selaku dosen penguji yang telah memberikan masukkan dan juga motivasi kepada penulis sehingga Tesis ini dapat terselesaikan dengan baik.
5. Seluruh dosen Matematika yang telah memberikan bekal dan ilmu pengetahuan serta staf administrasi Program Studi Magister Matematika atas segala bantuannya.
6. Geng belum tau namanya, rahma, winda, Saiful, teman senasib bidang graf dan sahabat penulis lainnya atas semua dukungan, bantuan, dan semangatnya selama proses penulisan Tesis ini.
Semoga Tuhan memberikan anugerah dan karunia-Nya kepada semua pihak yang telah membantu penulis dalam menyelesaikan Tesis ini.
Penulis menyadari bahwa dalam penulisan Tesis ini masih banyak kekurangan, sehingga kritik dan saran dari pembaca sangat penulis harapkan untuk perbaikan kedepannya. Akhirnya semoga Tesis ini dapat bermanfaat bagi pembaca, khususnya mahasiswa Institut Teknologi Sepuluh Nopember.
Surabaya, 23 Maret 2015
DAFTAR ISI
4.2 Pelabelan graceful pada graf dragon ganda ……… 18
4.3 Pelabelan graceful pada graf dragon pendant ……… 28
BAB V PENUTUP 5.1 Kesimpulan ………. 43
5.2 Saran………. 43
DAFTAR GAMBAR
Gambar 2.1 Graf Sederhana dan bukan sederhana………. 6
Gambar 2.2 Graf Lingkaran……… 6
Gambar 2.3 Graf Lintasan………... 7
Gambar 2.4 Fungsi Satu-satu……….. 7
Gambar 2.5 Fungsi Surjektif………... 8
Gambar 2.6 Fungsi Bijektif……….... 8
Gambar 2.7 Contoh operasi amalgamasi C3dan C4……….. 9
Gambar 2.8 Graf Dragon………. 9
Gambar 2.9 Graf Dragon Ganda………... 9
Gambar 2.10 Graf Dragon Pendant………... 10
Gambar 2.11 (a). Pelabelan Simpul, (b). Pelabelan Sisi c) Pelabelan Total…… 10
Gambar 2.12 (a). Pelabelan Graceful Skolem (b). Pelabelan Graceful Ganjil … 11 Gambar 2.13 Contoh pelabelan graceful pada graf dengan ‖ ‖ = | | -1 (a) dan graf dengan ‖ ‖ | | -1 (b)………... 12
Gambar 4.1 Contoh pelabelan menurut Lekha………. 16
Gambar 4.2 Pelabelan Graf dragon ganda 2 ……… 16
Gambar 4.3 Pelabelan Graf dragon ganda 2 ……… 17
Gambar 4.4 Graf Dragon Ganda 2 ……… 18
Gambar 4.5 Graf Dragon Ganda 2 ……… 23
Gambar 4.6 Graf Dragon Ganda 2 ……… 24
Gambar 4.7 Graf Dragon Ganda 2 ……… 27
Gambar 4.8 Graf Dragon Pendant ……… 29
Gambar 4.9 Graf Dragon Pendant ……… 32
Gambar 4.10 Graf Dragon Pendant ……… 32
Gambar 4.11 Graf Dragon Pendant ……… 34
Gambar 4.12 Graf Dragon Pendant ……… 35
Gambar 4.13 Graf Dragon Pendant ……… 37
Gambar 4.14 Graf Dragon Pendant ……… 38
DAFTAR SIMBOL
G = (V, E) Sebarang graf tak berarah dengan V adalah himpunan tak kosong dari semua simpul dan E adalah himpunan sisi
V (G) Himpunan simpul dari graf G E(G) Himpunan sisi dari graf G
Cn Notasi dari graf lingkaran order n Pn Notasi dari graf lintasan order n
Dn (m) Notasi dari graf dragon order n dan ukuran m
2Dn (m) DPn (m)
Notasi dari Graf dragon ganda order n dan ukuran m
Notasi dari Graf dragon pendant order n dan ukuran m
| | Order graf G
BAB I
PENDAHULUAN
1.1 Latar Belakang
Salah satu cabang ilmu di Matematika adalah teori graf. Teori graf pertama kali ditulis oleh ahli matematika dari Swiss, Leonhard Euler, pada tahun 1736. Euler mencoba menyelesaikan persoalan jembatan Konigsberg. Konigsberg sendiri adalah sebuah kota yang terletak di Prusia timur, sekarang bernama Kaliningrad, sebuah kota yang termasuk dalam wilayah Rusia. Dalam tulisannya, Euler mencoba solusi atas permasalahan bagaimana menyeberangi semua jembatan itu tepat satu kali dari tempat berangkat sampai kembali ke tempat semula.
Saat ini, pelabelan graf menjadi topik yang banyak mendapat perhatian, karena model- model yang ada pada pelabelan graf berguna untuk aplikasi yang luas antara lain pelabelan graf graceful pada graf pot, pelabelan graceful pada graf duplikasi simpul dan graf duplikasi sisi dari graf sikel Cn , pelabelan graceful pada
graf lintasan menggunakan program php dan javascrip, pelabelan harmonis, pelabelan super dan lain-lain. Hingga saat ini pemanfaatan teori pelabelan graf banyak memiliki peranan terutama pada sektor komunikasi, transportasi, penyimpanan data komputer, dan pemancar frekuensi radio.
Suatu graf G didefinisikan sebagai pasangan himpunan (V, E), dengan V
Pelabelan pada suatu graf adalah suatu pemetaan (fungsi) yang memasangkan unsur-unsur graf (simpul atau sisi) dengan bilangan (biasanya bilangan bulat). Jika domain dari fungsi adalah simpul, maka pelabelan disebut pelabelan simpul (vertex labeling). Jika domainnya adalah sisi, maka disebut pelabelan sisi (edge labeling), dan jika domainnya simpul dan sisi, maka disebut pelabelan total (total labeling). Pelabelan graceful pada graf G
adalah fungsi injektif f dari V (G) ke {0, 1, 2,…,q}sedemikian hingga jika sisi
uv dilabeli dengan | ( ) ( )| maka label sisinya akan berbeda untuk semua sisi di G. Graf yang memenuhi pelabelan graceful dinamakan graf
graceful.
Allesandra pada tahun 2014 menunjukkan bahwa graf pendant dengan dengan 3,4 (mod 8) memiliki pelabelan graceful, Cavalier pada tahun 2006 menunjukkan bahwa semua graf pohon adalah gracefuldan Eshghi pada tahun 2002 menunjukkan bahwa beberapa graf merupakan graf graceful antara lain graf roda dengan 3, R2n dengan n ≥ 3, graf helm dengan 3 dan graf dragon ( ) dengan 3 dan 1. Tri lusia (2008) menunjukkan bahwa graf digraf lintasan merupakan digraf graceful dengan n
genap dan digraf bipartite lengkap merupakan digraf graceful.
Beberapa contoh graf graceful dapat diperoleh dari Galian (2013) antara lain graf lingkaran ( ) dengan n adalah n 0 (mod 4) dan n 3 (mod 4), graf bintang, graf lintasan, graf dragon, graf gir, graf caterpillar, graf banana, pohon, graf lobster dan graf kembang api.
Hal yang menarik dalam pelabelan graceful adalah, pertama, pemberian label pada simpul sedemikian sehingga jika sisinya mendapat label harga mutlak dari selisih pelabelan kedua simpul yang terhubung langsung (adjacent) maka hasilnya berbeda. Kedua, pembentukan pola dari graf yang telah mendapatkan label sehingga dapat dirumuskan. Sebuah graf baru dapat dibangun dari sebuah graf yang well known dengan mengenakan operasi tertentu. Hal yang menarik dalam pelabelan graceful adalah membuktikan apakah graf baru tersebut juga memenuhi pelabelan graceful.
1.2 Rumusan Masalah
Berdasarkan latar belakang di atas, maka permasalahan dalam penelitian ini adalah :
1. Menunjukkan apakah graf dragon ganda dan graf dragon pendant merupakan graf graceful atau bukan.
2. Menentukan konstruksi pelabelan graceful pada graf dragon ganda dan graf dragon pendant.
1.3 Tujuan Penelitian
1. Mengetahui apakah graf dragon ganda dan graf dragon pendant merupakan graf graceful atau bukan.
2. Mengonstruksi pelabelan graceful apabila graf dragon ganda dan graf dragon pendant merupakan graf graceful.
1.4 Batasan Masalah
Pelabelan graceful pada sebuah graf merupakan NP-complete problem.
Oleh karenanya dalam penelitian tesis ini graf dibatasi pada graf dragon ganda dengan , dan dan graf dragon pendant dengan , dan , .
1.5 Manfaat Penelitian
BAB II
DASAR TEORI
2.1 Terminologi Dasar Graf
Sebuah Graf G didefinisikan sebagai pasangan himpunan (V, E), ditulis dengan notasi G = (V, E) terdiri atas himpunan V = { } dengan
V adalah himpunan tak kosong dari simpul (vertex) yang disebut himpunan simpul, dan himpunan E = { }, dimana anggotanya disebut sisi. Order dari G yang menyatakan banyaknya simpul di G dinotasikan dengan
| | dan ukuran dari G yang menyatakan banyaknya sisi di G dinotasikan dengan ‖ ‖ (Gross, 2006).
Sisi e = (u, v) dikatakan menghubungkan simpul u dan v. Jika e = (u, v) adalah sisi pada graf G, maka u dan v disebut terhubung langsung (adjacent),
u dan e serta v dan e disebut terkait langsung (incident). Untuk selanjutnya, sisi e = (u,v) akan ditulis e = uv. Banyak sisi yang terkait langsung dengan simpul v
dinamakan derajat simpul v, ditulis d(v).
Graf G disebut finite atau berhingga jika himpunan simpul adalah berhingga, atau graf yang jumlah simpulnya adalah n berhingga. Graf infinite atau tak berhingga adalah graf yang jumlah simpulnya tidak berhingga. Graf trivial
adalah graf berorder satu dengan himpunan sisinya merupakan himpunan kosong. Sebuah sisi graf yang menghubungkan sebuah simpul dengan dirinya sendiri dinamakan gelung (loop). Jika terdapat lebih dari satu sisi yang menghubungkan dua simpul u dan v pada suatu graf maka sisi-sisi tersebut disebut sisi rangkap (multiple edges).
Graf yang tidak memiliki sisi rangkap dan tidak memiliki gelung disebut graf sederhana. Sedangkan sebuah graf yang memiliki sisi rangkap tetapi tidak memiliki gelung disebut graf rangkap.
u
Gambar 2.1 Graf sederhana dan graf bukan sederhana
2.2 Beberapa Graf Sederhana
Terdapat beberapa jenis graf sederhana. Berikut ini contoh-contoh graf sederhana beserta definisinya.
a. Graf Lingkaran (Cycle Graph)
Graf lingkaran adalah sebuah graf yang setiap simpulnya
berderajat dua. Graf lingkaran dinotasikan dengan Cn, dengan n merupakan banyaknya simpul pada graf lingkaran. Penggambaran graf
lingkaran tidak penting, yang terpenting adalah setiap simpul pada graf lingkaran berderajat dua. Adapun gambar dari graf lingkaran disajikan pada Gambar 2.2. memiliki derajat dua. Simpul v1 disebut simpul ujung, sedangkan vn
disebut simpul akhir. Graf lintasan dinotasikan dengan Pn dengan n
adalah order pada graf lintasan. Adapun gambar dari graf lingkaran disajikan pada Gambar 2.3.
Gambar 2.3. Graf lintasan (P5)
2.3. Fungsi a. Injektif
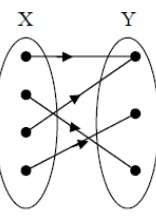
Suatu fungsi f dari X ke Y dikatakan fungsi satu satu (one to one) atau injective jika tidak ada dua elemen berbeda di X yang dipetakan kepada satu elemen yang sama di Y. Dengan kata lain, jika dan maka
Gambar 2.4 Fungsi satu-satu
b. Surjektif
Gambar 2.5 Fungsi Surjektif
c. Bijektif
Apabila fungsi f memenuhi fungsi injektif dan surjektif maka f dinamakan fungsi bijektif. Contoh fungsi bijektif disajikan pada
Gambar 2.6
Gambar 2.6 Fungsi Bijektif 2.4. Amalgamasi
Dalam membentuk sebuah graf baru, salah satu cara yang dapat dilakukan dengan menggunakan operasi amalgamasi. Amalgamasi simpul dari pasangan simpul graf bersama adalah graf yang diperoleh dengan menggabungkan simpul dan menjadi satu simpul. Notasi yang digunakan untuk menyatakan operasi amalgamasi adalah “ ” (Ardiansyah, 2013).
Selanjutnya, diberikan graf G dan H yang ditunjukkan pada Gambar 2.7, jika dilakukan amalgamasi dari simpul dan maka operasi amalgamasi dinotasikan dengan
Dimana R adalah graf baru yang terbentuk
Gambar 2.7. Contoh operasi amalgamasi C3dan C4
2.5 Graf Dragon
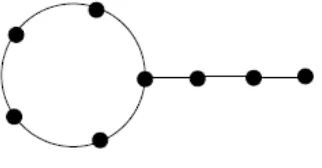
Graf dragon adalah graf yang diperoleh amalgamasi simpul graf lingkaran dan graf lingkaran. Graf lingkaran pada graf dragon dinamakan kepala dan graf lintasan pada graf dragon dinamakan ekor. Graf dragon dinotasikan dengan Dn(m) dimana n merupakan order pada graf lingkaran
dan m merupakan ukuran pada graf lintasan.
2.6 Graf Dragon Ganda
Graf dragon ganda adalah graf yang dibentuk dari amalgamasi simpul dari graf dragon dan graf lingkaran. Graf dragon ganda dinotasikan 2Dn (m).
Gambar 2.9. Graf dragon ganda 2
Gambar 2.8. Graf Dragon 𝐷
2.7 Graf Dragon Pendant
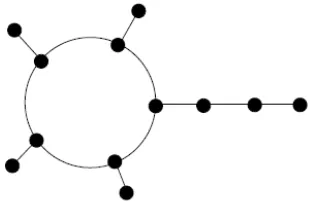
Graf dragon pendant adalah graf dragon yang pada setiap simpul bagian kepala yang tidak terhubung dengan ekor ditambahkan pendant. Graf dragon pendant dinotasikan DPn (m).
Gambar 2.10. Graf dragon pendant DP5 (3)
2.8 Pelabelan Graf
2.8.1 Definisi dan Jenis Pelabelan Graf
Pelabelan pada suatu graf adalah suatu pemetaan (fungsi) yang memasangkan unsur-unsur graf (simpul atau sisi) dengan bilangan (biasanya bilangan bulat). Jika domain dari fungsi adalah simpul, maka pelabelan disebut pelabelan simpul (vertex labeling). Jika domainnya adalah sisi, maka disebut pelabelan sisi (edge labeling), dan jika domainnya simpul dan sisi, maka disebut pelabelan total (total labeling) (Gallian, 2013). Pada Gambar 2.11 dapat dilihat perbedaan antara pelabelan ketiganya dimana pelabelan simpul hanya pada simpul saja yang dilabeli, pelabelan sisi hanya pada sisi saja yang dilabeli dan pelabelan total keduanya dilabeli yaitu sisi dan simpul.
Adapun beberapa jenis pelabelan antara lain pelabelan skolem graceful
dan pelabelan graceful ganjil. Pelabelan skolem graceful adalah fungsi injektif dari himpunan simpul V ke himpunan bilangan { 1, 2,…,n} sedemikian hingga jika sisi uv dilabeli dengan | | maka label sisinya { 1, 2,…,q}.
Pada Gambar 2.12 dapat dilihat perbedaan antara pelabelan skolem
graceful dan pelabelan graceful ganjil adalah pada pelabelan simpul pada
graceful ganjil menggunakan label 0 . Sedangkan pada skolem graceful
menggunakan label 1. Pada pelabelan sisi merupakan akibat dari pelabelan simpul yang diperoleh dari selisih dua simpul yang berhubungan langsung. Pada pelabelan graceful ganjil sisi terlabeli integer ganjil sedangkan pada pelabelan skolem graceful sisi terlabeli dengan integer tanpa 0.
2.8.2 Pelabelan Graceful
Pelabelan graceful pada graf G adalah fungsi injektif f dari V (G) ke {0, 1, 2,…,q} sedemikian hingga jika sisi uv dilabeli dengan | |
maka label sisinya akan berbeda untuk semua sisi di G (Gallian, 2013).
Adapun aturan pelabelan graceful sebagai berikut :
i. Memberikan label pada simpul suatu graf G yang memenuhi fungsi injektif dari himpunan simpul ke himpunan bilangan bulat tak negatif {0, 1, 2, ..., q}.
ii. Akibat dari point (i) adalah semua sisi uv yang dilabeli | f(u) – f(v) | memiliki hasilnya berbeda untuk semua sisi di G.
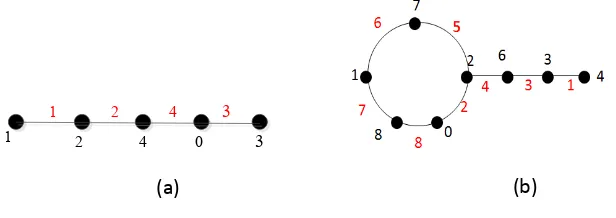
Pada Gambar 2.13 diberikan contoh pelabelan graceful pada graf lintasan dengan ‖ ‖ = | | -1 (a) dan graf dragon dengan ‖ ‖ | | -1 (b).
1 2 4 0 3
1 2 4 3
Gambar 2.13. Contoh pelabelan graceful pada graf dengan
‖ ‖ = | | - 1 (a) dan graf dengan ‖ ‖ | | -1 (b)
Dapat dilihat bahwa pada Gambar 2.11 (a) himpunan {0, 1, 2,3,4 } terpakai seluruhnya untuk melabelkan simpul pada graf. Sedangkan pada Gambar 2.12 (b), himpunan {0, 1, 2, ..,8} hanya terpakai sebagaian saja yaitu {0, 1,2,3,4,6,7,8} untuk melabelkan simpul pada graf. Secara umum bila graf G memiliki jumlah sisi ‖ ‖ =| | -1 , maka label terpakai seluruhnya, bila graf G memiliki jumlah sisi
‖ ‖ | | -1, maka label tidak seluruhnya terpakai. Pada Gambar 2.13 warna merah merupakan bobot sisi yang diperoleh dari selisih dua simpul yang berhubungan langsung. Pada Gambar 2.13 (a) terlihat bahwa semua sisinya berbeda yaitu {1, 2,3,4} dan pada Gambar 2.13 (b) semua sisinya berbeda yaitu {1, 2,3,4,6,7,8}.
BAB III
METODE PENELITIAN
Pada bagian ini diuraikan metode penelitian yang digunakan untuk mencapai tujuan penelitian.
3.1 Tahapan penelitian
1. Studi literatur dan pemahaman konsep
Pada tahap ini dilakukan studi literatur dari beberapa referensi buku, artikel, jurnal dari berbagai sumber mengenai penelitian pelabelan
graceful pada graf. 2. Analisis
a. Melakukan observasi terhadap graf yang diteliti.
b. Melakukan pelabelan graceful pada graf dragon ganda dan graf dragon pendant dengan menggunakan beberapa cara antara lain :
Trial
Trial yang dimaksudkan pada penelitian ini adalah mencoba kemungkinan-kemungkinan dalam melabeli simpul pada graf dragon ganda dan graf dragon pendant berdasarkan penelitian sebelumnya sedemikian sehingga jika sisinya mendapat label harga mutlak dari selisih kedua simpul yang terhubung langsung (adjacent) maka hasilnya berbeda.
Pendeteksian pola
Apabila ditemukan label simpul yang memenuhi pelabelan
Adapun cara pelabelan yang dilakukan pada graf dragon ganda dan graf dragon pandant adalah melabeli simpul kepala pada graf dragon ganda dan graf dragon pendant kemudian dilanjutkan melabeli simpul ekor pada graf dragon ganda dan graf dragon pendant.
3. Evaluasi
Pada tahap ini melakukan evaluasi terhadap analisa yang telah dilakukan pada pelabelan graceful pada graf dragon ganda dan graf dragon pendant. Apabila graf dragon ganda dan graf dragon pendant tidak memenuhi aturan pelabelan graceful maka dicari alasan mengapa graf tersebut tidak memenuhi aturan tersebut.
4. Menyusun laporan
BAB IV
HASIL DAN PEMBAHASAN
Pada bab ini dibahas mengenai pelabelan graceful pada graf dragon ganda dan graf dragon pendant. Pada penelitian ini graf dragon ganda yang diteliti adalah = 3, dan = 4, sedangkan graf dragon pendant yang diteliti adalah = 3,4, 5 dan 6 dengan .
4.1. Pelabelan graceful pada graf dragon ganda 2D3(2) dan graf Jointsum
dari dua copy sikel
Graf dragon ganda adalah graf yang dibentuk dari amalgamasi simpul dari graf dragon dan graf lingkaran. Graf dragon ganda dinotasikan 2Dn(m). Untuk m =1 graf dragon ganda mempunyai nama lain yang disebut dengan graf Jointsum
dari dua copy sikel.
Pelabelan graceful pada graf Jointsum dari dua copy sikel telah diteliti oleh Lekha menyatakan bahwa Jointsum dari dua copy sikel merupakan pelabelan
graceful (Lekha, 2012). Hanya saja setelah mencermati hasil dari pelabelan
tersebut dan mengimplementasikannya pada graf dengan n =3 dengan pola umum sebagai berikut
Untuk ≤ 𝑖 ≤ −
𝑓(𝑣) = ( + )−𝑖 + , untuk 𝑖 gasal
= + 𝑖 + , untuk 𝑖 genap
Untuk + ≤ 𝑖 ≤ −
𝑓(𝑣) = ( + )−𝑖 + , untuk 𝑖 genap
𝑓(𝑣 ) = 0
Untuk ≤ 𝑖 ≤
𝑓(𝑣) = ( + ) −𝑖 − , untuk 𝑖 gasal
=𝑖 + − , untuk 𝑖 genap
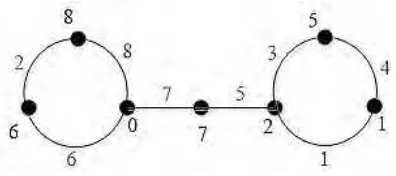
Penulis menemukan sebuah kesalahan bila pelabelan dilakukan. Berikut akan ditunjukkan pelabelan yang mengikuti hasil pelabelan pola umum dari Lekha
Gambar 4.1. Contoh pelabelan menurut Lekha
Dari gambar di atas dapat dilihat bahwa ada label sisi yang sama yaitu 5. Hal ini tidak sesuai dengan definisi dari pelabelan graceful yaitu fungsi injektif f dari V (G) ke {0, 1, 2,…,q}sedemikian hingga jika sisi uv dilabeli dengan |𝑓( ) − 𝑓(𝑣)| maka label sisinya akan berbeda. Dari permasalahan di atas peneliti melakukan revisi pada n = 3 yaitu sebagai berikut
Berikut akan ditunjukkan pelabelan graceful pada graf dragon ganda dengan = , hal ini dilakukan karena untuk = memiliki pelabelan yang unik. Adapun pelabelannya dapat dikonstruksi sebagai berikut
Gambar 4.3. Pelabelan graf dragon ganda 2D3(2)
4.2. Pelabelan graceful pada graf dragon ganda
Pada pelabelan graceful graf dragon ganda dalam tesis ini diklasifikasikan menjadi 2 bagian, yaitu
a. Pelabelan graceful pada graf dragon ganda ( ) untuk n = 3 dengan
b. Pelabelan graceful pada graf dragon ganda ( ) untuk n= 4 dengan .
Pada bab sebelumnya telah diberikan definisi pelabelan graceful. Perlu diingat bahwa pelabelan graceful pada graf G adalah fungsi injektif f dari V (G) ke
{0, 1, 2,…,q} sedemikian hingga jika sisi uv dilabeli dengan |𝑓( ) − 𝑓(𝑣)|
Teorema 4.1 Graf Dragon Ganda ( ) dengan adalah graf
graceful
Bukti : Misalkan graf dragon ganda ( ) dengan adalah graf dengan himpunan simpul dan himpunan sisi sebagai berikut
= *𝑣 𝑣 𝑣 𝑣 𝑣 } dan = * }
Dalam hal ini | | = + dan ‖ ‖ = + . Sehingga graf dragon ganda ( ) dapat digambarkan seperti pada Gambar 4.4
Gambar 4.4. Graf dragon ganda 2 ( )
Untuk = dapat dikonstruksikan pelabelan graceful sebagai berikut
v3
Untuk = dapat dikonstruksikan pelabelan graceful sebagai berikut
|𝑓(𝑣 ) − 𝑓(𝑣 )| = |𝑓(𝑣 ) − 𝑓(𝑣 )| 𝑖 = +
= { ( ) ( )
|𝑓(𝑣 ) − 𝑓(𝑣 )| = {
( ) ( )
Adapun label simpul yang tidak digunakan pada pelabelan graceful graf dragon ganda ( ) adalah sebagai berikut
Untuk 0( )
{ +
( − ) + }
Untuk ( )
{ + ( − ) + ( − )}
Untuk ( )
{ + +
( − ) }
Untuk ( )
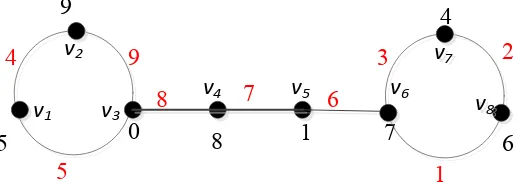
Sebagai contoh untuk graf dragon ganda = dapat dikonstruksi pelabelannya menurut teorema 4.1. Hasilnya diberikan seperti pada Gambar 4.5
6
Perhatikan Gambar 4.5.dapat dilihat bahwa simpul dilabeli sejumlah integer dari 0 sampai dengan 10 (sesuai dengan ukuran graf) dan tidak ada yang sama. Dapat dilihat bahwa label simpul yang digunakan hanya sebagai yaitu *0 0+ dikarenakan banyak simpul kurang dari banyak sisi. Selanjutnya pelabelan sisi pada graf tersebut dapat diperoleh dari selisih kedua simpul ujung sisi tersebut dan dapat dilihat juga pada Gambar 4.5 semua sisi terlabeli (warna merah) dengan bilangan integer yang berbeda.
Teorema 4.2 Graf Dragon Ganda ( ) dengan adalah graf
graceful;
Bukti : Misalkan graf dragon ganda ( ) dengan adalah graf dengan himpunan simpul dan himpunan sisi sebagai berikut :
= *𝑣 𝑣 𝑣 𝑣 𝑣 𝑣 }dan = * }
Dalam hal ini | | = + dan ‖ ‖ = + . Sehingga graf dragon ganda ( ) dapat digambarkan seperti pada Gambar 4.6
v2
Untuk = dapat dikonstruksikan pelabelan graceful sebagai berikut
4
Untuk = dapat dikonstruksikan pelabelan graceful sebagai berikut
5
Sedangkan untuk dapat dikonstruksikan pelabelan graceful secara umum. Adapun pengkonstruksiannya sebagai berikut
Pelabelan empat simpul pertama pada graf dragon ganda, yaitu 𝑣 𝑣 𝑣 𝑣
dapat dikonstruksikan sebagai berikut:
𝑓(𝑣 ) = + .
𝑓(𝑣 ) = ⌊ + ⌋
Untuk , konstruksi pelabelan sisi dengan cara sebagai berikut:
|𝑓(𝑣 ) − 𝑓(𝑣 )| = +
|𝑓(𝑣 ) − 𝑓(𝑣 )| = + − ⌊ + ⌋
|𝑓(𝑣 ) − 𝑓(𝑣 )| = + − ⌊ + ⌋ |𝑓(𝑣 ) − 𝑓(𝑣 )| = +
|𝑓(𝑣 ) − 𝑓(𝑣 )| = + − 𝑖 ≤ 𝑖 ≤ ⌊ + ⌋ +
|𝑓(𝑣 ) − 𝑓(𝑣)| = {
⌊ + ⌋
⌊ + ⌋ − 𝑖 = ⌊ +
⌋ +
⌊ + ⌋ + ≤ 𝑖 ≤ +
|𝑓(𝑣 ) − 𝑓(𝑣 )| = {
⌊ + ⌋ + − 𝑖 ⌊ + ⌋ + − 𝑖
|𝑓(𝑣 ) − 𝑓(𝑣 )| = |𝑓(𝑣 ) − 𝑓(𝑣 )| 𝑖 = +
= { 0 ( ) ( )( ) ( )
|𝑓(𝑣 ) − 𝑓(𝑣 )| = |𝑓(𝑣 ) − 𝑓(𝑣 )| 𝑖 = +
= 1
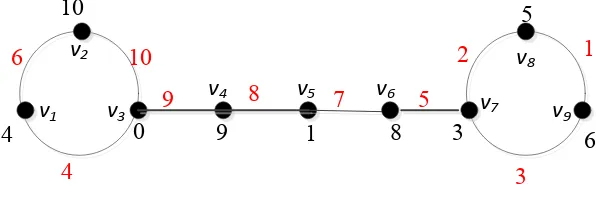
Adapun label simpul yang tidak digunakan pada pelabelan graceful graf dragon pelabelannya menurut teorema 4.2. Hasilnya diberikan seperti pada Gambar 4.7
7
Perhatikan Gambar 4.7 dapat dilihat bahwa simpul dilabeli sejumlah integer dari 0 sampai dengan 12 (sesuai dengan ukuran graf) dan tidak ada yang sama. Dapat dilihat bahwa label simpul yang digunakan hanya sebagai
yaitu *0 0 + dikarenakan banyak simpul kurang dari dengan banyak sisi.Selanjutnya pada pelabelan sisi pada graf tersebut dapat diperoleh dari selisih kedua simpul ujung sisi tersebut dan dapat dilihat juga pada Gambar 4.7 semua sisi terlabeli (warna merah) dengan bilangan integer yang berbeda.
4.3. Pelabelan graceful pada graf dragon pendant
Pada pelabelan graceful graf dragon pendant dalam tesis ini diklasifikasikan menjadi 4 bagian, yaitu
a. Pelabelan graceful pada graf dragon pendant ( ) untuk n = 3 dengan
b. Pelabelan graceful pada graf dragon pendant ( ) untuk n = 4 dengan .
c. Pelabelan graceful pada graf dragon pendant ( ) untuk n = 5 dengan .
d. Pelabelan graceful pada graf dragon pendant ( ) untuk n = 6 dengan .
Pada Teorema 4.3 diberikan konstruksi dari pelabelan graceful pada graf dragon pendant ( ) untuk n = 3 dengan . Selanjutnya pada Teorema 4.4 diberikan konstruksi dari pelabelan graceful pada graf dragon pendant ( ) untuk n = 4 dengan , Teorema 4.5 diberikan konstruksi dari pelabelan graceful pada graf dragon pendant ( ) untuk n = 5 dengan dan Teorema 4.6 diberikan konstruksi dari pelabelan graceful pada graf dragon pendant ( ) untuk n = 6 dengan .
Teorema 4.3 Graf dragon pendant ( ) dengan adalah graf graceful. Bukti : Misalkan graf dragon pendant ( ) dengan adalah graf dengan himpunan simpul dan himpunan sisi sebagai berikut
Dalam hal ini | | = + dan ‖ ‖ = + . Sehingga graf dragon pendant ( ) dapat digambarkan seperti pada Gambar 4.8
v2
v1 v3
v4
v5
v6 v7 vm+4 vm+5
v6 v7 vm+4 vm+5
Pelabelan lima simpul pertama pada graf dragon pendant, yaitu
𝑣 𝑣 𝑣 𝑣 𝑣 dapat dikonstruksikan sebagai berikut:
𝑓(𝑣 ) = ⌊ + ⌋
𝑓(𝑣 ) = {⌊ +
⌋ −
⌊ + ⌋ +
𝑓(𝑣 ) = {⌊ +
⌋ +
⌊ + ⌋ −
𝑓(𝑣 ) = ⌊ + ⌋ +
𝑓(𝑣 ) = {⌊ +
⌋ +
⌊ + ⌋ −
Sedangkan untuk simpul selanjutnya, yaitu 𝑣 𝑣 𝑣 dapat
dikonstruksikan sebagai berikut:
≤ 𝑖 ≤ +
𝑓(𝑣 ) = {⌊ +
⌋ − +𝑖 + 𝑖 ⌊ + ⌋ + −𝑖 + 𝑖
𝑓(𝑣 ) = {⌊ +
⌋ + −𝑖 + 𝑖 ⌊ + ⌋ − +𝑖 + 𝑖
Untuk , konstruksi pelabelan sisi dengan cara sebagai berikut:
|𝑓(𝑣 ) − 𝑓(𝑣 )| =
|𝑓(𝑣 ) − 𝑓(𝑣 )| =
|𝑓(𝑣 ) − 𝑓(𝑣 )| =
|𝑓(𝑣 ) − 𝑓(𝑣 )| =
|𝑓(𝑣 ) − 𝑓(𝑣 )| =
≤ 𝑖 ≤ +
𝑓( ) = |𝑓(𝑣 ) − 𝑓(𝑣)| = 𝑖
Adapun label simpul yang tidak digunakan pada pelabelan graceful graf dragon pendant ( ) adalah sebagai berikut
Sebagai contoh untuk graf dragon pendant = dapat dikonstruksi
Perhatikan gambar 4.9.dapat dilihat bahwa simpul dilabeli sejumlah integer dari 0 sampai dengan 7 (sesuai dengan ukuran graf) dan tidak ada yang sama. Dapat dilihat bahwa label simpul yang digunakan hanya sebagai yaitu *0 + dikarenakan banyak simpul sama dengan banyak sisi. Selanjutnya pelabelan sisi pada graf tersebut dapat diperoleh dari selisih kedua simpul ujung sisi tersebut dan dapat dilihat juga pada Gambar 4.9 semua sisi terlabeli (warna merah) dengan bilangan integer yang berbeda.
Teorema 4.4 Graf dragon pendant ( ) dengan adalah graf
graceful
Bukti : Misalkan graf dragon pendant ( ) dengan adalah graf dengan himpunan simpul dan himpunan sisi sebagai berikut :
= *𝑣 𝑣 𝑣 𝑣 𝑣 }dan = * }
𝑓(𝑣 ) = {⌊ +
⌋ −
⌊ + ⌋ +
Sedangkan untuk simpul selanjutnya, yaitu 𝑣 𝑣 𝑣 dapat
dikonstruksikan sebagai berikut:
≤ 𝑖 ≤ +
𝑓(𝑣) = {⌊ +
⌋ − +𝑖 + 𝑖 ⌊ + ⌋ + −𝑖 + 𝑖
𝑓(𝑣) = {⌊ +
⌋ + −𝑖 + 𝑖 ⌊ + ⌋ − +𝑖 + 𝑖
Untuk , konstruksi pelabelan sisi dengan cara sebagai berikut:
|𝑓(𝑣 ) − 𝑓(𝑣 )| =
|𝑓(𝑣 ) − 𝑓(𝑣 )| =
|𝑓(𝑣 ) − 𝑓(𝑣 )| =
|𝑓(𝑣 ) − 𝑓(𝑣 )| =
|𝑓(𝑣 ) − 𝑓(𝑣 )| =
|𝑓(𝑣 ) − 𝑓(𝑣 )| =
≤ 𝑖 ≤ +
Adapun label simpul yang tidak digunakan pada pelabelan graceful graf
Perhatikan gambar 4.11 dapat dilihat bahwa simpul dilabeli sejumlah integer dari 0 sampai dengan 9 (sesuai dengan ukuran graf) dan tidak ada yang sama. Dapat dilihat bahwa label simpul yang digunakan hanya sebagai yaitu *0 + dikarenakan banyak simpul sama dengan banyak sisi. Selanjutnya pelabelan sisi pada graf tersebut dapat diperoleh dari selisih kedua simpul ujung sisi tersebut dan dapat dilihat juga pada Gambar 4.11 semua sisi terlabeli (warna merah) dengan bilangan integer yang berbeda.
Teorema 4.5 Graf dragon pendant ( ) dengan adalah graf
graceful
= *𝑣 𝑣 𝑣 𝑣 𝑣 } dan = * }
Pelabelan sembilan simpul pertama pada graf dragon pendant, yaitu
𝑓(𝑣 ) = {⌊ +
⌋ −
⌊ + ⌋ +
𝑓(𝑣 ) = ⌊ + ⌋
𝑓(𝑣 ) = {⌊ +
⌋ +
⌊ + ⌋ −
𝑓(𝑣 ) = {⌊ +
⌋ −
⌊ + ⌋ +
Sedangkan untuk simpul selanjutnya, yaitu 𝑣 𝑣 𝑣 dapat
dikonstruksikan sebagai berikut:
0 ≤ 𝑖 ≤ +
𝑓(𝑣 ) = {⌊ +
⌋ − +𝑖 + 0 𝑖 ⌊ + ⌋ + −𝑖 + 𝑖
𝑓(𝑣 ) = {⌊ +
⌋ + −𝑖 + 0 𝑖 ⌊ + ⌋ − +𝑖 + 𝑖
Untuk , konstruksi pelabelan sisi dengan cara sebagai berikut:
|𝑓(𝑣 ) − 𝑓(𝑣 )| =
|𝑓(𝑣 ) − 𝑓(𝑣 )| =
Gambar 4.13. Graf Dragon Pendant ( )
Perhatikan gambar 4.13 dapat dilihat bahwa simpul dilabeli sejumlah integer dari 0 sampai dengan 11 (sesuai dengan ukuran graf) dan tidak ada yang sama. Dapat dilihat bahwa label simpul yang digunakan hanya sebagai yaitu *0 0 + dikarenakan banyak simpul sama dengan banyak sisi. Selanjutnya pelabelan sisi pada graf tersebut dapat diperoleh dari selisih kedua simpul ujung sisi tersebut dan dapat dilihat juga pada Gambar 4.13 semua sisi terlabeli (warna merah) dengan bilangan integer yang berbeda.
Teorema 4.6 Graf dragon pendant ( ) dengan adalah graf
graceful
Bukti : Misalkan graf dragon pendant ( ) dengan adalah graf dengan himpunan simpul dan himpunan sisi sebagai berikut
= *𝑣 𝑣 𝑣 𝑣 𝑣 }dan = * }
Pelabelan sebelas simpul pertama pada graf dragon pendant, yaitu 𝑣 𝑣 𝑣 𝑣 𝑣 𝑣 𝑣 𝑣 𝑣 𝑣 𝑣 dapat dikonstruksikan sebagai berikut:
𝑓(𝑣 ) = {
⌊ + ⌋ + ⌊ + ⌋ −
𝑓(𝑣 ) = {
⌊ + ⌋ − ⌊ + ⌋ +
Sedangkan untuk simpul selanjutnya, yaitu 𝑣 𝑣 𝑣 dapat
dikonstruksikan sebagai berikut:
≤ 𝑖 ≤ +
𝑓(𝑣 ) = {⌊
+
⌋ − +𝑖 + 𝑖 ⌊ + ⌋ + −𝑖 + 𝑖
𝑓(𝑣 ) = {⌊
+
⌋ + −𝑖 + 𝑖 ⌊ + ⌋ − +𝑖 + 𝑖
Untuk , konstruksi pelabelan sisi dengan cara sebagai berikut:
|𝑓(𝑣 ) − 𝑓(𝑣 )| =
|𝑓(𝑣 ) − 𝑓(𝑣 )| =
|𝑓(𝑣 ) − 𝑓(𝑣 )| =
|𝑓(𝑣 ) − 𝑓(𝑣 )| =
|𝑓(𝑣 ) − 𝑓(𝑣 )| = 0
|𝑓(𝑣 ) − 𝑓(𝑣 )| =
Adapun label simpul yang tidak digunakan pada pelabelan graceful graf dragon pendant ( ) adalah sebagai berikut
BAB V
KESIMPULAN DAN SARAN
Pada bab ini disampaikan kesimpulan dan saran yang diperoleh dari pembahasan konstruksi pelabelan graceful pada graf dragon ganda dan graf dragon pendant pada bab sebelumnya.
5.1 Kesimpulan
Dari hasil penelitian pada bab sebelumnya, diperoleh hasil sebagai berikut:
1. Graf dragon ganda dengan adalah graf graceful (Teorema 4.1).
2. Graf dragon ganda dengan adalah graf graceful (Teorema 4.2) .
3. Graf dragon pendant untuk n = 3 dengan adalah graf graceful (Teorema 4.3).
4. Graf dragon pendant untuk n = 4 dengan adalah graf graceful (Teorema 4.4) .
5. Graf dragon pendant untuk n = 5 dengan adalah graf graceful (Teorema 4.5) .
6. Graf dragon pendant untuk n = 6 dengan adalah graf graceful (Teorema 4.6).
5.2 Saran
DAFTAR PUSTAKA
Ahmad,Muzayyin, (2012), Pelabelan Graceful dan pelabelan ̂ pada graf pot bunga dan graf pohon palem, Universitas Indonesia.
Alessandra, (2014), “A new graceful labeling for pendant graphs”, Aequat. Math. Hal 135–145.
Ardiyansah, Ridwan dan Darmaji, (2013),” Bilangan Kromatik Graf Hasil Amalgamasi Dua Buah Graf ”. Jurnal Sains dan SENI POMITS Vol. 2, No.1, Institut Teknologi Sepuluh Nopember.
Budayasa, Ketut, (2007), Teori Graph dan Aplikasinya, Unesa University Press.
Cavalier, (2006),Graceful Labelings, Bachelor of Science Louisiana State University
Eshghi. Kourosh,(2013), Introduction To graceful graphs, Sharif University of Technology
Gallian J. A.,(2013), A dynamic survey of graph labeling, Department of Mathematics and Statistics University of Minnesota Duluth.
Gross, L. Jonathan dan Yellen, Jay,(2006), Graph Theory and Its Applications, Chapman& Hall/CRC, New York.
Lekha, Bijukumar, (2012), Some interesting results in the theory of Graphs, thesis PhD, Saurashtra University.
Narindra, dkk.(2011), pelabelan graceful pada graf duplikasi simpul dan graf duplikasi sisi dari graf sikel Cn, Universitas Diponegoro.
Riadi. Bambang,(2009), Menentukan Pelabelan Graceful pada Graf Lintasan (Pn ) dengan panjang n menggunakan program php dan javascript, Fakultas Sains dan Teknologi Universitas Islam Negeri (UIN) Maulana Malik Ibrahim Malang
Tri,Lusia,(2008), “Pelabelan graceful digraph lintasan dan digraph bipartite”, Jurnal MIPA, Nomer 1, hal 1-5. Universitas Jember
Zulfi.Amir, dkk,(2011), “pelabelan graceful, skolem graceful dan pelabelan
BIODATA PENULIS
Oktober 2011 dengan mendapat gelar Sarjana Pendidikan. Sebelum mendapat gelar Sarjana, penulis mendapat pekerjaan sebagai guru matematika di SMPK Angelus Custos II Surabaya pada tahun 2010 hingga 2012. Penulis melanjutkan studi S2 di Jurusan Matematika Institut Teknologi Sepuluh Nopember (ITS) Surabaya melalui program pra s2 pada tahun 2012 hingga tahun 2013 kemudian meneruskan program s2 tahun 2013 sampai 2015. Selama kuliah S2 di jurusan matematika, penulis mengambil bidang graf. Kritik dan saran ataupun pertanyaan yang berhubungan dengan tesis ini dapat menghubungi penulis melalui email resturiawantika@yahoo.com.