Statistika Dasar. Bagus Sartono

Statistika Dasar

Pokok Bahasan

• Pengenalan analisis dan deskripsi data

• Pendugaan parameter dan selang kepercayaan

• Pengujian hipotesis rata-rata

– One-Sample T-Test – Two-Sample T-Test – One-Way ANOVA

PENGENALAN ANALISIS STATISTIKA

DAN DESKRIPSI DATA KATEGORIK

Apa itu Statistika

• Ilmu yang mempelajari teknik-teknik

pengumpulan data, analisis data, hingga

proses pengambilan kesimpulan berdasarkan analisis tersebut.

Statistika bekerja dengan data contoh

• Populasi vs contoh

– Populasi (population): himpunan semua

individu/objek yang menjadi minat/perhatian

– Contoh (sample): himpunan bagian dari populasi

• Sensus vs Survei

– Sensus: proses pengumpulan data populasi – Survei: proses pengumpulan data contoh

Mengapa Contoh?

• Keterbatasan sumberdaya (tenaga, biaya, waktu, dll)

• Sensus tidak dapat dikerjakan untuk kasus

individu yang selalu bergerak ataupun bertambah jumlahnya.

• Proses pengumpulan data kadangkala bersifat merusak, misal: pemeriksaan kualitas kemasan, pemeriksaan rasa buah, dsb

Contoh harus representatif

• Representatif = mewakili  kesimpulan tidak bias. Contoh harus memiliki karakteristik yang sama dengan populasi karena data contoh

digunakan untuk menarik kesimpulan mengenai populasi.

• Contoh Acak (random sample)

Statistik sebagai penduga parameter

• Parameter vs Statistik

– Parameter: karakteristik numerik dari populasi – Statistik: karakteristik numerik dari contoh

– Statistik adalah penduga parameter

• Statistik selalu memiliki galat (error)

– Sampling error

Peubah dan Jenisnya

• Variable, karakteristik dari individu. Misal untuk individu

manusia, dapat dikumpulkan data mengenai: ukuran tubuh, usia, pekerjaan, penghasilan. Untuk individu tanaman

dapat dikumpulkan data peubah ukuran tanaman, produktivitas, daya tahan terhadap hama, dsb.

• Numerik vs Kategorik • Peubah Kategorik – Nominal – Ordinal • Peubah Numerik – Interval – Ratio

Peubah Kategorik

• Nominal

– Hanya berupa penggolongan. Urutan kelas atau kategorinya tidak memiliki makna.

– Misal: warna baju, pekerjaan, bentuk daun

• Ordinal

– Urutan kelas atau kategorinya dapat diurutkan. – Misal: intensitas serangan hama (parah, sedang,

ringan), tingkat pendidikan (SD, SMP, SMA, PT), tingkat kesetujuan masyarakat (sangat setuju, setuju, kurang setuju, tidak setuju)

Peubah Numerik

• Interval

– Nilai 0 pada peubah ini tidak bersifat mutlak, dan hanya berupa kesepakatan.

– Misal: temperatur benda/ruangan, nilai IPK

• Ratio

– Nilai 0 pada peubah ini bersifat mutlak.

– Misal: penghasilan per bulan, panjang benda,

jumlah daun per cabang, produktivitas tanaman, berat badan sapi.

Analisis Statistika

• Statistika Deskriptif

– Mempelajari teknik-teknik yang berguna dalam

peringkasan data dan pemberian gambaran umum tentang data yang dimiliki.

• Statistika Inferensia

– Mempelajari kaidah-kaidah pengambilan kesimpulan statistika dari data yang dimiliki dengan menggunakan ilmu peluang.

Deskripsi Data

• Menyajikan gambaran umum perilaku data yang dimiliki

• Deskripsi dilakukan di awal proses analisis data • Tujuan deskripsi data:

– Memberikan informasi yang cepat tentang data – Mendapatkan informasi keberadaan data dengan

karakteristik yang ‘aneh’

– Memperoleh informasi yang berguna bagi proses analisis selanjutnya

Deskripsi Data Kategorik

• Tabel Frekuensi (Frequency Table)

• Tabulasi Silang (Cross Tabulation) • Grafik

– Bar Chart, 3D Bar Chart, Multiple Bar Chart – Pie Chart

Deskripsi Data Kategorik

PROC FREQ DATA=stk.profile; TABLES transport / NOCUM; RUN;

Deskripsi Data Kategorik

PROC FREQ DATA=stk.profile; TABLES transport*budget; run;

Deskripsi Data Kategorik

PROC GCHART DATA=stk.profile; PIE transport;

Deskripsi Data Kategorik

PROC GCHART DATA=stk.profile; VBAR transport / GROUP=budget; where budget NE "";

DESKRIPSI DAN PENGENALAN

SEBARAN DATA NUMERIK

Deskripsi Data Numerik

• Ukuran Pemusatan (central tendency)

– Rataan – Median – Modus

• Ukuran Penyebaran (dispersion)

– Ragam (variance), simpangan baku (standard deviation) – Range

– Inter-Quartile Range

Nilai tengah (rataan/rata-rata)

• Definisi: merupakan ukuran yang menimbang data menjadi dua kelompok data yang memiliki massa yang sama

• Apabila x1, x2, ...,xN adalah anggota suatu populasi

terhingga berukuran N, maka nilai tengah populasinya adalah:   



1 N Xi i 1 N

Nilai tengah (rataan/rata-rata)

• sedangkan jika x1, x2, ...,xn adalah anggota

suatu contoh berukuran n, maka nilai tengah contoh tersebut adalah:

x

1 n Xi i 1 n  



dalam Bahasa Inggris, rata populasi disebut dengan mean dan rata-rata contoh disebut average

Median

• Definisi : suatu nilai data yang membagi dua sama banyak kumpulan data yang telah

diurutkan.

• Langkah Teknis:

– Urutkan data dari kecil ke besar – Cari posisi median (n_med=(n+1)/2) – Nilai median

• Jika n_med bulat, maka Median=X_(n+1)/2

• Jika n_med pecahan, maka Median=(X_[nmed]+ X_[nmed]+1)/2 (rata-rata dua pengamatan yang berada sebelum dan setelah posisi median)

Median vs Rataan

• Data: 20 34 45 89 120 122 129 130 150 152 180 Median = 122, Rataan = 106.45 • Data: 20 34 45 89 120 122 129 130 150 152 1800 Median = 122, Rataan = 253.73 24

Median vs Rataan

• Nilai rataan bersifat tidak kekar (robust), dan sangat terpengaruh oleh keberadaan nilai-nilai ekstrim.

[selanjutnya nanti akan dikenalkan istilah pencilan/outlier] • Adanya nilai ekstrim besar, akan menyebabkan nilai rataan

cenderung membesar. Sebaliknya, nilai rataan akan mengecil jika terdapat nilai ekstrim kecil.

• Median cenderung tidak demikian, hanya saja secara komputasi penghitungan median lebih lama karena ada proses pengurutan data.

• Rataan terpangkas (trimmed mean) adalah salah satu solusi mengatasi ketidakkekaran rataan, dengan tidak

menyertakan nilai ekstrim dalam penghitungan. Misal, membuang 5% data terbesar dan terkecil.

Ukuran Penyebaran

• Definisi : suatu ukuran untuk memberikan gambaran seberapa besar data menyebar dalam kumpulannya.

• Beberapa ukuran penyebaran:

– Wilayah (Range)

– Jarak Antar Kuartil (Interquartile Range) – Ragam (Variance)

– Simpangan Baku (Standard Deviation)

– dll

Wilayah (Range)

• Definisi : suatu ukuran yang dihitung dari selisih antara nilai pengamatan terbesar dengan pengamatan terkecil

W = X_[N]-X_[1]

• Ukuran ini cukup baik digunakan untuk mengukur penyebaran data yang simetrik dan nilai pengamatannya menyebar

merata.

• Tetapi ukuran ini akan menjadi tidak relevan jika nilai

pengamatan maksimum dan minimum merupakan data-data ekstrem

Kuartil (Quartile)

• Definisi :

suatu nilai data yang membagi

empat sama banyak kumpulan data yang telah diurutkan

• Q1, Q2, Q3

• Cara Penghitungan

– Metode Belah dua – Metode Interpolasi

Metode Belah dua

• Urutkan data dari kecil ke besar • Cari posisi kuartil

– n_q2=(n+1)/2

– n_q1=(n_q2*+1)/2= n_q3, n_q2* posisi kuartil dua terpangkas (pecahan dibuang)

• Nilai kuartil 2 ditentukan sama seperti mencari nilai median. Kuartil 1 dan 3 prinsipnya sama seperti

median tapi kuartil 1 dihitung dari kiri, sedangkan kuartil 3 dihitung dari kanan.

Kuartil – Metode Belah Dua

• Data terurut: 20 34 45 64 89 102 120 122 129 130 133 150 152 180 • Banyaknya data, n = 14 • Posisi median, n_Q2 = (14 + 1) / 2 = 7.5 • Posisi Q1, n_Q1 = (7 + 1) / 2 = 4 • Median = (120 + 122) / 2 = 121 • Q1 = 64 • Q3 = 133 30

Metode Interpolasi

• Urutkan data dari kecil ke besar

• Cari posisi kuartil

– n_q1=(1/4)(n+1) – n_q2=(2/4)(n+1) – n_q3=(3/4)(n+1)

• Nilai kuartil dihitung sebagai berikut:

– X_qi=X_a,i + h_i (X_b,i-X_a,i)

– X_a,i = pengamatan sebelum posisi kuartil ke-i, X_b,i =

pengamatan setelah posisi kuartil ke-i dan h_i adalah nilai pecahan dari posisi kuartil

Kuartil – Metode Interpolasi

• Data terurut: 20 34 45 64 89 102 120 122 129 130 133 150 152 180 • Banyaknya data, n = 14 • Posisi Q1, n_Q1 = (14 + 1) * 1/ 4 = 3.75 • Posisi Q2, n_Q2 = (14 + 1) * 2/ 4 = 7.5 • Posisi Q3, n_Q3 = (14 + 1) * 3/4 = 11.25 • Q1 = X3 + 0.75(X4 – X3) = 45 + 0.75(64-45) = 59.25 • Q2 = X7 + 0.5 (X8 – X7) = 120 + 0.5 (122-120) = 121 • Q3 = X11 + 0.25 (X12 – X11) = 133 + 0.25(150-133) = 137.25 32

Jarak antar kuartil (Interquartile Range)

• Definisi : Jarak antar kuartil mengukur

penyebaran 50% data ditengah-tengah setelah data diurut.

• Ukuran penyebaran ini merupakan ukuran penyebaran data yang terpangkas 25% yaitu dengan membuang 25% data yang terbesar dan 25% data terkecil.

Jarak antar kuartil (Interquartile Range)

• Jarak antar kuartil dihitung dari selisih antara kuartil 3 (Q3) dengan kuartil 1 (Q1):

JAK atau IQR = Q3 -Q1

• Ukuran ini sangat baik digunakan jika data

yang dikumpulkan banyak mengandung data pencilan

Ragam (Variance)

• Definisi : Ragam merupakan ukuran

penyebaran data yang mengukur rata-rata jarak kuadrat semua titik pengamatan

terhadap titik pusat (rataan).

• Apabila x₁, x₂, ...,x_N]adalah anggota suatu

populasi terhingga berukuran N, maka ragam populasinya adalah



2 _{ }



2 



1 N Xi i 1 N ( ) 35

Ragam (Variance)

• apabila x1, x2, ...,xn adalah anggota suatu contoh berukuran n, maka ragam contoh tersebut adalah: s2   x 2 



1 n - 1 Xi i 1 n ( ) 36

Simpangan Baku (Standard Deviation)

• Definisi : Merupakan akar dari ragam, yaitu  simpangan baku populasi dan s simpangan baku sampel.

 diperoleh satuan yang sama dengan data aslinya

Teladan

38

• Perhatikan hasil ringkasan terhadap data pendapatan masyarakat (juta rupiah per bulan) dari dua kabupaten berikut ini:

Teladan

• Jika kita hanya menyajikan nilai rata-rata saja dari kedua kabupaten, maka dinyatakan bahwa masyarakat di kedua kabupaten memiliki pendapatan yang relatif sama.

• Penjelasan yang lebih banyak akan diperoleh jika kita melihat nilai-nilai simpangan bakunya.

• Kabupaten A memiliki simpangan baku yang lebih besar daripada Kabupaten B. Artinya, pendapatan masyarakat di Kabupaten A lebih heterogen dibandingkan di Kabupaten B. Implikasi dari informasi ini terhadap kesimpulan bisa

Pengenalan Sebaran Data

• Data distribution • Statistik

– Statistik lima serangkai – Persentil

– Skewness, kurtosis

• Grafik

– Histogram – Boxplot

Pola Sebaran Data

• Selain menggunakan ukuran pemusatan dan ukuran penyebaran, pengenalan sebaran data dapat dilakukan menggunakan bantuan grafik:

– HISTOGRAM

– STEM & LEAF (Diagram Dahan Daun) – BOX-PLOT (Diagram Kotak Garis)

42

HISTOGRAM

• informasi penyebaran data dan bentuk sebarannya

• informasi ukuran pemusatan data

• informasi keberadaan data-data ekstrim dan pencilan (outliers)

Tahapan

• Buat beberapa selang nilai yang sama

lebarnya yang melingkupi semua nilai yang

ada di data. Banyaknya kelas sekitar 3.3Log(n) + 1

• Hitung banyaknya (frekuensi) data yang nilainya memenuhi setiap kelas

• Gambarkan batang setiap kelas yang tingginya proporsional dengan frekuensi

44

Ilustrasi

• Data n=48:

Kemungkinan Informasi yang diperoleh

dari bentuk sebaran

Nilai ukuran pemusatan di berbagai

bentuk sebaran

• Simetrik: rataan = rataan

• Menjulur ke kiri: rataan < median

STEM AND LEAF

• Mirip dengan Histogram, namun batangnya berupa nilai-nilai data

• Tahapan:

– bagi setiap data menjadi dua bagian :

• Dahan – Daun

– Letakkan nilai dahan pada sebuah kolom terurut – Pasangkan daun sesuai dengan letak dahannya – Urutkan nilai daun di setiap dahan

52

Ilustrasi

• Data: 17 21 22 12 27 13 30 24 29 15 18 10 13 14 28 09 02 20 07 09 00 01 13 02 17 03 17 14 18 19 11 19 02 10 29 04 20 28 09 04 03 02 34 25 09 21 07 24

• bagi setiap data menjadi dua bagian

1-7 2-1 2-2 1-2 2-7 1-3 3-0 2-4 2-9 1-5 1-8 1-0 1-3 1-4 2-8 0-9 0-2 2-0 0-7 0-9 0-0 0-1 1-3 0-2 1-7 0-3 1-7 1-4 1-8 1-9 1-1 1-9 0-2 1-0 2-9 0-4 2-0 2-8 0-9 0-4 0-3 0-2 3-4 2-5 0-9 2-1 0-7 2-4

• Letakkan nilai dahan pada sebuah kolom terurut 0

1 2 3

• Pasangkan daun sesuai dengan letak dahannya 0 79279012324943297 1 123580343774891904 2 27498090851 3 04

54

• Urutkan nilai daun di setiap dahan

0 0122223344779999 1 00123334457778899 2 0011244578899

• Jika mungkin perbaiki tampilan dengan memecah dahan 0- 0122223344 * 779999 1- 001233344 * 57778899 2- 0011244 * 578899 3- 04

56

• Aturan memecah dahan

– pecah jadi 2 : • - : 0, 1, 2, 3, 4 • * : 5, 6, 7, 8, 9 – pecah jadi 5 : • - : 0, 1 • t : 2, 3 • f : 4, 5 • s : 6, 7 • * : 8, 9

BOXPLOT

• informasi ukuran pemusatan dan penyebaran (berupa kuartil)

• informasi bentuk sebaran • informasi data ekstrim

Tahapan

• hitung statistik lima serangkai (Min, Q1, Q2, Q3, Max)

• hitung batas atas

BA = Q3 + 3/2 (Q3-Q1)

• hitung batas bawah

BB = Q1 - 3/2 (Q3-Q1)

• deteksi keberadaan pencilan, yaitu data yang

nilainya kurang dari BB atau data yang lebih besar dari BA

• gambar kotak, dengan batas Q1 sampai Q3, dan

letakkan tanda garis di tengah kotak pada posisi Q2

60

• Tarik garis ke kanan, mulai dari Q3 sampai data terbesar di dalam batas atas

• Tarik garis ke kiri, mulai dari Q1 sampai data terkecil di dalam batas bawah

Ilustrasi

• Dengan data sebelumnya diperoleh

– X[1] = Min = 0 – Q1 = 7.5 – Q2 = 14 – Q3 = 21 – X[n] = Max = 34 • Batas Bawah = 7.5 – 3/2(21 – 7.5) = -12.75 • Batas Atas = 21 + 3/2(21 – 7.5) = 41.25

Sebaran Nilai Statistik

• Statistik: karakteristik numerik yang diperoleh dari data contoh

• Dari sebuah populasi dapat diperoleh banyak contoh acak. • Dari setiap contoh acak, dapat dihitung sebuah nilai

statistik.

• Nilai statistik tersebut dapat berbeda-beda antar contohnya.





 





0.5

2.5

1.5

1.5

populasi

contoh

rata-rata

Rata-rata Contoh

• Misalkan terdapat suatu populasi dengan banyaknya anggota sebesar N, rata-rata sebesar  dan ragam sebesar 2_{, ditarik}

contoh berukuran n. Maka

– memiliki rata-rata sebesar  – memiliki ragam sebesar

• Dengan Pemulihan

• Tanpa Pemulihan untuk N -> ∞, n σ2         1 N n N n σ2 1 1 N n N _         x x

• Jika x₁, x₂, …, x_n adalah contoh acak berukuran n yang diambil dari populasi dengan sebaran N(µ, 2), maka rata-rata contoh akan

memiliki sebaran N(, 2/n)

• Dengan demikian memiliki sebaran N(0, 1) atau sebaran Z

n x

Ilustrasi

• Andaikan sebuah contoh acak berukuran 8

diambil dari populasi dengan sebaran N(5, 16). Maka rata-rata contoh akan memiliki sebaran N(5, 2).

• Peluang mendapatkan contoh dengan rata-rata kurang dari 4 adalah

P(xbar < 4) = P(Z < (4-5)/2)

Selang Kepercayaan bagi Rata-Rata

1 - 

x

Upper Limit Lower Limit

Selang Kepercayaan bagi Rata-Rata

1 - 

x

n z x _  2  n z x _  2 

Selang Kepercayaan bagi Rata-Rata

1 -  /2 Z_/2 99% 0.005 2.57 95% 0.025 1.96 90% 0.050 1.645

n

z

x

_



2



Ilustrasi

• Andaikan sebuah contoh acak berukuran 25 diambil dari

populasi yang menyebar normal dengan ragam 16. Jika rata-rata data contoh adalah 10, maka selang kepercayaan 95% bagi rata-rata adalah

11.568 s/d 8.432 1.568 10 s/d 568 . 1 10 568 . 1 10 25 4 ) 96 . 1 ( 10 2      n z x _ 

Ilustrasi

• Dengan tingkat keyakinan/kepercayaan 95%, kita yakin bahwa rata-rata populasi antara

Problem

• Pada banyak (semua) kasus,

ragam populasi atau



2

tidak

diketahui

• Jika x₁, x₂, …, x_n adalah contoh acak berukuran n yang diambil dari populasi dengan sebaran normal, maka

memiliki sebaran t-student dengan derajat bebas (n-1)

n s

Selang Kepercayaan bagi Rata-Rata:

ragam populasi tidak diketahui

1 - 

x

n s t x n 1) ; 2 (   _ n s t x n 1) ; 2 (   _

Ilustrasi

• Andaikan sebuah contoh acak berukuran 25 diambil dari

populasi yang menyebar normal. Jika rata-rata dan ragam dari data contoh masing-masing adalah 10 dan 20, maka selang

kepercayaan 95% bagi rata-rata adalah 11.846 s/d 8.154 1.846 10 s/d 846 . 1 10 846 . 1 10 25 20 ) 2.064 ( 10 ) 1 25 ; 025 . 0 (      _ n s t x

Teorema Limit Pusat

(central limit theorem)

• Jika x1, x2, …, xn adalah contoh acak berukuran n

dari populasi dengan sebaran tertentu yang memiliki rata-rata dan ragam masing-masing  dan 2, untuk

n (n sangat besar) maka

memiliki sebaran N(0, 1)

n x

Selang Kepercayaan bagi Proporsi

• Proporsi (p) adalah rata-rata dari peubah biner yang nilai datanya diganti 1 untuk kejadian yang diinginkan dan 0 untuk selainnya.

• Untuk contoh dengan ukuran yang besar, sebaran proporsi (p) mendekati sebaran normal.

• Ragam dari peubah biner adalah np(1-p), sehingga ragam proporsi adalah p(1-p)

Selang Kepercayaan bagi Proporsi

1 -  /2 Z_/2 99% 0.005 2.57 95% 0.025 1.96 90% 0.050 1.645

n

p

p

z

p

ˆ

ˆ

(

1

ˆ

)

2





_

Ilustrasi

• Pemeriksaan terhadap 1000 bayi berusia antara 2 hingga 6 bulan di Kota Bogor mendeteksi adanya 300 bayi yang

mendapat makanan dengan gizi kurang. Dengan demikian, selang kepercayaan 95% bagi proporsi bayi dengan gizi kurang adalah: 32.8% s/d 27.2% 0.328 s/d 272 . 0 028 . 0 3 . 0 1000 ) 7 . 0 )( 3 . 0 ( ) 96 . 1 ( 3 . 0 ) ˆ 1 ( ˆ ˆ 2     n p p z p _

Latihan (3)

• Dari pemeriksaan terhadap 200 lembar papan yang dihasilkan dari sebuah pabrik pemotongan kayu, diperoleh 8 lembar papan yang cacat. Buat selang kepercayaan 90% bagi proporsi papan cacat produksi pabrik tersebut.

• Wawancara terhadap 400 penumpang KRL Commuter Line menghasilkan sebanyak 285 orang yang tidak

setuju kenaikan harga tiket awal bulan ini. Buat selang kepercayaan 95% bagi proporsi penumpang yang tidak setuju kenaikan harga.

• n = 400

• p = 285 / 400 = 71.25%  penduga titik (point estimate) • 1 -  = 95%  z_/2 = 1.96 75.7% -% 8 . 66 04435 . 0 7125 . 0 400 ) 2875 . 0 )( 7125 . 0 ( ) 96 . 1 ( 7125 . 0 ) ˆ 1 ( ˆ ˆ 2     n p p z p _

Pengujian Hipotesis mengenai

Rataan Populasi

• Rataan populasi:

– nilainya tidak diketahui – nilainya diduga

– nilainya diasumsikan sama dengan, kurang dari atau lebih dari nilai tertentu

– nilainya dihipotesiskan

• Rataan Contoh

– digunakan untuk menduga rataan populasi

– digunakan untuk mengkonfirmasi hipotesis tentang rataan populasi

• Ditolak (rejected) : hipotesis tidak didukung oleh data, data tidak cukup mendukung

hipotesis

• Diterima (accepted): hipotesis didukung oleh data

Kesalahan Kesimpulan









Hipotesis Benar Hipotesis Salah

Diterima

Ditolak

Kondisi Sebenarnya (tapi tidak diketahui)

K esim pula n K on fir masi (be rda sar kan da ta con toh )

Apapun kesimpulan yang diambil berdasarkan data contoh, mengandung peluang membuat kesalahan.

Bentuk Hipotesis

 Hipotesis dalam statistika dinyatakan dalam dua

bentuk yaitu:

 _{H0 (hipotesis nol / null hypothesis)}

 _{H1 / HA (hipotesis alternatif / alternative hypothesis)}

 _{H0 dan H1 bertolak belakang, tidak mungkin}

dua-duanya ditolak dan tidak mungkin dua-dua-duanya diterima. Penolakan terhadap H0 berimplikasi pada penerimaan terhadap H1, dan sebaliknya.

Bentuk Hipotesis

H₀ :  = ₀ H₁ :   ₀ H₀ :   ₀ H₁ :  < ₀ H₀ :   ₀ H₁ :  > ₀ Two-Tail Hypothesis One-Tail Hypothesis

Kesalahan Kesimpulan



Type II Error

(



)

Type I Error

(



)



H₀ Benar H₀ Salah Terima H₀ Tolak H₀ Kondisi Sebenarnya (tapi tidak diketahui)

K esim pula n K on fir masi (be rda sar kan da ta con toh )

 ditentukan oleh pengambil kesimpulan. Secara umum

 membesar jika  mengecil.  disebut juga sebagai taraf nyata (significance level).

Pengambilan Kesimpulan

H₀ :  = ₀ H₁ :   ₀

Jika H₀ benar maka x-bar akan menyebar mengikuti sebaran N(₀, 2_/n)

Wilayah penolakan H₀:

1. x-bar lebih dari ₀ + z_/2 /n 2. x-bar kurang dari ₀ – z_/2 /  n

Pengambilan Kesimpulan

H₀ :  = ₀ H₁ :   ₀ n x z_hitung  _ 0

Tolak H₀ jika |z_hitung| > z_/2

Jika didefinisikan z_hitung sebagai

1 -  /2 Z_/2

99% 0.005 2.57 95% 0.025 1.96 90% 0.050 1.645

Pengambilan Kesimpulan

H₀ :  = ₀ H₁ :   ₀ n s x t_hitung   0

Tolak H₀ jika |t_hitung| > t_/2 dengan derajat bebas (n – 1) Pada kondisi nilai ragam (2_{) atau simpangan baku (}₎

Pengambilan Kesimpulan

Daerah penolakan H₀ sangat tergantung dari bentuk hipotesis alternatif (H₁) dan statistik uji

Uji Z (Z-test)

H₁:  < ₀  Tolak H₀ jika z_hitung < -z_(tabel) H₁:  > ₀  Tolak H₀ jika z_hitung > z_(tabel) H₁:   ₀  Tolak H₀ jika |z_hitung| > z_/2(tabel)

Uji t (t-test)

H₁:  < ₀  Tolak H₀ jika t_hitung < -t_{(; db=n-1)}(tabel) H₁:  > ₀  Tolak H₀ jika t_hitung > t_{(; db=n-1)}(tabel)

H₁:   ₀  Tolak H₀ jika |t_hitung| > t_{(/2; db=n-1)}(tabel)

daerah kritis (critical region)

Ilustrasi

• Batasan yang ditentukan oleh pemerintah terhadap emisi gas CO kendaraan bermotor adalah 50 ppm.

• Sebuah perusahaan baru yang sedang mengajukan ijin pemasaran mobil, diperiksa oleh petugas pemerintah untuk menentukan apakah perusahan tersebut layak diberikan ijin.

• Sebanyak 20 mobil diambil secara acak dan diuji emisi CO-nya.

• Dari data yang didapatkan, rata-ratanya adalah 55 dan ragamnya 4.2.

• Dengan menggunakan taraf nyata 5%, layakkah perusahaan tersebut mendapat ijin ?

• Hipotesis yang diuji:

H0 :   50 vs H1 :  > 50

• Statistik uji:

t_h= (55-50)/(4.2/20)=10.91

• Daerah kritis pada taraf nyata 0.05

• Kesimpulan:

Tolak H₀, artinya emisi gas CO kendaraan bermotor yang akan dipasarkan oleh

perusahaan tersebut melebihi batasan yang ditentukan oleh pemerintah sehingga

perusahaan tersebut tidak layak memperoleh ijin untuk memasarkan mobilnya.

Latihan

• CV Ayo Kurban menyatakan bahwa

kambing-kambing kurban yang mereka sediakan memiliki rata-rata bobot 48 kg. Pemeriksaan terhadap 15 ekor kambing memberikan data bobot sebagai berikut:

• Dengan taraf nyata 5%, apakah pernyataan CV Ayo Kurban didukung oleh data yang ada?

47 49 51 52 46 47 48 46 48 49 45 50 50 49 49 45

Outline

• Review Pengujian Hipotesis Pembandingan Nilai Tengah Dua Populasi

• Pengujian Hipotesis Pembandingan Nilai Tengah k Populasi, k > 2 : One-Way ANOVA

• Uji Perbandingan Berpasangan

– Fisher’s LSD – Tukey’s HSD

Pembandingan Nilai Tengah k Populasi

Populasi 1 Populasi 2 Populasi 3 Populasi 4

₁ ₂ ₃ ₄

dengan mengasumsikan ragam dari semua populasi sama besar, ingin diuji apakah populasi-populasi tersebut memiliki nilai tengah atau rata-rata yang sama besar.

H₀ : ₁ = ₂ = ₃ = ₄

Bagaimana membandingkannya?

Contoh 1 Contoh 2 Contoh 3 Contoh 4

1

x x₂ x₃ x₄

H₀ akan cenderung ditolak jika

perbedaan

antar x-bar semakin besar

H₀ akan cenderung ditolak jika

‘variasi’

antar x-bar semakin besar

Bagaimana membandingkannya?

Contoh 1 Contoh 2 Contoh 3 Contoh 4

1

x x₂ x₃ x₄

Jika didefinisikan

x

sebagai rataan umum (grand mean), yaitu rataan dari data gabungan semua contoh, maka selisih antara dan dapat dipandang sebagai ukuran variasi antar populasi

x

i

x

Variasi Total

• Ukuran variasi/perbedaan nilai setiap individu amatan dengan rata-rata umum.

• Diukur dalam bentuk SS(T), Sum of Squares Total [JKT = jumlah kuadrat total]



    k i ij n j x x T SS i 1 2 1 ) ( ) (

Variasi antar Populasi

• Diukur menggunakan SS(B), Sum of Squares Between

– Mengukur variasi antar rata-rata setiap contoh dengan rata-rata umum (grand mean)

– Diboboti oleh banyaknya amatan (sample size) dari masing-masing contoh



   k i i i x x n B SS 1 2 ) ( ) (

Variasi dalam Populasi

• Meskipun dari contoh yang sama, nilai amatan bisa berbeda-beda  ada variasi dalam populasi

• Diukur menggunakan SS(W), Sum of Squares Within

– Mengukur variasi antara nilai setiap amatan dengan rata-rata contoh                         







   k n j k kj n j j n j j x x x x x x W SS 1 2 1 2 2 2 1 2 1 1 ) ( ) ( ) ( ) ( 2 1 



   k i i i s n W SS 1 2 ) 1 ( ) (

One-Way ANOVA

• Memecah variasi total menjadi dua sumber yaitu variasi antar populasi dan variasi dalam populasi

• ANOVA: analysis of variance, analisis ragam, sidik ragam • Dapat ditunjukkan bahwa

SS(T) = SS(B) + SS(W)

• Penolakan terhadap H0 dilakukan jika porsi SS(B) jauh lebih besar dibandingkan porsi SS(W)

• SS(W) merupakan variasi yang diakibatkan oleh faktor lain selain faktor perbedaan populasi. Sehingga, SS(W) juga dikenal sebagai SS(E), sum of squares error.

One-Way ANOVA

• Direpresentasikan dalam bentuk tabel: Tabel ANOVA

Source df SS MS F Between k – 1 SS(B) MS(B) = SS(B)/ dfB Within n – k SS(W) MS(W) = SS(W)/dfW Total n – 1 SS(T) = SS(B ) + SS(W) Sumber db JK KT F Antar Populasi k – 1 Dalam Populasi n – k Total n – 1

df: degree of freedom, SS: sum of squares, MS: mean of squares = SS/df

One-Way ANOVA

• Uji F

• Kriteria penolakan H₀

F > F_tabel dengan derajat bebas (dfB, dfW) H₀ : ₁ = ₂ = ₃ = ₄

H₁ : setidaknya ada satu pasangan _i  _j

dfW W SS dfB B SS W MS B MS F ) ( ) ( ) ( ) (  

Permasalahan

• Suatu kelas dibagi dalam tiga kelompok

berdasarkan baris tempat duduk siswa: depan, tengah, belakang

• Seorang guru ingin mengetahui apakah posisi

tempat duduk mempengaruhi pemahaman siswa terhadap materi pelajaran.

• Ingin dibandingkan rata-rata nilai dari tiga kelompok tempat duduk.

Data

• Contoh acak dari setiap kelompok baris tempat duduk diambil.

• Data nilai ujian mata pelajaran yang berhasil dikumpulkan adalah sebagai berikut

– Depan : 82, 83, 97, 93, 55, 67, 53

– Tengah : 83, 78, 68, 61, 77, 54, 69, 51, 63

Statistik Deskriptif

Ringkasan statistik deskriptif dari data di slide sebelumnya adalah sebagai berikut

Depan Tengah Belakang

n 7 9 8

Rata-rata 75.71 67.11 53.50 St. Dev (simpangan baku) 17.63 10.95 8.96 Variance (ragam) 310.90 119.86 80.29

Rata-Rata Umum (grand mean)

08 . 65 24 1562 8 9 7 ) 50 . 53 ( 8 ) 11 . 67 ( 9 ) 71 . 75 ( 7 3 2 1 3 3 2 2 1 1             x x n n n x n x n x n x

SS(B)













1902 ) ( 08 . 65 50 . 53 8 08 . 65 11 . 67 9 08 . 65 71 . 75 7 ) ( ) ( ) ( 2 2 2 1 2         



 B SS B SS x x n B SS k i i i

SS(W)

3386 ) ( ) 29 . 80 ( 7 ) 86 . 119 ( 8 ) 90 . 310 ( 6 ) ( ) 1 ( ) ( 1 2      



 W SS W SS s n W SS k i i i

Tabel ANOVA

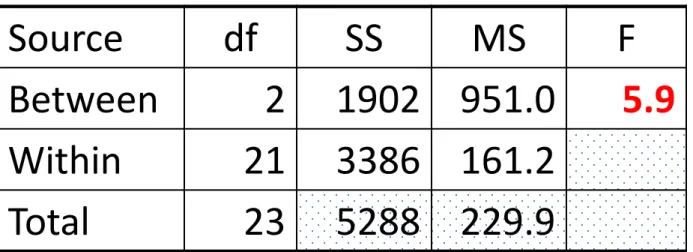
Source df SS MS F

Between 2 1902 951.0 5.9

Within 21 3386 161.2

Total 23 5288 229.9

F_tabel pada db1 = 2 dan db2 = 21, serta  = 5% adalah 3.4668

Karena nilai F lebih dari F_tabel, kita simpulkan Tolak H₀, dengan demikian dikatakan bahwa rata-rata tingkat penguasaan materi pelajaran di tiga tempat duduk tersebut tidak semuanya sama besar. Dalam bahasa lain, posisi tingkat duduk mempengaruhi tingkat pengusaan materi pelajaran.

Hubungan Antar Peubah

• Dari setiap objek/individu/tempat/dll dapat diukur/dicatat/diamati lebih dari satu buah peubah.

• Nilai dari suatu peubah bersifat:

– saling bebas dengan peubah lain – saling terkait dengan peubah lain

Hubungan antar Peubah

tinggi badan berat badan ketinggian tempat suhu rata-rata

Koefisien Korelasi

• Diperlukan sebuah ukuran yang dapat mencirikan keeratan hubungan antar dua peubah.

• Koefisien Korelasi ( ; baca: rho)

– nilainya: -1    1

– tanda menunjukkan arah hubungan

– besar/magnitude menunjukkan kekuatan hubungan – koefisien korelasi data contoh dinotasikan r

Koefisien Korelasi (Pearson)

1 ) ( dan 1 ) ( 1 ) )( ( 2 2           







n y y S n x x S n y y x x S S S S r i y i x i i xy y x xy xy

Jika ada dua peubah X dan Y, korelasi antara keduanya adalah

Koefisien Korelasi (+)

r = 0.58

r = 0.70

Koefisien Korelasi (-)

r = -0.58

r = -0.68

Ilustrasi

Tinggi Badan Berat Badan

165 49 159 58 166 60 173 67 179 69 164 56 163 53 154 51 170 60 158 44 40 45 50 55 60 65 70 150 160 170 180

Ilustrasi

x y x-xbar y-ybar (x-xbar)2 _(y-ybar)2 _{(x-xbar)(y-ybar)}

165 49 -0.1 -7.7 0.01 59.29 0.77 159 58 _{-6.1 1.3 37.21 1.69 -7.93} 166 60 0.9 3.3 0.81 10.89 2.97 173 67 7.9 10.3 62.41 106.09 81.37 179 69 13.9 12.3 193.21 151.29 170.97 164 56 -1.1 -0.7 1.21 0.49 0.77 163 53 -2.1 -3.7 4.41 13.69 7.77 154 51 -11.1 -5.7 123.21 32.49 63.27 170 60 4.9 3.3 24.01 10.89 16.17 158 44 -7.1 -12.7 50.41 161.29 90.17 165.1 56.7 jumlah 496.9 548.1 426.3 817 . 0 1 . 548 9 . 496 3 . 426    r

Regresi Linear: Pengantar

• Terdapat 2 peubah numerik : peubah yang satu mempengaruhi peubah yang lain

• Peubah yang mempengaruhi  X, peubah bebas (independent), peubah penjelas (explanatory) • Peubah yang dipengaruhi  Y, peubah tak bebas

Pengantar

Misalnya ingin melihat hubungan antara

pengeluaran untuk iklan (ads expenditures, X) dengan penerimaan melalui penjualan (sales revenue, Y)

Bulan 1 2 3 4 5 6 7 8 9 10

X 10 9 11 12 11 12 13 13 14 15

Pengantar

35 40 45 50 55 60 65 8 10 12 14 16 sa les revenue (m il lions of do ll ars )

Pengantar

35 40 45 50 55 60 65 8 10 12 14 16 sal es reve n ue (million s of do ll ars)

ads expenditures (millions of dollars)

Yˆ Y e Ingin dibuat model Y = a + bX Model memuat error, selisih nilai sebenarnya dengan dugaan berdasar model

Y

ˆ

-Y

e



Bagaimana mendapatkan a dan b?

Metode yang digunakan : OLS (ordinary least

squares/kuadrat terkecil), mencari a dan b sehingga jumlah kuadrat error paling kecil Cari penduga a dan b sehingga

minimum









   n i n i 1 2 i i 1 2 i Y - aˆ - bˆX e

Bagaimana mendapatkan a dan b?















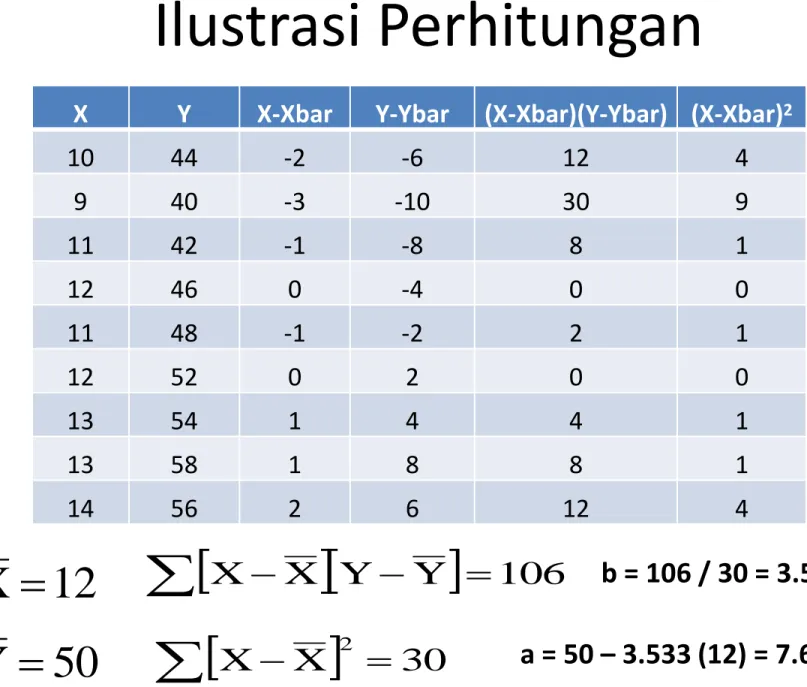
      _n 1 i 2 i n 1 i i i X X Y Y X X bˆ X bˆ Y aˆ   Rata-rata Y Rata-rata X

Ilustrasi Perhitungan

12 X  50 Y 



X  X



Y  Y



106 



X  X



2  30  b = 106 / 30 = 3.533 a = 50 – 3.533 (12) = 7.60

X Y X-Xbar Y-Ybar (X-Xbar)(Y-Ybar) (X-Xbar)2

10 44 -2 -6 12 4 9 40 -3 -10 30 9 11 42 -1 -8 8 1 12 46 0 -4 0 0 11 48 -1 -2 2 1 12 52 0 2 0 0 13 54 1 4 4 1 13 58 1 8 8 1 14 56 2 6 12 4

y = 3.5333x + 7.6 35 40 45 50 55 60 65 8 10 12 14 16 sa les revenue (m il lions of do ll ars )

Interpretasi a dan b

Y = 7.6 + 3.53 X

Pendapatan = 7.6 + 3.53 Belanja Iklan

• a = intersep/intercept = besarnya nilai Y ketika X sebesar 0

• b = gradient/slope = besarnya perubahan nilai Y ketika X berubah satu satuan. Tanda koefisien b menunjukkan arah hubungan X dan Y

Pada kasus ilustrasi

• a = 7.6  besarnya sales revenue jika tidak ada belanja iklan adalah 7.6 juta dolar

• b = 3.533  jika belanja iklan dinaikkan 1 juta dolar maka sales revenue naik 3.533 juta dolar

Uji Signifikasi Koefisien b

bˆ s bˆ t uji statistik 













      _n i i n i i i b X X n Y Y s 1 2 1 2 ˆ ) 2 ( ˆ

H₀ : b = 0 (artinya X tidak mempengaruhi Y)

H₁ : b  0 (artinya X mempengaruhi Y)

Tolak H₀ jika nilai |t| melebihi nilai t pada tabel dengan derajat bebas (n-2) dengan tingkat kesalahan /2

Uji signifikansi koefisien b

• Nilai s_b =  (65.47 / (8)(30)) = 0.52

• Nilai t = 3.53 / 0.52 = 6.79

• Nilai t pada tabel (db = 8,  = 5%) = 2.306 • Kesimpulan : Tolak H₀, data mendukung

kesimpulan adanya pengaruh ads expenditure terhadap sales revenue.

Ukuran Kebaikan Model

• Menggunakan koefisien determinasi (R2_,

R-squared)

• R-squared bernilai antara 0 s/d 1

• R-squared adalah persentase keragaman data yang mampu diterangkan oleh model

• R-squared tinggi adalah indikasi model yang baik

Ukuran Kebaikan Model

 





_























₂ 2 2 2 2

1

ˆ

Y

Y

e

Y

Y

Y

Y

R

i i i

• Model dalam ilustrasi bisa ditunjukkan memiliki R-squared 0.85 atau 85%