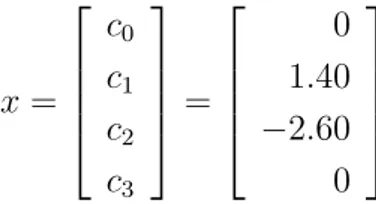Daftar Isi
Contents ii
Daftar Tabel iii
Daftar Gambar iv
1 Konsep Dasar 1
1.1 Definisi dan Teorema Dalam Kalkulus . . . 1
1.2 Representasi bilangan dalam komputer . . . 4
1.3 Algoritma . . . 6
1.4 Software Komputer . . . 7
2 Solusi Persamaan Fungsi Polinomial 10 2.1 Metoda Biseksi . . . 10
2.2 Metoda Newton-Raphson . . . 12
2.3 Metoda Posisi Palsu . . . 14
3 Interpolasi dan Aproksimasi Polinomial 18
3.1 Norm . . . 18
3.2 Konsep Masalah dalam Aproksimasi . . . 20
3.3 Solusi Iteratif Untuk Sistem Linier Ax=b . . . 21
3.4 Fungsi-Fungsi Aproksimasi . . . 24
3.4.1 Interpolasi dan Polinomial Lagrange . . . 24
3.4.2 Difrensi Terpisah . . . 25
3.4.3 Interpolasi Splin Kubik . . . 33
3.5 Solusi Iteratif Integral Terbatas . . . 40
4 Metoda Numeris untuk Sistem Nonlinier 52 4.1 Metoda Titik Tetap . . . 54
4.2 Metoda Newton . . . 58
5 Metoda Numeris Untuk Masalah Nilai Awal 64 5.1 Teori Dasar . . . 66
5.2 Beberapa Metoda Numeris . . . 68
5.2.1 Metoda Euler . . . 69
5.2.2 Metoda Runge-Kutta . . . 74
5.2.3 Metoda Multistep Linier (MML) . . . 79
Daftar Tabel
3.1 Difrensi terpisah langkah maju. . . 28
3.2 Difrensi terpisah langkah mundur. . . 31
3.3 Data f(x) . . . 32
4.1 Data hasil eksekusi program iterasi Newton . . . 61
5.1 Data hasil eksekusi program metoda Runge-Kutta . . . 79
1.1 Approksimasi oleh p1(x) . . . 2
1.2 Approksimasi oleh p2(x) . . . 3
3.1 Diagram aproksimasi . . . 20
3.2 Interpolasi polinomial Lagrange p2(x) terhadap f(x) . . . 26
3.3 Approksimasi NFDD p4(x) . . . 33
3.4 Approksimasi spline kubik S3(x) . . . 41
3.5 Aturan Trapesium. . . 43
3.6 Aturan Simpson. . . 44
3.7 Konstruksi automobile . . . 50
5.1 Diagram kekonvekan untuk D∈R2 . . . . 67
5.2 Metoda Euler dalam grafik . . . 74
5.3 Metoda Runge-Kutta order 2 . . . 80
BAB 1
Konsep Dasar
1.1
Definisi dan Teorema Dalam Kalkulus
Pengembangan metoda numerik tidak terlepas dari pengembangan beberapa definisi dan teorema dalam mata kuliah kalkulus yang berkenaan dengan fungsi polinomial f(x). Oleh karena itu dibawah ini akan diingatkan kembali beberapa definisi dan teorema tersebut.
Teorema 1.1.1 (Nilai Tengah) Jika f(x) adalah fungsi kontinyu pada interval
[a, b], dan didefinisikan m = Infa≤x≤b f(x) dan M = Supa≤x≤bf(x) maka ada
sebarangξpada interval[m, M], sehingga paling sedikit satu titikζ di dalam interval
[a, b] akan memenuhi f(ξ) = ζ
Teorema 1.1.2 (Nilai Rata-Rata) Jika f(x)adalah fungsi kontinyu pada inter-val[a, b] dan terdefrensialkan pada interval(a, b), maka paling sedikit ada satu titik
ξ dalam (a, b) yang memenuhi f(b)−f(a) =f0(ξ)(b−a)
Teorema 1.1.3 (Integral Nilai Rata-Rata) Jikaw(x)adalah fungsi tak negatif
dan terintegralkan pada interval [a, b], dan misal f(x) kontinyu pada [a, b] maka Z b a w(x)f(x)dx=f(ξ) Z b a w(x)dx
untuk semua ξ∈[a, b]
Teorema 1.1.4 (Teorema Taylor) Jikaf(x)mempunyain+1turunan kontinyu pada interval [a, b] untuk beberapa n ≥0 dan bila x, x0 ∈[a, b] maka
f(x) ≈ pn(x) +Rn+1(x) (1.1) pn(x) = f(x0) + (x−x0) 1! f 0(x 0) +· · ·+(x−x0) n n! f (n)(x 0) (1.2) Rn+1(x) = 1 n! Z x x0 (x−t)nf(n+1)(t)dt (1.3) = (x−x0) n+1 (n+ 1)! f (n+1)(ξ) (1.4)
untuk ξ antara x0 dan x
0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5 −5 −4 −3 −2 −1 0 1 2 3 4 f(x) p1(x)
Gambar 1.1: Approksimasi oleh p1(x)
Deret Taylor ini nantinya akan menjadi konsep dasar pengembangan metoda nu-meris. Beberapa metoda aproksimasi adalah merupakan hasil ekspansi dan
pe-menggalan dari deret ini. Sehingga deret ini sendiri juga merupakan model aproksi-masi terhadap suatu fungsi f(x) sebagaimana digambarkan dalam contoh berikut ini.
Contoh 1.1.1 Diketahuif(x) = lnx, tentukan fungsi aproksimasi linearp1(x)dan kuadratik p2(x) pada x0 = 1, dan gunakan p1(x), p2(x) untuk menghitung ln 1.5.
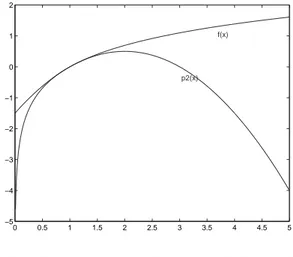
0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5 −5 −4 −3 −2 −1 0 1 2 f(x) p2(x)
Gambar 1.2: Approksimasi oleh p2(x)
Penyelesaian 1.1.1 f(x) = lnx maka f(x0) = ln 1 = 0, f0(x) = 1x maka f0(x0) =
1. Dengan menggunakan teori Taylor kita dapatkan
p1(x) = ln 1 + (x−1).1 =x−1 p2(x) = ln 1 + (x−1).1 + 1 2(x−1) 2.−1 = (x−1)−1 2(x−1) 2 Dengan demikian ln 1.5 dapat ditentukan dengan cara
ln 1.5 = p1(1.5) = 1.5−1 = 0.5
ln 1.5 = p2(1.5) = (1.5−1)−
1
2(1.5−1)
2 = 0.375
Secara grafis aproksimasi dari p1(x) dan p2(x) terhadap f(x) = lnx dapat
1.2
Representasi bilangan dalam komputer
Komputer dapat melakukan operasi pada bilangan dengan mudah, misal 2 + 2 = 4,6 : 2 = 3, dengan pasti komputer dapat menjawab dengan benar. Namun demikian bila komputer mengoperasikan (√3)2 maka operasi ini tidak dilakukan
dengan cara ¡312
¢2
= 3 akan tetapi dengan cara melakukan pengakaran bilangan tiga dua kali kemudian keduanya dikalikan. Dapat dipahami bahwa untuk √3 = 1.7320508. . . mempunyai jumlah desimal (digit) yang tidak terbatas sehingga nilai tersebut hanya merupakan nilai pendekatan.
Dalam hal melakukan pendekatan ini komputer melakukan pemotongan (Chop-ping) atau pembulatan (Rounding) dan selanjutnya dimungkinkan muncul bebe-rapa kesalahan yang secara umum dikenal dengan nama kesalahan pembulatan (Rounding error) dan kesalahan pemotongan (Chopping error).
Selanjutnya untuk merepresentasikan bilangan real, komputer pada umumnya meng-gunakan sistem ”floating-point” dengan basis bilangan 2 (biner), 8(octal) dan 16(hexadecimal). Sedangkan format penyimpanannya dalam memori komputer digambarkan sebagai berikut :
x=σ·(·a1a2. . . at)β ·βe, (1.5) dimana
• a1 6= 0, dan 0≤ai ≤β−1,a1 kemudian disebut titik radik.
• σ adalah tanda dengan nilai σ = +1 atau −1, dan β adalah basis.
• eadalah bilangan bulat denganL≤e≤U, dimanaL, U masing-masing nilai terkecil dan terbesar.
• (·a1a2. . . at)β adalah mantisa. Bila bilangan real x dinyatakan dalam
maka representasi pemotongan desimal dapat dinyatakan dalam bentuk floating point f l(x) sebagai berikut
f l(x) = σ·(·a1a2. . . at)β·βe (1.7) Sedangkan representasi pembulatan dapat ditampilkan sebagai
f l(x) = (
σ·(·a1a2. . . at)β ·βe; 0≤at+1 < β2
σ·[(·a1a2. . . at)β+ (·0. . .01)β]·βe; β2 ≤at+1 < β
Dalam hal ini f l(x) 6= x, oleh karena itu kesalahan dapat dimunculkan dalam bentuk ²=x−f l(x), dan kesalahan relatifnya
x−f l(x) x =²R dengan demikian
f l(x) = (1−²R)x (1.8)
Jika simbol-simbol operasi mesin komputer dinyatakan dalam⊕,ª,⊗dan ®maka operasi jumlah, kurang, kali dan bagi untuk x dan y dalam komputer dinyatakan sebagai berikut:
x⊕y = f l(f l(x) +f l(y)) xªy = f l(f l(x)−f l(y)) x⊗y = f l(f l(x)×f l(y)) x®y = f l(f l(x)÷f l(y)).
Dengan demikian komputer melakukan floating point terhadap masing-masing kom-ponen bilangan sebelum dan sesudah melakukan operasi. Hal ini bertujuan untuk meminimalkan kesalahan yang dihasilkannya.
Secara umum formulasi nilai kesalahannya dari perhitungan aproksimasi terhadap xA (niali eksak) oleh xT (nilai aproksimasi), dapat dinyatakan sebagai
dan kesalahan relatifnya adalah
Rel(xA) =
xT −xA
xT (1.10)
1.3
Algoritma
Teorema 1.3.1 (Algoritma) Algoritma adalah suatu prosedur yang menggam-barkan urut-urutan rapi dan logis dengan tujuan memudahkan pengimplementasian suatu masalah. Selanjutnya, sebagai prosedur logis algoritma harus dapat dengan mudah diinterpretasikan dalam fungsi-fungsi khusus pada komputer prog-ramming.
Dua simbol yang digunakan dalam algoritma adalah Period (·) dan menunjukan akhir prosedur, dan titik koma (;) memisahkan tugas dalam beberapa langkah. Teknik loop (pengulangan) dalam algoritma dapat dinyatakan dengan ’kontrol penyanggah’
F or i= 1,2, . . . , n Set xi =ai+i·h ataupun ’kontrol bersyarat’
W hile i < N do Steps3−6 if . . . then, if . . . then . . . else Misal suatu algoritma untuk menghitung
N X
i=1
xi =x1+x2 +· · ·+xN, dapat diuraikan adalah sebagai berikut
INPUT N, x1, x2, . . . , xn.
OUTPUT SUM=PNi=1xi.
Step 2 For i= 1,2,3, . . . , N do setSUM =SUM +xi.
Step 3 OUTPUT (SUM); STOP.
1.4
Software Komputer
Banyak software programming, baik compiler ataupun semi compiler, yang dapat digunakan untuk menyelesaikan masalah numerik, diantaranya adalah
1. Fortran (LINPACK, EISPACK, LAPACK, BLAS, NAG)
2. Matlab yang library-nya berdasarkan EISPACK dan LINPACK + beberapa Matlab Toolbox
Latihan Tutorial 1
1. Fungsi aproksimasi sebagian besar didasari oleh pengembangan deret Tay-lor sebutkan teorema Taylor ini. Bila diketahui f(x) = sinx terapkan deret Taylor ini untuk menentukan fungsi aproksimasi kuadratik terhadap f pada x = 0. Kemudian tentukan nilai aproksimasi dari sin 5. Disadari bahwa dalam menghitung nilai sin 5 anda akan mendapatkan kesalahan nu-meris sebutkan penyebab kesalahan itu. Selanjutnya untuk mengantisipasi kesalahan ini diperlukan format penyimpanan yang baik dalam memori kom-puter, tentukan format tersebut. Dan bila diberikan nilai eksak xA dan nilai aproksimasixT ,formulasikankesalahan E(xA) serta relatif kesalahan Rel(xA).
2. Tentukan konversi dari masing-masing bilangan dibawah ini kedalam bentuk desimal biasa.
(a) (1010101.101)2
(b) (2A3.F F)16
(c) (.101010101. . .)2
3. Tentukan fungsi aproksimasi p1(x), p2(x) dan p3(x) dari fungsi dibawah ini
pada x0 = 1.
(a) f(x) = lnx+x (b) g(x) = x2+ 4x+ 2
dan tentukan nilai dari ln 3, melalui fungsi aproksimasif(x).
4. Gunakan deret Taylor untuk menemukan rumusan dari ex,sinx,cosx, e−x2
dan 1
1−x pada x0 = 0
5. Lakukan pembulatan dan pemotongan terhadap bilangan dibawah ini sampai empat desimal dibelakang koma.
(a) 0.35745397 (b) 4.8975978
(c) −1.098904045 (d) 0.09874329873
dan tentukan nilai kesalahan dan kesalahan relatifnya.
6. Gunakan metoda biseksi untuk menyelesaikan persmaan dibawah ini pada interval yang diberikan
(a) √x−cosx= 0 pada interval [0,1]
(b) x3−7x2+ 14x−6 = 0 pada interval [1,1.32]
(c) 2xcosx−(x+ 1)2 = 0 pada interval [−3,−2]
Solusi Persamaan Fungsi
Polinomial
Definition 2.0.1 (Metoda numeris) Metoda numeris adalah suatu model pen-dekatan dengan menggunakan teknik-teknik kalkulasi berulang (teknik iterasi) untuk mecari penyelesaian hampiran suatu masalah tertentu. Selanjutnya teknik-teknik yang digunakan itu mempunyai potensi membuat suatu nilai kesalahan yang dieval-uasi secara bertahap untuk mendapatkan nilai kesalahan yang sangat kecil.
Untuk mengawali penjelasan teknik-teknik aproksimasi ini, dalam bab ini akan dimulai dengan pembahasan aproksimasi terhadap suatu titik melalui penyelesaian persamaan fungsi polinomial.
f :=a1xn+a2xn−1+a3xn−2+· · ·+an = 0
2.1
Metoda Biseksi
Definition 2.1.1 (Prosedur Biseksi) Misalf adalah fungsi kontinyu terdefi-nisi pada interval [a, b], dimana f(a) berbeda tanda dengan f(b). Dengan teori ”nilai
tengah” maka ada p ∈ (a, b) dengan f(p) = 0 dengan asumsi akar dalam interval
(a, b)adalah tungal. Selanjutnya untuk melakukan perhitungan yang akurat kita set
a1 =a dan b1 =b dan tentukan p1 lewat
p1 =
1
2(a1+b1)
Jika f(p1) = 0, maka p=p1. Jika tidak, f(p1) akan mempunyai tanda yang sama denganf(a1) atau f(b1). Jikaf(p1)dan f(a1)mempunyai tanda yang sama maka
p∈ (p1, b1) jika tidak maka p ∈ (a1, p1). Selanjutnya set a2 dan b2 yang baru dan tentukan p2 melalui perhitungan yang sama dengan p1, dan lakukan pengulangan sampai tingkat akurasi tertentu.
Untuk menghentikan pengulangan penghitungan dalam mencari solusi yang akurat harus dikonfirmasikan dengan nilai kesalahan ² (selanjuntya kita sebut toleransi) dimana toleransi dalam hal ini dapat dipilih
|pn−pn−1| < e
|pn−pn−1|
|pn|
< e, pn6= 0 |f(pn)| < e
Algoritma Metoda Biseksi
INPUT batas interval a, b, ² (Toleransi), Jumlah iterasi maximum (N) OUTPUT nilai aproksimasi p
Step 1 Set i=1;
F A=f(a)
Step 2 While i≤N do Steps 3-6
Step3 Set p=a+ (b−a)/2; F P =f(p)
Step4 IFF P = 0, atau (b−a)/2< ² OUTPUT(p)
Step5 Set i=i+ 1.
Step6 If F A·F P > 0 thena =p, F A=F P; else Set b=p.
Step 7 OUTPUT (Metoda gagal setelah N iterasi) STOP.
2.2
Metoda Newton-Raphson
Jika f ∈ C2[a, b], dan ¯x ∈ [a, b] adalah nilai aproksimasi terhadap p sehingga
f0(¯x) 6= 0 dan |¯x−p| sangat kecil, maka polynomial Taylor dapat dikembangkan
untuk ¯x sebagai: f(x) = f(¯x) + (x−x)f¯ 0(¯x) + (x−x)¯ 2 2! f 00(ξ(x)) +. . . f(x) = f(¯x) + (x−x)f¯ 0(¯x) + (x−x)¯ 2 2 f 00(ξ(x)); ξ(x)∈(x,x).¯ (2.1)
Jika f(p) = 0 maka untuk x=ppersamaan (5.1) menjadi 0 = f(¯x) + (p−x)f¯ 0(¯x) + (p−x)¯ 2
2 f
00(ξ(p))
Telah diasumsikan |¯x−p| sangat kecil, maka suku ketiga dapatlah diabaikan se-hingga
0 = f(¯x) + (p−x)f¯ 0(¯x).
Formulasikan untukp didapat
p≈x¯− f(¯x) f0(¯x).
Dengan menggati ¯x = pn−1 maka formulasi Newton-Raphson dapat diturunkan
untuk menggeneralisasi suatu deret {pn} melalui
Sama halnya dengan metoda biseksi, untuk menghentikan pengulangan penghitun-gan dalam mencari solusi yang akurat harus dikonfirmasikan denpenghitun-gan nilai kesalahan ² yang telah ditentukan sehingga
|pn−pn−1| < e
|pn−pn−1|
|pn|
< e pn6= 0 |f(pn)| < e
Algoritma Metoda Newton-Raphson
INPUT nilai awal p0, ² (Toleransi), Jumlah iterasi maximum (N)
OUTPUT nilai aproksimasi p
Step 1 Set i=1;
Step 2 While i≤N do Steps 3-6
Step3 Set p=p0−f(p0)/f0(p0); Step4 IF|p−p0|< ²
OUTPUT(p) STOP.
Step5 Set i=i+ 1.
Step6 Set p0 =p(Perbaharui p0)
Step 7 OUTPUT (Metoda gagal setelah N iterasi) STOP.
Metoda Newton ini lebih baik dibandingkan metoda Biseksi, namun demikian proses menentukan f0(x) kadangkala merupakan proses yang lebih susah
diban-dingkan dengan operasi artmatikanya. Untuk menghindari hal tersebut dikem-bangkan metoda berikut. Ingat definisi turunan
f0(pn−1) = lim x→pn−1 f(x)−f(pn−1) x−pn−1 . Misalx=pn−2 maka f0(p n−1)≈ f(pn−2)−f(pn−1) pn−2−pn−1 = f(pn−1)−f(pn−2) pn−1−pn−2 .
Substitusikan rumusan ini kedalam rumusan Newton diperoleh rumus:
pn =pn−1−f(fp(np−n1−)(1p)−n−f1(p−np−n2−)2). (2.3)
Rumus ini kemudian disebut Metoda Secant Algoritma Metoda Secant
INPUT nilai awal p0, p1, ² (Toleransi), Jumlah iterasi maximum (N)
OUTPUT nilai aproksimasi p
Step 1 Set i=2;
q0 =f(p0).
q1 =f(p1).
Step 2 While i≤N do Steps 3-6
Step3 Set p=p1−q1(p1−p0)/(q1−q0). (hitung pi)
Step4 IF|p−p1|< ²
OUTPUT(p) STOP.
Step5 Set i=i+ 1.
Step6 Set p0 =p1; (Perbaharui p0, q0, p1, q1)
q0 =q1;
p1 =p;
q1 =f(p).
Step 8 OUTPUT (Metoda gagal setelah N iterasi) STOP.
2.3
Metoda Posisi Palsu
Metoda ini menggabungkan ide metoda biseksi dan metoda secant. Dalam penyelesaian f(x) = 0, ditentukan suatu interval [p0, p1] dimana f kontinyu pada
interval ini, danf(p0).f(p1)<0 (berlawanan tanda). Prosedur selanjutnya dapat
Algoritma Metoda Posisi Palsu
INPUT nilai awal p0, p1, ² (Toleransi), Jumlah iterasi maximum (N)
OUTPUT nilai aproksimasi p
Step 1 Set i=2;
q0 =f(p0).
q1 =f(p1).
Step 2 While i≤N do Steps 3-7
Step3 Set p=p1−q1(p1−p0)/(q1−q0). (hitung pi)
Step4 IF|p−p1|< ² OUTPUT(p) STOP. Step5 Set i=i+ 1. q=f(p) Step6 IFq·q1 <0 maka p0 =p1, q0 =q1 Step7 p1 =p1, q1 =q
Step 8 OUTPUT (Metoda gagal setelah N iterasi) STOP.
Latihan Tutorial 2
1. Gunakan algoritma biseksi untuk menentukan anilai aproksimasi pada √3 dan 3√25
2. Suatu model yang dipakai untuk mengadakan aproksimasi terhadap suatu masalah adalah metoda numeris,sebutkandefinisi formal metoda ini. Selan-jutnya implikasi dari penggunaan metoda ini, komputer programming meru-pakan hal yang sangat penting. Untuk mempermudah menginterpretasikan suatu metoda menjadi suatu programming dibutuhkan algoritma, jelaskan apa yang disebut dengan algoritma.
Salah satu algoritma yang digunakan untuk menginterpretasikan proses kalku-lasi metoda numeris adalah metoda Newton-Raphson dengan rumusan
pn=pn−1−
f(pn−1)
f0(p
n−1)
, untuk n≥1
Metoda ini adalah metoda yang cukup terkenal, namun proses menentukan f0(x) kadangkala merupakan proses yang lebih sulit dibandingkan dengan
operasi artmatiknya. Untuk menghindari hal tersebut ditawarkan metoda lain yaitu Metode Secant dengan rumus
pn=pn−1−
f(pn−1)(pn−1−pn−2)
f(pn−1)−f(pn−2)
untuk n ≥1.
Uraikanbagaimana metoda Newton dikembangkan sehingga menjadi meto-da Secant ini. Kemudian bila kalkulasi iteratif diterapkan terhameto-dap metometo-da ini, maka kalkulasi berulang (looping) akan terus dilakukan, jelaskan apa yang harus dilakukanuntuk menghentikan kalkulasi tersebut.
3. f(x) = −x3−cosx dan p
0 = −1, gunakan metoda Newton Raphson untuk
menentukanp2
4. Gunakan algoritma Newton untuk menentukan masing-masing soal dibawah ini dengan tingkat ketelitian (toleransi) e= 1e−5
(a) ex+ 2−x+ 2 cosx−6 = 0 untuk [1,2] (b) ln(x−1) + cos(x−1) = 0 untuk [1.3,2]
(c) 2xcos 2x−(x−2)2 = 0 untuk [2,3]
5. Ulangi soal nomor 8 diatas dan gunakan metoda secant 6. Ulangi soal nomor 8 diatas dan gunakan metoda posisi palsu
Interpolasi dan Aproksimasi
Polinomial
3.1
Norm
Definisi 3.1.1 (Norm vektor) Norm vektor adalah pemetaan dari suatu fungsi terhadap setiapx∈IRN yang disimbolkan dengan||x||sedemikian hingga memenuhi sifat-sifat dibawah ini
1. ||x||>0 untuk x6= 0, atau ||x||= 0, untuk x= 0
2. ||αx||=α||x|| 3. ||x+y|| ≤ ||x||+||y|| Contoh ||x||1 = n X i=1 |xi| ||x||2 = µXn i=1 |xi|2 ¶1 2 , (Norm Euclid) 18
||x||p = µXn i=1 |xi|p ¶1 p ||x||∞ = max 1≤i≤n|xi|
Definisi 3.1.2 (Norm matrik) Norm matrik adalah pemetaan dari suatu fungsi terhadap setiapx∈IRN×N yang disimbolkan dengan||A||sedemikian hingga memenuhi
sifat-sifat dibawah ini
1. ||A||>0 untuk A6= 0, atau ||A||= 0, untuk A= 0
2. ||αA||=α||A|| 3. ||A+B|| ≤ ||A||+||B|| 4. ||AB|| ≤ ||A||||B|| Contoh ||A||F = µXn i=1 n X j=1 |aij|2 ¶1 2 (Norm F robenius) ||A||v = max x6=0 ||Ax|v ||x||v
Definisi 3.1.3 (Ruang Linier (RL)) HimpunanF dikatakan suatu ruang lini-er bila operasi penjumlahan dan perkalian terdefinisi didalamnya sehingga f ·g ∈ F
dan αf +βg ∈F untuk ∀f, g ∈F.
Definisi 3.1.4 (Ruang Linier Norm (RLN)) F dikatakan ruang linier norm bila F adalah merupakan RL dan terdapat fungsi norm sehingga
2. ||αf||=α||f||
3. ||f+g|| ≤ ||f||+||g||
untuk semua f, g∈F
3.2
Konsep Masalah dalam Aproksimasi
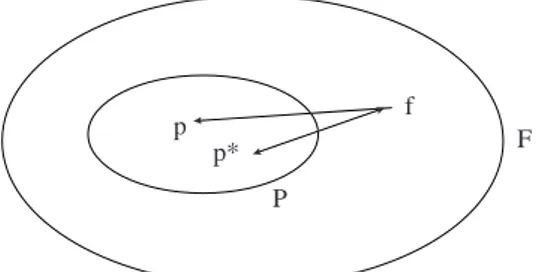
Misalf ∈ F dan f /∈ P maka masalah dalam aproksimasi sebenarnya adalah menentukanp∗ ∈P sedemikian hingga
||f−p∗|| ≤ ||f−p||, ∀p∈P
kemudianp∗dikatakan suatu aproksimasi terbaik terhadapf. Hal ini dapat
digam-barkan dalam diagram Venn berikut ini
p p*
P
F f
Gambar 3.1: Diagram aproksimasi
Beberapa fungsi aproksimasi p(x) untuk menghampiri fungsi f(x) dalam F = C[a, b] adalah sebagai berikut
• P ={p:p(x) = a1+a2x+· · ·+anxn−1}
• P ={p:p(x) = PPn0arxr n
0brxr} • P ={p:p(x) = Prn=1αreλrx}.
Sedangkan dalamF =IRN adalahP ={p:p(x) = Pnr=1arφr, ar ∈IRN, φrIRN} Teorema 3.2.1 (Teorema Weirstrass) Misal f terdefinisi dan terdifrensialkan pada interval [a, b] maka terdapat polinomial p(x) yang juga terdefinisi dan ter-difrensialkan pada interval tersebut sedemikian hingga untuk nilai ² >0 berlaku
||f(x)−p(x)||< ²,
dan ∀x∈[a, b] Contoh
F =C[a, b] dan f ∈F, tunjukkan bahwa berikut dibawah ini merupakan RLN ||f||p = µ Z b a |f(x)|pdx ¶1 p ; 1≤p≤ ∞ ||f||∞ = max a≤x≤b|f(x)|
3.3
Solusi Iteratif Untuk Sistem Linier A
x
=
b
Suatu sistem linier dapat digambarkan sebagai
a11x1+a12x2+· · ·+a1nxn = b1;
a21x1+a22x2+· · ·+a2nxn = b2;
a31x1+a32x2+· · ·+a3nxn = b3; (3.1)
... annx1+an2x2+· · ·+annxn = bn.
Bila A merupakan matrik yang memuat koefisien variabelx1, x2, . . . , xn maka
digunakan dalam menyelesaikan sistem ini. Diantaranya metoda langsung dan metoda iteratif. Namun demikian sesuai dengan perkembangan hardware dan soft-ware komputer solusi dengan metoda iteratif ini menjadi sangat populer dan terus dikembangkan.
Metoda langsung memanfaakan konsep invers dalam matrik sehingga sistemAx= b dapat diselesaikan melalui
A−1Ax = A−1b x = A−1b
Teknik ini dipandang tidak efisien dan efektif, bahkan dimungkinkan suatu sistem tidak dapat diselesaikan karena proses kalkulasi panjang yang harus dikerjakan, yaitu berkenaan dengan penghitungan invers matrik A.
Metoda iteratif menguraikan matrikA ini kedalam unsur matrik yang lebih seder-hana dan mudah dihitung oleh komputer. Misal A=D-L-U, dimana D adalah matrik diagonal,Ladalah negatif matrik segitiga bawah satu tahap dibawah diag-onal utama dan Uadalah negatif matrik segiatiga atas satu tahap diatas diagonal utama maka sistem diatas dapat dinyatakan sebagai berikut
(D−L−U)x = b (3.2)
Dx−(L+U)x = b
Dx = (L+U)x+b
x = D−1(L+U)x+D−1b x = D−1(L+U)x+D−1b.
MisalJ =D−1(L+U) maka secara iteratif dapat diformulasikan sebagai
xj+1 =Jxj +D−1b. (3.3) Metoda ini disebut metoda Jacobi.
Untuk meningkatkan kecepatan tingkat konvergensi dari metoda Jacobi, ditetap-kanlah suatu koefisien redaman ω ∈ < sebagai faktor akselerasi terhadap metoda
ini sedemikian hingga dapat disajikan dengan bentuk dibawah ini xj+1 =
£
(1−ω)I+ωJ¤xj +ωD−1b. (3.4) Metoda ini disebut metoda Jacobi teredam (damped Jacobi).
Bentuk lain dari penyederhanaan (3.2) adalah sebagai berikut (D−L)x−Ux = b
(D−L)x = Ux+b
x = (D−L)−1Ux+ (D−L)−1b
MisalG= (D−L)−1Umaka secara iteratif dapat diformulasikan sebagai
xj+1 =Gxj+ (D−L)−1b (3.5) Metoda ini disebut metoda Gauss-Seidel.
Metoda-metoda iteratif ini dihitung berdasarkan suatu nilai awal yang dalam hal ini x0, kemudian dengan rumusan itu dilanjutkan perhitungan untuk x1, x2, . . .
sehingga diperoleh deret {xi}ni=0. Deret ini akan konvergen terhadap nilai eksak
x. Dapat dilihat disini bahwa proses penghitungan secara berulang terjadi se-hingga dinamakan model solusi iteratif. Untuk menghentikan proses pengulangan ini, hasilnya harus dikonfirmasikan dengan toleransi ² yang dalam hal ini dapat ditentukan dari nilai dibawah ini
² = ||b−Ax||1
² = ||b−Ax||2
3.4
Fungsi-Fungsi Aproksimasi
3.4.1
Interpolasi dan Polinomial Lagrange
Polinomial Taylor yang sementara ini sudah cukup baik melakukan interpo-lasi terhadap suatu fungsi masih memiliki kelemahan diantaranya kekurangaku-ratan melakukan suatu aproksimasi. Hal ini disebabkan polinomial ini melakukan aproksimasi hanya berdasarkan satu titik tertentu. Dengan demikian interpolasi yang paling akurat hanya terjadi disekitar titik itu. Oleh karena itu diperlukan eksplorasi terhadap polinomial lainnya, polinomial Lagrange misalnya.
Polinomial ini mengembangkan interpolasi terhadap suatu fungsi dibeberapa titik terhubung, sehingga interpolasinya berdasarkan titik-titik yang telah ditentukan terlebih dahulu pada fungsi itu. Semakin dekat jarak penentuan titik yang satu dengan titik yang lainnya semakin akurat aproksimasinya. Dengan kata lain tingkat akurasinya ditentukan oleh kedekatan antara titik-titik (grid) pada fungsi tadi.
Teorema 3.4.1 (Polinomial Langrange ke-n) Jika x0, x1, x2, . . . adalah bilan-gan berbeda dan f adalah suatu fungsi yang terdefinisi pada titik-titik ini, maka ada dengan tungggal suatu polinomial p(x) berderajad paling besar n yang memenuhi sifat-sifat berikut f(x) =p(x) dimana pk(x) =f(x0)Ln,0(x) +· · ·+f(xn)Ln,n(x) = n X k=0 f(xk)Ln,k(x) dan Ln,k(x) = n Y i=0 i6=k (x−xi) (xk−xi) untuk k=0,1,2,. . . , n
Dalam hal ini Ln,k(x) dapat ditulis dngan Lk(x) bila dianggap rancu dengan pengertian derajad n. Polinomial Lagrange ini memenuhi sifat sebagai berikut:
Ln,k(xi) = (
0 jika i6=k 1 jika i=k
Contoh 1 Gunakan titik-titik x0 = 2, x1 = 2.5 dan x2 = 4 untuk menentukan interpolasi polinomial kedua terhadap f(x) = 1/x.
Solusi 1 L0(x) = (x−2.5)(x−4) (2−2.5)(2−4) = (x−6.5)x+ 10 L1(x) = (x−2)(x−4) (2.5−2)(2.5−4) = (−4x+ 24)x−32 3 L2(x) = (x−2)(x−2.5) (4−2)(4−2.5) = (x−4.5)x+ 5 3
jika f(x0) = f(2) = 0.5, f(x1) = f(2.5) = 0.4, f(x2) =f(4) = 0.25, maka didapat
p2(x) = 2 X k=0 f(xk)Lk(x) = 0.5((x−6.5)x+ 10) + 0.4(−4x+ 24)x−32 3 + 0.25 (x−4.5)x+ 5 3 = (0.05x−0.425)x+ 1.15
Interpolasi olehp2(x) terhadap f(x) dapat digambarkan dibawah ini
3.4.2
Difrensi Terpisah
Difrensi terpisah menyempurnakan interpolasi polinomial Lagrange dengan mengek-spresikan bentuk pn(x) dalam
pn(x) = a0+a1(x−x0) +a2(x−x0)(x−x1) +. . .
0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5 0 0.5 1 1.5 2 2.5 3 3.5 4 f(x) p2(x)
Gambar 3.2: Interpolasi polinomial Lagrange p2(x) terhadap f(x)
dimanaa0, a1, . . . , an adalah konstanta.
Selanjutnya bila kita tentukanx=x0 maka persamaan (3.6) menjadi
pn(x0) = a0 =f(x0)≈f[x0], (3.7) dan x=x1 maka pn(x1) =a0+a1(x1−x0) = f(x1), pn(x1) = f(x0) +a1(x1−x0) =f(x1), sehingga a1 = f(x1)−f(x0) x1−x0 ≈f[x0, x1], (3.8)
dengan demikian dapat dikatakan f[xi, xi+1] = f[xi+1]−f[xi] xi+1−xi (3.9) dan f[xi, xi+1, xi+2] = f[xi+1, xi+2]−f[xi, xi+1] xi+2−xi (3.10) sehingga difrensi terpisah ke k
f[xi, xi+1, . . . , xi+k] =
f[xi+1, xi+2, . . . , xi+k]−f[xi, xi+1, . . . , xi+(k−1)]
xi+k−xi
Dan terakhir persamaan (3.6) menjadi pn(x) = f[x0] +f[x0, x1](x−x0) +f[x0, x1, x2](x−x0)(x−x1) +. . . +f[x0, x1, . . . , xn](x−x0)(x−x1). . .(x−xn−1) (3.12) Selanjuntya untuk x = x0+sh x = xi+ (s−i)h atau h= x−xi s−i , i= 0,1,2, . . . , n maka pn(x) = pn(x0+sh) = f[x0] +shf[x0, x1] +s(s−1)h2f[x0, x1, x2] +· · ·+s(s−1). . . (s−(n−1))hnf[x0, x1, . . . , xn] (3.13) = n X k=0 s(s−1). . .(s−k+ 1)hkf[x 0, x1, . . . , xk] (3.14) Bukti
Pada suku kedua dari persamaan (3.13) h dapat diganti dengan h = x−x0
s , pada suku ketiga h2 dapat diganti dengan h ·h =
µ x−x0 s ¶µ x−x1 s−1 ¶
begitu juga suku keempat, kelima dan seterusnya.
Sekarang kita nyatakan (3.14) dalam ekspresi
pn(x) = pn(x0+sh) = n X k=0 à s k ! k!hkf[x0, x1, . . . , xk] dimana à s k ! = s(s−1). . .(s−k+ 1) k!
Dan diperkenalkan difrensi langkah maju sebagai berikut 4f(xn) = f(xn+1)−f(xn) f[x0, x1] = f(x1)−f(xn) x1−x0 = 1 h 4f(x0) f[x0, x1, x2] = f[x1, x2]−f[x0, x1] x2−x0 = 1 2h[ 1 h 4f(x2)− 1 h 4f(x0)] = 1 2h2 4f(x0) sehingga f[x0, . . . , xk] = 1 k!hk 4 kf(x 0) (3.15) x f(x) D. T. I D. T. II D. T. III x0 f[x0] f[x0, x1] x1 f[x1] f[x0, x1, x2] = f[x1,xx22]−−fx0[x0,x1] f[x1, x2] f[x0, x1, x2, x3] = f[x1,x2,x3]−f[x0,x1,x2] x3−x0 x2 f[x2] f[x1, x2, x3] = f[x2,xx33]−−fx1[x1,x2] f[x2, x3] f[x1, x2, x3, x4] = f[x2,x3,x4]−f[x1,x2,x3] x4−x1 x3 f[x3] f[x2, x3, x4] = f[x3,xx44]−−fx2[x2,x3] f[x3, x4] f[x2, x3, x4, x5] = f[x3,x4,x5]−f[x2,x3,x4] x5−x2 x4 f[x4] f[x3, x4, x5] = f[x4,xx55]−−fx3[x3,x4] f[x4, x5] x5 f[x5]
Substitusikan ini kedalam persamaan pn(x) = pn(x0+sh) = n X k=0 Ã s k ! k!hkf[x 0, x1, . . . , xk] maka diperoleh bentuk
pn(x) = pn(x0+sh) = Pn k=0 Ã s k ! 4kf(x 0).
Formulasi ini disebut Difrensi Terpisah Langkah Maju Newton (NFDD). Untuk mempermudah dapat disusun suatu tabel difrensi terpisah langkah maju seba-gaimana tabel 3.1.
Selanjutnya bila urutan itu dibalik yaitu xn, xn−1, xn−2, . . . , x0, maka pn(x) dapat dinyatakan dalam
pn(x) = a0+a1(x−xn) +a2(x−xn)(x−xn−1) +. . .
+an(x−xn)(x−xn−1). . .(x−x1) (3.16)
dimanaa0, a1, . . . , an adalah konstanta.
Misal kita tentukan x=xn maka persamaan (3.16) menjadi
pn(xn) = a0 =f(xn)≈f[xn], (3.17) dan untuk x=xn−1 maka
pn(xn−1) = a0+a1(xn−1−xn) =f(xn−1), pn(xn−1) = f(xn) +a1(xn−1−xn) = f(xn−1), sehingga a1 = f(xn−1)−f(xn) xn−1−xn = f(xn)−f(xn−1) xn−xn−1 ≈f[xn, xn−1]. (3.18)
Dengan demikian persamaan (3.16) menjadi pn(x) = f[xn] +f[xn, xn−1](x−xn) +f[xn, xn−1, xn−2](x−xn)(x−xn−1) +. . . +f[xn, xn−1, . . . , x0](x−xn)(x−xn−1). . .(x−x1) (3.19) Selanjutnya untuk x = xn+sh x = xn−i+ (s+i)h atau h= x−xn−i s+i , i= 0,1,2, . . . , n−1 maka pn(x) = pn(xn+sh) = f[xn] +shf[xn, xn−1] +s(s+ 1)h2f[xn, xn−1, xn−2] +· · ·+s(s+ 1). . . (s+ (n−1))hnf[x n, xn−1, . . . , x0] (3.20) = n X k=0 s(s+ 1). . .(s+k−1)hkf[x n, xn−1, . . . , x0] Bukti
Pada suku kedua dari persamaan (3.16)hdapat diganti dengan h= xn−xn−1
s , pada suku ketigah2 dapat diganti denganh·h=
µ xn−xn−1 s ¶µ x−xn−2 s+1 ¶
begitu juga suku keempat, kelima dan seterusnya.
Sehingga kita memiliki ekspresi pn(x) =pn(x0+sh) = n X k=0 (−1)k à −s k ! k!hkf[x n, xn−1, . . . , x0] dimana à s k ! = (−1)ks(s−1). . .(s−k+ 1) k!
Diperkenalkan juga bentuk difrensi langkah mundur
5f(xn) = f(xn)−f(xn−1); n ≥1
maka x f(x) D. T. I D. T. II D. T. III x0 f[x0] f[x1, x0] x1 f[x1] f[x2, x1, x0] = f[x1,xx00]−−fx2[x2,x1] f[x2, x1] f[x3, x2, x1, x0] = f[x2,x1,x0]−f[x3,x2,x1] x0−x3 x2 f[x2] f[x3, x2, x1] = f[x2,xx11]−−fx3[x3,x2] f[x3, x2] f[x4, x3, x2, x1] = f[x3,x2,x1]−f[x4,x3,x2] x1−x4 x3 f[x3] f[x4, x3, x2] = f[x3,xx22]−−fx4[x4,x3] f[x4, x3] f[x5, x4, x3, x2] = f[x4,x3,x2]−f[x5,x4,x3] x2−x5 x4 f[x4] f[x5, x4, x3] = f[x4,xx33]−−fx5[x5,x4] f[x5, x4] x5 f[x5]
Tabel 3.2: Difrensi terpisah langkah mundur.
f[xn, xn−1] = f(xn)−f(xn−1) xn−xn−1 = 1 h 5f(xn) f[xn, xn−1, xn−2] = f[xn, xn−1]−f[xn−1, xn−2] xn−xn−2 = 1 2h2 5 2f(x n) dan akhirnya f[xn, xn−1, . . . , x0] = 1 k!hk 5 kf(x n) (3.21)
Substitusikan ini kedalam persamaan pn(x) =pn(x0+sh) = n X k=0 (−1)k à −s k ! k!hkf[xn, xn−1, . . . , x0]
maka diperoleh bentuk pn(x) = pn(x0+sh) = Pn k=0(−1)k à −s k ! 5kf(x n).
Formulasi ini disebut Difrensi Terpisah Langkah Mundur Newton (NBDD).
Dalam hal ini dapat pula disusun suatu tabel difrensi terpisah langkah mudur yang disajikan dalam Tabel 3.2.
Contoh 2 Suatu data diberikan dalam tabel berikut ini Tentukan interpolasi difrensi
x f(x) 1.0 0.7651977 1.3 0.6200860 1.6 0.4554022 1.9 0.2818186 2.2 0.1103623 Tabel 3.3: Dataf(x)
terpisal langkah majup4 terhadap data tersebut dan tentukan nilai aproksimasi dari
f(1.5).
Solusi 2 Dengan menggunakan difrensi terpisah langkah maju didapatkan tabel berikut ini
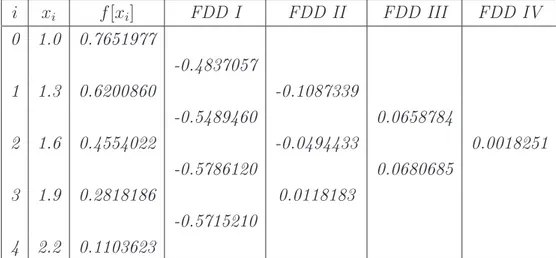
Sehingga formulasi dari NFDD adalah sebagai berikut
p4(x) = 0.7651977−0.4837057(x−1.0)−0.1087339(x−1.0)(x−1.3) + 0.0658784
i xi f[xi] FDD I FDD II FDD III FDD IV 0 1.0 0.7651977 -0.4837057 1 1.3 0.6200860 -0.1087339 -0.5489460 0.0658784 2 1.6 0.4554022 -0.0494433 0.0018251 -0.5786120 0.0680685 3 1.9 0.2818186 0.0118183 -0.5715210 4 2.2 0.1103623
Selanjutnya dapat ditentukan
f(1.5)≈p4(1.5) = 0.5118200
Gambar dibawah ini menunjukkan bagaimanap4(x) menginterpolasi data f(x)
0.5 1 1.5 2 2.5 3 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 p4(x) Gambar 3.3: Approksimasi NFDD p4(x)
3.4.3
Interpolasi Splin Kubik
Definisi 3.4.1 Fungsi f terdefinisi pada interval [a, b] dan diberikan himpunan titik x0, x1, . . . , xn dimana a = x0 < x1 < · · · < xn = b, maka interpolasi splin
kubik S untuk f adalah suatu fungsi yang memenuhi beberapa sarat berikut ini
1. S(x)adalah fungsi polinomial kubik, dinotasikan dengan Sj(x), yang
terdefin-isi pada subinterval [xj, xj+1] untuk masing-masing j = 0,1, . . . , n−1;
2. S(xj) =f(xj) untuk setiap j = 0,1, . . . , n; 3. Sj+1(xj+1) =Sj(xj+1) untuk setiap j = 0,1, . . . , n−2; 4. S0 j+1(xj+1) =Sj0(xj+1) untuk setiap j = 0,1, . . . , n−2; 5. S00 j+1(xj+1) =Sj00(xj+1) untuk setiap j = 0,1, . . . , n−2;
6. dan satu diantara sarat batas berikut terpenuhi
(a) S00(x
0) =S00(xn) = 0 (sarat batas bebas atau alami);
(b) S0(x
0) = f0(x0) dan S0(xn) =f0(xn) (sarat batas terikat);
Selanjutnya jika sarat batas bebas yang terjadi maka splin ini dinamakan Splin Alami, dan sebaliknya bila sarat batas terikat yang terjadi maka disebut Splin Terikat.
Splin Kubik Alami
Untuk membangun splin kubik ini pertama kali kita tulis interpolasi plonomial kubik
Sj(x) = aj+bj(x−xj) +cj(x−xj)2+dj(x−xj)3; j = 0,1, . . . , n−1 (3.22) Untuk x=xj, maka
Sj(xj) =aj =f(xj) (3.23) dan untuk x=xj+1 maka
j = 0,1, . . . , n−2. Bila hj =xj+1−xj
aj+1 =aj +bjhj +cjh2j +djh3j; j = 0,1, . . . , n−1 (3.24) Sekarang didefinisikanbn=Sn0(x) dan turunan pertama (3.22) adalah
S0
j(x) = bj + 2cj(x−xj) + 3dj(x−xj)2 sehingga
bj+1 = Sj0+1(xj+1) =Sj0(xj+1), (lihat poin5.pada definisi)
= bj+ 2cjhj + 3djh2j; j = 0,1, . . . , n−1. (3.25) Sekarang permisalkan c= S00n(x)
2 , dan turunan kedua dari (3.22) adalah
S00 j(x) = 2cj+ 6dj(x−xj) sehingga cj+1 = cj + 3djhj dj = (cj+1−cj) 3hj (3.26) Substitusikan persamaan ini ke (3.24)dan (3.25) didapat
aj+1 = aj+bjhj +cjh2j + (cj+1−cj)h3j 3hj ; = aj+bjhj +h 2 j 3 (2cj +cj+1) (3.27) dan bj+1 = bj+ 2cjhj+ 3 (cj+1−cj)h2j 3hj ; = bj+hj(cj+cj+1) (3.28)
Ekspresikan persamaan (3.27) dalam bj dan kemudian reduksi indeknya satu kali bj = 1 hj (aj+1−aj)− hj 3 (2cj +cj+1). (3.29) bj−1 = 1 hj−1 (aj −aj−1)− hj−1 3 (2cj−1+cj). (3.30)
Reduksi juga indek dari persamaan (3.28) satu kali bj =bj−1+hj−1(cj−1+cj) (3.31) Substitusikan (3.29) dan (3.30) ke (3.31) 1 hj (aj+1−aj)− hj 3 (2cj +cj+1) = 1 hj−1 (aj−aj−1)− hj−1 3 (2cj−1+cj) +hj−1 3 (2cj−1+cj). Kelompokkan seluruh variabelc keruas kiri
hj−1 3 (2cj−1+cj)−hj−1(cj−1+cj)− hj 3 (2cj+cj+1) = − 1 hj(aj+1−aj) + 1 hj−1 (aj−aj−1) −hj−1(2cj−1+cj) + 3hj−1(cj−1+cj) +hj(2cj+cj+1) = 3 hj(aj+1−aj) − 3 hj−1 (aj−aj−1)
Dengan demikian diperoleh bentuk indek berurut dari koefisienc hj−1cj−1+ 2(hj−1+hj)cj+hjcj+1 = 3 hj (aj+1−aj)− 3 hj−1 (aj−aj−1), (3.32) dimanaj = 1,2, . . . , n−1.
Splin kubik alami memenuhi kondisi S00(x
masing-masing j dapat diformulasikan sebagai berikut j = 0→c0 = 0; j = 1→h0c0+ 2(h0+h1)c1+h1c2 = 3 h1 (a2−a1)− 3 h0 (a1−a0); j = 2→h1c1+ 2(h1+h2)c2+h2c3 = 3 h2 (a3−a2)− 3 h1 (a2−a1); ; ... j = n−1→hn−2cn−2+ 2(hn−2+hn−1)cn−1+hn−1cn = 3 hn−1 (an−an−1) − 3 hn−2 (an−1 −an−2); j = n→cn= 0.
Persamaan ini terdiri darin persamaan dann variablecj yang akan dicari, dengan kata lain menyelesaikan persamaan ini adalah sama dengan menyelesaikan suatu sistem linierAx=b, dimana
A = 1 0 0 0 h0 2(h0+h1) h1 0 h1 2(h1+h2) h2 0 hn−2 2(hn−2+hn−1) hn−1 0 0 0 1 dan b= 0 3 h1(a2−a1)− 3 h0(a1−a0) 3 h2(a3−a2)− 3 h1(a2−a1) ... 3 hn−1(an−an−1)− 3 hn−2(an−1−an−2) 0 , x= c0 c1 c2 ... cn−1 cn
Matrik A adalah matrik yang elemennya mendominasi diagonal sejajar dengan diagonak utama (strictly diagonally dominant), diluar itu nilainya nol. Hal ini
membantu dalam melakukan kalkulasi untuk x. Dengan menggunakan metoda it-eratif, sistem linier itu dapat diselesaikan dengan mudah.
Algoritma splin kubik alami
INPUT n;x0, x1, . . . , xn;a0 =f(x0), . . . , an =f(xn).
OUTPUT aj, bj, cj, dj, untuk j = 1,2, . . . , n−1(Catatan : Sj(xj) = aj +bj(x−xj) +cj(x−xj)2+dj(x−xj)3 untuk xj ≤x≤xj+1.) Step 1 for i= 0,1, . . . , n−1 dan Set hi =xi+1−xi.
Step 2 for i= 1, . . . , n−1 dan Set αi = 3 hi(ai+1−ai)− 3 hi−1 (ai−ai−1)
Step 3 Set l0 = 1(Langkah 3,4,5 dan sebagian dari 6 adalah algoritma
untuk menyelesaikan sistem linier tridiagonalAx=b) µ0 = 0; z0 = 0. Step 4 for i= 1,2, . . . , n−1 setli = 2(xi+1−xi−1)−hi−1µi−1; µi =hi/li; zi = (αi−hi−1zi−1)/li. Step 5 Set ln= 1; zn= 0; cn = 0. Step 6 for j =n−1, n−2, . . . ,0 setcj =zj −µjcj+1; bj = (aj+1−aj)/hj−hj(cj+1+ 2cj)/3; dj = (cj+1−cj)/(3hj).
Step 7 OUTPUT(aj, bj, cj, dj, untuk j = 1,2, . . . , n−1); STOP.
Contoh 3 Tentukan interpolasi splin kubik pada data berikut ini xj aj =f(xj) 0 0 1 1 2 3 3 2
Solusi 3 Polinomial kubik dalam hal ini adalah
Sj(xj) =aj +bj(x−xj) +cj(x−xj)2 +dj(x−xj)3,
dimana j = 1, . . . , n−1. Karena n = 3 maka j = 1,2, dengan asumsi j = 0 → c0 = 0 dan j = 3 →c3 = 0 sehingga A = 1 0 0 0 h0 2(h0+h1) h1 0 0 h1 2(h1+h2) h2 0 0 0 1 dan b = 0 3 h1(a2−a1)− 3 h0(a1−a0) 3 h2(a3−a2)− 3 h1(a2−a1) 0 , x= c0 c1 c2 c3
Dengan memasukkan nilai hj dan aj dapatlah diperoleh matrik dan vektor sebagai
berikut A= 1 0 0 0 1 4 1 0 0 1 4 1 0 0 0 1
dan b = 0 3 −9 0
Dengan menyelesaikan sistem itu diperoleh vektor x sebagai berikut
x= c0 c1 c2 c3 = 0 1.40 −2.60 0
Sedang bj dan dj dapat dihitung dengan menggunakan rumus (3.29) dan (3.26).
Hasil selengkapnya dapat dilihat dalam tabel berikut
xj aj bj cj dj
0 0 0.53333 0 0.46667
1 1 1.93333 1.40 -13.33333
2 3 0.73333 -2.60 0.86667
3 2 − 0 −
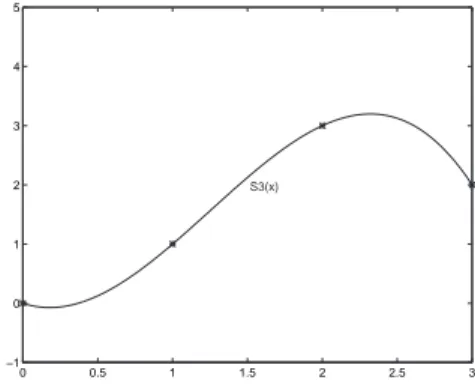
Grafik dibawah ini menunjukkan interpolasi splin kubik terhadap suatu data ’*’.
3.5
Solusi Iteratif Integral Terbatas
Teknik numeris untuk menghitung integral tertentu yang dikenal sebagai In-tegrasi Numeris dibutuhkan untuk menyelesaikan atau menghitung nilai integral dimana fungsi yang diintegralkan tidak mempunyai antiturunan yang eksplisit atau fungsi yang antiturunannya tidak mudah ditentukan. Suatu metoda yang cukup dasar sekali adalah metoda numeris kuadratur. Metoda ini menggunakan rumus jumlah Pni=0aif(xi) untuk menghitung nilai approksimasi terhadap
Rb
0 0.5 1 1.5 2 2.5 3 −1 0 1 2 3 4 5 S3(x)
Gambar 3.4: Approksimasi spline kubik S3(x)
Interpolasi fungsi approksimasi metoda ini didasarkan atas pemilihan dan pengem-bangan interpolasi polinomial Lagrange karena polinomial ini dianggap merupakan fungsi approksimasi yang terbaik p∗. Prosedur penurunannya diawali dengan menentukan himpunan titik-titik berbedax0, . . . , xndari interval [a, b], selanjutnya mengintegralkan polinomial Lagrange dan suku kesalahan pemenggalannya dalam interval [a, b]. Pn(x) = n X i=0 f(xi)Li(x) Z b a f(x)dx = Z b a n X i=0 f(xi)Li(x)dx+ Z b a n Y i=0 (x−xi) fn+1(ξ(x)) (n+ 1)! dx = n X i=0 aif(xi) + 1 (n+ 1)! Z b a n Y i=0 (x−xi)fn+1(ξ(x))dx, dimanaξ(x)∈[a, b] untuk setiap x dan
ai = Z b
a
Li(x)dx untuk setiap i= 0,1,2, . . . , n. Dengan demikian secara umum formula kuadratur numeris itu adalah
Z b a f(x)dx≈ n X i=0 aif(xi),
dengan kesalahan E(f) = 1 (n+ 1)! Z b a n Y i=0 (x−xi)f(n+1)(ξ(x))dx.
Metoda ini dipandang terlampau sederhana dan tidak cukup akurat untuk men-gatasi permasalahan yang lebih komplek. Bila kita cermati formulasi kesalahan-nya maka rumusan ini digeneralisasi dari pengembangan aproksimasi deret Taylor yang belum diekpansi, sedangkan disadari bahwa akurasi deret Taylor yang belum terekspansi level akurasinya rendah dan penetapan fungsi aproksimasinya hanya berdasarkan pada pengambilan satu titik sampel. Metoda lain yang dipandang lebih akurat adalah aturan Trapesium dan Simpson. Aturan ini dikembangkan dari perluasan interpolasi polinomial Lagrange kesatu dan kedua pada himpunan titik-titik sampel. Misal kita notasikan x0 = a, x1 = b, h = b−a dan polinomial
Lagrange linier P1(x) = (x−x1) (x0−x1) f(x0) + (x−x0) (x1−x0) f(x1). maka Z b a f(x)dx = Z x1 x0 · (x−x1) (x0−x1) f(x0) + (x−x0) (x1−x0) f(x1) ¸ dx +1 2 Z x1 x0 f00(ξ(x))(x−x 0)(x−x1)dx. (3.33)
Jika (x−x0)(x−x1) tidak berubah tanda dalam interval [x0, x1] maka teorema
nilai ”weighted mean” untuk integral dapat diterapkan dalam suku kesalahannya sehingga diperoleh Z x1 x0 f00(ξ(x))(x−x 0)(x−x1)dx = f00(ξ) Z x1 x0 (x−x0)(x−x1)dx = f00(ξ) · x3 3 − (x1+x0) 2 x 2 +x 0x1x ¸x1 x0 = −h3 6 f 00(ξ).
Sebagai konsukwensinya (3.33) akan menjadi Z b a f(x)dx = · (x−x1)2 2(x0−x1) f(x0) + (x−x0)2 2(x1−x0) f(x1) ¸x1 x0 − h 3 12f 00(ξ) = x1−x0 2 [f(x0) +f(x1)]− h3 12f 00(ξ).
Dengan demikian untukh=x1−x0 kita mendapatkan rumus berikut ini
Aturan Trapesium Rb
af(x)dx= h2[f(x0) +f(x1)]− h
3
12f00(ξ) (3.34)
Rumus ini disebut aturan Trapesium karena jika f adalah susatu fungsi positif, makaRabf(x)dx dapat diapproksimasikan dengan luas dari trapesium sebagaimana digambarkan dalam Gambar 3.5.
f P_1
a=x_0 b=x_1
y
x
Gambar 3.5: Aturan Trapesium.
Bila kita perhatikan rumus diatas, dapatlah disimpulkan bahwa aturan Trapesium itu akan memberikan solusi eksak terhadap sebarang fungsi yang turunan kedu-anya adalah sama dengan nol (sebarang polinomial berorder satu atau kurang), karena suku kesalahan trapesium ini meliputif00. Dengan kata lain aturan
Trape-sium dikatakan berorder satu, dan suku kesalahan pemenggalannya adalah suatu fungsi O(h2). Dari sisi ini kita dapat mengatakan bahwa aturan Trapesium juga
memandang rendahnya order dari aturan ini sehingga tetap dibutuhkan aturan lainnya. Salah satu metoda yang cukup terkenal adalah aturan Simpson.
Aturan Simpson didapat dari mengintegralkan polinomial Lagrange kedua dalam batas [a, b] dengan beberapa titik x0 =a, x2 =b dan x1 =a+h, untukh = (b−2a),
lihat Gambar 3.6. Polinomial Lagrange kedua disajikan dalam P2(x) = (x−x1)(x−x2) (x0−x1)(x0−x2) f(x0) + (x−x0)(x−x2) (x1−x0)(x1−x2) f(x1) + (x−x0)(x−x1) (x2−x0)(x2−x1) f(x2) Sehingga Z b a f(x)dx = · (x−x1)(x−x2) (x0−x1)(x0−x2) f(x0) + (x−x0)(x−x2) (x1−x0)(x1−x2) f(x1) + (x−x0)(x−x1) (x2−x0)(x2 −x1) f(x2) ¸ dx + Z x1 x0 (x−x0)(x−x1)(x−x2) 6 f (3)(ξ(x))dx. f P_1 a=x_0 b=x_2 y x x_1
Gambar 3.6: Aturan Simpson.
Sebagaimana aturan Trapesium, penentuan orde aturan Simpson juga dapat dil-ihat dari suku kesalahannya. Suku kesalahan rumus ini hanya sampai pada suku
kesalahan O(h4) yaitu hanya meliputi f(3) sehingga aturan Simpson yang
ditu-runkan dari interpolasi Lagrange hanya berorder dua. Versi yang lebih baik dari aturan Simpson order dua ini adalah aturan yang diturunkan dari ekspansi polino-mial Taylor ketigaf terhadap x1. Misalkan masing-masing x∈[a, b] ada bilangan
ξ(x)∈(x0, x1) maka ekspansi Taylor
f(x) = f(x1) +f0(x1)(x−x1) + f00(x 1) 2 (x−x1) 2+ f000(x1) 6 (x−x1) 3 +f(4)(ξ(x)) 24 (x−x1) 4 dan Z x2 x0 f(x)dx = · f(x1)(x−x1) + f0(x 1) 2 (x−x1) 2 +f 00(x 1) 6 (x−x1) 3+f000(x1) 24 (x−x1) 4 ¸x2 x0 + 1 24 Z x1 x0 f(4)(ξ(x))(x−x 1)4dx (3.35)
Karena (x−x1)4 tidak pernah bernilai negatif pada interval [x0, x1], maka teori
nilai ”Weighted Mean” untuk integral akan menjadi 1 24 Z x1 x0 f(4)(ξ(x))(x−x1)4dx = f(4)(ξ 1) 24 Z x2 x0 (x−x1)4dx = f(4)(ξ1) 120 (x−x1) 5 ¯ ¯ ¯ ¯ x2 x0 untuk sebarang ξ1 ∈(x0, x2).
Sementara kita tahu bahwa h=x2−x1 =x1−x0, sehingga
(x2−x1)2−(x0−x1)2 = (x2−x1)4−(x0−x1)4 = 0
(x2−x1)3−(x0−x1)3 = 2h3 dan (x2−x1)5−(x0−x1)5 = 2h5
Sebagai konsukwensinya persamaan (3.35) dapat ditulis sebagai Z x2 x0 f(x)dx= 2hf(x1) + h3 3 f 00(x 1) + h5 60f (4)(ξ 1) (3.36)
Disisi lain kita memiliki ekspresi f(x0+h) = f(x0) +f0(x0)h+ 1 2f 00(x 0)h2+ 1 6f 000(x 0)h3+ 1 24f (4)(ξ 1)h4 f(x0−h) = f(x0) +f0(x0)h− 1 2f 00(x 0)h2 + 1 6f 000(x 0)h3− 1 24f (4)(ξ −1)h4
dimanax0−h < ξ−1 < x0 < ξ1 < x0+h. Dan bila kita jumlahkan kedua ekspansi
Taylor ini f(x0+h) +f(x0 −h) = 2f(x0) +f00(x0)h2+ 1 24[f (4)(ξ 1+) +f(4)(ξ−1+)]h4 Sederhanakan untukf00(x 0) didapat f00(x0) = 1 h2[f(x0 −h)−2f(x0) +f(x0 +h)]− h2 24[f (4)(ξ 1) +f(4)(ξ −1+)]. (3.37)
Teorema nilai tengah mengatakan bahwa untukf(4) ∈C[x
0−h, x0+h] maka
f(4)(ξ) = 1
2[f
(4)(ξ
1+) +f(4)(ξ−1+)].
Dengan demikian kita dapat menulis (3.37) sebagai f00(x0) = 1
h2[f(x0−h)−2f(x0) +f(x0+h)]−
h2
12f
(4)(ξ), (3.38)
untuk sebarang ξ ∈ (x0 −h, x0 +h). Pada akhirnya (3.36) dapat ditulis dengan
menggantif00(x
0) dengan persamaan (3.38) adalah
Z x2 x0 f(x)dx = 2hf(x1) + h3 3 ½ 1 h2[f(x0)−2f(x1) +f(x2)] −h 2 12[f (4)(ξ 2) ¾ + h 5 60f (4)(ξ 1) = h 3 3 [f(x0) + 4f(x1) +f(x2)]− h5 12 · 1 3f (4)(ξ 2)− 1 5f (4)(ξ 1) ¸
Dan ingat sekali lagi bahwa kita dapat mengganti ekspresi ξ1 dan ξ2 dengan ξ ∈
Aturan Simpson Rx2 x0 f(x)dx= h 3[f(x0) + 4f(x1) +f(x2)]− h 5 90f(4)(ξ) (3.39)
Secara definitif perbincangan order itu dapat ditafsirkan sebagai barometer keaku-ratan suatu teknik approksimasi. Semakin tinggi order itu berarti semakin luas ekspansi suku kesalahannya, akibatnya kesalahan pemenggalan semakin kecil. Se-bagaimana dijelaskan dalam Burden dan Faires definisi derajad keakuratan dapat dijelaskan sebagai berikut:
Definisi 3.5.1 (Derajad keakuratan atau presesi) Derajad keakuratan atau presesi dari formulasi kuadratur adalah bilangan bulat positif terbesarn sedemikian hingga formula itu eksak untuk xk, dimana k = 1,2, . . . , n (1997 : 89).
Dengan definisi (5.1.1) ini ditambah kenyataan besarnya order pada masing-masing aturan, maka aturan Trapesium dan Simpson masing-masing mempunyai derajad presesi satu dan tiga. Maka dapatlah disimpulkan bahwa aturan Simpson akan lebih cepat konvergen dibandingkan aturan Trapesium. Artinya aturan Simpson dimungkinkan lebih akurat pendekatannya dalam menghitung nilai integral untuk jumlah iterasi yang sama dari kedua aturan tersebut.
Latihan Tutorial 3
1. Buktikan bahwa||f||=maxa≤x≤b|f(x)| merupakan norm pada C[a, b]. 2. Jika A ∈ IRN×N,A = AT dan A definit positif matrik, yakni xTAx > 0
untuk seberang vektorx, maka buktikan bahwa||x||A= (xTAx)1
2 merupakan
norm padaIRN
3. Mana diantara berikut ini merupakan norm. (a) dalam IR2, ||x||= max{3|x
1|+ 2|x2|,2|x1|+ 3|x2|}.
(b) dalam IRN, ||a||= max0≤x≤1|
Pn
k=1akxk−1|.
4. Nyatakan teorema aproksimasi Weirstrass untuk f ∈ C[a, b]. Selanjutnya tunjukkan bahwa untuk ||g||p =
( Rb a w(x)|g(x)|pdx )1 p dimana 1 ≤ p ≤ ∞, dan diberikan ² > 0, maka ∃N = N(²) dan polinomial pN(x) sedemikian hingga
||f−pN|| ≤K1p²,
untuk sebarang konstantaK >0
5. Gunakan interpolasi polinomial Lagrange derajad satu, dua dan tiga untuk menentukan nilai aproksimasi dari masing-masing dibawah ini
(a) tentukan nilai dari f(8.4) bila diketahui f(8.1) = 16.94410, f(8.3) = 17.56492, f(8.6) = 18.50515 dan f(8.7) = 18.82091.
(b) tentukan nilai darif(0.25) bila diketahuif(0.1) =−0.62049958, f(0.2) = −0.28398668, f(0.3) = 0.00660095 dan f(0.4) = 0.24842440.
(c) tentukan nilai daricos 0.750 bila diketahui cos 0.698 = 0.7661,cos 0.733 = 0.7432,cos 0.768 = 0.7193 dan cos 0.803 = 0.6946.
(a) f(x) =e2xcos 3x, x 0 = 0, x1 = 0.3, x2 = 0.6 (b) f(x) = sin lnx, x0 = 2.0, x1 = 2.4, x2 = 2.6 (c) f(x) = cosx+ sinx, x0 = 0, x1 = 0.25, x2 = 0.5, x3 = 1.0 (d) f(x) =e2xcos 3x, x 0 = 0, x1 = 0.3, x2 = 0.6
7. Suatu data disajikan dalam tabel dibawah ini maka tentukan
x 0.0 0.2 0.4 0.6 0.8
f(x) 1.00000 1.22140 1.49182 1.82212 2.22554
(a) nilai dari f(0.05) dengan menggunakan NFDD (b) nilai dari f(0.65) dengan menggunakan NBDD
8. Polinomial berderajad empatp(x) memenuhi sifat44p(0) = 24,43p(0) = 6,
dan 42p(0) = 0 dimana 4p(x) = p(x+ 1)−p(x). Hitung 42p(10).
9. Perbincangan aproksimasi lebih luas banyak dikaitkan dengan interpolasi ter-hadap suatu fungsi f dengan fungsi aproksimasi p. Selanjutnya akurasi in-terpolasi itu diukur dari kedekatan antaraf dan p, secara matematis ditulis dengan||f−p||(dibaca : norm(f-p)). Sebutkan definisinorm ini, baik vek-tor ataupun matrik. Kemudian dengan pemahaman akan norm inisebutkan apa sebenarnya inti permasalahan (konsep masalah) dalam aproksimasi itu. Jika kita memilih fungsi aproksimasi p tentunya kita pilih fungsi yang terbaik. Dalam hal ini ada beberapa fungsi aproksimasi yang dapat digu-nakan untuk menginterpolasi fungsi f itu, sebutkan nama-nama fungsi aproksimasi tersebut. Salah satu fungsi aproksimasi yang fleksibel adalah splin kubik. Dengan data dibawah ini tentukan fungsi aproksimasi splin kubik untuk menginterpolasi dataf(xj) dimana xj = 0,1,2.