BAB I
BAB I
INTEGRAL TENTU
INTEGRAL TENTU
Tujuan Pembelajaran Umum:
Tujuan Pembelajaran Umum:
1.1. Mahasiswa Mahasiswa mampu mampu memahami memahami konsep konsep dasar dasar integral.integral. 2.
2. Mahasiswa mampu Mahasiswa mampu menggunakan menggunakan konsep dasar konsep dasar integral untuk integral untuk menyelesaikanmenyelesaikan masalah teknik sipil.
masalah teknik sipil.
Tujuan Pembelajaran Khusus:
Tujuan Pembelajaran Khusus:
1.1. Mahasiswa mampu Mahasiswa mampu menghitung integral menghitung integral tentu dari tentu dari fungsi-fungsi dasar fungsi-fungsi dasar dengandengan menggunakan sifat-sifat integral tentu.
menggunakan sifat-sifat integral tentu. 2.
2. Mahasiswa mampu Mahasiswa mampu menghitung menghitung integral fungsi integral fungsi trigonometri, fungsi trigonometri, fungsi pecahanpecahan rasional, dan pengintegralan parsial.
rasional, dan pengintegralan parsial. 3.
3. Mahasiswa mampu Mahasiswa mampu menyelesaikan masalah menyelesaikan masalah pada pada penerapan integral penerapan integral untuk luasuntuk luas daerah, volume benda putar, dan penentuan pusat massa.
daerah, volume benda putar, dan penentuan pusat massa.
1.1 Pendahuluan
1.1 Pendahuluan
Pembahasan integral pada bab ini mencakup sifat-sifat integral tentu, teknik pengintegralan, dan Pembahasan integral pada bab ini mencakup sifat-sifat integral tentu, teknik pengintegralan, dan penerapan integral dalam beberapa masalah teknik mesin.
penerapan integral dalam beberapa masalah teknik mesin. Pembahasan dilakukan hanya
Pembahasan dilakukan hanya pada penghitungan praktis bidang pada penghitungan praktis bidang teknik. teknik. Misalnya, pada subbabMisalnya, pada subbab tentang sifat-sifat integral tentu tidak dijelaskan dengan terinci persyaratan secara matematis dari tentang sifat-sifat integral tentu tidak dijelaskan dengan terinci persyaratan secara matematis dari sebuah sifat integral tentu, tetapi diasumsikan bahwa sifat ini selalu dapat digunakan.
sebuah sifat integral tentu, tetapi diasumsikan bahwa sifat ini selalu dapat digunakan.
1.2
1.2 Sifat-sifa
Sifat-sifat
t Integral
Integral Tentu
Tentu
Integral tentu adalahIntegral tentu adalah integral yang integral yang memiliki batas (atas memiliki batas (atas dan bawah). dan bawah). Sifat-sifat pada integralSifat-sifat pada integral tentu sangat membantu penghitungan integral sehingga langkah-langkah penghitungannya tentu sangat membantu penghitungan integral sehingga langkah-langkah penghitungannya menjadi lebih
menjadi lebih pendek. pendek. Sifat-sifat integral tentu ySifat-sifat integral tentu yang sering ang sering digunakan dalam digunakan dalam masalah-masalahmasalah-masalah teknik yaitu
teknik yaitu 1. Jika
1. Jika aa konstanta, berlakukonstanta, berlaku
∫∫
contoh 1contoh 1::
∫∫
2. Untuk2. Untuk
maupunmaupun
, berlaku, berlaku∫∫
∫∫
Contoh 23.
3. Sifat Sifat penambahan penambahan selang, selang, yaituyaitu
∫∫
∫∫
∫∫
bagaimanapun urutanbagaimanapun urutan a, ba, b, dan, dancc.. Contoh 3
Contoh 3::
∫∫ √ √
∫∫ √ √
∫∫ √ √
4. Pendiferensialan4. Pendiferensialan suatu integral suatu integral tentu. tentu. JikaJika x x variabel di dalam selangvariabel di dalam selang
, berlaku, berlaku
––
Contoh 4
Contoh 4::
**∫∫
+
+
..5.
5. Nilai Nilai rata-rata rata-rata di di dalam dalam integral. integral. JikaJika ccsebuah bilangan di dalam selangsebuah bilangan di dalam selang
,, berlakuberlaku
∫∫
dengandengan
adalah nilai rata-rata fungsiadalah nilai rata-rata fungsi
pada intervalpada interval
Contoh 5Contoh 5: : Nilai Nilai rata-rata rata-rata fungsifungsi
pada interval [-1, 2] adalahpada interval [-1, 2] adalah∫∫
++
6. 6. Definisi:Definisi: f(x)f(x) fungsi genap jika dan hanya jikafungsi genap jika dan hanya jika
.. f(x)f(x) fungsi ganjil jika dan hanya jikafungsi ganjil jika dan hanya jika
.. Teorema Simetri:Teorema Simetri: Jika
Jika f(x) f(x) fungsi fungsi genap, genap, berlakuberlaku
∫∫
∫∫
JikaJika f(x) f(x) fungsi ganjil, berlakufungsi ganjil, berlaku
∫∫
Contoh 6Contoh 6: Karena: Karena
merupakan fungsi genap, berlakumerupakan fungsi genap, berlaku
Contoh 7: Karena
merupakan fungsi ganjil, berlaku
7. Teorema Periodik:
Jika f(x) fungsi periodik dengan periode p, berlaku
∫
∫
Contoh 8: Karena
adalah fungsi periodik dengan periode
,
Latihan 1
Andaikan∫
∫
∫
∫
hitunglah! 1.∫
6.∫
∫
7.∫
∫
8.∫
∫
9.∫
∫
∫
10.∫
∫
Carilah
jika 11.∫
12.∫
13.∫ √
14.∫
15.∫
16.∫
√
17.∫
1.3 Teknik Pengintegralan
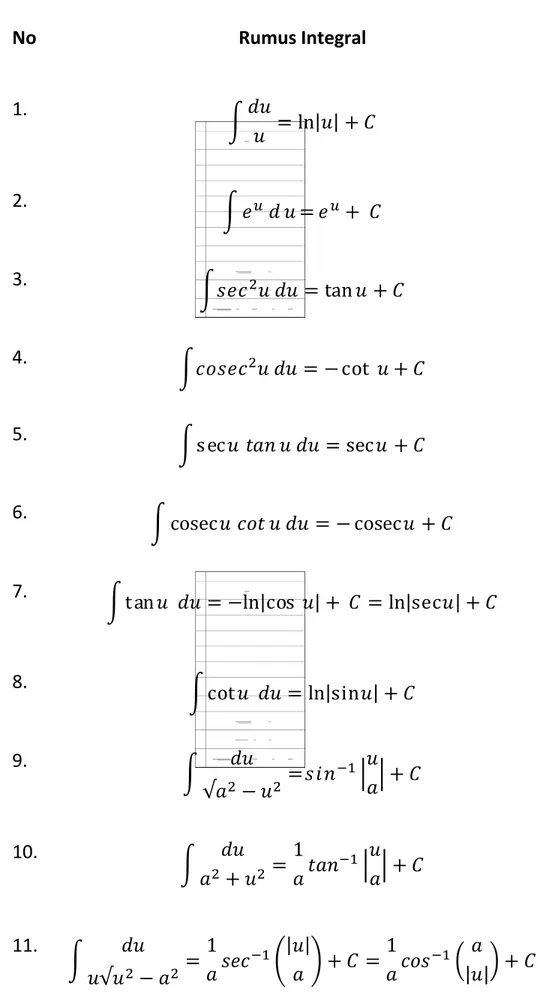
Tabel 1 Rumus-Rumus Integral
No Rumus Integral 1.
||
2.
3.
4.
5.
6.
7. | | ||
8. ||
9.
√
10.
11.
√
||
||
1.3.1 Penggunaan Rumus Dasar Integral
Contoh 1: Hitunglah∫
Misalnya
, sehingga
|| ||
Contoh 2:
Contoh 3:
√
Contoh 4:
Contoh 5:
√
||
||
1.3.2 Integral Fungsi Pecahan Rasional
Definisi:Sebuah fungsi rasional merupakan hasilbagi dua fungsi suku banyak, sehingga dapat ditulis sebagai
.Jika derajat p(x) kurang dari derajat q(x), fungsi ini disebut fungsi rasional sejati. Sebaliknya, jika derajat p(x) sama atau lebih dari derajat q(x), fungsi ini disebut fungsi rasional tidak sejati. Fungsi rasional tidak sejati selalu dapat ditulis sebagai jumlah fungsi suku banyak dan fungsi rasional sejati. Misalnya,
Fungsi suku banyak mudah diintegralkan, sedangkan fungsi rasional sejati sekalipun tidak selalu mudah, namun secara teori selalu dapat diintegralkan.
Contoh 1 (Faktor Linear Berbeda):
Fungsi integran (fungsi yang diintegralkan) dipecah menjadi fungsi-fungsi rasional dengan pembagi linear sebagai berikut
maka
. Dengan pemisalan
dan
maka diperoleh
Jadi,
||||
Contoh 2 (Faktor Linear Berulang):
Fungsi integran dipecah menjadi fungsi-fungsi rasional sebagai berikut
Jadi,
. Dengan pemisalan
dan
maka diperoleh
Jadi,
||
Contoh 3 (Faktor Kuadrat):Fungsi integran dipecah menjadi fungsi-fungsi rasional sebagai berikut
Jadi,
. Dengan pemisalan
dan
diperoleh
Jadi,
||
Contoh 4 (Faktor Kuadrat Berulang):
Fungsi integran dipecah menjadi fungsi-fungsi rasional sebagai berikut
Jadi,
. Dengan pemisalan
dan
diperoleh
Jadi,
Contoh 5 (Derajat pembilang sama atau lebih besar dari derajat penyebut):
Fungsi integran disederhanakan dengan melakukan pembagian terlebih dulu karena fungsi ini merupakan fungsi rasional tidak sejati (derajat polinom pembilang dan penyebutnya sama).
Hasil pembagiannya adalah
Jadi,1.3.3 Integral Parsial
Teknik pengintegralan yang terakhir dan jarang ditemui adalah pengintegralan parsial. Rumusnya adalah
∫ ∫
Contoh 1: Hitunglah∫
Misalnya
Menurut rumus (1.1)∫
∫
Contoh 2: Hitunglah∫
Misalnya
Menurut rumus (1.1)∫
∫
Untuk menyelesaikan
∫
, digunakan pengintegralan parsial lagi, yaitumisalnya
Menurut rumus (1.1)
∫
∫
. Jadi,
∫
Dengan demikian,
Latihan 2
Hitunglah!
√
⁄
∫
8.∫
9.∫
10.∫√
1.4 Penerapan Integral
Penerapan integral pada subbab ini mencakup luas daerah, volume benda putar, dan pusat massa. Penghitungan integral pada pusat massa memiliki kesamaan dengan luas daerah maupun volume benda putar. Oleh karena itu, pemahaman pada bahasan luas daerah akan membantu pada bahasan volume benda putar dan pusat massa.
1.4.1 Luas Daerah Bidang Rata
Terdapat dua cara menghitung luas daerah bidang rata ini, yaitu dengan mempartisi daerah secara vertikal atau secara horisontal. Jika mempartisi secara vertikal, bentuk integralnya dalam
dx dan mempartisi secara horisontal bentuk integralnya dy. Sebuah daerah yang dibatasi oleh kurva pertama di bagian atas dan kurva kedua di bagian bawah akan lebih mudah jika diselesaiakan dengan cara mempartisi secara vertikal. Demikian juga untuk daerah yang dibatasi oleh kurva pertama di sebelah kanan dan kurva kedua di sebelah kiri lebih mudah diselesaikan dengan cara mempartisi secara horisontal.
y
xi y = f ( x)
f(xi)-g(xi) y = g( x)
a b x
xi
G.1 Penghitungan Luas dengan Partisi Vertikal
Pada gambar G.1 diperlihatkan sebuah daerah yang dibatasi oleh kurva f ( x) di bagian atas dan kurva g( x) di bagian bawah, sedangkan sebelah kiri dibatasi oleh garis x = a dan sebelah kanan dibatasi oleh garis x = b. Karena kurva yang membatasinya di bagian atas dan bawah, digunakan cara yang pertama, yaitu mempartisi secara vertikal.
Daerah yang berwarna gelap adalah partisi ke-i. Misalnya daerah yang dibatasi oleh kurva f ( x), kurva g( x), garis x = a, dan garis x = b disebut L. Maka, luas partisi ke-i adalah
sehingga∑
∑
Jika
,
. Jadi,
∑
Contoh 1.Tentukan luas daerah bidang rata yang dibatasi oleh kurva dengan persamaan
, sumbu x, garis x = -1, dan garis x = 2!y x = 2 xi y=
-1 3 x -y xiG.2 Contoh Penggunaan Partisi Vertikal
Berdasarkan gambar G.2, penghitungan luas daerah digunakan cara pertama yaitu mempartisi secara vertikal. Penghitungannya dibagi dua bagian berdasarkan perbedaan rumus luas partisi, yaitu bagian pertama luas daerah pada nilai x antara
dan bagian kedua luas daerah pada
. Bagian pertama, luas partisinya adalah y x dan bagian kedua, luas partisinya adalah - y x. Jadi, luas seluruh daerah di atas adalah
Contoh 2. Tentukan luas daerah bidang rata yang dibatasi oleh kurva dengan persamaan
dan
!Sketsa daerah ini pada bidang xy, sebagai berikut
y y2=
xi y1 – y2 x y1=
G.3 Contoh Penggunaan Partisi Vertikal
Titik potong kedua kurva di titik (0, 0) dan titik (1, 1). Jadi, batas integralnya adalah 0 dan 1. Berdasarkan gambar G.3 penghitungan luas daerah digunakan cara pertama yaitu mempartisi secara vertikal, dengan 1uas partisi ( y1
–
y2) x sehingga luas seluruh daerah di atas adalah
Contoh 3. Tentukan luas daerah bidang rata yang dibatasi oleh kurva dengan persamaan
dan
! y
x1–
x2
yi xG.4 Contoh Penggunaan Partisi Horisontal
Titik potong kedua kurva di titik (1/4, -1) dan titik (4, 4). Pada gambar G.4, penghitungan luas daerah digunakan cara kedua yaitu mempartisi secara horisontal sehingga batas integralnya adalah -1 dan 4. Luas partisinya adalah ( x1
–
x2) y sehingga luas seluruh daerah di atas adalah
Latihan 3.
Hitunglah luas daerah yang dibatasi oleh kurva-kurva di bawah ini! 1.
,
,
, dan
. 2.
, dan
3.
, dan sumbu x 4.
, dan
.7.
||
dan
1.4.2 Volume Benda Putar
Terdapat tiga bagian bahasan dalam subbab ini, yaitu metode cakram, metode cincin, dan metode kulit tabung. Seperti ketika menghitung luas daerah, menghitung volume juga menggunakan pendekatan partisi. Untuk bagian pertama dan kedua digunakan pendekatan rumus volume tabung atau cakram sebagai berikut.
∑̅
̅
̅
adalah luas penampang benda pada partisi ke-i dan
adalah lebar partisi ke-i. Jika sebelah kiri dibatasi oleh garis x = a dan sebelah kanan dibatasi oleh garis x = b dan
, diperoleh
∑̅
Rumus di atas diperoleh jika mempartisi secara vertikal. Namun jika mempartisi secara horisontal maka bentuk integralnya dalam dy.
a. Metode Cakram Contoh 1.
Tentukan volume benda putar yang dibentuk oleh daerah R yang dibatasi oleh kurva
√
, sumbu x, dan garis x =4 jika R diputar mengelilingi sumbu x !Sketsa daerah R pada bidang xy, sebagai berikut y
xi
√
0 x 4 x
Daerah R diputar mengelilingi sumbu x, diperoleh benda putar
x
√
0 4 x
x
G.6 Daerah R diputar mengelilingi sumbu x
Gambar G.5 menunjukan daerah dengan sebuah jalur pemotongan (partisi). Jika daerah ini diputar mengelilingi sumbu x, daerah ini membentuk sebuah benda putar (gambar G.6) dan jalur ini membentuk sebuah cakram yang volumenya didekati (diaproksimasi) oleh volume tabung dengan tinggi tabung
dan jari-jari alas tabung√
. Jadi, volume tabung ini adalah
(√ )
Jika volume tabung-tabung ini dijumlahkan dan diintegralkan, diperoleh volume benda putar
Contoh 2.Tentukan volume benda putar yang dibentuk oleh daerah D yang dibatasi oleh kurva
, sumbu y, dan garis y = 3diputar mengelilingi sumbu y !y y = x3 3
y y 0 x G.7 Daerah Dx
y
y
x
G.8 Daerah D diputar mengelilingi sumbu y
Dalam kasus ini, lebih mudah y digunakan sebagai variabel pengintegralan atau mempartisi benda secara horisontal. Volume partisi adalah volume tabung dengan tinggi
dan jari-jari alas tabung
. Jadi, volume tabung ini adalah(
)
maka volume benda putar yang dibentuk oleh daerah D adalah
[
]
√
b. Metode Cincin
Metode ini digunakan jika partisi volumenya berupa cakram yang di tengahnya terdapat lubang atau berupa cincin.
Contoh 3.
Tentukan volume benda putar yang dibentuk oleh daerah A yang dibatasi oleh kurva
, dan
diputar mengelilingi sumbu x!y y = x2
4
√
x
x x2
0 x
G.9 Daerah A
x
G.10 Daerah A diputar mengelilingi sumbu x
Seperti sebelumnya, dalam proses penghitungan volume benda putar ini digunakan metode potong menjadi jalur-jalur, kemudian diaproksimasi dan diintegralkan. Volume cincin dengan
tebal x, jari-jari luar
√
dan jari-jari dalam
adalah*(√ )
+
maka volume benda putar yang dibentuk oleh daerah A dengan sumbu putar sumbu x adalah
c. Metode Kulit TabungUntuk beberapa kondisi, metode ini lebih mudah digunakan dari pada metode cakram atau metode cincin. Sebuah kulit tabung adalah sebuah benda yang dibatasi oleh dua tabung
lingkaran tegak yang sumbu simetrinya berimpit. Jika jari-jari tabung dalam adalah r 1 dan
jari- jari tabung dalam adalah r 2 , sedangkan tinggi tabung hmaka volume tabung adalah
Jadi, V = 2. (rata-rata jari-jari).(tinggi).(tebal) = 2rhr.
Contoh 4.Tentukan volume benda putar yang dibentuk oleh daerah B yang dibatasi oleh kurva
√
, sumbu x, garis x= 1, dan garis x= 4 diputar mengelilingi sumbu y!y y= f(x) x y x x G.11 Daerah B
Tebal kulit tabung yang dihasilkan setelah daerah B diputar adalah x, jari-jarinya x, sedangkan
tingginya y. Karena y = f(x), diperoleh volume kulit tabung yaitu
Jadi, volume benda putar yang dibentuk oleh daerah B dengan sumbu putar sumbu y adalah
jumlah semua kulit-kulit tabung yang terbentuk dari x = 1 hingga x = 4.
√
[
]
Latihan 4
A. Hitunglah volume benda putar yang dibentuk dari daerah yang dibatasi oleh kurva-kurva yang diberikan di bawah ini diputar mengelilingi sumbu x!
1.
, sumbu x, sumbu y, dan garis
.3.
, sumbu x, dan sumbu y4.
, sumbu x, dan sumbu y5.
√
,
antara garis
, dan
B. Hitunglah volume benda putar yang dibentuk dari daerah yang dibatasi oleh kurva-kurva yang diberikan di bawah ini diputar mengelilingi sumbu y!
1.
, sumbu x, dan sumbu y2.
, sumbu x, dan sumbu y3.
,
, dan
4.
,
,
dan
5.
dan
C. Hitunglah volume benda putar yang dibentuk dari daerah yang dibatasi oleh kurva-kurva yang diberikan di bawah ini diputar mengelilingi sumbu yang diberikan!
1.
,
,
dan
, mengelilingi sumbu y2.
, x= 0, y = 0 dan mengelilingi sumbu y3.
√
, x= 4, y= 0 dan mengelilingi garis x = 44.
,
, dan
, mengelilingi sumbu x5.
,
,
dan
mengelilingi garis y = 31.4.3 Pusat Massa (
Centroid
)
Pusat massa pada sebuah garis lurus adalah titik tengah garis lurus tersebut, sedangkan pada bidang rata beraturan seperti segitiga, persegi, maupun jajaran genjang adalah titik tengah bidang (untuk persegi dan jajaran genjang merupakan titik perpotongan diagonal-diagonalnya). Secara khusus untuk lingkaran, pusat massanya adalah titik pusat lingkaran.
Penentuan pusat massa seperti di atas adalah dengan asumsi garis atau bidang ini memiliki massa yang homogen. Jadi, massa tidak menentukan atau memengaruhi posisi pusat massa. Dengan
kata lain, garis atau bidang yang memiliki massa yang homogen, pusat massanya berimpit dengan pusat geometrinya (centroid -nya).
Pembahasan pusat massa pada subbab ini dikhususkan untuk bidang yang memiliki massa yang homogen. Karena bidang-bidang yang beraturan tidak membutuhkan integral untuk menentukan pusat massanya, pembahasan hanya untuk bidang yang tidak beraturan.
Lamina homogen adalah lempeng tipis yang rata dengan kepadatan massa, , konstan. Jadi, lamina homogen merupakan bidang rata yang memiliki massa yang homogen. Perhatikan ilustrasi dari sebuah lamina pada gambar berikut ini!
y y = f ( x) xi y = g( x) • ½( f(xi) + g(xi)) x a b xi
G.12 Penentuan Pusat Massa dengan Partisi Vertikal
Titik hitam di tengah-tengah partisi adalah pusat massa dari partisi. Pusat massa partisi ke- i adalah ( xi , ½( f(xi) + g(xi))). Pusat massa lamina adalah jumlah semua momen dari partisi dibagi massa lamina. Misalnya m adalah massa sebuah partisi maka m adalah massa lamina. Karena
, diperoleh
Misalnya M x dan M y berturut-turut adalah momen sebuah partisi terhadap sumbu x dan momen sebuah partisi terhadap sumbu ymaka
Maka M x dan M y adalah momen lamina terhadap sumbu x dan momen lamina terhadap sumbu y,
yaitu
Jadi, pusat massa lamina adalah̅
dengan̅
Karena konstan, dapat diabaikan dalam penghitungan.
Contoh:Tentukan pusat massa dari daerah yang dibatasi oleh kurva
dan√
! Sketsa daerah ini pada bidang xy, sebagai berikuty
y2=
xi y1=
√
x
G.13 Contoh Penentuan Pusat Massa dengan Partisi Vertikal Dari gambar G.13 diperoleh
(√
)
. Jadi,̅ ∫ (√
∫ (√
)
)
dan
∫
(√
∫ (√
)(√
)
)
Latihan 5.
Tentukan pusat massa dari daerah yang dibatasi oleh kurva
1.
,
,
,
. 2.
,√
, dan
.3.