PENYELESAIAN MASALAH PENJADWALAN MATA PELAJARAN SEKOLAH MENENGAH PERTAMA MENGGUNAKAN PEMROGRAMAN LINEAR INTEGER MAHNURI

PENYELESAIAN MASALAH PENJADWALAN MATA PELAJARAN

SEKOLAH MENENGAH PERTAMA MENGGUNAKAN

PEMROGRAMAN LINEAR INTEGER

MAHNURI

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM

INSTITUT PERTANIAN BOGOR

BOGOR

2009

ABSTRAK

MAHNURI. Penyelesaian Masalah Penjadwalan Mata Pelajaran Sekolah Menengah Pertama Menggunakan Pemrogramam Linear Integer. Dibimbing Oleh TONI BAKHTIAR dan PRAPTO TRI SUPRIYO.

Jadwal mata pelajaran pada Sekolah Menengah Pertama merupakan bagian yang sangat penting. Tujuan penyusunan jadwal adalah untuk menempatkan mata pelajaran dalam penjadwalan sesuai dengan klasifikasinya dan memenuhi preferensi guru dalam mengajar serta memenuhi kendala lainnya.

Dalam karya ilmiah ini, preferensi dan kendala diakomodasi oleh koefisien bobot yang diberikan terhadap mata pelajaran dan guru. Masalah penjadwalan di sini diformulasikan sebagai masalah minimisasi. Pemberian kerangka bobot yang kecil terhadap mata pelajaran dan guru menunjukkan periode waktu yang diinginkan dalam penjadwalan, begitu juga sebaliknya.

Masalah penjadwalan dalam karya ilmiah ini dimodelkan sebagai masalah pemrograman linear integer (Integer Linear Programing/ILP) dan untuk menyelesaiakan masalah penjadwalan di sini digunakan software Lingo 8.0. Hasil dari penelitian ini adalah jadwal mata pelajaran lengkap untuk Sekolah Menengah Pertama “Masa Depan”.

ABSTRACT

MAHNURI. Courses Scheduling Problem at Junior High School with Integer Linear Programming. Supervised by TONI BAKHTIAR and PRAPTO TRI SUPRIYO.

The course scheduling at junior high school is an important task. The purpose of course scheduling is to allocate courses according to their classification and to satisfy teachers preferences on teaching and other constraints.

In this paper, the preferences and constraints are accommodated by means of coefficients as weights attached into courses as well as teachers. The problem is formulated as a minimization problem. The preferences and constraints with smaller weights framework indicate more preffered time periods, and vice versa.

The scheduling problem in this paper is modeled in term of integer linear programming (ILP) and Lingo 8.0 is used to solve the problem. The result of the research is a fully defined schedule for “Masa Depan” junior high school.

PENYELESAIAN MASALAH PENJADWALAN MATA PELAJARAN

SEKOLAH MENENGAH PERTAMA MENGGUNAKAN

PEMROGRAMAN LINEAR INTEGER

Skripsi

Sebagai salah satu syarat untuk memperoleh gelar Sarjana Sains pada Fakultas Matematika dan Ilmu Pengetahuan Alam

Institut Pertanian Bogor

Oleh :

MAHNURI

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM

INSTITUT PERTANIAN BOGOR

BOGOR

2009

Judul

: Penyelesaian Masalah Penjadwalan Mata Pelajaran Sekolah Menengah

Pertama menggunakan Pemrograman Linear Integer

Nama : Mahnuri

NIM

: G54104064

Menyetujui,

Mengetahui,

Dekan Fakultas Matematika dan Ilmu Pengetahuan Alam

Institut Pertanian Bogor

Dr. Drh. Hasim, DEA.

NIP 19610328 198601 1 002

Tanggal Lulus :

Pembimbing I

Dr. Toni Bakhtiar, M.Sc.

NIP 19720627 199702 1 002

Pembimbing II

Drs. Prapto Tri Supriyo, M.Kom.

NIP 19630715 199002 1 002

KATA PENGANTAR

Puji dan syukur penulis panjatkan ke hadirat Allah Azza wa Jalla atas segala nikmat, karunia, izin, dan pertolongan-NYA sehingga penulisan skripsi ini berhasil diselesaikan. Shalawat serta salam tercurah kepada nabi Muhammad Shalallohu‘alaihi wasalam sebagai suri tauladan terbaik bagi umatnya hingga akhir zaman. Tema yang dipilih adalah Riset Operasi dengan judul Penyelesaian Masalah Penjadwalan Mata Pelajaran Sekolah Menengah Pertama Menggunakan Pemrogramam Linear Integer. Skripsi ini merupakan syarat untuk menyelesaikan studi pada Departemen Matematika, Fakultas Matematika dan Ilmu Pengetahuan Alam, Institut Pertanian Bogor.

Terima kasih penulis ucapkan kepada :

1. Bapak Dr. Toni Bakhtiar, M.Sc. dan Bapak Drs. Prapto Tri Supriyo, M.Kom. selaku dosen pembimbing, atas segala kesabaran dan masukannya selama membimbing penulis. Tak lupa kepada Bapak Drs. Siswandi, M.Si. selaku penguji, saran dan kritikan beliau sangat berharga buat penulis.

2. Ibunda Sinah dan bapak Kamso atas doa, nasehat, dan pengorbanan yang telah diberikan sampai saat ini yang tidak mungkin penulis balas dengan kebaikan apapun. Mbah (Alm.) Martawireja dan Mbok Sarkem atas kasih sayang dan bimbangan yang sangat berharga bagi kehidupan penulis. Adiku Siska dan Firman atas kasih sayang dan dukungan yang telah diberikan.

3. Teman-teman mahasiswa matematika angkatan 41: Udin, Grit, Aji, Fred, Racil, Idris, Triyadi, Yaya, Deni, Chubby, Mimin, Fariz, Zali, Mazid, Iboy, Amin, Dika, Racum, Yos, Mora, Hendri, Fitrie, Endhit, Sita, Rita, Diah, Dian, Liay, Sifa, Mukti, penny, Uwie, Ani, Liam, darwisah, Jannah, Ami, Intan, Enyon, Echi, Ria, Enny, Roma, Titis, Tia, Febrina., Ayu, Ika, Mahar, Eli, Rina Z, Eva, Roro, Nidia, atas segenap dukungan, suka-duka dan kebahagiaan selama penulis menempuh studi di Departemen Matematika IPB.

4. Sumar”dD”Wati atas dukungan dan bantuan yang telah diberikan. Teh Mayang atas bantuan yang telah diberikan. Warno, Sapto, dan Iput selaku pembahas, semoga cepat menyusul. Danar, Jaukhul, dan Sai atas persahabatan dan suka duka yang telah kita lalui bersama selama kurang lebih tiga tahun.

5. Teman-temanku di Wisma At-Tauhid : Hasan, Angga, Dimas, Ari, Abrar, Huri, Akhid, Yusuf, Dian, dan Mas Eko; di Wisma Al-Ghuroba : Rusmanto, Iksani, Fauzi, Aris, Joko, ngaToif, Risma, Irsal, dan Sarwanto; di Wisma Al-Furqon : Frendy, Bombai, Sugara, Mas Anri, Mas Wiji, dan Rifki; di wisma Al-Izzah : Auriza, dan Abdul atas persahabatan yang telah kalian berikan. Semoga tetap terjalin dan senantiasa dalam perlindunga-NYA.

6. Keluarga besar GUMATIKA periode 2006-2008 atas berbagai pengalaman yang kita lalui bersama.

7. Juga pihak-pihak lain yang telah membantu penyusunan skripsi ini, yang tidak dapat disebutkan satu persatu. Semoga Allah Azza wa Jalla mengganjar kalian dengan kebaikan. Penulis menyadari bahwa dalam tulisan ini masih terdapat kekurangan dan jauh dari kesempurnaan, oleh karena itu penulis mengharapkan kritik dan saran yang membangun dari pembaca. Semoga tulisan ini dapat bermanfaat.

Bogor, Juni 2009

RIWAYAT HIDUP

Penulis dilahirkan di Bogor pada tanggal 23 Mei 1986 dari pasangan Kamso dan Sinah. Penulis merupakan anak pertama dari tiga bersaudara.

Penulis memulai pendidikan di Sekolah Dasar Negeri 1 Karanganyar pada tahun 1992-1998. Selanjutnya di Sekolah Menengah Pertama Negeri 1 Jatilawang pada tahun 1998-2001. Kemudian penulis melanjutkan pendidikan di Sekolah Menengah Umum Negeri 5 Purwokerto pada tahun 2001-2004. Pada tahun 2004-2009 penulis melanjutkan pendidikan di Institut Pertanian Bogor Fakultas Matematika dan Ilmu Pengetahuan Alam Departemen Matematika.

Selama mengikuti kegiatan perkuliahan penulis aktif dalam HIMPRO (Himpunan Profesi) kemahasiswaan. Penulis aktif di HIMPRO GUMATIKA (Himpunan Profesi Gugus Mahasiswa Matematika) pada tahun 2005-2007. Penulis juga aktif dalam kegiatan kemahasiswaan diantaranya adalah Matematika Ria pada tahun 2006 (Sekretaris), Try Out SPMB Nasional pada tahun 2007 (Ketua), Matematika Ria pada tahun 2007 (Ketua).

Pada tahun 2006-2007 penulis menjadi asisten tutorial mata kuliah Pengantar Matematika dan Kalkulus.

DAFTAR ISI

Halaman

DAFTAR TABEL ... viii

DAFTAR GAMBAR ... viii

DAFTAR LAMPIRAN ... viii

1 PENDAHULUAN Latar Belakang ... 1

Tujuan ... 1

2 LANDASAN TEORI Fungsi Linear dan Pertidaksamaan Linear ... 1

Pemrograman Linear ... 2

Pemrograman Integer ... 3

Metode Branch-and-Bound ... 3

3 DESKRIPSI DAN FORMULASI MASALAH ... 7

4 STUDI KASUS DAN PENYELESAIAN ... 11

5 SIMPULAN DAN SARAN Simpulan ... 16

Saran ... 16

DAFTAR PUSTAKA ... 16

DAFTAR TABEL

Halaman

1 Daftar mata pelajaran untuk masing-masing kelas beserta periode waktu

yang dibutuhkan ... 11

2 Distribusi KBM dengan 10 kelas ... 11

3 Daftar periode waktu KBM ... 12

4 Hari guru mengajar ... 12

5 Permintaan periode waktu mengajar ... 13

6 Jadwal KBM SMP Masa Depan untuk setiap kelas ... 18

7 Jadwal mengajar guru untuk setiap hari dan setiap periode waktunya ... 19

DAFTAR GAMBAR

Halaman 1 Daerah fisibel untuk LP-relaksasi dari masalah ILP (6) ... 5

2 Daerah fisibel untuk Subproblem 2 dan Subproblem 3 ... 5

3 Seluruh pencabangan pada metode branch and bound untuk menentukan solusi optimal dari ILP ... 6

4 Bobot untuk mata pelajaran inti ... 8

5 Bobot untuk mata pelajaran biasa ... 8

6 Bobot untuk guru-guru yang mengajarkan mata pelajaran inti dan mata pelajaran biasa ... 8

7 Bobot untuk mata pelajaran yang diharapkan diajarkan di awal periode waktu ... 13

8 Bobot untuk mata pelajaran yang diharapkan diajarkan di akhir periode waktu ... 13

9 Bobot untuk mata pelajaran yang diharapkan diajarkan di periode waktu awal dan periode waktu akhir ... 13

10 Bobot untuk mata pelajaran yang diharapkan diajarkan di periode waktu pertengahan ... 14

11 Bobot untuk guru dengan preferensi mengajar di akhir periode waktu, kalau tidak terpenuhi menginginkan di awal periode waktu ... 14

12 Bobot untuk guru dengan preferensi mengajar di awal periode waktu, kalau tidak terpenuhi menginginkan di akhir periode waktu ... 14

13 Bobot untuk guru dengan preferensi mengajar di awal dan di akhir periode waktu ... 14

DAFTAR LAMPIRAN

Halaman 1 Jadwal Kegiatan Belajar Mengajar (KBM) yang Terbentuk untuk SMP Masa Depan ... 18

2 Syntax Program LINGO 8.0 untuk Menyelesaikan Masalah Pemrograman Linear dengan Metode Branch-and-Bound Beserta Hasil yang Diperoleh ... 24

3 Syntax dan Hasil Komputasi Program LINGO 8.0 untuk Masalah Penjadwalan Sekolah Menengah Masa Depan ... 27

I PENDAHULUAN

Latar Belakang

Sekolah merupakan salah satu bagian penting dalam pendidikan. Oleh karena itu sekolah harus memperhatikan bagian-bagian yang ada di dalamnya. Salah satu bagian penting yang tidak dapat dipisahkan dalam sekolah adalah masalah penjadwalan mata pelajaran. Oleh sebab itu perlu dibuat sebuah penjadwalan mata pelajaran berkualitas yang memuaskan guru, murid dan sekolah. Salah satu sekolah yang mempunyai masalah penjadwalan mata pelajaran adalah Sekolah Menengah Pertama (SMP).

Pada setiap SMP mata pelajaran yang diajarkan sesuai dengan kurikulum yang berlaku. Mata pelajaran yang diajarkan ada yang nantinya diujikan dalam Ujian Akhir Nasional (UAN), untuk selanjutnya kita sebut sebagai mata pelajaran inti (primary) dan ada pula mata pelajaran yang tidak diujikan dalam UAN, melainkan hanya diujikan oleh sekolah masing-masing atau biasa disebut Ujian Akhir Sekolah (UAS), untuk selanjutnya kita sebut sebagai mata pelajaran biasa (nonprimary). Begitu pula dengan gurunya, ada yang mengajar mata pelajaran inti, ataupun mata pelajaran biasa, namun ada pula yang mengajar keduanya. Setiap guru mempunyai

preferensi hari dan periode waktu dalam memberikan mata pelajaran yang akan diajarkannya. Atas dasar perbedaan di atas, masalah penjadwalan mata pelajaran akan dibuat.

Masalah penjadwalan mata pelajaran di sini dapat dimodelkan sebagai masalah pemrograman linear integer (Integer Linear Programing/ILP). ILP adalah masalah optimisasi dengan fungsi objektif dan kendala yang linear serta variabel integer.

Karya ilmiah ini merupakan rekonstruksi dari karya ilmiah T Birbas, S Daskalaki, dan E Housos (1997) yang berjudul “Timetabling for Greek high schools”. Dalam karya ilmiah ini akan diperlihatkan formulasi dan penyelesaian masalah penjadwalan mata pelajaran menggunakan bantuan software LINGO 8.0.

Tujuan

Tujuan penulisan karya ilmiah ini adalah menunjukan peranan pemrograman linear integer dalam menentukan penjadwalan mata pelajaran Sekolah Menengah Pertama yang memenuhi preferensi mata pelajaran dan preferensi guru.

II LANDASAN TEORI

Dalam menyelesaikan masalah penjadwalan mata pelajaran pada karya ilmiah ini digunakan suatu model ILP untuk proses penyelesaiannya. Supaya lebih memahami dalam pembuatan model ILP dan proses penyelesaiannya, beberapa definisi dan teori yang terkait dengan ILP perlu dijelaskan terlebih dahulu. Berikut ini akan dijelaskan definisi dan teori yang digunakan

Fungsi Linear dan Pertidaksamaan Linear Fungsi linear dan pertidaksamaan linear merupakan salah satu konsep dasar yang harus dipahami terkait dengan konsep pemrograman linear.

Definisi 1 (Fungsi Linear)

Suatu fungsi f(x1,x2,...,xn) dalam variabel-variabel x x₁, ₂,...,x adalah suatu _n fungsi linear jika dan hanya jika untuk suatu

himpunan konstanta c c₁, ₂,...,c , dapat ditulis _n sebagai; . ... ) ,..., , (x1 x2 xn c1x1 c2x2 cnxn f = + + + (Winston, 2004) Sebagai gambaran, f x x( ,_{1 2})=3x₁+5x₂ merupakan fungsi linear, sementara

2 3

1 2 1 2

( , )

f x x =x x bukan fungsi linear. Definisi 2 (Pertidaksamaan Linear)

Untuk sembarang fungsi linear )

,..., , (x1 x2 xn

f dan sembarang bilangan b , pertidaksamaan f(x1,x2,...,xn)≤b dan b x x x f( 1, 2,..., n)≥ adalah pertidaksamaan linear. (Winston, 2004)

Pemrograman Linear

Pemrograman linear (PL) adalah suatu masalah optimisasi yang memenuhi ketentuan-ketentuan sebagai berikut.

a) Tujuan masalah tersebut adalah memaksimumkan atau meminimumkan suatu fungsi linear dari sejumlah variabel keputusan. Fungsi yang akan dimaksimumkan atau diminimumkan ini disebut fungsi objektif.

b) Nilai variabel-variabel keputusannya harus memenuhi suatu himpunan kendala. Setiap kendala harus berupa persamaan linear atau pertidaksamaan linear.

c) Ada pembatasan tanda untuk setiap variabel dalam masalah ini. Untuk sembarang variabel x_i, pembatasan tanda menentukan x_i harus taknegatif (xi ≥0).

(Winston, 2004) Suatu PL mempunyai bentuk standar seperti yang didefinisikan sebagai berikut.

Definisi 3 (Bentuk Standar PL)

Suatu pemrograman linear didefinisikan mempunyai bentuk standar sebagai berikut: min z = cTx

terhadap Ax = b

x≥ 0. (1) di mana b

≥

0. Dengan x dan c berupa vektor berukuran n, vektor b berukuran m, sedangkan A berupa matriks berukuran m x n yang disebut juga matriks kendala.

(Nash & Sofer, 1996) Solusi Pemrograman Linear

Suatu masalah PL dapat diselesaikan dalam berbagai teknik, salah satunya adalah metode simpleks. Metode ini dapat menghasilkan suatu solusi optimal bagi masalah PL dan telah dikembangkan oleh Dantzig sejak tahun 1947, dan dalam perkembangannya merupakan metode yang paling umum digunakan untuk menyelesaikan PL. Metode ini berupa metode iteratif untuk menyelesaikan PL berbentuk standar.

Pada masalah PL (1), vektor x yang memenuhi kendala Ax=b disebut solusi PL (1). Misalkan matriks A dapat dinyatakan sebagai A=

(

B N

)

, dengan B adalah matriks berukuran m × m yang elemennya berupa koefisien variabel basis dan N merupakan matriks berukuran m× −(n m) yang elemen-elemennya berupa koefisien variabel nonbasis pada matriks kendala.

Dalam hal ini matriks B disebut matriks basis untuk PL (1).

Misalkan x dapat dinyatakan sebagai vektor =    B N x x

x , dengan x adalah vektor B variabel basis dan x adalah vektor variabel _N nonbasis, maka Ax=b dapat dinyatakan sebagai :

(

)

  =     B N x Ax B N x . =Bx + NxB N =b (2) Karena matriks B adalah matriks taksingular, maka B memiliki invers, sehingga dari (2)

B

x dapat dinyatakan sebagai:

- .

= -1 -1

B N

x B b B Nx (3) Definisi 4 (Solusi Basis)

Solusi dari suatu masalah PL disebut solusi basis jika memenuhi syarat berikut: a) Solusi tersebut memenuhi kendala pada

masalah PL.

b) Kolom-kolom dari matriks kendala yang berpadanan dengan komponen taknol dari solusi tersebut adalah bebas linear.

(Nash & Sofer, 1996) Definisi 5 (Solusi Fisibel Basis)

Vektor x disebut solusi fisibel basis jika x merupakan solusi basis dan x≥0.

(Nash & Sofer, 1996) Ilustrasi solusi basis dan solusi fisibel basis diberikan dalam Contoh 1.

Contoh 1

Misalkan diberikan masalah LP sebagai berikut 1 2 1 2 3 1 2 4 1 5 min -3 - 2 terhadap -2 3 - 2 8 5 z x x x x x x x x x x = + + = + + = + = 0 , 1, ..., 5 i x ≥ i= . (4) Dari masalah LP (4) diperoleh:

2 1 1 0 0 3 1 2 0 1 0 , 8 1 0 0 0 1 5 −         = −_{ } =_{ }         A b . Misalkan dipilih

(

x3 x4 x5

)

dan

(

x1 x2

)

, = T = T B N x x

1 0 0 0 1 0 0 0 1     =_{ }     B .

Dengan menggunakan matriks basis di atas didapatkan

(

0 0

)

, −

(

3 8 5

)

. = T = 1 = T N B x x B b (5) Solusi (5) merupakan solusi basis, karena memenuhi kendala pada LP (4) dan kolom-kolom pada matriks kendala yang berpadanan dengan komponen taknol dari (5), yaitu B

bebas linear (kolom yang satu bukan merupakan kelipatan dari kolom yang lain). Solusi (5) juga merupakan solusi fisibel basis, karena nilai-nilai variabelnya lebih dari atau sama dengan nol.

Hal yang juga penting dalam konsep pemrograman linear untuk model ini adalah daerah fisibel dan solusi optimal yang didefinisikan sebagai berikut.

Definisi 6 (Daerah Fisibel)

Daerah fisibel untuk suatu LP adalah himpunan semua titik yang memenuhi semua kendala dan pembatasan tanda pada LP tersebut.

(Winston, 2004) Definisi 7 (Solusi Optimal)

Untuk masalah maksimisasi, solusi optimal suatu LP adalah suatu titik dalam daerah fisibel dengan nilai fungsi objektif terbesar. Untuk masalah minimisasi, solusi optimal suatu LP adalah suatu titik dalam daerah fisibel dengan nilai fungsi objektif terkecil.

(Winston, 2004) Pemrograman Integer

Pemrograman integer (Integer Programing/IP) adalah suatu model pemrograman linear dengan variabel yang digunakan berupa bilangan bulat (integer). Jika semua variabel harus berupa integer, maka masalah tersebut dinamakan pure integer programming. Jika hanya sebagian yang harus berupa integer, maka disebut mixed integer programming. IP dengan semua variabelnya harus bernilai 0 atau 1 disebut 0-1 IP.

(Garfinkel & Nemhauser, 1972) Definisi 8 (Linear Programming Relaksasi)

Linear Programming relaksasi atau sering disebut LP-relaksasi merupakan suatu pemrograman linear yang diperoleh dari suatu

IP dengan menghilangkan kendala integer atau kendala 0-1 pada setiap variabelnya.

Untuk masalah maksimisasi, nilai optimal fungsi objektif LP-relaksasi lebih besar atau sama dengan nilai optimal fungsi objektif IP, sedangkan untuk masalah minimisasi, nilai optimal fungsi objektif LP-relaksasi lebih kecil atau sama dengan nilai optimal fungsi objektif IP.

(Winston, 1995) Metode Branch-and-Bound

Dalam penulisan karya ilmiah ini, untuk memperoleh solusi optimal dari masalah ILP digunakan software LINGO 8.0 yaitu sebuah program yang didesain untuk aplikasi riset operasi dalam membangun dan menentukan solusi model linear, nonlinear, dan optimisasi integer dengan salah satu prinsip pemecahannya berdasarkan metode branch and bound.

Branch and bound adalah algoritma umum untuk mencari solusi optimal dari berbagai masalah optimasi. Metode ini pertama kali diperkenalkan oleh A.H. Land dan A.G. Doig pada tahun 1960.

Prinsip dasar metode ini adalah memecah daerah fisibel suatu masalah LP-relaksasi dengan membuat subproblem-subproblem. Ada dua konsep dasar dalam algoritme branch and bound.

1. Branching

Branching adalah proses membagi-bagi permasalahan menjadi subproblem-subproblem yang mungkin mengarah ke solusi.

2. Bounding

Bounding adalah suatu proses untuk mencari/menghitung batas atas (dalam masalah minimisasi) dan batas bawah (dalam masalah maksimisasi) untuk solusi optimal pada subproblem yang mengarah ke solusi, di sini dilakukan LP-relaksasi pada ILP.

Metode branch and bound diawali dengan menyelesaikan LP-relaksasi dari suatu masalah integer programming. Jika semua nilai variabel keputusan solusi optimal sudah berupa integer, maka solusi tersebut merupakan solusi optimal ILP. Jika tidak, dilakukan pencabangan dan penambahan batasan pada LP-relaksasinya kemudian diselesaikan.

Winston (2004) menyebutkan bahwa nilai fungsi objektif optimal untuk ILP ≤ nilai fungsi objektif optimal untuk LP-relaksasi (masalah maksimisasi), sehingga nilai fungsi objektif optimal LP-relaksasi merupakan batas

atas bagi nilai fungsi objektif optimal untuk masalah ILP. Diungkapkan pula oleh Winston (2004) bahwa nilai fungsi objektif optimal untuk suatu kandidat solusi merupakan batas bawah nilai fungsi objektif optimal untuk masalah ILP asalnya. Suatu kandidat solusi diperoleh jika solusi dari suatu subproblem sudah memenuhi kendala integer pada masalah ILP, artinya semua variabelnya sudah bernilai integer.

Berikut ini adalah langkah-langkah penyelesaian suatu masalah maksimisasi dengan metode branch-and-bound.

1)Langkah 0

Didefinisikan z sebagai batas bawah dari nilai fungsi objektif (solusi) ILP yang optimal. Pada awalnya ditetapkan z =−∞ dan i=0.

2)Langkah 1

Subproblem LP dipilih sebagai bagian _{( )i} masalah berikutnya untuk dipecahkan. Subproblem LP diselesaikan. _{( )i}

a) Jika LP terukur dan solusi PL yang _{( )i} ditemukan lebih baik maka batas bawah z diperbarui. Jika tidak, bagian masalah (subproblem) baru i dipilih dan langkah 1 diulangi. Jika semua subproblem telah dipecahkan, maka proses dihentikan.

b) Jika LP tidak terukur, proses _{( )i} dilanjutkan ke langkah 2 untuk melakukan pencabangan LP . _{( )i} Suatu subproblem dikatakan terukur (fathomed) jika terdapat kondisi sebagai berikut.

1. Subproblem tersebut takfisibel, sehingga tidak dapat menghasilkan solusi optimal untuk ILP.

2. Subproblem tersebut menghasilkan suatu solusi optimal dengan semua variabelnya bernilai integer. Jika solusi optimal ini mempunyai nilai fungsi objektif yang lebih baik daripada solusi fisibel yang diperoleh sebelumnya, maka solusi ini menjadi kandidat solusi optimal dan nilai fungsi objektifnya menjadi batas bawah nilai fungsi objektif optimal bagi masalah ILP pada saat itu. Bisa jadi subproblem ini menghasilkan solusi optimal untuk masalah ILP.

3. Nilai fungsi objektif optimal untuk subproblem tersebut tidak melebihi batas bawah saat itu, maka subproblem ini dapat dieliminasi. 3). Langkah 2

Dipilih salah satu variabel x_j yang nilai optimalnya adalah x*_j yang tidak memenuhi batasan integer dalam solusi LPi. Bidang

1 ] [ ]

[x*_j <x_j < x*_j + disingkirkan dengan membuat dua subproblem PL, yaitu x_j <[x*_j] dan x_j >[x*_j]+1, sehingga diperoleh kendala subproblem baru sebagai berikut:

• Subproblem baru 1: kendala subproblem lama + kendala *

[ ]

j j

x ≤ x

• Subproblem baru 2: kendala subproblem lama + kendala x_j ≥[x*_j] 1+

dengan [x*_j] didefinisikan sebagai integer terbesar yang kurang dari atau sama dengan

.

*

j

x Selanjutnya kembali ke langkah 1. (Winston, 1975) Untuk memudahkan pemahaman metode branch-and-bound diberikan contoh sebagai berikut.

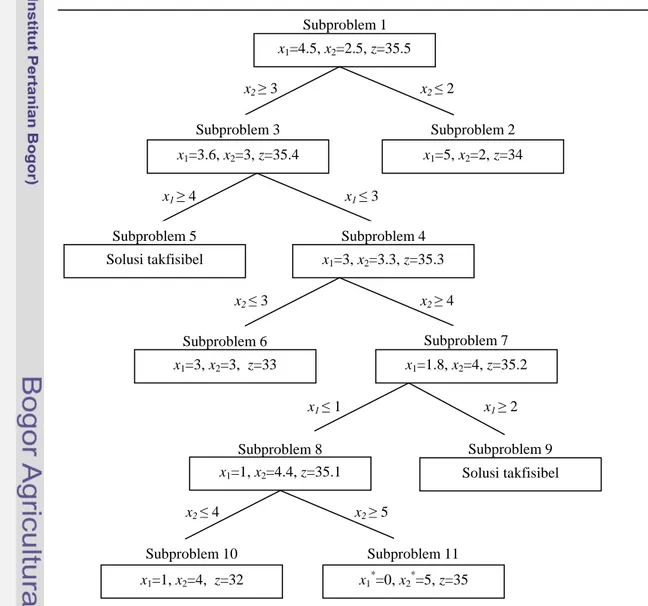
Contoh 2 (Metode Branch-and-Bound) Misalkan diberikan masalah ILP sebagai berikut : max z=4x₁+7x₂ terhadap 1 2 1 2 7 5 9 45 x x x x + ≤ + ≤

x

i

≥

0

, i = 1, 2. (6) Setelah diselesaiakan menggunakan software LINGO 8.0 didapatkan solusi optimal LP-relaksasi dari masalah ILP (6) adalah x₁=4.5 , x₂ =2.5, dan z=35.5 (lihat Lampiran 2). Batas atas nilai optimal fungsi objektif masalah ini adalah 35.5. Daerah fisibel LP-relaksasi masalah (6) ditunjukkan pada Gambar 1. Solusi optimal berada pada titik perpotongan dua garis yang berasal dari kendala pertidaksamaan masalah (6).

Gambar 1 Daerah fisibel untuk LP

relaksasi dari masalah IL

Langkah berikutnya adalah memartisi daerah fisibel LP-relaksasi

bagian berdasarkan variabel yang berbentuk pecahan (non integer). Karena nilai dari kedua variabel yang diperoleh bukan

dipilih salah satu variabel untuk dasar pencabangan. Misalkan dipilih

dasar pencabangan. Jika masalah

diberi nama Subproblem 1, maka pencabangan tersebut menghasilkan 2 subproblem, yaitu:

• Subproblem 2: Subproblem 1 ditambah kendala x₂ ≤2;

• Subproblem 3: Subproblem 1 ditambah kendala x₂≥3.

Secara grafis dapat dilihat pada gambar di bawah ini.

Gambar 2 Daerah fisibel untu Subproblem 2 dan Subproblem 3

Setiap titik (solusi) fisibel dari IP ( termuat dalam daerah fisibel Subproblem 2 atau Subproblem 3. Setiap subproblem ini saling lepas. Subproblem 2 dan Subproblem 3 dikatakan dicabangkan oleh

Daerah fisibel untuk LP-LP (6).

Langkah berikutnya adalah memartisi relaksasi menjadi dua bagian berdasarkan variabel yang berbentuk ). Karena nilai dari kedua variabel yang diperoleh bukan integer, maka dipilih salah satu variabel untuk dasar angan. Misalkan dipilih x₂ sebagai dasar pencabangan. Jika masalah LP-relaksasi diberi nama Subproblem 1, maka pencabangan tersebut menghasilkan 2 Subproblem 2: Subproblem 1 ditambah Subproblem 3: Subproblem 1 ditambah Secara grafis dapat dilihat pada gambar di

Daerah fisibel untuk Subproblem 2 dan Subproblem 3.

Setiap titik (solusi) fisibel dari IP (6) rah fisibel Subproblem 2 atau Subproblem 3. Setiap subproblem ini saling lepas. Subproblem 2 dan Subproblem 3 dikatakan dicabangkan oleh x₂.

Sekarang dipilih subproblem yang belum diselesaikan. Misalkan dipilih Subpr

solusi optimal untuk Subproblem 2

1 5

x = ,x₂ =2, dan z=34 2). Semua variabel bernilai

memenuhi kendala bilangan bulat), maka tidak perlu dilakukan pencabangan di Subproblem 2. Solusi dari

menjadi batas bawah yaitu sama dengan 3 Saat ini Subproblem yang belum diselesaiakan adalah Subproblem 3. Solusi optimal untuk Subproblem 3 adalah

2 3

x = , dan z=35.4 (lihat Karena solusi optim

bukan solusi integer dan masih mempunyai kemungkinan solusi lebih besar dari batas bawah, maka dipilih pencabangan pada Subproblem 3 pada x ₁,

dua subproblem lagi.

• Subproblem 4: Subproblem 3 ditambah kendala x₁≤3

• Subproblem 5: Subproblem 3 ditambah kendala x₁≥4

Sekarang dipilih Subproblem yang belum diselesaikan yaitu Subproblem 4 Subproblem 5. Subproblem 5 takfisibel ( Lampiran 2), maka subproblem ini tidak dapat menghasilkan solu

Subprolem yang belum diselesaiakan adalah Subproblem 4. Setelah diselesaiakan solusi optimal yang didapatkan untuk Subproblem 4 adalah x₁=3, x₂ =3.3, dan

dari subproblem 4 tidak integer

dari batas bawah, maka dipilih pencabangan pada Subproblem 4 sehingga diperoleh subproblem baru lagi

• Subproblem 6: Subproblem 4 ditambah kendala x₂ ≤3

• Subproblem 7: Subproblem 4 ditambah kendala x₂ ≥4

Solusi optimal untuk Subproblem 6 adalah

1 3

x = , x₂ =3, z=33 (lihat Lampiran Solusi optimal untuk Subproblem 6 memenuhi solusi integer, akan tetapi solusi pada Subproblem ini lebih kecil (tidak lebih dari batas bawah sehingga solusi pada Subproblem 6 tidak menjadi batas bawah baru. Subproblem 7 menghasilkan solusi optimal x₁ =1.8, x₂ =4

Lampiran 2). Solusi dari Subproblem 7 tidak integer dan lebih baik dari batas bawah, maka pada Subproblem ini dilakukan pencabangan lagi sehingga diperoleh Subproblem baru lagi

Sekarang dipilih subproblem yang belum diselesaikan. Misalkan dipilih Subproblem 2, optimal untuk Subproblem 2 adalah 34 (lihat Lampiran emua variabel bernilai integer (solusinya memenuhi kendala bilangan bulat), maka tidak perlu dilakukan pencabangan di . Solusi dari Subproblem 2 menjadi batas bawah yaitu sama dengan 34.

Saat ini Subproblem yang belum diselesaiakan adalah Subproblem 3. Solusi Subproblem 3 adalah x₁=3.6,

(lihat Lampiran 2). optimal Subproblem 3

dan masih mempunyai kemungkinan solusi lebih besar dari batas bawah, maka dipilih pencabangan pada , sehingga diperoleh Subproblem 4: Subproblem 3 ditambah Subproblem 5: Subproblem 3 ditambah ubproblem yang belum diselesaikan yaitu Subproblem 4 atau Subproblem 5. Subproblem 5 takfisibel (lihat maka subproblem ini tidak apat menghasilkan solusi optimal. Subprolem yang belum diselesaiakan adalah Subproblem 4. Setelah diselesaiakan solusi optimal yang didapatkan untuk Subproblem 4 , dan z=35.3. Solusi integer dan lebih baik maka dipilih pencabangan sehingga diperoleh Subproblem 6: Subproblem 4 ditambah Subproblem 7: Subproblem 4 ditambah Solusi optimal untuk Subproblem 6 adalah (lihat Lampiran 2). Solusi optimal untuk Subproblem 6 memenuhi akan tetapi solusi pada ebih kecil (tidak lebih baik) dari batas bawah sehingga solusi pada Subproblem 6 tidak menjadi batas bawah baru. Subproblem 7 menghasilkan solusi

4

= , z=35.2 (lihat ). Solusi dari Subproblem 7 tidak dan lebih baik dari batas bawah, maka pada Subproblem ini dilakukan pencabangan lagi sehingga diperoleh Subproblem baru lagi

• Subproblem 8: Subproblem 7 ditambah kendala x₁≤1

• Subproblem 9: Subproblem 7 ditambah kendala x₁≥2

Penyelesaian dari Subproblem 9 menghasilkan solusi yang takfisibel (lihat Lampiran 2), maka subproblem ini tidak dapat menghasilkan solusi optimal. Subproblem 8 menghasilkan solusi optimal

1 1

x = , x₂ =4.4, z=35.1 (lihat Lampiran 2). Solusi dari Subproblem 8 tidak integer dan lebih baik dari batas bawah, maka pada Subproblem ini dilakukan pencabangan lagi sehingga diperoleh Subproblem baru lagi • Subproblem 10: Subproblem 8 ditambah

kendala x₂≤4

• Subproblem 11: Subproblem 8 ditambah kendala x₂≥5

Subproblem 10 menghasilkan solusi optimal x₁=1, x₂ =4, z=32. Subproblem ini menghasilkan solusi integer, akan tetapi solusi yang dihasilkan pada subproblem ini tidak lebih baik dari batas bawah sehinggga solusi pada Subproblem 10 tidak menjadi batas bawah baru. Subproblem 11 menghasilkan solusi optimal x₁=0, x₂ =5,

35

z= . Solusi pada Subproblem ini menghasilkan solusi integer dan lebih baik dari batas bawah sehingga solusi pada Subproblem 11 menjadi batas bawah baru. Karena sudah tidak ada lagi subproblem baru yang dapat dibuat maka tidak perlu dilakukan pencabangan lagi. Dengan demikian, solusi optimal pada contoh 2 adalah x₁*=0,

2* 5

x = , z=35 .

Secara keseluruhan pencabangan semua Subproblem untuk masalah ILP pada contoh 2 ditunjukan pada gambar di bawah ini.

Gambar 3 Seluruh pencabangan pada metode branch and bound untuk menentukan solusi optimal dari ILP.

Subproblem 10 x1=1, x2=4, z=32 Subproblem 11 x1*=0, x2*=5, z=35 Subproblem 9 Solusi takfisibel Subproblem 8 x1=1, x2=4.4, z=35.1 x2 ≥ 5 x2 ≤ 4 Subproblem 2 x1=5, x2=2, z=34 Subproblem 1 x1=4.5, x2=2.5, z=35.5 x2 ≥ 3 x2 ≤ 2 Subproblem 3 x1=3.6, x2=3, z=35.4 x1 ≥ 4 x1 ≤ 3 Subproblem 5 Solusi takfisibel Subproblem 4 x1=3, x2=3.3, z=35.3 x2 ≥ 4 x2 ≤ 3 Subproblem 6 x1=3, x2=3, z=33 Subproblem 7 x1=1.8, x2=4, z=35.2 x1 ≥ 2 x1 ≤ 1

III DESKRIPSI DAN FORMULASI MASALAH

Jadwal Kegiatan Belajar Mengajar (KBM) di sekolah menengah pertama merupakan bagian yang sangat penting dan harus ada supaya proses belajar mengajar dapat berjalan dengan baik sehingga siswa ataupun guru dapat menikmati kegiatan belajar mengajar tersebut. Oleh karena itu harus dibuat jadwal yang mendukung terciptanya suasana di atas. Di bawah ini akan diuraikan bagaimana suatu penjadwalan dibuat.

Model penjadwalan pada karya ilmiah ini menggunakan lima parameter utama sebagai penyusun jadwal yaitu;

1. Hari, yaitu hari di mana mata pelajaran diberikan. Hari = {Senin, Selasa,...., Sabtu}

2. Periode waktu, yaitu waktu belajar di mana mata pelajaran diberikan. Periode waktu = {07.00-08.00, 08.00-09.00,...,(t – t+1)}.

3. Kelas, yaitu kelompok murid yang menghadiri mata pelajaran yang sama dan berada dalam satu ruangan. Kelas = {1A, 1B, ...,2A, 2B, ...,3A, 3B, ...}.

4. Guru, yaitu orang yang mengajar suatu mata pelajaran tertentu dalam suatu kelas. Guru = {Guru 1, ...., Guru n}.

5.

Mata pelajaran, yaitu pelajaran yang diajarkan di kelas oleh seorang guru. Mata pelajaran = {mata pelajaran1, ..., mata pelajaran n}.

Dalam menyusun suatu penjadwalan, ada dua macam kendala yang harus diperhatikan. Kendala yang pertama adalah kendala utama, yaitu kendala yang harus dipenuhi oleh setiap sekolah. Kendala ini dibuat oleh otorita pengelola pendidikan (Dinas Pendidikan). Kendala yang kedua adalah kendala tambahan, yaitu kendala yang diharapkan dapat dipenuhi atau dengan memasukan penalti pada fungsi objektif. Kendala ini biasanya dibuat oleh staf akademik pada setiap sekolah karena kondisi tertentu atau karena suatu peraturan yang ada dan bertujuan untuk meningkatkan prestasi murid dan guru. Berikut ini adalah beberapa contoh dari setiap kendala.

Kendala Utama

1. Kurikulum untuk setiap sekolah sudah ada. 2. Dalam satu minggu jumlah periode waktu untuk memberikan mata pelajaran di setiap kelas sudah ditentukan.

3. Setiap guru mengajar sesuai bidangnya untuk kelas yang sudah ditentukan. 4. Dalam satu minggu periode waktu total

untuk memberikan semua mata pelajaran di setiap kelas sudah ditentukan.

5. Guru tidak boleh mengajar lebih dari satu kelas pada periode waktu yang sama. 6. Jumlah jam mengajar setiap guru sudah

ditentukan sesuai dengan kemampuannya. 7. Jumlah jam mengajar untuk setiap kelas

sudah ditetapkan.

8. Setiap guru harus mengajar minimal satu periode waktu untuk beberapa hari di mana guru tersebut telah dijadwalkan. Kendala Tambahan

1. Distribusi periode waktu mengajar guru harus sama dalam seminggu.

2. Perbedaan periode waktu mengajar harian seorang guru paling banyak satu periode waktu dari periode waktu mengajar rata-rata di mana guru tersebut ditugaskan. 3. Beberapa mata pelajaran harus diajarkan

di awal jam pelajaran.

4. Beberapa mata pelajaran tidak diajarkan di akhir jam pelajaran.

5. Tidak boleh ada periode waktu kosong untuk setiap kelas.

6. Untuk keadaan khusus (contohnya; sakit, ibu yang mempunyai anak kecil), guru boleh meminta waktu untuk tidak mengajar pada periode waktu tertentu. 7. Terdapat batasan maksimal dan minimal

dalam menentukan beban mengajar. Model Matematika

Model matematika untuk masalah penjadwalan di sini adalah model integer linear programming (ILP). Pembuatan jadwal pada karya ilmiah ini tidak menggunakan semua kendala yang sudah disebutkan di atas, namun hanya beberapa kendala yang dipakai. Hal ini untuk menyesuaikan kondisi yang ada. Berikut ini kendala yang digunakan dalam pembuatan penjadwalan pada karya ilmiah ini. 1. Tidak boleh ada seorang guru yang mengajar di dua kelas atau lebih pada periode waktu yang sama.

2. Untuk setiap hari dan setiap periode waktunya, kecuali periode waktu terakhir, semua kelas akan diajar oleh seorang guru. 3. Terpenuhinya jumlah periode waktu total yang diperlukan setiap kelas selama seminggu.

4. Terpenuhinya jumlah periode waktu mengajar setiap guru di

5. Guru mengajar minimal satu perio waktu pada hari di mana

telah dijadwalkan

6. Semua mata pelajaran akan didistribusikan dengan seimbang selama seminggu

7. Beberapa guru tidak mengajar tertentu.

Dalam karya ilmiah ini diasumsikan ruangan yang digunakan untuk kegiatan belajar mengajar memiliki kapasitas yang mencukupi.

Tujuan dari model penjadwalan ini a mencari penjadwalan mata pelajaran optimal dengan cara meminimumkan

dengan koefisien-koefisi

bobot yang diberikan kepada guru atau mata pelajaran. Sebagai contoh :

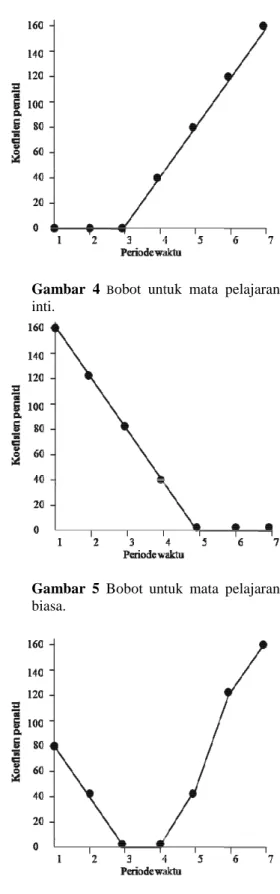
1) Mata pelajaran inti

diajarkan di awal periode waktu. Oleh karena itu mata pelajaran ini diberi bobot (koefisien) yang kecil

waktu dan bobot yang

periode waktu. Sehingga mata pelajaran ini memiliki peluang yang lebih besar untuk dijadwalkan di awal periode waktu (lihat Gambar 4).

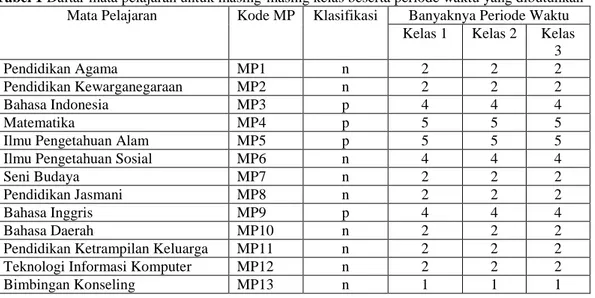
2) Mata pelajaran biasa diharapkan dapat diajarkan setelah jam istirahat (periode waktu akhir). Oleh karena i

pelajaran ini diberi bobot yang kecil di akhir periode waktu dan bobot yang besar di awal periode waktu. Sehingga mata pelajaran ini memiliki peluang yang lebih besar untuk dijadwalkan di akhir periode waktu (lihat Gambar 5).

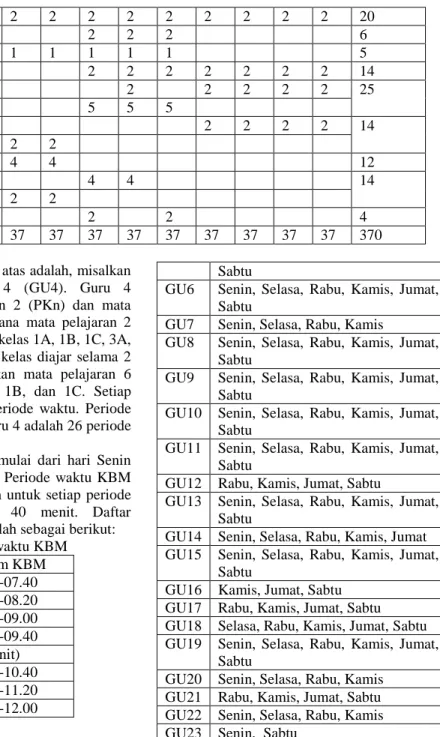
3) Guru-guru tertentu mem

untuk mengajarkan mata pelajaran periode waktu pertengahan. Guru tertentu merupakan guru mengajar mata pelajaran inti dan pelajaran biasa. Guru

mangajarkan mata pelajaran ini diberi bobot yang kecil di peri

pertengahan dan bobot

dan di akhir periode waktu (lihat Gambar 6).

Terpenuhinya jumlah periode waktu di kelas yang di ajar. inimal satu periode di mana guru tersebut mata pelajaran akan didistribusikan

selama seminggu. Beberapa guru tidak mengajar pada hari

Dalam karya ilmiah ini diasumsikan ruangan yang digunakan untuk kegiatan belajar mengajar memiliki kapasitas yang

penjadwalan ini adalah mata pelajaran optimal meminimumkan fungsi objektif koefisiennya merupakan bobot yang diberikan kepada guru atau mata

Sebagai contoh :

Mata pelajaran inti diharapkan dapat diajarkan di awal periode waktu. Oleh karena itu mata pelajaran ini diberi bobot yang kecil di awal periode yang besar di akhir periode waktu. Sehingga mata pelajaran ini memiliki peluang yang lebih besar untuk dijadwalkan di awal periode waktu Mata pelajaran biasa diharapkan dapat diajarkan setelah jam istirahat (periode waktu akhir). Oleh karena itu mata pelajaran ini diberi bobot yang kecil di akhir periode waktu dan bobot yang besar di awal periode waktu. Sehingga mata pelajaran ini memiliki peluang yang lebih besar untuk dijadwalkan di akhir periode waktu (lihat Gambar 5).

guru tertentu memiliki preferensi tuk mengajarkan mata pelajaran di periode waktu pertengahan. Guru-guru tertentu merupakan guru-guru yang mengajar mata pelajaran inti dan mata pelajaran biasa. Guru-guru yang mata pelajaran ini diberi yang kecil di periode waktu pertengahan dan bobot yang besar di awal iode waktu (lihat Gambar

Gambar 4 Bobot untuk inti.

Gambar 5 Bobot untuk mata pelajaran biasa.

Gambar 6 Bobot untuk guru mengajarkan mata pelajaran mata pelajaran biasa.

untuk mata pelajaran

Bobot untuk mata pelajaran

Bobot untuk guru-guru yang mengajarkan mata pelajaran inti dan

Bobot yang diberikan terhadap guru bersesuaian dengan variabel keputusan yang akan dipilih dalam penjadwalan. Variabel

keputusan dalam masalah penjadwalan adalah sebagai berikut :

{

, , , ,

1 , jika guru mengajar mata pelajaran di kelas pada hari diperiode ke-0 , selainnya i j k l m l m k i j

x

=

dengan : I = himpunan hari

J = himpunan periode waktu K = himpunan kelas

L = himpunan guru

M = himpunan mata pelajaran

i ϵ I, j ϵ J, k ϵ K, l ϵ L, m ϵ M.

Seperti telah disebutkan di atas bahwa model penjadwalan pada karya ilmiah ini bertujuan mencari penjadwalan mata pelajaran optimal dengan cara meminimumkan fungsi objektif dengan koefisien-koefisiennya merupakan bobot yang diberikan kepada guru atau mata pelajaran. Fungsi objektif untuk masalah penjadwalan ini dimodelkan sebagai berikut: , , , , , , , , min _{i j k l m i j k l m} i I j J k K l L m M

c

x

∈ ∈ ∈ ∈ ∈

∑ ∑ ∑ ∑ ∑

dengan : , , , , i j k l m c =

Pada model penjadwalan di sini untuk setiap kelas sudah ditentukan guru-guru yang akan mengajar di kelas tersebut, sehingga masing-masing guru hanya akan mengajar kelas tertentu. Begitu pula dengan mata pelajaran yang akan diajarkan oleh guru. Masing-masing guru hanya akan mengajar mata pelajaran tertentu. Atas dasar keterkaitan ini maka fungsi objektif dari model penjadwalan dapat ditulis menjadi ;

, , , , , , , , min l kl i j k l m i j k l m i I j J l L k K m M

c

x

∈ ∈ ∈ ∈ ∈

∑ ∑ ∑ ∑ ∑

dengan :

{ : kelas yang diajar oleh guru }, l K k K k l l L = ∈ = ∀ ∈

{ : pelajaran yang diajarkan di kelas oleh guru }, dan

kl

M m M m

k l k K l L

= ∈ =

∀ ∈ ∈

Fungsi kendala yang digunakan adalah sebagai berikut :

1. Tidak boleh ada seorang guru yang mengajar dalam dua kelas atau lebih pada periode waktu yang sama.

, , , , 1 ; , , l kl i j k l m k K m M x i I j J l L ∈ ∈ ≤ ∀ ∈ ∈ ∈

∑ ∑

Kendala 1 menjamin bahwa untuk setiap periode waktu setiap harinya hanya ada satu guru yang akan mengajarkan sebuah mata pelajaran. Misalkan pada hari 1 guru 2 mengajar di periode 3, maka variabel

1,3, ,2,k m

x akan bernilai satu, dan selain itu bernilai nol.

2. Untuk setiap hari dan setiap periode waktunya, kecuali periode waktu terakhir, semua kelas akan diajar seorang guru dan sebuah pelajaran.

(

)

, , , , 1 ; , 1, 2, ..., 1 , dan, k kl i j k l m l L m M n x i I j j k K ∈ ∈ = ∀ ∈ ∈ − ∈

∑ ∑

, , , , 1 ; , , k kl i j k l m n l L m M x i I j j k K ∈ ∈ ≤ ∀ ∈ ∈ ∈

∑ ∑

dengan:

{ : guru yang ditugasi untuk mengajar di kelas },

, periode waktu terakhir.

k n L l L l k k K j = ∈ = ∀ ∈ =

Kendala 2 menjamin bahwa pada setiap periode waktu setiap harinya kecuali mungkin periode waktu terakhir pasti akan diajar oleh seorang guru.

3. Terpenuhinya jumlah periode waktu total yang diperlukan setiap kelas selama seminggu. , , , , ; k kl i j k l m k i I j J l L m M x a k K ∈ ∈ ∈ ∈ = ∀ ∈

∑∑ ∑ ∑

dengan:

periode waktu total selama seminggu untuk kelas .

k

a

k =

Kendala 3 menjamin bahwa selama seminggu periode waktu total yang bobot yang diberikan kepada

dibutuhkan oleh setiap kelas pasti sudah diajarkan. Misalkan untuk kelas 3 periode waktu total yang dibutuhkan selama

seminggu 20, maka , ,3, , 20 k kl i j l m i I j J l L m M x ∈ ∈ ∈ ∈ =

∑∑ ∑ ∑

.

4. Terpenuhinya jumlah periode waktu mengajar setiap guru di kelas yang di ajar

, , , , ; , kl i j k l m kl i I j J m M x b k K l L ∈ ∈ ∈ = ∀ ∈ ∈

∑∑ ∑

dengan:

jumlah jam mengajar guru pada kelas .

kl

b l

k =

Kendala 4 menjamin bahwa periode waktu mengajar guru l di kelas k sudah terpenuhi. Misalkan periode waktu mengajar guru 5 dikelas 2 sebanyak 4 maka

, ,2,5, 4 kl i j m i I j J m M x ∈ ∈ ∈ =

∑∑ ∑

.

5. Guru mengajar minimal satu periode waktu pada hari di mana guru tersebut dijadwalkan.

, , , , 1 , , dengan :

hari dimana guru dijadwalkan.

l kl i j k l m l j J k K m M l x i I l L I l ∈ ∈ ∈ ≥ ∀ ∈ ∈ =

∑ ∑ ∑

Kendala 5 menjamin bahwa pada hari di mana guru dijadwalkan maka seorang guru harus mengajar sedikitnya satu periode waktu. Misalkan guru 4 mengajar pada hari 1, hari 2, dan hari 3 maka pada hari tersebut guru 4 harus mengajar paling sedikit 1 periode waktu.

6. Semua mata pelajaran akan didistribuskan dengan seimbang dalam seminggu.

, , , , ; , , , dan, i j k l m j J l kl x q i I l L k K m M ∈ ≤ ∀ ∈ ∈ ∈ ∈

∑

, , , , ; , , i j k l m mk i I j J l kl x d l L k K m M ∈ ∈ = ∀ ∈ ∈ ∈

∑ ∑

dengan:

jumlah periode waktu yang diperlukan untuk mengajar pelajaran di kelas . = periode waktu maksimal seorang guru memberikan sebuah mata pelajaran disetiap kelas mk d m k q =

untuk satu harinya. Kendala 6 menjamin setiap mata pelajaran akan distribusikan dengan seimbang dalam seminggunya. Misalkan mata pelajaran 7 diajarkan untuk kelas 5 sebanyak 3 periode waktu. Selama seminggu mata pelajaran tersebut akan diajarkan selama tiga hari dan setiap harinya satu periode waktu. Selain itu maka salah.

7. Untuk beberapa guru yang dijadwalkan pada beberapa hari saja dalam seminggu maka untuk hari di mana guru tersebut tidak dijadwalkan akan memenuhi kendala sebagai berikut : , , , ,

0

l l kl i j k l m i S j J k K m M i l L

x

∈ ∈ ∈ ∈ ∀ ∈

=

∑∑ ∑ ∑

dengan:

hari dimana guru tidak mengajar. guru yang tidak mengajar pada hari . l i S l L l i = =

IV STUDI KASUS DAN PENYELESAIANNYA

Studi kasus yang diambil dalam penelitian ini adalah menentukan penjadwalan mata pelajaran di SMP Masa Depan. Pada sekolah tersebut mata pelajaran yang akan diajarkan untuk setiap kelas sudah ditentukan berdasarkan kurikulum yang berlaku pada saat

itu. Kurikulum yang digunakan adalah Kurikulum Tingkat Satuan Pendidikan (KTSP). Tabel 1 merupakan daftar mata pelajaran untuk setiap kelas beserta jumlah periode waktu yang dibutuhkan.

Tabel 1 Daftar mata pelajaran untuk masing-masing kelas beserta periode waktu yang dibutuhkan Mata Pelajaran Kode MP Klasifikasi Banyaknya Periode Waktu

Kelas 1 Kelas 2 Kelas 3

Pendidikan Agama MP1 n 2 2 2

Pendidikan Kewarganegaraan MP2 n 2 2 2

Bahasa Indonesia MP3 p 4 4 4

Matematika MP4 p 5 5 5

Ilmu Pengetahuan Alam MP5 p 5 5 5

Ilmu Pengetahuan Sosial MP6 n 4 4 4

Seni Budaya MP7 n 2 2 2

Pendidikan Jasmani MP8 n 2 2 2

Bahasa Inggris MP9 p 4 4 4

Bahasa Daerah MP10 n 2 2 2

Pendidikan Ketrampilan Keluarga MP11 n 2 2 2

Teknologi Informasi Komputer MP12 n 2 2 2

Bimbingan Konseling MP13 n 1 1 1

Keterangan:

p : mata pelajaran inti (primary) n : mata pelajaran biasa (non-primary)

Jumlah guru di SMP Masa Depan sebanyak 23 orang. Dari 23 orang guru beban mengajar tidaklah sama, ada yang mengajar 5

periode waktu, ada pula yang mengajar lebih dari itu. Begitu juga dengan kelas yang akan diajar, setiap guru mengajar di kelas yang sudah ditentukan. Berikut ini akan diberikan contoh distribusi kegiatan belajar mengajar (KBM) untuk setiap kelas.

Tabel 2 Distribusi KBM dengan 10 kelas Guru Kode

MP

Penugasan guru Total

Periode Waktu 1A 1B 1C 2A 2B 2C 3A 3B 3C 3D GU1 MP9 4 4 4 12 GU2 MP13 1 1 1 1 1 5 GU3 MP4 5 5 5 5 5 25 GU4 MP2 2 2 2 2 2 2 2 26 MP6 4 4 4 GU5 MP2 2 2 2 22 MP3 4 4 4 4 GU6 MP5 5 5 5 5 20 GU7 MP3 4 4 4 12 GU8 MP6 4 4 4 4 4 20 GU9 MP1 2 2 2 2 2 2 2 2 2 2 20 GU10 MP4 5 5 5 5 5 25 GU11 MP8 2 2 2 2 2 2 2 2 2 2 20 GU12 MP9 4 4 4 12 GU13 MP5 5 5 5 21 MP11 2 2 2 GU14 MP 9 4 4 4 4 16

GU15 MP10 2 2 2 2 2 2 2 2 2 2 20 GU16 MP7 2 2 2 6 GU17 MP13 1 1 1 1 1 5 GU18 MP13 2 2 2 2 2 2 2 14 GU19 MP12 2 2 2 2 2 25 MP5 5 5 5 GU20 MP7 2 2 2 2 14 MP12 2 2 2 GU21 MP3 4 4 4 12 GU22 MP6 4 4 14 MP7 2 2 2 GU23 MP12 2 2 4 Total 37 37 37 37 37 37 37 37 37 37 370

Maksud dari tabel di atas adalah, misalkan diambil contoh guru 4 (GU4). Guru 4 mengajar mata pelajaran 2 (PKn) dan mata pelajaran 6 (IPS), di mana mata pelajaran 2 diajarkan oleh guru 4 di kelas 1A, 1B, 1C, 3A, 3B, 3C, dan 3D. Setiap kelas diajar selama 2 periode waktu, sedangkan mata pelajaran 6 diajarkan di kelas 1A, 1B, dan 1C. Setiap kelas diajar selama 4 periode waktu. Periode waktu total mengajar guru 4 adalah 26 periode waktu.

Hari untuk KBM dimulai dari hari Senin dan berakhir hari Sabtu. Periode waktu KBM dimulai pukul 07.00 dan untuk setiap periode waktunya berlangsung 40 menit. Daftar periode waktu KBM adalah sebagai berikut: Tabel 3 Daftar periode waktu KBM

Periode Jam KBM Periode 1 07.00-07.40 Periode 2 07.40-08.20 Periode 3 08.20-09.00 Periode 4 09.00-09.40 Istirahat (20 menit) Periode 5 10.00-10.40 Periode 6 10.40-11.20 Periode 7 11.20-12.00

Hari mengajar setiap guru tidaklah sama, hal ini tergantung dari permintaan dan kondisi guru yang bersangkutan. Berikut ini akan diberikan tabel distribusi hari mengajar berdasarkan preferensi guru.

Tabel 4 Hari guru mengajar

Guru Hari mengajar

GU1 Rabu, Kamis, Jumat, Sabtu GU2 Senin, Selasa, Rabu

GU3 Senin, Selasa, Rabu, Kamis, Jumat, Sabtu

GU4 Senin, Selasa, Rabu, Kamis, Jumat, Sabtu

GU5 Senin, Selasa, Rabu, Kamis, Jumat,

Sabtu

GU6 Senin, Selasa, Rabu, Kamis, Jumat, Sabtu

GU7 Senin, Selasa, Rabu, Kamis

GU8 Senin, Selasa, Rabu, Kamis, Jumat, Sabtu

GU9 Senin, Selasa, Rabu, Kamis, Jumat, Sabtu

GU10 Senin, Selasa, Rabu, Kamis, Jumat, Sabtu

GU11 Senin, Selasa, Rabu, Kamis, Jumat, Sabtu

GU12 Rabu, Kamis, Jumat, Sabtu

GU13 Senin, Selasa, Rabu, Kamis, Jumat, Sabtu

GU14 Senin, Selasa, Rabu, Kamis, Jumat GU15 Senin, Selasa, Rabu, Kamis, Jumat,

Sabtu

GU16 Kamis, Jumat, Sabtu GU17 Rabu, Kamis, Jumat, Sabtu GU18 Selasa, Rabu, Kamis, Jumat, Sabtu GU19 Senin, Selasa, Rabu, Kamis, Jumat,

Sabtu

GU20 Senin, Selasa, Rabu, Kamis GU21 Rabu, Kamis, Jumat, Sabtu GU22 Senin, Selasa, Rabu, Kamis GU23 Senin, Sabtu

Telah disebutkan di atas bahwa mata pelajaran diklasifikasikan menjadi 2 yaitu inti dan biasa. Mata pelajaran yang termasuk mata pelajaran inti yaitu Bahasa Indonesia, IPA, Matematika, dan Bahasa Inggris. Mengingat pentingnya keempat mata pelajaran tersebut maka sedapat mungkin mata pelajaran tersebut dijadwalkan di awal jam pelajaran. Dengan harapan siswa lebih mudah dalam menerima pelajaran-pelajaran tersebut. Untuk pelajaran biasa (selain keempat mata pelajaran yang telah disebutkan sebelumnya) penjadwalan sedapat mungkin ditempatkan setelah jam istirahat. Hal ini supaya siswa

sudah segar kembali dalam berfikir, sehingga siswa juga akan lebih mudah dalam memahami pelajaran.

Untuk memenuhi preferensi meng guru, pembuatan penjadwalan mungkin memenuhi permintaan guru dalam penentuan

mereka. Permintaan periode waktu mengajar guru secara lengkap adalah sebagai berikut:

Tabel 5 Permintaan periode

Guru Periode waktu

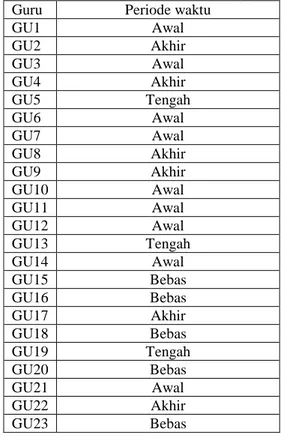
GU1 GU2 Akhir GU3 GU4 Akhir GU5 Tengah GU6 GU7 GU8 Akhir GU9 Akhir GU10 GU11 GU12 GU13 Tengah GU14 GU15 Bebas GU16 Bebas GU17 Akhir GU18 Bebas GU19 Tengah GU20 Bebas GU21 GU22 Akhir GU23 Bebas Keterangan;

Awal : periode1, periode2, periode3 Tengah : periode3, periode

Akhir : periode5, periode6, periode7 Bebas : available untuk semua periode

Atas pertimbangan di

(koefisien) yang mana penjelasan

disebutkan pada bagian sebelumnya. Penentuan bobot yang telah disebutkan pada bagian sebelumnya tidaklah mutlak harus seperti itu. Yang ada di sin

gambaran saja. Beberapa

mungkin dapat digunakan diperlihatkan sebagai berikut:

i dalam berfikir, sehingga siswa juga akan lebih mudah dalam preferensi mengajar penjadwalan sedapat mungkin memenuhi permintaan dan kondisi guru dalam penentuan waktu mengajar periode waktu mengajar lengkap adalah sebagai berikut:

taan periode waktu mengajar Periode waktu Awal Akhir Awal Akhir Tengah Awal Awal Akhir Akhir Awal Awal Awal Tengah Awal Bebas Bebas Akhir Bebas Tengah Bebas Awal Akhir Bebas

: periode1, periode2, periode3 , periode4

: periode5, periode6, periode7 untuk semua periode

atas, dibuatlah bobot penjelasan bobot telah disebutkan pada bagian sebelumnya. yang telah disebutkan pada tidaklah mutlak harus sini hanyalah sebagai Beberapa grafik bobot yang mungkin dapat digunakan diperlihatkan

Gambar 7 Bobot untuk mata pelajaran yang diharapkan diajarkan di awal periode waktu.

Gambar 8 Bobot untuk mata pelajaran yang diharapkan diajarkan di akhir periode waktu.

Gambar 9 Bobot untuk mata pelajaran yang diharapkan diajarkan

waktu awal dan periode waktu

Bobot untuk mata pelajaran diajarkan di awal

Bobot untuk mata pelajaran diajarkan di akhir

Bobot untuk mata pelajaran diajarkan di periode periode waktu akhir.

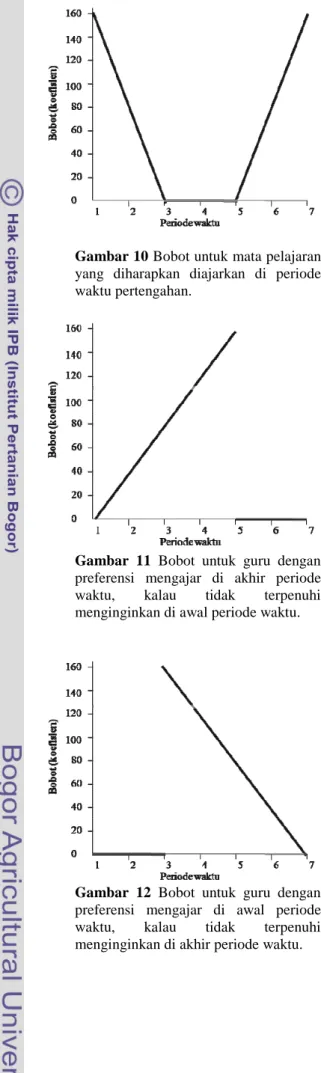
Gambar 10 Bobot untuk mata pelajaran yang diharapkan diajarkan di periode waktu pertengahan.

Gambar 11 Bobot untuk guru

preferensi mengajar di akhir periode waktu, kalau tidak terpenuhi menginginkan di awal periode waktu

Gambar 12 Bobot untuk guru dengan preferensi mengajar di awal periode waktu, kalau tidak terpenuhi menginginkan di akhir periode waktu

Bobot untuk mata pelajaran diajarkan di periode

Bobot untuk guru dengan preferensi mengajar di akhir periode waktu, kalau tidak terpenuhi

ginginkan di awal periode waktu.

Bobot untuk guru dengan preferensi mengajar di awal periode waktu, kalau tidak terpenuhi

inginkan di akhir periode waktu.

Gambar 13 Bobot untuk guru dengan preferensi mengajar di awal

periode waktu.

Dari studi kasus di atas formulasi model ILP-nya adalah sebagai berikut ;

Min i I j J l L k K m M

c

x

∈ ∈ ∈ ∈ ∈

∑ ∑ ∑ ∑ ∑

I = 1, 2, …, 6 J = 1, 2, …, 7 K = 1, 2, …, 10 L = 1, 2, …, 23 M = 1, 2, …, 13

Terhadap fungsi kendala sebagai berikut; 1. Tidak boleh ada seorang guru yang

mengajar di dua kelas atau lebih pada periode waktu yang sama.

, , , , 1 ; , , l kl i j k l m k K m M x i I j J l L ∈ ∈ ≤ ∀ ∈ ∈ ∈

∑ ∑

2. Untuk setiap hari dan setiap periode waktunya, kecuali periode waktu terakhir, semua kelas akan diajar seorang guru dengan sebuah mata pelajaran.

, , , , 1 ; , 1, 2, ..., 6 dan, k kl i j k l m l L m M x i I j k K ∈ ∈ = ∀ ∈ ∈ ∈

∑ ∑

, , , , 1 ; , 7, k kl i j k l m l L m M x i I j k K ∈ ∈ ≤ ∀ ∈ ∈ ∈

∑ ∑

dengan:

{ : guru yang ditugasi untuk mengajar di kelas },

, periode waktu terakhir.

k n L l L l k K J = ∈ = ∀ ∈ =

3. Terpenuhinya jumlah periode waktu total yang diperlukan setiap kelas selama seminggu. , , , , k kl i j k l m i I j J l L m M x k K ∈ ∈ ∈ ∈ = ∀ ∈

∑∑ ∑ ∑

Bobot untuk guru dengan preferensi mengajar di awal dan di akhir

Dari studi kasus di atas formulasi model nya adalah sebagai berikut ;

, , , , , , , ,

i j k l m i j k l m

c

x

Terhadap fungsi kendala sebagai berikut; Tidak boleh ada seorang guru yang

dua kelas atau lebih pada periode waktu yang sama.

1 ; , ,

x ≤ ∀ ∈i I j∈J l∈L

Untuk setiap hari dan setiap periode waktunya, kecuali periode waktu terakhir, semua kelas akan diajar seorang guru

pelajaran. 1 ; , 1, 2, ..., 6 dan, x i I j k K = ∀ ∈ ∈ ∈ 1 ; , 7, x ≤ ∀ ∈i I j∈ k∈K

{ : guru yang ditugasi untuk mengajar di kelas },

, periode waktu terakhir. k

Terpenuhinya jumlah periode waktu total yang diperlukan setiap kelas selama

37 ;

x = ∀ ∈k K

4. Terpenuhinya jumlah periode waktu mengajar untuk guru l dikelas k.

, , , , ; , kl i j k l m kl i I j J m M x b k K l L ∈ ∈ ∈ = ∀ ∈ ∈

∑∑ ∑

dengan:

jumlah jam mengajar guru pada kelas .

kl

b l

k =

Misalkan untuk guru 1. Guru 1 mengajar di kelas 1, 2, dan 3 masing-masing 4 periode waktu. , ,1,1, 4 kl i j m i I j J m M x ∈ ∈ ∈ =

∑∑ ∑

, ,2,1, 4 kl i j m i I j J m M x ∈ ∈ ∈ =

∑∑ ∑

, ,3,1, 4 kl i j m i I j J m M x ∈ ∈ ∈ =

∑∑ ∑

5. Guru mengajar minimal satu periode waktu pada hari di mana guru tersebut dijadwalkan.

, , , , 1 , , dengan :

hari dimana guru dijadwalkan.

l kl i j k l m l j J k K m M l x i I l L I l ∈ ∈ ∈ ≥ ∀ ∈ ∈ =

∑ ∑ ∑

Misalkan diambil contoh untuk guru 17. Guru ini mengajar pada hari 3, hari 4, hari 5 dan hari 6. 3, , ,17, 1 l kl j k m j J k K m M x ∈ ∈ ∈ ≥

∑ ∑ ∑

4, , ,17, 1 l kl j k m j J k K m M x ∈ ∈ ∈ ≥

∑ ∑ ∑

5, , ,17, 1 l kl j k m j J k K m M x ∈ ∈ ∈ ≥

∑ ∑ ∑

6, , ,17, 1 l kl j k m j J k K m M x ∈ ∈ ∈ ≥

∑ ∑ ∑

6. Semua mata pelajaran akan didistribusikan dengan seragam selama seminggu.

Pada karya ilmiah ini setiap mata pelajaran diajarkan paling banyak satu periode waktu untuk setiap harinya.

, , , , 1 ; , , , dan, i j k l m j J l kl x i I l L k K m M ∈ ≤ ∀ ∈ ∈ ∈ ∈

∑

, , , , ; , , i j k l m mk i I j J l kl x d l L k K m M ∈ ∈ = ∀ ∈ ∈ ∈

∑ ∑

dengan:

jumlah periode waktu yang diperlukan untuk mengajar pelajaran di kelas .

mk

d

m k

=

Misalkan diambil contoh mata pelajaran 1 yang diajarkan di kelas 10.

, ,10, ,1 2 ; , , i j l i I j J l kl x l L k K m M ∈ ∈ = ∀ ∈ ∈ ∈

∑ ∑

7.

Untuk beberapa guru yang dijadwalkan pada beberapa hari saja dalam seminggu maka untuk hari di mana guru tersebut tidak dijadwalkan akan memenuhi kendala sebagai berikut : , , , ,

0

l l kl i j k l m i S j J k K m M i

x

l

L

∈ ∈ ∈ ∈

=

∀ ∈

∑∑ ∑ ∑

Misalkan untuk guru 2. Guru 2 tidak mengajar pada hari Kamis, Jumat, dan Sabtu. Maka fungsi kendalanya adalah

, , ,2,

0

l l kl i j k m i S j J k K m M

x

∈ ∈ ∈ ∈

=

∑∑ ∑ ∑

l S

=

4, 5, 6.

Penyelesaian masalah penjadwalan mata pelajaran SMP Masa Depan pada karya ilmiah ini dilakukan dengan bantuan software LINGO 8.0. menggunakan metode branch and bound. Syntax program dan hasil komputasi dicantumkan pada Lampiran 3. Solusi yang didapat adalah solusi optimal dengan nilai fungsi objektifnya adalah 4760 didapatkan pada iterasi 40663. Waktu yang dibutuhkan untuk mendapatkan solusi tersebut sekitar 1,32 menit dengan menggunakan komputer Intel Pentium Dual Core CPU 2.80 GHz dengan RAM 960 MB. Hasil komputasi tidak semuanya dicantumkan, dikarenakan terlalu banyak. Hasil yang dicantumkan hanya untuk x yang bernilai satu saja. Daftar penjadwalan yang terbentuk untuk SMP Masa Depan dicantumkan pada Lampiran 1.

Dari hasil yang didapatkan bisa dilihat presentase rata-rata terpenuhinya preferensi setiap mata pelajaran dan preferensi setiap guru. Untuk mata pelajaran presentase rata-rata terpenuhinya preferensi sekitar 85%. Untuk guru presentase rata-rata terpenuhinya preferensi sekitar 79%. Secara keseluruhan presentase rata-rata terpenuhinya preferensi mata pelajaran dan guru sekitar 82%.

V SIMPULAN DAN SARAN

Simpulan

Dalam penulisan karya ilmiah ini telah diperlihatkan penyelesaian dari masalah penjadwalan mata pelajaran yang bertujuan mencari penjadwalan mata pelajaran optimal dengan cara meminimumkan fungsi objektif dengan koefisien-koefisiennya merupakan bobot (koefisien) yang diberikan kepada guru atau mata pelajaran. Di mana masalah penjadwalan disini dipandang sebagai masalah 0-1 ILP. Penyelesaian masalah ini menggunakan software LINGO 8.0 dengan metode branch and bound.

Penjadwalan yang dihasilkan sangat bergantung pada penentuan bobot yang akan diberikan terhadap mata pelajaran atau guru. Oleh karena itu semakin bagus (sesuai dengan kenyataan yang ada) penentuan bobotnya maka penjadwalan yang dihasilkan juga akan semakin memuaskan. Dalam hal ini antara guru dan murid serta pihak sekolah yang

terkait akan semakin menikmati kegiatan belajar mengajar. Penentuan penjadwalan menggunakan software LINGO 8.0 sangat memudahkan kita. Pengguna dapat dengan mudah menambahkan data maupun kendala-kendala baru supaya tercipta penjadwalan yang lebih baik lagi.

Saran

Pada penulisan karya ilmiah ini data yang digunakan terbatas hanya pada satu sekolah saja dan tidak dilakukan penelitian secara langsung ke sekolah yang terkait. Akan lebih baik jika data yang diambil berdasarkan penelitian secara langsung dan mengadakan kuisioner untuk menentukan bobot yang akan digunakan.

Penambahan kendala baru seperti guru yang menginginkan 2 periode waktu mengajar mereka secara berturutan setiap kali mengajar juga sangat menarik untuk ditambahkan.

DAFTAR PUSTAKA

Aprilia, S. Aplikasi Algoritma Branch and Bound Untuk Menyelesaikan Integer Programing.

http://www.informatika.org/~rinaldi/Stmi

k/2006-2007/Makalah_2007/MakalahSTMIK200 7-076.pdf

Birbas, T, Daskalaki, S, & Housos, E. 2000. Timetabling for Greek High Schools. The Journal of the Operational Research Society. 48: 1191-1200.

Chen, CY. 2008. Using Integer Programing to Solve School Timetabling at Chin-Min Institute of Technology. Journal of American Academy of Business. 13: 279-286

Garfinkel, RS. & GL. Nemhauser. 1972. Integer Programming. John Willey & Sons, New York.

Nash, SG. & A. Sofer. 1996. Linear and Nonlinear Programming McGraw-Hill, New York.

Taha, HA. 1975. Integer Programming. Academic Press, New York.

Winston, WL. 1995. Introduction to Mathematical Programming 2nded. Duxbury, New York.

Winston, WL. 2004. Operations Research Applications and Algorithms 4th ed. Duxbury, New York.